Рэлеевское замирание

редактировать

Рэлеевское замирание - это статистическая модель для эффекта среда распространения на радиосигнале, например, используемая беспроводными устройствами.

Модели рэлеевских замираний предполагают, что величина сигнала, прошедшего через такую среду передачи (также называемую каналом связи ), будет варьироваться случайным образом, или затухание, согласно распределению Рэлея - радиальная составляющая суммы двух некоррелированных гауссовских случайных величин.

замирание Рэлея рассматривается как разумная модель для распространения сигналов тропосферы и ионосферы, а также влияния сильно застроенных городских сред на радиосигналы. Рэлеевское замирание наиболее применимо, когда нет преобладающего распространения вдоль прямой видимости между передатчиком и приемником. Если есть доминирующая линия обзора, рисовское замирание может быть более применимым. Рэлеевское замирание - это частный случай двухволнового замирания с диффузной мощностью (TWDP).

Содержание

1 Модель
- 1.1 Применимость
2 Свойства
- 2.1 Скорость пересечения уровней
- 2.2 Средняя длительность замирания
- 2.3 Доплеровская спектральная плотность мощности
3 Создание рэлеевских замираний
- 3.1 Модель Джейкса
- 3.2 Фильтрованный белый шум
4 См. Также
5 Ссылки

Модель

Рэлеевское замирание является разумной моделью, когда в окружающей среде много объектов, рассеивающих радиосигнал до того, как он достигнет приемника. Центральная предельная теорема утверждает, что при достаточно большом разбросе импульсная характеристика канала будет хорошо смоделирована как гауссовский процесс независимо от распределения отдельные компоненты. Если в разбросе нет доминирующего компонента, то такой процесс будет иметь нулевое среднее и фазу , равномерно распределенные между 0 и 2π радиан. Таким образом, конверт отклика канала будет распределенным по Рэлею.

. Вызов этой случайной переменной $R {\ displaystyle R}$ $R$ будет иметь функция плотности вероятности :

п R (r) = 2 r Ω e - r 2 / Ω, r ≥ 0 {\ displaystyle p_ {R} (r) = {\ frac {2r} {\ Omega}} e ^ { -r ^ {2} / \ Omega}, \ r \ geq 0}

{\ displaystyle p_ {R} (r) = {\ frac {2 r} {\ Omega}} e ^ {- r ^ {2} / \ Omega}, \ r \ geq 0}

где $Ω = E ⁡ (R 2) {\ displaystyle \ Omega = \ operatorname {E} (R ^ {2}) }$ ${\ displaystyle \ Omega = \ operatorname {E} (R ^ {2})}$ .

Часто элементы усиления и фазы искажения канала удобно представлять в виде комплексного числа. В этом случае замирание Рэлея проявляется в предположении, что действительная и мнимая части отклика моделируются независимыми и одинаково распределенными гауссовскими процессами с нулевым средним. так что амплитуда отклика складывается из двух таких процессов.

Применимость

Было показано, что плотно построенный Манхэттен приближается к среде с рэлеевскими замираниями.

Одна секунда замирания Рэлея с максимальным доплеровским сдвигом 10 Гц.

Одна секунда замирания Рэлея с максимальное доплеровское смещение 100 Гц.

Требование наличия большого количества рассеивателей означает, что рэлеевские замирания могут быть полезной моделью в сильно застроенных центрах городов, где отсутствует прямая видимость между передатчик и приемник, а также многие здания и другие объекты ослабляют, отражают, преломляют и преломляют сигнал. Экспериментальная работа на Манхэттене обнаружила там затухание, близкое к рэлеевскому. При распространении сигналов тропосферы и ионосферы многие частицы в атмосферных слоях действуют как рассеиватели, и такая среда также может приближаться к рэлеевскому замиранию. Если окружающая среда такова, что в дополнение к рассеянию на приемнике наблюдается сильно доминирующий сигнал, обычно вызванный прямой видимостью, то среднее значение случайного процесса больше не будет равно нулю., вместо этого варьируя в зависимости от уровня мощности доминирующего пути. Такую ситуацию можно лучше смоделировать как рисовское замирание.

Обратите внимание, что рэлеевское замирание - это мелкомасштабный эффект. Будут присутствовать основные свойства среды, такие как потери на пути и затенение, на которые накладывается затухание.

Скорость затухания канала будет зависеть от скорости движения приемника и / или передатчика. Движение вызывает доплеровский сдвиг в компонентах принятого сигнала. На рисунках показано изменение мощности постоянного сигнала в течение 1 секунды после прохождения через однолучевой канал с рэлеевскими замираниями с максимальным доплеровским сдвигом 10 Гц и 100 Гц. Эти доплеровские сдвиги соответствуют скоростям около 6 км / ч (4 мили в час) и 60 км / ч (40 миль в час) соответственно на частоте 1800 МГц, одной из рабочих частот для мобильных телефонов GSM . Это классическая форма рэлеевского выцветания. Обратите внимание, в частности, на «глубокие затухания», когда уровень сигнала может упасть в несколько тысяч раз, или 30–40. dB.

Свойства

Поскольку он основан на хорошо изученном распределении с особыми свойствами, Рэлеевский Распределение поддается анализу, а ключевые особенности, влияющие на производительность беспроводной сети, имеют аналитические выражения.

. Обратите внимание, что параметры, обсуждаемые здесь, относятся к нестатическому каналу. Если канал не меняется со временем, он не исчезает, а вместо этого остается на определенном уровне. Отдельные экземпляры канала в этом случае не будут коррелированы друг с другом из-за предположения, что каждый из рассеянных компонентов затухает независимо. Как только относительное движение вводится между любым из передатчика, приемника и рассеивателя, замирание становится коррелированным и изменяется во времени.

Скорость пересечения уровней

Скорость пересечения уровней является мерой скорости замирания. Он определяет, как часто замирание пересекает некоторый порог, обычно в положительном направлении. Для рэлеевского замирания скорость пересечения уровней равна:

LCR = 2 π fd ρ e - ρ 2 {\ displaystyle \ mathrm {LCR} = {\ sqrt {2 \ pi}} f_ {d} \ rho e ^ { - \ rho ^ {2}}}

{\ mathrm {LCR}} = {\ sqrt {2 \ pi}} f_ {d} \ rho e ^ {{- \ rho ^ {2}}}

где $fd {\ displaystyle f_ {d}}$ $f_ {d}$ - максимальный доплеровский сдвиг, а $ρ {\ displaystyle \, \! \ rho }$ $\, \! \ rho$ - пороговый уровень, нормированный на среднеквадратичный (RMS) уровень сигнала:

ρ = R пороговое значение R среднеквадратичное. {\ displaystyle \ rho = {\ frac {R _ {\ mathrm {threshold}}} {R _ {\ mathrm {rms}}}}.}

{\ displaystyle \ rho = {\ frac {R _ {\ mathrm {threshold) }}} {R _ {\ mathrm {rms}}}}.}

Средняя длительность замирания

Средняя длительность замирания количественно определяет, насколько долго сигнал находится ниже порога $ρ {\ displaystyle \, \! \ rho}$ $\, \! \ rho$ . Для рэлеевских замираний средняя длительность замирания составляет:

A F D = e ρ 2 - 1 ρ f d 2 π. {\ displaystyle \ mathrm {AFD} = {\ frac {e ^ {\ rho ^ {2}} - 1} {\ rho f_ {d} {\ sqrt {2 \ pi}}}}.}

{\ displaystyle \ mathrm {AFD} = {\ frac {e ^ {\ rho ^ {2}} - 1} {\ rho f_ {d} {\ sqrt {2 \ pi}}}}.}

частота пересечения уровня и средняя длительность замирания, взятые вместе, дают полезные средства для характеристики степени замирания во времени.

Для конкретного нормализованного порогового значения $ρ {\ displaystyle \ rho}$ $\ rho$ произведение средней продолжительности замирания и скорости перехода уровня является константой и выражается как

AFD × LCR = 1 - e - ρ 2. {\ displaystyle \ mathrm {AFD} \ times \ mathrm {LCR} = 1-e ^ {- \ rho ^ {2}}.}

{\ mathrm {AFD}} \ times {\ mathrm {LCR}} = 1-e ^ {{- \ rho ^ {2}}}.

Доплеровская спектральная плотность мощности

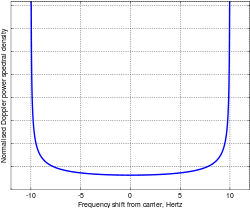Нормализованный доплеровский спектр мощности рэлеевского замирания с максимальное доплеровское смещение 10 Гц.

Доплеровская спектральная плотность мощности канала с замиранием описывает, насколько спектральное расширение это вызывает. Это показывает, как чистая частота, например, чистая синусоида, которая представляет собой импульс в частотной области, распространяется по частоте при прохождении через канал. Это преобразование Фурье функции автокорреляции времени. Было показано, что для рэлеевских замираний с вертикальной приемной антенной с одинаковой чувствительностью во всех направлениях:

S (ν) = 1 π fd 1 - (ν fd) 2, {\ displaystyle S (\ nu) = {\ frac {1} {\ pi f_ {d} {\ sqrt {1- \ left ({\ frac {\ nu} {f_ {d}}} \ right) ^ {2}}}}},}

{\ displaystyle S (\ nu) = {\ frac {1} {\ pi f_ {d} {\ sqrt {1- \ left ({\ frac {\ nu} {f_ {d }}} \ right) ^ {2}}}}},}

где $ν {\ displaystyle \, \! \ Nu}$ $\, \ ! \ nu$ - сдвиг частоты относительно несущей частоты. Это уравнение действительно только для значений $ν {\ displaystyle \, \! \ Nu}$ $\, \ ! \ nu$ между $± fd {\ displaystyle \ pm f_ {d}}$ $\ pm f_ {d}$ ; вне этого диапазона спектр равен нулю. Этот спектр показан на рисунке для максимального доплеровского сдвига 10 Гц. «Форма чаши» или «форма ванны» - классическая форма этого доплеровского спектра.

Создание рэлеевских замираний

Как описано выше, сам канал рэлеевских замираний может быть смоделирован путем генерации действительной и мнимой частей комплексного числа в соответствии с независимыми нормальными гауссовыми переменными. Однако иногда бывает так, что интерес представляют просто колебания амплитуды (например, на рисунке, показанном выше). Есть два основных подхода к этому. В обоих случаях цель состоит в том, чтобы произвести сигнал, который имеет доплеровский спектр мощности, указанный выше, и эквивалентные свойства автокорреляции.

Модель Джейкса

В своей книге Джейкс популяризировал модель замирания Рэлея, основанную на суммировании синусоид. Пусть рассеиватели равномерно распределены по окружности под углами $α n {\ displaystyle \ alpha _ {n}}$ $\ alpha_n$ с выходящими лучами $k {\ displaystyle k}$ $k$ от каждого рассеивателя. Доплеровский сдвиг на луче $n {\ displaystyle n}$ $n$ равен

fn = fd cos ⁡ α n {\ displaystyle \, \! F_ {n} = f_ {d} \ cos \ alpha _ {n}}

{\ displaystyle \, \! f_ {n} = f_ {d} \ cos \ alpha _ {n}}

и, с $M {\ displaystyle M}$ $M$ такими рассеивателями, рэлеевское замирание $k th {\ displaystyle k ^ {\ text {th }}}$ $k ^ {\ text {th }}$ форма волны во времени $t {\ displaystyle t}$ $t$ может быть смоделирована как:

R (t, k) = 2 2 [∑ n = 1 M (cos ⁡ β n + j sin ⁡ β n) cos ⁡ (2 π fnt + θ n, k) + 1 2 (cos ⁡ α + j sin ⁡ α) cos ⁡ (2 π fdt)]. {\ displaystyle {\ begin {align} R (t, k) = 2 {\ sqrt {2}} \ left [\ sum _ {n = 1} ^ {M} \ right. \ left (\ cos \ beta _ {n} + j \ sin \ beta _ {n} \ right) \ cos \ left (2 \ pi f_ {n} t + \ theta _ {n, k} \ right) \\ [4pt] \ left. {} + {\ frac {1} {\ sqrt {2}}} \ left (\ cos \ alpha + j \ sin \ alpha \ right) \ cos (2 \ pi f_ {d} t) \ right]. \ конец {выровнен}}}

{\ displaystyle {\ begin {выровнено} R (t, k) = 2 {\ sqrt {2}} \ left [\ sum _ {n = 1} ^ {M} \ right. \ left (\ cos \ beta _ {n} + j \ sin \ beta _ {n} \ right) \ cos \ left (2 \ pi f_ {n} t + \ theta _ {n, k} \ right) \\ [4pt] \ left. {} + {\ frac {1} {\ sqrt {2}}} \ left (\ cos \ alpha + j \ sin \ alpha \ right) \ cos (2 \ pi f_ {d} t) \ right]. \ End {выравнивается}}}

Здесь $α {\ displaystyle \, \! \ alpha}$ $\, \! \ alpha$ и $β n {\ displaystyle \, \! \ beta _ {n }}$ $\, \! \ Beta _ {n}$ и $θ n, k {\ displaystyle \, \! \ Theta _ {n, k}}$ $\, \! \ theta _ {{n, k}}$ - параметры модели с $α {\ displaystyle \, \! \ alpha}$ $\, \! \ alpha$ обычно устанавливается равным нулю, $β n {\ displaystyle \, \! \ beta _ {n}}$ $\, \! \ Beta _ {n}$ выбирается так, чтобы не было перекрестных корреляция между действительной и мнимой частями $R (t) {\ displaystyle R (t)}$ $R(t)$ :

β n = π n M + 1 {\ displaystyle \, \! \ beta _ {n} = {\ frac {\ pi n} {M + 1}}}

\, \! \ Beta _ {n} = {\ frac {\ pi n} {M + 1}}

и $θ n, k {\ displaystyle \, \! \ theta _ {n, k}}$ $\, \! \ theta _ {{n, k}}$ используется для генерации нескольких формы волны. Если моделируется однолучевой канал, так что имеется только одна форма сигнала, тогда $θ n {\ displaystyle \, \! \ Theta _ {n}}$ ${\ displaystyle \, \! \ theta _ {n}}$ может быть нулевым. Если многолучевой частотно-избирательный канал моделируется таким образом, что требуется несколько форм сигналов, Джейкс предполагает, что некоррелированные формы сигналов задаются как

θ n, k = β n + 2 π (k - 1) M + 1. {\ displaystyle \ theta _ {n, k} = \ beta _ {n} + {\ frac {2 \ pi (k-1)} {M + 1}}.}

\ theta _ {{n, k}} = \ beta _ {n} + {\ frac {2 \ pi (k-1)} {M + 1}}.

Фактически, это было показано что формы сигналов коррелированы между собой - они имеют ненулевую взаимную корреляцию - за исключением особых обстоятельств. Модель также является детерминированной (она не содержит случайных элементов после выбора параметров). Модифицированная модель Джейкса выбирает немного другие интервалы для рассеивателей и масштабирует их формы волны, используя последовательности Уолша – Адамара, чтобы гарантировать нулевую взаимную корреляцию. Установка

α n = π (n - 0,5) 2 M и β n = π n M, {\ displaystyle \ alpha _ {n} = {\ frac {\ pi (n-0,5)} {2M}} { \ text {and}} \ beta _ {n} = {\ frac {\ pi n} {M}},}

{\ displaystyle \ alpha _ {n} = {\ frac {\ pi (n-0,5)} {2M}} {\ text {and}} \ beta _ {n} = {\ frac {\ pi n} {M}},}

приводит к следующей модели, обычно называемой моделью Дента или модифицированной моделью Джейкса:

R (t, k) = 2 M n = 1 MA k (n) (cos ⁡ β n + j sin ⁡ β n) cos ⁡ (2 π fdt cos ⁡ α n + θ n). {\ Displaystyle R (t, k) = {\ sqrt {\ frac {2} {M}}} \ sum _ {n = 1} ^ {M} A_ {k} (n) \ left (\ cos \ beta _ {n} + j \ sin \ beta _ {n} \ right) \ cos \ left (2 \ pi f_ {d} t \ cos \ alpha _ {n} + \ theta _ {n} \ right).}

{\ displaystyle R (t, k) = {\ sqrt {\ frac {2} {M}}} \ sum _ {n = 1 } ^ {M} A_ {k} (n) \ left (\ cos \ beta _ {n} + j \ sin \ beta _ {n} \ right) \ cos \ left (2 \ pi f_ {d} t \ cos \ alpha _ {n} + \ theta _ {n} \ right).}

Весовые функции $A k (n) {\ displaystyle A_ {k} (n)}$ $A_{k}(n)$ - это $k {\ displaystyle k}$ $k$ Уолш– Последовательность Адамара в $n {\ displaystyle n}$ $n$ . Поскольку они имеют нулевую взаимную корреляцию по конструкции, эта модель приводит к некоррелированным сигналам. Фазы $θ n {\ displaystyle \, \! \ Theta _ {n}}$ ${\ displaystyle \, \! \ theta _ {n}}$ могут быть инициализированы случайным образом и не влияют на свойства корреляции. быстрое преобразование Уолша можно использовать для эффективного генерирования выборок с использованием этой модели.

Модель Джейкса также популяризировала спектр Доплера, связанный с замиранием Рэлея, и, как результат, этот спектр Доплера часто называют спектром Джейкса.

Фильтрованный белый шум

Другой способ генерировать сигнал с требуемым доплеровским спектром мощности - это пропустить сигнал белый гауссов шум через гауссовский фильтр с частотной характеристикой, равной квадратному корню из требуемого доплеровского спектра. Хотя он проще, чем модели, приведенные выше, и недетерминирован, он представляет некоторые вопросы реализации, связанные с необходимостью фильтров высокого порядка для аппроксимации иррациональной функции квадратного корня в отклике и выборки гауссовой формы волны с соответствующей частотой.

См. Также

Ссылки