Модель Рэмси-Касса-Купманса

Модель Рэмси-Касса-Купманса или Модель роста Рэмси, является неоклассической моделью экономического роста, основанной в основном на работе Фрэнка П. Рэмси, со значительными расширениями Дэвида Касса и Тьяллинг Купманс. Модель Рэмси – Касса – Купманса отличается от модели Солоу – Свона тем, что выбор потребления явно микрооснован в определенный момент времени и, таким образом, эндогенизирует норма экономии. В результате, в отличие от модели Солоу – Суона, уровень сбережений может не быть постоянным при переходе к долгосрочному устойчивому состоянию. Другое следствие модели состоит в том, что результат оптимален по Парето или эффективен по Парето.

Первоначально Рэмси изложил модель как проблему социального планировщика по максимизации уровней потребление в последовательных поколениях. Лишь позже Касс и Купманс приняли модель как описание децентрализованной динамической экономики с репрезентативным агентом. Модель Рэмси-Касса-Купманса направлена ​​только на объяснение долгосрочного экономического роста, а не колебаний бизнес-цикла, и не включает никаких источников нарушений, таких как несовершенство рынка, неоднородность среди домашних хозяйств или экзогенные шоки. Поэтому последующие исследователи расширили модель, допустив потрясения, связанные с государственными закупками, колебания в занятости и другие источники нарушений, что известно как теория реального делового цикла.

• 1 Математическое описание
• 2 История
• 3 Примечания
• 4 Ссылки
• 5 Дополнительная литература
• 6 Внешние ссылки

Модель Рамси – Касса – Купманса начинается с агрегированной производственной функции, который удовлетворяет условиям Инада, часто указывается как относящийся к типу Кобба – Дугласа, $F\; (K,\; L)\; \{\backslash \; displaystyle\; F\; (K,\; L)\}$, с факторами капитал $K\; \{\backslash \; displaystyle\; K\}$и труд $L\; \{\backslash \; displaystyle\; L\}$. Поскольку предполагается, что эта производственная функция однородна степени 1, ее можно выразить в единицах на душу, $F\; (K,\; L)\; =\; L\; \cdot \; F\; (KL,\; 1)\; знак\; равно\; L\; \cdot \; е\; (К)\; \{\backslash \; Displaystyle\; F\; (К,\; L)\; =\; L\; \backslash \; CDOT\; F\; \backslash \; влево\; (\{\backslash \; гидроразрыва\; \{K\}\; \{L\}\},\; 1\; \backslash \; вправо)\; =\; L\; \backslash \; CDOT\; F\; (K)\}$. Количество рабочей силы равно численности населения в экономике и растет с постоянной скоростью $n\; \{\backslash \; displaystyle\; n\}$, т.е. $L\; =\; L\; 0\; ent\; \{\backslash \; displaystyle\; L\; =\; L\_\; \{0\}\; e\; ^\; \{nt\}\}$где $L\; 0>0\; \{\backslash \; displaystyle\; L\_\; \{0\}>0\}$- это численность населения в начальный период.

Первое ключевое уравнение модели Рэмси – Касса – Купманса представляет собой уравнение состояния для накопления капитала:

$k\; \dot{}\; =\; f\; (k)\; -\; (n\; +\; \delta )\; k\; -\; c\; \{\backslash \; displaystyle\; \{\backslash \; dot\; \{k\}\}\; =\; f\; (k)\; -\; (n\; +\; \backslash \; delta)\; kc\}$

нелинейное дифференциальное уравнение, подобное модели Солоу – Свона, где $k\; \{\backslash \; displaystyle\; k\}$равно капиталоемкость (т.е. капитал на одного работника), $k\; \dot{}\; =\; dkdt\; \{\backslash \; displaystyle\; \{\backslash \; dot\; \{k\}\}\; =\; \{\backslash \; tfrac\; \{\backslash \; mathrm\; \{d\}\; k\}\; \{\; \backslash \; mathrm\; \{d\}\; t\}\}\}$- это сокращение в нотации Ньютона для изменения капиталоемкости с течением времени, $c\; \{\backslash \; displaystyle\; c\}$- потребление на одного работника, $f\; (k)\; \{\backslash \; displaystyle\; f\; (k)\}$- вывод на одного рабочего для данного $k\; \{\backslash \; displaystyle\; k\}$и $\delta \; \{\backslash \; displaystyle\; \backslash \; delta\; \backslash ,\}$- норма амортизации капитала. При упрощающем предположении об отсутствии роста населения это уравнение утверждает, что инвестиции или увеличение капитала на одного работника - это та часть продукции, которая не потребляется, за вычетом нормы амортизации. капитала. Таким образом, инвестиции - это то же самое, что и сбережения.

. Второе уравнение модели - это решение проблемы специалиста по социальному планированию по максимизации функции общественного благосостояния, $U\; 0\; знак\; равно\; \int \; 0\; \infty \; е\; -\; \rho \; T\; U\; (C)\; dt\; \{\backslash \; displaystyle\; U\_\; \{0\}\; =\; \backslash \; int\; \_\; \{0\}\; ^\; \{\backslash \; infty\}\; e\; ^\; \{-\; \backslash \; rho\; t\}\; U\; (C)\; \backslash ,\; \backslash \; mathrm\; \{d\}\; t\}$, который состоит из потока экспоненциально дисконтированной мгновенной полезности от потребления, где $\rho \; \in \; (0,\; \infty )\; \{\backslash \; displaystyle\; \backslash \; rho\; \backslash \; in\; (0,\; \backslash \; infty)\}$- это ставка дисконтирования, отражающая временные предпочтения. Предполагается, что экономика населена идентичными людьми, так что проблема оптимального управления может быть сформулирована в терминах бесконечно живущего репрезентативного агента с неизменной во времени полезностью: $U\; (C)\; знак\; равно\; L\; u\; (c)\; =\; L\; 0\; entu\; (c)\; \{\backslash \; displaystyle\; U\; (C)\; =\; Lu\; (c)\; =\; L\_\; \{0\}\; e\; ^\; \{nt\}\; u\; (c)\}$. Предполагается, что функция полезности строго возрастает (т. Е. Отсутствует точка блаженства ) и вогнута в $c\; \{\backslash \; displaystyle\; c\}$, с $lim\; c\; \to \; 0\; uc\; =\; \infty \; \{\backslash \; displaystyle\; \backslash \; lim\; \_\; \{c\; \backslash \; to\; 0\}\; u\_\; \{c\}\; =\; \backslash \; infty\}$, где $uc\; \{\backslash \; displaystyle\; u\_\; \{c\}\}$сокращенное обозначение предельной полезности потребления $\partial \; u\; \partial \; c\; \{\backslash \; displaystyle\; \{\backslash \; tfrac\; \{\backslash \; partial\; u\}\; \{\backslash \; partial\; c\}\}\}$. Нормализуя исходную совокупность $L\; 0\; \{\backslash \; displaystyle\; L\_\; \{0\}\}$к единице, проблему можно сформулировать так:

$max\; c\; U\; 0\; =\; \int \; 0\; \infty \; e\; -\; (\rho \; -\; n)\; ту\; (с)\; dt\; \{\backslash \; displaystyle\; \backslash \; max\; \_\; \{c\}\; U\_\; \{0\}\; =\; \backslash \; int\; \_\; \{0\}\; ^\; \{\backslash \; infty\}\; e\; ^\; \{-\; (\backslash \; rho\; -n)\; t\}\; u\; (c)\; \backslash ,\; \backslash \; mathrm\; \{d\}\; t\}$

$при\; условии\; c\; =\; f\; (k)\; -\; (n\; +\; \delta )\; k\; -\; k\; \dot{}\; \{\backslash \; displaystyle\; \{\backslash \; text\; \{при\; условии\}\}\; \backslash \; quad\; c\; =\; f\; (k)\; -\; (n\; +\; \backslash \; дельта)\; k\; -\; \{\backslash \; dot\; \{k\}\}\}$

где начальный ненулевой акционерный капитал $k\; (0)\; =\; k\; 0>0\; \{\backslash \; displaystyle\; k\; (0)\; =\; k\_\; \{0\}>0\}$Решение этой проблемы, обычно находящееся с использованием функции Гамильтона, представляет собой нелинейное дифференциальное уравнение, описывающее оптимальную эволюцию потребления,

$c\; \dot{}\; =\; -\; uc\; (c)\; c\; \cdot \; ucc\; (c)\; [fk\; (k)\; -\; \delta \; -\; \rho ]\; \cdot \; c\; \{\backslash \; displaystyle\; \{\backslash \; dot\; \{c\}\}\; =\; -\; \{\backslash \; frac\; \{u\_\; \{c\}\; (c)\}\; \{c\; \backslash \; cdot\; u\_\; \{cc\}\; (c)\}\}\; \backslash \; left\; [f\_\; \{k\}\; (k)\; -\; \backslash \; delta\; -\; \backslash \; rho\; \backslash \; right]\; \backslash \; cdot\; c\}$

который известен wn как правило Кейнса – Рэмси. Термин $fk\; (k)\; -\; \delta \; \{\backslash \; displaystyle\; f\_\; \{k\}\; (k)\; -\; \backslash \; delta\}$, где $fk\; \{\backslash \; displaystyle\; f\_\; \{k\}\}$- это сокращенное обозначение предельного продукта капитала $\partial \; f\; \partial \; k\; \{\backslash \; displaystyle\; \{\backslash \; tfrac\; \{\backslash \; partial\; f\}\; \{\backslash \; partial\; k\}\}\}$, отражает предельную доходность чистых инвестиций. Выражение $-\; uc\; (c)\; /\; c\; \cdot \; ucc\; (c)\; \{\backslash \; displaystyle\; -\; \backslash \; left.u\_\; \{c\}\; (c)\; \backslash \; right\; /\; c\; \backslash \; cdot\; u\_\; \{cc\}\; (c)\}$отражает кривизну функции полезности; его обратный известен как (межвременная) эластичность замещения и указывает, насколько репрезентативный агент желает сгладить потребление с течением времени. Часто предполагается, что эта эластичность является положительной константой, т.е. $\sigma \; =\; -\; c\; \cdot \; ucc\; (c)\; /\; uc\; (c)>0\; \{\backslash \; displaystyle\; \backslash \; sigma\; =\; -\; \backslash \; left.c\; \backslash \; cdot\; u\_\; \{cc\}\; (\; c)\; \backslash \; right\; /\; u\_\; \{c\}\; (c)>0\}$.

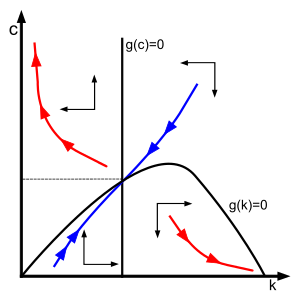Фазовое пространство график (или фазовая диаграмма) модели Рамсея. Синяя линия представляет динамический (или седловой) путь регулирования экономики в которой удовлетворяются все ограничения, присутствующие в модели. Это устойчивая траектория динамической системы. Красные линии представляют динамические траектории, которые исключаются условием трансверсальности.

Два связанных дифференциальных уравнения для $k\; \{\; \backslash \; displaystyle\; k\}$и $c\; \{\backslash \; displaystyle\; c\}$образуют динамическую систему Рэмси – Касса – Купманса. Ее устойчивое состояние, который можно найти, задав $k\; \dot{}\; \{\backslash \; displaystyle\; \{\backslash \; dot\; \{k\}\}\}$и $c\; \dot{}\; \{\backslash \; displaystyle\; \{\backslash \; dot\; \{c\}\}\}$равно нулю, задается парой $(k\; \ast ,\; c\; \ast )\; \{\backslash \; displaystyle\; (k\; ^\; \{\backslash \; ast\},\; c\; ^\; \{\backslash \; ast\})\}$неявно определяется формулами

$fk\; (k\; \ast )\; =\; \delta \; +\; \rho \; и\; c\; \ast \; =\; f\; (k\; \ast )\; -\; (n\; +\; \delta )\; k\; \ast \; \{\backslash \; displaystyle\; f\_\; \{k\}\; \backslash \; left\; (k\; ^\; \{\backslash \; ast\}\; \backslash \; right)\; =\; \backslash \; delta\; +\; \backslash \; rho\; \backslash \; quad\; \{\backslash \; text\; \{and\}\}\; \backslash \; quad\; c\; ^\; \{\backslash \; ast\}\; =\; f\; \backslash \; left\; (k\; ^\; \{\backslash \; ast\}\; \backslash \; right)\; -\; (n\; +\; \backslash \; delta)\; k\; ^\; \{\backslash \; ast\}\; \}$

Качественное утверждение об устойчивости решения $(k\; \ast ,\; c\; \ast )\; \{\backslash \; displaystyle\; (k\; ^\; \{\backslash \; ast\},\; c\; ^\; \{\backslash \; ast\})\}$требует линеаризации с помощью полинома Тейлора первого порядка

$[k\; \dot{}\; c\; \dot{}]\; \approx \; J\; (k\; \ast ,\; c\; \ast )\; [(k\; -\; k\; \ast )\; (c\; -\; c\; \ast )]\; \{\; \backslash \; Displaystyle\; \{\backslash \; begin\; \{bmatrix\}\; \{\backslash \; dot\; \{k\}\}\; \backslash \backslash \; \{\backslash \; dot\; \{c\}\}\; \backslash \; end\; \{bmatrix\}\}\; \backslash \; приблизительно\; \backslash \; mathbf\; \{J\}\; (k\; ^\; \{\backslash \; ast\},\; c\; ^\; \{\backslash \; ast\; \})\; \{\backslash \; begin\; \{bmatrix\}\; (kk\; ^\; \{\backslash \; ast\})\; \backslash \backslash \; (cc\; ^\; \{\backslash \; ast\})\; \backslash \; end\; \{bmatrix\}\}\}$

где $J\; (k\; \ast ,\; c\; \ast )\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{J\}\; (k\; ^\; \{\backslash \; ast\},\; c\; ^\; \{\backslash \; ast\})\}$- это матрица Якоби, вычисляемая в установившемся состоянии, заданная как

$J\; (\; k\; \ast ,\; c\; \ast )\; =\; [\rho \; -\; n\; -\; 1\; 1\; \sigma \; fkk\; (k)\; \cdot \; c\; \ast \; 0]\; \{\backslash \; displaystyl\; e\; \backslash \; mathbf\; \{J\}\; \backslash \; left\; (k\; ^\; \{\backslash \; ast\},\; c\; ^\; \{\backslash \; ast\}\; \backslash \; right)\; =\; \{\backslash \; begin\; \{bmatrix\}\; \backslash \; rho\; -n\; -1\; \backslash \backslash \; \{\backslash \; frac\; \{1\}\; \{\backslash \; sigma\}\; \}\; f\_\; \{kk\}\; (k)\; \backslash \; cdot\; c\; ^\; \{\backslash \; ast\}\; 0\; \backslash \; end\; \{bmatrix\}\}\}$

, который имеет определитель , поскольку $c\; \{\backslash \; displaystyle\; c\}$всегда положительно, $\sigma \; \{\backslash \; displaystyle\; \backslash \; sigma\}$равно положительно по предположению, и только $fkk\; \{\backslash \; displaystyle\; f\_\; \{kk\}\}$отрицательно, поскольку $f\; \{\backslash \; displaystyle\; f\}$равно вогнутый. Поскольку определитель равен произведению собственных значений, собственные значения должны быть действительными и противоположными по знаку. Следовательно, согласно теореме об устойчивом многообразии, равновесие - это седловая точка и существует единственное устойчивое плечо, или «седловой путь», который сходится к точке равновесия, обозначенной синей кривой. на фазовой диаграмме. Система называется «стабильной по седловому пути», поскольку все неустойчивые траектории исключаются условием «нет схемы Понци »:

$lim\; t\; \to \; \infty \; k\; \cdot \; e\; -\; \int \; 0\; t\; (fk\; -\; n\; -\; \delta )\; ds\; \ge \; 0\; \{\backslash \; displaystyle\; \backslash \; lim\; \_\; \{t\; \backslash \; to\; \backslash \; infty\}\; k\; \backslash \; cdot\; e\; ^\; \{-\; \backslash \; int\; \_\; \{0\}\; ^\; \{t\}\; \backslash \; left\; (f\_\; \{k\}\; -n-\; \backslash \; delta\; \backslash \; right)\; \backslash \; mathrm\; \{d\}\; s\}\; \backslash \; geq\; 0\}$

подразумевая, что приведенная стоимость акционерного капитала не может быть отрицательной.

Спир и Янг повторно исследуют история оптимального роста в течение 1950-х и 1960-х годов, частично сосредотачиваясь на правдивости заявленной одновременной и независимой разработки «Оптимального роста в агрегированной модели накопления капитала» Касса (опубликованной в 1965 году в Обзоре экономических исследований ), и «О концепции оптимального экономического роста» Тьяллинга Купмана (опубликовано в «Неделе исследований эконометрического подхода к планированию развития», 1965, Рим: Папская академия наук).

За время своей жизни ни Кэсс, ни Купманс никогда не предполагали, что их результаты, характеризующие оптимальный рост в односекторной модели непрерывного роста, были чем-то иным, кроме «одновременного и независимого». То, что вопрос о приоритете когда-либо стал предметом обсуждения, было связано только с тем фактом, что в опубликованной версии работы Купманса он процитировал главу из тезиса Касса, которая позже стала статьей RES. В своей статье Купманс заявляет в сноске, что Касс независимо получил условия, аналогичные тем, что находит Купманс, и что Касс также рассматривает в своей статье предельный случай, когда учетная ставка стремится к нулю. Со своей стороны Касс отмечает, что «после того, как первоначальная версия этой статьи была завершена, наше внимание привлек очень похожий анализ Купманса. Мы опираемся на его результаты при обсуждении предельного случая, когда эффективная социальная ставка дисконтирования стремится к нулю».. В интервью, которое Касс дал Macroeconomic Dynamics, он благодарит Купманса за то, что он указал ему на предыдущую работу Фрэнка Рэмси, утверждая, что был смущен тем, что не знал о ней, но ничего не говорит, чтобы развеять основное утверждение, что его работа и Купманс были в ней. факт независимый.

Спир и Янг оспаривают эту историю, основываясь на ранее упущенной версии рабочего документа Купманса, которая послужила основой для часто цитируемой презентации Купманса на конференции, проведенной Папской академией наук в октябре 1963 года. В этом документе для обсуждения Cowles есть ошибка. Купманс утверждает в своем основном результате, что уравнения Эйлера необходимы и достаточны для характеристики оптимальных траекторий в модели, потому что любые решения уравнений Эйлера, которые не сходятся к оптимальному установившемуся состоянию, столкнутся либо с нулевым потреблением, либо с нулевой границей капитала в конечное время. Эта ошибка, по-видимому, была представлена ​​на конференции в Ватикане, хотя на момент ее представления Купмансом ни один из участников не прокомментировал проблему. Это можно сделать вывод, потому что обсуждение после каждой презентации доклада на конференции в Ватикане дословно сохраняется в томе конференции.

В обсуждении тома Ватикана после презентации статьи Эдмонда Малинво проблема действительно возникает из-за явного включения Малинво так называемого «условия трансверсальности» (которое Малинво называет Условием I) в его статье. В конце презентации Купманс спрашивает Малинво, не так ли, что Условие I просто гарантирует, что решения уравнений Эйлера, которые не сходятся к оптимальному установившемуся состоянию, достигают границы за конечное время. Малинво отвечает, что это не так, и предлагает Купману взглянуть на пример с функциями полезности журнала и производственными функциями Кобба-Дугласа.

На этом этапе Купманс, очевидно, осознает, что у него есть проблема, но, судя по сбивающему с толку добавлению к более поздней версии статьи, подготовленной после конференции в Ватикане, он, кажется, не может решить, как решить поднятую проблему. по условию I. Малинво

Из интервью Macroeconomic Dynamics с Кассом ясно, что Купманс встречался с научным руководителем Касса, Хирофуми Удзава, на зимних собраниях Эконометрического Общество в январе 1964 года, когда Узава сообщил ему, что его ученик [Касс] уже решил эту проблему. Затем Удзава, должно быть, предоставил Купмансу копию главы диссертации Касса, которую он, по-видимому, прислал под видом Технического отчета IMSSS, который Купманс цитировал в опубликованной версии своей статьи. Слово «обличие» здесь уместно, потому что номер ТУ, указанный в цитировании Купманса, указывал бы на дату выпуска отчета в начале 1950-х годов, чего явно не было.

В опубликованной версии статьи Купманса он налагает новое условие альфа в дополнение к уравнениям Эйлера, утверждая, что единственная допустимая траектория среди тех, которые удовлетворяют уравнениям Эйлера, - это та, которая сходится к оптимальной установившейся траектории. состояние равновесия модели. Этот результат получен в статье Касса посредством наложения условия трансверсальности, которое Касс вывел из соответствующих разделов книги Льва Понтрягина. Спир и Янг предполагают, что Купманс выбрал этот путь, потому что не хотел, чтобы он «заимствовал» технологию трансверсальности Малинво или Касса.

Основываясь на этом и другом исследовании вклада Малинво в 1950-е годы - в частности, на его интуиции важности условия трансверсальности - Спир и Янг предполагают, что неоклассическую модель роста лучше назвать моделью Рамсея-Малинво-Касса. модель, чем установленная почетная Рэмси-Касс-Купманса.

• Аджемоглу, Дарон (2009). «Неоклассическая модель роста». Введение в современный экономический рост. Принстон: Издательство Принстонского университета. С. 287–326. ISBN 978-0-691-13292-1.
• Барро, Роберт Дж. ; Сала-и-Мартин, Ксавье (2004). «Модели роста с оптимизацией потребителей». Экономический рост (второе изд.). Нью-Йорк: Макгроу-Хилл. С. 85–142. ISBN 978-0-262-02553-9.
• (2011). «Модель Рэмси». Макроэкономическая теория. Нью-Йорк: Издательство Оксфордского университета. С. 145–160. ISBN 978-0-19-538771-1.
• Бланшар, Оливье Жан ; Фишер, Стэнли (1989). «Потребление и инвестиции: основные модели бесконечного горизонта». Лекции по макроэкономике. Кембридж: MIT Press. С. 37–89. ISBN 978-0-262-02283-5.
• (2014). «Неоклассические модели роста». Экономическая динамика в дискретном времени. Кембридж: MIT Press. С. 353–364. ISBN 978-0-262-02761-8.
• ; Фернандес, Эстер; Руис, Хесус (2009). «Оптимальный рост: анализ непрерывного времени». Экономический рост: теория и численные методы решения. Берлин: Springer. С. 101–154. ISBN 978-3-540-68665-1.
• Ромер, Дэвид (2011). «Модели бесконечного горизонта и перекрывающихся поколений». Продвинутая макроэкономика (четвертое изд.). Нью-Йорк: Макгроу-Хилл. С. 49–77. ISBN 978-0-07-351137-5.

• Обсуждение оригинальной статьи Рэмси Орацио Аттанасио на YouTube