Алгоритм БПФ Рейдера

Алгоритм Рейдера (1968), названный в честь Чарльза М. Рейдера из лаборатории Линкольна Массачусетского технологического института, представляет собой алгоритм быстрого преобразования Фурье (БПФ), который вычисляет дискретное преобразование Фурье (ДПФ) простых размеров путем повторного выражения ДПФ в виде циклической свертки ( другой алгоритм для БПФ простых размеров, алгоритм Блюстейна, также работает, переписывая ДПФ как свертку).

Поскольку алгоритм Рейдера зависит только от периодичности ядра ДПФ, он напрямую применим к любому другому преобразованию (простого порядка) с аналогичным свойством, например, теоретико-числовому преобразованию или дискретному преобразованию Хартли.

Алгоритм можно модифицировать, чтобы получить двукратную экономию для случая ДПФ реальных данных, используя слегка измененную повторную индексацию / перестановку для получения двух циклических сверток половинного размера реальных данных; альтернативная адаптация для ДПФ реальных данных использует дискретное преобразование Хартли.

Виноград расширил алгоритм Рейдера, включив в него размеры ДПФ с простой степенью, и сегодня алгоритм Рейдера иногда описывается как частный случай алгоритма Винограда БПФ, также называемого алгоритмом мультипликативного преобразования Фурье (Tolimieri et al., 1997), который применяется к еще большим класс размеров. Однако для составных размеров, таких как степени простых чисел, алгоритм БПФ Кули – Тьюки намного проще и практичнее в реализации, поэтому алгоритм Рейдера обычно используется только для базовых случаев с большими простыми числами рекурсивного разложения Кули – Тьюки ДПФ. ${\ displaystyle p ^ {m}}$

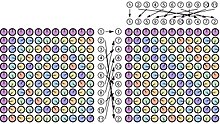Визуальное представление матрицы ДПФ в алгоритме БПФ Рейдера. Массив состоит из цветных часов, представляющих матрицу ДПФ размера 11. Путем перестановки строк и столбцов (кроме первого каждого из них) в соответствии с последовательностями, сгенерированными степенями первообразного корня из 11, исходная матрица ДПФ становится циркулянтной матрицей. Умножение последовательности данных на циркулянтную матрицу эквивалентно циклической свертке с вектором-строкой матрицы. Это соотношение представляет собой пример того, что мультипликативная группа является циклической:.${\ Displaystyle (\ mathbb {Z} / p \ mathbb {Z}) ^ {\ times} \ cong C_ {p-1}}$

Начнем с определения дискретного преобразования Фурье:

${\ displaystyle X_ {k} = \ sum _ {n = 0} ^ {N-1} x_ {n} e ^ {- {\ frac {2 \ pi i} {N}} nk} \ qquad k = 0, \ точки, N-1.}$

Если N является простым числом, то множество ненулевых индексов образует группу относительно умножения по модулю N. Одним из следствий теории чисел таких групп является то, что существует генератор группы (иногда называемый примитивным корнем, который можно быстро найти с помощью исчерпывающего поиска или немного лучших алгоритмов). Этот генератор представляет собой целое число g такое, что для любого ненулевого индекса n и для уникального (формирующего биекцию от q к ненулевому n). Аналогичным образом, для любого ненулевого индекса к и уникальный, где отрицательный показатель обозначает мультипликативный обратный из. Это означает, что мы можем переписать ДПФ, используя эти новые индексы p и q, как: ${\ Displaystyle п \ в {} \ {1, \ точки, N-1 \}}$ ${\ Displaystyle п = г ^ {д} {\ pmod {N}}}$${\ displaystyle q \ in {} \ {0, \ dots, N-2 \}}$ ${\ Displaystyle к = г ^ {- р} {\ pmod {N}}}$${\ displaystyle p \ in {} \ {0, \ dots, N-2 \}}$ ${\ displaystyle g ^ {p} \ mod N}$

${\ displaystyle X_ {0} = \ sum _ {n = 0} ^ {N-1} x_ {n},}$

${\ displaystyle X_ {g ^ {- p}} = x_ {0} + \ sum _ {q = 0} ^ {N-2} x_ {g ^ {q}} e ^ {- {\ frac {2 \ pi i} {N}} g ^ {- (pq)}} \ qquad p = 0, \ dots, N-2.}$

(Напомним, что x n и X k неявно периодичны по N, а также это ( тождество Эйлера ). Таким образом, все индексы и показатели берутся по модулю N, как того требует групповая арифметика.) ${\ Displaystyle е ^ {2 \ пи я} = 1}$

Заключительное суммирование, приведенное выше, представляет собой в точности циклическую свертку двух последовательностей a q и b q (длины N –1, потому что), определяемых следующим образом: ${\ displaystyle q \ in {} \ {0, \ dots, N-2 \}}$

${\ displaystyle a_ {q} = x_ {g ^ {q}}}$

${\ displaystyle b_ {q} = e ^ {- {\ frac {2 \ pi i} {N}} g ^ {- q}}.}$

Оценка свертки

Поскольку N –1 является составным, эту свертку можно выполнить непосредственно с помощью теоремы свертки и более традиционных алгоритмов БПФ. Однако это может быть неэффективным, если само N –1 имеет большие простые множители, что требует рекурсивного использования алгоритма Рейдера. Вместо этого, можно вычислить длина- ( N -1) циклическую свертку точно с помощью нулевого заполнения его к длине по меньшей мере 2 ( N - 1) -1, скажем, до степени двух, которые затем могут быть оценены в O ( N log N) время без рекурсивного применения алгоритма Рейдера.

Таким образом, этот алгоритм требует O ( N) сложений плюс O ( N log N) времени для свертки. На практике сложения O ( N) часто могут быть выполнены путем поглощения добавлений в свертку: если свертка выполняется парой БПФ, то сумма x n задается выходом DC (0-й) БПФ. из в д плюс х 0 и х 0 может быть добавлен ко всем выходам, добавляя его в перспективе постоянного тока свертки до обратного БПФ. Тем не менее, этот алгоритм требует больше операций, чем БПФ близких составных размеров, и на практике обычно занимает в 3–10 раз больше времени.

Если алгоритм Рейдера выполняется с использованием БПФ размера N –1 для вычисления свертки, а не с помощью заполнения нулями, как упомянуто выше, эффективность сильно зависит от N и количества раз, которое алгоритм Рейдера должен применяться рекурсивно. Наихудший случай был бы, если бы N –1 было 2 N 2, где N 2 - простое число, с N 2 –1 = 2 N 3, где N 3 - простое число, и так далее. В таких случаях, если предположить, что цепочка простых чисел расширяется до некоторого ограниченного значения, рекурсивное применение алгоритма Рейдера фактически потребует времени O ( N ²). Такие N j называются простыми числами Софи Жермен, а такая их последовательность - цепью Каннингема первого рода. Однако длина цепочек Каннингема растет медленнее, чем log 2 ( N), поэтому алгоритм Рейдера, примененный таким образом, вероятно, не O ( N ²), хотя он, возможно, хуже, чем O ( N log N) для худшие случаи. К счастью, гарантия сложности O ( N log N) может быть достигнута нулевым заполнением.

1. ^ CM Rader, "Дискретное преобразование Фурье, когда количество выборок данных простое", Proc. IEEE 56, 1107–1108 (1968).
2. ^ С. Чу и К. Буррус, "АлгоритмFTT [ sic ]простого множителя,использующий распределенную арифметику", IEEE Transactions on Acoustics, Speech, and Signal Processing 30 (2), 217–227 (1982).
3. ^ ^{a b} Маттео Фриго и Стивен Джонсон, « Разработка и реализация FFTW3 », Протоколы IEEE 93 (2), 216–231 (2005).
4. ^ С. Виноград, "О вычислении дискретного преобразования Фурье", Proc. Национальная академия наук США, 73 (4), 1005–1006 (1976).
5. ^ С. Виноград, "О вычислении дискретного преобразования Фурье", Математика вычислений, 32 (141), 175–199 (1978).
6. ^ Р. Толимьери, М. Ан и К. Лу, Алгоритмы дискретного преобразования Фурье и свертки, Springer-Verlag, 2-е изд., 1997.
7. ^ Дональд Э. Кнут, Искусство компьютерного программирования, т. 2: Получисловые алгоритмы, 3-е издание, раздел 4.5.4, стр. 391 (Аддисон – Уэсли, 1998).