| B А | B молчит | B предает |
|---|---|---|
| Остается молчать | -1 -1 | 0 -3 |
| А предает | -3 0 | -2 -2 |
В Дилемма заключенного стандартный пример игры анализировались в теории игр, которая показывает, почему два совершенно рациональные люди не могли бы сотрудничать, даже если кажется, что это в их интересах, чтобы сделать это. Первоначально она была создана Мерриллом Флудом и Мелвином Дрешером во время работы в RAND в 1950 году. Альберт У. Такер формализовал игру с помощью награды за тюремное заключение и назвал ее «дилеммой заключенного», представив ее следующим образом:
Два члена преступной организации арестованы и заключены в тюрьму. Каждый заключенный находится в одиночном заключении, не имея возможности общаться друг с другом. У прокуратуры нет достаточных доказательств, чтобы осудить эту пару по основному обвинению, но у них есть достаточно, чтобы осудить обоих по менее серьезному обвинению. Одновременно прокуратура предлагает каждому заключенному выгодную сделку. Каждому заключенному предоставляется возможность либо предать другого, дав показания о том, что другой совершил преступление, либо сотрудничать с другим, сохраняя молчание. Возможные результаты:
Подразумевается, что у заключенных не будет возможности вознаградить или наказать своего партнера, кроме приговоров к тюремному заключению, которые они получат, и что их решение не повлияет на их репутацию в будущем. Поскольку предательство партнера предлагает большую награду, чем сотрудничество с ним, все чисто рациональные эгоистичные заключенные предадут друг друга, а это означает, что единственный возможный исход для двух чисто рациональных заключенных - это предать друг друга, даже если взаимное сотрудничество принесет больше пользы. награда. На самом деле люди демонстрируют системную предвзятость в отношении кооперативного поведения в этой и подобных играх, несмотря на то, что предсказывают простые модели «рационального» эгоистичного действия. Этот уклон в сторону сотрудничества известен с тех пор, как испытание было впервые проведено в RAND; секретари доверяли друг другу и работали вместе для достижения наилучшего общего результата. Дилемма заключенного стала предметом обширных экспериментальных исследований.
Также существует расширенная «повторная» версия игры. В этой версии классическая игра многократно разыгрывается между одними и теми же заключенными, у которых постоянно есть возможность наказать другого за предыдущие решения. Если игрокам известно, сколько раз игра будет сыграна, то (посредством обратной индукции ) два классически рациональных игрока будут многократно предавать друг друга по тем же причинам, что и вариант с одиночным выстрелом. В игре с бесконечной или неизвестной продолжительностью не существует фиксированной оптимальной стратегии, и были проведены турниры по дилемме заключенного, чтобы соревноваться и проверять алгоритмы для таких случаев.
Игра «Дилемма заключенного» может использоваться в качестве модели для многих ситуаций реального мира, связанных с совместным поведением. При случайном использовании ярлык «дилемма заключенного» может применяться к ситуациям, не строго соответствующим формальным критериям классических или итеративных игр: например, те, в которых два объекта могут получить важные выгоды от сотрудничества или пострадать от его отказа., но им сложно или дорого - не обязательно невозможно - координировать свою деятельность.
Двое заключенных разделены по отдельным комнатам и не могут общаться друг с другом. Обычная игра показана ниже:
| Заключенный B Заключенный А | Заключенный B молчит ( сотрудничает) | Заключенный B предает ( дефекты) |
|---|---|---|
| Заключенный А молчит ( сотрудничает) | Каждый обслуживает 1 год | Заключенный A: 3 года Заключенный B: выходит на свободу |
| Узник А предает ( пороки) | Заключенный A: выходит на свободу Заключенный B: 3 года | Каждый служит 2 года |
Предполагается, что оба заключенных понимают природу игры, не лояльны друг к другу и не будут иметь возможности для возмездия или вознаграждения вне игры. Независимо от того, что решит другой, каждый заключенный получает более высокую награду, предав другого («дезертирство»). Рассуждение включает анализ лучших ответов обоих игроков: B будет либо сотрудничать, либо отступать. Если B будет сотрудничать, A должен уйти, потому что переходить бесплатно лучше, чем служить 1 год. Если B отказывает, A также должен отказываться, потому что служить 2 года лучше, чем обслуживать 3. Так что в любом случае A должен отказаться, поскольку отказ - лучший ответ A, независимо от стратегии B. Параллельное рассуждение покажет, что B должен уйти.
Поскольку отступничество всегда приводит к лучшему выигрышу, чем сотрудничество, независимо от выбора другого игрока, это строго доминирующая стратегия как для А, так и для Б. Взаимный отказ - единственное сильное равновесие по Нэшу в игре (т.е. только хуже, если в одностороннем порядке изменить стратегию). Таким образом, дилемма состоит в том, что взаимное сотрудничество дает лучший результат, чем взаимное отступничество, но не является рациональным результатом, потому что выбор сотрудничества с эгоистической точки зрения иррационален. Таким образом, дилемма заключенного - это игра, в которой равновесие по Нэшу не является эффективным по Парето.
Структуру традиционной дилеммы заключенного можно обобщить, исходя из исходной ситуации с заключенным. Предположим, что два игрока представлены красным и синим цветами и что каждый игрок выбирает либо «сотрудничать» (молчать), либо «отступить» (предать).
Если оба игрока сотрудничают, они оба получают вознаграждение R за сотрудничество. Если оба игрока дефект, они оба получают наказание выигрыша P. Если Синие дефекты в то время как Red сотрудничает, то синий получают соблазн выигрыша Т, в то время как Red получает «неудачник» выигрыш, S. Аналогичным образом, если в то время как синие взаимодействует красные дефекты, а затем Синий получает неудачник выигрыша S, в то время как красный получает соблазн выигрыша Т.
Это можно выразить в нормальной форме :
| красный Синий | Сотрудничать | Дефект |
|---|---|---|
| Сотрудничать | р р | Т S |
| Дефект | S Т | п п |
и чтобы быть игрой-дилеммой заключенного в строгом смысле слова, для выплат должно выполняться следующее условие:
Отношения взятка подразумевает, что взаимное сотрудничество превосходит взаимное предательство, в то время как платежные отношения и предполагают, что отступничество является доминирующей стратегией для обоих агентов.
«Игра с пожертвованиями» - это форма дилеммы заключенного, в которой сотрудничество соответствует предложению другому игроку выгоды b за личные расходы c при b gt; c. Отклонение означает ничего не предлагать. Таким образом, матрица выплат имеет вид
| красный Синий | Сотрудничать | Дефект |
|---|---|---|
| Сотрудничать | б - в б - в | б - с |
| Дефект | - с б | 0 0 |
Обратите внимание на то (т.е.), которое квалифицирует игру с пожертвованиями как повторяющуюся игру (см. Следующий раздел).
Игра в пожертвования может применяться к рынкам. Предположим, X выращивает апельсины, Y выращивает яблоки. Предельная полезность яблока к оранжево-ростовому X является Ь, что выше предельной полезности ( гр) апельсина, так как Х имеет избыток апельсинов и без каких - либо яблок. Точно так же для производителя яблок Y предельная полезность апельсина равна b, а предельная полезность яблока - c. Если X и Y заключают договор об обмене яблоком и апельсином, и каждый выполняет свою часть сделки, то каждый получает выплату b - c. Если один «дефект» и не доставит, как обещал, перебежчик получит выплату b, а кооператор проиграет c. Если оба ошибаются, то ни один из них ничего не приобретает и не теряет.
Если два игрока играют в дилемму заключенного более одного раза подряд и помнят предыдущие действия своего противника и соответственно меняют свою стратегию, игра называется повторной дилеммой заключенного.
В дополнение к общей форме, приведенной выше, итеративная версия также требует этого, чтобы предотвратить чередование сотрудничества и отступничества, дающее большую награду, чем взаимное сотрудничество.
Повторяющаяся игра «дилемма заключенного» является фундаментальной для некоторых теорий человеческого сотрудничества и доверия. Исходя из предположения, что игра может моделировать транзакции между двумя людьми, требующими доверия, совместное поведение популяций может быть смоделировано многопользовательской повторяющейся версией игры. Следовательно, на протяжении многих лет он очаровывал многих ученых. В 1975 году Грофман и Пул подсчитали, что количество научных статей, посвященных этой теме, превысило 2000. Повторяющаяся дилемма заключенного также упоминается как « игра мир-война ».
Если игра проводится ровно N раз, и оба игрока знают об этом, то оптимальным вариантом будет отказать во всех раундах. Единственное возможное равновесие по Нэшу - всегда отклоняться. Доказательство носит индуктивный характер : с таким же успехом можно отступить на последнем ходу, так как у оппонента не будет шанса нанести ответный удар. Следовательно, оба дезертируют в последний ход. Таким образом, игрок может также дезертировать на предпоследнем ходу, так как противник отступит на последнем, что бы ни было сделано, и так далее. То же самое применимо, если продолжительность игры неизвестна, но имеет известный верхний предел.
В отличие от стандартной дилеммы заключенного, в повторяющейся дилемме заключенного стратегия отступничества противоречит интуиции и плохо предсказывает поведение игроков-людей. Однако в рамках стандартной экономической теории это единственно правильный ответ. Сверхрациональный стратегия в дилемме Итерированного заключенной с фиксированным N является сотрудничество против сверхрационального противника, и в пределе больших N, экспериментальные результаты по стратегии согласуются с сверхрациональными версиями, а не теоретико-игровой рациональным.
Чтобы возникло сотрудничество между теоретически рациональными игроками, игрокам должно быть неизвестно общее количество раундов N. В этом случае «всегда дефект» может больше не быть строго доминирующей стратегией, а только равновесием по Нэшу. Среди результатов, показанных Робертом Ауманом в статье 1959 года, рациональные игроки, неоднократно взаимодействующие в течение бесконечно длинных игр, могут поддерживать совместный исход.
Согласно экспериментальному исследованию 2019 года, опубликованному в American Economic Review, в котором проверялось, какие стратегии реальные субъекты использовали в повторяющихся ситуациях дилеммы заключенных при идеальном мониторинге, большинство выбранных стратегий всегда были дефектными, « око за око» и мрачным спусковым крючком. Выбор стратегии зависел от параметров игры.
Интерес к повторной дилемме заключенного (IPD) пробудил Роберт Аксельрод в его книге «Эволюция сотрудничества» (1984). В нем он сообщает о организованном им турнире по дилемме заключенного N-го шага (с фиксированным N), в котором участники должны снова и снова выбирать свою общую стратегию и помнить о своих предыдущих встречах. Аксельрод пригласил академических коллег со всего мира разработать компьютерные стратегии для участия в турнирах IPD. Программы, которые были введены, сильно различались по алгоритмической сложности, начальной враждебности, способности прощать и так далее.
Аксельрод обнаружил, что, когда эти встречи повторялись в течение длительного периода времени со многими игроками, у каждого из которых была своя стратегия, жадные стратегии, как правило, очень плохо работали в долгосрочной перспективе, в то время как более альтруистические стратегии работали лучше, если судить по чисто личным интересам. Он использовал это, чтобы показать возможный механизм эволюции альтруистического поведения из механизмов, которые изначально были чисто эгоистичными, путем естественного отбора.
Выигрышная детерминированная стратегия была «око за око», которую Анатолий Рапопорт разработал и принял участие в турнире. Это была самая простая программа, содержащая всего четыре строки BASIC, и она выиграла конкурс. Стратегия состоит в том, чтобы просто сотрудничать на первой итерации игры; после этого игрок делает то же, что и его противник на предыдущем ходу. В зависимости от ситуации немного лучшей стратегией может быть «око за око с прощением». Когда противник отступает, на следующем ходу игрок иногда все равно сотрудничает с небольшой вероятностью (около 1–5%). Это позволяет время от времени выздоравливать, чтобы не попасть в ловушку цикла дезертирства. Точная вероятность зависит от состава противников.
Анализируя стратегии, набравшие наибольшее количество очков, Аксельрод сформулировал несколько условий, необходимых для успеха стратегии.
Оптимальная стратегия (максимизация очков) для одноразовой игры PD - это просто отступничество; как объяснялось выше, это верно независимо от состава оппонентов. Однако в игре с итеративным PD оптимальная стратегия зависит от стратегий вероятных противников и от того, как они будут реагировать на отступничество и сотрудничество. Например, представьте себе популяцию, в которой все каждый раз сбегают, за исключением одного человека, который следует стратегии «око за око». Этот человек находится в небольшом невыгодном положении из-за проигрыша на первом ходу. В такой популяции оптимальная стратегия для этого человека - каждый раз дезертировать. В популяции с определенным процентом постоянных перебежчиков и остальными игроками, играющими за око, оптимальная стратегия для отдельного человека зависит от процента и от продолжительности игры.
В стратегии под названием «Павлов» « выиграть - остаться, проиграть - переключиться», столкнувшись с отказом от сотрудничества, игрок меняет стратегию на следующем ходу. В определенных обстоятельствах Павлов превосходит все другие стратегии, отдавая предпочтение товарищам по игре, используя аналогичную стратегию.
Получение оптимальной стратегии обычно осуществляется двумя способами:
Хотя «око за око» считается самой надежной базовой стратегией, команда из Саутгемптонского университета в Англии представила новую стратегию на повторном соревновании «дилемма заключенного», посвященном 20-летию, которое оказалось более успешным, чем «око за око». Эта стратегия основывалась на сговоре между программами для достижения максимального количества баллов за одну программу. Университет представил на конкурс 60 программ, которые были разработаны так, чтобы узнавать друг друга через серию из пяти-десяти ходов на старте. Как только это признание будет сделано, одна программа всегда будет сотрудничать, а другая всегда будет давать сбой, обеспечивая максимальное количество баллов для перебежчика. Если бы программа понимала, что играет игрок, не являющийся игроком Саутгемптона, она бы постоянно нарушала правила, пытаясь минимизировать счет конкурирующей программы. В результате результаты турнира 2004 года «Дилемма заключенных» показывают, что стратегии Саутгемптонского университета занимают первые три места, несмотря на меньшее количество побед и намного больше поражений, чем стратегия GRIM. (В турнире PD цель игры не в том, чтобы «выиграть» матчи - этого легко добиться частым дезертирством). Кроме того, даже без неявного сговора между стратегиями программного обеспечения (используемого командой Саутгемптона) «око за око» не всегда является абсолютным победителем любого данного турнира; точнее было бы сказать, что его долгосрочные результаты по серии турниров превосходят его соперников. (В любом случае данная стратегия может быть немного лучше приспособлена к соревнованиям, чем «око за око», но «око за око» более надежна). То же самое относится к варианту «око за око» с вариантом прощения и другим оптимальным стратегиям: в любой конкретный день они могут не «выиграть» против определенного набора контр-стратегий. Альтернативный способ выразить это - использование дарвиновского ESS- моделирования. В такой симуляции принцип «око за око» почти всегда будет преобладать, хотя неприятные стратегии будут приходить и уходить из популяции, потому что популяция «око за око» проницаема для хороших стратегий без ответных действий, которые, в свою очередь, становятся легкой добычей для противных. стратегии. Ричард Докинз показал, что здесь никакое статическое сочетание стратегий не формирует устойчивого равновесия, и система всегда будет колебаться между границами. В итоге эта стратегия заняла три верхних позиции в конкурсе, а также несколько позиций в нижней части.
Стратегия Саутгемптона использует тот факт, что в этом конкретном соревновании было разрешено несколько участников и что производительность команды измерялась показателем игрока, набравшего наибольшее количество очков (это означает, что использование самоотверженных игроков было формой минимизации ). В соревновании, где у вас есть контроль только над одним игроком, «око за око», безусловно, лучшая стратегия. Из-за этого нового правила это соревнование также имеет небольшое теоретическое значение при анализе стратегий одного агента по сравнению с основополагающим турниром Аксельрода. Тем не менее, это послужило основой для анализа того, как достичь кооперативных стратегий в многоагентных средах, особенно в присутствии шума. Фактически, задолго до того, как был проведен этот турнир по новым правилам, Докинз в своей книге «Эгоистичный ген» указал на возможность выигрыша таких стратегий, если бы было разрешено несколько входов, но он заметил, что, скорее всего, Аксельрод не позволил бы их, если бы они был отправлен. Он также основан на обходе правил в отношении дилеммы заключенного в том смысле, что между двумя игроками не разрешается общаться, что, возможно, сделали программы Саутгемптона с их открывающим «танцем из десяти движений», чтобы узнавать друг друга; это только подтверждает, насколько ценным может быть общение для изменения баланса в игре.
В стохастической повторяющейся игре «дилемма заключенного» стратегии задаются в терминах «вероятностей сотрудничества». В столкновении между игроком в X и игрока Y, X Стратегия «ы определяется набором вероятностей P взаимодействующих с Y. P является функцией результатов их предыдущих встреч или некоторого их подмножества. Если P является функцией только их последних n встреч, это называется стратегией «памяти n». Затем стратегия памяти-1 определяется четырьмя вероятностями сотрудничества:, где - вероятность того, что X будет сотрудничать в настоящем столкновении, учитывая, что предыдущее столкновение характеризовалось (ab). Например, если в предыдущем столкновении X сотрудничал, а Y дезертировал, то это вероятность того, что X будет сотрудничать в нынешнем столкновении. Если каждая из вероятностей равна 1 или 0, стратегия называется детерминированной. Примером детерминированной стратегии является стратегия «око за око», записанная как P = {1,0,1,0}, в которой X отвечает так же, как Y в предыдущем столкновении. Другой вариант - это стратегия « выиграть - остаться, проиграть - переключиться», записанная как P = {1,0,0,1}, в которой X отвечает, как и в предыдущем столкновении, если это была «победа» (т.е. cc или dc), но изменения стратегия, если это была потеря (например, cd или dd). Было показано, что для любой стратегии memory-n существует соответствующая стратегия memory-1, которая дает те же статистические результаты, поэтому необходимо рассматривать только стратегии memory-1.
Если мы определим P как вышеупомянутый 4-элементный вектор стратегии X и как 4-элементный вектор стратегии Y, матрица перехода M может быть определена для X, ij- я запись которого представляет собой вероятность того, что результат конкретной встречи между X и Y будет j, учитывая, что предыдущая встреча была i, где i и j - один из четырех индексов результата: cc, cd, dc или dd. Например, с точки зрения X, вероятность того, что исход данной встречи будет cd, при условии, что предыдущая встреча была cd, равна. (Индексы для Q взяты с точки зрения Y: результат cd для X является результатом dc для Y.) В соответствии с этими определениями повторяющаяся дилемма заключенного квалифицируется как случайный процесс, а M - это стохастическая матрица, допускающая все теория случайных процессов.
Одним из результатов стохастической теории является то, что существует стационарный вектор v для матрицы M такой, что. Без ограничения общности можно указать, что v нормализована так, что сумма его четырех компонентов равна единице. IJ й записи в даст вероятность того, что исход встречи между X и Y будет J, учитывая, что столкновение п шаги предыдущего это я. В пределе, когда n приближается к бесконечности, M будет сходиться к матрице с фиксированными значениями, давая долгосрочные вероятности встречи, производящей j, которая не будет зависеть от i. Другими словами, строки будут идентичными, что даст долгосрочные равновесные вероятности результата повторяющейся дилеммы заключенных без необходимости явно оценивать большое количество взаимодействий. Можно видеть, что v является стационарным вектором для и, в частности, так что каждая строка будет равна v. Таким образом, стационарный вектор определяет равновесный исход вероятность для X. Определяя и в качестве векторов краткосрочных выплат для результатов {cc, cd, dc, dd} ( с точки зрения X), равновесные выплаты для X и Y теперь могут быть указаны как и, что позволяет использовать две стратегии P и Q, чтобы сравнить их долгосрочную отдачу.
 Взаимосвязь между стратегиями нулевого детерминанта (ZD), сотрудничества и отказа в повторяющейся дилемме заключенного (IPD), проиллюстрированная на диаграмме Венна. Стратегии сотрудничества всегда взаимодействуют с другими стратегиями сотрудничества, а стратегии отклонения всегда противоречат другим стратегиям отклонения. Оба содержат подмножества стратегий, которые устойчивы при строгом отборе, что означает, что никакая другая стратегия памяти-1 не выбрана для вторжения в такие стратегии, когда они являются резидентными в популяции. Только взаимодействующие стратегии содержат подмножество, которое всегда является устойчивым, что означает, что никакая другая стратегия памяти-1 не выбрана для вторжения и замены таких стратегий как при сильном, так и при слабом отборе. Пересечение между ZD и хорошими стратегиями сотрудничества - это набор щедрых ZD-стратегий. Стратегии вымогательства - это пересечение ZD и ненадежных дефектных стратегий. «Око за око» лежит на пересечении стратегий сотрудничества, отказа и ZD.
Взаимосвязь между стратегиями нулевого детерминанта (ZD), сотрудничества и отказа в повторяющейся дилемме заключенного (IPD), проиллюстрированная на диаграмме Венна. Стратегии сотрудничества всегда взаимодействуют с другими стратегиями сотрудничества, а стратегии отклонения всегда противоречат другим стратегиям отклонения. Оба содержат подмножества стратегий, которые устойчивы при строгом отборе, что означает, что никакая другая стратегия памяти-1 не выбрана для вторжения в такие стратегии, когда они являются резидентными в популяции. Только взаимодействующие стратегии содержат подмножество, которое всегда является устойчивым, что означает, что никакая другая стратегия памяти-1 не выбрана для вторжения и замены таких стратегий как при сильном, так и при слабом отборе. Пересечение между ZD и хорошими стратегиями сотрудничества - это набор щедрых ZD-стратегий. Стратегии вымогательства - это пересечение ZD и ненадежных дефектных стратегий. «Око за око» лежит на пересечении стратегий сотрудничества, отказа и ZD. В 2012 году Уильям Х. Пресс и Фримен Дайсон опубликовали новый класс стратегий для решения стохастической повторяющейся дилеммы заключенного, названный стратегиями «нулевого детерминанта» (ZD). Долгосрочные выигрыши от встреч между X и Y могут быть выражены как определитель матрицы, которая является функцией двух стратегий и векторов краткосрочных выигрышей: и, которые не включают стационарный вектор v. Поскольку детерминантная функция линейна по f, отсюда следует, что (где U = {1,1,1,1}). Любые стратегии, для которых по определению является ZD-стратегией, и долгосрочные выплаты подчиняются этому соотношению.
Око за око - это стратегия ZD, которая «справедлива» в том смысле, что не получает преимущества над другим игроком. Тем не менее, пространство ZD также содержит стратегии, которые в случае двух игроков могут позволить одному игроку в одностороннем порядке установить счет другого игрока или, альтернативно, заставить эволюционирующего игрока достичь выигрыша на несколько процентов ниже, чем его собственный. Вымогаемый игрок может дезертировать, но тем самым причинит себе вред, получив меньший выигрыш. Таким образом, решения о вымогательстве превращают повторяющуюся дилемму заключенного в своего рода игру в ультиматум. В частности, X может выбрать стратегию, для которой, в одностороннем порядке устанавливая определенное значение в определенном диапазоне значений, независимо от стратегии Y, предлагая X возможность «вымогать» игрока Y (и наоборот). (Оказывается, что если X пытается установить определенное значение, диапазон возможностей намного меньше и состоит только из полного сотрудничества или полного отступничества.)
Расширением IPD является эволюционный стохастический IPD, в котором относительное количество конкретных стратегий может изменяться, при этом более успешные стратегии относительно увеличиваются. Этот процесс может быть осуществлен за счет того, что менее успешные игроки имитируют более успешные стратегии, или путем исключения менее успешных игроков из игры при умножении более успешных. Было показано, что несправедливые стратегии ZD не являются эволюционно устойчивыми. Ключевая интуиция состоит в том, что эволюционно стабильная стратегия должна не только иметь возможность вторгаться в другую популяцию (что могут делать стратегии вымогательства ZD), но также должна хорошо работать против других игроков того же типа (которые игроки-вымогатели ZD делают плохо, потому что они уменьшают каждый чужой излишек).
Теория и моделирование подтверждают, что за пределами критического размера популяции вымогательство ZD проигрывает в эволюционной конкуренции с более кооперативными стратегиями, и в результате средний выигрыш в популяции увеличивается, когда популяция становится больше. Кроме того, в некоторых случаях вымогатели могут даже стимулировать сотрудничество, помогая вырваться из противостояния между единообразными перебежчиками и агентами, которые побеждают, а потом проигрывают.
В то время как стратегии вымогательства ZD нестабильны в больших популяциях, другой класс ZD, называемый «щедрыми» стратегиями, является одновременно стабильным и надежным. Фактически, когда популяция не слишком мала, эти стратегии могут вытеснить любую другую стратегию ZD и даже хорошо работать с широким набором общих стратегий для повторяющейся дилеммы заключенного, в том числе «победить - остаться, проиграть - переключиться». Это было специально доказано Александром Стюартом и Джошуа Плоткиным в 2013 году для игры с пожертвованиями. Щедрые стратегии будут взаимодействовать с другими игроками, которые сотрудничают, и перед лицом отступничества щедрый игрок теряет больше полезности, чем его соперник. Щедрые стратегии - это пересечение стратегий ZD и так называемых «хороших» стратегий, которые были определены Akin (2013) как те, за которые игрок реагирует на прошлое взаимное сотрудничество будущим сотрудничеством и делит ожидаемые выплаты поровну, если он получает по крайней мере ожидаемая отдача кооператива. Среди хороших стратегий подмножество щедрых (ZD) хорошо работает, когда популяция не слишком мала. Если популяция очень мала, преобладают стратегии дезертирства.
Большая часть работ по повторной дилемме заключенного сосредоточена на дискретном случае, в котором игроки либо сотрудничают, либо отступают, потому что эту модель относительно просто анализировать. Тем не менее, некоторые исследователи рассмотрели модели постоянно повторяющейся дилеммы заключенного, в которой игроки могут вносить переменный вклад в пользу другого игрока. Ле и Бойд обнаружили, что в таких ситуациях развивать сотрудничество намного труднее, чем в дискретной повторяющейся дилемме заключенного. Основная интуиция для этого результата проста: в постоянной дилемме заключенного, если популяция начинается в некооперативном равновесии, игроки, которые лишь незначительно более склонны к сотрудничеству, чем не сотрудничающие, получают небольшую выгоду от сортировки друг с другом. Напротив, в дилемме дискретного заключенного, кооператоры «око за око» получают большую выгоду от сортировки друг с другом в некооперативном равновесии по сравнению с теми, кто не сотрудничает. Поскольку природа, вероятно, предлагает больше возможностей для разнообразного сотрудничества, чем строгую дихотомию сотрудничества или отступничества, постоянная дилемма заключенного может помочь объяснить, почему реальные примеры сотрудничества, похожего на око за око, чрезвычайно редки в природе (например, Хаммерштейн), хотя око за око кажется надежным в теоретических моделях.
Кажется, что игроки не могут координировать взаимное сотрудничество, поэтому часто попадают в низшую, но стабильную стратегию отступничества. Таким образом, повторяющиеся раунды способствуют развитию стабильных стратегий. Повторяющиеся раунды часто приводят к новым стратегиям, которые имеют последствия для сложного социального взаимодействия. Одна из таких стратегий - беспроигрышный вариант - оставаться проигрышным. Эта стратегия превосходит простую стратегию «око за око» - то есть, если вы можете избежать мошенничества, повторите это поведение, однако, если вас поймают, переключитесь.
Единственная проблема этой стратегии «око за око» состоит в том, что они уязвимы для ошибки сигнала. Проблема возникает, когда один человек обманывает в отместку, но другой интерпретирует это как обман. В результате второй человек теперь обманывает, а затем начинает цепную реакцию обмана.
Обстановка заключенного может показаться надуманной, но на самом деле существует множество примеров человеческого взаимодействия, а также взаимодействия в природе, которые имеют одинаковую матрицу выигрыша. Таким образом, дилемма заключенного представляет интерес для социальных наук, таких как экономика, политика и социология, а также для биологических наук, таких как этология и эволюционная биология. Многие естественные процессы были абстрагированы в модели, в которых живые существа участвуют в бесконечных играх с дилеммой заключенного. Такая широкая применимость PD придает игре существенное значение.
В экологических исследованиях ЧР проявляется в кризисных ситуациях, таких как глобальное изменение климата. Утверждается, что от стабильного климата выиграют все страны, но ни одна страна в отдельности часто не решается сдерживать выбросы CO. 2 выбросы. Непосредственная выгода для любой страны от сохранения текущего поведения ошибочно воспринимается как большая, чем предполагаемая конечная выгода для этой страны, если поведение всех стран изменится, что объясняет тупик, связанный с изменением климата в 2007 году.
Важное различие между политикой в области изменения климата и дилеммой заключенного - неопределенность; степень и скорость, с которой загрязнение может изменить климат, неизвестны. Таким образом, дилемма, стоящая перед правительством, отличается от дилеммы заключенного тем, что отдача от сотрудничества неизвестна. Это различие предполагает, что государства будут сотрудничать в гораздо меньшей степени, чем в реальной повторяющейся дилемме заключенного, так что вероятность избежать возможной климатической катастрофы намного меньше, чем предполагает теоретико-игровой анализ ситуации с использованием реальной повторяющейся дилеммы заключенного.
Осанг и Нанди (2003) предоставляют теоретическое объяснение с доказательствами беспроигрышной ситуации, основанной на регулировании, в соответствии с гипотезой Майкла Портера, в которой государственное регулирование конкурирующих фирм является существенным.
Кооперативное поведение многих животных можно рассматривать как пример дилеммы заключенного. Часто животные вступают в долгосрочные партнерские отношения, что более конкретно можно смоделировать как повторяющуюся дилемму заключенного. Например, гуппи совместно осматривают хищников группами и, как считается, наказывают инспекторов, не сотрудничающих с ними.
Летучие мыши-вампиры - социальные животные, которые участвуют во взаимном обмене пищей. Объяснить такое поведение можно, применяя выплаты из дилеммы заключенного:
В наркомании исследований / поведенческой экономике, Джордж Эйнсли указует, что наркомания может быть брошена как межвременные проблемы PD между настоящим и будущим самих наркомана. В этом случае, дезертировать средства рецидивирующий, и легко видеть, что не дезертировать и сегодня, и в будущем, безусловно, лучший результат. Случай, когда человек воздерживается сегодня, но возвращается в будущем, является наихудшим исходом - в некотором смысле дисциплина и самопожертвование, связанные с воздержанием сегодня, были «потрачены впустую», потому что будущий рецидив означает, что наркоман вернулся туда, откуда они начали, и будет приходится начинать заново (что довольно деморализует и затрудняет начало работы). Рецидив сегодня и завтра - это немного «лучший» результат, потому что, хотя наркоман все еще остается зависимым, он не прилагает усилий, чтобы попытаться остановиться. Последний случай, когда человек проявляет аддиктивное поведение сегодня, воздерживаясь от «завтра», будет знаком каждому, кто боролся с зависимостью. Проблема здесь в том, что (как и в других ВД) существует очевидная выгода от отказа «сегодня», но завтра вы столкнетесь с тем же самым ВД, и тогда будет присутствовать такая же очевидная выгода, что в конечном итоге приведет к бесконечной череде дезертирства.
Джон Готтман в своем исследовании, описанном в «Науке о доверии», определяет хорошие отношения как отношения, в которых партнеры знают, что они не должны входить в (D, D) ячейку или, по крайней мере, не застревать там динамически в петле. В когнитивной нейробиологии быстрая передача сигналов в мозг, связанная с обработкой различных раундов, может указывать на выбор в следующем раунде. Результаты взаимного сотрудничества влекут за собой изменения активности мозга, которые позволяют прогнозировать, насколько быстро человек будет сотрудничать в натуральном выражении при следующей возможности; эта деятельность может быть связана с основными гомеостатическими и мотивационными процессами, возможно, увеличивая вероятность кратчайшего пути к ячейке (C, C) игры.
Дилемма заключенного получила название кишечной палочки социальной психологии, и она широко использовалась для исследования различных тем, таких как олигополистическая конкуренция и коллективные действия для создания коллективного блага.
Рекламу иногда приводят как реальный пример дилеммы заключенного. Когда реклама сигарет была законной в Соединенных Штатах, конкурирующие производители сигарет должны были решать, сколько денег потратить на рекламу. Эффективность рекламы фирмы A частично определялась рекламой, проводимой фирмой B. Аналогичным образом, прибыль, полученная от рекламы для фирмы B, зависит от рекламы, проводимой фирмой A. Если и фирма A, и фирма B решили размещать рекламу в течение заданного периода времени. периода, то реклама одной фирмы отрицает рекламу другой, выручка остается неизменной, а расходы увеличиваются из-за стоимости рекламы. Обе фирмы выиграют от сокращения рекламы. Однако, если фирма B решит не рекламировать, фирма A может получить большую выгоду от рекламы. Тем не менее, оптимальный объем рекламы одной фирмы зависит от того, сколько рекламы берет на себя другая. Поскольку лучшая стратегия зависит от того, что выберет другая фирма, доминирующей стратегии не существует, что несколько отличается от дилеммы заключенного. Однако результат схож: обеим фирмам было бы лучше, если бы они рекламировали меньше, чем в состоянии равновесия. Иногда в деловых ситуациях проявляется кооперативное поведение. Например, производители сигарет одобрили принятие законов, запрещающих рекламу сигарет, понимая, что это снизит затраты и увеличит прибыль во всей отрасли. Этот анализ, вероятно, будет уместен во многих других бизнес-ситуациях, связанных с рекламой.
Без обязательных соглашений члены картеля также оказываются вовлеченными в дилемму заключенного (многопользовательской). «Сотрудничество» обычно означает поддержание цен на заранее согласованном минимальном уровне. «Отклонение от ответственности» означает продажу ниже этого минимального уровня, мгновенно отнимая бизнес (и прибыль) у других членов картеля. Антимонопольные органы хотят, чтобы потенциальные участники картеля взаимно отступали, обеспечивая потребителям максимально низкие цены.
Допинг в спорте приводился как пример дилеммы заключенного.
Два соревнующихся спортсмена имеют возможность использовать запрещенные и / или опасные препараты для повышения своих результатов. Если ни один из спортсменов не принимает препарат, ни один из них не получает преимущества. Если это сделает только один, то этот спортсмен получает значительное преимущество перед своим конкурентом, уменьшенное за счет юридических и / или медицинских опасностей, связанных с приемом препарата. Однако, если оба спортсмена принимают препарат, преимущества отменяются, и остаются только опасности, что ставит их обоих в худшее положение, чем если бы ни один из них не принимал допинг.
В международной политической теории дилемма заключенного часто используется для демонстрации последовательности стратегического реализма, согласно которому в международных отношениях все государства (независимо от их внутренней политики или декларируемой идеологии) будут действовать в своих рациональных личных интересах в условиях международной анархии.. Классический пример - гонка вооружений, подобная холодной войне и подобным конфликтам. Во время холодной войны у противостоящих альянсов НАТО и Варшавского договора был выбор: вооружиться или разоружиться. С точки зрения каждой стороны, разоружение, пока их противник продолжал вооружаться, привело бы к военному проигрышу и возможному уничтожению. И наоборот, вооружение, в то время как их противник разоружен, привело бы к превосходству. Если бы обе стороны предпочли вооружиться, ни одна из них не могла позволить себе атаковать другую, но обе понесли высокие затраты на создание и поддержание ядерного арсенала. Если бы обе стороны предпочли разоружиться, войны можно было бы избежать и не было бы никаких затрат.
Хотя «лучший» общий результат - разоружение для обеих сторон, рациональным курсом для обеих сторон является вооружение, и именно это действительно произошло. Обе стороны вложили огромные ресурсы в военные исследования и вооружения в войне на истощение в течение следующих тридцати лет, пока Советский Союз не смог противостоять экономическим издержкам. Та же самая логика может быть применена в любом подобном сценарии, будь то экономическая или технологическая конкуренция между суверенными государствами.
Многие дилеммы реальной жизни связаны с несколькими игроками. Несмотря на метафорическую формулировку, трагедия Хардина с общим достоянием может рассматриваться как пример многопользовательского обобщения PD: каждый сельский житель делает выбор в пользу личной выгоды или сдержанности. Коллективная награда за единодушное (или даже частое) дезертирство - очень низкие выплаты (представляющие собой уничтожение «общего»). Дилемма общего пользования, с которой может столкнуться большинство людей, - это мытье посуды в общем доме. Не мыть посуду, человек может сэкономить свое время, но если это поведение будет принято каждым жителем, коллективные издержки - это не чистые тарелки для кого-либо.
Общественное достояние не всегда эксплуатируется: Уильям Паундстон в книге о дилемме заключенного описывает ситуацию в Новой Зеландии, где коробки с газетами остаются незапертыми. Люди могут взять бумагу, не заплатив ( дефект), но очень немногие делают это, чувствуя, что если они не заплатят, то и другие тоже не будут, разрушая систему. Последующее исследование Элинор Остром, лауреата Нобелевской премии по экономическим наукам 2009 года, выдвинуло гипотезу о том, что трагедия общин слишком упрощена, а отрицательный результат зависит от внешних влияний. Не усложняя давление, группы общаются и управляют обществом между собой для их взаимной выгоды, обеспечивая соблюдение социальных норм для сохранения ресурса и достижения максимальной пользы для группы, что является примером достижения наилучшего результата для PD.
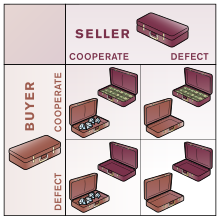 Дилемма заключенного как обмен портфелем
Дилемма заключенного как обмен портфелем Дуглас Хофштадтер однажды предположил, что люди часто находят такие проблемы, как проблема частичного разряда, более понятной, когда она проиллюстрирована в форме простой игры или компромисса. Одним из нескольких примеров, которые он использовал, был «закрытый обмен сумок»:
Два человека встречаются и обмениваются закрытыми мешками, при этом понимая, что в одном из них лежат деньги, а в другом - покупка. Либо игрок может решить выполнить сделку, положив в свою сумку то, что он или она согласился, либо он или она может отказаться, передав пустую сумку.
Друг или враг? это игровое шоу, которое транслировалось с 2002 по 2003 год на Game Show Network в США. Это пример игры-дилеммы заключенного, проверенной на реальных людях, но в искусственной обстановке. На игровом шоу соревнуются три пары людей. Когда пара выбывает, они играют в игру, похожую на дилемму заключенного, чтобы определить, как делятся выигрыши. Если они оба сотрудничают (Друг), они делят выигрыш 50–50. Если один сотрудничает, а другой отказывает (Враг), перебежчик получает весь выигрыш, а кооператор ничего не получает. Если оба неисправны, оба уходят ни с чем. Обратите внимание на то, что матрица вознаграждения немного отличается от стандартной, приведенной выше, поскольку вознаграждения в случаях «оба дефекта» и «сотрудничать, пока оппонент ошибается» идентичны. Это делает случай «оба дефекта» слабым равновесием по сравнению со строгим равновесием в стандартной дилемме заключенного. Если участник знает, что его противник проголосует «за врага», то его собственный выбор не влияет на его собственный выигрыш. В определенном смысле « Друг или враг » использует модель вознаграждения между дилеммой заключенного и игрой «Курица».
Матрица вознаграждений:
| Пара 2 Пара 1 | «Друг» (сотрудничать) | «Враг» (дефект) |
|---|---|---|
| «Друг» (сотрудничать) | 1 1 | 2 0 |
| «Враг» (дефект) | 0 2 | 0 0 |
Эта матрица выплат также использовалась в британских телевизионных программах Trust Me, Shafted, The Bank Job и Golden Balls и в американских игровых шоу Take It All, а также для пары победителей в реалити-шоу шоу Bachelor Pad и Love Остров. Игровые данные из серии Golden Balls были проанализированы группой экономистов, которые обнаружили, что сотрудничество было «на удивление высоким» для денежных сумм, которые могли бы иметь важное значение в реальном мире, но были сравнительно низкими в контексте игры.
Исследователи из Лозаннского и Эдинбургского университетов предположили, что «Итерационная игра в снежный занос» может более точно отражать реальные социальные ситуации. Хотя эта модель на самом деле представляет собой игру про цыплят, здесь она будет описана. В этой модели риск эксплуатации через дезертирство ниже, и люди всегда выигрывают от совместного выбора. В игре «Сугроб» изображены два водителя, застрявшие по разные стороны сугроба, и каждому из них предоставляется возможность расчистить лопатой снег, чтобы расчистить путь, или остаться в машине. Самый высокий выигрыш для игрока - это предоставление противнику возможности самостоятельно очистить весь снег, но противник все равно номинально награждается за свою работу.
Это может лучше отражать сценарии реального мира. Исследователи приводят пример двух ученых, сотрудничающих над отчетом, и оба выиграют, если другой будет работать усерднее. «Но когда ваш соавтор не выполняет никакой работы, вам, вероятно, лучше делать всю работу самому. У вас все равно будет завершенный проект».
|
|
В координационных играх игроки должны координировать свои стратегии для достижения хорошего результата. Примером могут служить две машины, которые резко встречаются в метель; каждый должен выбрать, свернуть влево или вправо. Если оба повернут налево или оба повернут направо, машины не столкнутся. Соглашение о местном левостороннем и правостороннем движении помогает координировать их действия.
Симметричные координационные игры включают " Охоту на оленя" и " Баха или Стравинского".
Более общий набор игр асимметричен. Как и в случае с дилеммой заключенного, лучший выход - это сотрудничество, и есть мотивы для отступничества. Однако, в отличие от симметричной дилеммы заключенного, один игрок может больше терять и / или больше приобретать, чем другой. Некоторые такие игры были описаны как дилемма заключенного, в которой у одного заключенного есть алиби, отсюда и термин «игра алиби».
В экспериментах игроки, получающие неравные выплаты в повторяющихся играх, могут стремиться максимизировать прибыль, но только при условии, что оба игрока получают равные выплаты; это может привести к стратегии стабильного равновесия, при которой проигравший игрок отказывается от всех X игр, в то время как другой всегда сотрудничает. Такое поведение может зависеть от социальных норм эксперимента в отношении справедливости.
Было создано несколько программных пакетов для моделирования дилемм заключенного и проведения турниров, некоторые из которых имеют доступный исходный код.
Ханну Раджаниеми положил начало своей трилогии «Квантовый вор » в «тюрьме дилеммы». Основная тема сериала описывается как «неадекватность бинарной вселенной», а главный антагонист - персонаж по имени Все-Перебежчик. Раджаниеми особенно интересен как художник, занимающийся этим предметом, поскольку он математик, получивший образование в Кембридже, и имеет докторскую степень в области математической физики - взаимозаменяемость материи и информации - главная особенность книг, происходящих в "пост-сингулярности". " будущее. Первая книга этой серии была опубликована в 2010 году, а два продолжения - «Фрактальный принц» и «Причинный ангел» - в 2012 и 2014 годах соответственно.
Игра, созданная по образцу (повторной) дилеммы заключенного, является центральным элементом видеоигры 2012 года Zero Escape: Virtue's Last Reward и второстепенной частью ее сиквела 2016 года Zero Escape: Zero Time Dilemma.
В «Таинственном обществе Бенедикта и дилемме заключенного » Трентона Ли Стюарта главные герои начинают с игры в одну из версий игры и в целом сбегают из «тюрьмы». Позже они становятся настоящими пленниками и снова сбегают.
В поддуге «Зона приключений : равновесие» во время игры «Страдания» игровые персонажи дважды сталкиваются с дилеммой заключенного за время их пребывания в владениях двух личей: один раз сотрудничают, а другой - дезертируют.
В 8 - й роман от автора Джеймса С. А. Corey аурой Тиамат, Уинстон Дуарте объясняет заключенные дилемму к его 14-летней дочери, Тереза, чтобы обучать ее в стратегическом мышлении.
Пример дилеммы заключенного показан в фильме 2008 года «Темный рыцарь», в котором Джокер устанавливает два парома, один из которых содержит заключенных, а другой - гражданских лиц. В конце концов, обе стороны решают не взрывать бомбу.