Целочисленная факторизация

редактировать

Разложение целого числа в продукт

Нерешенная проблема в информатике :. Можно ли решить целочисленную факторизацию за полиномиальное время на классический компьютер? (больше нерешенных проблем в информатике)

В теории чисел, целочисленная факторизация - это разложение составного числа на продукт меньших целых чисел. Если эти множители дополнительно ограничиваются простыми числами, процесс называется простой факторизацией .

. Когда числа достаточно большие, неэффективные, неквантовые целочисленный факторизация алгоритм известен. В 2019 году Фабрис Будо, Пьерк Годри, Аврора Гильевич, Надя Хенингер, Эммануэль Томе и Пол Циммерманн разложили на множители 240-значное число (RSA-240 ), используя примерно 900 основных лет вычислительной мощности. Исследователи подсчитали, что 1024-битный модуль RSA займет примерно в 500 раз больше времени. Однако не было доказано, что не существует эффективного алгоритма. Предполагаемая сложность этой проблемы лежит в основе широко используемых алгоритмов в криптографии, таких как RSA. Многие области математики и информатики были задействованы в решении этой проблемы, включая эллиптические кривые, теорию алгебраических чисел и квантовые вычисления.

Не все числа заданной длины одинаково сложно разложить на множители. Самыми сложными примерами этих проблем (для известных в настоящее время методов) являются полупростые числа, произведение двух простых чисел. Когда они оба большие, например, более двух тысяч битов длиной, выбираются случайным образом и примерно одинакового размера (но не слишком близко, например, чтобы избежать эффективной факторизации методом факторизации Ферма ), даже самые быстрые алгоритмы разложения на простые множители на самых быстрых компьютерах могут занять достаточно времени, чтобы сделать поиск непрактичным; то есть по мере увеличения числа разрядов простых чисел, разлагаемых на множители, количество операций, необходимых для выполнения факторизации на любом компьютере, резко возрастает.

Многие криптографические протоколы основаны на сложности разложения больших составных целых чисел на множители или на связанной проблеме, например, на проблеме RSA. Алгоритм, который эффективно множит произвольное целое число, сделает криптографию на основе RSA с открытым ключом небезопасной.

Содержание

1 Разложение на простые числа
2 Текущее состояние
- 2.1 Сложность и сложность
3 Алгоритмы факторинга
- 3.1 Специальное назначение
- 3.2 Универсальное
- 3.3 Другие известные алгоритмы
4 Время выполнения эвристики
5 Строгое время выполнения
- 5.1 Алгоритм Шнорра – Зейсена – Ленстры
- 5.2 Ожидаемое время выполнения
6 См. Также
7 Примечания
8 Ссылки
9 Внешние ссылки

Разложение на простые числа

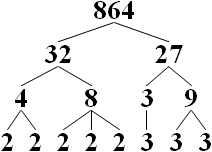Разложение на простые числа n = 864 как 2 × 3

По основной теореме арифметики каждое положительное целое число имеет уникальное простое число факторизация. (По соглашению, 1 - это пустой продукт.) Проверка того, является ли целое число простым, может выполняться за полиномиальное время, например, с помощью Тест на простоту AKS. Однако, если они составные, тесты на полиномиальное время не дают понимания того, как получить коэффициенты.

Учитывая общий алгоритм целочисленной факторизации, любое целое число может быть разложено на составляющие простые множители путем повторного применения этого алгоритма. Ситуация усложняется со специальными алгоритмами факторизации, преимущества которых могут не быть реализованы также или даже не реализованы с факторами, полученными во время разложения. Например, если n = 171 × p × q, где p < q are very large primes, пробное деление быстро произведет факторы 3 и 19, но потребует p делений, чтобы найти следующий фактор. В качестве противоположного примера, если n является произведением простых чисел 13729, 1372933 и 18848997161, где 13729 × 1372933 = 18848997157, метод факторизации Ферма начнется с a = √n⌉ = 18848997159, что сразу дает b = √a - n = √4 = 2 и, следовательно, множители a - b = 18848997157 и a + b = 18848997161. Хотя они легко распознаются как составные и простые соответственно, метод Ферма потребует гораздо больше времени для разложения составного числа на множители, поскольку начальное значение ⌈√ 18848997157⌉ = 137292 для a - это далеко не 1372933.

Текущее состояние дел

Среди b-битных чисел наиболее сложно учесть на практике существующие алгоритмы те, которые являются продуктами двух простых чисел одинакового размера. По этой причине эти целые числа используются в криптографических приложениях. Самым крупным из таких полупростых чисел, который когда-либо учитывался, был RSA-250, 829-битное число с 250 десятичными знаками, в феврале 2020 года. Общее время вычислений составило примерно 2700 ядерно-лет вычислений с использованием Intel Xeon Gold 6130 на частоте 2,1 ГГц. Как и все недавние записи факторизации, эта факторизация была завершена высокооптимизированной реализацией сита общего числового поля, запущенной на сотнях машин.

Сложность и сложность

Не опубликовано ни одного алгоритма , который может разложить на множители все целые числа за полиномиальное время, то есть, который может разложить на множители b- бит номер n во времени O (b) для некоторой константы k. Ни существование, ни отсутствие таких алгоритмов не было доказано, но обычно предполагается, что их не существует и, следовательно, проблема не в классе P. Проблема явно в классе NP, но обычно предполагается, что она не является NP-полным, хотя это не было доказано.

Существуют опубликованные алгоритмы, которые быстрее, чем O ((1 + ε)) для всех положительных ε, то есть субэкспоненциальный. Опубликованный алгоритм с наилучшим асимптотическим временем выполнения - это решето общего числового поля (GNFS ), работающее на b-битном числе n во времени:

exp ⁡ ((64 9 3 + o (1)) (ln ⁡ n) 1 3 (ln ⁡ ln ⁡ n) 2 3). {\ displaystyle \ exp \ left (\ left ({\ sqrt [{3}] {\ frac {64} {9}}} + o (1) \ right) (\ ln n) ^ {\ frac {1}) {3}} (\ ln \ ln n) ^ {\ frac {2} {3}} \ right).}

{\ displaystyle \ exp \ left (\ left ({\ sqrt [{3 }] {\ frac {64} {9}}} + o (1) \ right) (\ ln n) ^ {\ frac {1} {3}} (\ ln \ ln n) ^ {\ frac {2 } {3}} \ right).}

Для современных компьютеров GNFS - лучший опубликованный алгоритм для больших n (более 400 бит). Однако для квантового компьютера Питер Шор открыл в 1994 году алгоритм, который решает его за полиномиальное время. Это будет иметь серьезные последствия для криптографии, если квантовые вычисления станут масштабируемыми. Алгоритм Шора занимает только O (b) времени и O (b) пространства на входах b-битных чисел. В 2001 году алгоритм Шора был впервые реализован с использованием методов ЯМР на молекулах, дающих 7 кубитов.

Точно неизвестно, какие классы сложности содержат версия решения задачи целочисленной факторизации (то есть: имеет ли n множитель меньше k?). Известно, что оно присутствует как в NP, так и в co-NP, что означает, что оба ответа «да» и «нет» могут быть проверены за полиномиальное время. Ответ «да» может быть подтвержден факторизацией n = d (n / d) с d ≤ m. Ответ «нет» может быть подтвержден демонстрацией факторизации n на различные простые числа, все больше m; можно проверить их простоту, используя тест на простоту AKS, а затем умножить их, чтобы получить n. Фундаментальная арифметическая теорема гарантирует, что будет принята только одна возможная строка возрастающих простых чисел, что показывает, что проблема как в UP, так и в co-UP. Известно, что он находится в BQP из-за алгоритма Шора.

Предполагается, что проблема находится за пределами всех трех классов сложности P, NP-полная и co-NP-complete. Следовательно, он является кандидатом для класса сложности NP-промежуточный. Если бы можно было доказать, что он является либо NP-полным, либо co-NP-полным, это означало бы NP = co-NP, очень неожиданный результат, и поэтому многие подозревают, что целочисленная факторизация находится вне обоих этих классов. Многие люди пытались найти для него классические алгоритмы с полиномиальным временем и потерпели неудачу, поэтому многие подозревают, что он находится за пределами P.

В отличие от проблемы решения "Является ли n составным числом?" (или, что эквивалентно: «Является ли n простым числом?») оказывается намного проще, чем проблема определения множителей n. Задача составного / простого числа может быть решена за полиномиальное время (в количестве b цифр n) с помощью теста простоты AKS. Кроме того, существует несколько вероятностных алгоритмов , которые могут очень быстро проверить простоту на практике, если кто-то готов допустить исчезающе малую вероятность ошибки. Простота проверки простоты является важной частью алгоритма RSA, так как для начала необходимо найти большие простые числа.

Алгоритмы факторинга

Специальные

Время работы специального алгоритма факторинга зависит от свойств числа, подлежащего факторизации, или от одного из его неизвестных факторов: размера, специальная форма и т. д. Параметры, определяющие время работы, варьируются в зависимости от алгоритма.

Важным подклассом специализированных алгоритмов факторизации являются алгоритмы Категории 1 или Первой категории, время работы которых зависит от размера наименьшего простого множителя. Учитывая целое число неизвестной формы, эти методы обычно применяются перед методами общего назначения для удаления небольших факторов. Например, наивное пробное деление - это алгоритм Категории 1.

универсальное

универсальное разложение алгоритм, также известный как алгоритм категории 2, второй категории или Крайчик, имеет время работы, которое зависит исключительно от размера целого числа, которое нужно разложить на множители. Это тип алгоритма, который используется для факторизации чисел RSA. Большинство алгоритмов факторинга общего назначения основаны на методе сравнения квадратов.

Другие известные алгоритмы

алгоритм Шора для квантовых компьютеров

Эвристическое время выполнения

В теории чисел существует множество алгоритмов целочисленного разложения, которые эвристически ожидали время выполнения

L п [1 2, 1 + о (1)] = е (1 + о (1)) (журнал ⁡ N) (журнал ⁡ журнал ⁡ п) {\ Displaystyle L_ {п} \ влево [{\ tfrac {1} {2}}, 1 + o (1) \ right] = e ^ {(1 + o (1)) {\ sqrt {(\ log n) (\ log \ log n)}}}}

{\ displaystyle L_ {n} \ left [{\ tfrac {1} {2}}, 1 + o (1) \ right] = e ^ {(1 + o (1)) {\ sqrt {(\ log n) (\ log \ log n)}}}}

в little-o и L-notation. Некоторыми примерами этих алгоритмов являются метод эллиптической кривой и квадратное решето. Другой такой алгоритм - это метод групповых отношений классов, предложенный Шнорром, Сейсеном и Ленстрой, который они доказали, только предполагая недоказанную Обобщенную гипотезу Римана (GRH).

Жесткое время выполнения

Вероятностный алгоритм Шнорра – Зейсена – Ленстры был строго доказан Ленстра и Померанс как ожидаемое время выполнения $L n [1 2, 1 + o (1)] {\ displaystyle L_ {n} \ left [{ \ tfrac {1} {2}}, 1 + o (1) \ right]}$ ${\ displaystyle L_ {n} \ left [{\ tfrac {1} {2}}, 1 + o (1) \ right]}$ путем замены предположения GRH на использование множителей. Алгоритм использует группу классов положительных двоичных квадратичных форм дискриминанта Δ , обозначенную G Δ. G Δ - это набор троек целых чисел (a, b, c), в котором эти числа являются относительными простыми числами.

Алгоритм Шнорра – Сейсена – Ленстры

Дано целое число n, которое будет факторизовано, где n - нечетное положительное целое число, большее определенной константы. В этом алгоритме факторизации дискриминант Δ выбирается как кратное n, Δ = −dn, где d - некоторый положительный множитель. Алгоритм ожидает, что для одного d существует достаточно гладких форм в G Δ. Ленстра и Померанс показывают, что выбор d может быть ограничен небольшим набором, чтобы гарантировать результат гладкости.

Обозначим через P Δ множество всех простых чисел q с символом Кронекера $(Δ q) = 1 {\ displaystyle \ left ({\ tfrac { \ Delta} {q}} \ right) = 1}$ $\ left ({ \ tfrac {\ Delta} {q}} \ right) = 1$ . Путем построения набора образующих группы G Δ и простых форм f q группы G Δ с q в P Δ создается последовательность отношений между набором генераторов и f q. Размер q может быть ограничен $c 0 (log ⁡ | Δ |) 2 {\ displaystyle c_ {0} (\ log | \ Delta |) ^ {2}}$ $c_ {0} (\ log | \ Delta |) ^ {2}$ для некоторой константы. $c 0 {\ displaystyle c_ {0}}$ $c_ {0}$ .

Используемое отношение представляет собой отношение между произведением степеней, равным нейтральному элементу группы G Δ. Эти отношения будут использоваться для построения так называемой неоднозначной формы G Δ, которая является элементом G Δ деления порядка 2. Путем вычисления соответствующей факторизации Δ и взяв gcd, эта неоднозначная форма обеспечивает полную факторизацию числа n на простые множители. Этот алгоритм состоит из следующих основных этапов:

Пусть n будет факторизованным числом.

Пусть Δ - отрицательное целое число с Δ = −dn, где d - множитель, а Δ - отрицательный дискриминант некоторой квадратичной формы.
Возьмем t первых простых чисел $p 1 = 2, p 2 = 3, p 3 = 5,…, pt {\ displaystyle p_ {1} = 2, p_ {2} = 3, p_ {3} = 5, \ dots, p_ {t}}$ $p_ {1} = 2, p_ {2} = 3, p_ {3} = 5, \ dots, p_ {t}$ , для некоторого $t ∈ N {\ displaystyle t \ in {\ mathbb {N}}}$ $t \ in {\ mathbb {N}}$ .
Пусть $fq {\ displaystyle f_ {q}}$ $f_ {q}$ будет случайным простым числом форма G Δ с $(Δ q) = 1 {\ displaystyle \ left ({\ tfrac {\ Delta} {q}} \ right) = 1}$ $\ left ({ \ tfrac {\ Delta} {q}} \ right) = 1$ .
Найдите генераторную установку X of G Δ
Соберите последовательность отношений между множеством X и {f q : q ∈ P Δ }, удовлетворяющую: $(∏ x ∈ X xr (x)). (∏ q ∈ п Δ fqt (q)) знак равно 1 {\ displaystyle \ left (\ prod _ {x \ in X _ {}} x ^ {r (x)} \ right). \ Left (\ prod _ {q \ in P _ {\ Delta}} f_ {q} ^ {t (q)} \ right) = 1}$ $\ left (\ prod _ {x \ in X _ {}} x ^ {r (x)} \ right). \ Left (\ prod _ {q \ in P _ {\ Delta }} f_ {q} ^ {t (q)} \ right) = 1$
Построить неоднозначную форму $(a, b, c) {\ displaystyle (a, b, c)}$ $(a, b, в)$ , который является элементом f ∈ G Δ порядка деления 2 для получения взаимно-простого факторизации наибольшего нечетного делителя Δ, в котором $Δ = - 4 ас или a (a - 4 c) или (b - 2 a) (b + 2 a) {\ displaystyle \ Delta = -4ac {\ text {or}} a (a-4c) {\ text {or}} (b -2a) (b + 2a)}$ ${\ displaystyle \ Delta = -4ac {\ text {or}} a (a-4c) {\ text {or}} (b-2a) (b + 2a)}$
Если неоднозначная форма обеспечивает факторизацию n, тогда остановитесь, иначе найдите другую неоднозначную форму, пока не будет найдено факторизация n. Чтобы предотвратить создание бесполезных неоднозначных форм, создайте 2-силовскую группу Sll 2 (Δ) из G (Δ).

Чтобы получить алгоритм факторизации любых положительное целое число, необходимо добавить несколько шагов к этому алгоритму, например, пробное деление и тест суммы Якоби.

Ожидаемое время выполнения

. Указанный алгоритм является вероятностным алгоритмом , поскольку он делает случайный выбор. Ожидаемое время работы не более $L n [1 2, 1 + o (1)] {\ displaystyle L_ {n} \ left [{\ tfrac {1} {2}}, 1 + o (1) \ right]}$ ${\ displaystyle L_ {n} \ left [{\ tfrac {1} {2}}, 1 + o (1) \ right]}$ .

См. также

алгоритм Баха для генерации случайных чисел с их факторизацией
Каноническое представление положительного целого числа
Факторизация
Мультипликативное разбиение
Разделение (теория чисел) - способ записи числа как суммы положительных целых чисел.

Примечания

Ссылки

Ричард Крэндалл и Карл Померанс (2001). Простые числа: вычислительная перспектива. Springer. ISBN 0-387-94777-9.Глава 5: Алгоритмы экспоненциального факторинга, стр. 191–226. Глава 6: Алгоритмы субэкспоненциального факторинга, стр. 227–284. Раздел 7.4: Метод эллиптических кривых, стр. 301–313.
Дональд Кнут. Искусство программирования, Том 2: Получисленные алгоритмы, третье издание. Addison-Wesley, 1997. ISBN 0-201-89684-2. Раздел 4.5.4: Факторинг в простые числа, стр. 379–417.
Сэмюэл С. Вагстафф, младший (2013). Радость факторинга. Провиденс, Род-Айленд: Американское математическое общество. ISBN 978-1-4704-1048-3..
Уоррен-младший, Генри С. (2013). Восторг хакера (2-е изд.). Эддисон Уэсли - Pearson Education, Inc. ISBN 978-0-321-84268-8.

Внешние ссылки

msieve - SIQS и NFS - помог завершить некоторые из крупнейших известных публичных факторизаций
Ричард П. Брент, "Недавний прогресс и перспективы алгоритмов целочисленной факторизации", Вычисления и комбинаторика ", 2000, стр. 3–22. загрузить
Маниндра Агравал, Нирадж Каял, Нитин Саксена, «ПРИМЕС в П.» Annals of Mathematics 160 (2): 781-793 (2004). Версия от августа 2005 г. PDF
Эрик У. Вайсштейн, «RSA-640 Factored» MathWorld Headline News, 8 ноября 2005 г.