Разделение (теория чисел)

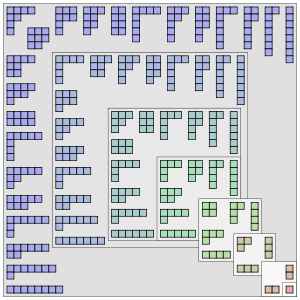
Диаграммы Юнга, связанные с разбиениями натуральных чисел от 1 до 8. Они расположены так, что изображения под отражением относительно главной диагонали квадрата являются сопряженными разбиениями. 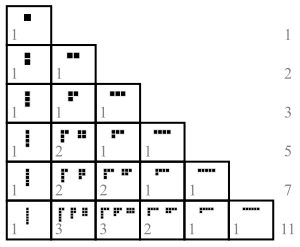Разделы n с наибольшим слагаемым k

В теории чисел и комбинаторике, разбиение положительного целого числа п, также называется целое число разделы, является способом записи п в виде суммы положительных целых чисел. Две суммы, различающиеся только порядком слагаемых, считаются одним и тем же разбиением. (Если порядок имеет значение, сумма становится составом. ) Например, 4 можно разделить пятью различными способами:

4

3 + 1

2 + 2

2 + 1 + 1

1 + 1 + 1 + 1

Зависимая от порядка композиция 1 + 3 является тем же разбиением, что и 3 + 1, в то время как две различные композиции 1 + 2 + 1 и 1 + 1 + 2 представляют собой одно и то же разбиение 2 + 1 + 1.

Слагаемое в разбиении также называется частью. Количество разбиений n определяется статистической суммой p ( n). Таким образом, p (4) = 5. Обозначение λ ⊢ n означает, что λ является разбиением числа n.

Разделы могут быть графически визуализированы с помощью диаграмм Юнга или Феррерса. Они встречаются в ряде разделов математики и физики, включая изучение симметрических многочленов и симметрической группы, а также в теории представлений групп в целом.

СОДЕРЖАНИЕ

• 1 Примеры
• 2 Представления перегородок
  • 2.1 Диаграмма Феррерса
  • 2.2 Диаграмма Юнга
• 3 Функция разделения
• 4 Ограниченные разделы
  • 4.1 Сопряженные и самосопряженные перегородки
  • 4.2 Нечетные части и отдельные части
  • 4.3 Ограниченный размер или количество деталей
    • 4.3.1 Асимптотика
  • 4.4 Разбиения в прямоугольнике и гауссовские биномиальные коэффициенты
• 5 Ранг и площадь Дерфи
• 6 решетка Юнга
• 7 См. Также
• 8 Примечания
• 9 ссылки
• 10 Внешние ссылки

Примеры

Семь разделов из пяти:

• 5
• 4 + 1
• 3 + 2
• 3 + 1 + 1
• 2 + 2 + 1
• 2 + 1 + 1 + 1
• 1 + 1 + 1 + 1 + 1

В некоторых источниках разбиения трактуются как последовательность слагаемых, а не как выражение со знаком плюс. Например, раздел 2 + 2 + 1 вместо этого может быть записан как кортеж (2, 2, 1) или в еще более компактной форме (2 ², 1), где верхний индекс указывает количество повторений термина.

Представления перегородок

Существует два распространенных схематических метода представления разбиений: в виде диаграмм Феррерса, названных в честь Нормана Маклеода Феррерса, и в виде диаграмм Юнга, названных в честь британского математика Альфреда Янга. У обоих есть несколько возможных соглашений; здесь мы используем английскую нотацию, а диаграммы выровнены в верхнем левом углу.

Диаграмма Феррерса

Разделение 6 + 4 + 3 + 1 положительного числа 14 можно представить в виде следующей диаграммы:

14 кругов выстроены в 4 ряда, каждый размером с часть перегородки. Схемы для 5 разделов числа 4 приведены ниже:

4	знак равно	3 + 1	знак равно	2 + 2	знак равно	2 + 1 + 1	знак равно	1 + 1 + 1 + 1

Диаграмма Юнга

Основная статья: диаграмма Юнга

Альтернативным визуальным представлением целочисленного разбиения является его диаграмма Юнга (часто также называемая диаграммой Феррерса). Вместо того, чтобы представлять разбиение точками, как на диаграмме Феррерса, диаграмма Юнга использует прямоугольники или квадраты. Таким образом, диаграмма Юнга для разбиения 5 + 4 + 1 имеет вид

а диаграмма Феррерса для того же разбиения имеет вид

Хотя этот, казалось бы, тривиальный вариант не заслуживает отдельного упоминания, диаграммы Юнга оказались чрезвычайно полезными при изучении симметрических функций и теории представлений групп : заполнение ящиков диаграмм Юнга числами (или иногда более сложными объектами), подчиняющимися различным rules приводит к семейству объектов, называемых таблицами Юнга, и эти таблицы имеют комбинаторное и теоретико-представительное значение. Диаграммы Юнга - это особый вид полимино, состоящий из смежных квадратов, соединенных вместе.

Функция разделения

Используя метод Эйлера, чтобы найти p (40): линейка со знаками плюс и минус (серая рамка) сдвигается вниз, соответствующие термины добавляются или вычитаются. Положение знаков дано разностью чередующихся натуральных (синий) и нечетных (оранжевый) чисел. В файле SVG наведите указатель мыши на изображение, чтобы переместить линейку. Основная статья: Функция разделения (теория чисел)

Статсумма равно число возможных разбиений целого неотрицательного. Например, поскольку целое число имеет пять разделов,,,, и. Значения этой функции для: ${\ Displaystyle р (п)}$ ${\ displaystyle n}$${\ Displaystyle p (4) = 5}$${\ displaystyle 4}$${\ displaystyle 1 + 1 + 1 + 1}$${\ displaystyle 1 + 1 + 2}$${\ displaystyle 1 + 3}$${\ displaystyle 2 + 2}$${\ displaystyle 4}$${\ Displaystyle п = 0,1,2, \ точки}$

1, 1, 2, 3, 5, 7, 11, 15, 22, 30, 42, 56, 77, 101, 135, 176, 231, 297, 385, 490, 627, 792, 1002, 1255, 1575, 1958, 2436, 3010, 3718, 4565, 5604,... (последовательность A000041 в OEIS ).

Производящая функция IS ${\ displaystyle p}$

${\ displaystyle \ sum _ {n = 0} ^ {\ infty} p (n) q ^ {n} = \ prod _ {j = 1} ^ {\ infty} \ sum _ {i = 0} ^ {\ infty} q ^ {ji} = \ prod _ {j = 1} ^ {\ infty} (1-q ^ {j}) ^ {- 1}.}.$

Нет замкнутая форма выражения для функции разбиения не известно, но она имеет как асимптотические разложения, которые точно аппроксимировать его и рекуррентные соотношения, с помощью которого он может быть рассчитаны точно. Он растет как экспоненциальная функция от квадратного корня из аргумента. Мультипликативный обратное его порождающей функции является функция Эйлера ; по теореме Эйлера о пятиугольных числах эта функция представляет собой переменную сумму пятиугольных числовых степеней своего аргумента.

${\ Displaystyle п (п) = п (п-1) + п (п-2) -р (п-5) -р (п-7) + \ cdots}$

Шриниваса Рамануджан первым обнаружил, что статистическая сумма имеет нетривиальные закономерности в модульной арифметике, теперь известные как сравнения Рамануджана. Например, всякий раз, когда десятичное представление чисел заканчивается цифрой 4 или 9, количество разделов будет делиться на 5. ${\ displaystyle n}$${\ displaystyle n}$

Ограниченные разделы

И в комбинаторике, и в теории чисел часто изучаются семейства разбиений с различными ограничениями. В этом разделе рассматривается несколько таких ограничений.

Сопряженные и самосопряженные перегородки

Если перевернуть диаграмму разбиения 6 + 4 + 3 + 1 по его главной диагонали, мы получим еще одно разбиение 14:

	↔
6 + 4 + 3 + 1	знак равно	4 + 3 + 3 + 2 + 1 + 1

Превращая строки в столбцы, мы получаем разбиение 4 + 3 + 3 + 2 + 1 + 1 числа 14. Такие разбиения называются сопряженными друг другу. В случае числа 4 разбиения 4 и 1 + 1 + 1 + 1 являются сопряженными парами, а разбиения 3 + 1 и 2 + 1 + 1 сопряжены друг другу. Особый интерес представляет разбиение 2 + 2, которое само является сопряженным. Такое разбиение называется самосопряженным.

Требование: Количество самосопряженных перегородок является таким же, как число разделов с различными нечетными частями.

Доказательство (схема): ключевое наблюдение состоит в том, что каждую нечетную часть можно « сложить » посередине, чтобы сформировать самосопряженную диаграмму:

↔

Затем можно получить биекцию между набором разделов с различными нечетными частями и набором самосопряженных разделов, как показано в следующем примере:

	↔
9 + 7 + 3	знак равно	5 + 5 + 4 + 3 + 2
Расст. странный		самосопряженный

Нечетные части и отдельные части

Среди 22 разбиений числа 8 есть 6, которые содержат только нечетные части:

• 7 + 1
• 5 + 3
• 5 + 1 + 1 + 1
• 3 + 3 + 1 + 1
• 3 + 1 + 1 + 1 + 1 + 1
• 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1

В качестве альтернативы мы могли бы подсчитать разделы, в которых ни одно число не встречается более одного раза. Такой раздел называется разделом с отдельными частями. Если мы посчитаем разбиения 8 с отдельными частями, мы также получим 6:

• 8
• 7 + 1
• 6 + 2
• 5 + 3
• 5 + 2 + 1
• 4 + 3 + 1

Это общее свойство. Для каждого положительного числа количество разделов с нечетными частями равно количеству разделов с отдельными частями, обозначенным q ( n). Этот результат был доказан Леонардом Эйлером в 1748 году и позже был обобщен в виде теоремы Глейшера.

Для каждого типа ограниченного раздела существует соответствующая функция для количества разделов, удовлетворяющих данному ограничению. Важный пример - q ( n). Первые несколько значений q ( n) (начиная с q (0) = 1):

1, 1, 1, 2, 2, 3, 4, 5, 6, 8, 10,... (последовательность A000009 в OEIS ).

Производящая функция для д ( п) (разбиения на отдельные части) задается

${\ displaystyle \ sum _ {n = 0} ^ {\ infty} q (n) x ^ {n} = \ prod _ {k = 1} ^ {\ infty} (1 + x ^ {k}) = \ prod _ {k = 1} ^ {\ infty} {\ frac {1} {1-x ^ {2k-1}}}.}.$

Теорема о пятиугольном числе дает рекуррент для q:

q ( k) = a k + q ( k - 1) + q ( k - 2) - q ( k - 5) - q ( k - 7) + q ( k - 12) + q ( k - 15) - q ( k - 22) -...

где a k равно (−1) ^m, если k = 3 m ² - m, или k = 3 m ² + m для некоторого целого числа m, и равно 0 в противном случае.

Ограниченный размер детали или количество деталей

Используя сопряжения, количество p k ( n) разбиений n ровно на k частей равно количеству разбиений n, в которых наибольшая часть имеет размер k. Функция p k ( n) удовлетворяет рекуррентности

p k ( n) = p k ( n - k) + p k −1 ( n - 1)

с начальными значениями p 0 (0) = 1 и p k ( n) = 0, если n ≤ 0 или k ≤ 0 и n и k не равны нулю.

Восстанавливают функцию p ( n) следующим образом:

${\ displaystyle p (n) = \ sum _ {k = 0} ^ {n} p_ {k} (n).}$

Одна из возможных производящих функций для таких разбиений при фиксированном k и переменном n:

${\ displaystyle \ sum _ {n \ geq 0} p_ {k} (n) x ^ {n} = x ^ {k} \ cdot \ prod _ {i = 1} ^ {k} {\ frac {1} {1-x ^ {i}}}.}$

В более общем смысле, если T - это набор положительных целых чисел, то количество разбиений n, все части которых принадлежат T, имеет производящую функцию

${\ displaystyle \ prod _ {t \ in T} (1-x ^ {t}) ^ {- 1}.}$

Это можно использовать для решения проблем с внесением сдачи (где набор T указывает доступные монеты). В качестве двух частных случаев можно сказать, что количество разбиений n, в которых все части равны 1 или 2 (или, что то же самое, количество разбиений n на 1 или 2 части) равно

${\ displaystyle \ left \ lfloor {\ frac {n} {2}} + 1 \ right \ rfloor,}$

и число перегородок п, в которых все части являются 1, 2 или 3 (или, что то же самое, число разбиений п на не более трех частей) является ближайшим целым числом к ( п + 3) ² /12.

Асимптотика

Основная статья: Partition_function_ (number_theory) § Приближенные_формулы

Асимптотическая скорость роста для р ( п) задаются

${\ displaystyle \ log p (n) \ sim C {\ sqrt {n}} {\ text {as}} n \ rightarrow \ infty}$

где. Более точная асимптотическая формула ${\ displaystyle C = \ pi {\ sqrt {\ frac {2} {3}}}.}$

${\ displaystyle p (n) \ sim {\ frac {1} {4n {\ sqrt {3}}}} \ exp \ left ({\ pi {\ sqrt {\ frac {2n} {3}}}} \ Правильно)}$ в качестве ${\ Displaystyle п \ rightarrow \ infty}$

был впервые получен Г. Х. Харди и Рамануджаном в 1918 г. и независимо И. В. Успенским в 1920 г. Полное асимптотическое разложение было дано в 1937 г. Гансом Радемахером.

Если является множество натуральных чисел, пусть р ( п) обозначает число разбиений п на элементы А. Если A имеет положительную естественную плотность α, то

${\ displaystyle \ log p_ {A} (n) \ sim C {\ sqrt {\ alpha n}}}$

и наоборот, если это асимптотическое свойство выполняется для p A ( n), то A имеет естественную плотность α. Этот результат был сформулирован с наброском доказательства Эрдёшем в 1942 году.

Если A - конечное множество, этот анализ неприменим (плотность конечного множества равна нулю). Если в A есть k элементов, наибольший общий делитель которых равен 1, то

${\ displaystyle p_ {A} (n) = \ left (\ prod _ {a \ in A} a ^ {- 1} \ right) \ cdot {\ frac {n ^ {k-1}} {(k- 1)!}} + O (n ^ {k-2}).}$

Разбиения в прямоугольнике и гауссовские биномиальные коэффициенты

Основная статья: биномиальный коэффициент Гаусса

Также можно одновременно ограничить количество и размер деталей. Пусть р ( N, M ; п) обозначает число разбиений п с не более чем М частей, каждая из размера не более N. Эквивалентно, это разбиения, диаграмма Юнга которых помещается внутри прямоугольника M × N. Есть рекуррентное отношение

${\ Displaystyle п (N, M; N) = п (N, M-1; n) + p (N-1, M; nM)}$

полученный путем наблюдения, которое подсчитывает разбиения n на ровно M частей размером не более N, и вычитание 1 из каждой части такого разбиения дает разбиение n - M на не более M частей. ${\ Displaystyle п (N, M; N) -p (N, M-1; N)}$

Гауссовский биномиальный коэффициент определяется следующим образом:

${\ displaystyle {k + \ ell \ choose \ ell} _ {q} = {k + \ ell \ choose k} _ {q} = {\ frac {\ prod _ {j = 1} ^ {k + \ ell} (1 -q ^ ​​{j})} {\ prod _ {j = 1} ^ {k} (1-q ^ {j}) \ prod _ {j = 1} ^ {\ ell} (1-q ^ {j })}}.}$

Гауссовский биномиальный коэффициент связан с порождающей функцией от р ( Н, М, п) равенство

${\ displaystyle \ sum _ {n = 0} ^ {MN} p (N, M; n) q ^ {n} = {M + N \ select M} _ {q}.}$

Рэнк и Дерфи-сквер

Основная статья: Дерфи-сквер

Оценка перегородки является наибольшим числом к таким образом, что перегородка содержит, по меньшей мере, K части размера по крайней мере, к. Например, разбиение 4 + 3 + 3 + 2 + 1 + 1 имеет ранг 3, потому что оно содержит 3 части ≥ 3, но не содержит 4 частей ≥ 4. В диаграмме Феррерса или диаграмме Юнга разбиения ранга r, квадрат r × r элементов в верхнем левом углу известен как квадрат Дёрфи :

Квадрат Дёрфи находит применение в комбинаторике при доказательстве различных тождеств разбиения. Он также имеет некоторое практическое значение в виде индекса Хирша.

Другой статистический показатель также иногда называют рангом разбиения (или рангом Дайсона), а именно разницей для разбиения k частей с наибольшей частью. Эта статистика (которая не связана со статистикой, описанной выше) появляется в исследовании конгруэнций Рамануджана. ${\ displaystyle \ lambda _ {k} -k}$${\ displaystyle \ lambda _ {k}}$

Решетка Юнга

Основная статья: решетка Юнга

Существует естественный частичный порядок на разбиениях, задаваемый включением диаграмм Юнга. Этот частично упорядоченный набор известен как решетка Юнга. Решетки были первоначально определены в контексте теории представлений, где он используется для описания неприводимых представлений о симметрических группах S п для все п, вместе с их свойствами ветвления, в нулевой характеристике. Он также получил значительные исследования из-за своих чисто комбинаторных свойств; в частности, это мотивирующий пример дифференциального положения.

Смотрите также

• Ранг раздела, другое понятие ранга
• Кривошип перегородки
• Порядок доминирования
• Факторизация
• Целочисленная факторизация
• Разделение набора
• Звезды и стержни (комбинаторика)
• Плоская перегородка
• Вежливое число, определяемое разбиением на последовательные целые числа
• Мультипликативный раздел
• Двенадцатикратный путь
• Формула выборки Ювенса
• Формула Фаа ди Бруно
• Многораздельный
• Личности Ньютона
• Функция наименьших частей
• Разбиение Гольдбаха - это разбиение четного числа на простые числа (см . Гипотезу Гольдбаха )
• Статистическая сумма Костанта

Примечания

использованная литература

• Абрамовиц, Милтон ; Стегун, Ирен (1964). Справочник по математическим функциям с формулами, графиками и математическими таблицами. Министерство торговли США, Национальное бюро стандартов. ISBN   0-486-61272-4.
• Эндрюс, Джордж Э. (1976). Теория перегородок. Издательство Кембриджского университета. ISBN   0-521-63766-X.
• Эндрюс, Джордж Э.; Эрикссон, Киммо (2004). Целочисленные разделы. Издательство Кембриджского университета. ISBN   0-521-60090-1.
• Апостол, Том М. (1990) [1976]. Модулярные функции и ряды Дирихле в теории чисел. Тексты для выпускников по математике. 41 (2-е изд.). Нью-Йорк и др.: Springer-Verlag. ISBN   0-387-97127-0. Zbl   0697.10023. (См. Главу 5 с современным педагогическим введением к формуле Радемахера).
• Бона, Миклош (2002). Прогулка по комбинаторике: введение в теорию перечисления и графов. Мировое научное издательство. ISBN   981-02-4900-4. (элементарное введение в тему целочисленных разбиений, включая обсуждение графов Феррерса)
• Харди, GH ; Райт, EM (2008) [1938]. Введение в теорию чисел. Отредактировано Д. Р. Хитом-Брауном и Дж. Х. Сильверманом. Предисловие Эндрю Уайлса. (6-е изд.). Оксфорд: Издательство Оксфордского университета. ISBN   978-0-19-921986-5. Руководство по ремонту   2445243. Zbl   1159.11001.
• Лемер, Д.Х. (1939). «Об остатке и сходимости ряда для статистической суммы». Пер. Амер. Математика. Soc. 46: 362–373. DOI : 10.1090 / S0002-9947-1939-0000410-9. MR   0000410. Zbl   0022.20401. Предоставляет основную формулу (без производных), остаток и старую форму для A k ( n).)
• Гупта, Хансрадж; Gwyther, CE; Миллер, JCP (1962). Королевское математическое общество. Таблицы. Том 4, Таблицы перегородок. |volume=имеет дополнительный текст ( справка ) (Имеет текст, почти полную библиографию, но они (и Абрамовиц) пропустили формулу Сельберга для A k ( n), которая есть у Уайтмана.)
• Макдональд, Ян Г. (1979). Симметричные функции и многочлены Холла. Оксфордские математические монографии. Издательство Оксфордского университета. ISBN   0-19-853530-9. Zbl   0487.20007. (См. Раздел I.1)
• Натансон, МБ (2000). Элементарные методы теории чисел. Тексты для выпускников по математике. 195. Springer-Verlag. ISBN   0-387-98912-9. Zbl   0953.11002.
• Радемахер, Ганс (1974). Собрание статей Ганса Радемахера. v II. MIT Press. С. 100–07, 108–22, 460–75.
• Сотуа, Маркус Ду. (2003). Музыка премий. Нью-Йорк: Многолетник-ХарперКоллинз.
• Стэнли, Ричард П. (1999). Перечислительная комбинаторика. Тома 1 и 2. Издательство Кембриджского университета. ISBN   0-521-56069-1. |volume=имеет дополнительный текст ( справка )
• Whiteman, AL (1956). «Сумма, связанная с рядом для статистической суммы». Тихоокеанский математический журнал. 6 (1): 159–176. DOI : 10,2140 / pjm.1956.6.159. Zbl   0071.04004. (Предоставляет формулу Сельберга. Более старая форма - это конечное разложение Фурье Сельберга.)

внешние ссылки

• "Разделение", Энциклопедия математики, EMS Press, 2001 [1994]
• Калькулятор разбиения и состава
• Вайсштейн, Эрик В. «Раздел». MathWorld.
• Уилф, Герберт С. Лекции по целочисленным разделам (PDF), архив (PDF) из оригинала на 2021-02-24, извлечение 2021-02-28
• Подсчет с помощью разделов со ссылочными таблицами на Он-лайн энциклопедию целочисленных последовательностей
• Запись целочисленных разделов в базе данных FindStat
• Модуль Integer:: Partition Perl из CPAN
• Быстрые алгоритмы генерации целочисленных разделов
• Создание всех разделов: сравнение двух кодировок
• Грайм, Джеймс (28 апреля 2016 г.). «Перегородки - Numberphile» (видео). Брэди Харан. Дата обращения 5 мая 2016.