Распределение Парето

Тип Парето I

Функция плотности вероятности Функции плотности вероятности Парето типа I для различных с При приближении распределения где - дельта-функция Дирака. ${\ displaystyle \ alpha}$${\ displaystyle x _ {\ mathrm {m}} = 1.}$${\ displaystyle \ alpha \ rightarrow \ infty,}$${\ Displaystyle \ дельта (х-х _ {\ mathrm {m}}),}$${\ displaystyle \ delta}$
Кумулятивная функция распределения Функции кумулятивного распределения Парето типа I для различных с${\ displaystyle \ alpha}$${\ displaystyle x _ {\ mathrm {m}} = 1.}$
Параметры	${\ displaystyle x _ {\ mathrm {m}}gt; 0}$ масштаб ( реальная ) форма (реальная) ${\ displaystyle \ alphagt; 0}$
Служба поддержки	${\ Displaystyle х \ в [х _ {\ mathrm {m}}, \ infty)}$
PDF	${\ displaystyle {\ frac {\ alpha x _ {\ mathrm {m}} ^ {\ alpha}} {x ^ {\ alpha +1}}}}$
CDF	${\ displaystyle 1- \ left ({\ frac {x _ {\ mathrm {m}}} {x}} \ right) ^ {\ alpha}}$
Квантиль	${\ displaystyle x _ {\ mathrm {m}} {(1-p)} ^ {- {\ frac {1} {\ alpha}}}}$
Иметь в виду	${\ displaystyle {\ begin {cases} \ infty amp; {\ text {for}} \ alpha \ leq 1 \\ {\ dfrac {\ alpha x _ {\ mathrm {m}}} {\ alpha -1}} amp; { \ text {for}} \ alphagt; 1 \ end {case}}}$
Медиана	${\ Displaystyle х _ {\ mathrm {m}} {\ sqrt [{\ alpha}] {2}}}$
Режим	${\ Displaystyle х _ {\ mathrm {m}}}$
Дисперсия	${\ displaystyle {\ begin {cases} \ infty amp; {\ text {for}} \ alpha \ leq 2 \\ {\ dfrac {x _ {\ mathrm {m}} ^ {2} \ alpha} {(\ alpha - 1) ^ {2} (\ alpha -2)}} amp; {\ text {for}} \ alphagt; 2 \ end {case}}}$
Асимметрия	${\ displaystyle {\ frac {2 (1+ \ alpha)} {\ alpha -3}} {\ sqrt {\ frac {\ alpha -2} {\ alpha}}} {\ text {for}} \ alphagt; 3}$
Бывший. эксцесс	${\ Displaystyle {\ гидроразрыва {6 (\ альфа ^ {3} + \ альфа ^ {2} -6 \ альфа -2)} {\ альфа (\ альфа-3) (\ альфа -4)}} {\ текст {for}} \ alphagt; 4}$
Энтропия	${\ displaystyle \ log \ left (\ left ({\ frac {x _ {\ mathrm {m}}} {\ alpha}} \ right) \, e ^ {1 + {\ tfrac {1} {\ alpha}} }\Правильно)}$
MGF	не существует
CF	${\ Displaystyle \ альфа (-ix _ {\ mathrm {m}} t) ^ {\ alpha} \ Gamma (- \ alpha, -ix _ {\ mathrm {m}} t)}$
Информация Fisher	${\ Displaystyle {\ mathcal {I}} (х _ {\ mathrm {m}}, \ alpha) = {\ begin {bmatrix} {\ dfrac {\ alpha} {x _ {\ mathrm {m}} ^ {2} }} amp; - {\ dfrac {1} {x _ {\ mathrm {m}}}} \\ - {\ dfrac {1} {x _ {\ mathrm {m}}}} amp; {\ dfrac {1} {\ альфа ^ {2}}} \ конец {bmatrix}}}$ Верно: ${\ Displaystyle {\ mathcal {I}} (х _ {\ mathrm {m}}, \ alpha) = {\ begin {bmatrix} {\ dfrac {\ alpha ^ {2}} {x _ {\ mathrm {m}} ^ {2}}} amp; 0 \\ 0 amp; {\ dfrac {1} {\ alpha ^ {2}}} \ end {bmatrix}}}$

Распределение Парето, названный в честь итальянского инженера, экономиста и социолога Вильфредо Парето ( итал  [ р т е ː т о ] США : / р ə г eɪ т oʊ / pə- RAY -toh ), является степенное распределение вероятностей, которое используется в описании социального, контроля качества, научных, геофизических, актуарных и многих других видов наблюдаемых явлений. Первоначально применялся для описания распределения богатства в обществе, соответствуя тенденции, согласно которой большая часть богатства принадлежит небольшой части населения. Принцип Парето или «правило 80-20», утверждающий, что 80% результатов обусловлены 20% причин, был назван в честь Парето, но концепции различны, и только распределения Парето со значением формы ( α) log 4 5 ≈ 1.16 это точно отражает. Эмпирические наблюдения показали, что это распределение 80-20 подходит для широкого круга случаев, включая природные явления и деятельность человека.

СОДЕРЖАНИЕ

• 1 Определения
  • 1.1 Кумулятивная функция распределения
  • 1.2 Функция плотности вероятности
• 2 свойства
  • 2.1 Моменты и характеристическая функция
  • 2.2 Условные распределения
  • 2.3 Характеризационная теорема
  • 2.4 Среднее геометрическое
  • 2.5 Гармоническое среднее
  • 2.6 Графическое представление
• 3 Связанные дистрибутивы
  • 3.1 Обобщенные распределения Парето
    • 3.1.1 Типы Парето I – IV
    • 3.1.2 Распределение Феллера – Парето
  • 3.2 Связь с экспоненциальным распределением
  • 3.3 Связь с логнормальным распределением
  • 3.4 Связь с обобщенным распределением Парето
  • 3.5 Ограниченное распределение Парето
    • 3.5.1 Генерация ограниченных случайных величин Парето
  • 3.6 Симметричное распределение Парето
  • 3.7 Многомерное распределение Парето
• 4 Статистический вывод
  • 4.1 Оценка параметров
  • 4.2 Доверительные интервалы
• 5 Возникновение и применение
  • 5.1 Общие
  • 5.2 Связь с законом Ципфа
  • 5.3 Связь с «принципом Парето»
  • 5.4 Связь с законом Прайса
  • 5.5 Кривая Лоренца и коэффициент Джини
• 6 Вычислительные методы
  • 6.1 Генерация случайной выборки
• 7 См. Также
• 8 ссылки
• 9 Примечания
• 10 Внешние ссылки

Определения

Если X - случайная величина с распределением Парето (тип I), то вероятность того, что X больше некоторого числа x, то есть функция выживания (также называемая хвостовой функцией), определяется выражением

${\ displaystyle {\ overline {F}} (x) = \ Pr (Xgt; x) = {\ begin {cases} \ left ({\ frac {x _ {\ mathrm {m}}} {x}} \ right) ^ {\ alpha} amp; x \ geq x _ {\ mathrm {m}}, \\ 1 amp; x lt;x _ {\ mathrm {m}}, \ end {cases}}}$

где x m - (обязательно положительное) минимально возможное значение X, а α - положительный параметр. Распределение Парето типа I характеризуется масштабным параметром x m и параметром формы α, который известен как хвостовой индекс. Когда это распределение используется для моделирования распределения богатства, параметр α называется индексом Парето.

Кумулятивная функция распределения

Согласно определению, кумулятивная функция распределения случайной величины Парето с параметрами α и x m равна

${\ Displaystyle F_ {X} (х) = {\ begin {case} 1- \ left ({\ frac {x _ {\ mathrm {m}}} {x}} \ right) ^ {\ alpha} amp; x \ geq x _ {\ mathrm {m}}, \\ 0 amp; x lt;x _ {\ mathrm {m}}. \ end {case}}}$

Функция плотности вероятности

Отсюда (путем дифференцирования ) следует, что функция плотности вероятности равна

${\ displaystyle f_ {X} (x) = {\ begin {cases} {\ frac {\ alpha x _ {\ mathrm {m}} ^ {\ alpha}} {x ^ {\ alpha +1}}} amp; x \ geq x _ {\ mathrm {m}}, \\ 0 amp; x lt;x _ {\ mathrm {m}}. \ end {case}}}$

При нанесении на линейные оси распределение принимает знакомую J-образную кривую, которая асимптотически приближается к каждой из ортогональных осей. Все сегменты кривой самоподобны (с учетом соответствующих масштабных коэффициентов). На графике логарифмического графика распределение представлено прямой линией.

Характеристики

Моменты и характерная функция

• Ожидаемое значение из случайной величины после распределения Парето

${\ displaystyle \ operatorname {E} (X) = {\ begin {case} \ infty amp; \ alpha \ leq 1, \\ {\ frac {\ alpha x _ {\ mathrm {m}}} {\ alpha -1} } amp; \ alphagt; 1. \ end {case}}}$

• Дисперсия из случайной величины после распределения Парето

${\ displaystyle \ operatorname {Var} (X) = {\ begin {cases} \ infty amp; \ alpha \ in (1,2], \\\ left ({\ frac {x _ {\ mathrm {m}}} { \ alpha -1}} \ right) ^ {2} {\ frac {\ alpha} {\ alpha -2}} amp; \ alphagt; 2. \ end {ases}}}$

(Если α ≤ 1, дисперсия не существует.)

• Сырьевые моменты являются

${\ displaystyle \ mu _ {n} '= {\ begin {case} \ infty amp; \ alpha \ leq n, \\ {\ frac {\ alpha x _ {\ mathrm {m}} ^ {n}} {\ alpha -n}} amp; \ alphagt; n. \ end {case}}}$

• Функция, производящая момент, определена только для неположительных значений t  ≤ 0 как

${\ displaystyle M \ left (t; \ alpha, x _ {\ mathrm {m}} \ right) = \ operatorname {E} \ left [e ^ {tX} \ right] = \ alpha (-x _ {\ mathrm { m}} t) ^ {\ alpha} \ Gamma (- \ alpha, -x _ {\ mathrm {m}} t)}$

${\ displaystyle M \ left (0, \ alpha, x _ {\ mathrm {m}} \ right) = 1.}$

Таким образом, поскольку математическое ожидание не сходится на открытом интервале, содержащем, мы говорим, что функция, производящая момент, не существует. ${\ displaystyle t = 0}$

• Характеристическая функция задается

${\ displaystyle \ varphi (t; \ alpha, x _ {\ mathrm {m}}) = \ alpha (-ix _ {\ mathrm {m}} t) ^ {\ alpha} \ Gamma (- \ alpha, -ix_ { \ mathrm {m}} t),}$

где Γ ( a,  x) - неполная гамма-функция.

Параметры могут быть решены методом моментов.

Условные распределения

Условное распределение вероятностей из Парето- распределенной случайной величины, учитывая событие, которое оно больше или равно определенный номер  превышения, является распределение Парето с тем же индексом паретовского , но с минимумом  вместо. Это означает, что условное ожидаемое значение (если оно конечно, т. Е.) Пропорционально. В случае случайных величин, которые описывают время жизни объекта, это означает, что продолжительность жизни пропорциональна возрасту и называется эффектом Линди или законом Линди. ${\ displaystyle x_ {1}}$${\ displaystyle x _ {\ text {m}}}$${\ displaystyle \ alpha}$${\ displaystyle x_ {1}}$${\ displaystyle x _ {\ text {m}}}$${\ displaystyle \ alphagt; 1}$${\ displaystyle x_ {1}}$

Характеризационная теорема

Предположим, что это независимые одинаково распределенные случайные величины, распределение вероятностей которых поддерживается на интервале для некоторых. Предположим, что для всех две случайные величины и независимы. Тогда обычное распределение - это распределение Парето. ${\ Displaystyle X_ {1}, X_ {2}, X_ {3}, \ dotsc}$ ${\ Displaystyle [х _ {\ текст {м}}, \ infty)}$${\ displaystyle x _ {\ text {m}}gt; 0}$${\ displaystyle n}$${\ displaystyle \ min \ {X_ {1}, \ dotsc, X_ {n} \}}$${\ displaystyle (X_ {1} + \ dotsb + X_ {n}) / \ min \ {X_ {1}, \ dotsc, X_ {n} \}}$

Среднее геометрическое

Геометрическое среднее ( G) является

${\ displaystyle G = x _ {\ text {m}} \ exp \ left ({\ frac {1} {\ alpha}} \ right).}$

Гармоническое среднее

Гармоническое среднее ( Н) является

${\ displaystyle H = x _ {\ text {m}} \ left (1 + {\ frac {1} {\ alpha}} \ right).}$

Графическое представление

Характерное криволинейное распределение с `` длинным хвостом '' при построении в линейном масштабе маскирует лежащую в основе простоту функции при нанесении на логарифмический график, который затем принимает форму прямой линии с отрицательным градиентом: это следует из формулы для функция плотности вероятности, что для x ≥ x m,

${\ displaystyle \ log f_ {X} (x) = \ log \ left (\ alpha {\ frac {x _ {\ mathrm {m}} ^ {\ alpha}} {x ^ {\ alpha +1}}}} \ справа) = \ log (\ alpha x _ {\ mathrm {m}} ^ {\ alpha}) - (\ alpha +1) \ log x.}$

Поскольку α положительно, градиент - ( α  + 1) отрицательный.

Связанные дистрибутивы

Обобщенные распределения Парето

Смотрите также: Обобщенное распределение Парето

Существует иерархия распределений Парето, известная как распределения Парето типа I, II, III, IV и распределения Феллера – Парето. Тип Парето IV содержит Типы Парето I – III как особые случаи. Распределение Феллера – Парето обобщает тип Парето IV.

Типы Парето I – IV

Иерархия распределения Парето суммирована в следующей таблице, в которой сравниваются функции выживаемости (дополнительная функция CDF).

Когда μ = 0, тип распределения Парето II также известен как распределение Ломакса.

В этом разделе символ x m, использовавшийся ранее для обозначения минимального значения x, заменен на  σ.

Распределения Парето

	${\ Displaystyle {\ overline {F}} (х) = 1-F (х)}$	Служба поддержки	Параметры
Тип I	${\ displaystyle \ left [{\ frac {x} {\ sigma}} \ right] ^ {- \ alpha}}$	${\ Displaystyle х \ geq \ sigma}$	${\ displaystyle \ sigmagt; 0, \ альфа}$
Тип II	${\ displaystyle \ left [1 + {\ frac {x- \ mu} {\ sigma}} \ right] ^ {- \ alpha}}$	${\ Displaystyle х \ geq \ mu}$	${\ displaystyle \ mu \ in \ mathbb {R}, \ sigmagt; 0, \ alpha}$
Lomax	${\ displaystyle \ left [1 + {\ frac {x} {\ sigma}} \ right] ^ {- \ alpha}}$	${\ Displaystyle х \ geq 0}$	${\ displaystyle \ sigmagt; 0, \ альфа}$
Тип III	${\ displaystyle \ left [1+ \ left ({\ frac {x- \ mu} {\ sigma}} \ right) ^ {1 / \ gamma} \ right] ^ {- 1}}$	${\ Displaystyle х \ geq \ mu}$	${\ displaystyle \ mu \ in \ mathbb {R}, \ sigma, \ gammagt; 0}$
Тип IV	${\ displaystyle \ left [1+ \ left ({\ frac {x- \ mu} {\ sigma}} \ right) ^ {1 / \ gamma} \ right] ^ {- \ alpha}}$	${\ Displaystyle х \ geq \ mu}$	${\ displaystyle \ mu \ in \ mathbb {R}, \ sigma, \ gammagt; 0, \ alpha}$

Параметр формы α - индекс хвоста, μ - местоположение, σ - масштаб, γ - параметр неравенства. Некоторые частные случаи типа Парето (IV):

${\ Displaystyle Р (IV) (\ сигма, \ сигма, 1, \ альфа) = Р (I) (\ сигма, \ альфа),}$

${\ Displaystyle Р (IV) (\ му, \ сигма, 1, \ альфа) = Р (II) (\ му, \ сигма, \ альфа),}$

${\ Displaystyle P (IV) (\ mu, \ sigma, \ gamma, 1) = P (III) (\ mu, \ sigma, \ gamma).}$

Конечность среднего, а также существование и конечность дисперсии зависят от хвостового индекса α (индекса неравенства γ). В частности, дробные δ- моменты конечны для некоторого δ gt; 0, как показано в таблице ниже, где δ не обязательно является целым числом.

Моменты распределений Парето I – IV (случай μ = 0)

	${\ displaystyle \ operatorname {E} [X]}$	Состояние	${\ displaystyle \ operatorname {E} [X ^ {\ delta}]}$	Состояние
Тип I	${\ displaystyle {\ frac {\ sigma \ alpha} {\ alpha -1}}}$	${\ displaystyle \ alphagt; 1}$	${\ displaystyle {\ frac {\ sigma ^ {\ delta} \ alpha} {\ alpha - \ delta}}}$	${\ Displaystyle \ дельта lt;\ альфа}$
Тип II	${\ displaystyle {\ frac {\ sigma} {\ alpha -1}} + \ mu}$	${\ displaystyle \ alphagt; 1}$	${\ displaystyle {\ frac {\ sigma ^ {\ delta} \ Gamma (\ alpha - \ delta) \ Gamma (1+ \ delta)} {\ Gamma (\ alpha)}}}$	${\ Displaystyle 0 lt;\ дельта lt;\ альфа}$
Тип III	${\ Displaystyle \ сигма \ Гамма (1- \ гамма) \ Гамма (1+ \ гамма)}$	${\ Displaystyle -1 lt;\ гамма lt;1}$	${\ displaystyle \ sigma ^ {\ delta} \ Gamma (1- \ gamma \ delta) \ Gamma (1+ \ gamma \ delta)}$	${\ Displaystyle - \ гамма ^ {- 1} lt;\ дельта lt;\ гамма ^ {- 1}}$
Тип IV	${\ Displaystyle {\ гидроразрыва {\ сигма \ Гамма (\ альфа - \ гамма) \ Гамма (1+ \ гамма)} {\ Гамма (\ альфа)}}}$	${\ Displaystyle -1 lt;\ гамма lt;\ альфа}$	${\ displaystyle {\ frac {\ sigma ^ {\ delta} \ Gamma (\ alpha - \ gamma \ delta) \ Gamma (1+ \ gamma \ delta)} {\ Gamma (\ alpha)}}}$	${\ Displaystyle - \ гамма ^ {- 1} lt;\ дельта lt;\ альфа / \ гамма}$

Распределение Феллера – Парето

Валочно определяет переменную Парето с помощью преобразования U  =  Y ^-1  - 1 из в бета случайной величины Y, чья вероятность того, функция плотности

${\ displaystyle f (y) = {\ frac {y ^ {\ gamma _ {1} -1} (1-y) ^ {\ gamma _ {2} -1}} {B (\ gamma _ {1}, \ gamma _ {2})}}, \ qquad 0 lt;y lt;1; \ gamma _ {1}, \ gamma _ {2}gt; 0,}$

где B () - бета-функция. Если

${\ Displaystyle W = \ mu + \ sigma (Y ^ {- 1} -1) ^ {\ gamma}, \ qquad \ sigmagt; 0, \ gammagt; 0,}$

то W имеет распределение Феллера – Парето FP ( μ, σ, γ, γ 1, γ 2).

Если и являются независимыми гамма-переменными, другая конструкция переменной Феллера – Парето (FP): ${\ Displaystyle U_ {1} \ sim \ Gamma (\ delta _ {1}, 1)}$${\ Displaystyle U_ {2} \ sim \ Gamma (\ delta _ {2}, 1)}$

${\ displaystyle W = \ mu + \ sigma \ left ({\ frac {U_ {1}} {U_ {2}}} \ right) ^ {\ gamma}}$

и пишем W ∼ FP ( μ, σ, γ, δ 1, δ 2). Частные случаи распределения Феллера – Парето:

${\ Displaystyle FP (\ sigma, \ sigma, 1,1, \ альфа) = P (I) (\ sigma, \ alpha)}$

${\ Displaystyle FP (\ му, \ сигма, 1,1, \ альфа) = п (II) (\ му, \ сигма, \ альфа)}$

${\ Displaystyle FP (\ му, \ сигма, \ гамма, 1,1) = п (III) (\ му, \ сигма, \ гамма)}$

${\ displaystyle FP (\ mu, \ sigma, \ gamma, 1, \ alpha) = P (IV) (\ mu, \ sigma, \ gamma, \ alpha).}$

Связь с экспоненциальным распределением

Распределение Парето связано с экспоненциальным распределением следующим образом. Если X распределено по Парето с минимумом x m и индексом  α, то

${\ displaystyle Y = \ log \ left ({\ frac {X} {x _ {\ mathrm {m}}}} \ right)}$

будет распределено экспоненциально с параметром скорости  альфа. Эквивалентно, если Y экспоненциально распределено со скоростью  α, то

${\ Displaystyle х _ {\ mathrm {m}} е ^ {Y}}$

распределено по Парето с минимумом x m и индексом  α.

Это можно показать, используя стандартные методы замены переменных:

${\ Displaystyle {\ begin {align} \ Pr (Y lt;y) amp; = \ Pr \ left (\ log \ left ({\ frac {X} {x _ {\ mathrm {m}}}} \ right) lt;y \ right) \\ amp; = \ Pr (X lt;x _ {\ mathrm {m}} e ^ {y}) = 1- \ left ({\ frac {x _ {\ mathrm {m}}} {x _ {\ mathrm {m}} e ^ {y}}} \ right) ^ {\ alpha} = 1-e ^ {- \ alpha y}. \ end {выравнивается}}}$

Последнее выражение представляет собой кумулятивную функцию распределения экспоненциального распределения со скоростью  α.

Распределение Парето можно построить с помощью иерархических экспоненциальных распределений. Пусть и. Тогда у нас есть и, как следствие,. ${\ Displaystyle \ фи | а \ сим {\ текст {Exp}} (а)}$${\ Displaystyle \ эта | \ фи \ сим {\ текст {Exp}} (\ фи)}$${\ displaystyle p (\ eta | a) = {\ frac {a} {(a + \ eta) ^ {2}}}}$${\ displaystyle a + \ eta \ sim {\ text {Pareto}} (a, 1)}$

В общем, если (параметризация скорости формы) и, то. ${\ displaystyle \ lambda \ sim {\ text {Gamma}} (\ alpha, \ beta)}$${\ displaystyle \ eta | \ lambda \ sim {\ text {Exp}} (\ lambda)}$${\ Displaystyle \ бета + \ эта \ сим {\ текст {Парето}} (\ бета, \ альфа)}$

Равнозначно, если и, то. ${\ displaystyle Y \ sim {\ text {Gamma}} (\ alpha, 1)}$${\ displaystyle X \ sim {\ text {Exp}} (1)}$${\ displaystyle x _ {\ text {m}} \! \ left (1 + {\ frac {X} {Y}} \ right) \ sim {\ text {Pareto}} (x _ {\ text {m}}, \ alpha)}$

Отношение к логнормальному распределению

Распределение Парето и логнормальное распределение - это альтернативные распределения для описания одних и тех же типов величин. Одна из связей между ними заключается в том, что они оба являются распределениями экспоненты случайных величин, распределенных согласно другим общим распределениям, соответственно экспоненциальному распределению и нормальному распределению. (См. Предыдущий раздел.)

Связь с обобщенным распределением Парето

Распределение Парето - это частный случай обобщенного распределения Парето, которое представляет собой семейство распределений аналогичной формы, но содержит дополнительный параметр таким образом, что носитель распределения либо ограничен снизу (в переменной точке), либо ограничены как сверху, так и снизу (где оба являются переменными), причем распределение Ломакса является частным случаем. Это семейство также содержит экспоненциальные распределения без сдвига и со сдвигом.

Распределение Парето с масштабом и формой эквивалентно обобщенному распределению Парето с расположением, масштабом и формой. И наоборот, можно получить распределение Парето из GPD с помощью и. ${\ displaystyle x_ {m}}$${\ displaystyle \ alpha}$${\ displaystyle \ mu = x_ {m}}$${\ displaystyle \ sigma = x_ {m} / \ alpha}$${\ Displaystyle \ xi = 1 / \ альфа}$${\ displaystyle x_ {m} = \ sigma / \ xi}$${\ Displaystyle \ альфа = 1 / \ xi}$

Ограниченное распределение Парето

См. Также: Усеченное распределение

Ограниченный Парето

Параметры	${\ displaystyle Lgt; 0}$ местоположение ( реальное ) местоположение ( реальное ) ${\ displaystyle Hgt; L}$ ${\ displaystyle \ alphagt; 0}$ форма (реальная)
Служба поддержки	${\ Displaystyle L \ leqslant x \ leqslant H}$
PDF	${\ displaystyle {\ frac {\ alpha L ^ {\ alpha} x ^ {- \ alpha -1}} {1- \ left ({\ frac {L} {H}} \ right) ^ {\ alpha}} }}$
CDF	${\ displaystyle {\ frac {1-L ^ {\ alpha} x ^ {- \ alpha}} {1- \ left ({\ frac {L} {H}} \ right) ^ {\ alpha}}}}$
Иметь в виду	${\ displaystyle {\ frac {L ^ {\ alpha}} {1- \ left ({\ frac {L} {H}} \ right) ^ {\ alpha}}} \ cdot \ left ({\ frac {\ alpha} {\ alpha -1}} \ right) \ cdot \ left ({\ frac {1} {L ^ {\ alpha -1}}} - {\ frac {1} {H ^ {\ alpha -1} }} \ right), \ alpha \ neq 1}$ ${\ displaystyle {\ frac {{H} {L}} {{H} - {L}}} \ ln {\ frac {H} {L}}, \ alpha = 1}$
Медиана	${\ displaystyle L \ left (1 - {\ frac {1} {2}} \ left (1- \ left ({\ frac {L} {H}} \ right) ^ {\ alpha} \ right) \ right)) ^ {- {\ frac {1} {\ alpha}}}}$
Дисперсия	${\ displaystyle {\ frac {L ^ {\ alpha}} {1- \ left ({\ frac {L} {H}} \ right) ^ {\ alpha}}} \ cdot \ left ({\ frac {\ альфа} {\ alpha -2}} \ right) \ cdot \ left ({\ frac {1} {L ^ {\ alpha -2}}} - {\ frac {1} {H ^ {\ alpha -2} }} \ right), \ alpha \ neq 2}$ ${\ displaystyle {\ frac {2 {H} ^ {2} {L} ^ {2}} {{H} ^ {2} - {L} ^ {2}}} \ ln {\ frac {H} { L}}, \ alpha = 2}$ (это второй необработанный момент, а не дисперсия)
Асимметрия	${\ displaystyle {\ frac {L ^ {\ alpha}} {1- \ left ({\ frac {L} {H}} \ right) ^ {\ alpha}}} \ cdot {\ frac {\ alpha * ( L ^ {k- \ alpha} -H ^ {k- \ alpha})} {(\ alpha -k)}}, \ alpha \ neq j}$ (это k-й необработанный момент, а не перекос)

Ограничена (или усеченный) распределение Парето имеет три параметра: α, L и H. Как и в стандартном распределении Парето, α определяет форму. L обозначает минимальное значение, а H обозначает максимальное значение.

Функция плотности вероятности :

${\ displaystyle {\ frac {\ alpha L ^ {\ alpha} x ^ {- \ alpha -1}} {1- \ left ({\ frac {L} {H}} \ right) ^ {\ alpha}} }}$,

где L  ≤  x  ≤  H и α  gt; 0.

Генерация ограниченных случайных величин Парето

Если U будет равномерно распределено на интервале (0, 1), а затем применяя метод обратного преобразования

${\ Displaystyle U = {\ гидроразрыва {1-L ^ {\ alpha} x ^ {- \ alpha}} {1 - ({\ frac {L} {H}}) ^ {\ alpha}}}}$

${\ displaystyle x = \ left (- {\ frac {UH ^ {\ alpha} -UL ^ {\ alpha} -H ^ {\ alpha}} {H ^ {\ alpha} L ^ {\ alpha}}} \ справа) ^ {- {\ frac {1} {\ alpha}}}}$

является ограниченным распределением по Парето.

Симметричное распределение Парето

Целью симметричного распределения Парето и нулевого симметричного распределения Парето является получение некоторого специального статистического распределения с острым пиком вероятности и симметричными длинными хвостами вероятности. Эти два распределения получены из распределения Парето. Длинный хвост вероятности обычно означает, что вероятность медленно убывает. Распределение Парето во многих случаях выполняет подгоночную работу. Но если распределение имеет симметричную структуру с двумя медленно затухающими хвостами, Парето не смог бы этого сделать. Тогда вместо этого применяется симметричное распределение Парето или нулевое симметричное распределение Парето.

Кумулятивная функция распределения (CDF) симметричного распределения Парето определяется следующим образом:

${\ Displaystyle F (X) = P (x lt;X) = {\ begin {cases} {\ tfrac {1} {2}} ({b \ over 2b-X}) ^ {a} amp; X lt;b \\ 1 - {\ tfrac {1} {2}} ({\ tfrac {b} {X}}) ^ {a} amp; X \ geq b \ end {case}}}$

Соответствующая функция плотности вероятности (PDF):

${\ displaystyle p (x) = {ab ^ {a} \ over 2 (b + \ left \ vert xb \ right \ vert) ^ {a + 1}}, X \ in R}$

Это распределение имеет два параметра: a и b. Он симметричен по b. Тогда математическое ожидание равно b. Когда он имеет следующие отклонения:

${\ Displaystyle E ((xb) ^ {2}) = \ int _ {- \ infty} ^ {\ infty} (xb) ^ {2} p (x) dx = {2b ^ {2} \ over (a -2) (а-1)}}$

CDF нулевого симметричного распределения Парето (ZSP) определяется следующим образом:

${\ Displaystyle F (X) = P (x lt;X) = {\ begin {cases} {\ tfrac {1} {2}} ({b \ over bX}) ^ {a} amp; X lt;0 \\ 1- {\ tfrac {1} {2}} ({\ tfrac {b} {b + X}}) ^ {a} amp; X \ geq 0 \ end {case}}}$

Соответствующий PDF-файл:

${\ displaystyle p (x) = {ab ^ {a} \ over 2 (b + \ left \ vert x \ right \ vert) ^ {a + 1}}, X \ in R}$

Это распределение симметрично нулю. Параметр a связан со скоростью убывания вероятности, а (a / 2b) представляет собой пиковую величину вероятности.

Многомерное распределение Парето

Одномерное распределение Парето было расширено до многомерного распределения Парето.

Статистические выводы

Оценка параметров

Функция правдоподобия для параметров распределения Парето α и x m для независимой выборки x = ( x 1,  x 2,...,  x n) равна

${\ displaystyle L (\ alpha, x _ {\ mathrm {m}}) = \ prod _ {i = 1} ^ {n} \ alpha {\ frac {x _ {\ mathrm {m}} ^ {\ alpha}} {x_ {i} ^ {\ alpha +1}}} = \ alpha ^ {n} x _ {\ mathrm {m}} ^ {n \ alpha} \ prod _ {i = 1} ^ {n} {\ frac {1} {x_ {i} ^ {\ alpha +1}}}.}$

Следовательно, функция логарифмического правдоподобия имеет вид

${\ displaystyle \ ell (\ alpha, x _ {\ mathrm {m}}) = п \ ln \ alpha + n \ alpha \ ln x _ {\ mathrm {m}} - (\ alpha +1) \ sum _ {i = 1} ^ {n} \ ln x_ {i}.}$

Видно, что он монотонно возрастает с увеличением x m, то есть чем больше значение x m, тем больше значение функции правдоподобия. Отсюда, поскольку x ≥ x m, заключаем, что ${\ Displaystyle \ ell (\ альфа, х _ {\ mathrm {m}})}$

${\ displaystyle {\ widehat {x}} _ {\ mathrm {m}} = \ min _ {i} {x_ {i}}.}$

Чтобы найти оценку для α, мы вычисляем соответствующую частную производную и определяем, где она равна нулю:

${\ displaystyle {\ frac {\ partial \ ell} {\ partial \ alpha}} = {\ frac {n} {\ alpha}} + n \ ln x _ {\ mathrm {m}} - \ sum _ {i = 1} ^ {n} \ ln x_ {i} = 0.}$

Таким образом, оценка максимального правдоподобия для α равна:

${\ displaystyle {\ widehat {\ alpha}} = {\ frac {n} {\ sum _ {i} \ ln (x_ {i} / {\ widehat {x}} _ {\ mathrm {m}})} }.}$

Ожидаемая статистическая ошибка:

${\ displaystyle \ sigma = {\ frac {\ widehat {\ alpha}} {\ sqrt {n}}}.}$

Малик (1970) дает точное совместное распределение. В частности, и являются независимыми и является Парето с параметром масштаба x m и параметром формы nα, тогда как имеет обратное гамма-распределение с параметрами формы и масштаба n  - 1 и nα, соответственно. ${\ displaystyle ({\ hat {x}} _ {\ mathrm {m}}, {\ hat {\ alpha}})}$${\ displaystyle {\ hat {x}} _ {\ mathrm {m}}}$${\ displaystyle {\ hat {\ alpha}}}$ ${\ displaystyle {\ hat {x}} _ {\ mathrm {m}}}$${\ displaystyle {\ hat {\ alpha}}}$

Доверительные интервалы

Рассматривая как известные (т.е.) и используя результат выше Малика (1970), CDF распределения Парето (,) можно инвертировать, чтобы сформировать доверительный интервал для, то есть CDF () =. Дополнительно возможно профилирование. То есть для каждой гипотезы производят переоценку в ограниченном нулевом пространстве и считают это известным. Нижний односторонний доверительный интервал 97,5% является гипотезой о том, что вероятность того, что верхний хвост или что-то более экстремальное, составляет 2,5%. Аналогичный подход может быть использован для получения доверительного интервала для путем инвертирования CDF обратного гамма-распределения с параметрами формы и масштаба и, соответственно, т.е. CDF () =. Двусторонние 95% доверительные интервалы - это гипотезы, согласно которым односторонняя вероятность или что-то более экстремальное составляет 2,5%. ${\ displaystyle {\ hat {\ alpha}}}$${\ displaystyle \ alpha = {\ hat {\ alpha}}}$${\ displaystyle x_ {m}}$${\ displaystyle n {\ hat {\ alpha}}}$${\ displaystyle x_ {m}}$${\ displaystyle {\ hat {x}} _ {m}}$${\ displaystyle 1 - {\ Bigl (} {\ frac {x_ {m}} {{\ hat {x}} _ {m}}} {\ Bigr)} ^ {n {\ hat {\ alpha}}} }$${\ displaystyle \ alpha}$${\ displaystyle H_ {0}: x_ {m} \ leq x_ {m_ {0}}}$${\ displaystyle \ alpha}$${\ displaystyle {\ hat {\ alpha}} _ {0}}$${\ displaystyle x_ {m}}$${\ displaystyle {\ hat {x}} _ {m}}$${\ displaystyle \ alpha}$${\ displaystyle n-1}$${\ Displaystyle п \ альфа}$${\ displaystyle {\ hat {\ alpha}}}$${\ displaystyle {\ frac {\ Gamma {\ Bigl (} n-1, {\ frac {n \ alpha} {\ hat {\ alpha}}} {\ Bigr)}} {\ Gamma (n-1)} }}$${\ displaystyle \ alpha}$${\ displaystyle {\ hat {\ alpha}}}$

Возникновение и приложения

Общий

Первоначально Вильфредо Парето использовал это распределение для описания распределения богатства между людьми, поскольку оно, казалось, довольно хорошо показывает, что большая часть богатства любого общества принадлежит меньшему проценту людей в этом обществе. Он также использовал его для описания распределения доходов. Эта идея иногда выражается проще как принцип Парето или «правило 80-20», согласно которому 20% населения контролируют 80% богатства. Однако правило 80-20 соответствует определенному значению α, и на самом деле данные Парето о британских подоходных налогах в его Cours d'économie politique показывают, что около 30% населения имели около 70% дохода. Функция плотности вероятности (PDF) график, в начале этой статьи показывает, что «вероятность» или часть населения, которой принадлежит небольшое количество богатства на человека достаточно высока, а затем постепенно уменьшается по мере увеличения благосостояния. (Однако распределение Парето нереально для богатства на нижнем уровне. Фактически, чистая стоимость может быть даже отрицательной.) Это распределение не ограничивается описанием богатства или дохода, но во многих ситуациях, в которых равновесие находится в распределение от «малого» к «большому». Следующие примеры иногда рассматриваются как приблизительно распределенные по Парето:

• Размеры населенных пунктов (несколько городов, много деревень / деревень)
• Распределение размера файлов интернет-трафика, использующего протокол TCP (много файлов меньшего размера, несколько файлов большего размера)
• Частота ошибок жесткого диска
• Кластеры конденсата Бозе – Эйнштейна вблизи абсолютного нуля

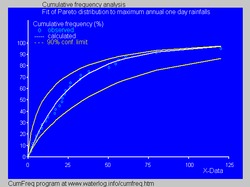
Подгонка кумулятивного распределения Парето (Lomax) к максимальным однодневным осадкам с использованием CumFreq, см. Также подгонку распределения

• Значения запасов нефти на нефтяных месторождениях (несколько крупных месторождений, много мелких месторождений )
• Распределение длин в заданиях суперкомпьютеров (несколько крупных, много мелких)
• Стандартизированная доходность по отдельным акциям
• Размеры песчинок
• Размер метеоритов
• Серьезность крупных потерь в результате несчастных случаев для определенных сфер деятельности, таких как общая ответственность, коммерческие автомобили и компенсация рабочим.
• Количество времени, которое пользователь Steam будет проводить, играя в разные игры. (В некоторые игры играют много, но в большинство почти никогда не играют.) [2]
• В гидрологии распределение Парето применяется к экстремальным явлениям, таким как годовые максимальные однодневные осадки и сток рек. На синем рисунке показан пример подгонки распределения Парето к ранжированным годовым максимальным однодневным осадкам, показывающий также пояс уверенности 90%, основанный на биномиальном распределении. Данные об осадках представлены в виде точек на графике как часть кумулятивного частотного анализа.
• В отношении надежности распределения электроэнергии (80% минут, в течение которых клиент прерывает работу, происходит примерно в 20% дней в году).

Связь с законом Ципфа

Распределение Парето - это непрерывное распределение вероятностей. Закон Ципфа, также иногда называемый дзета-распределением, представляет собой дискретное распределение, разделяющее значения на простое ранжирование. Оба представляют собой простой степенной закон с отрицательной экспонентой, масштабированный таким образом, чтобы их кумулятивные распределения равнялись 1. Коэффициенты Ципфа можно получить из распределения Парето, если значения (доходы) разделены на ранги, так что количество людей в каждой ячейке соответствует единице. / шаблон ранга. Распределение нормализуется путем определения так, что где - обобщенный номер гармоники. Это делает функцию плотности вероятности Ципфа выводимой из функции Парето. ${\ displaystyle x}$${\ displaystyle N}$${\ displaystyle x_ {m}}$${\ displaystyle \ alpha x _ {\ mathrm {m}} ^ {\ alpha} = {\ frac {1} {H (N, \ alpha -1)}}}$${\ Displaystyle Н (N, \ альфа -1)}$

${\ displaystyle f (x) = {\ frac {\ alpha x _ {\ mathrm {m}} ^ {\ alpha}} {x ^ {\ alpha +1}}} = {\ frac {1} {x ^ { s} H (N, s)}}}$

где и - целое число, представляющее ранг от 1 до N, где N - категория с наивысшим доходом. Таким образом, случайно выбранный человек (или слово, ссылка на веб-сайт или город) из населения (или языка, Интернета или страны) имеет вероятность ранжирования. ${\ displaystyle s = \ alpha -1}$${\ displaystyle x}$${\ displaystyle f (x)}$${\ displaystyle x}$

Отношение к «принципу Парето»

« Закон 80–20 », согласно которому 20% всех людей получают 80% всего дохода, а 20% наиболее богатых 20% получают 80% этих 80%, и так далее, выполняется именно тогда, когда индекс Парето есть. Этот результат может быть получен из формулы кривой Лоренца, приведенной ниже. Более того, было показано, что следующее математически эквивалентно: ${\ displaystyle \ alpha = \ log _ {4} 5 = {\ cfrac {\ log _ {10} 5} {\ log _ {10} 4}} \ приблизительно 1,161}$

• Доход распределяется по распределению Парето с индексом α  gt; 1.
• Существует некоторое число 0 ≤  p  ≤ 1/2 такое, что 100 p  % всех людей получают 100 (1 -  p)% всего дохода, и аналогично для каждого действительного (не обязательно целого) n  gt; 0, 100 p ⁿ  % от общего дохода. все люди получают 100 (1 -  p) ⁿ процентов от всех доходов. α и p связаны соотношением

${\ displaystyle 1 - {\ frac {1} {\ alpha}} = {\ frac {\ ln (1-p)} {\ ln (p)}} = {\ frac {\ ln ((1-p) ^ {n})} {\ ln (p ^ {n})}}}$

Это относится не только к доходу, но и к богатству или ко всему, что можно смоделировать с помощью этого распределения.

Это исключает распределения Парето, в которых 0 lt;  α  ≤ 1, которые, как отмечалось выше, имеют бесконечное ожидаемое значение и поэтому не могут разумно моделировать распределение доходов.

Связь с законом Прайса

Закон квадратного корня Прайса иногда предлагается как свойство или аналогично распределению Парето. Однако закон действует только в том случае, если это. Обратите внимание, что в этом случае общая и ожидаемая сумма богатства не определены, и правило применяется только асимптотически к случайным выборкам. Упомянутый выше расширенный принцип Парето является гораздо более общим правилом. ${\ Displaystyle \ альфа = 1}$

Кривая Лоренца и коэффициент Джини

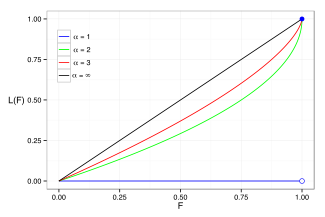
Кривые Лоренца для ряда распределений Парето. Случай α  = ∞ соответствует идеально равному распределению ( G  = 0), а линия α  = 1 соответствует полному неравенству ( G  = 1)

Кривая Лоренца часто используется для характеристики распределения доходов и богатства. Для любого распределения кривая Лоренца L ( F) записывается в терминах PDF f или CDF F как

${\ Displaystyle L (F) = {\ гидроразрыва {\ int _ {x _ {\ mathrm {m}}} ^ {x (F)} xf (x) \, dx} {\ int _ {x _ {\ mathrm { m}}} ^ {\ infty} xf (x) \, dx}} = {\ frac {\ int _ {0} ^ {F} x (F ') \, dF'} {\ int _ {0} ^ {1} х (F ') \, dF'}}}$

где x ( F) - обратная функция CDF. Для распределения Парето

${\ displaystyle x (F) = {\ frac {x _ {\ mathrm {m}}} {(1-F) ^ {\ frac {1} {\ alpha}}}}}$

а кривая Лоренца рассчитывается как

${\ Displaystyle L (F) = 1- (1-F) ^ {1 - {\ frac {1} {\ alpha}}},}$

Поскольку знаменатель бесконечен, получаем L = 0. Примеры кривой Лоренца для ряда распределений Парето показаны на графике справа. ${\ Displaystyle 0 lt;\ альфа \ leq 1}$

По данным Oxfam (2016) 62 самых богатых человека имеют такое же состояние, как и беднейшая половина населения мира. Мы можем оценить индекс Парето, который применим к этой ситуации. Приравнивая ε, имеем: ${\ displaystyle 62 / (7 \ times 10 ^ {9})}$

${\ Displaystyle L (1/2) = 1-L (1- \ varepsilon)}$

или

${\ displaystyle 1- (1/2) ^ {1 - {\ frac {1} {\ alpha}}} = \ varepsilon ^ {1 - {\ frac {1} {\ alpha}}}}$

Решение состоит в том, что α равно примерно 1,15, и около 9% богатства принадлежит каждой из двух групп. Но на самом деле 69% беднейшего взрослого населения мира владеют лишь 3% богатства.

Коэффициент Джини - это мера отклонения кривой Лоренца от линии равнораспределения, которая представляет собой линию, соединяющую [0, 0] и [1, 1], которая показана черным ( α  = ∞) на графике Лоренца на Правильно. В частности, коэффициент Джини в два раза больше площади между кривой Лоренца и линией равнораспределения. Затем рассчитывается коэффициент Джини для распределения Парето (для) ${\ displaystyle \ alpha \ geq 1}$

${\ displaystyle G = 1-2 \ left (\ int _ {0} ^ {1} L (F) \, dF \ right) = {\ frac {1} {2 \ alpha -1}}}$

(см. Aaberge 2005).

Вычислительные методы

Генерация случайной выборки

Случайные выборки могут быть сгенерированы с использованием выборки с обратным преобразованием. Для случайной переменной U, взятой из равномерного распределения на единичном интервале (0, 1], переменная T, заданная формулой

${\ Displaystyle Т = {\ гидроразрыва {х _ {\ mathrm {m}}} {U ^ {1 / \ alpha}}}}$

распределено по Парето. Если U равномерно распределен на [0, 1), его можно заменить на (1 -  U).

Смотрите также

• Закон Брэдфорда
• Закон Гутенберга – Рихтера
• Эффект Мэтью
• Парето анализ
• Парето эффективность
• Интерполяция Парето
• Распределения вероятностей степенного закона
• Закон осетровых рыб
• Модель генерации трафика
• Закон Ципфа
• Распределение с тяжелым хвостом

использованная литература

Примечания

• М.О. Лоренц (1905). «Методы измерения концентрации богатства». Публикации Американской статистической ассоциации. 9 (70): 209–19. Bibcode : 1905PAmSA... 9..209L. DOI : 10.2307 / 2276207. JSTOR   2276207.
• Парето, Вильфредо (1965). Librairie Droz (ред.). Ecrits sur la courbe de la répartition de la richesse. Uvres complete: T. III. п. 48. ISBN   9782600040211.

• Парето, Вильфредо (1895). "La legge della domanda". Giornale Degli Economisti. 10: 59–68.
• Парето, Вильфредо (1896). "Cours d'économie politique". DOI : 10,1177 / 000271629700900314. S2CID   143528002. Цитировать журнал требует |journal=( помощь )

внешние ссылки

• "Распределение Парето", Математическая энциклопедия, EMS Press, 2001 [1994]
• Вайсштейн, Эрик В. «Распределение Парето». MathWorld.
• Оберже, Рольф (май 2005 г.). «Ядерная семья Джини». Международная конференция, посвященная двум выдающимся социологам (PDF).

• Crovella, Mark E. ; Беставрос, Азер (декабрь 1997 г.). Самоподобие в интернет-трафике: доказательства и возможные причины (PDF). Транзакции IEEE / ACM в сети. 5. С. 835–846. Архивировано из оригинального (PDF) 04 марта 2016 года. Проверено 25 февраля 2019.

• syntraf1.c - это программа на языке C для генерации синтетического пакетного трафика с ограниченным размером пакета Парето и экспоненциальным временем между пакетами.