Демпфирование

редактировать

Эта статья о затухании в колебательных системах. Для использования в других целях, см Демпфирование (значения).

Классическая механика
Часть серии по
${\ displaystyle {\ textbf {F}} = {\ frac {d} {dt}} (м {\ textbf {v}})}$ ${\ displaystyle {\ textbf {F}} = {\ frac {d} {dt}} (м {\ textbf {v}})}$ Второй закон движения
История Лента новостей Учебники
ветви
Основы
Составы
Основные темы
Вращение
Ученые
Физический портал Категория
v т е

Недемпфированная система пружина – масса с ζ lt;1

Демпфирование - это влияние внутри колебательной системы или на нее, которое снижает или предотвращает ее колебания. В физических системах затухание вызывается процессами, которые рассеивают энергию, запасенную в колебаниях. Примеры включают вязкое сопротивление (вязкость жидкости может препятствовать колебательной системе, вызывая ее замедление) в механических системах, сопротивление в электронных генераторах, а также поглощение и рассеяние света в оптических генераторах. Демпфирование, не основанное на потерях энергии, может быть важным в других колебательных системах, например, в биологических системах и велосипедах (например, подвеска (механика) ). Не следует путать с трением, которое представляет собой диссипативную силу, действующую на систему. Трение может быть причиной или быть фактором демпфирования.

Коэффициент демпфирования - это безразмерная мера, описывающая, как колебания в системе затухают после возмущения. Многие системы демонстрируют колебательное поведение, когда они выходят из положения статического равновесия. Например, масса, подвешенная на пружине, может, если ее потянуть и отпустить, подпрыгнуть вверх и вниз. При каждом отскоке система стремится вернуться в свое положение равновесия, но проскакивает его. Иногда потери (например, фрикционные ) демпфируют систему и могут вызывать постепенное затухание амплитуды колебаний до нуля или ослабление. Коэффициент затухания - это мера, описывающая, насколько быстро колебания затухают от одного отскока к другому.

Коэффициент демпфирования - это системный параметр, обозначаемый ζ (дзета), который может варьироваться от незатухающего ( ζ = 0), слабозатухающего ( ζ lt;1) до критически затухающего ( ζ = 1) до чрезмерного демпфирования ( ζ gt; 1).

Поведение колебательных систем часто представляет интерес в самых разных дисциплинах, включая технику управления, химическую инженерию, машиностроение, структурную инженерию и электротехнику. Физическая величина, которая колеблется, сильно варьируется и может быть колебанием высокого здания на ветру или скоростью электродвигателя, но нормализованный или безразмерный подход может быть удобным для описания общих аспектов поведения.

СОДЕРЖАНИЕ

1 Колебательные корпуса
2 Затухающая синусоида
3 Определение коэффициента демпфирования
4 Вывод
5 Q- фактор и скорость затухания
6 Логарифмический декремент
7 Процент превышения
8 примеров и приложений
- 8.1 Вязкое сопротивление
- 8.2 Демпфирование в электрических системах
- 8.3 Магнитное демпфирование
9 ссылки

Колебательные случаи

В зависимости от степени демпфирования система демонстрирует различные колебательные режимы и скорости.

Там, где система пружина-масса полностью без потерь, масса будет колебаться бесконечно, причем каждый отскок будет иметь одинаковую высоту с последним. Этот гипотетический случай называется незатухающим.
Если бы система имела большие потери, например, если бы эксперимент с пружиной и массой проводился в вязкой жидкости, масса могла бы медленно возвращаться в исходное положение, никогда не превышая ее. Этот случай называется сверхдемпфированием.
Обычно масса имеет тенденцию выходить за пределы своего начального положения, а затем возвращаться, снова выскакивая за пределы. При каждом выбросе некоторая энергия в системе рассеивается, и колебания затухают до нуля. Этот случай называется недемпфированным.
Между случаями с избыточным и недостаточным демпфированием существует определенный уровень демпфирования, при котором система просто не сможет перескочить и не совершит ни одного колебания. Этот случай называется критическим демпфированием. Ключевое различие между критическим демпфированием и избыточным демпфированием состоит в том, что при критическом демпфировании система возвращается в состояние равновесия за минимальное время.

Затухающая синусоида

Не путать с затухающей волной (радиопередача).

{\ Displaystyle у (т) = е ^ {- т} \ cdot \ соз (2 \ пи т)}

y (t) = e ^ {{- t}} \ cdot \ cos (2 \ pi t)

Затухать синусоидой или затухающая синусоида является синусоидальной функцией, амплитуда которого приближается к нулю при возрастании времени, соответствующем underdamped случае затухающих систем второго порядка, или underdamped дифференциальных уравнений второго порядка. Затухающие синусоидальные волны обычно встречаются в науке и технике, где гармонический осциллятор теряет энергию быстрее, чем подается. Истинная синусоида, начинающаяся в момент времени = 0, начинается в начале координат (амплитуда = 0). Косинусоидальная волна начинается с максимального значения из-за разницы фаз от синусоидальной волны. Данная синусоидальная форма волны может иметь промежуточную фазу, имеющую как синусоидальную, так и косинусоидальную составляющие. Термин «затухающая синусоида» описывает все такие затухающие формы волны, независимо от их начальной фазы.

Наиболее распространенная форма демпфирования, которая обычно принимается, - это форма, встречающаяся в линейных системах. Эта форма представляет собой экспоненциальное затухание, при котором внешняя огибающая последовательных пиков представляет собой кривую экспоненциального затухания. То есть, когда вы соединяете максимальную точку каждой последующей кривой, результат напоминает функцию экспоненциального затухания. Общее уравнение для экспоненциально затухающей синусоиды может быть представлено как:

{\ Displaystyle у (T) = A \ CDOT е ^ {- \ лямбда т} \ CDOT \ соз (\ омега т- \ фи)}

{\ Displaystyle у (T) = A \ CDOT е ^ {- \ лямбда т} \ CDOT \ соз (\ омега т- \ фи)}

куда:

{\ Displaystyle у (т)}

у (т)

- мгновенная амплитуда в момент времени t ;

{\ displaystyle A}

А

- начальная амплитуда огибающей;

{\ displaystyle \ lambda}

\ lambda

- скорость убывания, обратная единицам времени независимой переменной t ;

{\ displaystyle \ phi}

\ phi

- фазовый угол при t = 0;

{\ displaystyle \ omega}

\омега

- угловая частота.

К другим важным параметрам относятся:

Частота :, количество циклов в единицу времени. Он выражается в обратных единицах времени или герцах. ${\ Displaystyle е = \ омега / (2 \ пи)}$ ${\ Displaystyle е = \ омега / (2 \ пи)}$ ${\ displaystyle t ^ {- 1}}$ $t ^ {- 1}$
Постоянная времени :, время уменьшения амплитуды в е раз. ${\ Displaystyle \ тау = 1 / \ лямбда}$ ${\ Displaystyle \ тау = 1 / \ лямбда}$
Период полураспада - это время, необходимое для уменьшения огибающей экспоненциальной амплитуды в 2 раза. Оно равно примерно. ${\ displaystyle \ ln (2) / \ lambda}$ ${\ displaystyle \ ln (2) / \ lambda}$ ${\ displaystyle 0.693 / \ lambda}$ ${\ displaystyle 0.693 / \ lambda}$
Коэффициент демпфирования: безразмерная характеристика скорости затухания относительно частоты, приблизительно или точно. ${\ displaystyle \ zeta}$ $\ zeta$ ${\ displaystyle \ zeta = \ lambda / \ omega}$ ${\ displaystyle \ zeta = \ lambda / \ omega}$ ${\ displaystyle \ zeta = \ lambda / {\ sqrt {\ lambda ^ {2} + \ omega ^ {2}}} lt;1}$ ${\ displaystyle \ zeta = \ lambda / {\ sqrt {\ lambda ^ {2} + \ omega ^ {2}}} lt;1}$
Q-фактор : это еще одна безразмерная характеристика величины демпфирования; высокий Q указывает на медленное затухание относительно колебаний. ${\ Displaystyle Q = 1 / (2 \ zeta)}$ ${\ Displaystyle Q = 1 / (2 \ zeta)}$

Определение коэффициента демпфирования

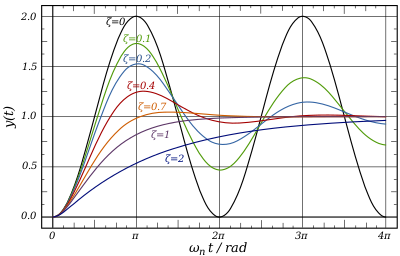Влияние изменения коэффициента демпфирования на систему второго порядка.

Коэффициент затухания является параметром, обычно обозначается z, (греческой буквы дзета), который характеризует частотный отклик в виде обыкновенного дифференциального уравнения второго порядка. Это особенно важно при изучении теории управления. Это также важно в гармоническом осцилляторе. В общем, системы с более высокими коэффициентами демпфирования (один или больше) будут демонстрировать больший эффект демпфирования. Системы с недостаточным демпфированием имеют значение меньше единицы. Системы с критическим демпфированием имеют коэффициент демпфирования ровно 1 или, по крайней мере, очень близок к нему.

Коэффициент демпфирования представляет собой математическое средство выражения уровня демпфирования в системе относительно критического демпфирования. Для затухающего гармонического осциллятора с массой m, коэффициентом демпфирования c и жесткостью пружины k его можно определить как отношение коэффициента демпфирования в дифференциальном уравнении системы к критическому коэффициенту демпфирования:

{\ displaystyle \ zeta = {\ frac {c} {c_ {c}}} = {\ frac {\ text {фактическое демпфирование}} {\ text {критическое демпфирование}}},}

{\ displaystyle \ zeta = {\ frac {c} {c_ {c}}} = {\ frac {\ text {фактическое демпфирование}} {\ text {критическое демпфирование}}},}

где уравнение движения системы

{\ displaystyle m {\ frac {d ^ {2} x} {dt ^ {2}}} + c {\ frac {dx} {dt}} + kx = 0}

m {\ frac {d ^ {2} x} {dt ^ {2}}} + c {\ frac {dx} {dt}} + kx = 0

а соответствующий критический коэффициент демпфирования равен

{\ displaystyle c_ {c} = 2 {\ sqrt {км}}}

{\ displaystyle c_ {c} = 2 {\ sqrt {км}}}

или

{\ displaystyle c_ {c} = 2m {\ sqrt {\ frac {k} {m}}} = 2m \ omega _ {n}}

{\ displaystyle c_ {c} = 2m {\ sqrt {\ frac {k} {m}}} = 2m \ omega _ {n}}

куда

{\ displaystyle \ omega _ {n} = {\ sqrt {\ frac {k} {m}}}}

{\ displaystyle \ omega _ {n} = {\ sqrt {\ frac {k} {m}}}}

- собственная частота системы.

Коэффициент демпфирования безразмерен и представляет собой отношение двух коэффициентов одинаковых единиц.

Вывод

Используя собственную частоту гармонического осциллятора и определение коэффициента демпфирования выше, мы можем переписать это как: ${\ textstyle \ omega _ {n} = {\ sqrt {{k} / {m}}}}$ ${\ textstyle \ omega _ {n} = {\ sqrt {{k} / {m}}}}$

{\ displaystyle {\ frac {d ^ {2} x} {dt ^ {2}}} + 2 \ zeta \ omega _ {n} {\ frac {dx} {dt}} + \ omega _ {n} ^ {2} x = 0.}

{\ frac {d ^ {2} x} {dt ^ {2}}} + 2 \ zeta \ omega _ {n} {\ frac {dx} {dt}} + \ omega _ {n} ^ {2} х = 0.

Это уравнение является более общим, чем просто система масса-пружина, а также применимо к электрическим цепям и другим областям. Это можно решить с помощью подхода.

{\ displaystyle x (t) = Ce ^ {st},}

{\ displaystyle x (t) = Ce ^ {st},}

где C и s - комплексные константы, причем s удовлетворяет

{\ displaystyle s = - \ omega _ {n} \ left (\ zeta \ pm i {\ sqrt {1- \ zeta ^ {2}}} \ right).}

{\ displaystyle s = - \ omega _ {n} \ left (\ zeta \ pm i {\ sqrt {1- \ zeta ^ {2}}} \ right).}

Два таких решения для двух значений s, удовлетворяющих уравнению, могут быть объединены для получения общих реальных решений с колебательными и затухающими свойствами в нескольких режимах:

Незатухающий: Это случай, когда соответствует незатухающему простому гармоническому осциллятору, и в этом случае решение выглядит так, как ожидалось. Этот случай чрезвычайно редок в мире природы, и наиболее близкими примерами являются случаи, когда трение было целенаправленно снижено до минимальных значений. ${\ displaystyle \ zeta = 0}$ ${\ displaystyle \ zeta = 0}$ ${\ Displaystyle \ ехр (я \ омега _ {п} т)}$ $\ ехр (я \ омега _ {п} т)$
Недостаточно демпфированный: Если s - это пара комплексных значений, то каждый член комплексного решения представляет собой убывающую экспоненту в сочетании с колеблющейся частью, которая выглядит так. Этот случай имеет место и называется недостаточным демпфированием (например, эластичный кабель). ${\ textstyle \ exp \ left (я \ omega _ {n} {\ sqrt {1- \ zeta ^ {2}}} t \ right)}$ ${\ textstyle \ exp \ left (я \ omega _ {n} {\ sqrt {1- \ zeta ^ {2}}} t \ right)}$ ${\ Displaystyle \ 0 \ Leq \ zeta lt;1}$ ${\ Displaystyle \ 0 \ Leq \ zeta lt;1}$
Сверхдемпфированный: Если s - пара действительных значений, то решение представляет собой просто сумму двух убывающих экспонент без колебаний. Этот случай имеет место и называется сверхдемпфированием. Ситуации, в которых чрезмерное демпфирование практично, имеют тенденцию к трагическим последствиям, если происходит перенапряжение, обычно электрическое, а не механическое. Например, посадка самолета на автопилоте: если система пролетит мимо и выпустит шасси слишком поздно, это приведет к катастрофе. ${\ displaystyle \ zetagt; 1}$ $\ zetagt; 1$
Критически затухающий: Случай, когда является границей между случаями сверхдемпфирования и недостаточного демпфирования, называется критически демпфированным. Это оказывается желательным результатом во многих случаях, когда требуется инженерное проектирование демпфирующего генератора (например, механизма закрытия двери). ${\ displaystyle \ zeta = 1}$ $\ zeta = 1$

Q - фактор и скорость распада

Q - фактор, коэффициент демпфирования ζ, и экспоненциальной скорости распада α связаны таким образом, что

{\ displaystyle \ zeta = {\ frac {1} {2Q}} = {\ alpha \ over \ omega _ {n}}.}

{\ displaystyle \ zeta = {\ frac {1} {2Q}} = {\ alpha \ over \ omega _ {n}}.}

Когда система второго порядка имеет (то есть, когда система underdamped), она имеет два комплексно - сопряженных полюсов, каждый из которых имеет действительную часть из ; то есть параметр скорости затухания представляет собой скорость экспоненциального затухания колебаний. Более низкий коэффициент демпфирования подразумевает меньшую скорость затухания, и поэтому системы с очень слабым демпфированием колеблются в течение длительного времени. Например, высококачественный камертон с очень низким коэффициентом демпфирования имеет длительные колебания, которые очень медленно затухают после удара молотком. ${\ displaystyle \ zeta lt;1}$ $\ zeta lt;1$ ${\ displaystyle - \ alpha}$ $-\альфа$ ${\ displaystyle \ alpha}$ $\альфа$

Логарифмический декремент

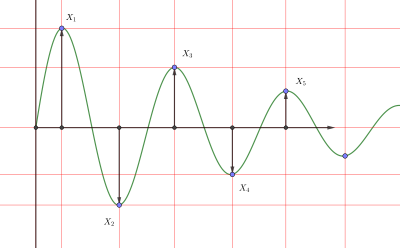
Для недостаточно затухающих колебаний коэффициент демпфирования также связан с логарифмическим декрементом. Коэффициент затухания может быть найден для любых двух пиков, даже если они не являются смежными. Для соседних пиков: ${\ displaystyle \ delta}$ $\ дельта$

{\ displaystyle \ zeta = {\ frac {\ delta} {\ sqrt {\ delta ^ {2} + \ left (2 \ pi \ right) ^ {2}}}}}

{\ displaystyle \ zeta = {\ frac {\ delta} {\ sqrt {\ delta ^ {2} + \ left (2 \ pi \ right) ^ {2}}}}}

куда

{\ displaystyle \ delta = \ ln {\ frac {x_ {0}} {x_ {1}}}}

{\ displaystyle \ delta = \ ln {\ frac {x_ {0}} {x_ {1}}}}

где x 0 и x 1 - амплитуды любых двух последовательных пиков.

Как показано на правом рисунке:

{\ displaystyle \ delta = \ ln {\ frac {x_ {1}} {x_ {3}}} = \ ln {\ frac {x_ {2}} {x_ {4}}} = \ ln {\ frac { x_ {1} -x_ {2}} {x_ {3} -x_ {4}}}}

{\ displaystyle \ delta = \ ln {\ frac {x_ {1}} {x_ {3}}} = \ ln {\ frac {x_ {2}} {x_ {4}}} = \ ln {\ frac { x_ {1} -x_ {2}} {x_ {3} -x_ {4}}}}

где, - амплитуды двух последовательных положительных пиков и, - амплитуды двух последовательных отрицательных пиков. ${\ displaystyle x_ {1}}$ $х_ {1}$ ${\ displaystyle x_ {3}}$ $x_ {3}$ ${\ displaystyle x_ {2}}$ $x_ {2}$ ${\ displaystyle x_ {4}}$ $x_ {4}$

Процент превышения

В теории управления, перерегулирование относится к выходу превышает его окончательное, стационарное значение. Для пошагового ввода, то процент перерегулирование (РО) представляет собой максимальное значение минус значение шага, деленное на значение шага. В случае единичного шага перерегулирование - это просто максимальное значение реакции на скачок минус один.

Процент превышения (PO) связан с коэффициентом демпфирования ( ζ) следующим образом:

{\ displaystyle \ mathrm {PO} = 100 \ exp \ left ({- {\ frac {\ zeta \ pi} {\ sqrt {1- \ zeta ^ {2}}}}} \ right)}

{\ displaystyle \ mathrm {PO} = 100 \ exp \ left ({- {\ frac {\ zeta \ pi} {\ sqrt {1- \ zeta ^ {2}}}}} \ right)}

И наоборот, коэффициент демпфирования ( ζ), который приводит к заданному процентному превышению, определяется как:

{\ displaystyle \ zeta = {\ frac {- \ ln \ left ({\ frac {\ rm {PO}} {100}} \ right)} {\ sqrt {\ pi ^ {2} + \ ln ^ {2 } \ left ({\ frac {\ rm {PO}} {100}} \ right)}}}}

{\ displaystyle \ zeta = {\ frac {- \ ln \ left ({\ frac {\ rm {PO}} {100}} \ right)} {\ sqrt {\ pi ^ {2} + \ ln ^ {2 } \ left ({\ frac {\ rm {PO}} {100}} \ right)}}}}

Примеры и приложения

Вязкое сопротивление

Представьте, что вы роняете предмет. Пока этот объект падает в воздухе, единственная сила, препятствующая его свободному падению, - это сопротивление воздуха. Если вы уроните объект в воду или масло, он начнет замедляться с большей скоростью, пока в конечном итоге не достигнет установившейся скорости, поскольку сила сопротивления уравновесится с силой тяжести. Это концепция вязкого сопротивления. Применение этой концепции в повседневной жизни объясняет физику автоматических дверей или дверей с защитой от захлопывания.

Демпфирование в электрических системах

Электрические системы, работающие с переменным током (AC), используют резисторы для гашения электрического тока, поскольку они являются периодическими. Диммерные переключатели или ручки регулировки громкости являются примерами демпфирования в электрической системе.

Магнитное демпфирование

Кинетическая энергия, вызывающая колебания, рассеивается в виде тепла электрическими вихревыми токами, которые индуцируются при прохождении через полюса магнита катушкой или алюминиевой пластиной. Другими словами, сопротивление, вызванное магнитными силами, замедляет работу системы. Примером применения этой концепции в реальном мире являются тормоза на американских горках.

использованная литература

11. Британника, Энциклопедия. «Демпфирование». Британская энциклопедия, Британская энциклопедия, Inc., www.britannica.com/science/damping.

12. OpenStax, Колледж. «Физика». Lumen, course.lumenlearning.com/physics/chapter/23-4-eddy-currents-and-mintage-damping/.