Константы Оорта

редактировать

Константы Оорта (обнаружил Ян Оорт ) $A {\ displaystyle A}$ $A$ и $B {\ displaystyle B}$ $B$ - это эмпирически полученные параметры, которые характеризуют локальные свойства вращения нашей галактики Млечный Путь в следующим образом:

A = 1 2 (V 0 R 0 - dvdr | R 0) B = - 1 2 (V 0 R 0 + dvdr | R 0) {\ displaystyle {\ begin {align} A = { \ frac {1} {2}} \ left ({\ frac {V_ {0}} {R_ {0}}} - {\ frac {dv} {dr}} {\ Bigg \ vert} _ {R_ {0 }} \ right) \\ B = - {\ frac {1} {2}} \ left ({\ frac {V_ {0}} {R_ {0}}} + {\ frac {dv} {dr}} {\ Bigg \ vert} _ {R_ {0}} \ right) \\\ конец {выровнено}}}

{\ displaystyle {\ begin {align} A = {\ frac {1} {2}} \ left ({\ frac { В_ {0}} {Р _ {0}}} - {\ frac {dv} {dr}} {\ Bigg \ vert} _ {R_ {0}} \ right) \\ B = - {\ frac {1} {2}} \ left ({\ frac {V_ {0}} {R_ {0}}} + {\ frac {dv} {dr}} {\ Bigg \ vert} _ {R_ {0}} \ right) \\\ конец {выровнен }}}

где $V 0 {\ displaystyle V_ {0}}$ $V_{0}$ и $R 0 {\ displaystyle R_ {0}}$ $R_{0}$ - скорость вращения и расстояние до центра Галактики соответственно, измеренные в положении Солнца, а vи r- скорости и расстояния в других положениях в нашей части галактика. Как показано ниже, Aи Bзависят только от движений и положений звезд в окрестности Солнца. По состоянию на 2018 год наиболее точные значения этих констант: $A {\ displaystyle A}$ $A$ = 15,3 ± 0,4 км с kpc, $B {\ displaystyle B}$ $B$ = -11,9 ± 0,4 км с kpc . Из констант Оорта можно определить орбитальные свойства Солнца, такие как орбитальная скорость и период, и вывести локальные свойства галактического диска, такие как массовая плотность и как скорость вращения изменяется в зависимости от радиуса от центра Галактики.

Содержание

1 Историческое значение и история вопроса
2 Вывод
3 Измерения
4 Значение
- 4.1 Вращение твердого тела
- 4.2 Кеплеровское вращение
- 4.3 Плоская кривая вращения
5 Использование
6 См. Также
7 Ссылки
8 Внешние ссылки

Историческое значение и предыстория

К 1920-м годам большая часть астрономического сообщества осознала, что некоторые из распространенных, облакоподобные объекты или туманности, наблюдаемые в ночном небе, представляли собой совокупность звезд, расположенных за пределами нашей локальной совокупности звездных скоплений. Эти галактики имели разнообразную морфологию, от эллипсоидов до дисков. Концентрированная полоса звездного света, которая является видимым признаком Млечного Пути, указывает на структуру диска нашей галактики; однако наше положение в нашей галактике затрудняло определение структуры на основе наблюдений.

Классическая механика предсказывала, что совокупность звезд может поддерживаться против гравитационного коллапса либо случайными скоростями звезд, либо их вращением вокруг своего центра масс. Для дисковой коллекции опора должна быть в основном поворотной. В зависимости от плотности массы или распределения массы в диске скорость вращения может быть разной на каждом радиусе от центра диска до внешнего края. График зависимости этих скоростей вращения от радиусов, на которых они измеряются, называется кривой вращения. Для внешних дисковых галактик можно измерить кривую вращения, наблюдая доплеровские сдвиги спектральных характеристик, измеренные по разным галактическим радиусам, поскольку одна сторона галактики будет двигаться к нашему лучу зрения, а другая - в сторону. Однако наше положение в средней плоскости Галактики Млечного Пути, где пыль в молекулярных облаках заслоняет большую часть оптического света во многих направлениях, делало получение нашей собственной кривой вращения технически трудным до открытия 21 см. водородная линия в 1930-е гг.

Чтобы подтвердить вращение нашей галактики до этого, в 1927 году Ян Оорт разработал способ измерения вращения Галактики по небольшой части звезд в окрестностях. Как описано ниже, значения, которые он нашел для $A {\ displaystyle A}$ $A$ и $B {\ displaystyle B}$ $B$ , доказали не только то, что Галактика вращалась, но и что он вращается дифференциально или как жидкость, а не твердое тело.

Вывод

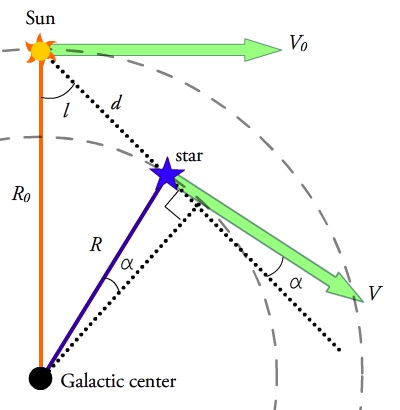
Рис. 1: Геометрия вывода констант Оорта, с полевой звездой, расположенной близко к Солнцу в средней плоскости Галактики.

Рассмотрим звезду в средней плоскости диска Галактики с Галактическая долгота $l {\ displaystyle l}$ $l$ на расстоянии $d {\ displaystyle d}$ $d$ от Солнца. Предположим, что и звезда, и Солнце имеют круговые орбиты вокруг центра Галактики с радиусами $R {\ displaystyle R}$ $R$ и $R 0 {\ displaystyle R_ {0}}$ $R_{0}$ от галактического центра и скорости вращения $V {\ displaystyle V}$ $V$ и $V 0 {\ displaystyle V_ {0}}$ $V_{{0}}$ соответственно. Движение звезды вдоль луча зрения, или лучевая скорость, и движение звезды по плоскости неба, или поперечная скорость, наблюдаемые из положения Солнце тогда:

V набл, r = V звезда, r - V солнце, r = V cos ⁡ (α) - V 0 sin ⁡ (l) V набл, t = V звезда, t - V солнце, t Знак равно V грех ⁡ (α) - V 0 соз ⁡ (l) {\ displaystyle {\ begin {align} V _ {\ text {obs, r}} = V _ {\ text {star, r}} - V _ {\ text {солнце, r}} = V \ cos \ left (\ alpha \ right) -V_ {0} \ sin \ left (l \ right) \\ V _ {\ text {obs, t}} = V _ {\ text { звезда, t}} - V _ {\ text {солнце, t}} = V \ sin \ left (\ alpha \ right) -V_ {0} \ cos \ left (l \ right) \\\ end {выровнено}} }

{\ displaystyle {\ begin {align} V _ {\ text {obs, r}} = V _ {\ text {star, r}} - V _ {\ text {sun, r}} = V \ cos \ left (\ alpha \ right) -V_ {0} \ sin \ left (l \ right) \\ V _ {\ text {obs, t}} = V _ {\ text {star, t}} - V _ {\ text {sun, t}} = V \ sin \ left (\ alpha \ right) -V_ {0} \ cos \ left (l \ right) \\\ конец {выровнен}}}

В предположении кругового движения скорость вращения связана с угловой скоростью соотношением $v = Ω r {\ displaystyle v = \ Omega r}$ ${\ displaystyle v = \ Omega r}$ и мы можем подставить это в выражения для скорости:

V obs, r = Ω R cos ⁡ (α) - Ω 0 R 0 sin ⁡ (l) V obs, t = Ω R sin ⁡ (α) - Ω 0 R 0 соз ⁡ (l) {\ displaystyle {\ begin {align} V _ {\ text {obs, r}} = \ Omega R \ cos \ left (\ alpha \ right) - \ Omega _ {0} R_ {0} \ sin \ left (l \ right) \\ V _ {\ text {obs, t}} = \ Omega R \ sin \ left (\ alpha \ right) - \ Omega _ {0} R_ {0} \ cos \ left (l \ right) \\\ end {align}}}

{\ displaystyle {\ begin {align} V _ {\ text {obs, r}} = \ Omega R \ cos \ left (\ alpha \ right) - \ Omega _ {0} R_ {0} \ sin \ left (l \ right) \\ V _ {\ text {obs, t}} = \ Omega R \ sin \ left (\ alpha \ right) - \ Omega _ {0} R_ {0} \ cos \ left (l \ right) \\\ конец {выровнено}}}

Из геометрии на Рисунке 1 видно, что треугольники, образованные между центром Галактики, Солнцем и звездой, имеют одну или несколько сторон, поэтому следующие соотношения сохраняются и могут быть сделаны замены:

R cos ⁡ (α) = R 0 sin ⁡ (l) R грех ⁡ (α) знак равно р 0 соз ⁡ (л) - d {\ Displaystyle {\ begin {выровнено} R \ соз \ влево (\ альфа \ вправо) = R_ {0} \ грех \ влево (л \ вправо) \ \ R \ sin \ left (\ alpha \ right) = R_ {0} \ cos \ left (l \ right) -d \\\ end {align}}}

{\begin{aligned}R\cos \left(\alpha \right)=R_{0}\sin \left(l\right)\\R\sin \left(\alpha \right)=R_{0}\cos \left(l\right)-d\\\end{aligned}}

и с ними мы получаем

V obs, r знак равно (Ω - Ω 0) R 0 грех ⁡ (l) V obs, t = (Ω - Ω 0) R 0 соз ⁡ (l) - Ω d {\ displaystyle {\ begin {align} V _ {\ text {obs, r}} = \ left (\ Omega - \ Omega _ {0} \ right) R_ {0} \ sin \ left (l \ right) \\ V _ {\ text {obs, t}} = \ left (\ Omega - \ Omega _ {0} \ right) R_ {0} \ cos \ left (l \ right) - \ Omega d \\\ end {align}}}

{\ displaystyle {\ begin {align} V _ {\ текст {obs, r}} = \ left (\ Omega - \ Omega _ {0} \ right) R_ {0} \ sin \ left (l \ right) \\ V _ {\ text {obs, t}} = \ слева (\ Omega - \ Omega _ {0} \ right) R_ {0} \ cos \ left (l \ right) - \ Omega d \\\ конец {выровнено}}}

Чтобы поместить эти выражения только в терминах т Если известны величины $l {\ displaystyle l}$ $l$ и $d {\ displaystyle d}$ $d$ , мы берем разложение Тейлора из $Ω - Ω 0 {\ displaystyle \ Omega - \ Omega _ {0}}$ ${\ displaystyle \ Omega - \ Omega _ {0}}$ около $R 0 {\ displaystyle R_ {0}}$ $R_{0}$ .

(Ω - Ω 0) = (R - R 0) d Ω dr | R 0 +... {\ displaystyle \ left (\ Omega - \ Omega _ {0} \ right) = \ left (R-R_ {0} \ right) {\ frac {d \ Omega} {dr}} {\ Bigg \ vert} _ {R_ {0}} +...}

{\ displaystyle \ left (\ Omega - \ Omega _ {0} \ right) = \ left (R-R_ {0} \ right) {\ frac {d \ Omega} {dr}} {\ Bigg \ vert} _ {R_ {0 }} +...}

Кроме того, мы используем предположение о том, что звезды, используемые для этого анализа, являются локальными, т.е. $R - R 0 {\ displaystyle R-R_ {0}}$ ${\ displaystyle R-R_ {0}}$ мало, а расстояние d до звезды меньше, чем $R {\ displaystyle R}$ $R$ или $R 0 {\ displaystyle R_ {0}}$ $R_{0}$ , и берем:

R - R 0 = - d ⋅ cos ⁡ (l) {\ displaystyle R-R_ {0} = - d \ cdot \ cos \ left (l \ right)}

R-R_{0}=-d\cdot \cos \left(l\right)

Итак:

V obs, r = - R 0 d Ω dr | R 0 d ⋅ cos ⁡ (l) sin ⁡ (l) V obs, t = - R 0 d Ω d r | R 0 d ⋅ соз 2 ⁡ (l) - Ω d {\ displaystyle {\ begin {выровнено} V _ {\ text {obs, r}} = - R_ {0} {\ frac {d \ Omega} {dr}} {\ Bigg \ vert} _ {R_ {0}} d \ cdot \ cos \ left (l \ right) \ sin \ left (l \ right) \\ V _ {\ text {obs, t}} = - R_ { 0} {\ frac {d \ Omega} {dr}} {\ Bigg \ vert} _ {R_ {0}} d \ cdot \ cos ^ {2} \ left (l \ right) - \ Omega d \\\ end {align}}}

{\begin{aligned}V_{\text{obs, r}}=-R_{0}{\frac {d\Omega }{dr}}{\Bigg \vert }_{R_{0}}d\cdot \cos \left(l\right)\sin \left(l\right)\\V_{\text{obs, t}}=-R_{0}{\frac {d\Omega }{dr}}{\Bigg \vert }_{R_{0}}d\cdot \cos ^{2}\left(l\right)-\Omega d\\\end{aligned}}

Используя формулы синуса и косинуса половинного угла, эти скорости могут быть переписаны как:

V obs, r = - R 0 d Ω dr | R 0 d sin ⁡ (2 l) 2 V набл., T = - R 0 d Ω d r | R 0 d (cos ⁡ (2 l) + 1) 2 - Ω d = - R 0 d Ω d r | R 0 d соз ⁡ (2 l) 2 + (- 1 2 R 0 d Ω dr | R 0 - Ω) d {\ displaystyle {\ begin {align} V _ {\ text {obs, r}} = - R_ { 0} {\ frac {d \ Omega} {dr}} {\ Bigg \ vert} _ {R_ {0}} d {\ frac {\ sin \ left (2l \ right)} {2}} \\ V_ { \ text {obs, t}} = - R_ {0} {\ frac {d \ Omega} {dr}} {\ Bigg \ vert} _ {R_ {0}} d {\ frac {\ left (\ cos \ left (2l \ right) +1 \ right)} {2}} - \ Omega d = -R_ {0} {\ frac {d \ Omega} {dr}} {\ Bigg \ vert} _ {R_ {0} } d {\ frac {\ cos \ left (2l \ right)} {2}} + \ left (- {\ frac {1} {2}} R_ {0} {\ frac {d \ Omega} {dr} } {\ Bigg \ vert} _ {R_ {0}} - \ Omega \ right) d \\\ end {align}}}

{\ displaystyle {\ begin {align} V _ {\ text {obs, r}} = - R_ {0} {\ frac {d \ Omega} {dr}} {\ Bigg \ vert} _ {R_ {0}} d {\ frac { \ sin \ left (2l \ right)} {2}} \\ V _ {\ text {obs, t}} = - R_ {0} {\ frac {d \ Omega} {dr}} {\ Bigg \ vert} _ {R_ {0}} d {\ frac {\ left (\ cos \ left (2l \ right) +1 \ right)} {2}} - \ Omega d = -R_ {0} {\ frac {d \ Омега} {dr}} {\ Bigg \ vert} _ {R_ {0}} d {\ frac {\ cos \ left (2l \ right)} {2}} + \ left (- {\ frac {1} { 2}} R_ {0} {\ frac {d \ Omega} {dr}} {\ Bigg \ vert} _ {R_ {0}} - \ Omega \ right) d \\\ конец {выровнено}}}

Запись скоростей через известные нам величины и два коэффициента $A { \ displaystyle A}$ $A$ и $B {\ displaystyle B}$ $B$ дает:

V obs, r = A d sin ⁡ (2 l) V obs, t = A d соз ⁡ (2 л) + В d {\ displaystyle {\ begin {align} V _ {\ text {obs, r}} = Ad \ sin \ left (2l \ right) \\ V _ {\ text {obs, t }} = Ad \ cos \ left (2l \ right) + Bd \\\ конец {выровнено}}}

{\begin{aligned}V_{\text{obs, r}}=Ad\sin \left(2l\right)\\V_{\text{obs, t}}=Ad\cos \left(2l\right)+Bd\\\end{aligned}}

где

A = - 1 2 R 0 d Ω dr | R 0 B = - 1 2 R 0 d Ω d r | R 0 - Ω {\ displaystyle {\ begin {align} A = - {\ frac {1} {2}} R_ {0} {\ frac {d \ Omega} {dr}} {\ Bigg \ vert} _ { R_ {0}} \\ B = - {\ frac {1} {2}} R_ {0} {\ frac {d \ Omega} {dr}} {\ Bigg \ vert} _ {R_ {0}} - \ Omega \\\ end {align}}}

{\ displaystyle {\ begin {align} A = - {\ frac {1} {2}} R_ {0} {\ frac {d \ Omega} {dr}} {\ Bigg \ vert} _ {R_ {0}} \\ B = - {\ frac {1 } {2}} R_ {0} {\ frac {d \ Omega} {dr}} {\ Bigg \ vert} _ {R_ {0}} - \ Omega \\\ конец {выровнено}}}

На этом этапе наблюдаемые скорости связаны с этими коэффициентами и положением звезды. Теперь можно связать эти коэффициенты со свойствами вращения галактики. Для звезды, движущейся по круговой орбите, мы можем выразить производную угловой скорости по радиусу через скорость вращения и радиус и оценить это в местоположении Солнца:

Ω = v r d Ω d r | R 0 = d (v / r) d r | R 0 = - V 0 R 0 2 + 1 R 0 d v d r | R 0 {\ displaystyle {\ begin {align} \ Omega = {\ frac {v} {r}} \\ {\ frac {d \ Omega} {dr}} {\ Bigg \ vert} _ {R_ { 0}} = {\ frac {d (v / r)} {dr}} {\ Bigg \ vert} _ {R_ {0}} = - {\ frac {V_ {0}} {R_ {0} ^ { 2}}} + {\ frac {1} {R_ {0}}} {\ frac {dv} {dr}} {\ Bigg \ vert} _ {R_ {0}} \\\ конец {выровнено}}}

{\ displaystyle {\ begin {align} \ Omega = {\ frac {v} {r}} \\ {\ frac {d \ Omega} {dr}} {\ Bigg \ vert} _ {R_ {0}} = {\ frac {d (v / r)} {dr}} {\ Bigg \ vert} _ {R_ {0}} = - {\ frac {V_ {0}} {R_ {0 } ^ {2}}} + {\ frac {1} {R_ {0}}} {\ frac {dv} {dr}} {\ Bigg \ vert} _ {R_ {0}} \\\ end {выровнено }}}

итак

Константы Оорта на стене в Лейдене

A = 1 2 (V 0 R 0 - dvdr | R 0) B = - 1 2 (V 0 R 0 + dvdr | R 0) {\ displaystyle {\ begin {align} A = {\ frac {1} {2}} \ left ({\ frac {V_ {0}} {R_ {0}}} - {\ frac {dv} {dr}} { \ Bigg \ vert} _ {R_ {0}} \ right) \\ B = - {\ frac {1} {2}} \ left ({\ frac {V_ {0}} {R_ {0}}} + {\ frac {dv} {dr}} {\ Bigg \ vert} _ {R_ {0}} \ right) \\\ конец {выровнено}}}

{\ displaystyle {\ begin {align} A = {\ frac {1} {2}} \ left ({\ frac { В_ {0}} {Р _ {0}}} - {\ frac {dv} {dr}} {\ Bigg \ vert} _ {R_ {0}} \ right) \\ B = - {\ frac {1} {2}} \ left ({\ frac {V_ {0}} {R_ {0}}} + {\ frac {dv} {dr}} {\ Bigg \ vert} _ {R_ {0}} \ right) \\\ конец {выровнен }}}

$A {\ displaystyle A}$ $A$ - константа Оорта, описывающая сдвиговое движение, а $B {\ displaystyle B}$ $B$ - постоянная Оорта, описывающая вращение Галактики. Как описано ниже, можно измерить $A {\ displaystyle A}$ $A$ и $B {\ displaystyle B}$ $B$ , построив эти скорости, измеренные для многих звезд, в зависимости от галактические долготы этих звезд.

Измерения

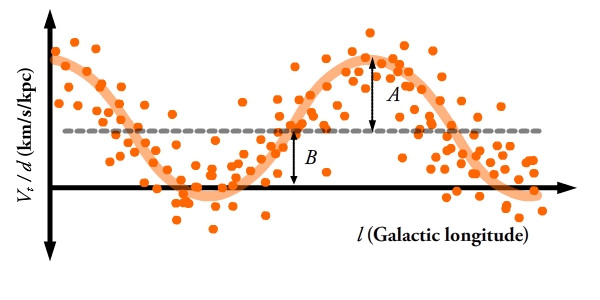
Рис. 2: Измерение констант Оорта путем подбора к большим наборам данных. Обратите внимание, что этот график ошибочно показывает B как положительный. Отрицательное значение B вносит западный компонент в поперечные скорости.

Как упоминалось на промежуточном этапе в приведенном выше выводе:

V obs, r = A d sin ⁡ (2 l) V obs, t = A d соз ⁡ (2 l) + B d {\ displaystyle {\ begin {align} V _ {\ text {obs, r}} = A \, d \, \ sin \ left (2l \ right) \\ V _ {\ text {obs, t}} = A \, d \, \ cos \ left (2l \ right) + B \, d \\\ end {align}}}

{\ displaystyle {\ begin {align} V _ {\ text {obs, r}} =A\,d\,\sin \left(2l\right)\\V_{\text{obs, t}}=A\,d\,\cos \left(2l\right)+B\,d\ \\end{aligned}}}

Следовательно, мы можем записать константы Оорта $A {\ displaystyle A}$ $A$ и $B {\ displaystyle B}$ $B$ как:

A = V obs, rd sin ⁡ (2 l) B = V obs, td - A соз ⁡ (2 l) {\ displaystyle {\ begin {align} A = {\ frac {V _ {\ text {obs, r}}} {d \, \ sin \ left (2l \ right)}} \\ B = {\ frac {V _ {\ text {obs, t}}} {d}} - A \, \ cos \ left (2l \ right) \\\ end {align}}}

{\ displaystyle {\ begin {align} A = {\ frac {V _ {\ text {obs, r}}} {d \, \ sin \ left (2l \ right)}} \\ B = {\ frac {V _ {\ text {obs, t}}} { d}} - A \, \ cos \ left (2l \ right) \\\ конец {выровнено}}}

Таким образом, константы Оорта могут быть выражены через лучевые и поперечные скорости, расстояния и галактические долготы объектов в нашей Галактике - все из которых, в принципе, являются наблюдаемыми величинами.

Однако есть ряд осложнений. Приведенный выше простой вывод предполагает, что и Солнце, и рассматриваемый объект движутся по круговым орбитам вокруг центра Галактики. Это неверно для Солнца (скорость Солнца относительно местного стандарта покоя составляет приблизительно 13,4 км / с), и не обязательно верно и для других объектов в Млечном Пути. Вывод также неявно предполагает, что гравитационный потенциал Млечного Пути осесимметричен и всегда направлен к центру. Это игнорирует эффекты спиральных рукавов и полосы Галактики. Наконец, как поперечная скорость, так и расстояние, как известно, трудно измерить для объектов, которые не находятся относительно близко друг к другу.

Поскольку некруглая составляющая скорости Солнца известна, ее можно вычесть из наших наблюдений для компенсации. Мы не знаем, однако, некруглых составляющих скорости каждой отдельной звезды, которую мы наблюдаем, поэтому их нельзя компенсировать таким образом. Но если мы построим график зависимости поперечной скорости, деленной на расстояние, от галактической долготы для большой выборки звезд, мы знаем из приведенных выше уравнений, что они будут следовать синусоидальной функции. Некруговые скорости приведут к рассеянию вокруг этой линии, но с достаточно большой выборкой можно подобрать истинную функцию и измерить значения констант Оорта, как показано на рисунке 2. $A {\ displaystyle A}$ $A$ - это просто амплитуда синусоиды, а $B {\ displaystyle B}$ $B$ - вертикальное смещение от нуля. Однако точное измерение поперечных скоростей и расстояний без ошибок остается сложной задачей, и наборы производных значений для $A {\ displaystyle A}$ $A$ и $B {\ displaystyle B}$ $B$ Часто не согласен.

Большинство методов измерения $A {\ displaystyle A}$ $A$ и $B {\ displaystyle B}$ $B$ принципиально похожи, следуя указанным выше шаблонам. Основные различия обычно заключаются в том, какие типы объектов используются и в деталях того, как измеряется расстояние или собственное движение. Оорт в своей оригинальной статье 1927 года о выводе констант получил $A {\ displaystyle A}$ $A$ = 31,0 ± 3,7 км с кпк. Он не получил явно значение для $B {\ displaystyle B}$ $B$ , но, исходя из его заключения, что Галактика почти находилась в кеплеровском вращении (как в примере 2 ниже), мы можем предположить, что он получил значение около -10 км / с кпк. Они существенно отличаются от современных значений, что свидетельствует о сложности измерения этих констант. Измерения $A {\ displaystyle A}$ $A$ и $B {\ displaystyle B}$ $B$ с того времени сильно различались; в 1964 г. IAU принял $A {\ displaystyle A}$ $A$ = 15 км / сек, тыс. пк и $B {\ displaystyle B}$ $B$ = -10 км с кпк в качестве стандартных значений. Хотя более поздние измерения продолжают варьироваться, они, как правило, находятся около этих значений.

Спутник Hipparcos, запущенный в 1989 году, был первой космической астрометрической миссией, а его точные измерения параллакса и собственного движения позволили гораздо лучше измерить константы Оорта. В 1997 году данные Hipparcos были использованы для получения значений $A {\ displaystyle A}$ $A$ = 14,82 ± 0,84 км / с, тыс. Пк и $B {\ displaystyle B}$ $B$ = - 12,37 ± 0,64 км с кпк. Космический корабль Gaia, запущенный в 2013 году, является обновленным преемником Hipparcos; что позволило получить новый и улучшенный уровень точности измерения четырех констант Оорта $A {\ displaystyle A}$ $A$ = 15,3 ± 0,4 км с кпк, $B {\ displaystyle B}$ $B$ = -11,9 ± 0,4 км с тыс. Пк / с, $C {\ displaystyle C}$ $C$ = -3,2 ± 0,4 км с тыс. Пк / с и $K {\ displaystyle K}$ $K$ = -3,3 ± 0,6 км / с кпк.

Используя значения Gaia, мы находим

dvdr | R 0 = - A - B = - 3,4 км / с / кпк V 0 R 0 = Ω = A - B = 27,2 км / с / кпк {\ displaystyle {\ begin {align} {\ frac {dv} {dr }} {\ Bigg \ vert} _ {R_ {0}} = - AB = -3,4 {\ text {км / с / kpc}} \\ {\ frac {V_ {0}} {R_ {0}} } = \ Omega = AB = 27,2 {\ text {км / с / kpc}} \\\ end {align}}}

{\ displaystyle {\ begin {align} { \ frac {dv} {dr}} {\ Bigg \ vert} _ {R_ {0}} = - AB = -3,4 {\ text {км / с / kpc}} \\ {\ frac {V_ {0} } {R_ {0}}} = \ Omega = AB = 27,2 {\ text {км / с / kpc}} \\\ end {align}}}

Это значение Ω соответствует периоду в 226 миллионов лет, в течение которого нынешнее окружение Солнца должно пройти. вокруг Млечного Пути. Однако время, необходимое солнцу, чтобы обойти Млечный Путь (галактический год ), может быть больше, потому что (в простой модели) оно обращается вокруг точки, находящейся дальше от центра галактики, где Ω меньше (см. Солнце № Орбита в Млечном Пути ).

Значения в км / с кпк можно преобразовать в миллисекунды в год путем деления на 4,740. Это дает следующие значения для среднего собственного движения звезд в нашем районе на разных галактических долготах после поправки на эффект, обусловленный скоростью Солнца по отношению к местному стандарту покоя:

Галактическая долгота	Созвездие	среднее собственное движение	mas / год	приблизительное направление
0°	Стрелец	B+A	0,7	северо-восток
45 °	Аквила	B	2.5	юго-запад
90 °	Лебедь	B − A	5,7	запад
135 °	Кассиопея	B	2,5	запад
180 °	Возничий	B + A	0,7	юго-восток
225 °	Моноцерос	B	2,5	северо-запад
270 °	Вела	B − A	5,7	запад
315 °	Кентавр	B	2,5	запад

Движение Солнца к вершине Солнца в Геркулесе добавляет обычно западный компонент к наблюдаемым собственным движениям звезд вокруг Велы или Центавра и обычно восточный компонент для звезд вокруг Лебедя или Кассиопеи. Этот эффект уменьшается с увеличением расстояния, поэтому значения в таблице более характерны для звезд, находящихся дальше. С другой стороны, более далекие звезды или объекты не будут следовать за таблицей, которая предназначена для объектов в нашем районе. Например, Стрелец A *, радиоисточник в центре галактики, будет иметь собственное движение примерно на Ω или 5,7 мсд / год на юго-запад (с небольшой корректировкой из-за движения Солнца по направлению к Солнцу. апекс), даже если он находится в Стрельце. Обратите внимание, что эти собственные движения не могут быть измерены относительно «фоновых звезд» (потому что фоновые звезды будут иметь аналогичные собственные движения), но должны быть измерены по более стационарным ориентирам, таким как квазары.

Значение

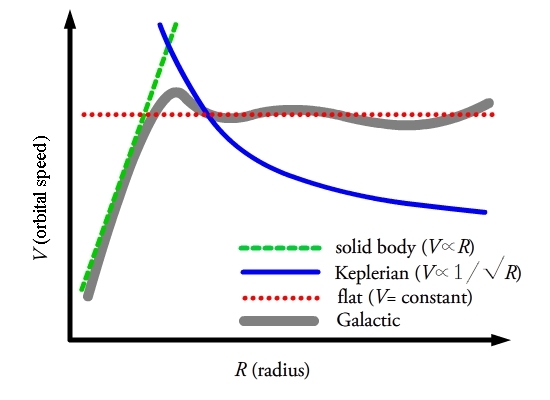
Рисунок 3: Диаграмма различных кривых вращения в галактике

Константы Оорта могут пролить свет на то, как вращается Галактика. Как можно видеть, $A {\ displaystyle A}$ $A$ и $B {\ displaystyle B}$ $B$ являются функциями орбитальной скорости Солнца, а также первой производной от скорость Солнца. В результате $A {\ displaystyle A}$ $A$ описывает сдвиговое движение в диске, окружающем Солнце, а $B {\ displaystyle B}$ $B$ описывает угловой момент градиент в окрестности Солнца, также называемый завихренностью.

Чтобы прояснить этот момент, можно рассмотреть три примера, описывающих орбиту звезд и газа внутри Галактики, что дает интуитивное представление о значении $A { \ displaystyle A}$ $A$ и $B {\ displaystyle B}$ $B$ . Эти три примера - вращение твердого тела, кеплеровское вращение и постоянное вращение в различных кольцах. Эти три типа поворота изображены как функция радиуса ( $R {\ displaystyle R}$ $R$ ) и показаны на рисунке 3 в виде зеленой, синей и красной кривых соответственно. Серая кривая приблизительно соответствует кривой вращения Млечного Пути.

Вращение твердого тела

Для начала предположим, что вращение Млечного Пути можно описать вращением твердого тела, как показано зеленой кривой на рисунке 3. Вращение твердого тела предполагает, что вся система движется как твердое тело без дифференциального вращения. В результате получается постоянная угловая скорость, $Ω {\ displaystyle \ Omega}$ $\ Omega$ , которая не зависит от $R {\ displaystyle R}$ $R$ . После этого мы видим, что скорость линейно масштабируется с $R {\ displaystyle R}$ $R$ , $v ∝ r {\ displaystyle v \ propto r}$ $v\propto r$ , таким образом,

dvdr = vr = Ω { \ displaystyle {\ begin {align} {\ frac {dv} {dr}} = {\ frac {v} {r}} = \ Omega \\\ end {align}}}

{\ displaystyle { \ begin {align} {\ frac {dv} {dr}} = {\ frac {v} {r}} = \ Omega \\\ end {align}}}

Использование двух констант Оорта идентичности, затем можно определить, какими будут константы $A {\ displaystyle A}$ $A$ и $B {\ displaystyle B}$ $B$ ,

A = 1 2 (Ω 0 R 0 R 0 - Ω | R 0) знак равно 0 B = - 1 2 (Ω 0 R 0 R 0 + Ω | R 0) = - Ω 0 {\ Displaystyle {\ begin {align} A = {\ гидроразрыв {1} {2}} \ left ({\ frac {\ Omega _ {0} R_ {0}} {R_ {0}}} - {\ Omega} {\ Bigg \ vert} _ {R_ {0} } \ right) = 0 \\ B = - {\ frac {1} {2}} \ left ({\ frac {\ Omega _ {0} R_ {0}} {R_ {0}}} + {\ Omega } {\ Bigg \ vert} _ {R_ {0}} \ right) = - \ Omega _ {0} \\\ end {align}}}

{\ displaystyle {\ begin {align} A = {\ frac {1} {2}} \ left ({\ frac {\ Omega _ {0} R_ {0}} {R_ {0}}} - {\ Omega} {\ Bigg \ vert} _ {R_ {0}} \ right) = 0 \\ B = - {\ frac {1} {2}} \ left ({\ frac {\ Omega _ {0} R_ {0}} {R_ {0}}} + {\ Omega} {\ Bigg \ vert} _ {R_ {0}} \ right) = - \ Omega _ {0} \\\ конец {выровнено}}}

Это демонстрирует, что при вращении твердого тела сдвиговое движение отсутствует, т.е. $A = 0 {\ displaystyle A = 0}$ $A=0$ , а завихренность - это просто угловое вращение, $B = - Ω {\ displaystyle B = - \ Omega}$ $B=-\Omega$ . Это то, чего можно было ожидать, потому что нет никакой разницы в орбитальной скорости при увеличении радиуса, следовательно, нет напряжения между кольцами. Кроме того, при вращении твердого тела единственное вращение происходит вокруг центра, поэтому разумно, что результирующая завихренность в системе описывается единственным вращением в системе. Фактически можно измерить и найти, что оно не равно нулю ( $A = 14 {\ displaystyle A = 14}$ ${\ displaystyle A = 14}$ км с кпк.). Таким образом, галактика не вращается как твердое тело в наших окрестностях, но может вращаться во внутренних областях Галактики.

Кеплеровское вращение

Второй проясняющий пример - предположить, что орбиты в локальной окрестности следуют кеплеровской орбите, как показано синей линией на рисунке 3. орбитальное движение по кеплеровской орбите описывается следующим образом:

v = GM r {\ displaystyle v = {\ sqrt {\ frac {GM} {r}}}}

{\ displaystyle v = {\ sqrt {\ frac {GM} {r}}}}

где $G {\ displaystyle G}$ $G$ - гравитационная постоянная, а $M {\ displaystyle M}$ $M$ - масса, заключенная в радиусе $r {\ displaystyle r}$ $r$ . Производная скорости по радиусу равна,

dvdr = - 1 2 GMR 3 = - 1 2 vr {\ displaystyle {\ frac {dv} {dr}} = - {\ frac {1} {2 }} {\ sqrt {\ frac {GM} {R ^ {3}}}} = - {\ frac {1} {2}} {\ frac {v} {r}}}

{\ displaystyle {\ frac {dv} {dr}} = - {\ frac {1} {2}} {\ sqrt {\ frac {GM} {R ^ {3}}}} = - {\ frac {1} {2}} {\ гидроразрыв {v} {r}}}

Константы Оорта могут тогда записывается следующим образом:

A = 1 2 (V 0 R 0 + v 2 r | R 0) = 3 V 0 4 R 0 B = - 1 2 (V 0 R 0 - v 2 r | R 0) = - 1 V 0 4 R 0 {\ displaystyle {\ begin {align} A = {\ frac {1} {2}} \ left ({\ frac {V_ {0}} {R_ {0}}} + {\ frac {v} {2r}} {\ Bigg \ vert} _ {R_ {0}} \ right) = {\ frac {3V_ {0}} {4R_ {0}}} \\ B = - {\ frac {1} {2}} \ left ({\ frac {V_ {0}} {R_ {0}}} - {\ frac {v} {2r}} {\ Bigg \ vert} _ {R_ {0}) } \ right) = - {\ frac {1V_ {0}} {4R_ {0}}} \\\ end {align}}}

{\ displaystyle {\ begin {align} A = {\ frac {1} {2}} \ left ({\ frac {V_ {0}} {R_ {0}}} + {\ frac {v} {2r}} {\ Bigg \ vert} _ {R_ {0}} \ right) = {\ frac {3V_ {0}} {4R_ {0}}} \\ B = - {\ frac {1} {2}} \ left ({ \ frac {V_ {0}} {R_ {0}}} - {\ frac {v} {2r}} {\ Bigg \ v ert} _ {R_ {0}} \ right) = - {\ frac {1V_ {0}} {4R_ {0}}} \\\ конец {выровнено}}}

Для значений скорости Солнца $V 0 = 218 {\ displaystyle V_ {0} = 218}$ $V _{0}=218$ км / с и радиус до центра Галактики, $R 0 = 8 {\ displaystyle R_ {0} = 8}$ ${\ displaystyle R_ {0} = 8}$ кпк, константы Оорта равны $A = 20 {\ displaystyle A = 20}$ $A=20$ km s kpc и $B = - 7 {\ displaystyle B = -7}$ $B=-7$ км с кпк. Однако наблюдаемые значения равны $A = 14 {\ displaystyle A = 14}$ ${\ displaystyle A = 14}$ км с кпк и $B = - 12 {\ displaystyle B = -12}$ $B=-12$ км с кпк. Таким образом, кеплеровское вращение - не лучшее описание вращения Млечного Пути. Более того, хотя этот пример не описывает локальное вращение, его можно рассматривать как предельный случай, который описывает минимальную скорость, которую объект может иметь на стабильной орбите.

Плоская кривая вращения

В последнем примере предполагается, что кривая вращения Галактики плоская, т.е. $v {\ displaystyle v}$ $v$ постоянна и независимо от радиуса, $r {\ displaystyle r}$ $r$ . Скорость вращения находится между скоростью твердого тела и кеплеровским вращением и обозначена красной пунктирной линией на рисунке 3. При постоянной скорости следует, что радиальная производная от $v {\ displaystyle v}$ $v$ равно 0,

dvdr = 0 {\ displaystyle {\ frac {dv} {dr}} = 0}

{\frac {dv}{dr} }=0

и, следовательно, константы Оорта равны,

A = 1 2 (V 0 R 0 - 0 | R 0) знак равно 1 2 (V 0 R 0) B = - 1 2 (V 0 R 0 + 0 | R 0) = - 1 2 (V 0 R 0) {\ displaystyle {\ begin {align} A = {\ frac {1} {2}} \ left ({\ frac {V_ {0}} {R_ {0}}} - 0 {\ Bigg \ vert} _ {R_ {0}} \ right) = { \ frac {1} {2}} \ left ({\ frac {V_ {0}} {R_ {0}}} \ right) \\ B = - {\ frac {1} {2}} \ left ({ \ frac {V_ {0}} {R_ {0}}} + 0 {\ Bigg \ vert} _ {R_ {0}} \ right) = - {\ frac {1} {2}} \ left ({\ frac {V_ {0}} {R_ {0}}} \ right) \\\ end {align}}}

{\begin{aligned}A={\frac {1}{2}}\left({\frac {V_{0}}{R_{0}}}-0{\Bigg \vert }_{R_{0}}\right)={\frac {1}{2}}\left({\frac {V_{0}}{R_{0}}}\right)\\B=-{\frac {1}{2}}\left({\frac {V_{0}}{R_{0}}}+0{\Bigg \vert }_{R_{0}}\right)=-{\frac {1}{2}}\left({\frac {V_{0}}{R_{0}}}\right)\\\end{aligned}}

Используя локальную скорость и радиус, указанные в последнем примере, можно найти $A = 13,6 { \ displaystyle A = 13,6}$ ${\ displaystyle A = 13.6}$ км с тыс. пк / с и $B = - 13,6 {\ displaystyle B = -13,6}$ $B=-13.6$ км с тыс. пк. Это близко к фактически измеренным константам Оорта и говорит нам, что модель постоянной скорости является наиболее близкой из этих трех к реальности в окрестностях Солнца. Но на самом деле, как упоминалось выше, $- A - B {\ displaystyle -A-B}$ ${\ displaystyle -AB}$ отрицательно, что означает, что на нашем расстоянии скорость уменьшается с удалением от центра галактики.

Из этих трех примеров следует сделать вывод о том, что с помощью удивительно простой модели вращение Млечного Пути можно описать этими двумя константами. Первые два примера используются в качестве ограничений для вращения Галактики, поскольку они показывают самое быстрое и самое медленное вращение Галактики с заданным радиусом. Плоская кривая вращения служит промежуточным звеном между двумя кривыми вращения и фактически дает наиболее разумные константы Оорта по сравнению с измерениями тока.

Использует

Одно из основных применений констант Оорта - калибровка кривой вращения галактики. Относительная кривая может быть получена при изучении движения газовых облаков в Млечном Пути, но для калибровки соответствующих фактических абсолютных скоростей требуется знание V 0. Мы знаем, что:

V 0 = R 0 (A - B) {\ displaystyle V_ {0} = R_ {0} (AB) \, \!}

V_{0}=R_{0}(A-B)\,\!

Поскольку R 0 может определяться другими способами (например, путем тщательного отслеживания движения звезд около центральной сверхмассивной черной дыры Млечного Пути), зная $A {\ displaystyle A}$ $A$ и $B {\ displaystyle B}$ $B$ позволяет нам определить V 0.

. Также можно показать, что массовая плотность $ρ R {\ displaystyle \ rho _ {R}}$ $\rho _{R}$ может быть задано следующим образом:

ρ R = B 2 - A 2 2 π G {\ displaystyle \ rho _ {R} = {\ frac {B ^ {2} -A ^ {2}} {2 \ pi G}}}

{ \ displaystyle \ rho _ {R} = {\ frac {B ^ {2} -A ^ {2}} {2 \ pi G}}}

Итак, константы Оорта могут кое-что сказать нам о плотности массы на заданном радиусе в диске. Они также полезны для ограничения моделей распределения массы Галактики. Кроме того, в эпициклическом приближении для почти круговых звездных орбит в диске эпициклическая частота $κ {\ displaystyle \ kappa}$ $\ каппа$ задается как $κ 2 = - 4 В Ω {\ displaystyle \ kappa ^ {2} = - 4B \ Omega}$ $\kappa ^{2}=-4B\Omega$ , где $Ω {\ displaystyle \ Omega}$ $\ Omega$ - угловая скорость . Следовательно, константы Оорта могут многое рассказать нам о движениях в галактике.

См. Также

Ссылки

Внешние ссылки

СМИ, связанные с константами Оорта в Wikimedia Commons