Фигура, образованная двумя лучами, встреча с одной точкой

Угол, образованный двумя лучами, исходящими из вершины.
В Евклидова геометрия, - это фигура, образованная двумя лучами, называемыми сторонами, имеющими общую конечную точку, называемую вершиной угол. Углы, образованные двумя лучами, лежат в плоскости , данным лучи. Углы также образуются пересечением двух плоскостей. Эти углы называются двугранными углами. Две пересекающиеся кривые определяют также угол, который является углом касательных в точке пересечения. Например, сферический угол , образованный двумя большими кругами на сфере, равенство двугранному углу между плоскостями, содержащими большие круги.
Угол также используется для обозначения меры угла или поворота. Эта мера представляет собой длину дуги окружности к ее радиусу. В случае геометрического угла дуга центрируется в вершине и ограничивается. В случае вращения дуга центрируется в центре вращения и ограничивается любая другая точка и ее изображение путем поворота.
Содержание
- 1 История и этимология
- 2 Определение углов
- 3 Типы углов
- 3.1 Отдельные углы
- 3.2 Эквивалентные пары углов
- 3.3 Вертикальные и совместные пары углов
- 3.4 Объединение пар углов
- 3.5 Углы, связанные с многоугольником
- 3.6 Углы, связанные с плоскостью
- 4 Измерение углов
- 4.1. Постулат сложения углов
- 4.2 Единицы
- 4.3 Положительные и отрицательные углы
- 4.4 Альтернатива измерения размера угла
- 4.5 Астрономические приближения
- 5 Углы между кривыми
- 6 Биссектрисы и трисекции углов
- 7 Точечное произведение и обобщения
- 7.1 Внутреннее произведение
- 7.2 Углы между подпространствами
- 7.3 Углы в римановой геометрии
- 7.4 Гиперболический угол
- 8 Углы в географии и астрономии
- 9 См. Также
- 10 Примечания
- 11 Ссылки
- 12 Библиография
- 13 Внешние ссылки
История и этимология
Слово угол происходит от латинского слова angulus, означающего « угол »; родственными словами греческое ἀγκύλος (ankylοs), означающее «изогнутый, изогнутый», и английское слово «лодыжка ». Оба связаны с протоиндоевропейским корнем * ank-, что означает «сгибаться» или «кланяться».
Евклид определяет угол плоскости как наклон друг к другу в плоскость из двух линий, которые встречаются друг с другом и не лежат прямо относительно друг друга. Согласно Проклу, угол должен быть либо качеством, либо просто либо отношением. Первую концепцию использовал Евдем, который рассматривал угол как отклонение от прямой линии ; второй - Карпом Антиохийским, который считал его промежутком или пространством между пересекающимися линиями; Евклид принял третью концепцию.
Определение углов
В математических выражениях обычно используются греческие буквы (α, β, γ, θ, φ,...) как переменные, обозначающие размер некоторого угла (чтобы избежать путаницы с другим его значением, символ π обычно для этой цели не используется). Также используются строчные латинские буквы (a, b, c,...), а также прописные латинские буквы в контексте многоугольников. Примеры смотрите на рисунках в этой статье.
В геометрических фигурах углы также идентифицировать по меткам, прикрепленным к тремкам точкам, которые их определяют. Например, угол при вершине A, заключенный между лучами AB и AC (т.е. прямыми от точки A до точки B и от точки A до точки C) обозначается ∠BAC (в Unicode U + 2220 ANGLE) или  . Если нет риска путаницы, угол иногда можно обозначать просто по его вершине (в данном случае «угол А»).
. Если нет риска путаницы, угол иногда можно обозначать просто по его вершине (в данном случае «угол А»).
Потенциально, угол, обозначенный, например, как ∠BAC, может относиться к любому из четырех углов: угол по часовой стрелке от B до C, угол против часовой стрелки от B до C, угол по стрелке от C до B, или угол против часовой стрелки от C до B, где, в котором измеряется угол, определяет его знак (см. Положительные и отрицательные углы). Однако во многих случаях из контекста очевидно, что имеется в виду положительный угол, меньший или равный 180 градусам, в этом случае двусмысленности не возникает. В случае заключения соглашения, согласно которому ∠BAC всегда относится к положительному углу против часовой стрелки от B к C, а ∠CAB - к углу против часовой стрелки (положительному) от C к B.
Типы углов
Отдельные углы
Существует некоторая общая терминология, величина которой всегда неотрицательна (см. # Положительные и отрицательные углы):
- Угол, равный 0 ° или не повернутый, считается нулевым
- Углы, меньшие прямого угла (менее 90 °), называются острыми углами («острый», что означает «острый»).
- Угол, равный 1/4 поворот (90 ° или π / 2 радиан) называется прямым углом. Две прямые, образующие угол, называются нормальными, ортогональными или перпендикуляр.
- Углы больше прямого и прямого (от 90 ° до 180 °) называются тупыми углами («тупой» означает «тупой»).
- , равный до 1/2 оборота (180 ° или π угол радиан) называется меньше прямым углом. 3 03>
- Углы больше прямого t угол, но менее 1 оборота (от 180 ° до 360 °), называются углами отражения.
- Угол, равный 1 обороту (360 ° или 2π радиан), называется полным углом, полным углом, круглым углом. или перигон.
- Углы, которые не являются прямыми или кратными прямыми, называются наклонными углами.
Названия, интервалы и единицы измерения отображаются в таблице ниже:
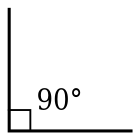 Справа угол
Справа угол 
Острый (
a), тупой (
b) и прямой (
c) углы. Острый и тупой углы также известны как косые углы.

Угол отражения
| Название | ноль | острый | прямой угол | тупой | прямой | рефлекс | перигон |
| Единицы | Интервал |
|---|
| Обороты | 0 | (0, 1/4) | 1/4 | (1/4, 1/2) | 1/2 | (1/2, 1) | 1 |
| Радианы | 0 | (0, 1 / 2π) | 1 / 2π | (1 / 2π, π) | π | (π, 2π) | 2π |
| Градусы | 0 ° | (0, 90) ° | 90 ° | (90, 180) ° | 180 ° | (180, 360) ° | 360 ° |
| Гонс | 0 | (0, 100) | 100 | (100, 200) | 200 | (200, 400) | 400 |
Пары эквивалентных углов
- Углы, имеющие одинаковую меру (т.е. одинаковую равную), называютсяными или конгруэнтными. Угол определяет его размер и не зависит от длины стороннего угла (например, все прямые углы равны по размеру).
- Два угла, которые имеют общие концевые стороны, но отличаются по размеру на целое число, кратное повороту, называются концевыми углами.
- Опорный угол - это острая версия любого угла, определяемого путем многократного вычитания или добавления прямого угла (1/2 оборота, 180 ° или π радиан) к результатам по мере необходимости, пока результат не станет острым углом, размером от 0 до 1/4 оборота, 90 ° или π / 2 радиан. Например, угол 30 градусов имеет опорный угол 30 градусов, а угол 150 градусов также имеет опорный угол 30 градусов (180–150). Угол 750 градусов имеет опорный угол 30 градусов (750–720).
Вертикальные и соответствующие пары углов

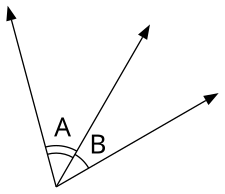
Углы A и B - это пара вертикальных углов; углы C и D представить собой пару вертикальных углов.
Когда две прямые линии пересекаются в точке, образуются четыре угла. Попарно эти углы названы в соответствии с их расположением друг друга.
- Пара углов, противоположных друг другу, образованная двумя пересекающимися прямыми линиями, которые образуют «X» -подобную форму, называемые вертикальными углами, или противоположными углами, или вертикально противоположными углами. Они сокращенно обозначаются как верт. опп. ∠s.
- Равенство вертикально противоположных углов называется теоремой вертикального угла. Евдем с Родоса приписал доказательство Фалесу Милетскому. Предложение, поскольку оба вертикальных угла пары обеспечивают дополнительные к обоим соседним углам, вертикальные углы равны в меру. Согласно исторической заметке, когда Фалес посетил Египет, он заметил, что всякий раз, когда египтяне рисовали две пересекающиеся линии, они измеряли вертикальные углы, чтобы убедиться, что они равны. Фалес пришел к выводу, что можно доказать, что все вертикальные углы равны, если принять некоторые общие понятия, такие как:
- Все прямые углы равны.
- Равные, добавленные к равным, равны.
- Равные, вычтенные из равных, равны.
- Когда два соседних угла образуют прямую линию, они являются дополнительными. Следовательно, если мы предположим, что мера угла A равна x, то мера угла C будет 180 - x. Точно так же угол D будет равен 180 x. И угол C, и угол D имеют размер 180 - x и конгруэнтны. Угол B, используя меру угла C или угол D, мы находим, что величина B равна 180 - (180 - х) = 180 - 180 + х = х. Следовательно, и угол A, и угол B меры, равные x имеют и равны по размеру.
Углы A и B являются семейными.
- Смежные углы, сокращенно обозначаемые как прил. ∠s - это углы, которые имеют общие вершину и ребро, но не имеют внутренних общих точек. Другими словами, это углы расположенные бок о бок или другие, имеющие общую «руку». Смежные углы, которые в сумме составляют прямой, прямой или полный угол, являются особыми и соответственно называются дополнительными, дополнительными и дополнительными углами (см. «Объединение пар углов» ниже).
A поперечный - это линия, пересекающая пара (часто параллельных) линий и связ с чередующимися внутренними углами, углами, внутренними углами и внешними углами.
Объединение пар углов
Есть три специальные пары углов, которые включают суммирование углов:

Дополнительные углы
aи
b(
bявляются дополнением к
a, а
aявляются дополнением к
b).
- дополнительным углам. - пары углов, сумма измерений равна одному прямому углу (1/4 оборота, 90 ° или π / 2 радиана). Если два дополнительных угла наклона, их необщие стороны образуют прямой угол. В евклидовой геометрии два острых угла в прямоугольном треугольнике дополняют друг друга, потому что сумма внутренних углов треугольника равна 180 градусам, а сам прямой угол составляет 90 градусов.
- Прилагательное дополнительное происходит от латинского complementum, связанного с глаголом Complere, «заполнять». Острый угол «заполняется» его дополнением, образуя прямой угол.
- Разница между углом и прямым углом называется дополнением угла.
- Если углы A и B используются дополнительными, выполняются следующие соотношения:
![{\ displaystyle {\ begin {align} \ sin ^ {2} A + \ sin ^ {2} B = 1 \ cos ^ {2 } A + \ cos ^ {2} B = 1 \\ [3pt] \ tan A = \ cot B \ sec A = \ csc B \ end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/47aa6b35b8e53468f73d7ec051d55371da314fba)
- (касательная угол равна котангенсу его дополнения, а его секанс равен косеканс его дополнения.)
- Префикс «со- » в названиях некоторых тригонометрических называться относится к слову « дополнительный ».
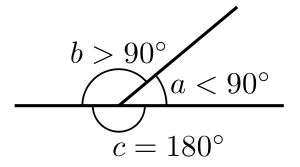
Углы
aи
bдополнительные углами.
- Два угла, сумма которых составляет прямой угол (1/2 оборота, 180 ° или π радиан), называются дополнительные углы.
- Если два дополнительных угла дополнительных углов (т. Е. Имеют общие ve rtex и имеют только одну сторону), их необщие стороны образуют прямую линию. Такие углы называются линейной парой углов. Однако дополнительные углы не обязательно должны быть разделены на линии. Например, дополнительные углы параллелограмма дополнительные, противоположные углы циклического четырехугольника (тот, у которого все вершины лежат на одной окружности) являются дополнительными.
- Если точка P находится вне окружности с центром O, и если касаются от P касаются окружности в точках T и Q, то ∠TPQ и ∠TOQ являются дополнительными.
- Синусы дополнительных углов равны. Их косинусы и касательные (если они не проявляют) равны по величине, но имеют противоположные знаки.
- В евклидовой геометрии любая сумма двух углов в треугольнике является дополнительной к третьему, потому что сумма внутренних углов треугольника является прямым углом.

Сумма двух дополнительных углов является полным углом.
- Два угла, которые в сумме составляют полный угол (1 поворот, 360 ° или 2π радиан), называются дополнительными углами или сопряженными углами.
- Разница между углом и полным углом называется угла или сопряженным углом.
Углы, связанные с многоугольниками

Внутренний и внешний углы.
- Угол, который является Часть простого многоугольника называется внутренним углом, если он лежит внутри этого простого многоугольника. Простой вогнутый многоугольник имеет по крайней мере один внутренний угол, который является углом отражения.
- В евклидовой геометрии размеры внутренних углов треугольника в сумме составляют π радиан, 180 ° или 1/2 оборота; Измерения внутренних углов простого выпуклого четырехугольника в сумме составляют 2π радиан, 360 ° или 1 оборот. В общем, внутренние углы простого выпуклого многоугольника с участием в сумме составляют (n - 2) π радиан, или 180 (n - 2) градусов, (2n - 4) прямых углов, или (n / 2 - 1) поворот.
- Дополнение к внутреннему углу называется внешний угол, то есть внутренний угол и внешний угол образуют линейную пару углы. В каждой вершине многоугольника есть два внешних угла, каждый определяется одной из двух сторон многоугольника, которые встречаются в вершине; эти два угла являются вертикальными и, следовательно, равны. Внешний угол измеряет поворот, который необходимо сделать в вершине, чтобы очертить многоугольник. Если соответствующий внутренний угол должен быть углом отражения, внешний угол считать отрицательным. Даже в непростом многоугольнике можно определить внешний угол, но нужно будет выбрать ориентацию плоскости (или поверхности ) определить знак меры внешнего угла.
- Вклидовой геометрии сумма евклидовой геометрии внешнего углового простого выпуклого многоугольника составляет один полный оборот (360 °). Внешний угол здесь можно назвать дополнительным внешним углом. Внешние углы обычно используются в программах Logo Turtle при рисовании правильных многоугольников.
- В треугольнике , биссектрисы двух внешних углов и биссектриса другие внутренние углы являются параллельными (встречаются в одной точке).
- В треугольнике три точки пересечения, каждая из которых представляет собой биссектрису внешнего угла с противоположной расширенной стороной, коллинеарны.
- В треугольнике три точки пересечения, две из которых находятся между биссектрисой Внутренний угол и противоположной стороной, а третье - между биссектрисой другого внешнего угла и вытянутой противоположной стороной, коллинеарны.
- Некоторые используют название «внешний угол» простого многоугольника, чтобы просто обозначить внешний угол расширения (не дополнительный!) Внутреннего угла. Это противоречит приведенному выше использованию.
Углы, относящиеся к плоскости
- Углы между двумя плоскостями (например, двумя смежными гранями многогранника ) называется двугранный угол. Его можно определить как острый угол между двумя прямыми нормальными к плоскостям.
- Угол между плоскостью и пересекающейся прямой девяноста градусам минус угол между пересекающейся линией. и линия, проходящая через точку пересечения и перпендикулярная плоскость.
Измерение углов
Размер геометрического угла обычно характеризуется величиной наименьшего поворота, который отображает один из лучей в другой. Углы, имеющие одинаковый размер, называются равными, равными или равными по мере.
В некоторых контекстах, таких как определение точки окружающей среды или описание ориентации объекта в двух измерениях исходной ориентации, углы, которые отличаются точным числом, кратным полному повороту эффективно эквивалентны. В других контекстах, таких как определение точки спиральной кривой или описание совокупного вращения объекта в двух измерениях относительно исходной ориентации, углы, которые отличаются ненулевым кратным полному обороту, являются не эквивалентными.

Мера угла
θ(в радианах) представляет собой частное от
sи
r.
. Чтобы измерить угол θ , дугу окружности с центром в вершине угла рисуется, например с парой циркуля . Отношение длины sдуги к радиусу rокружности - это мера угла в радианах.
Мера угла в другом угловомировании получается единица измерения путем умножения меры в радианах на коэффициент масштабирования k / 2π, где k - это мера полного поворота в выбранной единице (например, 360 для градусов или 400 для градианов ):

Определенное таким образом значение θне зависит от размера круга: если длина изменяется, тогда длина дуги изменяется в той же пропорции, поэтому отношение s / r не изменяется. (Доказательство. Формулу выше можно переписать как k = θr / s. Один оборот, для которого θ = n единиц, соответствует дуге, равной длине окружности окружности, которая равна 2πr, поэтому s = 2πr. Подстановка n вместо θ и 2πr вместо s в формуле дает k = nr / 2πr = n / 2π.)
Постулат сложения углов
Постулат сложения углов утверждает, что если B находится внутри угла AOC, тогда

Мера угла. AOC - это сумма угла AOB и угла BOC. В этом постулате не имеет значения, в какой единице угол измеряется, если каждый угол измеряется в одной и той же единице.
Единицы
Единицы, используемые для представления углов, перечислены ниже в порядке убывания величины. Из этих единиц наиболее часто используются градус и радиан. Углы, выраженные в радианах, безразмерны для целей анализа размеров .
Большинство единиц углового измерения определены таким образом, что один оборот (т.е. один полный круг) равен n единицам для некоторого целого номер n. Двумя исключениями являются радианы и диаметр.
- Поворот (n = 1)
- Поворот, а также цикл, полный круг, оборот и вращение - это полное круговое движение или измерение (чтобы вернуться в ту же точку) с кругом или эллипс. Оборот обозначается сокращенно τ, cyc, rev или rot в зависимости от приложения, но в аббревиатуре rpm (оборотов в минуту) используется только r. Оборот на n единиц получается путем установки k = 1 / 2π в формуле выше. Эквивалент 1 поворота составляет 360 °, 2π рад, 400 град и 4 прямых угла. Символ τ также может использоваться как математическая константа для представления 2π радиан. Используемый таким образом (k = τ / 2π) позволяет выражать радианы в долях оборота. Например, половина оборота равна τ / 2 = π.
- Квадрант (n = 4)
- Квадрант составляет 1/4 оборота, т.е. прямой угол. Это единица, используемая в Элементах Евклида. 1 квад. = 90 ° = π / 2 рад = 1/4 оборота = 100 град. В немецком языке этот символ использовался для обозначения квадранта.
- Секстант (n = 6)
- Секстант (угол равностороннего треугольника ) составляет 1/6 очередь. Эту единицу использовали вавилоняне, и ее особенно легко построить с помощью линейки и циркуля. Градус, угловая минута и дуговая секунда - это шестидесятеричные субъединицы вавилонской единицы. 1 вавилонская единица = 60 ° = π / 3 рад ≈ 1,047197551 рад.
 θ
θ=
s/
rрад = 1 рад.
- Радиан (n = 2π = 6,283...)
- радиан - это угол, образованный дугой окружности, имеющей ту же длину, что и радиус окружности. В случае радиана для формулы, приведенной ранее, радиан из n = 2π единиц получается путем установки k = 2π / 2π = 1. Один поворот равен 2π радиан, а один радиан равен 180 / π градусов, или примерно 57,2958 градусов. Радиан сокращенно обозначается как рад, хотя этот символ часто опускается в математических текстах, где подразумеваются радианы, если не указано иное. При использовании радианов углы считаются безразмерными. Радианы используются практически во всех математических работах, помимо простой практической геометрии, из-за, например, приятных и «естественных» свойств, которые тригонометрические функции отображают, когда их аргументы выражены в радианах. Радиан - это (производная) единица измерения угла в системе SI.
- Положение часов (n = 12)
- Положение часов - это относительное направление объекта описывается аналогично 12-часовым часам. Представьте себе циферблат, лежащий прямо или прямо перед собой, и отождествите двенадцать часовых отметок с направлениями, в которые они указывают.
- Часовой угол (n = 24)
- Астрономический часовой угол составляет 1/24 оборота. Поскольку эта система предназначена для измерения объектов, которые совершают цикл один раз в день (например, относительного положения звезд), шестидесятеричные единицы называются минутами времени и секундами времени. Они отличаются от угловых минут и секунд и в 15 раз больше их. 1 час = 15 ° = π / 12 рад = 1/6 квад. = 1/24 оборота = 16 + 2/3 град.
- (Компас) точка или ветер (n = 32)
- Точка, используемая в навигации, является 1/32 оборота. 1 балл = 1/8 прямого угла = 11,25 ° = 12,5 град. Каждая точка разделена на четыре четверти точки, так что 1 оборот равен 128 четвертям.
- (n = 60)
- Гексаконтада - это единица измерения 6 °, которую использовал Эратосфен, так что весь ход был разделен на 60 единиц.
- (n = 144–180)
- Печус был вавилонским единицей, равным примерно 2 ° или 2 + 1 / 2 °.
- Двоичная степень (n = 256)
- Двоичная степень, также известная как двоичный радиан (или штифт), составляет 1/256 оборота.. Двоичная степень используется в вычислениях, так что угол может быть эффективно представлен в одном байте (хотя и с ограниченной точностью). Другие меры угла, используемые при вычислении, могут быть основаны на делении одного целого поворота на 2 равные части для других значений n.
- Степень (n = 360)
- Степень, обозначенная небольшим надстрочный кружок (°) составляет 1/360 оборота, поэтому один оборот равен 360 °. В случае градусов для формулы, приведенной ранее, степень n = 360 ° единиц получается путем установки k = 360 ° / 2π. Одним из преимуществ этой старой шестидесятеричной субъединицы является то, что многие углы, общие для простой геометрии, измеряются как целое число градусов. Доли градуса могут быть записаны в обычной десятичной системе счисления (например, 3,5 ° для трех с половиной градусов), но также используются шестидесятеричные субъединицы «минута» и «секунда» системы «градус-минута-секунда», особенно для географических координат и в астрономии и баллистике.
- (n = 376,99....)
- Часть диаметра (иногда используется в исламской математике) составляет 1/60 радиана. Одна «часть диаметра» составляет приблизительно 0,95493 °. На оборот приходится около 376,991 частей диаметра.
- Град (n = 400)
- Град, также называемый уклоном, градианом или гоном, составляет 1/400 от поворот, поэтому прямой угол равен 100 град. Это десятичная единица квадранта. километр исторически определялся как сенти -градус дуги вдоль большого круга Земли, поэтому километр является десятичным аналогом шестидесятеричной морской мили.. Град используется в основном в триангуляции.
- Миллирадиан
- Миллирадиан (мил или мрад) определяется как одна тысячная радиана, что означает, что поворот на один оборот состоит из 2000π мил (или примерно 6283,185... мил), и почти все прицелы для огнестрельного оружия откалиброваны по этому определению. Вдобавок есть три других производных определения, используемых для артиллерии и навигации, которые приблизительно равны миллирадиану. В соответствии с этими тремя другими определениями один оборот составляет ровно 6000, 6300 или 6400 мил, что соответствует диапазону от 0,05625 до 0,06 градуса (от 3,375 до 3,6 минут). Для сравнения, истинный миллирадиан составляет приблизительно 0,05729578... градуса (3,43775... минуты). Один «NATO mil» определяется как 1/6400 круга. Как и в случае с истинным миллирадианом, каждое из других определений использует свойство вытягивания миллидиана, то есть то, что значение в один миллирадиан приблизительно равно углу, образуемому шириной 1 метр, если смотреть с расстояния 1 км (2π / 6400 = 0,0009817... ≈ 1/1000).
- Угловая минута (n = 21,600)
- Угловая минута (или MOA, угловая минута или просто минута) составляет 1/60 градуса = 1 / 21,600 об. Обозначается простым штрихом (′). Например, 3 ° 30 ′ равно 3 × 60 + 30 = 210 минут или 3 + 30/60 = 3,5 градуса. Также иногда используется смешанный формат с десятичными дробями, например 3 ° 5,72 ′ = 3 + 5,72 / 60 градусов. морская миля исторически определялась как угловая минута вдоль большого круга Земли.
- Угловая секунда (n = 1,296,000)
- Секунда дуги (или секунда дуги, или просто секунда) составляет 1/60 угловой минуты и 1/3600 градуса. Обозначается двойным штрихом (″). Например, 3 ° 7 ′ 30 ″ равно 3 + 7/60 + 30/3600 градусов, или 3,125 градуса.
- Миллисекунда (n = 1 296 000 000)
- mas
- Микродуговая секунда (n = 1,296,000,000,000)
- µas
Положительные и отрицательные углы
Хотя определение измерения угла не поддерживает концепцию отрицательного угла, это часто полезно для наложения соглашения, которое позволяет положительным и отрицательным угловым значениям представлять ориентации и / или вращения в противоположных направлениях относительно некоторой ссылки.
В двумерной декартовой системе координат угол обычно определяется двумя его сторонами с вершиной в начале координат. Начальная сторона находится на положительной оси x, а другая сторона или конечная сторона определяется измерением от начальной стороны в радианах, градусах или поворотах. С положительными углами, представляющими повороты к положительной оси y, и отрицательными углами, представляющими повороты к отрицательной оси y. Когда декартовы координаты представлены стандартным положением, определяемым осью x вправо и осью y вверх, положительные повороты составляют против часовой стрелки, а отрицательные повороты составляют по часовой стрелке.
Во многих контекстах угол −θ фактически эквивалентен углу «один полный оборот минус θ». Например, ориентация, представленная как -45 °, фактически эквивалентна ориентации, представленной как 360 ° - 45 ° или 315 °. Хотя конечное положение такое же, физическое вращение (движение) на -45 ° не то же самое, что вращение на 315 ° (например, вращение человека, держащего метлу, лежащую на пыльном полу, оставит визуально разные следы подметаемых областей на полу).
В трехмерной геометрии «по часовой стрелке» и «против часовой стрелки» не имеют абсолютного значения, поэтому направление положительных и отрицательных углов должно быть определено относительно некоторой ссылки, которая обычно является вектором проходящий через вершину угла и перпендикулярный плоскости, в которой лежат лучи угла.
В навигации, пеленги или азимут измеряются относительно севера. По соглашению, если смотреть сверху, углы пеленга положительные по часовой стрелке, поэтому пеленг 45 ° соответствует ориентации на северо-восток. Отрицательные пеленги не используются в навигации, поэтому ориентация на северо-запад соответствует пеленгу 315 °.
Альтернативные способы измерения размера угла
Существует несколько альтернатив измерению размера угла по углу поворота. Уровень уклона или градиента равен касательной угла или иногда (редко) синусу . Градиент часто выражается в процентах. Для очень малых значений (менее 5%) крутизна уклона приблизительно равна величине угла в радианах.
В рациональной геометрии расстояние между двумя линиями определяется как квадрат синуса угла между линиями. Поскольку синус угла и синус его дополнительного угла одинаковы, любой угол поворота, который отображает одну из линий в другую, приводит к тому же значению для разброса между линиями.
Астрономические приближения
Астрономы измеряют угловое расстояние между объектами в градусах от точки наблюдения.
- 0,5 ° приблизительно соответствует ширине солнца или луны.
- 1 ° приблизительно соответствует ширине мизинца на расстоянии вытянутой руки.
- 10 ° приблизительно соответствует ширине закрытого кулак на расстоянии вытянутой руки.
- 20 ° - это примерно ширина размаха руки на длине руки.
Эти размеры явно зависят от индивидуального объекта, и вышеизложенное следует рассматривать как грубое практическое правило только приблизительные значения.
Углы между кривыми

Угол между двумя кривыми в точке P определяется как угол между касательными
Aи
Bв точке
P.
Угол между прямая и кривая (смешанный угол) или между двумя пересекающимися кривыми (криволинейный угол) определяется как угол между касательными в точке пересечения. Различные названия (сейчас они используются редко, если вообще используются) были даны отдельным случаям: - амфициртический (греч. Ἀμφί, с обеих сторон, κυρτός, выпуклый) или циссоидальный (греч. Κισσός, плющ), двояковыпуклый; ксистроидальный или систроидальный (греч. ξυστρίς, инструмент для соскабливания), вогнуто-выпуклый; амфикоэльский (греч. κοίλη, пустота) или angulus lunularis, двояковыпуклый.
Биссектриса и трисекция углов
древнегреческие математики умели делить угол пополам (делить его на два угла равной меры), используя только циркуль и линейку, но можно было разрезать только определенные углы пополам. В 1837 году Пьер Ванцель показал, что для большинства углов это построение невозможно.
Dot product and generalisations
In the Euclidean space, the angle θ between two Euclidean vectors uand vis related to their dot product and their lengths by the formula

This formula supplies an easy method to find the angle between two planes (or curved surfaces) from their normal vectors and between skew lines from their vector equations.
Inner product
To define angles in an abstract real inner product space, we replace the Euclidean dot product ( ·) by the inner product  , i.e.
, i.e.

In a complex inner product space, the expression for the cosine above may give non-real values, so it is replaced with

or, more commonly, using the absolute value, with

The latter definition ignores the direction of the vectors and thus describes the angle between one-dimensional subspaces  and
and  spanned by the vectors
spanned by the vectors  and
and  correspondingly.
correspondingly.
Angles between subspaces
The definition of the angle between one-dimensional subspaces  and
and  given by
given by

in a Hilbert space can be extended to subspaces of any finite dimensions. Given two subspaces  ,
,  with
with  , this leads to a definition of
, this leads to a definition of  angles called canonical or principal angles between subspaces.
angles called canonical or principal angles between subspaces.
Angles in Riemannian geometry
In Riemannian geometry, the metric tensor is used to define the angle between two tangents. Where U and V are tangent vectors and gijare the components of the metric tensor G,

Hyperbolic angle
A hyperbolic angle is an argument of a hyperbolic function just as the circular angle is the argument of a circular function. The comparison can be visualized as the size of the openings of a hyperbolic sector and a circular sector since the areas of th Эти секторы в каждом случае соответствуют значениям углов. В отличие от кругового угла, гиперболический угол не ограничен. Когда круговые и гиперболические функции рассматриваются как бесконечный ряд в их угловом аргументе, круговые функции представляют собой просто чередующиеся последовательности форм гиперболических функций. Это переплетение двух типов угла и функции было объяснено Леонардом Эйлером в Введение в анализ бесконечности.
Углы в географии и астрономии
в geography, местоположение любой точки на Земле можно определить с помощью географической системы координат. Эта система определяет широту и долготу любого местоположения в терминах углов в центре Земли, используя экватор и (обычно) Гринвичский меридиан в качестве ориентира.
В астрономии заданная точка на небесной сфере (то есть видимое положение астрономического объекта) может быть идентифицирована с использованием из нескольких астрономических систем координат, где ссылки меняются в зависимости от конкретной системы. Астрономы измеряют угловое разделение двух звезд, представляя две линии, проходящие через центр Земли, каждая из которых пересекает одну из звезд. Угол между этой линией можно измерить, и это угловое расстояние между двумя звездами.
И в географии, и в астрономии направление визирования может быть указано в виде вертикального угла, например, высота / высота относительно горизонт, а также азимут относительно севера.
Астрономы также измеряют видимый размер объектов как угловой диаметр. Например, полная луна имеет угловой диаметр приблизительно 0,5 °, если смотреть с Земли. Можно сказать: «Диаметр Луны составляет угол в полградуса». Формула <малого измерения в отношении расстояния / размера.
См. Также
Примечания
Ссылки
Библиография
- Henderson, David W.; Таймина, Дайна (2005), Опыт геометрии Евклидово и неевклидово с историей (3-е изд.), Пирсон Прентис Холл, стр. 104, ISBN 978-0-13-143748-7
- Heiberg, Johan Ludvig (1908), Heath, TL (ed.), Euclid, Тринадцать книг элементов Евклида, 1, Кембридж : Cambridge University Press.
- Сидоров, Л.А. (2001) [1994], Энциклопедия математики, EMS Press
- Джейкобс, Гарольд Р. (1974), Геометрия, У.Х. Фриман, стр.97, 255, ISBN 978-0-7167-0456-0
- Слокум, Джонатан (2007), Предварительный индоевропейский лексикон - данные Pokorny PIE, Исследовательский отдел Техасского университета: лингвистический исследовательский центр, данные получены 2 февраля 2010 г.
- Шут, Уильям Дж.; Ширк, Уильям В.; Портер, Джордж Ф. (1960), Американская книжная компания, Плоская и сплошная геометрия, стр. 25–27
- Вонг, Так-ва; Вонг, Мин-сим (2009), «Углы на пересекающихся и параллельных линийх», New Century Mathematics, 1B (1 ed.), Гонконг: Oxford University Press, стр. 161–163, ISBN 978-0-19-800177-5
 В этой статье включен текст из публикации, которая сейчас находится в общественном достоянии : Чисхолм, Хью, изд. (1911), «Угол », Британская энциклопедия, 2(11-е изд.), Cambridge University Press, стр. 14
В этой статье включен текст из публикации, которая сейчас находится в общественном достоянии : Чисхолм, Хью, изд. (1911), «Угол », Британская энциклопедия, 2(11-е изд.), Cambridge University Press, стр. 14
Внешние ссылки
 | На Викискладе есть материалы, связанные с Углами (геометрия). |
 Угол, образованный двумя лучами, исходящими из вершины.
Угол, образованный двумя лучами, исходящими из вершины. 
 Справа угол
Справа угол  Острый (a), тупой (b) и прямой (c) углы. Острый и тупой углы также известны как косые углы.
Острый (a), тупой (b) и прямой (c) углы. Острый и тупой углы также известны как косые углы.  Угол отражения
Угол отражения  Углы A и B - это пара вертикальных углов; углы C и D представить собой пару вертикальных углов.
Углы A и B - это пара вертикальных углов; углы C и D представить собой пару вертикальных углов.  Углы A и B являются семейными.
Углы A и B являются семейными.  Дополнительные углы aи b(bявляются дополнением к a, а aявляются дополнением к b).
Дополнительные углы aи b(bявляются дополнением к a, а aявляются дополнением к b).![{\ displaystyle {\ begin {align} \ sin ^ {2} A + \ sin ^ {2} B = 1 \ cos ^ {2 } A + \ cos ^ {2} B = 1 \\ [3pt] \ tan A = \ cot B \ sec A = \ csc B \ end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/47aa6b35b8e53468f73d7ec051d55371da314fba)
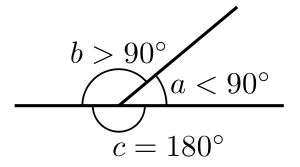 Углы aи bдополнительные углами.
Углы aи bдополнительные углами.  Сумма двух дополнительных углов является полным углом.
Сумма двух дополнительных углов является полным углом.  Внутренний и внешний углы.
Внутренний и внешний углы.  Мера угла θ(в радианах) представляет собой частное от sи r.
Мера угла θ(в радианах) представляет собой частное от sи r.

 θ= s/rрад = 1 рад.
θ= s/rрад = 1 рад.  Угол между двумя кривыми в точке P определяется как угол между касательными Aи Bв точке P.
Угол между двумя кривыми в точке P определяется как угол между касательными Aи Bв точке P.
















![]() В этой статье включен текст из публикации, которая сейчас находится в общественном достоянии : Чисхолм, Хью, изд. (1911), «Угол », Британская энциклопедия, 2(11-е изд.), Cambridge University Press, стр. 14
В этой статье включен текст из публикации, которая сейчас находится в общественном достоянии : Чисхолм, Хью, изд. (1911), «Угол », Британская энциклопедия, 2(11-е изд.), Cambridge University Press, стр. 14