Конструкция носового обтекателя

Учитывая проблему аэродинамической конструкции носового конуса часть любого транспортного средства или тела, предназначенная для перемещения через сжимаемую текучую среду среду (например, ракета или самолет, ракета или пуля ), важной проблемой является определение геометрической формы носового конуса для оптимальных характеристик. Для многих приложений такая задача требует определения формы тела вращения, которая испытывает минимальное сопротивление быстрому движению через такую ​​текучую среду, которая состоит из упругих частиц.

Содержание

• 1 Формы носового конуса и уравнения
  • 1.1 Общие размеры
  • 1.2 Конический
    • 1.2.1 Сферически затупленный конический
  • 1.3 Биконический
  • 1.4 Касательная огиба
    • 1.4.1 Сферически затупленная касательная оживляющая
  • 1.5 Секущая оживляющая
  • 1.6 Эллиптическая
  • 1.7 Параболическая
  • 1.8 Силовая серия
  • 1.9 Серия Хаака
  • 1.10 Фон Карман
  • 1.11 Aerospike
• 2 Нос Характеристики лобового сопротивления конуса
  • 2.1 Влияние общей формы
  • 2.2 Влияние тонкости помола
• 3 Дополнительная литература
• 4 Ссылки

Формы и уравнения носового конуса

Общие размеры

Общие параметры, используемые для построения профилей носового конуса.

Во всех следующих уравнениях формы носового конуса L - это общая длина носового конуса, а R - радиус основания носового конуса. y - это радиус в любой точке x, поскольку x изменяется от 0 на кончике носового конуса до L. Уравнения определяют двумерный профиль формы носа. Полное тело вращения носового конуса формируется путем поворота профиля вокруг центральной линии ⁄ L. Хотя уравнения описывают «идеальную» форму, на практике носовые конусы часто притупляются или усекаются по производственным или аэродинамическим причинам.

Конический

Конический рендеринг и профиль носового конуса с показанными параметрами.

Очень распространенный Форма носового конуса представляет собой простой конус. Эту форму часто выбирают из-за простоты изготовления. Более оптимальные, обтекаемые формы (описанные ниже) зачастую намного сложнее создать. Стороны конического профиля представляют собой прямые линии, поэтому уравнение диаметра выглядит просто:

$y\; =\; x\; RL\; \{\backslash \; displaystyle\; y\; =\; \{xR\; \backslash \; over\; L\}\}$

Конусы иногда определяются их половинным углом φ:

$\varphi \; =\; arctan\; \; (RL)\; \{\backslash \; displaystyle\; \backslash \; phi\; =\; \backslash \; arctan\; \backslash \; left\; (\{R\; \backslash \; over\; L\}\; \backslash \; right)\}$и $y\; =\; x\; tan\; \; (\varphi )\; \{\; \backslash \; displaystyle\; y\; =\; x\; \backslash \; tan\; (\backslash \; phi)\; \backslash ;\}$

Сферически затупленный конус

Визуализация и профиль сферически затупленного конического носового конуса с указанными параметрами.

В практических приложениях конический нос часто притупляется за счет покрытия это с отрезком сферы сферы. Точку касания, в которой сфера пересекает конус, можно найти по следующей формуле:

$xt\; =\; L\; 2\; R\; rn\; 2\; R\; 2\; +\; L\; 2\; \{\backslash \; displaystyle\; x\_\; \{t\}\; =\; \{\backslash \; frac\; \{L\; ^\; \{2\}\}\; \{R\}\; \}\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{r\_\; \{n\}\; ^\; \{2\}\}\; \{R\; ^\; \{2\}\; +\; L\; ^\; \{2\}\}\}\}\}$

$yt\; =\; xt\; RL\; \{\backslash \; displaystyle\; y\_\; \{t\}\; =\; \{\backslash \; frac\; \{x\_\; \{t\}\; R\}\; \{L\}\}\}$

, где r n - радиус сферической головной части.

Центр сферической носовой крышки, x o, можно найти по следующей формуле:

$xo\; =\; xt\; +\; rn\; 2\; -\; yt\; 2\; \{\backslash \; displaystyle\; x\_\; \{o\}\; =\; x\_\; \{\; t\}\; +\; \{\backslash \; sqrt\; \{r\_\; \{n\}\; ^\; \{2\}\; -y\_\; \{t\}\; ^\; \{2\}\}\}\}$

И точку вершины, x a можно найти из:

$xa\; =\; xo\; -\; rn\; \{\backslash \; displaystyle\; x\_\; \{a\}\; =\; x\_\; \{o\}\; -r\_\; \{n\}\}$

Биконический

Визуализация и профиль биконического носового конуса с показанными параметрами.

A bi -коническая форма носового конуса - это просто конус длиной L 1, уложенный поверх усеченного конуса конуса (обычно известного как форма конического переходного участка) длиной L. 2, где основание верхнего конуса равно радиусу R 1 вершине меньшей усеченной вершины с радиусом основания R 2.

$L\; =\; L\; 1\; +\; L\; 2\; \{\backslash \; displaystyle\; L\; =\; L\_\; \{1\}\; +\; L\_\; \{2\}\}$

Для $0\; \le \; x\; \le \; L\; 1\; \{\backslash \; displaystyle\; 0\; \backslash \; leq\; x\; \backslash \; leq\; L\_\; \{1\}\}$: $y\; =\; x\; R\; 1\; L\; 1\; \{\backslash \; displaystyle\; y\; =\; \{xR\_\; \{1\}\; \backslash \; over\; L\_\; \{1\}\}\}$

для $L\; 1\; \le \; x\; \le \; L\; \{\backslash \; displaystyle\; L\_\; \{1\}\; \backslash \; leq\; x\; \backslash \; leq\; L\}$: $y\; =\; R\; 1\; +\; (Икс\; -\; L\; 1)\; (R\; 2\; -\; R\; 1)\; L\; 2\; \{\backslash \; displaystyle\; y\; =\; R\_\; \{1\}\; +\; \{(x-L\_\; \{1\})\; (R\_\; \{2\}\; -R\_\; \{1\})\; \backslash \; ov\; er\; L\_\; \{2\}\}\}$

Половинные углы:

$\varphi \; 1\; =\; arctan\; \; (R\; 1\; L\; 1)\; \{\backslash \; displaystyle\; \backslash \; phi\; \_\; \{1\}\; =\; \backslash \; arctan\; \backslash \; left\; (\{R\_\; \{1\}\; \backslash \; over\; L\_\; \{1\}\}\; \backslash \; right)\}$и $y\; =\; x\; загар\; \; (\varphi \; 1)\; \{\backslash \; displaystyle\; y\; =\; x\; \backslash \; tan\; (\backslash \; phi\; \_\; \{1\})\; \backslash ;\}$

$\varphi \; 2\; знак\; равно\; arctan\; \; (R\; 2\; -\; R\; 1\; L\; 2)\; \{\backslash \; displaystyle\; \backslash \; phi\; \_\; \{2\}\; =\; \backslash \; arctan\; \backslash \; left\; (\{R\_\; \{2\}\; -R\_\; \{1\}\; \backslash \; над\; L\_\; \{2\}\}\; \backslash \; right)\}$и $y\; =\; R\; 1\; +\; (x\; -\; L\; 1)\; tan\; \; (\varphi \; 2)\; \{\backslash \; displaystyle\; y\; =\; R\_\; \{1\}\; +\; (x-L\_\; \{1\})\; \backslash \; tan\; (\backslash \; phi\; \_\; \{2\})\; \backslash ;\}$

Касательный огив

Рендеринг и профиль носового конуса касательного огива с параметрами и показанным кругом.

Рядом с простым конусом фигура касательного огива - это наиболее знакомый в хобби ракетостроение. Профиль этой формы образован сегментом окружности таким образом, что корпус ракеты касается изгиба носового конуса в его основании, а основание находится на радиусе круга. Популярность этой формы во многом объясняется простотой построения ее профиля, так как это просто круглое сечение.

Радиус круга, образующего ожив, называется радиусом огива, ρ, и он связан с длиной и радиусом основания носового конуса, как выражается формулой:

$\rho \; =\; R\; 2\; +\; L\; 2\; 2\; R\; \{\backslash \; displaystyle\; \backslash \; rho\; =\; \{R\; ^\; \{2\}\; +\; L\; ^\; \{2\}\; \backslash \; over\; 2R\}\}$

Радиус y в любой точке x, когда x изменяется от 0 до L:

$Y\; =\; \rho \; 2\; -\; (L\; -\; x)\; 2\; +\; R\; -\; \rho \; \{\backslash \; displaystyle\; y\; =\; \{\backslash \; sqrt\; \{\backslash \; rho\; ^\; \{2\}\; -\; (Lx)\; ^\; \{2\}\}\}\; +\; R-\; \backslash \; rho\}$

Длина носового конуса L должна быть меньше или равна ρ. Если они равны, то форма представляет собой полусферу.

Сферически притупленная касательная оживляющая часть

Сферически притупленная касательная оживляющая конусная рендеринг и профиль с показанными параметрами.

Касательная оживляющая носовая часть часто притупляется, закрывая ее с сегментом сферы. Точка касания, в которой сфера пересекает касательную огиву, находится по формуле

$xo\; =\; L\; -\; (\rho \; -\; rn)\; 2\; -\; (\rho \; -\; R)\; 2\; yt\; =\; rn\; (\rho \; -\; R)\; \rho \; -\; rnxt\; =\; xo\; -\; rn\; 2\; -\; yt\; 2\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; x\_\; \{o\}\; =\; L\; -\; \{\backslash \; sqrt\; \{\backslash \; left\; (\backslash \; rho\; -r\_\; \{n\}\; \backslash \; right)\; ^\; \{2\}\; -\; (\backslash \; rho\; -R)\; ^\; \{2\}\}\}\; \backslash \backslash \; y\_\; \{t\}\; =\; \{\backslash \; frac\; \{r\_\; \{n\}\; (\backslash \; rho\; -R)\}\; \{\backslash \; rho\; -r\_\; \{n\}\}\}\; \backslash \backslash \; x\_\; \{t\}\; =\; x\_\; \{o\}\; -\; \{\backslash \; sqrt\; \{r\_\; \{n\}\; ^\; \{2\}\; -y\_\; \{t\}\; ^\; \{2\}\}\}\; \backslash \; end\; \{align\}\}\}$

где r n - радиус, а x o - центр сферической носовой насадки.

Наконец, точку апекса можно найти из:

$xa\; =\; xo\; -\; rn\; \{\backslash \; displaystyle\; x\_\; \{a\}\; =\; x\_\; \{o\}\; -r\_\; \{n\}\}$

Secant ogive

Секущий рендеринг конуса носа и профиль с показанными параметрами и кругом.

Профиль этой формы также образован сегментом круга, но основание формы не находится на радиусе определенного круга по радиусу оживления. Корпус ракеты не будет касаться изгиба носовой части у ее основания. Радиус оживления ρ не определяется R и L (как для касательного огива), а скорее является одним из факторов, которые необходимо выбрать для определения формы носа. Если выбранный радиус оживления секущего оживляющего элемента больше, чем радиус оживления касательного оживляющего элемента с теми же R и L, то результирующее секущее оживляющее действие выглядит как касательное оживляющее с усеченной частью основания.

$\rho >R\; 2\; +\; L\; 2\; 2\; R\; \{\backslash \; displaystyle\; \backslash \; rho>\{R\; ^\; \{2\}\; +\; L\; ^\; \{2\}\; \backslash \; over\; 2R\}\}$и $\alpha \; знак\; равно\; arccos\; \; (L\; 2\; +\; R\; 2\; 2\; \rho )\; -\; arctan\; \; (RL)\; \{\backslash \; displaystyle\; \backslash \; alpha\; =\; \backslash \; arccos\; \backslash \; left\; (\{\{\backslash \; sqrt\; \{L\; ^\; \{2\}\; +\; R\; ^\; \{2\}\}\})\; \backslash \; over\; 2\; \backslash \; rho\}\; \backslash \; right)\; -\; \backslash \; arctan\; \backslash \; left\; (\{R\; \backslash \; over\; L\}\; \backslash \; right)\}$

Тогда радиус y в любой точке x при изменении x от 0 до L равен:

$y\; =\; \rho \; 2\; -\; (\rho \; соз\; \; (\alpha )\; -\; Икс)\; 2\; -\; \rho \; грех\; \; (\alpha )\; \{\backslash \; Displaystyle\; у\; =\; \{\backslash \; sqrt\; \{\backslash \; rho\; ^\; \{2\}\; -\; (\backslash \; rho\; \backslash \; cos\; (\backslash \; alpha)\; -x)\; ^\; \{2\}\}\}\; -\; \backslash \; rho\; \backslash \; sin\; (\backslash \; alpha)\}$

Альтернативный рендер и профиль секущих огибающих, которые показывают выпуклость из-за меньшего радиуса.

Если выбранное значение ρ меньше тангенциального оживления ρ и больше чем половина длины носового конуса, то в результате получится секущая оживляющая часть, которая выступает до максимального диаметра, превышающего диаметр основания. Классическим примером такой формы является носовой конус Ho nest John.

Elliptical

Эллиптический рендеринг и профиль носового конуса с показанными параметрами.

Профиль этой формы составляет половину эллипса с большой осью является центральной линией, а малая ось - основанием носового конуса. Вращение полного эллипса вокруг его главной оси называется вытянутым сфероидом, поэтому эллиптическая форма носа правильно будет известна как вытянутый полусфероид. Эта форма популярна в дозвуковом полете (например, ракетная модель ) из-за тупого носа и касательного основания. Это не та форма, которая обычно встречается в профессиональной ракетной технике, которая почти всегда летает с гораздо более высокими скоростями, чем другие конструкции более подходят. Если R равно L, это полушарие.

$y\; =\; R\; 1\; -\; x\; 2\; L\; 2\; \{\backslash \; displaystyle\; y\; =\; R\; \{\backslash \; sqrt\; \{1-\; \{x\; ^\; \{2\}\; \backslash \; over\; L\; ^\; \{2\}\}\; \}\}\}$

Параболический

Половина (K ′ = 1/2) Три четверти (K ′ = 3/4) Полный (K ′ = 1) Визуализация обычных параболических Форма носового конуса.

Эта форма носа не является тупой формой, которую обычно представляют, когда люди обычно называют «параболический» носовой конус. Форма носа параболической серии создается путем вращения сегмента параболы вокруг линии, параллельной его прямой кишке. Эта конструкция похожа на конструкцию касательной огива, за исключением того, что определяющей формой является парабола, а не круг. Как и на живике, эта конструкция создает форму носа с острым кончиком. Относительно тупой формы, обычно связанной с параболическим носом, см. степенной ряд ниже. (Параболическую форму также часто путают с эллиптической.)

Для $0\; \le \; K\; \prime \; \le \; 1\; \{\backslash \; displaystyle\; 0\; \backslash \; leq\; K\; \text{'}\backslash \; leq\; 1\}$: $y\; =\; R\; (2\; (Икс\; L)\; -\; К\; \text{'}(Икс\; L)\; 2\; 2\; -\; К\text{'})\; \{\backslash \; Displaystyle\; у\; =\; R\; \backslash \; влево\; (\{2\; \backslash \; влево\; (\{х\; \backslash \; над\; L\}\; \backslash \; вправо)\; -K\; \text{'}\backslash \; влево\; (\{х\; \backslash \; над\; L\}\; \backslash \; right)\; ^\; \{2\}\; \backslash \; over\; 2-K\; \text{'}\}\; \backslash \; right)\}$

K' может варьироваться от 0 до 1, но наиболее распространенные значения, используемые для форм носового конуса:

Тип параболы	K ′ Value
Конус	0
Половина	1/2
Три четверти	3/4
Полный	1

Для корпуса полной параболы (K '= 1) форма имеет касательную к телу в его основании, а основание находится на оси параболы. Значения K 'меньше 1 приводят к более тонкой форме, внешний вид которой подобен таковому у секущего огива. Форма больше не касается основания, а основание параллельно, но смещено от оси параболы.

Степенный ряд

Графики, иллюстрирующие формы носового конуса степенного ряда Половина (n = 1/2) Три четверти (n = 3/4) Визуализация обычных степенных рядов Форма носового конуса.

Степенной ряд включает форму, обычно называемую «параболическим» носовым конусом, но форма, правильно известная как параболический носовой конус, является членом параболического ряда (описанного выше). Форма силового ряда характеризуется (обычно) тупым концом и тем фактом, что его основание не касается корпуса. На стыке носового конуса и корпуса всегда есть разрыв, который выглядит явно неаэродинамическим. Форма может быть изменена в основании, чтобы сгладить этот разрыв. И цилиндр с плоской поверхностью, и конус являются формами, которые являются членами степенного ряда.

Форма носа степенного ряда генерируется путем вращения кривой y = R (x / L) вокруг оси x для значений n меньше 1. Коэффициент n управляет тупостью формы. Для значений n выше примерно 0,7 кончик довольно острый. Когда n уменьшается до нуля, форма носа степенного ряда становится все более тупой.

Для $0\; \le \; n\; \le \; 1\; \{\backslash \; displaystyle\; 0\; \backslash \; leq\; n\; \backslash \; leq\; 1\}$: $y\; =\; R\; (x\; L)\; n\; \{\backslash \; displaystyle\; y\; =\; R\; \backslash \; left\; (\{x\; \backslash \; over\; L\}\; \backslash \; справа)\; ^\; \{n\}\}$

Общие значения n включают:

Тип мощности	n Значение
Цилиндр	0
Половина (Парабола)	1/2
Три четверти	3/4
Конус	1

Серия Хаака

Графики, иллюстрирующие формы носового конуса серии Хаак LD-Haack (Фон Карман) (C = 0) LV-Haack (C = 1/3) Визуализирует обычные формы носового конуса серии Хаак.

В отличие от всех форм носового конуса, описанных выше, формы серий Вольфганга Хаака не построены из геометрические фигуры. Вместо этого формы выводятся математически с целью минимизировать перетаскивание ; см. также тело Сирса – Хаака. Хотя серия представляет собой непрерывный набор форм, определяемых значением C в приведенных ниже уравнениях, два значения C имеют особое значение: когда C = 0, обозначение LD означает минимальное сопротивление для данной длины и диаметра, а когда C = 1/3, LV указывает минимальное сопротивление для данной длины и объема. Носовые обтекатели серии Haack не совсем касаются тела в их основании, за исключением случая, когда C = 2/3. Однако прерывистость обычно настолько незначительна, что ее нельзя не заметить. При C>2/3 носовые конусы Хаака выпирают до максимального диаметра, превышающего диаметр основания. Кончики носа Хаака не заостряются, а слегка закруглены.

$\theta \; =\; arccos\; \; (1-2\; x\; L)\; y\; =\; R\; \pi \; \theta \; -\; sin\; \; (2\; \theta )\; 2\; +\; C\; sin\; 3\; \; (\theta )\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; theta\; =\; \backslash \; arccos\; \backslash \; left\; (1-\; \{2x\; \backslash \; over\; L\}\; \backslash \; right)\; \backslash \backslash \; y\; =\; \{R\; \backslash \; over\; \{\backslash \; sqrt\; \{\backslash \; pi\}\}\}\; \{\backslash \; sqrt\; \{\backslash \; theta\; -\; \{\backslash \; sin\; (2\; \backslash \; theta)\; \backslash \; over\; 2\}\; +\; C\; \backslash \; sin\; ^\; \{3\}\; (\backslash \; theta)\}\}\; \backslash \; end\; \{align\}\}\}$

Специальные значения C (как описано выше) включают:

Тип серии Хаака	Значение C
Л.Д.-Хаак (Фон Карман)	0
Л.В.-Хаак	1/3
Касательная	2/3

Фон Карман

Хаак Конструкции серии, обеспечивающие минимальное сопротивление для данной длины и диаметра, LD-Haack, где C = 0, обычно называют Фон Карман или Фон Карман огив.

Aerospike

Характеристики аэродинамического сопротивления носового конуса

Для самолетов и ракет ниже Маха.8 сопротивление давлением носового конуса практически равно нулю для всех форм. Основным существенным фактором является сопротивление трением, которое в значительной степени зависит от смоченной области , гладкости поверхности этой области и наличия каких-либо неоднородностей в форме. Например, для дозвуковых ракет лучше всего подходит короткая, тупая, гладкая эллиптическая форма. В трансзвуковой области и за ее пределами, где сопротивление давления резко возрастает, влияние формы носа на сопротивление становится очень значительным. Факторами, влияющими на сопротивление давлению, являются общая форма носового конуса, его коэффициент тонкости и его коэффициент крутизны.

Влияние общей формы

Крупным планом вид носового обтекателя на Боинг 737

Многие ссылки на конструкцию носового обтекателя содержат эмпирические данные, сравнивающие характеристики лобового сопротивления различных форм носовой части в разных полётах. режимы. Представленная здесь диаграмма представляется наиболее полной и полезной компиляцией данных для наиболее интересного режима полета. Эта диаграмма в целом согласуется с более подробными, но менее исчерпывающими данными, содержащимися в других источниках (в первую очередь, USAF Datcom ).

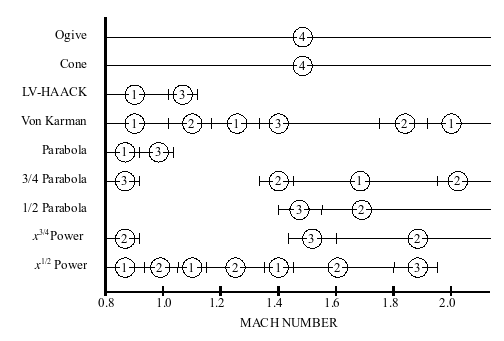Сравнение характеристик лобового сопротивления различных форм носового конуса в трансзвуковой и низко-маховых областях. Рейтинги следующие: превосходно (1), хорошо (2), удовлетворительно (3), низко (4).

Во многих конструкциях носового обтекателя наибольшее беспокойство вызывают летные характеристики в околозвуковой области от 0,8 до 1,2 Маха. Хотя данные не доступны для многих форм в трансзвуковой области, таблица ясно показывает, что либо форма фон Кармана, либо форма степенного ряда с n = 1/2, будет предпочтительнее популярных конических или оживленных форм. формы для этой цели.

General Dynamics F-16 с носовым конусом, очень близким к форме фон Кармана

Это наблюдение противоречит часто повторяемому общепринятому мнению о том, что конический нос является оптимальным для «взлома по Маху». Истребители, вероятно, являются хорошими примерами формы носа, оптимизированной для околозвуковой области, хотя форма их носа часто искажается из-за других соображений авионики и воздухозаборников. Например, нос F-16 Fighting Falcon выглядит очень близко к форме фон Кармана.

Влияние коэффициента тонкости

Отношение длины носового конуса к его диаметру основания известно как коэффициент тонкости. Иногда это также называют соотношением сторон, хотя этот термин обычно применяется к крыльям и хвосту. Коэффициент тонкости часто применяется ко всему транспортному средству с учетом его общей длины и диаметра. Отношение длины к диаметру также часто называют калибром носового конуса.

На сверхзвуковых скоростях коэффициент крупности оказывает существенное влияние на лобовое сопротивление волнового сопротивления, особенно при низких передаточных числах; но есть очень небольшой дополнительный выигрыш для соотношений, превышающих 5: 1. По мере увеличения степени измельчения смачиваемая площадь и, следовательно, составляющая сопротивления поверхностного трения также увеличиваются. Следовательно, минимальный коэффициент тонкости сопротивления в конечном итоге будет компромиссом между уменьшением волнового сопротивления и увеличением сопротивления трения.

Дополнительная литература

• Дизайн конфигурации ракеты
• Дизайн аэродинамически стабилизированных свободных ракет
• статья на немецком языке Вольфганга Хаака
• таблица носового конуса

Ссылки