Войти
Сетевые мотивы являются повторяющимися и статистически значимыми подграфы или паттерны большего графа. Все сети, включая биологические сети, социальные сети, технологические сети (например, компьютерные сети и электрические схемы) и другие, могут быть представлены в виде графов, которые включают большое количество подграфов.
Сетевые мотивы - это подграфы, которые повторяются в конкретной сети или даже среди различных сетей. Каждый из этих подграфов, определяемый конкретным шаблоном взаимодействий между вершинами, может отражать структуру, в которой конкретные функции выполняются эффективно. В самом деле, мотивы имеют важное значение в основном потому, что они могут отражать функциональные свойства. Недавно они привлекли большое внимание как полезная концепция для раскрытия принципов структурного проектирования сложных сетей. Хотя сетевые мотивы могут обеспечить глубокое понимание функциональных возможностей сети, их обнаружение является сложной вычислительной задачей.
Пусть G = (V, E) и G ′ = (V ′, E ′) - два графа. Граф G ′ является подграфом графа G (записывается как G ′ ⊆ G), если V ′ ⊆ V и E ′ ⊆ E ∩ (V ′ × V ′). Если G ′ ⊆ G и G ′ содержит все ребра ⟨u, v⟩ ∈ E, u, v ∈ V ′, то G ′ является индуцированным подграфом G. Мы называем G ′ и G изоморфными (записываемыми как G ′ ↔ G), если существует биекция (взаимно однозначное соответствие) f: V ′ → V с ⟨u, v⟩ ∈ E ′ ⇔ ⟨f (u), f (v)⟩ ∈ E для всех u, v ∈ V ′. Отображение f называется изоморфизмом между G и G ′.
Когда G ″ ⊂ G и существует изоморфизм между подграфом G ″ и графом G ′, это отображение представляет собой вид G ′ в G. Число появлений графа G 'в G называется частотой F G G' в G. Граф называется повторяющимся (или частым) в G, если его частота F G (G ') выше заранее определенного порога или значения отсечки. В этом обзоре мы используем термины «шаблон» и «частый подграф» как синонимы. Существует ансамбль Ω (G) случайных графов, соответствующий нулевой модели, связанной с G. Мы должны выбрать N случайных графов равномерно из Ω (G) и вычислить частоту для конкретный частый подграф G 'в G. Если частота G' в G выше, чем его средняя арифметическая частота в N случайных графах R i, где 1 ≤ i ≤ N, мы называем этот повторяющийся паттерн является значимым и, следовательно, рассматривать G 'как сетевой мотив для G.Для небольшого графа G' сеть G и набор рандомизированных сетей R (G) ⊆ Ω (R), где R (G) = N, Z-оценка частоты G ′ определяется как
где μ R (G ′) и σ R (G ′) обозначают среднее и стандартное отклонение частоты в наборе R (G) соответственно. Чем больше Z (G '), тем более значимым является подграф G' как мотив. В качестве альтернативы, другое измерение при проверке статистической гипотезы, которое может рассматриваться при обнаружении мотива, - это p-значение, заданное как вероятность F R (G ') ≥ F G (G ') (как его нулевая гипотеза), где F R (G') указывает частоту G 'в рандомизированной сети. Подграфик с p-значением меньше порога (обычно 0,01 или 0,05) будет рассматриваться как значимый образец. Значение p для частоты G ′ определяется как
Различные вхождения подграфа в граф. (M1 - M4) - это разные вхождения подграфа (b) в графе (a). Для концепции частоты F 1 набор M1, M2, M3, M4 представляет все совпадения, поэтому F 1 = 4. Для F 2 одно из два набора M1, M4 или M2, M3 - возможные совпадения, F 2 = 2. Наконец, для концепции частоты F 3 допускается только одно из совпадений (M1 - M4), поэтому F 3 = 1. Частота этих трех частотных концепций уменьшается по мере ограничения использования сетевых элементов. где N указывает количество рандомизированных сетей, i определяется по ансамблю рандомизированных сетей, а дельта-функция Кронекера δ (c (i)) равна единице, если выполняется условие c (i). Концентрация конкретного подграфа G 'размера n в сети G относится к отношению внешнего вида подграфа в сети к общей частоте неизоморфных подграфов размера n, которая формулируется как
где индекс i определен на множестве всех неизоморфных графов размера n. Другое статистическое измерение определено для оценки сетевых мотивов, но оно редко используется в известных алгоритмах. Это измерение введено Пикардом и др. в 2008 г. и использовал распределение Пуассона, а не гауссово нормальное распределение, которое неявно использовалось выше.
Кроме того, были предложены три конкретных концепции частоты подграфов. Как показано на рисунке, первое понятие частоты F 1 рассматривает все совпадения графа в исходной сети. Это определение похоже на то, что мы ввели выше. Вторая концепция F 2 определяется как максимальное количество непересекающихся по ребрам экземпляров данного графа в исходной сети. И, наконец, концепция частоты F 3 влечет за собой совпадения с непересекающимися ребрами и узлами. Следовательно, две концепции F 2 и F 3 ограничивают использование элементов графа, и, как можно заключить, частота подграфа снижается за счет наложения ограничений на сеть. использование элемента. В результате алгоритм обнаружения сетевых мотивов пропустит большее количество подграфов-кандидатов, если мы будем настаивать на частотных концепциях F 2 и F 3.
Изучение сетевых мотивов было начато. Холландом и Лейнхардтом, которые представили концепцию трехкомпонентной переписи сетей. Они представили методы для перечисления различных типов конфигураций подграфов и проверки того, отличаются ли подсчеты подграфов статистически от ожидаемых в случайных сетях.
Эта идея была далее обобщена в 2002 году Ури Алоном и его группой, когда сетевые мотивы были обнаружены в сети регуляции (транскрипции) генов бактерий E. coli, а затем в большом наборе естественных сетей. С тех пор по этой теме было проведено значительное количество исследований. Некоторые из этих исследований сосредоточены на биологических приложениях, другие - на вычислительной теории сетевых мотивов.
Биологические исследования направлены на интерпретацию мотивов, обнаруженных для биологических сетей. Например, в следующей работе сетевые мотивы найдены в E. coli были обнаружены в сетях транскрипции других бактерий, а также дрожжей и высших организмов. Отдельный набор сетевых мотивов был идентифицирован в других типах биологических сетей, таких как нейронные сети и сети взаимодействия белков.
Вычислительные исследования были сосредоточены на улучшении существующих инструментов обнаружения мотивов, чтобы помочь биологическим исследованиям и позволить более крупным сетям быть проанализированы. К настоящему времени было предоставлено несколько различных алгоритмов, которые подробно описаны в следующем разделе в хронологическом порядке.
Совсем недавно был выпущен инструмент acc-MOTIF для обнаружения сетевых мотивов.
Были предложены различные решения сложной проблемы сетевых мотивов (NM) открытие. Эти алгоритмы можно классифицировать по различным парадигмам, таким как методы точного подсчета, методы выборки, методы роста паттернов и так далее. Однако проблема обнаружения мотива состоит из двух основных этапов: во-первых, вычисление числа вхождений подграфа, а затем оценка значимости подграфа. Повторение является значительным, если обнаруживается намного больше, чем ожидалось. Грубо говоря, ожидаемое количество появлений подграфа можно определить с помощью Null-модели, которая определяется ансамблем случайных сетей с некоторыми из тех же свойств, что и исходная сеть.
До 2004 г. единственным точным методом подсчета для обнаружения ЯМ был метод грубой силы, предложенный Milo et al. Этот алгоритм оказался успешным для обнаружения небольших мотивов, но использование этого метода для поиска даже мотивов размера 5 или 6 было невозможно с вычислительной точки зрения. Следовательно, требовался новый подход к этой проблеме.
Здесь дается обзор вычислительных аспектов основных алгоритмов и обсуждаются связанные с ними преимущества и недостатки с алгоритмической точки зрения.
Каштан и др. опубликовал mfinder, первый инструмент для поиска мотивов, в 2004 году. Он реализует два типа алгоритмов поиска мотивов: полное перечисление и первый метод выборки.
Их алгоритм обнаружения выборки был основан на выборке краев по всей сети. Этот алгоритм оценивает концентрации индуцированных подграфов и может использоваться для обнаружения мотивов в направленных или неориентированных сетях. Процедура выборки алгоритма начинается с произвольного края сети, которая приводит к подграфу размера два, а затем расширяет подграф, выбирая случайное ребро, которое инцидентно текущему подграфу. После этого он продолжает выбирать случайные соседние ребра до тех пор, пока не будет получен подграф размера n. Наконец, выбранный подграф расширяется, чтобы включить все ребра, которые существуют в сети между этими n узлами. Когда алгоритм использует метод выборки, выборка объективных выборок является наиболее важной проблемой, которую алгоритм может решить. Однако процедура отбора проб не позволяет брать пробы равномерно, поэтому Каштан и др. предложил схему взвешивания, которая присваивает разные веса разным подграфам в сети. Базовый принцип распределения весов использует информацию о вероятности выборки для каждого подграфа, то есть вероятные подграфы получат сравнительно меньшие веса по сравнению с невероятными подграфами; следовательно, алгоритм должен вычислять вероятность выборки каждого подграфа, который был выбран. Этот метод взвешивания помогает mfinder беспристрастно определять концентрации на подграфе.
В расширенном, чтобы включить резкий контраст с исчерпывающим поиском, вычислительное время алгоритма на удивление асимптотически не зависит от размера сети. Анализ вычислительного времени алгоритма показал, что для каждой выборки подграфа размера n из сети требуется O (n). С другой стороны, нет анализа времени классификации выбранных подграфов, который требует решения проблемы изоморфизма графов для каждой выборки подграфов. Кроме того, на алгоритм накладываются дополнительные вычислительные усилия из-за вычисления веса подграфа. Но неизбежно сказать, что алгоритм может выполнять выборку одного и того же подграфа несколько раз, тратя время, не собирая никакой информации. В заключение, используя преимущества выборки, алгоритм работает более эффективно, чем алгоритм исчерпывающего поиска; однако он лишь приблизительно определяет концентрации подграфиков. Этот алгоритм может находить мотивы размером до 6 из-за его основной реализации, и в результате он дает наиболее значимый мотив, а не все остальные. Также необходимо отметить, что этот инструмент не имеет возможности визуального представления. Кратко показан алгоритм выборки:
| mfinder |
|---|
| Определения: Es- это набор выбранных ребер. V s - это набор всех узлов, которых касаются ребра в E. |
| Init V s и E s как пустые множества. 1. Выберите случайное ребро e 1 = (v i, v j). Обновите E s = {e 1 }, V s = {v i, v j} 2. Составьте список L всех соседних ребер E s. Опустите из L все ребра между элементами V s. 3. Выберите случайное ребро e = {v k,vl} из L. Обновите E s = E s ⋃ {e}, V s = V s ⋃ {v k, v l }. 4. Повторите шаги 2-3 до завершения подграфа из n узлов (пока | V s | = n). 5. Вычислите вероятность выборки выбранного подграфа с n узлами. |
Шрайбер и Швёббермейер предложили алгоритм, названный гибким поиском шаблонов (FPF), для извлечения частых подграфов входной сети и реализовали его в системе с именем Mavisto. Их алгоритм использует свойство закрытия вниз, которое применимо для частотных концепций F 2 и F 3. Свойство нисходящего закрытия утверждает, что частота для подграфов монотонно уменьшается за счет увеличения размера подграфов; однако это свойство не обязательно выполняется для частотной концепции F 1. FPF основан на дереве паттернов (см. Рисунок), состоящем из узлов, которые представляют различные графы (или паттерны), где родительский элемент каждого узла является подграфом его дочерних узлов; другими словами, соответствующий граф каждого узла дерева паттернов расширяется путем добавления нового ребра к графу его родительского узла.
Иллюстрация дерева шаблонов в алгоритме FPF. Сначала алгоритм FPF перечисляет и поддерживает информацию обо всех совпадениях подграфа, расположенного в корне дерева шаблонов. Затем, один за другим, он создает дочерние узлы предыдущего узла в дереве шаблонов, добавляя одно ребро, поддерживаемое совпадающим ребром в целевом графе, и пытается развернуть всю предыдущую информацию о совпадениях в новый подграф. (дочерний узел). На следующем этапе он решает, ниже ли частота текущего шаблона, чем предварительно определенный порог, или нет. Если он ниже и если закрытие вниз сохраняется, FPF может покинуть этот путь и не пройти дальше в этой части дерева; в результате можно избежать ненужных вычислений. Эта процедура продолжается до тех пор, пока не останется оставшегося пути для перемещения.
Преимущество алгоритма в том, что он не учитывает редко встречающиеся подграфы и пытается завершить процесс перечисления как можно скорее; поэтому он тратит время только на перспективные узлы в дереве шаблонов и отбрасывает все остальные узлы. В качестве дополнительного бонуса понятие дерева шаблонов позволяет реализовать и выполнять FPF параллельно, поскольку можно проходить каждый путь дерева шаблонов независимо. Однако FPF наиболее полезен для частотных концепций F 2 и F 3, потому что закрытие вниз не применимо к F 1. Тем не менее, дерево шаблонов все еще практично для F 1, если алгоритм работает параллельно. Еще одно преимущество алгоритма состоит в том, что реализация этого алгоритма не имеет ограничений на размер мотива, что делает его более поддающимся усовершенствованиям. Псевдокод FPF (Mavisto) показан ниже:
| Mavisto |
|---|
| Данные: График G, размер целевого шаблона t, концепция частоты F Результат: Набор R шаблонов размер t с максимальной частотой. |
| R ← φ, f max ← 0 P ← начальный шаблон p1 размера 1 Mp1← все совпадения p 1 в G Пока P ≠ φ do Pmax ← выбрать все шаблоны из P с максимальным размером. P ← выбрать шаблон с максимальной частотой из P max Ε = ExtensionLoop (G, p, M p) Foreach pattern p ∈ E IfF = F 1затем f ← size (M p) Else f ← Максимальный независимый набор (F, M p) End Ifsize (p) = t, затем Iff = f max, затем R ← R ⋃ {p} Иначе, если f>f max, то R ← {p} ; f max ← f Конец Иначе IfF = F 1orf ≥ f max затем P ← P ⋃ { p} Конец Конец Конец Конец |
Смещение выборки Каштана и др. дало большой импульс для разработки лучших алгоритмов обнаружения ЯМ Проблема. Хотя Каштан и др. пытались решить этот недостаток с помощью схемы взвешивания, этот метод привел к нежелательным накладным расходам на время работы, а также к более сложной реализации. Этот инструмент является одним из самых полезных, поскольку он поддерживает визуальный options, а также является эффективным алгоритмом относительно времени. Но у него есть ограничение на размер мотива, так как он не позволяет искать f или мотивы размера 9 или выше в зависимости от способа реализации инструмента.
Вернике представил алгоритм под названием RAND-ESU, который обеспечивает значительное улучшение по сравнению с mfinder. Этот алгоритм, основанный на алгоритме точного перечисления ESU, был реализован в виде приложения под названием FANMOD. RAND-ESU - это алгоритм обнаружения NM, применимый как для направленных, так и для неориентированных сетей, эффективно использует несмещенную выборку узлов по всей сети и предотвращает более чем однократный пересчет подграфов. Кроме того, RAND-ESU использует новый аналитический подход под названием DIRECT для определения значимости подграфа вместо использования ансамбля случайных сетей в качестве нулевой модели. Метод DIRECT оценивает концентрацию подграфов без явного создания случайных сетей. Эмпирически метод DIRECT более эффективен по сравнению со случайным сетевым ансамблем в случае подграфов с очень низкой концентрацией; однако классическая Null-модель работает быстрее, чем метод DIRECT для высококонцентрированных подграфов. Далее мы подробно описываем алгоритм ESU, а затем показываем, как этот точный алгоритм может быть эффективно модифицирован в RAND-ESU, который оценивает концентрации подграфов.
Алгоритмы ESU и RAND-ESU довольно просты и, следовательно, их легко реализовать. ESU сначала находит набор всех индуцированных подграфов размера k, пусть S k будет этим набором. ESU может быть реализован как рекурсивная функция; выполнение этой функции может быть отображено в виде древовидной структуры глубины k, называемой ESU-Tree (см. рисунок). Каждый из узлов ESU-Tree указывает состояние рекурсивной функции, которая влечет за собой два последовательных набора SUB и EXT. SUB относится к узлам целевой сети, которые являются смежными и образуют частичный подграф размером | SUB | ≤ к. Если | SUB | = k, алгоритм нашел индуцированный полный подграф, поэтому S k = SUB ∪ S k. Однако если | SUB | < k, the algorithm must expand SUB to achieve cardinality k. This is done by the EXT set that contains all the nodes that satisfy two conditions: First, each of the nodes in EXT must be adjacent to at least one of the nodes in SUB; second, their numerical labels must be larger than the label of first element in SUB. The first condition makes sure that the expansion of SUB nodes yields a connected graph and the second condition causes ESU-Tree leaves (see figure) to be distinct; as a result, it prevents overcounting. Note that, the EXT set is not a static set, so in each step it may expand by some new nodes that do not breach the two conditions. The next step of ESU involves classification of sub-graphs placed in the ESU-Tree leaves into non-isomorphic size-k graph classes; consequently, ESU determines sub-graphs frequencies and concentrations. This stage has been implemented simply by employing McKay's nauty algorithm, which classifies each sub-graph by performing a graph isomorphism test. Therefore, ESU finds the set of all induced k-size sub-graphs in a target graph by a recursive algorithm and then determines their frequency using an efficient tool.
Процедура внедрения RAND-ESU довольно проста и является одним из основных преимуществ FANMOD. Можно изменить алгоритм ESU, чтобы исследовать только часть листьев ESU-Tree, применив значение вероятности 0 ≤ p d ≤ 1 для каждого уровня ESU-Tree и обязав ESU пройти каждый дочерний узел узла на уровне d-1 с вероятностью p d. Этот новый алгоритм называется RAND-ESU. Очевидно, когда p d = 1 для всех уровней, RAND-ESU действует как ESU. При p d = 0 алгоритм ничего не находит. Обратите внимание, что эта процедура гарантирует, что шансы посещения каждого листа ESU-Tree одинаковы, что приводит к несмещенной выборке подграфов по сети. Вероятность посещения каждого листа равна ∏ dpd, и она идентична для всех листьев ESU-Tree; следовательно, этот метод гарантирует беспристрастную выборку подграфов из сети. Тем не менее, определение значения p d для 1 ≤ d ≤ k - это еще одна проблема, которая должна быть решена вручную экспертом, чтобы получить точные результаты концентраций подграфика. Хотя на этот счет нет четких предписаний, Вернике дает некоторые общие наблюдения, которые могут помочь в определении значений p_d. Таким образом, RAND-ESU - это очень быстрый алгоритм обнаружения ЯМ в случае индуцированных подграфов, поддерживающих метод несмещенной выборки. Хотя основной алгоритм ESU и, следовательно, инструмент FANMOD известен тем, что обнаруживает индуцированные подграфы, в ESU есть тривиальная модификация, которая позволяет также находить неиндуцированные подграфы. Псевдокод ESU (FANMOD) показан ниже:
(a) Целевой граф размера 5, (b) ESU-дерево глубины k, которое связано с извлечением подграфов размера 3 в целевой граф. Листья соответствуют набору S3 или всем индуцированным подграфам размера 3 целевого графа (а). Узлы в дереве ESU включают два смежных набора, первый набор содержит смежные узлы, называемые SUB, а второй набор с именем EXT содержит все узлы, которые примыкают по крайней мере к одному из узлов SUB и где их числовые метки больше, чем узлы SUB этикетки. Набор EXT используется алгоритмом для расширения набора SUB до тех пор, пока он не достигнет желаемого размера подграфа, который помещается на самый нижний уровень ESU-Tree (или его листья). | Перечисление ESU (FANMOD) |
|---|
| EnumerateSubgraphs (G, k) Ввод: Граф G = (V, E) и целое число 1 ≤ k ≤ | V |. Вывод: Все подграфы размера k в G. для каждой вершины v ∈ V do VExtension ← {u ∈ N ({v}) | u>v} вызов ExtendSubgraph ({v}, VExtension, v) endfor |
| ExtendSubgraph (VSubgraph, VExtension, v) if| VSubgraph | = k затем вывести G [VSubgraph] и вернуть пока VExtension ≠ ∅ do Удалить произвольно выбранную вершину w из VExtension VExtension ′ ← VExtension ∪ {u ∈ N excl (w, VS подграф) | u>v} вызов ExtendSubgraph (VSubgraph ∪ {w}, VExtension ′, v) return |
Chen et al. представил новый алгоритм обнаружения NM под названием NeMoFinder, который адаптирует идею SPIN для извлечения часто встречающихся деревьев, а затем расширяет их в неизоморфные графы. NeMoFinder использует частые деревья размера n для разделения входной сети на коллекцию графов размера n, а затем находит частые подграфы размера n путем расширения частых деревьев по ребру до получения полного графа размера n K п. Алгоритм находит NM в неориентированных сетях и не ограничивается извлечением только индуцированных подграфов. Кроме того, NeMoFinder представляет собой алгоритм точного подсчета и не основан на методе выборки. Как пишет Chen et al. Согласно заявлению авторов, NeMoFinder применим для обнаружения относительно больших ЯМ, например, для обнаружения ЯМ размером до 12 из всей сети PPI S. cerevisiae (дрожжевые).
NeMoFinder состоит из трех основных этапов. Во-первых, поиск часто встречающихся деревьев размера n, затем использование повторяющихся деревьев размера n для разделения всей сети на коллекцию графов размера n, наконец, выполнение операций соединения подграфов, чтобы найти частые подграфы размера n. На первом этапе алгоритм обнаруживает все неизоморфные деревья размера n и отображения дерева в сеть. На втором этапе диапазоны этих отображений используются для разделения сети на графы размера n. Вплоть до этого шага не существует различия между NeMoFinder и методом точного перечисления. Однако большая часть неизоморфных графов размера n все еще остается. NeMoFinder использует эвристику для перечисления недревесных графов размера n на основе информации, полученной на предыдущих шагах. Основное преимущество алгоритма заключается в третьем шаге, который генерирует подграфы-кандидаты из ранее пронумерованных подграфов. Это создание новых подграфов размера n выполняется путем объединения каждого предыдущего подграфа с производными подграфами от самого себя, называемыми подграфами-родственниками. Эти новые подграфы содержат одно дополнительное ребро по сравнению с предыдущими подграфами. Тем не менее, существуют некоторые проблемы при создании новых подграфов: не существует четкого метода получения родственников из графа, соединение подграфа с его кузенами приводит к избыточности в создании определенного подграфа более одного раза, а определение кузенов является выполняется каноническим представлением матрицы смежности, которая не закрывается при операции соединения. NeMoFinder - это эффективный алгоритм поиска сетевых мотивов для мотивов размером до 12 только для сетей белок-белковых взаимодействий, которые представлены в виде неориентированных графов. И он не может работать в направленных сетях, которые так важны в области сложных и биологических сетей. Псевдокод NeMoFinder показан ниже:
| NeMoFinder |
|---|
| Input: G - сеть PPI; N - Количество рандомизированных сетей; K - максимальный размер сетевого мотива; F - Порог частоты; S - Порог уникальности; Вывод: U - повторяющийся и уникальный набор сетевых мотивов; D ← ∅; для размера мотива k из 3 toK do T ← FindRepeatedTrees (k); GDk← GraphPartition (G, T) D ← D ∪ T; D ′ ← T; i ← k; в то время как D ′ ≠ ∅ и i ≤ k × (k - 1) / 2 do D ′ ← FindRepeatedGraphs (k, i, D ′); D ← D ∪ D '; i ← i + 1; конец, а конец для для счетчик i из 1 toN do Grand ← RandomizedNetworkGeneration (); для каждого g ∈ D do GetRandFrequency (g, G rand); конец для конец для U ← ∅; для каждого g ∈ D do s ← GetUniqunessValue (g); ifs ≥ S, затем U ← U ∪ {g}; конец, если конец для return U; |
Грохов и Келлис предложили точный алгоритм для перечисления появлений подграфов. Алгоритм основан на подходе, ориентированном на мотив, что означает, что частота данного подграфа, называемого графом запроса, исчерпывающе определяется путем поиска всех возможных отображений из графа запроса в большую сеть. Утверждается, что мотивно-ориентированный метод по сравнению с сетецентрическими методами имеет некоторые полезные особенности. Прежде всего, это позволяет избежать повышенной сложности перебора подграфов. Кроме того, использование сопоставления вместо перечисления позволяет улучшить тест на изоморфизм. Чтобы улучшить производительность алгоритма, поскольку это неэффективный алгоритм точного перебора, авторы ввели быстрый метод, который называется условиями нарушения симметрии. Во время простых тестов на изоморфизм подграфа подграф может быть отображен на один и тот же подграф графа запроса несколько раз. В алгоритме Грохов-Келлиса (GK) нарушение симметрии используется для предотвращения таких множественных отображений. Здесь мы вводим алгоритм GK и условие нарушения симметрии, которое устраняет избыточные тесты изоморфизма.
(a) граф G, (b) иллюстрация всех автоморфизмов G, показанных в (a). Из множества AutG мы можем получить набор условий нарушения симметрии группы G, заданных SymG в (c). Только первое отображение в AutG удовлетворяет условиям SynG; в результате, применяя SymG в модуле расширения изоморфизма, алгоритм перечисляет каждый совместимый подграф в сети только один раз. Обратите внимание, что SynG не обязательно является уникальным набором для произвольного графа G. Алгоритм GK обнаруживает весь набор отображений данного графа запроса в сеть за два основных шага. Он начинается с вычисления условий нарушения симметрии графа запроса. Затем с помощью метода ветвей и границ алгоритм пытается найти все возможные отображения из графа запроса в сеть, которая удовлетворяет связанным условиям нарушения симметрии. Пример использования условий нарушения симметрии в алгоритме GK показан на рисунке.
Как упоминалось выше, метод нарушения симметрии - это простой механизм, который не позволяет тратить время на поиск подграфа более одного раза из-за его симметрии. Обратите внимание, что для вычисления условий нарушения симметрии требуется найти все автоморфизмы заданного графа запросов. Несмотря на то, что не существует эффективного (или полиномиального по времени) алгоритма для проблемы автоморфизма графа, эта проблема может быть эффективно решена на практике с помощью инструментов Маккея. Как утверждается, использование условий нарушения симметрии при обнаружении ЯМ позволяет значительно сэкономить время работы. Более того, из результатов можно сделать вывод, что использование условий нарушения симметрии приводит к высокой эффективности, особенно для направленных сетей по сравнению с неориентированными сетями. Условия нарушения симметрии, используемые в алгоритме GK, аналогичны ограничению, которое алгоритм ESU применяет к меткам в наборах EXT и SUB. В заключение, алгоритм GK вычисляет точное количество появлений заданного графа запроса в большой сложной сети, а использование условий нарушения симметрии улучшает производительность алгоритма. Кроме того, алгоритм GK является одним из известных алгоритмов, не имеющих ограничений по размеру мотива в реализации, и потенциально он может находить мотивы любого размера.
Большинство алгоритмов в области обнаружения ЯМ используются для поиска индуцированных подграфов сети. В 2008 году Нога Алон и др. представил подход для поиска неиндуцированных подграфов. Их методика работает в неориентированных сетях, таких как PPI. Кроме того, он считает неиндуцированные деревья и подграфы с ограниченной шириной дерева. Этот метод применяется для подграфов размером до 10.
Этот алгоритм подсчитывает количество неиндуцированных вхождений дерева T с k = O (logn) вершинами в сети G с n вершинами как следующим образом:
Поскольку доступные сети PPI далеки от завершения и отсутствия ошибок, этот подход подходит для обнаружения NM для таких сетей. Поскольку алгоритм Грохоу – Келлиса и этот являются популярными для неиндуцированных подграфов, стоит упомянуть, что алгоритм, представленный Alon et al. занимает меньше времени, чем алгоритм Грохоу-Келлиса.
Omidi et al. представил новый алгоритм для обнаружения мотивов под названием MODA, который применим для индуцированного и неиндуцированного обнаружения ЯМ в ненаправленных сетях. Он основан на подходе, ориентированном на мотив, который обсуждается в разделе, посвященном алгоритму Грохова – Келлиса. Очень важно различать алгоритмы, ориентированные на мотивы, такие как MODA и алгоритм GK, из-за их способности работать как алгоритмы поиска запросов. Эта функция позволяет таким алгоритмам находить отдельный запрос мотива или небольшое количество запросов мотива (не все возможные подграфы заданного размера) с большими размерами. Поскольку количество возможных неизоморфных подграфов экспоненциально увеличивается с размером подграфа, для мотивов большого размера (даже больше 10) сетецентрические алгоритмы, ищущие все возможные подграфы, сталкиваются с проблемой. Хотя алгоритмы, ориентированные на мотивы, также имеют проблемы с обнаружением всех возможных подграфов большого размера, их способность находить небольшое количество из них иногда является важным свойством.
Используя иерархическую структуру, называемую деревом расширения, алгоритм MODA может извлекать NM заданного размера систематически и аналогично FPF, что позволяет избежать перечисления бесперспективных подграфов; MODA учитывает потенциальные запросы (или возможные подграфы), которые могут привести к частым подграфам. Несмотря на то, что MODA напоминает FPF в использовании древовидной структуры, дерево расширения применимо только для вычисления концепции частоты F 1. Как мы обсудим далее, преимущество этого алгоритма состоит в том, что он не выполняет проверку изоморфизма подграфов для недревесных графов запросов. Кроме того, он использует метод выборки, чтобы ускорить время работы алгоритма.
Вот основная идея: с помощью простого критерия можно обобщить отображение графа размера k в сеть на его суперграфы того же размера. Например, предположим, что есть отображение f (G) графа G с k узлами в сеть, и у нас есть граф G 'того же размера с еще одним ребром lang, v⟩; f G отобразит G 'в сеть, если в сети есть ребро ⟨f G (u), f G (v)⟩. В результате мы можем использовать набор отображений графа для определения частот его суперграфов того же порядка просто за время O (1) без выполнения проверки изоморфизма подграфов. Алгоритм изобретательно начинается с минимально связанных графов запросов размера k и находит их отображения в сети через изоморфизм подграфов. После этого, с сохранением размера графа, он расширяет ранее рассмотренные графы запросов по ребру и вычисляет частоту этих расширенных графов, как упомянуто выше. Процесс расширения продолжается до достижения полного графа K k (полностью связанного с ребром ⁄ 2).
Как обсуждалось выше, алгоритм начинается с вычисления частот поддеревьев в сети, а затем расширяет поддеревья по краям. Один из способов реализации этой идеи - это дерево расширения T k для каждого k. На рисунке показано дерево расширения для подграфов размера 4. T k организует выполняющийся процесс и предоставляет графы запросов в иерархическом порядке. Строго говоря, дерево расширения T k - это просто ориентированный ациклический граф или DAG, с его корневым номером k, указывающим размер графа, существующего в дереве расширения, и каждый из его других узлов, содержащих матрица смежности отдельного графа запросов размера k. Все узлы на первом уровне T k являются отдельными деревьями размера k, и при обходе T k по глубине графы запросов расширяются с одним ребром на каждом уровне. Граф запроса в узле - это подграф графа запроса в дочернем узле с одной разностью ребер. Самый длинный путь в T k состоит из (k-3k + 4) / 2 ребер и является путем от корня до листового узла, содержащего полный граф. Создание деревьев расширения может быть выполнено с помощью простой процедуры, которая объясняется в.
MODA проходит через T k и когда он извлекает деревья запросов из первого уровня T k он вычисляет их наборы отображений и сохраняет эти отображения для следующего шага. Для запросов без дерева из T k алгоритм извлекает отображения, связанные с родительским узлом в T k, и определяет, какое из этих отображений может поддерживать текущие графы запросов. Процесс будет продолжаться до тех пор, пока алгоритм не получит полный граф запроса. Отображения дерева запросов извлекаются с использованием алгоритма Грохоу – Келлиса. Для вычисления частоты недревесных графов запросов алгоритм использует простую процедуру, которая занимает O (1) шагов. Кроме того, MODA использует метод выборки, при котором выборка каждого узла в сети линейно пропорциональна степени узла, распределение вероятностей точно аналогично хорошо известному Барабаши-Альберту. предпочтительная модель присоединения в области сложных сетей. Этот подход генерирует приближения; однако результаты практически стабильны в различных исполнениях, поскольку подграфы объединяются вокруг узлов с высокой связью. Псевдокод MODA показан ниже:
Иллюстрация дерева раскрытия T4 для графов запросов с 4 узлами. На первом уровне есть неизоморфные деревья размера k, и на каждом уровне к родительскому графу добавляется ребро, чтобы сформировать дочерний граф. На втором уровне есть граф с двумя альтернативными ребрами, который показан красным пунктиром. Фактически, этот узел представляет два развернутых графика, которые являются изоморфными. | MODA |
|---|
| Входные данные: G: Входной график, k: размер подграфа, Δ: пороговое значение Выходные данные: Список часто встречающихся подграфов: список всех частых подграфов размера k Примечание: FG: набор отображений из G во входном графе G выборка Tk do G ′ = Get-Next-BFS (T k) // G ′ - это граф запроса , если | E (G ′) | = (k - 1) call Mapping-Module (G ', G) else call Enumerating-Module (G', G, T k) end if сохранить F2 if|FG|>Δ затем добавить G 'в список часто встречающихся подграфов end if До | E (G') | = (k - 1) / 2 return Список часто встречающихся подграфов |
Недавно представленный алгоритм под названием Кавош направлен на улучшение использования основной памяти. Кавош может использоваться для обнаружения NM как в направленных, так и в неориентированных сетях. Основная идея Перечисление аналогично алгоритмам GK и MODA, которые сначала находят все подграфы размера k, в которых участвовал конкретный узел, затем удаляют узел и впоследствии повторяют этот процесс для оставшихся узлов.
Для подсчета подграфы размера k, которые включают в себя конкретный узел, деревья с максимальной глубиной k, укорененные в этом узле и основанные на взаимосвязи соседства, строятся неявно. Потомки каждого узла включают как входящие, так и исходящие смежные узлы. Чтобы спуститься по дереву, ребенок выбирается на каждом уровне с разрешением Уловка, что конкретный дочерний элемент может быть включен только в том случае, если он не был включен ни на одном из более высоких уровней. После спуска на самый нижний возможный уровень дерево снова поднимается, и процесс повторяется с условием, что узлы, посещенные на более ранних путях потомка, теперь считаются непосещенными узлами. Последнее ограничение при построении деревьев состоит в том, что все дочерние элементы в конкретном дереве должны иметь числовые метки, превышающие метку корня дерева. Ограничения на метки дочерних элементов аналогичны условиям, которые используют алгоритмы GK и ESU, чтобы избежать пересчета подграфов.
Протокол для извлечения подграфов использует составы целого числа. Для извлечения подграфов размера k необходимо учитывать все возможные комбинации целого числа k-1. Композиции k-1 состоят из всех возможных способов выражения k-1 как суммы положительных целых чисел. Суммирования, в которых порядок слагаемых различается, считаются различными. Состав может быть выражен как k 2,k3,…, k m, где k 2 + k 3 +… + k m = к-1. Для подсчета подграфов на основе композиции k i узлов выбираются из i-го уровня дерева в качестве узлов подграфов (i = 2,3,…, m). Выбранные узлы k-1 вместе с узлом в корне определяют подграф в сети. После обнаружения подграфа, участвующего в качестве соответствия в целевой сети, для того, чтобы иметь возможность оценить размер каждого класса в соответствии с целевой сетью, Кавош использует алгоритм красоты так же, как FANMOD. Перечислимая часть алгоритма Кавоша показана ниже:
| Перечисление Кавоша |
|---|
| Enumerate_Vertex (G, u, S, Remainder, i) Вход: G: Входной граф. u: Корневая вершина. S: выбор (S = {S 0,S1,..., S k-1 } - это массив набора всех S i). Remainder: количество оставшихся вершин, которые будут selected. i: Текущая глубина дерева.. Вывод: все подграфы размера k графа G с корнем u. ifОстаток = 0, затем . return . else . ValList ← Validate (G, S i-1, u). ni← Min (| ValList |, Remainder). для ki= 1 tonido. C ← Initial_Comb (ValList, k i). (Сделать выбор первой комбинации вершин в соответствии с). repeat . Si← C. Enumerate_Vertex (G, u, S, Remainder -k i, i + 1). Next_Comb (ValList, k i). (Сделать выбор следующей комбинации вершин соответственно). до C = NILL. конец для . для каждого v ∈ ValList do. Visited [v] ← false. конец для . end if |
| Validate (G, Parents, u) . Ввод: G: ввод гр. aph, Родители: выбранные вершины последнего слоя, u: Корневая вершина.. Вывод: Действительные вершины текущего уровня. ValList ← NILL. для каждого v ∈ Parents do. для каждого w ∈ Neighbor [u] do. iflabel [u] |
Недавно для этого программного обеспечения был разработан плагин Cytoscape под названием CytoKavosh. Он доступен на веб-странице Cytoscape [1].
В 2010 году Педро Рибейро и Фернандо Силва предложили новую структуру данных для хранения коллекции подграфов, названную g -три. Эта структура данных, которая концептуально сродни префиксному дереву, хранит подграфы в соответствии с их структурами и находит вхождения каждого из этих подграфов в более крупном графе. Одним из заметных аспектов этой структуры данных является то, что при обнаружении сетевого мотива необходимо оценить подграфы в основной сети. Таким образом, нет необходимости находить в случайной сети те, которых нет в основной сети. Это может быть одна из трудоемких частей в алгоритмах, в которых выводятся все подграфы в случайных сетях.
g-trie - это многостороннее дерево, которое может хранить коллекцию графов. Каждый узел дерева содержит информацию об одной вершине графа и соответствующих ребрах узлов-предков. Путь от корня до листа соответствует одному графу. Потомки узла g-trie имеют общий подграф. Построение g-дерева хорошо описано в разделе. После построения g-дерева выполняется подсчет. Основная идея в процессе подсчета - вернуться по всем возможным подграфам, но в то же время выполнить тесты на изоморфизм. Этот метод поиска с возвратом - это, по сути, тот же метод, который используется другими подходами, ориентированными на мотив, такими как алгоритмы MODA и GK. Использование преимуществ общих подструктур в том смысле, что в данный момент существует частичное изоморфное совпадение для нескольких различных подграфов-кандидатов.
Среди упомянутых алгоритмов G-Tries является самым быстрым. Но чрезмерное использование памяти является недостатком этого алгоритма, который может ограничивать размер обнаруживаемых мотивов персональным компьютером со средней памятью.
ParaMODA и NemoMap - быстрые алгоритмы, опубликованные в 2017 и 2018 годах соответственно. Они не так масштабируемы, как многие другие.
Таблицы и рисунок ниже показывают результаты выполнения упомянутых алгоритмов в различных стандартных сетях. Эти результаты взяты из соответствующих источников, поэтому к ним следует относиться индивидуально.
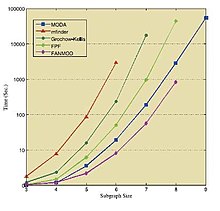Время выполнения Grochow – Kellis, mfinder, FANMOD, FPF и MODA для подграфов от трех узлов до девяти узлов. | Сеть | Размер | Исходная сеть переписи | Средняя перепись в случайных сетях | ||||
|---|---|---|---|---|---|---|---|
| FANMOD | GK | G-Trie | FANMOD | GK | G-Trie | ||
| Дельфины | 5 | 0.07 | 0.03 | 0,01 | 0,13 | 0,04 | 0,01 |
| 6 | 0,48 | 0,28 | 0,04 | 1,14 | 0,35 | 0,07 | |
| 7 | 3,02 | 3,44 | 0,23 | 8,34 | 3,55 | 0,46 | |
| 8 | 19.44 | 73.16 | 1.69 | 67.94 | 37.31 | 4,03 | |
| 9 | 100,86 | 2984,22 | 6,98 | 493,98 | 366,79 | 24,84 | |
| Контур | 6 | 0,49 | 0,41 | 0,03 | 0,55 | 0,24 | 0,03 |
| 7 | 3,28 | 3,73 | 0,22 | 3,53 | 1,34 | 0,17 | |
| 8 | 17,78 | 48,00 | 1,52 | 21,42 | 7,91 | 1,06 | |
| Социальные | 3 | 0,31 | 0,11 | 0,02 | 0,35 | 0,11 | 0,02 |
| 4 | 7,78 | 1,37 | 0,56 | 13,27 | 1,86 | 0,57 | |
| 5 | 208,30 | 31,85 | 14,88 | 531,65 | 62,66 | 22,11 | |
| Дрожжи | 3 | 0,47 | 0,33 | 0,02 | 0,57 | 0,35 | 0,02 |
| 4 | 10,07 | 2,04 | 0,36 | 12,90 | 2,25 | 0,41 | |
| 5 | 268,51 | 34,10 | 12,73 | 400,13 | 47,16 | 14,98 | |
| Мощность | 3 | 0,51 | 1,46 | 0,00 | 0,91 | 1,37 | 0,01 |
| 4 | 1,38 | 4,34 | 0,02 | 3,01 | 4,40 | 0,03 | |
| 5 | 4,68 | 16,95 | 0,10 | 12,38 | 17,54 | 0,14 | |
| 6 | 20,36 | 95,58 | 0,55 | 67,65 | 92,74 | 0,88 | |
| 7 | 101,04 | 765,91 | 3.36 | 408.15 | 630.65 | 5.17 | |
| Размер → | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|
| Сети ↓ | Алгоритмы ↓ | ||||||||
| E. coli | Кавош | 0.30 | 1.84 | 14.91 | 141.98 | 1374.0 | 13173,7 | 121110.3 | 1120560.1 |
| FANMOD | 0.81 | 2.53 | 15.71 | 132.24 | 1205.9 | 9256.6 | - | - | |
| Mavisto | 13532 | - | - | - | - | - | - | - | |
| Mfinder | 31.0 | 297 | 23671 | - | - | - | - | - | |
| Электронный | Кавош | 0.08 | 0.36 | 8.02 | 11.39 | 77.22 | 422,6 | 2823,7 | 18037,5 |
| FANMOD | 0,53 | 1,06 | 4,34 | 24,24 | 160 | 967,99 | - | - | |
| Мависто | 210,0 | 1727 | - | - | - | - | - | - | |
| Mfinder | 7 | 14 | 109,8 | 2020,2 | - | - | - | - | |
| Социальные сети | Кавош | 0,04 | 0,23 | 1,63 | 10,48 | 69,43 | 415,66 | 2594,19 | 14611,23 |
| FANMOD | 0,46 | 0,84 | 3,07 | 17,63 | 117,43 | 845.93 | - | - | |
| Mavisto | 393 | 1492 | - | - | - | - | - | - | |
| Mfinder | 12 | 49 | 798 | 181077 | - | - | - | - |
Как видно из таблицы, Алгоритмы обнаружения мотивов можно разделить на две общие категории: алгоритмы, основанные на точном подсчете, и алгоритмы, использующие вместо этого статистическую выборку и оценки. Поскольку вторая группа не учитывает все вхождения подграфа в основной сети, алгоритмы, принадлежащие этой группе, работают быстрее, но они могут давать предвзятые и нереалистичные результаты.
На следующем уровне алгоритмы точного подсчета можно разделить на сетецентрические и подграф-ориентированные методы. Алгоритмы первого класса ищут в данной сети все подграфы заданного размера, тогда как алгоритмы, попадающие во второй класс, сначала генерируют различные возможные неизоморфные графы заданного размера, а затем исследуют сеть для каждого сгенерированного подграфа отдельно. У каждого подхода есть свои преимущества и недостатки, о которых говорилось выше.
С другой стороны, методы оценки могут использовать подход цветового кодирования, как описано ранее. Другие подходы, используемые в этой категории, обычно пропускают некоторые подграфы во время перечисления (например, как в FANMOD) и основывают свою оценку на перечисленных подграфах.
Кроме того, таблица указывает, можно ли использовать алгоритм для направленных или неориентированных сетей, а также для индуцированных или неиндуцированных подграфов. Для получения дополнительной информации см. Предоставленные веб-ссылки или адреса лабораторий.
| Метод подсчета | Основа | Имя | Направленный / Неориентированный | Индуцированный / Неиндуцированный |
|---|---|---|---|---|
| Exact | Network-Centric | mfinder | Оба | Индуцированный |
| ESU (FANMOD) | Оба | Индуцированный | ||
| Кавош (используется в CytoKavosh ) | Оба | Индуцированные | ||
| G- Попытки | Оба | Индуцированные | ||
| ПГД | Ненаправленные | Индуцированные | ||
| Subgraph-Centric | FPF (Mavisto) | Оба | Индуцированные | |
| NeMoFinder | Непрямые | Индуцированные | ||
| Грохоу – Келлис | Оба | Оба | ||
| MODA | Оба | Оба | ||
| Оценка / выборка | Подход цветового кодирования | Н. Алон и др. ' s Алгоритм | Ненаправленный | Неиндуцированный |
| Другие подходы | mfinder | Оба | Индуцированный | |
| ESU (FANMOD) | Оба | Индуцированные |
| Алгоритм | Название лаборатории / отдела | Отдел / школа | Институт | Адрес ss | Электронная почта |
|---|---|---|---|---|---|
| mfinder | Группа Ури Алона | Департамент молекулярной клеточной биологии | Институт науки Вейцмана | Реховот, Израиль, Вольфсон, Rm. 607 | уриалон на weizmann.ac.il |
| FPF (Mavisto) | ---- | ---- | Leibniz-Institut für Pflanzengenetik und Kulturpflanzenforschung (IPK) | Corrensstraße 3, D-06466 Stadt Seeland, OT Gatersleben, Deutschland | schreibe at ipk-gatersleben.de |
| ESU (FANMOD) | Информационная теория | Institut für Informatik | Йенский университет Фридриха Шиллера | Ernst-Abbe-Platz 2, D-07743 Jena, Deutschland | sebastian.wernicke at gmail.com |
| NeMoFinder | ---- | Школа вычислительной техники | Национальный университет Сингапура | Сингапур 119077 | chenjin at comp.nus.edu.sg |
| Grochow – Kellis | CS Theory Group Complex Systems Group | Компьютерные науки | Университет Колорадо, Боулдер | 1111 Доктор технических наук. ECOT 717, 430 UCB Boulder, CO 80309-0430 USA | jgrochow at colorado.edu |
| N. Алгоритм Алона и др. | Департамент чистой математики | Школа математических наук | Тель-Авивский университет | Тель-Авив 69978, Израиль | nogaa at post.tau.ac.il |
| MODA | Лаборатория системной биологии и биоинформатики (LBB) | Институт биохимии и биофизики (IBB) | Тегеранский университет | Площадь Энгелаб, проспект Энгелаб, Тегеран, Иран | amasoudin at ibb.ut.ac.ir |
| Кавош (используется в CytoKavosh ) | Лаборатория системной биологии и биоинформатики (LBB) | Институт биохимии и биофизики (IBB) | Тегеранский университет | Площадь Энгелаб, проспект Энгелаб, Тегеран, Иран | amasoudin на ibb.ut.ac.ir |
| G-Tries | Центр исследований передовых вычислительных систем | Компьютерные науки | Университет Порту | Rua Campo Alegre 1021/1055, Porto, Portugal | pribeiro at dcc.fc.up.pt |
| PGD | Network Learning and Discovery Lab | Департамент компьютерных наук | Университет Пердью | Университет Пердью, 305 N University St, West Lafayette, IN 47907 | [email#160;protected] |
Много экспериментальных работ было посвящено пониманию сетевых мотивов в генных регуляторных сетях. Эти сети контролируют, какие гены экспрессируются в клетке в ответ на биологические сигналы. Сеть определяется так, что гены являются узлами, а направленные края представляют собой контроль одного гена фактором транскрипции (регуляторный белок, связывающий ДНК), кодируемый другим геном. Таким образом, сетевые мотивы представляют собой паттерны генов, регулирующих скорость транскрипции друг друга. При анализе сетей транскрипции видно, что одни и те же сетевые мотивы появляются снова и снова у разных организмов от бактерий до человека. Сеть транскрипции E. coli и дрожжи, например, состоят из трех основных семейств мотивов, которые составляют почти всю сеть. Основная гипотеза заключается в том, что сетевой мотив был независимо выбран эволюционными процессами сходящимся образом, поскольку создание или устранение регуляторных взаимодействий происходит быстро в эволюционной временной шкале относительно скорости, с которой изменяются гены. Сетевые мотивы в живых клетках указывают на то, что они обладают характерными динамическими функциями. Это предполагает, что сетевой мотив служит строительным блоком в сетях регуляции генов, которые полезны для организма.
Функции, связанные с общими сетевыми мотивами в сетях транскрипции, были исследованы и продемонстрированы в нескольких исследовательских проектах как теоретически, так и экспериментально. Ниже приведены некоторые из наиболее распространенных сетевых мотивов и связанные с ними функции.
Схематическое изображение мотива саморегуляции Один из простейших и наиболее распространенных сетевых мотивов в E. coli - отрицательная саморегуляция, при которой фактор транскрипции (TF) репрессирует собственную транскрипцию. Было показано, что этот мотив выполняет две важные функции. Первая функция - это ускорение реакции. Было показано, что NAR ускоряет реакцию на сигналы как теоретически, так и экспериментально. Это было сначала показано в синтетической сети транскрипции, а затем в естественном контексте в системе репарации ДНК SOS E.coli. Вторая функция - это повышенная стабильность концентрации саморегулируемого генного продукта по отношению к стохастическому шуму, что снижает различия в уровнях белка между разными клетками.
Положительная авторегуляция регуляция (PAR) происходит, когда фактор транскрипции увеличивает скорость собственной продукции. В отличие от мотива NAR этот мотив замедляет время ответа по сравнению с простой регуляцией. В случае сильного PAR мотив может привести к бимодальному распределению уровней белка в популяциях клеток.
Схематическое изображение мотива с прямой связью Это мотив обычно встречается во многих генных системах и организмах. Мотив состоит из трех генов и трех регуляторных взаимодействий. Целевой ген C регулируется 2 TF A и B, и, кроме того, TF B также регулируется TF A. Поскольку каждое из регуляторных взаимодействий может быть положительным или отрицательным, возможно, имеется восемь типов мотивов FFL. Два из этих восьми типов: когерентный FFL типа 1 (C1-FFL) (где все взаимодействия положительны) и некогерентный FFL типа 1 (I1-FFL) (A активирует C, а также активирует B, который репрессирует C) обнаруживаются гораздо чаще. часто в сети транскрипции E. coli и дрожжи, чем другие шесть типов. В дополнение к структуре схемы также следует учитывать способ, которым сигналы от A и B интегрируются промотором C. В большинстве случаев FFL является либо логическим элементом И (A и B требуются для активации C), либо логическим элементом OR (либо A, либо B достаточно для активации C), но возможны и другие входные функции.
Было показано, что C1-FFL с логическим элементом И имеет функцию элемента «знакочувствительной задержки» и детектора послесвечения как теоретически и экспериментально с арабинозной системой E. coli. Это означает, что этот мотив может обеспечить фильтрацию импульсов, при которой короткие импульсы сигнала не будут генерировать ответ, а постоянные сигналы будут генерировать ответ после короткой задержки. Отключение выхода по окончании постоянного импульса будет быстрым. Противоположное поведение проявляется в случае суммирования ворот с быстрым откликом и отложенным отключением, как было продемонстрировано в системе жгутиков E. coli. De novo эволюция C1-FFL в генных регуляторных сетях была продемонстрирована с помощью вычислений в ответ на отбор для фильтрации идеализированного короткого сигнального импульса, но для неидеализированного шума - динамическая система прямой связи. Вместо этого предпочтение было отдано регулированию с другой топологией.
I1-FFL - это генератор импульсов и ускоритель отклика. Два сигнальных пути I1-FFL действуют в противоположных направлениях, где один путь активирует Z, а другой подавляет его. Когда репрессия завершена, это приводит к импульсной динамике. Экспериментально также было продемонстрировано, что I1-FFL может служить ускорителем реакции, подобно мотиву NAR. Разница в том, что I1-FFL может ускорять ответ любого гена и не обязательно гена фактора транскрипции. Мотиву сети I1-FFL была назначена дополнительная функция: как теоретически, так и экспериментально было показано, что I1-FFL может генерировать немонотонную функцию ввода как в синтетической, так и в нативной системах. Наконец, единицы экспрессии, которые включают некогерентный прямой контроль продукта гена, обеспечивают адаптацию к количеству матрицы ДНК и могут превосходить простые комбинации конститутивных промоторов. Регулирование с прямой связью показало лучшую адаптацию, чем отрицательная обратная связь, а схемы, основанные на интерференции РНК, были наиболее устойчивы к вариациям в количестве матриц ДНК.
В некоторых случаях одни и те же регуляторы X и Y регулируют несколько генов Z одной и той же системы. Было показано, что путем регулирования силы взаимодействий этот мотив определяет временной порядок активации гена. Это было экспериментально продемонстрировано на системе жгутиков E. coli.
Этот мотив возникает, когда один регулятор регулирует набор генов без дополнительной регуляции. Это полезно, когда гены совместно выполняют определенную функцию и, следовательно, всегда должны активироваться синхронно. Регулируя силу взаимодействий, он может создать программу временной экспрессии генов, которые он регулирует.
В литературе модули с множественным входом (MIM) возникли как обобщение SIM. Однако точные определения SIM и MIM были источником несогласованности. Предпринимаются попытки предоставить ортогональные определения канонических мотивов в биологических сетях и алгоритмы их перечисления, особенно SIM, MIM и Bi-Fan (2x2 MIM).
Этот мотив возникает в том случае, если несколько регуляторов комбинаторно контролируют набор генов с различными регуляторными комбинациями. Этот мотив был найден в E. coli в различных системах, таких как использование углерода, анаэробный рост, реакция на стресс и другие. Чтобы лучше понять функцию этого мотива, необходимо получить больше информации о том, как множественные входы интегрируются генами. Каплан и др. картировал входные функции генов утилизации сахара в E. coli, имеющий разнообразную форму.
Интересное обобщение сетевых мотивов, мотивы активности перекрывают повторяющиеся шаблоны, которые можно найти, когда узлы и края в сети аннотируются количественными функции. Например, когда края метаболических путей аннотируются величиной или временем экспрессии соответствующего гена, некоторые закономерности повторяются с учетом базовой сетевой структуры.
Мотивы были обнаружены в сети купли-продажи. Например, если два человека покупают у одного и того же продавца, а один из них покупает также у второго продавца, то высока вероятность, что второй покупатель купит у второго продавца
Предположение (иногда более иногда менее неявное) за сохранением топологической подструктуры заключается в том, что она имеет особое функциональное значение. Это предположение недавно было поставлено под сомнение. Некоторые авторы утверждали, что мотивы, такие как мотивы двух вееров, могут проявлять разнообразие в зависимости от сетевого контекста, и, следовательно, структура мотива не обязательно определяет функцию. Структура сети, конечно, не всегда указывает на функцию; это идея, которая существует уже некоторое время, например, см. оперон Sin.
Большинство анализов функции мотива проводится, глядя на мотив, действующий изолированно. Недавнее исследование предоставляет убедительные доказательства того, что сетевой контекст, то есть связи мотива с остальной частью сети, слишком важен, чтобы делать выводы о функции только на основе локальной структуры - в цитируемой статье также рассматриваются критические замечания и альтернативные объяснения наблюдаемых данных. Анализ влияния одного мотивационного модуля на глобальную динамику сети изучается в. Еще одна недавняя работа предполагает, что определенные топологические особенности биологических сетей естественным образом приводят к общему появлению канонических мотивов, тем самым подвергая сомнению частоту встречаемости являются разумным доказательством того, что структуры мотивов выбраны с учетом их функционального вклада в работу сетей.
В то время как изучение мотивов в основном применялось к статическим сложным сетям, исследование временных сложных сетей предложило значительную переосмысление сети мотивы и представил концепцию темпоральных сетевых мотивов . Браха и Бар-Ям изучили динамику структуры локальных мотивов во временных / временных сетях и обнаружили повторяющиеся паттерны, которые могли бы предоставить эмпирические доказательства циклов социального взаимодействия. Вопреки перспективе стабильных мотивов и профилей мотивов в сложных сетях, они продемонстрировали, что для временных сетей локальная структура зависит от времени и может со временем развиваться. Браха и Бар-Ям далее предположили, что анализ временной локальной структуры может предоставить важную информацию о динамике задач и функций системного уровня.
