Чистая сила

Общая сила, действующая на объект. Чтобы вычислить чистую силу, тело изолировано, и взаимодействия с окружающей средой или другие ограничения представлены в виде сил и моментов на диаграмме свободного тела

Чистая сила - это векторная сумма сил, действующих на частицу или тело. Суммарная сила - это единственная сила, которая заменяет влияние исходных сил на движение частицы. Он дает частице такое же ускорение, что и все эти действительные силы вместе, как описано вторым законом движения Ньютона.

В физике можно определить крутящий момент связан с точкой приложения чистой силы, так что он поддерживает движение струй объекта под действием исходной системы сил. Связанный с ним крутящий момент, чистая сила, становится равнодействующей силой и оказывает такое же влияние на вращательное движение объекта, как и все действительные силы вместе взятые. Система сил может определять равнодействующую силу без крутящего момента. В этом случае результирующая сила, приложенная к правильному направлению действия, оказывает на тело такое же воздействие, как и все силы в точках их приложения. Не всегда можно найти равнодействующую силу без крутящего момента.

• 1 Суммарная сила
• 2 Правило параллелограмма для сложения сил
• 3 Смещение и вращение под действием силы
  • 3.1 Точечные силы
  • 3.2 Жесткие тела
• 4 Результирующая сила
• 5 Использование
• 6 См. Также
• 7 Ссылки

Схематический метод сложения сил.

Сила - это векторная величина, что означает что он имеет величину и направление и обычно обозначается жирным шрифтом, например F, или стрелкой над символом, например $F\; \to \; \{\backslash \; displaystyle\; \backslash \; scriptstyle\; \{\backslash \; vec\; \{\; F\}\}\}$.

Графически сила представлена ​​в виде отрезка линии от точки ее приложения A до точки B, которая определяет ее направление и величину. Длина отрезка AB представляет величину силы.

Векторное исчисление было разработано в конце 1800-х - начале 1900-х годов. Однако правило параллелограмма, используемое для сложения сил, восходит к древности и явно отмечено Галилеем и Ньютоном.

На диаграмме показано сложение сил $F\; \to \; 1\; \{\backslash \; displaystyle\; \backslash \; scriptstyle\; \{\backslash \; vec\; \{F\}\}\; \_\; \{1\}\}$и $F\; \to \; 2\; \{\backslash \; displaystyle\; \backslash \; scriptstyle\; \{\backslash \; vec\; \{F\}\}\; \_\; \{2\}\}$. Сумма $F\; \to \; \{\backslash \; displaystyle\; \backslash \; scriptstyle\; \{\backslash \; vec\; \{F\}\}\}$двух сил изображается как диагональ параллелограмма, определяемого двумя силами.

Силы, приложенные к вытянутому телу, могут иметь разные точки приложения. Силы являются связанными векторами и могут добавляться только в том случае, если они применяются в одной и той же точке. Суммарная сила, полученная от всех сил, действующих на тело, не сохраняет его движения, если не прикладывается в той же точке и не определяется соответствующий крутящий момент, связанный с новой точкой приложения. Чистая сила, приложенная к телу в одной точке с соответствующим крутящим моментом, известна как равнодействующая сила и крутящий момент.

Сила известна как связанный вектор - что означает, что у нее есть направление, величина и точка приложения. Удобный способ определить силу - это отрезок прямой от точки A до точки B. Если мы обозначим координаты этих точек как A = (A x, A y, A z) и B = (B x, B y, B z), то вектор силы, приложенный к точке A, определяется как

$F\; =\; B\; -\; A\; =\; (B\; x\; -\; A\; x,\; B\; y\; -\; A\; y,\; B\; z\; -\; A\; z).\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{F\}\; =\; \backslash \; mathbf\; \{B\}\; -\; \backslash \; mathbf\; \{A\}\; =\; (B\_\; \{x\}\; -A\_\; \{x\},\; B\_\; \{y\}\; -A\_\; \{y\},\; B\_\; \{z\}\; -A\_\; \{z)\; \}).\}$

Длина вектора B-Aопределяет величину F и задается как

$|\; F\; |\; =\; (B\; x\; -\; A\; x)\; 2\; +\; (B\; y\; -\; A\; y)\; 2\; +\; (B\; z\; -\; A\; z)\; 2.\; \{\backslash \; displaystyle\; |\; \backslash \; mathbf\; \{F\}\; |\; =\; \{\backslash \; sqrt\; \{(B\_\; \{x\}\; -A\_\; \{x\})\; ^\; \{2\}\; +\; (B\_\; \{y\}\; -A\_\; \{y\})\; ^\; \{2\}\; +\; (B\_\; \{\; z\}\; -A\_\; \{z\})\; ^\; \{2\}\}\}.\}$

Сумма двух сил F1и F2, приложенных в A, может быть вычислена из суммы сегментов, которые их определяют. Пусть F1=B-Aи F2=D-A, тогда сумма этих двух векторов равна

$F\; =\; F\; 1\; +\; F\; 2\; =\; B\; -\; A\; +\; D\; -\; A,\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{F\}\; =\; \backslash \; mathbf\; \{F\}\; \_\; \{1\}\; +\; \backslash \; mathbf\; \{F\}\; \_\; \{2\}\; =\; \backslash \; mathbf\; \{B\}\; -\; \backslash \; mathbf\; \{A\}\; +\; \backslash \; mathbf\; \{D\}\; -\; \backslash \; mathbf\; \{A\},\}$

что может быть записано как

$F\; =\; F\; 1\; +\; F\; 2\; =\; 2\; (B\; +\; D\; 2\; -\; A)\; =\; 2\; (E\; -\; A),\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{F\}\; =\; \backslash \; mathbf\; \{F\}\; \_\; \{1\}\; +\; \backslash \; mathbf\; \{F\}\; \_\; \{2\}\; =\; 2\; (\{\backslash \; frac\; \{\backslash \; mathbf\; \{B\}\; +\; \backslash \; mathbf\; \{D\}\}\; \{2\}\}\; -\; \backslash \; mathbf\; \{A\})\; =\; 2\; (\backslash \; mathbf\; \{E\}\; -\; \backslash \; mathbf\; \{A\}),\; \}$

где E - средняя точка отрезка BD, который соединяет точки B и D.

Таким образом, сумма сил F1и F2- это удвоенный отрезок, соединяющий A со средней точкой E отрезка, соединяющего конечные точки B и D двух сил. Удвоение этой длины легко достигается путем определения сегментов BC и DC, параллельных AD и AB, соответственно, чтобы завершить параллелограмм ABCD. Диагональ AC этого параллелограмма представляет собой сумму двух векторов силы. Это известно как правило параллелограмма для сложения сил.

Точечные силы

Когда сила действует на частицу, она применяется к одной точке (объем частицы незначителен): это точечная сила, а частица - ее точка приложения. Но внешняя сила, действующая на протяженное тело (объект), может быть приложена к ряду составляющих его частиц, т.е. может «распространяться» по некоторому объему или поверхности тела. Однако определение его вращательного воздействия на тело требует, чтобы мы указали его точку приложения (фактически, линию приложения, как объяснено ниже). Проблема обычно решается следующими способами:

• Часто объем или поверхность, на которую действует сила, относительно малы по сравнению с размером тела, так что его можно аппроксимировать точкой. Обычно нетрудно определить, является ли ошибка, вызванная такой аппроксимацией, приемлемой.
• Если она неприемлема (очевидно, например, в случае силы тяжести), такую ​​силу "объем / поверхность" следует описать как система сил (компонентов), каждая из которых действует на отдельную частицу, и тогда расчет следует производить для каждой из них отдельно. Такой расчет обычно упрощается за счет использования дифференциальных элементов объема / поверхности тела и интегрального исчисления. Однако в ряде случаев можно показать, что такая система сил может быть заменена одноточечной силой без фактического расчета (как в случае однородной гравитационной силы).

В любом случае анализ движения твердого тела начинается с модели точечной силы. И когда сила, действующая на тело, отображается графически, ориентированный линейный сегмент, представляющий силу, обычно рисуется так, чтобы «начать» (или «закончить») в точке приложения.

Жесткие тела

Как сила ускоряет тело.

В примере, показанном на диаграмме напротив, единственная сила $F\; \to \; \{\backslash \; displaystyle\; \backslash \; scriptstyle\; \{\backslash \; vec\; \{F\}\}\; \}$действует в точке приложения H на свободном твердом теле. Тело имеет массу $m\; \{\backslash \; displaystyle\; \backslash \; scriptstyle\; m\}$, а его центр масс находится в точке C . В приближении постоянной массы сила вызывает изменения в движении тела, описываемые следующими выражениями:

$a\; \to \; =\; F\; \to \; m\; \{\backslash \; displaystyle\; \{\backslash \; vec\; \{a\}\}\; =\; \{\{\backslash \; vec\; \{F\}\}\; \backslash \; over\; m\}\}$- центр ускорения масс; и

$\alpha \; \to \; =\; \tau \; \to \; I\; \{\backslash \; displaystyle\; \{\backslash \; vec\; \{\backslash \; alpha\}\}\; =\; \{\{\backslash \; vec\; \{\backslash \; tau\}\}\; \backslash \; over\; I\}\}$- угловое ускорение тела.

Во втором выражении $\tau \; \to \; \{\backslash \; displaystyle\; \backslash \; scriptstyle\; \{\backslash \; vec\; \{\backslash \; tau\}\}\}$- это крутящий момент или момент силы, тогда как $I\; \{\backslash \; displaystyle\; \backslash \; scriptstyle\; I\}$- это момент инерции тела. Крутящий момент, вызванный силой $F\; \to \; \{\backslash \; displaystyle\; \backslash \; scriptstyle\; \{\backslash \; vec\; \{F\}\}\}$, является векторной величиной, определенной относительно некоторой контрольной точки:

$\tau \; \to \; =\; r\; \to \; \times \; F\; \to \; \{\backslash \; displaystyle\; \{\backslash \; vec\; \{\backslash \; tau\}\}\; =\; \{\backslash \; vec\; \{r\}\}\; \backslash \; times\; \{\backslash \; vec\; \{F\}\}\}$- вектор крутящего момента, а

$\tau \; =\; F\; k\; \{\backslash \; displaystyle\; \backslash \; \backslash \; tau\; =\; Fk\}$- величина крутящего момента.

Вектор $r\; \to \; \{\backslash \; displaystyle\; \backslash \; scriptstyle\; \{\backslash \; vec\; \{r\}\}\}$это вектор положения от точки приложения силы, и в этом примере он обращается от центра масс в качестве опорной точки (см диаграмму). Отрезок прямой $k\; \{\backslash \; displaystyle\; \backslash \; scriptstyle\; k\}$- это плечо рычага силы $F\; \to \; \{\backslash \; displaystyle\; \backslash \; scriptstyle\; \{\backslash \; vec\; \{F\}\}\}$относительно центра масс. Как показано на рисунке, крутящий момент не изменяется (то же плечо рычага), если точка приложения перемещается вдоль линии приложения силы (пунктирная черная линия). Более формально это следует из свойств векторного произведения и показывает, что вращательное действие силы зависит только от положения линии ее приложения, а не от конкретного выбора точки приложения вдоль этой линии.

Вектор крутящего момента перпендикулярен плоскости, определяемой силой, и вектором $r\; \to \; \{\backslash \; displaystyle\; \backslash \; scriptstyle\; \{\backslash \; vec\; \{r\}\}\}$, и в этом примере он направлен на наблюдателя; вектор углового ускорения имеет то же направление. Правило правой руки связывает это направление с вращением по часовой стрелке или против часовой стрелки в плоскости чертежа.

Момент инерции $I\; \{\backslash \; displaystyle\; \backslash \; scriptstyle\; I\}$вычисляется относительно оси, проходящей через центр масс, параллельной крутящему моменту. Если тело, показанное на рисунке, представляет собой однородный диск, этот момент инерции равен $I\; =\; m\; r\; 2/2\; \{\backslash \; displaystyle\; \backslash \; scriptstyle\; I\; =\; mr\; ^\; \{2\}\; /\; 2\}$. Если диск имеет массу 0,5 кг и радиус 0,8 м, момент инерции составляет 0,16 кгм. Если сила составляет 2 Н, а плечо рычага 0,6 м, величина крутящего момента составляет 1,2 Нм. В показанный момент сила дает диску угловое ускорение α = τ / I = 7,5 рад / с, а его центру масс - линейное ускорение a = F / m = 4 м / с.

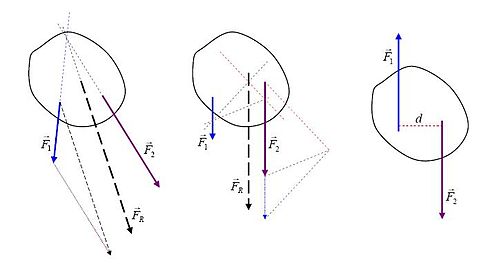Графическое изображение результирующей силы.

Результирующая сила и крутящий момент заменяют эффекты системы сил, действующих на движение твердого тела. Интересным частным случаем является результат без крутящего момента, который можно найти следующим образом:

1. Сложение векторов используется для нахождения чистой силы;
2. Используйте уравнение для определения точки приложения с нулевым крутящим моментом:

$р\; \to \; \times \; F\; \to \; R\; =\; \sum \; я\; =\; 1\; N\; (г\; \to \; я\; \times \; F\; \to \; я)\; \{\backslash \; displaystyle\; \{\backslash \; vec\; \{r\}\}\; \backslash \; times\; \{\backslash \; vec\; \{F\}\}\; \_\; \{\backslash \; mathrm\; \{R\}\; \}\; =\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{N\}\; (\{\backslash \; vec\; \{r\}\}\; \_\; \{i\}\; \backslash \; times\; \{\backslash \; vec\; \{F\}\}\; \_\; \{i\})\}$

где $F\; \to \; R\; \{\backslash \; displaystyle\; \{\backslash \; vec\; \{F\}\}\; \_\; \{\backslash \; mathrm\; \{R\}\}\}$- чистая сила, $r\; \to \; \{\backslash \; displaystyle\; \{\backslash \; vec\; \{r\}\}\}$определяет точку приложения, и отдельные силы равны $F\; \to \; i\; \{\backslash \; displaystyle\; \{\backslash \; vec\; \{F\}\}\; \_\; \{i\}\}$с точками приложения $r\; \to \; i\; \{\backslash \; displaystyle\; \{\backslash \; vec\; \{r\}\}\; \_\; \{i\}\}$. Может оказаться, что нет точки приложения, которая дает результат без крутящего момента.

На диаграмме напротив показаны простые графические методы нахождения линии приложения результирующей силы простых плоских систем:

1. Линии приложения действительных сил $F\; \to \; 1\; \{\backslash \; displaystyle\; \{\backslash \; vec\; \{F\}\}\; \_\; \{1\}\}$и $F\; \to \; 2\; \{\backslash \; displaystyle\; \{\backslash \; vec\; \{F\}\}\; \_\; \{2\}\}$на крайней левой иллюстрации пересекаются. После выполнения сложения вектора «в местоположении $F\; \to \; 1\; \{\backslash \; displaystyle\; \{\backslash \; vec\; \{F\}\}\; \_\; \{1\}\}$» полученная результирующая сила переводится так, что его линия приложение проходит через общую точку пересечения. Относительно этой точки все крутящие моменты равны нулю, поэтому крутящий момент результирующей силы $F\; \to \; R\; \{\backslash \; displaystyle\; \{\backslash \; vec\; \{F\}\}\; \_\; \{\backslash \; mathrm\; \{R\}\}\}$равен сумме моментов действительных сил.
2. На рисунке в середине диаграммы показаны две параллельные действительные силы. После сложения вектора "в местоположении $F\; \to \; 2\; \{\backslash \; displaystyle\; \{\backslash \; vec\; \{F\}\}\; \_\; \{2\}\}$" чистая сила преобразуется в соответствующую строку приложения, где она становится равнодействующей силой $F\; \to \; R\; \{\backslash \; displaystyle\; \backslash \; scriptstyle\; \{\backslash \; vec\; \{F\}\}\; \_\; \{\backslash \; mathrm\; \{R\}\}\}$. Процедура основана на разложении всех сил на составляющие, для которых линии приложения (бледные пунктирные линии) пересекаются в одной точке (так называемый полюс, произвольно установленный в правой части иллюстрации). Затем аргументы из предыдущего случая применяются к силам и их компонентам, чтобы продемонстрировать взаимосвязь крутящего момента.
3. Крайняя правая иллюстрация показывает пару, две равные, но противоположные силы, для которых величина чистая сила равна нулю, но они создают чистый крутящий момент $\tau \; =\; F\; d\; \{\backslash \; displaystyle\; \backslash \; scriptstyle\; \backslash \; tau\; =\; Fd\}$, где $d\; \{\backslash \; displaystyle\; \backslash \; scriptstyle\; \backslash \; d\}$- это расстояние между линиями их применения. Поскольку нет равнодействующей силы, этот крутящий момент может быть описан как «чистый» крутящий момент.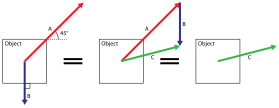

Векторная диаграмма для сложения непараллельных сил.

В общем, система действующих сил на твердом теле всегда можно заменить одной силой плюс один чистый (см. предыдущий раздел) крутящий момент. Сила - это чистая сила, но для расчета дополнительного крутящего момента чистая сила должна быть задана направлением действия. Линия действия может быть выбрана произвольно, но дополнительный чистый крутящий момент зависит от этого выбора. В особом случае можно найти такую ​​линию действия, при которой этот дополнительный крутящий момент равен нулю.

равнодействующая сила и крутящий момент могут быть определены для любой конфигурации сил. Однако интересным частным случаем является результат без крутящего момента. Это полезно как с концептуальной, так и с практической точки зрения, потому что тело движется без вращения, как если бы оно было частицей.

Некоторые авторы не отделяют результирующую силу от чистой силы и используют эти термины как синонимы.

• Теория винта
• Центр масс
• Центры тяжести в неоднородные поля