Условие, при котором угол отклонения минимален в призме
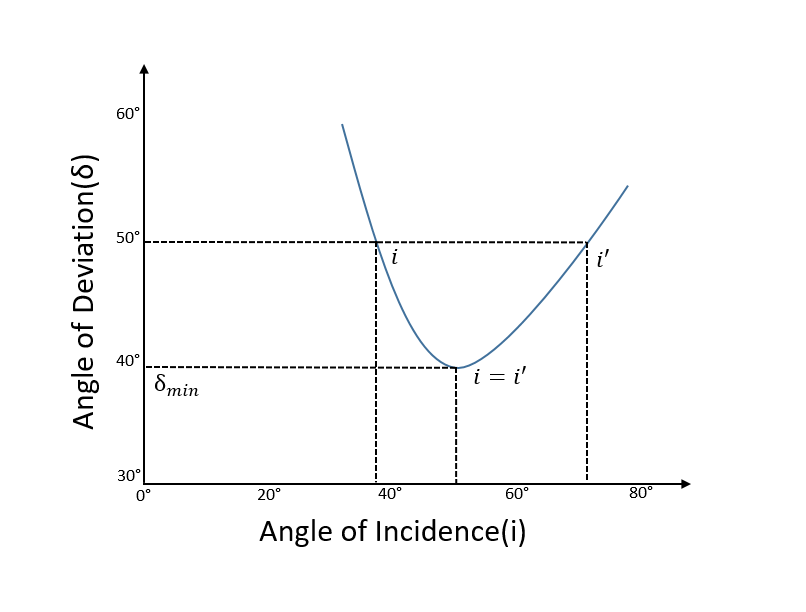
В призме угол отклонения ( ) уменьшается с увеличением угла падения (
) уменьшается с увеличением угла падения ( ) до определенного угла. Этот угол падения, при котором угол отклонения призмы минимален, называется положением минимального отклонения призмы, а сам угол отклонения известен как минимальный угол отклонения (обозначен на
) до определенного угла. Этот угол падения, при котором угол отклонения призмы минимален, называется положением минимального отклонения призмы, а сам угол отклонения известен как минимальный угол отклонения (обозначен на  ,
,  или
или  ).
).

Свет отклоняется при попадании в материал с показателем преломления>1.

Луч света дважды отклоняется в призме. Сумма этих отклонений и составляет угол отклонения.

Когда углы входа и выхода равны, угол отклонения луча, проходящего через призму, будет минимальным.
В режиме минимального отклонения преломленный луч в призме равен параллельно его основанию. Другими словами, световой луч симметричен относительно оси симметрии призмы. Кроме того, углы преломления равны, то есть  . И угол падения и угол выхода равны друг другу (
. И угол падения и угол выхода равны друг другу ( ). Это хорошо видно на графике в следующем разделе.
). Это хорошо видно на графике в следующем разделе.
Содержание
- 1 Формула и график
- 2 Экспериментальное определение
- 3 Минимальный угол рассеивания
- 4 Применения
- 5 См. Также
- 6 Ссылки / дополнительная информация Чтение
- 7 Внешние ссылки
Формула и график
Формула для минимального отклонения может быть получена путем использования геометрии призмы. Подход включает замену переменных в Законе Снеллиуса с точки зрения отклонения и углов призмы с использованием вышеуказанных свойств.

.
Из суммы углов из  ,
,



Использование теоремы о внешнем угле в  ,
,





Это также можно получить, поместив  в:
в: 
Из закона Снеллиуса,



(где  - показатель преломления,
- показатель преломления,  - угол призмы и
- угол призмы и  - минимальный угол отклонения.)
- минимальный угол отклонения.)
Это удобный способ, используемый для измерения показателя преломления материала (жидкости или газа) путем направления светового луча через призму пренебрежимо малого толщина при минимальном отклонении заполненного материала или погруженной в него стеклянной призмы.
Проработанные примеры:
| Показатель преломления стекла 1,5. Желателен минимальный угол отклонения для равносторонней призмы вместе с соответствующим углом падения. |
|---|
|
Ответ: 
Сол.:
Здесь  , , 
Подключив их к формула выше,







Кроме того,

Это также видно на графике ниже. |
| Если минимальный угол отклонения призмы с показателем преломления 1,4 равен ее углу преломления, желателен угол призмы. |
|---|
|
Ответ: 
Сол.:
Здесь 

Используя приведенную выше формулу,




|
Кроме того, изменение угла отклонения с вилкой Маршрутный угол падения можно заключить в одно уравнение, выразив  через
через  в формуле призмы используя закон Снеллиуса:
в формуле призмы используя закон Снеллиуса:

Нахождение минимумов этого уравнения также даст такое же соотношение для минимального отклонения, как указано выше.
Для тонкой призмы
В тонкой или малоугловой призме, когда углы становятся очень маленькими, синус угла почти равен самому углу, и это дает много полезных результатов.
 и
и  очень маленькие,
очень маленькие,




Интересно, что использование аналогичного подхода с законом Снеллиуса и для тонкой призмы в целом приводит к тому же результату для угла отклонения.
 и
и  маленькие,
маленькие,
 и
и

Из,





Таким образом, можно сказать, что тонкая призма всегда находится в минимальном отклонении .
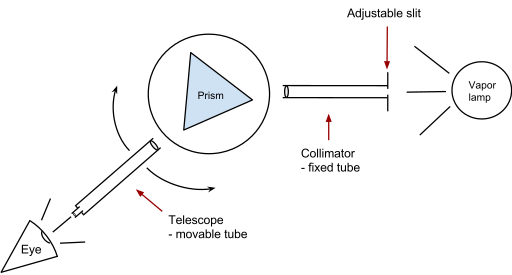
Экспериментальное определение
Минимальное отклонение можно найти вручную или с помощью спектрометра . Либо призма остается фиксированной и угол падения регулируется, либо призма поворачивается, сохраняя источник света фиксированным.
Минимальный угол рассеивания
Минимальный угол рассеивания для белого света - это разница в минимальном отклонении угол между красными и фиолетовыми лучами светового луча через призму.

Применение

Рисование радиусов в точках интерференции показывает, что углы преломления равны, что доказывает минимальное отклонение.
Один из факторов, которые вызывает радугу - это группирование световых лучей при минимальном угле отклонения, который близок к углу радуги (42 °).

Он также отвечает за такие явления, как гало и песы, полученные отклонением солнечного света в мини-призмах гексагональных кристаллов льда в воздухе, изгибающем свет с минимальным отклонением 22 °.
См. Также
 физический портал
физический портал
.
Ссылки / Дополнительная литература
- ^ "Глава 9, ЛУЧЕВАЯ ОПТИКА И ОПТИЧЕСКИЕ ПРИБОРЫ ». Учебник по физике для IX класса (PDF). NCERT. п. 331.
- ^ "Оптика-призма". Репетитор физики A-Level.
- ^ Марк А. Петерсон. «Минимальное отклонение призмы». mtholyoke. Колледж Маунт-Холиок. Архивировано из оригинала 23.05.2019.
- ^ «Refraction through Prisms». SchoolPhysics.
- ^ "Призма". HyperPhysics.
- ^«Определение показателя преломления материала призмы». BrainKart.
- ^«Угол минимального отклонения». Scribd.
- ^"Теория призменного спектрометра". www.ukessays.com.
- ^«Экспериментальная установка для измерения угла минимального отклонения призменным спектрометром». ResearchGate.
- ^«Измерение дисперсии стекла призменным спектрометром». studylib.net.
- ^«Определение минимального отклонения для данной призмы». BYJU'S.
- ^"Радуга". www.schoolphysics.co.uk.
- ^"Halo 22 °". HyperPhysics.
.
.
Внешние ссылки
Минимальное отклонение Часть 1 и Часть 2 в Академии Хана
Преломление через призму в NCERT Tectbook
Минимальное отклонение по призме Марк А. Петерсон, Колледж Маунт-Холиок





 Свет отклоняется при попадании в материал с показателем преломления>1.
Свет отклоняется при попадании в материал с показателем преломления>1.  Луч света дважды отклоняется в призме. Сумма этих отклонений и составляет угол отклонения.
Луч света дважды отклоняется в призме. Сумма этих отклонений и составляет угол отклонения.  Когда углы входа и выхода равны, угол отклонения луча, проходящего через призму, будет минимальным.
Когда углы входа и выхода равны, угол отклонения луча, проходящего через призму, будет минимальным. 






















 Рисование радиусов в точках интерференции показывает, что углы преломления равны, что доказывает минимальное отклонение.
Рисование радиусов в точках интерференции показывает, что углы преломления равны, что доказывает минимальное отклонение. 