Марковский процесс принятия решений

В математике марковский процесс принятия решений ( MDP) - это стохастический процесс управления с дискретным временем. Он обеспечивает математическую основу для моделирования принятия решений в ситуациях, когда результаты частично случайны, а частично находятся под контролем лица, принимающего решения. MDP полезны для изучения задач оптимизации, решаемых с помощью динамического программирования. MDP были известны, по крайней мере, еще в 1950-х годах; Основной объем исследований марковских процессов принятия решений стал результатом книги Рональда Ховарда 1960 года « Динамическое программирование и марковские процессы». Они используются во многих дисциплинах, включая робототехнику, автоматическое управление, экономику и производство. Название MDP происходит от русского математика Андрея Маркова, поскольку они являются продолжением цепей Маркова.

На каждом временном шаге процесс находится в некотором состоянии, и лицо, принимающее решение, может выбрать любое действие, доступное в состоянии. На следующем временном шаге процесс реагирует случайным переходом в новое состояние и дает лицу, принимающему решение, соответствующее вознаграждение. ${\ displaystyle s}$${\ displaystyle a}$${\ displaystyle s}$${\ displaystyle s '}$${\ displaystyle R_ {a} (s, s ')}$

Вероятность того, что процесс переходит в новое состояние зависит от выбранного действия. В частности, он задается функцией перехода состояния. Таким образом, следующее состояние зависит от текущего состояния и действий лица, принимающего решение. Но данное и условно не зависит от всех предыдущих состояний и действий; другими словами, переходы состояний MDP удовлетворяют свойству Маркова. ${\ displaystyle s '}$${\ displaystyle P_ {a} (s, s ')}$${\ displaystyle s '}$${\ displaystyle s}$${\ displaystyle a}$${\ displaystyle s}$${\ displaystyle a}$

Марковские процессы принятия решений являются продолжением цепей Маркова ; разница заключается в добавлении действий (предоставление возможности выбора) и поощрений (мотивация). И наоборот, если для каждого состояния существует только одно действие (например, «ожидание») и все вознаграждения одинаковы (например, «ноль»), процесс принятия решения Маркова сводится к цепи Маркова.

СОДЕРЖАНИЕ

• 1 Определение
  • 1.1 Цель оптимизации
  • 1.2 Модели симуляторов
• 2 Алгоритмы
  • 2.1 Известные варианты
    • 2.1.1 Итерация значений
    • 2.1.2 Итерация политики
    • 2.1.3 Итерация модифицированной политики
    • 2.1.4 Приоритетное подметание
• 3 Расширения и обобщения
  • 3.1 Частичная наблюдаемость
  • 3.2 Обучение с подкреплением
  • 3.3 Обучающие автоматы
  • 3.4 Теоретико-категориальная интерпретация
• 4 Марковский процесс принятия решений в непрерывном времени
  • 4.1 Определение
  • 4.2 Проблема
  • 4.3 Формулировка линейного программирования
  • 4.4 Уравнение Гамильтона – Якоби – Беллмана
  • 4.5 Применение
• 5 Альтернативные обозначения
• 6 Ограниченные марковские процессы принятия решений
• 7 См. Также
• 8 ссылки
• 9 Дальнейшее чтение
• 10 Внешние ссылки

Определение

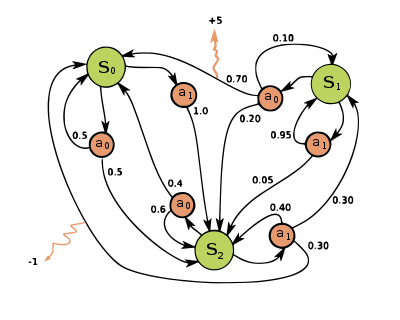Пример простой MDP с тремя состояниями (зеленые кружки) и двумя действиями (оранжевые кружки) с двумя наградами (оранжевые стрелки).

Марковский процесс принятия решения представляет собой четырехкортежный процесс, в котором: ${\ displaystyle (S, A, P_ {a}, R_ {a})}$

• ${\ displaystyle S}$представляет собой набор состояний называется пространством состояний,
• ${\ displaystyle A}$- это набор действий, называемый пространством действий (альтернативно, это набор действий, доступных из состояния),${\ displaystyle A_ {s}}$${\ displaystyle s}$
• ${\ Displaystyle P_ {a} (s, s ') = \ Pr (s_ {t + 1} = s' \ mid s_ {t} = s, a_ {t} = a)}$это вероятность того, что действие в состоянии во времени приведет к состоянию во времени,${\ displaystyle a}$${\ displaystyle s}$${\ displaystyle t}$${\ displaystyle s '}$${\ displaystyle t + 1}$
• ${\ displaystyle R_ {a} (s, s ')}$это немедленное вознаграждение (или ожидаемое немедленное вознаграждение), полученное после перехода из состояния в состояние в результате действия${\ displaystyle s}$${\ displaystyle s '}$${\ displaystyle a}$

Пространства состояний и действий могут быть конечными или бесконечными, например набор действительных чисел. Некоторые процессы со счетно бесконечными пространствами состояний и действий могут быть сведены к процессам с конечными пространствами состояний и действий.

Функция политики - это (потенциально вероятностное) отображение пространства состояний () в пространство действий (). ${\ displaystyle \ pi}$${\ displaystyle S}$${\ displaystyle A}$

Цель оптимизации

Цель марковского процесса принятия решений - найти хорошую «политику» для лица, принимающего решения: функцию, которая определяет действие, которое лицо, принимающее решения, выберет, находясь в состоянии. Как только процесс принятия решения Маркова таким образом объединяется с политикой, это фиксирует действие для каждого состояния, и результирующая комбинация ведет себя как цепь Маркова (поскольку действие, выбранное в состоянии, полностью определяется матрицей перехода Маркова и сводится к ней). ${\ displaystyle \ pi}$${\ displaystyle \ pi (s)}$${\ displaystyle s}$ ${\ displaystyle s}$${\ displaystyle \ pi (s)}$${\ Displaystyle \ Pr (s_ {t + 1} = s '\ mid s_ {t} = s, a_ {t} = a)}$${\ Displaystyle \ Pr (s_ {t + 1} = s '\ mid s_ {t} = s)}$

Цель состоит в том, чтобы выбрать политику, которая максимизирует некоторую кумулятивную функцию случайных вознаграждений, обычно ожидаемую дисконтированную сумму на потенциально бесконечном горизонте: ${\ displaystyle \ pi}$

${\ displaystyle E \ left [\ sum _ {t = 0} ^ {\ infty} {\ gamma ^ {t} R_ {a_ {t}} (s_ {t}, s_ {t + 1})} \ right ]}$(где мы выбираем, т.е. действия, заданные политикой). И ожидание возобладает${\ displaystyle a_ {t} = \ pi (s_ {t})}$${\ Displaystyle s_ {t + 1} \ sim P_ {a_ {t}} (s_ {t}, s_ {t + 1})}$

где - удовлетворяющий коэффициент дисконтирования, который обычно близок к 1 (например, для некоторой ставки дисконтирования r). Более низкий коэффициент дисконтирования побуждает лиц, принимающих решения, предпочесть ранние действия, а не откладывать их на неопределенный срок. ${\ Displaystyle \ \ gamma \}$${\ Displaystyle 0 \ Leq \ \ гамма \ \ Leq \ 1}$${\ Displaystyle \ гамма = 1 / (1 + г)}$

Политика, которая максимизирует указанную выше функцию, называется оптимальной политикой и обычно обозначается. Конкретный MDP может иметь несколько различных оптимальных политик. Благодаря марковскому свойству можно показать, что оптимальная политика является функцией текущего состояния, как предполагалось выше. ${\ displaystyle \ pi ^ {*}}$

Модели симуляторов

Во многих случаях трудно точно представить распределения вероятностей перехода,,. В таких случаях симулятор может использоваться для неявного моделирования MDP путем предоставления выборок из распределений переходов. Одной из распространенных форм неявной модели MDP является симулятор эпизодической среды, который можно запустить из начального состояния и получить последующее состояние и вознаграждение каждый раз, когда он получает входное действие. Таким образом могут создаваться траектории состояний, действий и вознаграждений, часто называемые эпизодами. ${\ displaystyle P_ {a} (s, s ')}$

Другой формой симулятора является генеративная модель, одношаговый симулятор, который может генерировать образцы следующего состояния и вознаграждать за любое состояние и действие. (Обратите внимание, что это значение отличается от термина « генеративная модель» в контексте статистической классификации.) В алгоритмах, которые выражаются с помощью псевдокода, часто используется для представления генеративной модели. Например, выражение может обозначать действие выборки из генеративной модели, где и - текущее состояние и действие, а и - новое состояние и награда. По сравнению с эпизодическим симулятором, генеративная модель имеет то преимущество, что она может предоставлять данные из любого состояния, а не только из тех, которые встречаются на траектории. ${\ displaystyle G}$${\ displaystyle s ', r \ получает G (s, a)}$${\ displaystyle s}$${\ displaystyle a}$${\ displaystyle s '}$${\ displaystyle r}$

Эти классы моделей образуют иерархию информационного содержания: явная модель тривиально дает генеративную модель посредством выборки из распределений, а повторное применение генеративной модели дает эпизодический симулятор. В обратном направлении можно изучать только приблизительные модели с помощью регрессии. Тип модели, доступной для конкретного MDP, играет важную роль в определении подходящих алгоритмов решения. Например, для алгоритмов динамического программирования, описанных в следующем разделе, требуется явная модель, а для поиска по дереву Монте-Карло требуется генеративная модель (или эпизодический симулятор, который можно скопировать в любом состоянии), тогда как для большинства алгоритмов обучения с подкреплением требуется только эпизодический симулятор..

Алгоритмы

Решения для MDP с конечными состояниями и пространствами действий можно найти с помощью различных методов, таких как динамическое программирование. Алгоритмы в этом разделе применяются к MDP с конечным пространством состояний и действий и явно заданными вероятностями перехода и функциями вознаграждения, но основные концепции могут быть расширены для обработки других классов проблем, например, с использованием аппроксимации функций.

Стандартное семейство алгоритмов для расчета оптимальных политик для MDP с конечным состоянием и действием требует хранения для двух массивов, индексированных по состоянию: значение, которое содержит реальные значения, и политика, которая содержит действия. В конце алгоритма будет содержать решение и дисконтированную сумму вознаграждений, которые будут получены (в среднем), следуя этому решению из состояния. ${\ displaystyle V}$ ${\ displaystyle \ pi}$${\ displaystyle \ pi}$${\ Displaystyle V (s)}$${\ displaystyle s}$

Алгоритм состоит из двух шагов: (1) обновление значения и (2) обновление политики, которые повторяются в некотором порядке для всех состояний до тех пор, пока не прекратятся дальнейшие изменения. Оба рекурсивно обновляют новую оценку оптимальной политики и значения состояния, используя более старую оценку этих значений.

${\ Displaystyle V (s): = \ сумма _ {s '} P _ {\ pi (s)} (s, s') \ left (R _ {\ pi (s)} (s, s ') + \ gamma V (s ') \ right)}$

${\ displaystyle \ pi (s): = \ operatorname {argmax} _ {a} \ left \ {\ sum _ {s '} P (s' \ mid s, a) \ left (R (s '\ mid s, а) + \ gamma V (s ') \ right) \ right \}}$

Их порядок зависит от варианта алгоритма; их также можно сделать для всех состояний сразу или для каждого состояния, и чаще для одних состояний, чем для других. Пока ни одно состояние не исключено навсегда из любого из шагов, алгоритм в конечном итоге придет к правильному решению.

Известные варианты

Итерация значения

В итерации значений ( Bellman 1957), которую также называют обратной индукцией, функция не используется; вместо этого значение вычисляется внутри всякий раз, когда это необходимо. Подстановка вычисления в вычисление дает объединенный шаг: ${\ displaystyle \ pi}$${\ displaystyle \ pi (s)}$${\ Displaystyle V (s)}$${\ displaystyle \ pi (s)}$${\ Displaystyle V (s)}$

${\ Displaystyle V_ {я + 1} (s): = \ max _ {a} \ left \ {\ sum _ {s '} P_ {a} (s' | s) \ left (R_ {a} (s, s ') + \ gamma V_ {i} (s') \ right) \ right \},}$

где - номер итерации. Итерация значения начинается с и как предположение функции значения. Затем он выполняет итерацию, многократно вычисляя для всех состояний, пока не сойдется с левой частью, равной правой части (которая является « уравнением Беллмана » для этой задачи). Статья Ллойда Шепли 1953 года о стохастических играх включала как частный случай метод итерации значений для MDP, но это было признано только позже. ${\ displaystyle i}$${\ displaystyle i = 0}$${\ displaystyle V_ {0}}$ ${\ Displaystyle V_ {я + 1}}$${\ displaystyle s}$${\ displaystyle V}$

Повторение политики

В итерации политики ( Howard 1960) первый шаг выполняется один раз, а затем второй шаг повторяется до тех пор, пока он не сойдется. Затем снова выполняется первый шаг и так далее.

Вместо повторения второго шага до сходимости его можно сформулировать и решить как набор линейных уравнений. Эти уравнения просто получаются путем составления на втором этапе уравнения. Таким образом, повторение шага два до сходимости можно интерпретировать как решение линейных уравнений с помощью релаксации (итерационный метод) ${\ displaystyle s = s '}$

Преимущество этого варианта в том, что существует определенное условие остановки: когда массив не изменяется в процессе применения шага 1 ко всем состояниям, алгоритм завершается. ${\ displaystyle \ pi}$

Итерация политики обычно медленнее, чем итерация значения для большого количества возможных состояний.

Измененная итерация политики

В итерации модифицированной политики ( van Nunen 1976 ; Puterman amp; Shin 1978) первый шаг выполняется один раз, а затем второй шаг повторяется несколько раз. Затем снова выполняется первый шаг и так далее.

Приоритетное подметание

В этом варианте шаги предпочтительно применяются к состояниям, которые в некотором роде важны - будь то на основе алгоритма (в последнее время произошли большие изменения в этих состояниях или вокруг них) или на основе использования (эти состояния находятся рядом с начальным состоянием или иным образом. представляющих интерес для человека или программы, использующей алгоритм). ${\ displaystyle V}$${\ displaystyle \ pi}$

Расширения и обобщения

Марковский процесс принятия решений - это стохастическая игра только с одним игроком.

Частичная наблюдаемость

Основная статья: Частично наблюдаемый марковский процесс принятия решений

Приведенное выше решение предполагает, что состояние известно, когда необходимо предпринять действие; в противном случае невозможно рассчитать. Когда это предположение неверно, проблема называется частично наблюдаемым марковским процессом принятия решений или POMDP. ${\ displaystyle s}$${\ displaystyle \ pi (s)}$

Большой прогресс в этой области был сделан Бернетасом и Катехакисом в статье «Оптимальные адаптивные политики для марковских процессов принятия решений». В этой работе класс адаптивных политик, которые обладают свойствами равномерно максимальной скорости сходимости для общего ожидаемого вознаграждения за конечный горизонт, был построен в предположениях конечного состояния пространств действия и неприводимости закона перехода. Эти политики предписывают, что выбор действий в каждом состоянии и в каждый период времени должен основываться на показателях, которые представляют собой инфляцию правой части уравнений оптимальности расчетного среднего вознаграждения.

Обучение с подкреплением

Основная статья: Обучение с подкреплением

Обучение с подкреплением использует MDP, где вероятность или вознаграждение неизвестны.

Для этой цели полезно определить дополнительную функцию, которая соответствует выполнению действия и последующему его оптимальному продолжению (или в соответствии с той политикой, которая у вас есть в настоящее время): ${\ displaystyle a}$

${\ Displaystyle \ Q (s, a) = \ sum _ {s '} P_ {a} (s, s') (R_ {a} (s, s ') + \ gamma V (s')). \ }$

Хотя эта функция также неизвестна, опыт во время обучения основан на парах (вместе с результатом ; то есть «Я был в состоянии, я пытался сделать, и получилось»). Таким образом, у человека есть массив, и он использует опыт для его непосредственного обновления. Это известно как Q-обучение. ${\ Displaystyle (s, а)}$${\ displaystyle s '}$${\ displaystyle s}$${\ displaystyle a}$${\ displaystyle s '}$${\ displaystyle Q}$

Обучение с подкреплением может решать процессы Маркова-принятия решений без явной спецификации переходных вероятностей; значения вероятностей перехода необходимы в итерациях значения и политики. В обучении с подкреплением вместо явного указания вероятностей переходов доступ к вероятностям перехода осуществляется через симулятор, который обычно перезапускается много раз из однородно случайного начального состояния. Обучение с подкреплением также можно комбинировать с аппроксимацией функций для решения задач с очень большим количеством состояний.

Обучающие автоматы

Основная статья: Обучающие автоматы

Еще одно применение процесса MDP в теории машинного обучения называется обучающимися автоматами. Это также один из типов обучения с подкреплением, если среда является стохастической. Обзор первой статьи по детально обучающимся автоматам был проведен Нарендрой и Татхачаром (1974), которые изначально были явно описаны как конечные автоматы. Подобно обучению с подкреплением, алгоритм обучающихся автоматов также имеет преимущество в решении проблемы, когда вероятность или вознаграждение неизвестны. Разница между обучающими автоматами и Q-обучением заключается в том, что в первом методе не сохраняется память о Q-значениях, но напрямую обновляется вероятность действия, чтобы найти результат обучения. Обучающиеся автоматы - это обучающая схема со строгим доказательством сходимости.

В теории обучающих автоматов стохастический автомат состоит из:

• набор x возможных входов,
• множество Φ = {Φ 1,..., Φ s } возможных внутренних состояний,
• набор α = {α 1,..., α r } возможных выходов или действий при r ≤ s,
• вектор вероятности начального состояния p (0) = ≪ p 1 (0),..., p s (0) ≫,
• вычислимая функция, которая после каждого временного шага т генерирует р ( т + 1) из р ( т), текущий входной сигнал и текущее состояние, и
• функция G: Φ → α, которая генерирует выходной сигнал на каждом временном шаге.

Состояния такого автомата соответствуют состояниям « марковского процесса с дискретными параметрами ». На каждом временном шаге t = 0,1,2,3,... автомат считывает входные данные из своей среды, обновляет P ( t) до P ( t + 1) с помощью A, случайным образом выбирает состояние-преемник в соответствии с вероятностей P ( t + 1) и выдает соответствующее действие. Среда автомата, в свою очередь, считывает действие и отправляет автомату следующий ввод.

Теоретико-категориальная интерпретация

Помимо вознаграждения, марковский процесс принятия решений можно понять с точки зрения теории категорий. А именно, пусть обозначим свободный моноид с порождающим множеством A. Пусть Dist обозначать категорию Клейсли из монады Жири. Тогда функтор кодирует оба множества S состояний и функция вероятности Р. ${\ displaystyle (S, A, P)}$ ${\ displaystyle {\ mathcal {A}}}$ ${\ displaystyle {\ mathcal {A}} \ to \ mathbf {Dist}}$

Таким образом, марковские процессы принятия решений могут быть обобщены от моноидов (категорий с одним объектом) до произвольных категорий. Можно назвать результат в процесс принятия решений Маркова контекстно-зависимые, так как переход от одного объекта к другому в изменении набора доступных действий и набор возможных состояний. ${\ displaystyle ({\ mathcal {C}}, F: {\ mathcal {C}} \ to \ mathbf {Dist})}$${\ displaystyle {\ mathcal {C}}}$

Марковский процесс принятия решений в непрерывном времени

В процессах принятия решений Маркова с дискретным временем решения принимаются через дискретные интервалы времени. Однако для процессов принятия решений Маркова с непрерывным временем решения могут приниматься в любое время по выбору лица, принимающего решения. По сравнению с марковскими процессами принятия решений с дискретным временем, марковские процессы принятия решений с непрерывным временем могут лучше моделировать процесс принятия решений для системы, которая имеет непрерывную динамику, т. Е. Динамика системы определяется уравнениями в частных производных (PDE).

Определение

Чтобы обсудить марковский процесс принятия решений в непрерывном времени, мы введем два набора обозначений:

Если пространство состояний и пространство действий конечны,

• ${\ Displaystyle {\ mathcal {S}}}$: Государственное пространство;
• ${\ displaystyle {\ mathcal {A}}}$: Пространство действий;
• ${\ Displaystyle д (я \ середина J, а)}$:, функция скорости перехода;${\ Displaystyle {\ mathcal {S}} \ times {\ mathcal {A}} \ rightarrow \ треугольник {\ mathcal {S}}}$
• ${\ Displaystyle R (я, а)}$:, функция вознаграждения.${\ Displaystyle {\ mathcal {S}} \ times {\ mathcal {A}} \ rightarrow \ mathbb {R}}$

Если пространство состояний и пространство действий непрерывны,

• ${\ displaystyle {\ mathcal {X}}}$: пространство состояний;
• ${\ displaystyle {\ mathcal {U}}}$: пространство возможного контроля;
• ${\ Displaystyle f (х, и)}$:, функция скорости перехода;${\ Displaystyle {\ mathcal {X}} \ times {\ mathcal {U}} \ rightarrow \ треугольник {\ mathcal {X}}}$
• ${\ Displaystyle г (х, и)}$:, функция коэффициента вознаграждения такая, что, где - функция вознаграждения, которую мы обсуждали в предыдущем случае.${\ Displaystyle {\ mathcal {X}} \ раз {\ mathcal {U}} \ rightarrow \ mathbb {R}}$${\ Displaystyle г (х (т), и (т)) \, dt = dR (х (т), и (т))}$${\ Displaystyle R (х, и)}$

Проблема

Подобно процессам Маркова с дискретным временем, в процессах Маркова с непрерывным временем мы хотим найти оптимальную политику или управление, которые могли бы дать нам оптимальное ожидаемое интегрированное вознаграждение:

${\ displaystyle \ max \ operatorname {E} _ {u} \ left [\ left. \ int _ {0} ^ {\ infty} \ gamma ^ {t} r (x (t), u (t)) \, dt \; \ right | x_ {0} \ right]}$

куда ${\ Displaystyle 0 \ Leq \ gamma lt;1.}$

Формулировка линейного программирования

Если пространство состояний и пространство действий конечны, мы могли бы использовать линейное программирование для поиска оптимальной политики, что было одним из первых применявшихся подходов. Здесь мы рассматриваем только эргодическую модель, что означает, что наша MDP с непрерывным временем становится эргодической марковской цепью с непрерывным временем при стационарной политике. В соответствии с этим предположением, хотя лицо, принимающее решение, может принять решение в любое время в текущем состоянии, оно не может получить больше, если предпримет более одного действия. Им лучше действовать только в тот момент, когда система переходит из текущего состояния в другое. При некоторых условиях (для подробностей проверьте следствие 3.14 марковских процессов принятия решений с непрерывным временем ), если наша функция оптимального значения не зависит от состояния, мы будем иметь следующее неравенство: ${\ Displaystyle V ^ {*}}$${\ displaystyle i}$

${\ Displaystyle г \ geq R (я, а) + \ сумма _ {j \ in S} q (j \ mid i, a) h (j) \ quad \ forall i \ in S {\ text {и}} а \ в А (я)}$

Если существует функция, то будет наименьшая, удовлетворяющая приведенному выше уравнению. Чтобы найти, мы могли бы использовать следующую модель линейного программирования: ${\ displaystyle h}$${\ displaystyle {\ bar {V}} ^ {*}}$${\ displaystyle g}$${\ displaystyle {\ bar {V}} ^ {*}}$

• Первичная линейная программа (P-LP)

${\ displaystyle {\ begin {align} {\ text {Minimize}} \ quad amp; g \\ {\ text {st}} \ quad amp; g- \ sum _ {j \ in S} q (j \ mid i, a) h (j) \ geq R (i, a) \, \, \ forall i \ in S, \, a \ in A (i) \ end {выравнивается}}}$

• Двойная линейная программа (D-LP)

${\ displaystyle {\ begin {align} {\ text {Maximize}} amp; \ sum _ {i \ in S} \ sum _ {a \ in A (i)} R (i, a) y (i, a) \\ {\ text {st}} amp; \ sum _ {i \ in S} \ sum _ {a \ in A (i)} q (j \ mid i, a) y (i, a) = 0 \ quad \ forall j \ in S, \\ amp; \ sum _ {i \ in S} \ sum _ {a \ in A (i)} y (i, a) = 1, \\ amp; y (i, a) \ geq 0 \ qquad \ forall a \ in A (i) {\ text {and}} \ forall i \ in S \ end {align}}}$

${\ Displaystyle у (я, а)}$является допустимым решением D-LP, если не является родным и удовлетворяет ограничениям в задаче D-LP. Допустимое решение D-LP называется оптимальным решением, если ${\ Displaystyle у (я, а)}$${\ Displaystyle у ^ {*} (я, а)}$

${\ Displaystyle {\ begin {align} \ sum _ {я \ in S} \ sum _ {a \ in A (i)} R (i, a) y ^ {*} (i, a) \ geq \ sum _ {я \ в S} \ sum _ {а \ в А (я)} R (я, а) у (я, а) \ конец {выровнено}}}$

для всех посильно решение D-LP. Найдя оптимальное решение, мы можем использовать его для разработки оптимальных политик. ${\ Displaystyle у (я, а)}$${\ Displaystyle у ^ {*} (я, а)}$

Уравнение Гамильтона – Якоби – Беллмана.

В MDP с непрерывным временем, если пространство состояний и пространство действий непрерывны, оптимальный критерий может быть найден путем решения уравнения в частных производных Гамильтона – Якоби – Беллмана (HJB). Чтобы обсудить уравнение HJB, нам нужно переформулировать нашу проблему

${\ displaystyle {\ begin {align} V (x (0), 0) = {} amp; \ max _ {u} \ int _ {0} ^ {T} r (x (t), u (t)) \, dt + D [x (T)] \\ {\ text {st}} \ quad amp; {\ frac {dx (t)} {dt}} = f [t, x (t), u (t) ] \ end {выровнен}}}$

${\ Displaystyle D (\ cdot)}$- функция конечного вознаграждения, - это вектор состояния системы, - это вектор управления системой, который мы пытаемся найти. показывает, как вектор состояния изменяется с течением времени. Уравнение Гамильтона – Якоби – Беллмана выглядит следующим образом: ${\ Displaystyle х (т)}$${\ Displaystyle и (т)}$${\ Displaystyle е (\ cdot)}$

${\ displaystyle 0 = \ max _ {u} (r (t, x, u) + {\ frac {\ partial V (t, x)} {\ partial x}} f (t, x, u))}$

Мы могли бы решить уравнение, чтобы найти оптимальное управление, которое могло бы дать нам функцию оптимального значения ${\ Displaystyle и (т)}$ ${\ Displaystyle V ^ {*}}$

заявка

Марковские процессы принятия решений с непрерывным временем находят применение в системах массового обслуживания, эпидемических процессах и демографических процессах.

Альтернативные обозначения

Терминология и обозначения для MDP полностью не определены. Существует два основных потока: один фокусируется на задачах максимизации из таких контекстов, как экономика, с использованием терминов действие, вознаграждение, ценность и вызов коэффициента скидки, или, в то время как другой фокусируется на проблемах минимизации из инженерии и навигации, используя термины контроль, стоимость, себестоимость и коэффициент дисконтирования. Кроме того, различаются обозначения вероятности перехода. ${\ displaystyle \ beta}$${\ displaystyle \ gamma}$${\ displaystyle \ alpha}$

в этой статье	альтернатива	комментарий
действие ${\ displaystyle a}$	контроль ${\ displaystyle u}$
награда ${\ displaystyle R}$	Стоимость ${\ displaystyle g}$	${\ displaystyle g}$ это отрицание ${\ displaystyle R}$
ценить ${\ displaystyle V}$	себестоимость ${\ displaystyle J}$	${\ displaystyle J}$ это отрицание ${\ displaystyle V}$
политика ${\ displaystyle \ pi}$	политика ${\ displaystyle \ mu}$
коэффициент дисконтирования ${\ Displaystyle \ \ gamma \}$	коэффициент дисконтирования ${\ displaystyle \ alpha}$
вероятность перехода ${\ displaystyle P_ {a} (s, s ')}$	вероятность перехода ${\ displaystyle p_ {ss '} (а)}$

Кроме того, вероятность перехода иногда пишется, или, реже,${\ Displaystyle \ Pr (s, a, s ')}$${\ Displaystyle \ Pr (s '\ mid s, а)}$${\ displaystyle p_ {s's} (а).}$

Ограниченные марковские процессы принятия решений

Марковские процессы принятия решений с ограничениями (CMDP) являются расширением марковских процессов принятия решений (MDP). Между MDP и CMDP есть три фундаментальных различия.

• После применения действия вместо одного возникает несколько затрат.
• CMDP решаются только с помощью линейных программ, а динамическое программирование не работает.
• Окончательная политика зависит от начального состояния.

Существует ряд приложений для CMDP. Недавно он был использован в сценариях планирования движения в робототехнике.

Смотрите также

• Вероятностные автоматы
• Квантовые конечные автоматы
• Частично наблюдаемый марковский процесс принятия решений
• Динамическое программирование
• Уравнение Беллмана в приложениях к экономике.
• Уравнение Гамильтона – Якоби – Беллмана.
• Оптимальный контроль
• Рекурсивная экономика
• Проблема овец мабиногиона
• Стохастические игры
• Q-обучение

использованная литература

дальнейшее чтение

• Bellman., RE (2003) [1957]. Динамическое программирование (Дувр, мягкая обложка, ред.). Принстон, Нью-Джерси: Издательство Принстонского университета. ISBN   978-0-486-42809-3.
• Бертсекас, Д. (1995). Динамическое программирование и оптимальное управление. 2. МА: Афина.
• Дерман, К. (1970). Конечные марковские процессы принятия решений. Академическая пресса.
• Файнберг, EA; Шварц, А., ред. (2002). Справочник по марковским процессам принятия решений. Бостон, Массачусетс: Клувер. ISBN   9781461508052.
• Guo, X.; Эрнандес-Лерма, О. (2009). Марковские процессы принятия решений в непрерывном времени. Стохастическое моделирование и прикладная вероятность. Springer. ISBN   9783642025464.
• Мейн, СП (2007). Методы управления сложными сетями. Издательство Кембриджского университета. ISBN   978-0-521-88441-9. Архивировано из оригинального 19 июня 2010 года.Приложение содержит сокращенное «Meyn amp; Tweedie». Архивировано из оригинального 18 декабря 2012 года.
• Путерман., М.Л. (1994). Марковские процессы принятия решений. Вайли.
• Росс, С.М. (1983). Введение в стохастическое динамическое программирование (PDF). Академическая пресса.
• Саттон, РС; Барто, AG (2017). Обучение с подкреплением: Введение. Кембридж, Массачусетс: MIT Press.
• Tijms., HC (2003). Первый курс стохастических моделей. Вайли. ISBN   9780470864289.

внешние ссылки

• Научиться решать марковские процессы принятия решений по Сатиндеру П. Сингх