Войти
Открытый конный тур по шахматной доске 
Анимация открытого конного похода на доске 5х5 Маршрут коня - это последовательность ходов коня на шахматной доске, при которой конь посещает каждую клетку ровно один раз. Если конь заканчивается на поле, которое находится на один ход коня от начального поля (так, чтобы он мог немедленно обойти доску, следуя тем же путем), тур закрывается; в противном случае он открыт.
Задача рыцарского тура - это математическая задача поиска рыцарского тура. Создание программы для поиска рыцарского тура - распространенная проблема, которую ставят перед студентами, изучающими информатику. Варианты задачи конного тура включают в себя шахматные доски разных размеров, чем обычные 8 × 8, а также доски неправильной (непрямоугольной) формы.
График коня, показывающий все возможные пути коня на стандартной шахматной доске 8 × 8. Цифры на каждом узле указывают количество возможных ходов, которые можно сделать из этой позиции. Проблема рыцарского тура является примером более общей проблемы гамильтонова пути в теории графов. Проблема поиска замкнутого рыцарского тура аналогична проблеме гамильтонова цикла. В отличие от общей гамильтоновой проблемы пути, задача рыцарского тура может быть решена за линейное время.
Маршрут коня, раскрытый Турком, розыгрыш шахматной машины. Это конкретное решение является замкнутым (круговым) и, таким образом, может быть выполнено из любой точки на доске. Самое раннее известное упоминание о путешествии рыцарей относится к IX веку нашей эры. В « Кавьяланкаре» Рудраны (5.15), санскритском труде по поэтике, модель рыцарского похода на полупансионе представлена в виде тщательно продуманной поэтической фигуры ( читра-аланкара), называемой турагападабандхой или «расположением в следах лошади».. Один и тот же стих в четырех строках по восемь слогов в каждой можно читать слева направо или следуя по пути путешествующего рыцаря. Поскольку индийские системы письма, используемые для санскрита, являются слоговыми, каждый слог можно представить себе как квадрат на шахматной доске. Пример Рудраты таков:
| से | ना | ली | ली | ली | ना | ना | ली |
| ली | ना | ना | ना | ना | ली | ली | ली |
| न | ली | ना | ली | ले | ना | ली | ना |
| ली | ली | ली | ना | ना | ना | ना | ली |
транслитерированный:
| se | нет | ли | ли | ли | нет | нет | ли |
| ли | нет | нет | нет | нет | ли | ли | ли |
| на | ли | нет | ли | ле | нет | ли | нет |
| ли | ли | ли | нет | нет | нет | нет | ли |
Например, первую строку можно читать слева направо или переходя от первого квадрата ко второй строке, к третьему слогу (2.3), а затем к 1,5–2,7–4,8–3,6–4,4–3,2.
Шри вайшнавский поэт и философ Веданта Десика во 14 - м веке в его 1008-куплет опус восхваление Господа Ранганатхи Божественные сандалии «s из Шрирангам, т.е. Paduka Sahasram (в главе 30: Chitra Паддхати) сочинил два последовательных санскрите стихи, содержащие 32 букв каждая ( в метре Ануштуб ), где второй стих может быть получен из первого стиха, выполнив тур Рыцаря на доске 4 × 8, начиная с верхнего левого угла. Транслитерированный 19-й стих выглядит следующим образом:
| sThi (1) | rA (30) | га (9) | Сэм (20) | са (3) | dhA (24) | rA (11) | дхья (26) |
| vi (16) | ха (19) | thA (2) | ка (29) | тха (10) | thA (27) | ма (4) | thA (23) |
| са (31) | thpA (8) | ду (17) | kE (14) | са (21) | rA (6) | SA (25) | мА (12) |
| побежал (18) | га (15) | rA (32) | я (7) | па (28) | дха (13) | нна (22) | я (5) |
20-й куплет, который можно получить, выполнив Knight's Tour в вышеприведенном стихе, выглядит следующим образом:
шти тха са ма я ра джа тпа
га тха ра ма дха кэ га ви |
дху ран ха сам сан нна тха дха
СА ДХЯ ТА ПА КАРА СА РА ||
Считается, что Десика сочинил все 1008 стихов (включая особую Чатуранга Туранга Падабандхам, упомянутую выше) за одну ночь в качестве испытания.
Путешествие, описанное в пятой книге Бхагавантабаскараби Бхат Нилакантхой, циклопедическом труде на санскрите о ритуалах, законе и политике, написанном около 1600 или около 1700 годов, описывает три рыцарских похода. Экскурсии не только реентерабельные, но и симметричные, а стихи основаны на одном туре, начиная с разных площадей. Работа Бхата Нилакантхи - это выдающееся достижение, представляющее собой полностью симметричный закрытый тур, предшествующий работе Эйлера (1759 г.) как минимум на 60 лет.
Одним из первых математиков, исследовавших рыцарский тур, был Леонард Эйлер. Первой процедурой завершения рыцарского тура было правило Варнсдорфа, впервые описанное в 1823 году ХК фон Варнсдорф.
В 20 веке группа писателей Улипо использовала его среди многих других. Наиболее ярким примером является рыцарский тур 10 × 10, который устанавливает порядок глав в романе Жоржа Перека « Жизнь и руководство пользователя».
В шестой партии чемпионата мира по шахматам 2010 года между Вишванатаном Анандом и Веселином Топаловым Ананд сделал 13 последовательных ходов конем (хотя и двумя конями); Интернет-комментаторы шутили, что Ананд во время игры пытался решить задачу с рыцарским туром.
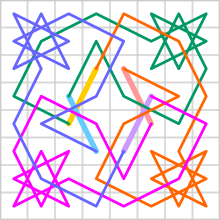Радиально-симметричный замкнутый рыцарский тур Швенк доказал, что для любой доски m × n с m ≤ n замкнутый конный тур всегда возможен, если не выполняется одно или несколько из этих трех условий:
Cull et al. и Конрад и др. Доказано, что на любой прямоугольной доске, меньшая размерность которой не менее 5, существует (возможно, открытый) конный тур.
На доске 8 × 8 имеется ровно 26 534 728 821 064 направленных замкнутых маршрута (т. Е. Два маршрута по одному и тому же пути, которые проходят в противоположных направлениях, считаются отдельно, как и вращения и отражения ). Количество неориентированных закрытых туров составляет половину этого числа, поскольку каждый тур можно проследить в обратном порядке. На доске 6 × 6 имеется 9862 неориентированных закрытых маршрута.
| п | Количество направленных обходов (открытых и закрытых) на доске n × n (последовательность A165134 в OEIS ) |
|---|---|
| 1 | 1 |
| 2 | 0 |
| 3 | 0 |
| 4 | 0 |
| 5 | 1,728 |
| 6 | 6 637 920 |
| 7 | 165 575 218 320 |
| 8 | 19 591 828 170 979 904 |
Есть несколько способов найти рыцарский тур на заданной доске с помощью компьютера. Некоторые из этих методов являются алгоритмами, а другие - эвристиками.
Полный перебор для тура рыцарского непрактичен на всех, кроме самых маленьких плат. Например, существует приблизительно 4 × 10 51 возможных последовательностей ходов на доске 8 × 8, и современные компьютеры (или компьютерные сети) не в состоянии выполнять операции с таким большим набором. Однако размер этого числа не указывает на сложность проблемы, которую можно решить «без особого труда, используя человеческую проницательность и изобретательность...».
Разделив доску на более мелкие части, построив туры на каждой части и склеив части вместе, можно построить туры на большинстве прямоугольных досок за линейное время, то есть за время, пропорциональное количеству квадратов на доске.
| а | б | c | d | е | ж | грамм | час | ||
| 8 |       | 8 | |||||||
| 7 | 7 | ||||||||
| 6 | 6 | ||||||||
| 5 | 5 | ||||||||
| 4 | 4 | ||||||||
| 3 | 3 | ||||||||
| 2 | 2 | ||||||||
| 1 | 1 | ||||||||
| а | б | c | d | е | ж | грамм | час | ||
Очень большой (130 × 130) квадратный открытый рыцарский тур, созданный с использованием правила Варнсдорфа. Правило Варнсдорфа - это эвристика для поиска одиночного рыцарского тура. Конь перемещается так, что он всегда переходит на поле, с которого у коня будет наименьшее количество дальнейших ходов. При подсчете количества дальнейших ходов для каждого квадрата-кандидата мы не учитываем ходы, которые возвращаются к любому уже посещенному квадрату. Возможны два или более выбора, для которых количество дальнейших ходов одинаково; Существуют различные методы разрыва таких связей, в том числе один разработан Полом, а другой - Белкой и Каллом.
Это правило также может быть применено к любому графу в более общем смысле. В терминах теории графов каждый переход выполняется в соседнюю вершину с наименьшей степенью. Хотя проблема гамильтонова пути в целом является NP-сложной, на многих графах, которые встречаются на практике, эта эвристика может успешно найти решение за линейное время. Рыцарский тур - такой особенный случай.
Впервые эта эвристика была описана в "Des Rösselsprungs einfachste und allgemeinste Lösung" ХК фон Варнсдорф в 1823 году.
Компьютерная программа, которая находит путь рыцаря для любой исходной позиции с использованием правила Варнсдорфа, была написана Гордоном Хорсингтоном и опубликована в 1984 году в книге Century / Acorn User Book of Computer Puzzles.
Закрытый конный тур на доске 24 × 24, решенный нейронной сетью Задача рыцарского тура также поддается решению с помощью реализации нейронной сети. Сеть настроена таким образом, что каждый разрешенный ход коня представлен нейроном, и каждый нейрон случайным образом инициализируется как «активный» или «неактивный» (выход 1 или 0), причем 1 означает, что нейрон является частью решение. Каждый нейрон также имеет функцию состояния (описанную ниже), которая инициализируется значением 0.
Когда сети разрешено работать, каждый нейрон может изменять свое состояние и выход в зависимости от состояний и выходов своих соседей (тех, кто отошел ровно на один конь) в соответствии со следующими правилами перехода:
где представляет дискретные интервалы времени, - состояние нейрона, соединяющего квадрат с квадратом, - выход нейрона от до и - набор соседей нейрона.
Хотя возможны расходящиеся случаи, сеть должна в конечном итоге сойтись, что происходит, когда ни один нейрон не меняет свое состояние время от времени на. Когда сеть сходится, либо сеть кодирует рыцарский тур, либо серию из двух или более независимых цепей на одной плате.
