Связка струй

редактировать

В дифференциальной топологии связка струй представляет собой определенную конструкцию, которая создает новую гладкий пучок волокон из заданного гладкого пучка волокон. Это позволяетывать дифференциальные уравнения записывать на участках пучка волокон в инвариантной форме. Струи также можно рассматривать как свободные от координат версии расширений Тейлора.

Исторически связки струй приписывались Чарльзу Эресманну и были продвижением методом (продолжение ) Эли Картана, геометрической работы с высшими производными путем наложения условий дифференциальной на вновь введенные формальные переменные. Пучки струй иногда называют спреями, хотя спреи обычно более конкретно к ассоциированному векторному полю, наведенному на соответствующий пучок (например, геодезический спрей на финслеровских разнообразиях.)

С начала 1980-х годов струйные пучки появились как краткий способ описания явлений, связанных с производными карт, особенно тех, которые связаны с вариационное исчисление. Следовательно, расслоение струй теперь признано правильной областью для геометрической ковариантной теории поля, и большая работа проделана в общих релятивистских формулировках полей с использованием этого подхода.

Содержание

1 Форсунки
2 Форсунки
3 Жгуты форсунок
- 3.1 Алгебро-геометрическая перспектива
- 3.2 Пример
4 Структура контактов
- 4.1 Пример
5 Вектор поля
6 Уравнения с частными производными
- 6.1 Пример
7 Удлинение струи
- 7.1 Пример
8 Бесконечные пространства для струй
- 8.1 Бесконечно протяженные УЧП
9 Примечание
10 См. также
11 Ссылки
12 Дополнительная литература

Jets

Предположим, что M - это m-мерное многообразие и что (E, π, M) - пучок волокон . Для p ∈ M через Γ (p) обозначим множество всех локальных секций, область определения которых содержит p. Пусть $I = (I (1), I (2),..., I (m)) {\ displaystyle I = (I (1), I (2),..., I (m))}$ ${\ Displaystyle I = (Я (1), Я (2),..., Я (м))}$ быть мультииндексом (набором m целых чисел, не обязательно в возрастании), затем определите:

| Я | : = ∑ i = 1 m I (i) ∂ | Я | ∂ x I: = ∏ i = 1 м (∂ ∂ x i) I (i). {\ displaystyle {\ begin {align} | Я | : = \ sum _ {i = 1} ^ {m} I (i) \\ {\ frac {\ partial ^ {| I |}} {\ partial x ^ {I}}} : = \ prod _ {i = 1} ^ {m} \ left ({\ frac {\ partial} {\ partial x ^ {i}}} \ справа) ^ {I (i)}. \ end {align}}}

{\ displaystyle {\ begin {align} | Я | : = \ sum _ {i = 1} ^ {m} I (i) \\ {\ frac {\ partial ^ {| I |}} {\ partial x ^ {I}}} : = \ prod _ {i = 1} ^ {m} \ left ({\ frac {\ partial} {\ partial x ^ {i}}} \ справа) ^ {I (i)}. \ end {align}}}

Определите локальные сечения σ, η ∈ Γ (p) так, чтобы они имели одинаковую r-струю в точке p, если

∂ | Я | σ α ∂ x I | p = ∂ | Я | η α ∂ x I | p, 0 ≤ | Я | ≤ r. {\ displaystyle \ left. {\ frac {\ partial ^ {| I |} \ sigma ^ {\ alpha}} {\ partial x ^ {I}}} \ right | _ {p} = \ left. {\ frac {\ partial ^ {| I |} \ eta ^ {\ alpha}} {\ partial x ^ {I}}} \ right | _ {p}, \ quad 0 \ leq | Я | \ leq r.}

{\ displaystyle \ left. {\ Frac {\ partial ^ {| I |} \ sigma ^ {\ alpha}} {\ partial x ^ {I}}} \ right | _ {p} = \ left. {\ Frac {\ partial ^ {| I |} \ eta ^ {\ alpha}} {\ partial x ^ {I}}} \ right | _ {p}, \ quad 0 \ leq | Я | \ leq r.}

Отношение, что две карты имеют одну и ту же r-струю, является отношением эквивалентности. В соответствии с этим использованием r-струя является классом эквивалентности, а r-струя с представительным σ обозначается $jpr σ {\ displaystyle j_ {p} ^ {r} \ sigma}$ ${\ displaystyle j_ {p} ^ {r} \ sigma}$ . Целое число r также называется порядком струи, p - ее со ссылкой на, а σ (p) - ее .

Коллекторы струи

r-м разнообразием струй множества π является множеством

J r (π) = {jpr σ: p ∈ M, σ ∈ Γ (p)}. {\ Displaystyle J ^ {r} (\ pi) = \ left \ {j_ {p} ^ {r} \ sigma: p \ in M, \ sigma \ in \ Gamma (p) \ right \}.}

{\ displaystyle J ^ {r} (\ pi) = \ left \ {j_ {p} ^ {r} \ sigma: p \ in M, \ sigma \ в \ Gamma ( p) \ right \}.}

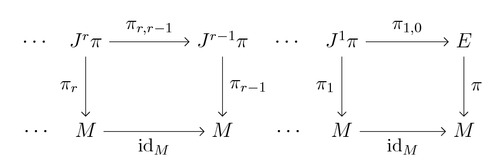
Мы можем определить проекции π r и π r, 0, называемые исходной и проекциями соответственно, как

{π r: J r (π) → M jpr σ ↦ п, {π r, 0: J r (π) → E jpr σ ↦ σ (p) {\ displaystyle {\ begin {cases} \ pi _ {r}: J ^ {r} ( \ pi) \ to M \\ j_ {p} ^ {r} \ sigma \ mapsto p \ end {cases}}, \ qquad {\ begin {cases} \ pi _ {r, 0}: J ^ {r} (\ pi) \ to E \\ j_ {p} ^ {r} \ sigma \ mapsto \ sigma (p) \ end {cases} Если}}

{ \ Displaystyle {\ begin {cases} \ pi _ {r}: J ^ {r} (\ pi) \ to M \\ j_ {p} ^ {r} \ sigma \ mapsto p \ end {cases}}, \ qquad {\ begin {cases} \ pi _ {r, 0}: J ^ {r} (\ pi) \ к E \\ j_ {p} ^ {r} \ sigma \ mapsto \ sigma (p) \ end { case}}}

1 ≤ k ≤ r, то k- проекция струи - это функция π r, k, определенная как

{π r, k: J r (π) → J k (π) jpr σ ↦ jpk σ {\ displaystyle {\ begin {case} \ pi _ {r, k}: J ^ {r} (\ pi) \ to J ^ {k} (\ pi) \\ j_ {p} ^ {r} \ sigma \ mapsto j_ {p } ^ {k} \ sigma \ end {cases}}}

{\ displaystyle {\ begin {case} \ pi _ {r, k}: J ^ {r} (\ pi) \ to J ^ {k} (\ pi) \\ j_ {p} ^ {r} \ sigma \ mapsto j_ {p} ^ {k} \ sigma \ end {cases}}}

Из этого определения ясно, что π r = π o πr, 0 и что если 0 ≤ m ≤ k, тогда π r, m = π k, m o πг, к. Принято рассматривать π r, r как тождественное отображение на J (π) и отождествлять J (π) с E.

Функции π r, k, π r, 0 и π r - это плавные цели погружения.

A система координат на E создаст систему координат на J (π). Пусть (U, u) - адаптированная координатная карта на E, где u = (x, u). индуцированная координатная карта (U, u) на J (π) означает как

U r = {jpr σ: σ (p) ∈ U} ur = (xi, u α, u I α) {\ Displaystyle {\ begin {align} U ^ {r} = \ left \ {j_ {p} ^ {r} \ sigma: \ sigma (p) \ in U \ right \} \\ u ^ {r} = \ left (x ^ {i}, u ^ {\ alpha}, u_ {I} ^ {\ alpha} \ right) \ end {align}}}

{\ displaystyle {\ begin {align} U ^ {r} = \ left \ {j_ {p} ^ {r} \ sigma: \ сигма (p) \ в U \ right \} \\ u ^ {r} = \ left (x ^ {i}, u ^ {\ alpha}, u_ {I} ^ {\ alpha} \ right) \ end {выровнено}}}

где

xi (jpr σ) знак равно Икси (п) U α (JPR σ) = U α (σ (р)) {\ Displaystyle {\ begin {Выровнено} х ^ {я} \ влево (J_ {р} ^ {г} \ сигма \ вправо) = x ^ {i} (p) \\ u ^ {\ alpha} \ left (j_ {p} ^ {r} \ sigma \ right) = u ^ {\ alpha} (\ sigma (p)) \ конец {align}}}

{\ displaystyle {\ begin { align} x ^ {i} \ left (j_ {p} ^ {r} \ sigma \ справа) = x ^ {i} (p) \\ u ^ {\ alpha} \ left (j_ {p} ^ { r} \ sigma \ right) = u ^ {\ alpha} (\ sigma (p)) \ end {align}}}

и $n ((m + rr) - 1) {\ displaystyle n \ left ({\ binom {m + r} {r}} - 1 \ right)}$ ${\ displaystyle n \ left ({\ binom {m + r } {r}} - 1 \ right)}$ функции, известные как координаты производной :

{u I α: U k → R u I α (jpr σ) = ∂ | Я | σ α ∂ x I | п {\ displaystyle {\ begin {cases} u_ {I} ^ {\ alpha}: U ^ {k} \ to \ mathbf {R} \\ u_ {I} ^ {\ alpha} \ left (j_ {p} ^ {г} \ sigma \ right) = \ left. {\ frac {\ partial ^ {| I |} \ sigma ^ {\ alpha}} {\ partial x ^ {I}}} \ right | _ {p} \ end {cases}}}

{\ displaystyle {\ беги n {case} u_ {I} ^ {\ alpha}: U ^ {k} \ to \ mathbf {R} \\ u_ {I} ^ {\ alpha} \ left (j_ {p} ^ {r} \ sigma \ right) = \ left. {\ frac {\ partial ^ {| I |} \ sigma ^ {\ alpha}} {\ partial x ^ {I}}} \ right | _ {p} \ end {case}}}

Учитывая атлас адаптированных карт (U, u) на E, соответствующий набор карт (U, u) является конечным C-атласом на J (π).

Связки струй

Горнолыжный атлас на каждом J (π) многообразие, тройки (J (π), π r, k, J (π)), ( J (π), π r, 0, E) и (J (π), π r, M) все определяют расслоенные многообразия. В частности, если (E, π, M) - расслоение слоев, тройка (J (π), π r, M) определяет r-й пучок струй для π .

Если W ⊂ M - открытое подмногообразие, то

J r (π | π - 1 (W)) ≅ π r - 1 (W). {\ Displaystyle J ^ {r} \ left (\ pi | _ {\ pi ^ {- 1} (W)} \ right) \ cong \ pi _ {r} ^ {- 1} (W). \,}

{\ displaystyle J ^ {r} \ left ( \ pi | _ {\ pi ^ {- 1} (W)} \ right) \ cong \ pi _ {r} ^ {- 1} (W). \,}

Если p ∈ M, то волокно $π r - 1 (p) {\ displaystyle \ pi _ {r} ^ {- 1} (p) \,}$ ${\ displaystyle \ pi _ {r} ^ {- 1} (p) \,}$ обозначается $J pr (π) {\ displaystyle J_ {p} ^ {r} (\ pi)}$ ${\ displaystyle J_ {p} ^ {r} (\ pi)}$ .

Пусть σ - локальное сечение π с областью определения W ⊂ M. r-ое продолжение струи σ - это отображение jσ: W → J (π), определенное формулой

(jr σ) (p) = jpr σ. {\ Displaystyle (j ^ {r} \ sigma) (p) = j_ {p} ^ {r} \ sigma. \,}

{\ displaystyle (j ^ {r} \ sigma) (p) = j_ {p} ^ {r} \ sigma. \,}

Обратите внимание, что π ro jσ = id W, так что jσ действительно является разделом. В локальных координатах jσ задается как

(σ α, ∂ | I | σ α ∂ x | I |) 1 ≤ | Я | ≤ r. {\ displaystyle \ left (\ sigma ^ {\ alpha}, {\ frac {\ partial ^ {| I |} \ sigma ^ {\ alpha}} {\ partial x ^ {| I |}}} \ right) \ qquad 1 \ leq | Я | \ leq r. \,}

{\ displaystyle \ left (\ sigma ^ {\ alpha}, {\ frac {\ частичный ^ { | I |} \ sigma ^ {\ alpha}} {\ partial x ^ {| I |}}} \ right) \ qquad 1 \ leq | Я | \ leq r. \,}

Мы отождествляем jσ с σ.

Алгебро-геометрическая перспектива

Независимо мотивированное построение связки секций $Γ J k (π TM) {\ displaystyle \ Gamma J ^ {k} \ left (\ pi _ {TM} \ right)}$ ${\ displaystyle \ Gamma J ^ {k} \ left (\ pi _ {TM} \ right)}$ дано.

Рассмотрим диагональное отображение $Δ n: M → ∏ i = 1 n + 1 M {\ textstyle \ Delta _ {n}: M \ to \ prod _ {i = 1} ^ {n + 1} M}$ ${\ textstyle \ Delta _ {n}: M \ to \ prod _ {i = 1} ^ {n + 1} M}$ , где гладкое многообразие $M {\ displaystyle M}$ $M$ является локально окольцованным пространством на $C k (U) {\ displaystyle C ^ {k} (U)}$ ${\ displaystyle C ^ {k} (U)}$ для каждого открытого $U {\ displaystyle U}$ $U$ . Пусть $I {\ displaystyle {\ mathcal {I}}}$ ${\ mathcal {I}}$ будет идеальным пучком для $Δ n (M) {\ displaystyle \ Delta _ {n} (M)}$ ${\ displaystyle \ Delta _ {n} (M)}$ , пусть $I {\ displaystyle {\ mathcal {I}}}$ ${\ mathcal {I}}$ будет связкой гладких ростков, которые исчезают на $Δ N (M) {\ displaystyle \ Delta _ {n} (M)}$ ${\ displaystyle \ Delta _ {n} (M)}$ для всех $0 < n ≤ k {\displaystyle 0$ ${\ displaystyle 0 <n \ leq k}$ . откат частного пучка $Δ n ∗ (I / I n + 1) {\ displaystyle {\ Delta _ {n}} ^ {*} \ left ({\ mathcal {I}} / {\ mathcal {I}} ^ {n + 1} \ right)}$ ${\ displaystyle {\ Delta _ {n}} ^ {*} \ left ({\ mathcal {I}} / {\ mathcal {I}} ^ {n + 1} \ right)}$ из $∏ я = 1 n + 1 M {\ textstyle \ prod _ {я = 1 } ^ {n + 1} M}$ ${\ textstyle \ prod _ {i = 1} ^ {n + 1} M}$ до $M {\ displaystyle M}$ $M$ на $Δ n {\ displaystyle \ Delta _ {n}}$ $\ Delta _ {n}$ - пучок к-струй.

прямой предел следовать инъекций, задаваемых каноническими включениями $I n + 1 ↪ I n {\ displaystyle {\ mathcal {I}} ^ {n + 1} \ hookrightarrow {\ mathcal {I}} ^ {n}}$ ${\ displaystyle {\ mathcal {I}} ^ {n + 1} \ hookrightarrow {\ mathcal {I}} ^ {n}}$ пучков, приводит к бесконечному пучку струй $J ∞ (TM) {\ displaystyle {\ mathcal {J}} ^ {\ infty} (TM)}$ ${\ displaystyle { \ mathcal {J}} ^ {\ infty} (TM)}$ . Заметим, что по построению прямого предела это фильтрованное кольцо.

Пример

Если π является тривиальным набором (M × R, pr 1, M), тогда там каноническим диффеоморфизмом между первым пучком струй J (π) и T * M × R . Чтобы построить этот диффеоморфизм, для каждого σ в Γ M (π) напишите $σ ¯ = pr 2 ∘ σ ∈ C ∞ (M) {\ displaystyle {\ bar {\ sigma}} = pr_ {2} \ circ \ sigma \ in C ^ {\ infty} (M) \,}$ ${\ displaystyle {\ bar {\ sigma}} = pr_ {2} \ circ \ sigma \ in C ^ {\ infty} (M) \,}$ .

Тогда, если p ∈ M

jp 1 σ = {ψ: ψ ∈ Γ p (π); ψ ¯ (p) = σ ¯ (p); d ψ ¯ p = d σ ¯ p}. {\ Displaystyle j_ {p} ^ {1} \ sigma = \ left \ {\ psi: \ psi \ in \ Gamma _ {p} (\ pi); {\ bar {\ psi}} (p) = {\ bar {\ sigma}} (p); d {\ bar {\ psi}} _ {p} = d {\ bar {\ sigma}} _ {p} \ right \}. \,}

{\ displaystyle j_ {p} ^ {1} \ sigma = \ left \ {\ psi: \ psi \ in \ Gamma _ {p} (\ pi); {\ bar {\ psi}} (p) = {\ bar {\ sigma}} (p); d {\ bar {\ psi}} _ {p} = d {\ bar {\ sigma}} _ {p} \ right \}. \,}

Следовательно, отображение

{J 1 (π) → T ∗ M × R jp 1 σ ↦ (d σ ¯ p, σ ¯ (p)) {\ displaystyle {\ begin {cases} J ^ {1} (\ pi) \ to T ^ {*} M \ times \ mathbf {R} \\ j_ {p} ^ {1} \ sigma \ mapsto \ left (d {\ bar {\ sigma}} _ {p}, {\ bar {\ sigma}} (p) \ right) \ end {cases}}}

{\ displaystyle {\ begin {cases} J ^ {1} (\ pi) \ to T ^ {*} M \ times \ mathbf {R} \\ j_ {p} ^ {1} \ sigma \ mapsto \ left (d {\ bar {\ sigma}} _ {p}, {\ bar {\ sigma}} (p) \ right) \ end {case}}}

четко определен и явно инъективен. Запись в координатах показывает, что это диффеоморфизм, потому что если (x, u) - координаты на M × R, где u = id R- единичные координаты, то производные координаты u i на J (π) координатам ∂ i на T * M.

Аналогично, если π - тривиальное расслоение (R × M, pr 1, R), то существует канонический диффеоморфизм между J (π) и R × TM.

Контактная структура

Пространство J (π) несет естественное распределение, то есть под-расслоение касательного тела TJ (π)), называемое распределением Картана. Распределение Картана натянуто на все касательные плоскости к графам голономных сечений; то есть сечения вида jφ для φ сечения π.

Аннигилятор распределения Картана - это пространство дифференциальных одноформ, называемых контактными формами, на J (π). Пространство дифференциальных одноформ на J (π) обозначается $Λ 1 J r (π) {\ displaystyle \ Lambda ^ {1} J ^ {r} (\ pi)}$ $\ Lambda ^ 1J ^ r (\ pi)$ а пространство контактных форм обозначается $Λ С р π {\ Displaystyle \ Lambda _ {C} ^ {r} \ pi}$ $\ Lambda_C ^ r \ pi$ . Единичная форма является контактной, если ее откат при каждом продлении равенство нулю. Другими словами, $θ ∈ Λ 1 J r π {\ displaystyle \ theta \ in \ Lambda ^ {1} J ^ {r} \ pi}$ $\ theta \ in \ Lambda ^ 1J ^ r \ pi$ является контактной формой тогда и только тогда, когда

(jr + 1 σ) ∗ θ = 0 {\ displaystyle \ left (j ^ {r + 1} \ sigma \ right) ^ {*} \ theta = 0}

{\ displaystyle \ left (j ^ {r + 1} \ sigma \ right) ^ {*} \ theta = 0}

для всех локальных участков σ из π над М.

Распределение Картана является основной геометрической структурой на пространствех уравнения в частных производных. Распределения Картана полностью не интегрируемы. В частности, они не инволютивные. Размер распределения Картана растет с порядком пространства струи. Однако в пространстве бесконечных струй J распределение Картана становится инволюционным и конечным: его размер совпадает с размером базового многообразия M.

Пример

Рассмотрим случай (E, π, M), где E ≃ R и M R . Тогда (J (π), π, M) определяет первое расслоение струй и может быть скоординировано с помощью (x, u, u 1), где

x (jp 1 σ) = x (p) = xu (jp 1 σ) = u (σ (p)) = u (σ (x)) = σ (x) u 1 (jp 1 σ) = ∂ σ ∂ x | п знак равно σ ′ (Икс) {\ Displaystyle {\ begin {выровнено} х \ влево (j_ {p} ^ {1} \ sigma \ right) = x (p) = x \\ u \ left (j_ { p} ^ {1} \ sigma \ right) = u (\ sigma (p)) = u (\ sigma (x)) = \ sigma (x) \\ u_ {1} \ left (j_ {p} ^ {1} \ sigma \ right) = \ left. {\ Frac {\ partial \ sigma} {\ partial x}} \ right | _ {p} = \ sigma '(x) \ end {align}}}

{\begin{aligned}x\left(j_{p}^{1}\sigma \right)=x(p)=x\\u\left(j_{p}^{1}\sigma \right)=u(\sigma (p))=u(\sigma (x))=\sigma (x)\\u_{1}\left(j_{p}^{1}\sigma \right)=\left.{\frac {\partial \sigma }{\partial x}}\right|_{p}=\sigma '(x)\end{aligned}}

для всех p ∈ M и σ в Γ p (π). Общая 1-форма на J (π) принимает вид

θ = a (x, u, u 1) dx + b (x, u, u 1) du + c (x, u, u 1) du 1 { \ displaystyle \ theta = a (x, u, u_ {1}) dx + b (x, u, u_ {1}) du + c (x, u, u_ {1}) du_ {1} \,}

{\ displaystyle \ theta = a (x, u, u_ {1}) dx + b (x, u, u_ {1}) du + c (x, u, u_ {1}) du_ {1} \,}

Сечение σ в Γ p (π) имеет первое продолжение

j 1 σ = (u, u 1) = (σ (p), ∂ σ ∂ x | p). {\ displaystyle j ^ {1} \ sigma = (u, u_ {1}) = \ left (\ sigma (p), \ left. {\ frac {\ partial \ sigma} {\ partial x}} \ right | _ {p} \ right).}

{\ displaystyle j ^ {1} \ sigma = (u, u_ {1}) = \ left (\ sigma (p), \ осталось. {\ frac {\ partial \ sigma} {\ partial x}} \ right | _ {p} \ right).}

Следовательно, (jσ) * θ можно вычислить как

(jp 1 σ) ∗ θ = θ ∘ jp 1 σ = a (x, σ (x), σ ′ (X)) dx + b (x, σ (x), σ ′ (x)) d (σ (x)) + c (x, σ (x), σ ′ (x)) d (σ ′ (x)) = a (x, σ (x), σ ′ (x)) dx + b (x, σ (x), σ ′ (x)) σ ′ (x) dx + c (x, σ (x))., σ ′ (x)) σ ″ (x) dx = [a (x, σ (x), σ ′ (x)) + b (x, σ (x), σ ′ (x)) σ ′ (Икс) + с (Икс, σ (Икс), σ '(Икс)) σ ″ (Икс)] dx {\ Displaystyle {\ begin {align} \ left (j_ {p} ^ {1} \ sigma \ right) ^ {*} \ theta = \ theta \ circ j_ {p} ^ {1} \ sigma \\ = a (x, \ sigma (x), \ sigma '(x)) dx + b (x, \ sigma) (х), \ sigma '(x)) d (\ sigma (x)) + c (x, \ sigma (x), \ sigma' (x)) d (\ sigma '(x)) \\ = а (х, \ sigma (x), \ sigma '(x)) dx + b (x, \ sigma (x), \ sigma' (x)) \ sigma '(x) dx + c (x, \ sigma (x), \ sigma '(x)) \ sigma' '(x) dx \\ = [a (x, \ sigma (x), \ sigma' (x)) + b (x, \ sigma (х), \ sigma '(x)) \ sigma' (x) + c (x, \ sigma (x), \ s igma '(x)) \ sigma' '(x)] dx \ end {align} }}

{\begin{aligned}\left(j_{p}^{1}\sigma \right)^{*}\theta =\theta \circ j_{p}^{1}\sigma \\=a(x,\sigma (x),\sigma '(x))dx+b(x,\sigma (x),\sigma '(x))d(\sigma (x))+c(x,\sigma (x),\sigma '(x))d(\sigma '(x))\\=a(x,\sigma (x),\sigma '(x))dx+b(x,\sigma (x),\sigma '(x))\sigma '(x)dx+c(x,\sigma (x),\sigma '(x))\sigma ''(x)dx\\=[a(x,\sigma (x),\sigma '(x))+b(x,\sigma (x),\sigma '(x))\sigma '(x)+c(x,\sigma (x),\sigma '(x))\sigma ''(x)]dx\end{aligned}}

Это исчезнет для всех секций σ тогда и только тогда, когда c = 0 и a = −bσ ′ (x). Следовательно, θ = b (x, u, u 1)θ0обязательно должно быть кратным основной контактной формой θ 0 = du - u 1 dx. Переход ко второй струе пространство J (π) с дополнительной координатой u 2, такое что

u 2 (jp 2 σ) = ∂ 2 σ ∂ x 2 | p = σ ″ (x) {\ displaystyle u_ {2} (j_ { p} ^ {2} \ sigma) = \ left. {\ frac {\ partial ^ {2} \ sigma} {\ partial x ^ {2}}} \ right | _ {p} = \ sigma '' (x) \,}

u_{2}(j_{p}^{2}\sigma)=\left.{\frac {\partial ^{2}\sigma }{\partial x^{2}}}\right|_{p}=\sigma ''(x)\,

общая 1-форма имеет конструкцию

θ = a (x, u, u 1, u 2) dx + b (x, u, u 1, u 2) ду + ​​с (Икс, U, U 1, U 2) ду 1 + е (Икс, U, U 1, U 2) дю 2 {\ Displaystyle \ theta = а (х, и, и_ {1}, и_ {2}) dx + b (x, u, u_ {1}, u_ {2}) du + c (x, u, u_ {1}, u_ {2}) du_ {1} + e (x, u, u_ {1}, u_ {2}) du_ {2} \,}

{\ displaystyle \ theta = a (x, u, u_ {1}, u_ {2}) dx + b (x, u, u_ {1}, u_ {2}) du + c (x, u, u_ {1}, u_ {2}) du_ {1} + е (x, u, u_ {1}, u_ {2}) du_ {2} \,}

Это контактная форма тогда и только тогда, когда

(jp 2 σ) ∗ θ = θ ∘ jp 2 σ = a (x, σ (x), σ ′ (X), σ ″ (x)) dx + b (x, σ (x), σ ′ (x), σ ″ (x)) d (σ (x)) + c (x, σ (x))., σ ′ (x), σ ″ (x)) d (σ ′ (x)) + e (x, σ (x), σ ′ (x), σ ″ (x)) d. (σ ″ (x)) = adx + b σ ′ (X) dx + c σ ″ (x) dx + e σ ‴ (x) dx = [a + b σ ′ (x) + c σ ″ (x) + e σ ‴ (x)] dx = 0 { \ Displaystyle {\ begin {выровнено} \ left (j_ {p} ^ {2} \ sigma \ right) ^ {*} \ theta = \ theta \ circ j_ {p} ^ {2} \ sigma \\ = a (x, \ sigma (x), \ sigma '(x), \ sigma' '(x)) dx + b (x, \ sigma (x), \ sigma' (x), \ sigma '' (x))) d (\ sigma (x)) + {} \\ \ qquad \ qquad c (x, \ sigma (x), \ sigma '(x), \ sigma' '(x)) d (\ sigma' (х)) + е (х, \ sigma (x), \ sigma '(x), \ sigma' '(x)) d (\ sigma' '(x)) \\ = adx + b \ sigma' (x) dx + c \ sigma '' (x) dx + e \ sigma '' '(x) dx \\ = [a + b \ sigma' (x) + c \ sigma '' '(x) + e \ sigma '' '(x)] dx \\ = 0 \ end {align}}}

{\begin{aligned}\left(j_{p}^{2}\sigma \right)^{*}\theta =\theta \circ j_{p}^{2}\sigma \\=a(x,\sigma (x),\sigma '(x),\sigma ''(x))dx+b(x,\sigma (x),\sigma '(x),\sigma ''(x))d(\sigma (x))+{}\\\qquad \qquad c(x,\sigma (x),\sigma '(x),\sigma ''(x))d(\sigma '(x))+e(x,\sigma (x),\sigma '(x),\sigma ''(x))d(\sigma ''(x))\\=adx+b\sigma '(x)dx+c\sigma ''(x)dx+e\sigma '''(x)dx\\=[a+b\sigma '(x)+c\sigma ''(x)+e\sigma '''(x)]dx\\=0\end{aligned}}

, что означает, что e = 0 и a = −bσ ′ (x) - cσ ′ ′ (x). Следовательно, θ является контактной формой тогда и только тогда, когда

θ = b (x, σ (x), σ ′ (x)) θ 0 + c (x, σ (x), σ ′ (x)) θ 1, {\ Displaystyle \ theta = б (х, \ sigma (x), \ sigma '(x)) \ theta _ {0} + с (x, \ sigma (x), \ sigma' (x)) \ theta _ {1},}

\theta =b(x,\sigma (x),\sigma '(x))\theta _{0}+c(x,\sigma (x),\sigma '(x))\theta _{1},

где θ 1 = du 1 - u 2 dx - это следующая основная контактная форма (обратите внимание, что здесь мы идентифицируем форму θ 0 с ее откатом $(π 2, 1) ∗ θ 0 {\ displaystyle \ left (\ pi _ {2,1} \ right) ^ {*} \ theta _ {0}}$ ${\ displaystyle \ left (\ pi _ {2, 1} \ right) ^ {*} \ theta _ {0}}$ в Дж (π)).

В общем случае, если x, u ∈ R, контактная форма на J (π) может быть записана как линейная комбинация линейная комбинация основных форм

θ К знак равно Дук - uk + 1 dxk = 0,…, r - 1 {\ displaystyle \ theta _ {k} = du_ {k} -u_ {k + 1} dx \ qquad k = 0, \ ldots, r -1 \,}

{\ displaystyle \ th eta _ {k} = du_ {k} -u_ {k + 1} dx \ qquad k = 0, \ ldots, г-1 \,}

где

uk (jk σ) = ∂ k σ ∂ xk | п. {\ displaystyle u_ {k} \ left (j ^ {k} \ sigma \ right) = \ left. {\ frac {\ partial ^ {k} \ sigma} {\ partial x ^ {k}}} \ right | _ {p}.}

{\ displaystyle u_ {k} \ left ( j ^ {k} \ sigma \ right) = \ left. {\ frac {\ partial ^ {k} \ sigma} {\ partial x ^ {k}}} \ right | _ {p}.}

Подобные аргументы приводят к полной характеристике всех контактных форм.

В локальных координатах каждая контактная форма на J (π) может быть записана как линейная комбинация

θ = ∑ | Я | Знак равно 0 р п α я θ я α {\ displaystyle \ theta = \ sum _ {| Я | = 0} ^ {r} P _ {\ alpha} ^ {I} \ theta _ {I} ^ {\ alpha}}

{\ displaystyle \ theta = \ sum _ {| Я | = 0} ^ {r} P _ {\ альфа} ^ {I} \ theta _ {I} ^ {\ alpha}}

с гладкими коэффициентами $P i α (xi, u α, u I α) {\ displaystyle P_ {i} ^ {\ alpha} (x ^ {i}, u ^ {\ alpha}, u_ {I} ^ {\ alpha})}$ ${\ displaystyle P_ {i} ^ {\ alph а} (х ^ {я }, и ^ {\ альфа}, и_ {I} ^ {\ альфа})}$ основных контактных форм

θ я α знак равно ду я α - U я, я α dxi {\ displaystyle \ theta _ {I} ^ {\ alpha} = du_ {I} ^ {\ alpha} -u_ {I, i} ^ {\ alpha} dx ^ {i} \,}

{\ displaystyle \ theta _ {I} ^ {\ alpha} = du_ {I} ^ {\ alpha} -u_ {I, i} ^ {\ alpha} dx ^ {я} \,}

| Я | известен как порядок контактной формы $θ i α {\ displaystyle \ theta _ {i} ^ {\ alpha}}$ ${\ displaystyle \ theta _ {i} ^ {\ alpha}}$ . Отметим, что контактные формы на J (π) имеют порядки не выше r. Контактные формы характеристики тех локальных участков π r + 1, которые являются продолжением участков π.

Пусть ψ ∈ Γ W(πr + 1), тогда ψ = jσ, где σ ∈ Γ W (π) тогда и только тогда, когда $ψ ∗ (θ | W) = 0, ∀ θ ∈ Λ C 1 π r + 1, r. {\ Displaystyle \ psi ^ {*} (\ theta | _ {W}) = 0, \ forall \ theta \ in \ Lambda _ {C} ^ {1} \ pi _ {r + 1, r}. \,}$ ${\ displaystyle \ psi ^ {*} (\ theta | _ {W}) = 0, \ forall \ theta \ in \ Lambda _ {C} ^ {1} \ pi _ {r + 1, r}. \,}$

Векторные поля

Общее векторное поле на всем пространстве E, координируемое с помощью $(x, u) = def (xi, u α) {\ displaystyle (x, u) \ {\ stackrel {\ mathrm {def}} {=}} \ left (x ^ {i}, u ^ {\ alpha} \ right) \,}$ ${\ displaystyle (x, u) \ {\ stackrel {\ mathrm {def}} {=}} \ left (x ^ {i}, u ^ {\ alpha} \ right) \,}$ , равно

V = def ρ i (x, u) ∂ ∂ xi + ϕ α (x, u) ∂ ∂ u α. {\ Displaystyle V \ {\ stackrel {\ mathrm {def}} {=}} \ \ rho ^ {i} (x, u) {\ frac {\ partial} {\ partial x ^ {i}}} + \ phi ^ {\ alpha} (x, u) {\ frac {\ partial} {\ partial u ^ {\ alpha}}}. \,}

{\ displaystyle V \ {\ stackrel {\ mathrm {def}} {=}} \ \ rho ^ {i} (x, u) {\ frac {\ parti al} { \ partial x ^ {i}}} + \ phi ^ {\ alpha} (x, u) {\ frac {\ partial} {\ partial u ^ {\ alpha}}}. \,}

векторное поле называется горизонтальным, что означает что все вертикальные коэффициенты равны нулю, если $ϕ α {\ displaystyle \ phi ^ {\ alpha}}$ ${\ displaystyle \ phi ^ {\ alpha}}$ = 0.

Векторное поле называется вертикальным, что означает, что все горизонтальные коэффициенты обращаются в нуль, если ρ = 0.

Для фиксированного (x, u) мы отождествляем

В (Икс, и) знак равно деф ρ я (Икс, и) ∂ ∂ Икс + ϕ α (Икс, и) ∂ ∂ U α {\ Displaystyle V _ {(х, u)} \ {\ stackrel { \ mathrm {def}} {=}} \ \ rho ^ {i} (x, u) {\ frac {\ partial} {\ partial x ^ {i}}} + \ phi ^ {\ alpha} (x, u) {\ frac {\ partial} {\ partial u ^ {\ alpha}}} \,}

{\ displaystyle V _ {(x, u)} \ {\ stackrel { \ mathrm {def}} {=}} \ \ rho ^ {i} (x, u) {\ frac {\ partial} {\ частичный x ^ {i}}} + \ phi ^ {\ alpha} (x, u) {\ frac {\ partial} {\ partial u ^ {\ alpha}}} \,}

, имеющий координаты (x, u, ρ, φ), с элементом в волокне T xu E TE над (x, u) в E, называемым a касательный вектор в TE . Раздел

{ψ: E → TE (x, u) ↦ ψ (x, u) = V {\ displaystyle {\ begin {cases} \ psi: E \ to TE \\ (x, u) \ mapsto \ psi (x, u) = V \ end {ases}}}

{\ displa ystyle {\ begin {cases} \ psi: E \ to TE \\ (x, u) \ mapsto \ psi (x, u) = V \ end {cases}}}

называется векторным полем на E с

V = ρ i (x, u) ∂ ∂ xi + ϕ α (Икс, U) ∂ ∂ U α {\ Displaystyle V = \ rho ^ {i} (x, u) {\ frac {\ partial} {\ partial x ^ {i}}} + \ phi ^ {\ alpha} (x, u) {\ frac {\ partial} {\ partial u ^ {\ alpha}}}}

{\ displaystyle V = \ rho ^ {i} (x, u) {\ frac {\ partial} {\ partial x ^ {i}}} + \ phi ^ {\ alpha} (x, u) {\ frac {\ partial} {\ partial u ^ {\ alpha}}}}

и ψ в Γ (TE).

Пучок струй J (π) координируется с помощью $(x, u, w) = def (xi, u α, wi α) {\ displaystyle (x, u, w) \ {\ stackrel {\ mathrm {def}} {=}} \ (x ^ {i}, u ^ {\ alpha}, w_ {i} ^ {\ alpha}) \,}$ ${\ Displaystyle (х, и, ш) \ {\ stackrel {\ mathrm {def}} {=} } \ (x ^ {i}, u ^ {\ alpha}, w_ {i} ^ {\ alpha}) \,}$ . Для фиксированных (x, u, w) отождествляем

V (x, u, w) = def V i (x, u, w) ∂ ∂ xi + V α (x, u, w) ∂ ∂ u α + V i α (x, u, w) ∂ ∂ wi α + V i 1 i 2 α (x, u, w) ∂ ∂ wi 1 i 2 α + ⋯ + V i 1 ⋯ ir α (x, u, вес) ∂ ∂ вес 1 ⋯ ir α {\ Displaystyle V _ {(x, u, w)} \ {\ stackrel {\ mathrm {def}} {=}} \ V ^ {i} (x, u, w) {\ frac {\ partial} {\ partial x ^ {i}}} + V ^ {\ alpha} (x, u, w) {\ frac {\ partial} {\ partial u ^ {\ alpha}}} + V_ {i} ^ {\ alpha} (x, u, w) {\ frac {\ partial} {\ partial w_ {i} ^ {\ alpha}}} + V_ {i_ {1} i_ {2}} ^ {\ alpha} (x, u, w) {\ frac {\ partial} {\ partial w_ {i_ {1} i_ {2}} ^ {\ alpha}}} + \ cdots + V_ {i_ {1} \ cdots i_ {r}} ^ {\ alpha} (x, u, w) {\ frac {\ partial} {\ partial w_ {i_ {1} \ cdots i_ {r}} ^ {\ alpha}}}}

{\ displaystyle V _ {(x, u, w)} \ {\ stackrel {\ mathrm {def}} {=}} \ V ^ {i} (x, u, w) {\ frac {\ partial} {\ partial x ^ {i}}} + V ^ {\ alpha} (x, u, w) {\ frac {\ partial} {\ partial u ^ {\ alpha}}} + V_ { i} ^ {\ альфа} (x, u, w) {\ frac {\ partial} {\ partial w_ {i} ^ {\ alpha}}} + V_ {i_ {1} i_ {2}} ^ {\ альфа} (x, u, w) {\ frac {\ partial} {\ partial w_ {i_ {1} i_ {2}} ^ {\ alpha}}} + \ cdots + V_ {i_ {1} \ cdots i_ {r}} ^ {\ alpha} (x, u, w) {\ frac {\ partial} {\ partial w_ {i_ {1} \ cdots i_ {r}} ^ {\ alpha}}}}

с координатами

(x, u, w, vi α, vi 1 i 2 α, ⋯, vi 1 ⋯ ir α), {\ displaystyle \ left (x, u, w, v_ {i} ^ { \ alpha}, v_ {i_ {1} i_ {2}} ^ {\ alpha}, \ cdots, v_ {i_ {1} \ cdots i_ {r}} ^ {\ alpha} \ right),}

{\ displaystyle \ left (x, u, w, v_ {i} ^ {\ alpha}, v_ {i_ {1} i_ {2}} ^ {\ alpha}, \ cdots, v_ {i_ {1} \ cdots i_ {r}} ^ {\ alpha} \ right),}

с элементом в волокне $Т xuw (J r π) {\ displaystyle T_ {xuw} (J ^ {r} \ pi)}$ ${\ displaystyle T_ {xuw} (J ^ {r} \ pi)}$ из TJ (π) над (x, u, w) ∈ J (π), называемый касательным вектором в TJ (π) . Здесь

vi α, vi 1 я 2 α, ⋯, vi 1 ⋯ ir α {\ displaystyle v_ {i} ^ {\ alpha}, v_ {i_ {1} i_ {2}} ^ {\ alpha}, \ cdots, v_ {i_ {1} \ cdots i_ {r}} ^ {\ alpha}}

{\ displaystyle v_ {i} ^ {\ alpha}, v_ {i_ {1} i_ {2}} ^ {\ alpha}, \ cdots, v_ {i_ { 1)} \ cdots i_ {r}} ^ {\ alpha}}

- функции с действительными значениями на J (π). Раздел

{Ψ: J r (π) → TJ r (π) (x, u, w) ↦ Ψ (u, w) = V {\ displaystyle {\ begin {cases} \ Psi: J ^ {r } (\ pi) \ to TJ ^ {r} (\ pi) \\ (x, u, w) \ mapsto \ Psi (u, w) = V \ end {cases}}}

{\ displaystyle {\ begin {cases}) \ Psi: J ^ {r} (\ пи) \ к TJ ^ {r} (\ pi) \\ (x, u, w) \ mapsto \ Psi (u, w) = V \ end {cases}}}

равно Векторное поле на J (π), и мы говорим $Ψ ∈ Γ (T (J r π)). {\ displaystyle \ Psi \ in \ Gamma (T (J ^ {r} \ pi)).}$ ${\ displaystyle \ Psi \ in \ Gamma (T (J ^ {r} \ pi)).}$

Уравнения в частных производных

Пусть (E, π, M) - пучок волокон. Уравнение в частных производных r-го порядка на π является замкнутым вложенным подмногообразием S многообразия струй J (π). Решение - это локальное сечение σ ∈ Γ W (π), удовлетворяющее $jpr σ ∈ S {\ displaystyle j_ {p} ^ {r} \ sigma \ in S}$ ${\ Displaystyle j_ {p} ^ {r} \ sigma \ in S}$ , для всех p в M.

Рассмотрим пример уравнения в частных производных первого порядка.

Пример

Пусть π будет тривиальным набором (R× R, pr 1, R) с глобальными координатами (x, x, u). Тогда карта F: J (π) → R определяется как

F = u 1 1 u 2 1-2 x 2 u 1 {\ displaystyle F = u_ {1} ^ {1} u_ { 2} ^ {1} -2x ^ {2} u ^ {1}}

{\ displaystyle F = u_ {1} ^ {1} u_ {2} ^ {1} -2x ^ {2} u ^ {1}}

дает начало дифференциальному уравнению

S = {jp 1 σ ∈ J 1 π: (u 1 1 u 2 1 - 2 Икс 2 U 1) (jp 1 σ) знак равно 0} {\ displaystyle S = \ left \ {j_ {p} ^ {1} \ sigma \ in J ^ {1} \ pi \: \ left (u_ {1} ^ {1} u_ {2} ^ {1} -2x ^ {2} u ^ {1} \ right) \ left (j_ {p} ^ {1} \ sigma \ right) = 0 \ right \} }

{\ displaystyle S = \ left \ {j_ {p} ^ {1} \ sigma \ in J ^ {1} \ pi \: \ left (u_ {1} ^ {1} u_ {2} ^ {1} -2x ^ {2} u ^ {1} \ right) \ left (j_ {p} ^ {1} \ sigma \ right) = 0 \ right \}}

который можно записать как

∂ σ ∂ x 1 ∂ σ ∂ x 2 - 2 x 2 σ = 0. {\ displaystyle {\ frac {\ partial \ sigma} {\ partial x ^ {1}} } {\ frac {\ partial \ sigma} {\ partial x ^ {2}}} - 2x ^ {2} \ sigma = 0.}

{\ displaystyle {\ frac {\ partial \ sigma) } {\ partial x ^ {1}}} {\ frac {\ partial \ sigma} {\ partial x ^ {2}}} - 2x ^ {2} \ sigma = 0.}

Частное

{σ: R 2 → R 2 × R σ (п 1, п 2) знак равно (п 1, п 2, п 1 (п 2) 2) {\ Displaystyle {\ begin {cases} \ sigma: \ mathbf {R} ^ {2} \ to \ mathbf { R} ^ {2} \ times \ mathbf {R} \\\ sigma (p_ {1}, p_ {2}) = \ left (p ^ {1}, p ^ {2}, p ^ {1} ( p ^ { 2}) ^ {2} \ right) \ end {ases}}}

{\ displaystyle {\ begin {cases} \ sigma: \ mathbf {R} ^ {2} \ to \ mathbf {R} ^ {2} \ times \ mathbf {R} \\\ sigma (p_ {1}, p_ {2}) = \ left (p ^ {1}, p ^ {2}, p ^ {1} (p ^ { 2}) ^ {2} \ right) \ end {case}}}

имеет первое продолжение, рав ное

j 1 σ (p 1, p 2) = (p 1, p 2, p 1 (п 2) 2, (п 2) 2, 2 п 1 п 2) {\ displaystyle j ^ {1} \ sigma \ left (p_ {1}, p_ {2} \ right) = \ left (p ^ {1}, p ^ {2}, p ^ {1} \ left (p ^ {2} \ right) ^ {2}, \ left (p ^ {2} \ right) ^ {2}, 2p ^ {1} p ^ {2} \ right)}

{\ displaystyle j ^ {1} \ sigma \ left (p_ {1}, p_ {2} \ right) = \ left (p ^ {1}, p ^ {2}, p ^ {1} \ left (p ^ {2} \ right) ^ {2}, \ left (p ^ {2} \ right) ^ {2}, 2p ^ {1} p ^ {2} \ right)}

и является решением этого дифференциального уравнения, поскольку

(u 1 1 u 2 1 - 2 x 2 u 1) ( jp 1 σ) = u 1 1 (jp 1 σ) u 2 1 (jp 1 σ) - 2 x 2 (jp 1 σ) u 1 (jp 1 σ) = (p 2) 2 ⋅ 2 p 1 p 2 - 2 ⋅ п 2 ⋅ п 1 (п 2) 2 знак равно 2 п 1 (п 2) 3 - 2 п 1 (п 2) 3 = 0 {\ displaystyle {\ begin {align} \ left (u_ {1} ^ { 1} u_ {2} ^ {1} -2x ^ {2} u ^ {1} \ right) \ left (j_ {p} ^ {1} \ sigma \ right) = u_ {1} ^ {1} \ left (j_ {p} ^ {1} \ sigma \ right) u_ {2} ^ {1} \ left (j_ {p} ^ {1} \ sigma \ right) -2x ^ {2} \ left (j_ {p} ^ {1} \ sigma \ right) u ^ {1} \ left (j_ {p} ^ {1} \ sigma \ right) \\ = \ left (p ^ {2} \ right) ^ { 2} \ cdot 2p ^ {1} p ^ {2} -2 \ cdot p ^ {2} \ cdot p ^ {1} \ left (p ^ {2} \ right) ^ {2} \\ = 2p ^ { 1} \ left (p ^ {2} \ right) ^ {3} -2p ^ {1} \ left (p ^ {2} \ right) ^ {3} \\ = 0 \ end {выровнено} }}

{\ displaystyle {\ begin {align} \ left (u_ {1} ^ {1} u_ {2} ^ {1} -2x ^ {2} u ^ {1} \ right) \ left (j_ {p} ^ {1} \ sigma \ справа) = u_ {1} ^ {1} \ left (j_ {p} ^ {1} \ sigma \ right) u_ {2} ^ {1} \ left (j_ {p} ^ {1} \ sigma \ справа) -2x ^ {2} \ left (j_ {p} ^ {1} \ sigma \ right) u ^ {1} \ left (j_ {p} ^ {1} \ sigma \ right) \\ = \ влево (p ^ {2} \ right) ^ {2} \ cdot 2p ^ {1} p ^ {2} -2 \ cdot p ^ {2} \ cdot p ^ {1} \ left (p ^ {2} \ right) ^ {2} \\ = 2p ^ {1} \ left (p ^ {2} \ right) ^ {3} -2p ^ {1} \ left (p ^ {2} \ right) ^ {3} \\ = 0 \ end {align}}}

и поэтому $jp 1 σ ∈ S {\ displaystyle j_ {p} ^ {1} \ sigma \ in S}$ ${\ displaystyle j_ {p} ^ {1} \ sigma \ in S}$ для каждого p ∈ R.

удлинение струи

Локальный диффеоморфизм ψ: J (π) → J (π) определяет контактное преобразование порядка r, если он сохраняет контактный идеал, что означает, что если θ - любая контактная форма на J (π), то ψ * θ также является контактной формой.

Поток, генерируемый векторным полем V на пространстве джетов J (π), образует однопараметрическую группу контактных преобразований тогда и только тогда, когда производная Ли $LV r ( θ) {\ displaystyle {\ mathcal {L}} _ {V ^ {r}} (\ theta)}$ ${\ displaystyle {\ mathcal {L}}) _ {V ^ {r}} (\ theta)}$ любой контактной формы θ сохраняет контактный идеал.

Начнем с дела первого порядка. Рассмотрим общее векторное поле V на J (π), задаваемое формулой

V 1 = def ρ i (xi, u α, u I α) ∂ ∂ xi + ϕ α (xi, u α, u I α) ∂ ∂ u α + χ i α (xi, u α, u I α) ∂ ∂ ui α. {\ displaystyle V ^ {1} \ {\ stackrel {\ mathrm {def}} {=}} \ \ rho ^ {i} \ left (x ^ {i}, u ^ {\ alpha}, u_ {I} ^ {\ alpha} \ right) {\ frac {\ partial} {\ partial x ^ {i}}} + \ phi ^ {\ alpha} \ left (x ^ {i}, u ^ {\ alpha}, u_ {I} ^ {\ alpha} \ right) {\ frac {\ partial} {\ partial u ^ {\ alpha}}} + \ chi _ {i} ^ {\ alpha} \ left (x ^ {i}, u ^ {\ alpha}, u_ {I} ^ {\ alpha} \ right) {\ frac {\ partial} {\ partial u_ {i} ^ {\ alpha}}}.}

{\ displaystyle V ^ {1} \ {\ stackrel {\ mathrm {def}} {=}} \ \ rho ^ {i} \ left (x ^ {i}, u ^ {\ alpha}, u_ {I} ^ {\ alpha} \ right) {\ frac {\ partial} {\ partial x ^ {i}}} + \ phi ^ {\ alpha} \ left (x ^ {i}, u ^ {\ alpha}, u_ {I} ^ {\ alpha} \ right) {\ frac {\ partial} {\ partial u ^ {\ alpha}}} + \ chi _ {i} ^ {\ alpha} \ left (x ^ {i}, u ^ {\ alpha}, u_ {I} ^ {\ alpha} \ right) {\ frac {\ partial} {\ partial u_ {i} ^ {\ alpha}}}. }

Теперь применим $LV 1 {\ displaystyle {\ mathcal {L}} _ {V ^ {1}}}$ ${\ displaystyle {\ mathcal {L}} _ {V ^ {1}}}$ к основным контактным формам $θ 0 α = du α - ui α dxi, {\ displaystyle \ theta _ {0} ^ {\ alpha} = du ^ {\ alpha} -u_ {i} ^ {\ alpha} dx ^ {i},}$ ${\ displaystyle \ theta _ {0} ^ {\ alpha} = du ^ {\ alpha} -u_ {i} ^ {\ alpha} dx ^ {i},}$ и развернуть внешнюю производную функций в терминах их координат, чтобы получить:

LV 1 (θ 0 α) = LV 1 (du α - ui α dxi) = LV 1 du α - (LV 1 ui α) dxi - ui α (LV 1 dxi) = d (V 1 u α) - V 1 ui α dxi - ui α d (V 1 xi) = d ϕ α - χ i α dxi - ui α d ρ i = ∂ ϕ α ∂ xidxi + ∂ ϕ α ∂ ukduk + ∂ ϕ α ∂ uikdui k - χ i α dxi - ui α [∂ ρ i ∂ xmdxm + ∂ ρ i ∂ ukduk + ∂ ρ i ∂ umkdumk] = ∂ ϕ α ∂ xidxi + ∂ ϕ α ∂ uk (θ k + uikdxi) + ∂ ϕ α ∂ uikduik - χ i α dxi - ul α [∂ ρ l ∂ xidxi + ∂ ρ l ∂ uk (θ k + uikdxi) + ∂ ρ l ∂ uikduik] = [∂ ϕ α ∂ xi + ∂ ϕ α ∂ ukuik - ul α (∂ ρ l ∂ xi + ∂ ρ l ∂ ukuik) - χ i α] dxi + [∂ ϕ α ∂ uik - ul α ∂ ρ l ∂ uik] duik + (∂ ϕ α ∂ uk - ul α ∂ ρ l ∂ uk) θ K {\ displaystyle {\ begin {align} { \ mathcal {L}} _ {V ^ {1}} \ left (\ theta _ {0} ^ {\ alpha} \ right) = {\ mathcal {L}} _ {V ^ {1}} \ left (du ^ {\ alpha} -u_ {i} ^ {\ alpha} dx ^ {i} \ right) \\ = {\ mathcal {L}} _ {V ^ {1}} du ^ {\ alpha} - \ left ({\ mathcal {L}} _ {V ^ {1}} u_ {i} ^ {\ alpha} \ right) dx ^ {i} -u_ {i} ^ {\ alpha} \ left ({ \ mathcal {L}} _ {V ^ {1}} dx ^ {i} \ right) \\ = d \ left (V ^ {1} u ^ {\ alpha} \ right) -V ^ {1} u_ {i} ^ {\ alpha} dx ^ {i} -u_ {i} ^ {\ alpha} d \ left (V ^ {1} x ^ {i} \ right) \\ = d \ phi ^ { \ alpha} - \ chi _ {i} ^ {\ alpha} dx ^ {i} -u_ {i} ^ {\ alpha} d \ rho ^ {i} \\ = {\ frac {\ partial \ phi ^ {\ alpha}} {\ partial x ^ {i}}} dx ^ {i} + {\ frac {\ partial \ phi ^ {\ alpha}} {\ pa rtial u ^ {k}}} du ^ {k} + {\ frac {\ partial \ phi ^ {\ alpha}} {\ partial u_ {i} ^ {k}}} du_ {i} ^ {k} - \ chi _ {i} ^ {\ alpha} dx ^ {i} -u_ {i} ^ {\ alpha} \ left [{\ frac {\ partial \ rho ^ {i}} {\ partial x ^ {m} }} dx ^ {m} + {\ frac {\ partial \ rho ^ {i}} {\ partial u ^ {k}}} du ^ {k} + {\ frac {\ partial \ rho ^ {i}} {\ partial u_ {m} ^ {k}}} du_ {m} ^ {k} \ right] \\ = {\ frac {\ partial \ phi ^ {\ alpha}} {\ partial x ^ {i} }} dx ^ {i} + {\ frac {\ partial \ phi ^ {\ alpha}} {\ partial u ^ {k}}} \ left (\ theta ^ {k} + u_ {i} ^ {k} dx ^ {i} \ right) + {\ frac {\ partial \ phi ^ {\ alpha}} {\ partial u_ {i} ^ {k}}} du_ {i} ^ {k} - \ chi _ {i } ^ {\ alpha} dx ^ {i} -u_ {l} ^ {\ alpha} \ left [{\ frac {\ partial \ rho ^ {l}} {\ partial x ^ {i}}} dx ^ { i} + {\ frac {\ partial \ rho ^ {l}} {\ partial u ^ {k}}} \ left (\ theta ^ {k} + u_ {i} ^ {k} dx ^ {i} \ справа) + {\ frac {\ partial \ rho ^ {l}} {\ partial u_ {i} ^ {k}}} du_ {i} ^ {k} \ right] \\ = \ left [{\ frac {\ partial \ phi ^ {\ alpha}} {\ partial x ^ {i}}} + {\ frac {\ partial \ phi ^ {\ alpha}} {\ partial u ^ {k}}} u_ {i} ^ {k} -u_ {l} ^ {\ alpha} \ left ({\ frac {\ partial \ rho ^ {l}} {\ partial x ^ {i}}} + {\ frac {\ partial \ rho ^ {l}} {\ partial u ^ {k}}} u_ {i} ^ {k} \ right) - \ chi _ {i} ^ {\ alpha} \ right] dx ^ {i} + \ left [{\ frac {\ partial \ phi ^ {\ alpha}} {\ partial u_ { i} ^ {k}}} - u_ {l} ^ {\ alpha} {\ frac {\ partial \ rho ^ {l}} {\ partial u_ {i} ^ {k}}} \ right] du_ {i } ^ {k} + \ left ({\ frac {\ partial \ phi ^ {\ alpha}} {\ partial u ^ {k}}} - u_ {l} ^ {\ alpha} {\ frac {\ partial \ rho ^ {l}} {\ partial u ^ {k}}} \ right) \ theta ^ {k} \ end {align}}}

{\ displaystyle {\ begin {align} {\ mathcal {L}} _ {V ^ { 1}} \ left (\ theta _ {0} ^ {\ alpha} \ right) = {\ mathcal {L}} _ {V ^ {1}} \ left (du ^ {\ alpha} -u_ {i } ^ {\ alpha} dx ^ {i} \ right) \\ = {\ mathcal {L}} _ {V ^ {1}} du ^ {\ alpha} - \ left ({\ mathcal {L}} _ {V ^ {1}} u_ {i} ^ {\ alpha} \ right) dx ^ {i} -u_ {i} ^ {\ alpha} \ left ({\ mathcal {L}} _ {V ^ {1}} dx ^ {i} \ right) \\ = d \ left (V ^ {1} u ^ {\ alpha} \ справа) -V ^ {1} u_ {i} ^ {\ alpha} dx ^ {i} -u_ {i} ^ {\ alpha} d \ left (V ^ {1} x ^ {i} \ right) \ \ = d \ phi ^ {\ alpha} - \ chi _ {i} ^ {\ alpha} dx ^ {i } -u_ {i} ^ {\ alpha} d \ rho ^ {i} \\ = {\ frac {\ partial \ phi ^ {\ alpha}} {\ partial x ^ {i}}} dx ^ {i } + {\ frac {\ partial \ phi ^ {\ alpha}} {\ partial u ^ {k}}} du ^ {k} + {\ frac {\ partial \ phi ^ {\ alpha}} {\ partial u_ {i} ^ {k}}} du_ {i} ^ {k} - \ chi _ {i} ^ {\ alpha} dx ^ {i} -u_ {i} ^ {\ alpha} \ left [{\ frac {\ partial \ rho ^ {i}} {\ partial x ^ {m}}} dx ^ {m} + {\ frac {\ partial \ rho ^ {i}} {\ partial u ^ {k}}} du ^ {k} + {\ frac {\ partial \ rho ^ {i}} {\ partial u_ {m} ^ {k}}} du_ {m} ^ {k} \ справа] \\ = {\ frac { \ partial \ phi ^ {\ alpha}} {\ частичный x ^ {i}}} dx ^ {i} + {\ frac {\ partial \ phi ^ {\ alpha}} {\ partial u ^ {k}}} \ left (\ theta ^ {k} + u_ { i} ^ {k} dx ^ {i} \ right) + {\ frac {\ partial \ phi ^ {\ alpha}} {\ partial u_ {i} ^ {k}}} du_ {i} ^ {k} - \ chi _ {i} ^ {\ alpha} dx ^ {i} -u_ {l} ^ {\ alpha} \ left [{\ frac {\ partial \ rho ^ {l}} {\ partial x ^ {i }}} dx ^ {i} + {\ frac {\ partial \ rho ^ {l}} {\ partial u ^ {k}}} \ left (\ theta ^ {k} + u_ {i} ^ {k} dx ^ {i} \ right) + {\ frac {\ partial \ rho ^ {l}} {\ partial u_ {i} ^ {k}}} du_ {i} ^ {k} \ right] \\ = \ left [{\ frac {\ partial \ phi ^ {\ alpha}} {\ partial x ^ {i}}} + {\ frac {\ partial \ phi ^ {\ alpha}} {\ partial u ^ {k} }} u_ {i} ^ {k} -u_ {l} ^ {\ alpha} \ left ({\ frac {\ частичный \ rho ^ {l}} {\ partial x ^ {i}}} + {\ frac {\ partial \ rho ^ {l}} {\ partial u ^ {k}}} u_ {i} ^ {k} \ right) - \ chi _ {i} ^ {\ alpha} \ right] dx ^ {i } + \ left [{\ frac {\ partial \ phi ^ {\ alpha}} {\ partial u_ {i} ^ {k}}} - u_ {l} ^ {\ alpha} {\ frac {\ partial \ rho ^ {l}} {\ partial u_ {i} ^ {k}}} \ right] du_ {i} ^ {k} + \ left ({\ frac {\ partial \ phi ^ {\ alpha }} {\ частичное u ^ {k}}} - u_ {l} ^ {\ alpha} {\ frac {\ partial \ rho ^ {l}} {\ partial u ^ {k}}} \ right) \ theta ^ {k} \ end {align}}}

Следовательно, V определяет преобразование контакта тогда и только тогда, когда коэффициенты при dx и $duik {\ displaystyle du_ {i} ^ {k}}$ ${\ displaystyle du_ {i} ^ {k}}$ в формуле исчезают. Последние требования подразумевают условия контакта

∂ ϕ α ∂ uik - ul α ∂ ρ l ∂ uik = 0 {\ displaystyle {\ frac {\ partial \ phi ^ {\ alpha}} {\ partial u_ { i} ^ {k}}} - u_ {l} ^ {\ alpha} {\ frac {\ partial \ rho ^ {l}} {\ partial u_ {i} ^ {k}}} = 0}

{\ displaystyle {\ frac {\ partial \ phi ^ {\ alpha}} {\ partial u_ {i} ^ {k}}} - u_ {l} ^ {\ alpha} {\ frac {\ partial \ rho ^ {l}} {\ partial u_ {i} ^ {k}}} = 0}

Первые требования предусматривают явные формулы для коэффициентов членов первой производной в V:

χ i α = D ^ i ϕ α - ul α (D ^ i ρ l) {\ displaystyle \ chi _ {i} ^ { \ alpha} = {\ widehat {D}} _ {i} \ phi ^ {\ alpha} -u_ {l} ^ {\ alpha} \ left ({\ widehat {D}} _ {i} \ rho ^ { l} \ right)}

{\ displaystyle \ chi _ {i} ^ {\ alpha} = {\ widehat {D}} _ {i} \ phi ^ {\ alpha} -u_ {l} ^ {\ alpha} \ left ({\ widehat {D}} _ {я} \ rho ^ {l} \ right)}

где

D ^ i = ∂ ∂ xi + uik ∂ ∂ uk {\ displaystyle {\ widehat {D}} _ {i} = {\ frac {\ partial} {\ partial x ^ {i}}} + u_ {i} ^ {k} {\ frac {\ partial} {\ partial u ^ {k}}}}

{\ displaystyle {\ widehat {D}} _ {i} = {\ frac {\ partial} {\ partial x ^ {i}}} + u_ {i} ^ {k} {\ frac {\ partial} {\ partial u ^ {k}}}}

обозначает усечение нулевого порядка полной производной D i.

Таким образом, условия контакта однозначно предписывают продолжение любого точечного или контактного векторного поля. То есть, если $LV r {\ displaystyle {\ mathcal {L}} _ {V ^ {r}}}$ ${\ displaystyle {\ mathcal {L}} _ {V ^ {r}}}$ удовлетворяет этим уравнениям, V называется r-м продолжением V в векторное поле на J (π) .

Эти результаты лучше всего понятны в применении к конкретному примеру. Поэтому рассмотрим следующее.

Пример

Рассмотрим случай (E, π, M), где E ≅ R и M ≃ R . Тогда (J (π), π, E) определяет первое расслоение струй и может быть скоординировано с помощью (x, u, u 1), где

x (jp 1 σ) = x (p) = xu (jp 1 σ) = u (σ (p)) = u (σ (x)) = σ (x) u 1 (jp 1 σ) = ∂ σ ∂ x | п знак равно σ ˙ (Икс) {\ Displaystyle {\ begin {align} х (j_ {p} ^ {1} \ sigma) = x (p) = x \\ u (j_ {p} ^ {1} \ sigma) = u (\ sigma (p)) = u (\ sigma (x)) = \ sigma (x) \\ u_ {1} (j_ {p} ^ {1} \ sigma) = \ left. {\ frac {\ partial \ sigma} {\ partial x}} \ right | _ {p} = {\ dot {\ sigma}} (x) \ end {align}}}

{\ displaystyle {\ begin {align} x (j_ {p } ^ {1 } \ sigma) = x (p) = x \\ u (j_ {p} ^ {1} \ sigma) = u (\ sigma (p)) = u (\ sigma (x)) = \ sigma ( x) \\ u_ {1} (j_ {p} ^ {1} \ sigma) = \ left. {\ гидроразрыв {\ partial \ sigma} {\ partial x}} \ right | _ {p} = {\ dot {\ sigma}} (x) \ end {align}}}

для всех p ∈ M и σ в Γ p (π). Контактная форма на J (π) имеет вид

θ = du - u 1 dx {\ displaystyle \ theta = du-u_ {1} dx}

{\ displaystyle \ theta = du-u_ {1} dx}

Рассмотрим вектор V на E, имеющий форму

V = x ∂ ∂ u - u ∂ ∂ x {\ displaystyle V = x {\ frac {\ partial} {\ partial u}} - u {\ frac {\ partial} {\ partial x}}}

{\ displaystyle V = x {\ frac {\ partial} {\ partial u}} - u {\ frac {\ partial} {\ partial x}}}

Тогда первое продолжение этого векторного поля на J (π) будет

V 1 = V + Z = x ∂ ∂ u - u ∂ ∂ x + Z = x ∂ ∂ u - u ∂ ∂ x + ρ (x, u, u 1) ∂ ∂ U 1 {\ displaystyle {\ begin {align} V ^ {1} = V + Z \\ = x {\ frac {\ partial} {\ partial u}} - u { \ frac {\ partial} {\ partial x}} + Z \\ = x {\ frac {\ partial} {\ partial u}} - u {\ frac {\ partial} {\ partial x}} + \ rho (x, u, u_ {1}) {\ frac {\ partial} {\ partial u_ {1}}} \ end {align}}}

{\ displaystyle {\ begin {выровнено} V ^ {1} = V + Z \\ = x {\ frac {\ partial} {\ partial u}} - u {\ frac {\ partial} {\ partial x}} + Z \\ = x {\ frac {\ partial } {\ partial u}} - u {\ frac {\ partial} {\ partial x}} + \ rho (x, u, u_ {1}) {\ frac {\ partial} {\ partial u_ {1}} } \ конец {выровнено}}

Если мы теперь возьмем производную Ли контактной формы относительно это продолженное векторное поле, $LV 1 (θ), {\ displaystyle {\ mathcal {L}} _ {V ^ {1}} (\ theta),}$ ${\ displaystyle {\ mathcal {L}} _ {V ^ {1}} (\ theta),}$ мы получаем

LV 1 (θ) = LV 1 (du - u 1 dx) = LV 1 du - (LV 1 u 1) dx - u 1 (LV 1 dx) = d (V 1 u) - V 1 u 1 dx - u 1 d (V 1 x) = dx - ρ ( x, u, u 1) d x + u 1 d u = ( 1 − ρ ( x, u, u 1)) d x + u 1 d u = [ 1 − ρ ( x, u, u 1) ] d x + u 1 ( θ + u 1 d x) d u = θ + u 1 d x = [ 1 + u 1 u 1 − ρ ( x, u, u 1) ] d x + u 1 θ {\displaystyle {\begin{aligned}{\mathcal {L}}_{V^{1}}(\theta)={\mathcal {L}}_{V^{1}}(du-u_{1}dx)\\={\mathcal {L}}_{V^{1}}du-\left({\mathcal {L}}_{V^{1}}u_{1}\right)dx-u_{1}\left({\mathcal {L}}_{V^{1}}dx\right)\\=d\left(V^{1}u\right)-V^{1}u_{1}dx-u_{1}d\left(V^{1}x\right)\\=dx-\rho (x,u,u_{1})dx+u_{1}du\\=(1-\rho (x,u,u_{1}))dx+u_{1}du\\=[1-\rho (x,u,u_{1})]dx+u_{1}(\theta +u_{1}dx)du=\theta +u_{1}dx\\=[1+u_{1}u_{1}-\rho (x,u,u_{1})]dx+u_{1}\theta \end{aligned}}}

{\ displaystyle {\ begin {align} {\ mathcal {L}} _ {V ^ {1}} (\ theta) = {\ mathcal {L}} _ {V ^ {1}} (du-u_ {1} dx) \\ = {\ mathcal {L}} _ {V ^{1}} du- \ left ({\ mathcal {L}} _ {V ^ {1}} u_ {1} \ right) dx-u_ {1} \ left ({\ mathcal {L}} _ {V ^ {1}} dx \ right) \\ = d \ left (V ^ {1} u \ right) -V ^ {1} u_ {1} dx-u_ {1} d \ left (V ^ {1 } x \ right) \\ = dx- \ rho (x, u, u_ {1}) dx + u_ {1} du \\ = (1- \ rho (x, u, u_ {1})) dx + u_ {1} du \\ = [1- \ rho (x, u, u_ {1})] dx + u_ {1} (\ theta + u_ {1} dx) du = \ theta + u_ {1} dx \\ = [1 + u_ {1} u_ {1} - \ rho (x, u, u_ {1})] dx + u_ {1} \ theta \ end {выровнено}}}

Hence, for preservation of the contact ideal, we require

1 + u 1 u 1 − ρ ( x, u, u 1) = 0 ⇔ ρ ( x, u, u 1) = 1 + u 1 u 1. {\displaystyle 1+u_{1}u_{1}-\rho (x,u,u_{1})=0\quad \Leftrightarrow \quad \rho (x,u,u_{1})=1+u_{1}u_{1}.}

{\ displaystyle 1 + u_ {1} u_ {1) } - \ rho (x, u, u_ {1}) = 0 \ quad \ Leftrightarrow \ quad \ rho (x, u, u_ {1}) = 1 + u_ {1} u_ {1}.}

And so the first prolongation of V to a vector field on J(π) is

V 1 = x ∂ ∂ u − u ∂ ∂ x + ( 1 + u 1 u 1) ∂ ∂ u 1. {\displaystyle V^{1}=x{\frac {\partial }{\partial u}}-u{\frac {\partial }{\partial x}}+(1+u_{1}u_{1}){\frac {\partial }{\partial u_{1}}}.}

{\ displaystyle V ^ {1} = x {\ frac {\ partial} {\ partial u}} -u {\ frac {\ partial} {\ partial x}} + (1 + u_ {1} u_ {1}) {\ frac {\ partial} {\ partial u_ {1}}}.}

Let us also calculate the second prolongation of V to a vector field on J(π). We have ${ x, u, u 1, u 2 } {\displaystyle \{x,u,u_{1},u_{2}\}}$ ${\ displaystyle \ {x, u, u_ {1}, u_ {2} \}}$ as coordinates on J(π). Hence, the prolonged vector has the form

V 2 = x ∂ ∂ u − u ∂ ∂ x + ρ ( x, u, u 1, u 2) ∂ ∂ u 1 + ϕ ( x, u, u 1, u 2) ∂ ∂ u 2. {\displaystyle V^{2}=x{\frac {\partial }{\partial u}}-u{\frac {\partial }{\partial x}}+\rho (x,u,u_{1},u_{2}){\frac {\partial }{\partial u_{1}}}+\phi (x,u,u_{1},u_{2}){\frac {\partial }{\partial u_{2}}}.}

{\ displaystyle V ^ {2} = x {\ frac {\ partial} {\ partial u}} - u {\ frac {\ partial} {\ partial x}} + \ rho (x, u, u_ {1}, u_ {2}) {\ frac {\ partial} {\ partial u_ {1}}} + \ phi (x, u, u_ {1}, u_ {2}) {\ frac { \ partial} {\ partial u_ {2}}}.}

The contact forms are

θ = d u − u 1 d x θ 1 = d u 1 − u 2 d x {\displaystyle {\begin{aligned}\theta =du-u_{1}dx\\\theta _{1}=du_{1}-u_{2}dx\end{aligned}}}

{\ Displaystyle {\ begin {align} \ theta = du-u_ {1} dx \\\ theta _ {1} = du_ {1} -u_ {2} dx \ end {выровнено}}}

To preserve the contact ideal, we require

L V 2 ( θ) = 0 L V 2 ( θ 1) = 0 {\displaystyle {\begin{aligned}{\mathcal {L}}_{V^{2}}(\theta)=0\\{\mathcal {L}}_{V^{2}}(\theta _{1})=0\end{aligned}}}

{\ displaystyle {\ begin {выравнивается} {\ mathcal {L}} _ {V ^ {2}} (\ theta) = 0 \\ {\ mathcal {L}} _ {V ^ {2}} (\ theta _ { 1}) = 0 \ конец {выровнен}}}

Now, θ has no u2dependency. Hence, from this equation we will pick вверх по формуле для ρ, которая обязательно будет тем же результатом, что мы нашли для V. Следовательно, задача аналогична продолжению векторного поля V до J (π). Другими словами, мы можем сгенерировать r-е продолжение векторного поля, рекурсивно применяя производную Ли контактных форм по отношению к продолженным векторным полям r раз. Итак, мы имеем

ρ (x, u, u 1) = 1 + u 1 u 1 {\ displaystyle \ rho (x, u, u_ {1}) = 1 + u_ {1} u_ {1}}

{\ displaystyle \ rho (x, u, u_ {1}) = 1 + u_ {1} u_ {1}}

и поэтому

V 2 = V 1 + ϕ (x, u, u 1, u 2) ∂ ∂ u 2 = x ∂ ∂ u - u ∂ ∂ x + (1 + u 1 u 1) ∂ ∂ U 1 + ϕ (x, u, u 1, u 2) ∂ ∂ u 2 {\ displaystyle {\ begin {align} V ^ {2} = V ^ {1} + \ phi (x, u, u_ {1}, u_ {2}) {\ frac {\ partial} {\ partial u_ {2}}} \\ = x {\ frac {\ partial} {\ partial u}} - u {\ frac {\ partial} {\ partial x}} + (1 + u_ {1} u_ {1}) {\ frac {\ partial} {\ partial u_ {1}}} + \ phi (x, u, u_ {1}, u_ {2}) {\ frac {\ partial} {\ partial u_ {2}}} \ end {align}}}

{\ displaystyle {\ begin {align} V ^ {2} = V ^ {1} + \ phi (x, u, u_ {1}, u_ {2}) {\ frac {\ partial} {\ partial u_ {2}}} \\ = x {\ frac {\ partial } {\ partial u}} -u {\ frac {\ partial} {\ partial x}} + (1 + u_ {1} u_ {1}) {\ frac {\ partial} {\ partial u_ {1}} } + \ phi (x, u, u_ {1}, u_ {2}) {\ frac {\ partial} {\ partial u_ {2}}} \ end {выравнивается}}}

Следовательно, производная Ли второй контактной формы по V равна

LV 2 (θ 1) = LV 2 (du 1 - u 2 dx) = LV 2 du 1 - (LV 2 u 2) dx - u 2 (LV 2 dx) = d (V 2 u 1) - V 2 u 2 dx - u 2 d (V 2 x) = d (1 + u 1 u 1) - ϕ (x, u, u 1, u 2) dx + u 2 du = 2 u 1 du 1 - ϕ (x, u, u 1, u 2) dx + u 2 du = 2 u 1 du 1 - ϕ (x, u, u 1, u 2) dx + u 2 (θ + u 1 dx) du = θ + u 1 dx = 2 u 1 (θ 1 + u 2 dx) - ϕ (x, u, u 1, u 2) dx + u 2 (θ + u 1 dx) du 1 = θ 1 + u 2 dx = [3 u 1 u 2 - ϕ (x, u, u 1, u 2)] dx + u 2 θ + 2 U 1 θ 1 {\ Displaystyle {\ begin {align} {\ mathcal {L}} _ {V ^ {2}} (\ theta _ {1}) = {\ mathcal {L}} _ {V ^ {2}} (du_ {1} -u_ {2} dx) \\ = {\ mathcal {L}} _ {V ^ {2}} du_ {1} - \ left ({\ mathcal { L}} _ {V ^ {2}} u_ {2} \ right) dx-u_ {2} \ left ({\ mathcal {L}} _ {V ^ {2}} dx \ right) \\ = d (V ^ {2} u_ {1}) - V ^ {2} u_ {2} dx-u_ {2} d (V ^ {2} x) \\ = d (1 + u_ {1} u_ {1}) - \ phi (x, u, u_ {1}, u_ {2}) dx + u_ {2} du \\ = 2u_ {1} du_ {1} - \ phi (x, u, u_ {1}, u_ {2}) dx + u_ {2} du \\ = 2u_ {1} du_ {1} - \ phi (x, u, u_ {1}, u_ {2}) dx + u_ { 2} (\ theta + u_ {1} dx) du = \ theta + u_ {1} dx \\ = 2u_ {1} (\ theta _ {1} + u_ {2} dx) - \ phi (x, u, u_ {1}, u_ {2}) dx + u_ {2} (\ theta + u_ {1} dx) du_ {1} = \ theta _ {1} + u_ {2} dx \\ = [3u_ {1} u_ {2} - \ phi (x, u, u_ {1}, u_ {2})] dx + u_ {2} \ theta + 2u_ {1} \ theta _ {1} \ end { выровнено}}}

{\ displaystyle {\ begin {align} {\ mathcal {L}} _ {V ^ {2}} (\ theta _ {1}) = {\ mathcal {L}} _ {V ^ {2}} (du_ {1} -u_ {2} dx) \\ = {\ mathcal {L}} _ {V ^ {2}} du_ {1} - \ left ({\ mathcal {L}} _ {V ^ {2}} u_ {2} \ right) dx-u_ {2} \ left ({\ mathcal {L}} _ {V ^ {2}} dx \ right) \\ = d (V ^ {2} u_ {1}) - V ^ {2} u_ {2} dx-u_ {2} d (V ^ {2} x) \\ = d (1 + u_ {1} u_ {1}) - \ phi (x, u, u_ {1}, u_ {2}) dx + u_ {2} du \\ = 2u_ {1} du_ {1} - \ phi (x, u, u_ {1}, u_ {2}) dx + u_ {2} du \\ = 2u_ {1} du_ {1} - \ phi (x, u, u_ {1}, u_ {2}) dx + u_ {2} (\ theta + u_ {1} dx) du = \ theta + u_ {1} dx \\ = 2u_ {1} (\ theta _ {1} + u_ {2} dx) - \ phi (x, u, u_ {1}, u_ {2}) dx + u_ {2} (\ theta + u_ {1} dx) du_ {1} = \ theta _ {1} + u_ {2} dx \\ = [3u_ {1} u_ {2} - \ phi (x, u, u_ {1}, u_ {2})] dx + u_ {2} \ theta + 2u_ {1} \ theta _ {1 } \ end {align}}}

Следовательно, для $LV 2 (θ 1) {\ displaystyle {\ mathcal {L}} _ {V ^ {2}} (\ theta _ {1})}$ ${\ displaystyle {\ mathcal {L}} _ {V ^ {2}} (\ theta _ {1})}$ , чтобы сохранить контактный идеал, потребуем

3 u 1 u 2 - ϕ (x, u, u 1, u 2) = 0 ⇔ ϕ (x, u, u 1, u 2) = 3 u 1 u 2. {\ displaystyle 3u_ {1} u_ {2} - \ phi (x, u, u_ {1}, u_ {2}) = 0 \ quad \ Leftrightarrow \ quad \ phi (x, u, u_ {1}, u_ {2}) = 3u_ {1} u_ {2}.}

{\ displaystyle 3u_ {1} u_ {2 } - \ phi (x, u, u_ {1}, u_ {2}) = 0 \ quad \ Leftrightarrow \ quad \ phi (x, u, u_ {1}, u_ {2}) = 3u_ {1} u_ {2}.}

Итак, второе продолжение V до векторного поля на J (π) равно

V 2 = x ∂ ∂ u - u ∂ ∂ x + (1 + u 1 u 1) ∂ ∂ u 1 + 3 u 1 u 2 ∂ ∂ u 2. {\ displaystyle V ^ {2} = x {\ frac {\ partial} {\ partial u}} - u {\ frac {\ partial} {\ partial x}} + (1 + u_ {1} u_ {1}) {\ frac {\ partial} {\ partial u_ {1}}} + 3u_ {1} u_ {2} {\ frac {\ partial} {\ partial u_ {2}}}.}

{\ displaystyle V ^ {2} = x {\ frac {\ partial} {\ partial u}} - u {\ frac {\ partial} {\ partial x} } + (1 + u_ {1} u_ {1}) {\ frac {\ partial} {\ partial u_ {1}}} + 3u_ {1} u_ {2} {\ frac {\ partial} {\ partial u_ {2}}}.}

Обратите внимание, первое продолжение V можно восстановить, опуская член второй производной в V или проецируя обратно на J (π).

Бесконечные пространства струй

обратный предел следовать проекций $π k + 1, k: J k + 1 (π) → J k (π) {\ displaystyle \ pi _ {k + 1, k}: J ^ {k + 1} (\ pi) \ to J ^ {k} (\ pi)}$ $\ pi _ {{k + 1, k}}: J ^ {{k + 1}} (\ pi) \ к J ^ {k} (\ pi)$ дает начало бесконечное реактивное пространство J (π). Точка $jp ∞ (σ) {\ displaystyle j_ {p} ^ {\ infty} (\ sigma)}$ $j_ {p} ^ {\ infty} (\ sigma)$ - это класс эквивалентности секций π, которые имеют одинаковую k-струю в p как σ для всех значений k. Естественная проекция π ∞ отображает $j p ∞ (σ) {\ displaystyle j_ {p} ^ {\ infty} (\ sigma)}$ $j_ {p} ^ {\ infty} (\ sigma)$ в p.

Если просто мыслить в терминах координат, J (π) кажется бесконечномерным геометрическим объектом. Фактически, самый простой способ добиться дифференцируемой структуры на J (π), не опираясь на дифференцируемые карты, дает дифференциальное исчисление над коммутативными алгебрами. Двойственный к последовательным проекциям $π k + 1, k: J k + 1 (π) → J k (π) {\ displaystyle \ pi _ {k + 1, k}: J ^ {k + 1} (\ pi) \ to J ^ {k} (\ pi)}$ ${\ displaystyle \ pi _ {k + 1, k}: J ^ {k + 1} (\ pi) \ to J ^ {k} (\ pi)}$ разнообразий - это последовательность вложений $π k + 1, k ∗: C ∞ (J k (π)) → С ∞ (J К + 1 (π)) {\ Displaystyle \ pi _ {k + 1, k} ^ {*}: C ^ {\ infty} (J ^ {k} (\ pi)) \ к C ^ {\ infty} \ left (J ^ {k + 1} (\ pi) \ right)}$ ${\ displaystyle \ pi _ {k + 1, k} ^ {*}: C ^ {\ infty} (J ^ {k} (\ pi)) \ to C ^ {\ infty} \ left (J ^ {k + 1} ( \ pi) \ right)}$ коммутативных алгебр. Обозначим $C ∞ (J k (π)) {\ displaystyle C ^ {\ infty} (J ^ {k} (\ pi))}$ $C ^ {\ infty} (J ^ {{k}} (\ pi))$ просто как $F k (π) {\ Displaystyle {\ mathcal {F}} _ {k} (\ pi)}$ ${\ mathcal {F}} _ {k} (\ pi)$ . Теперь возьмем прямой предел $F (π) {\ displaystyle {\ mathcal {F}} (\ pi)}$ ${\ mathcal {F}} (\ pi)$ $F k (π) {\ Displaystyle { \ mathcal {F}} _ {k} (\ pi)}$ ${\ mathcal {F}} _ {k} (\ pi)$ . Это будет коммутативная алгебра, которую можно считать алгеброй гладких функций над геометрическим объектом J (π). Обратите внимание, что $F (π) {\ displaystyle {\ mathcal {F}} (\ pi)}$ ${\ mathcal {F}} (\ pi)$ , имеет прямой предел, несет дополнительную структуру: это фильтрованная коммутативная алгебра.

Грубо говоря, конкретный элемент $φ ∈ F (π) {\ displaystyle \ varphi \ in {\ mathcal {F}} (\ pi)}$ $\ varphi \ in {\ mathcal {F}} (\ pi)$ всегда будет принадлежать some $F k (π) {\ displaystyle {\ mathcal {F}} _ {k} (\ pi)}$ ${\ mathcal {F}} _ {k} (\ pi)$ , поэтому это гладкая функция на конечном разнообразии J (π) в обычном понимании.

Бесконечно продолженные УЧП

Для системы УЧП k-го порядка E ⊆ J (π) набор I (E) исчезающих на E гладких функций на J (π) является идеал в алгебре $F k (π) {\ displaystyle {\ mathcal {F}} _ {k} (\ pi)}$ ${\ mathcal {F}} _ {k} (\ pi)$ и, следовательно, в прямом пределе $F (π) {\ displaystyle {\ mathcal {F}} (\ pi)}$ ${\ mathcal {F}} (\ pi)$ тоже.

Улучшите I (E), добавив все возможные композиции полных производных, примененные ко всем его элементам. Таким образом, мы получаем новый идеал I в $F (π) {\ displaystyle {\ mathcal {F}} (\ pi)}$ ${\ mathcal {F}} (\ pi)$ , который теперь замкнут при операции взятия полной производной. Подмногообразие E (∞) в J (π), вырезанное I, называется бесконечным продолжением массива E.

Геометрически E (∞) - это многообразие формальных решений уравнения E. Точка $jp ∞ (σ) {\ displaystyle j_ {p} ^ {\ infty} (\ sigma)}$ $j_ {p} ^ {\ infty} (\ sigma)$ of E (∞), как легко увидеть, представление сечением σ, график k-струи которого касается E в точке $jpk (σ) {\ displaystyle j_ {p} ^ {k} (\ sigma)}$ $j_ {p} ^ {к} (\ sigma)$ с произвольно высоким порядком касания.

Аналитически, если E задается с помощью φ = 0, формальное решение можно понимать как набор коэффициентов Тейлора сечения σ в точке p, которые обращают в нуль ряд Тейлора $φ ∘ jk ( σ) {\ displaystyle \ varphi \ circ j ^ {k} (\ sigma)}$ $\ varphi \ circ j ^ {k} (\ sigma)$ в точке p.

Наиболее важно то, что свойства замыкания I подразумевают, что E (∞) касается контактной структуры бесконечного порядка $C {\ displaystyle {\ mathcal {C }}}$ ${\ mathcal {C}}$ на J (π), так что, ограничивая $C {\ displaystyle {\ mathcal {C}}}$ ${\ mathcal {C}}$ до E (∞) получаем различие $(E (∞), C | E (∞)) {\ displaystyle (E _ {(\ infty)}, {\ mathcal {C}} | _ {E _ {(\ infty)})}$ $(E _ {{(\ infty)}}, {\ mathcal {C}} | _ {{E _ {{(\ infty)}}}})$ , и может использовать связанную последовательность Виноградова (C-спектральная).

Замечание

В статье струи локальные сечения расслоения, но можно определить струи функций f: M → N, где M и N - многообразия; тогда струя f просто соответствует струе секции

grf: M → M × N

grf(p) = (p, f (p))

(gr f является известным как график функции f ) тривиального пучка (M × N, π 1, M). Однако это ограничение не упрощает теорию, поскольку глобальная тривиальность π не означает глобальной тривиальности π 1.

См. Также

Ссылки

Дополнительная литература

Ehresmann, C., "Введение в теорию бесконечных симметричных структурных" и псевдогруппы Ли ". Geometrie Differentielle, коллок. Интер. du Centre Nat. de la Recherche Scientifique, Страсбург, 1953, 97–127.
Коларж, И., Михор, П., Словак, Дж., Естественные операции в дифференциальной геометрии. Springer-Verlag: Berlin Heidelberg, 1993. ISBN 3-540-56235-4, ISBN 0-387-56235-4.
Сондерс, ди-джей "Геометрия струйных связок", Cambridge University Press, 1989, ISBN 0-521-36948-7
Красильщик, И.С., Виноградов, AM, [и др.], «Симметрии и законы для различных условий математической физики», Ам. Математика. Soc., Providence, RI, 1999, ISBN 0-8218 -0958-X.
Олвер, П.Дж., «Эквивалентность, инварианты и симметрия», Cambridge University Press, 1995, ISBN 0-521-47811-1
Джакетта, Г., Манджиаротти, Л., Сарданашвили, Г., «Продвинутая классика Теория поля», World Scientific, 2009, ISBN 978-981 -283-895-7
Сарданашвили Г., Продвинутая дифференциальная геометрия для теоретиков. Пучки волокон, струйные многообразия и теория Лагранжа », Lambert Academic Publishing, 2013, ISBN 978-3-659-37815-7 ; arXiv : 0908.1886