Обратная кинематика

редактировать

Прямая и обратная кинематика

В компьютерной анимации и робототехнике, обратная кинематика - это математический процесс вычисления переменных параметров соединения, необходимых для размещения конца кинематической цепочки, такой как робот-манипулятор или скелет анимационного персонажа, в заданное положение и ориентация относительно начала цепочки. При заданных параметрах соединения положение и ориентация конца цепи, например рука персонажа или робота, как правило, может быть вычислена напрямую с использованием нескольких приложений тригонометрических формул, процесса, известного как прямая кинематика. Однако обратная операция, как правило, намного сложнее.

Обратная кинематика также используется для восстановления движений объекта в мире из некоторых других данных, таких как фильм этих движений или фильм о мире, видимом камерой, которая сама делает эти движения. Это происходит, например, когда записанные движения актера-человека должны быть дублированы анимированным персонажем.

Содержание

1 Робототехника
2 Кинематический анализ
3 Обратная кинематика и 3D-анимация
4 Аналитические решения обратной кинематики
5 Численные решения задач IK
- 5.1 Обратный метод Якоби
- 5.2 Эвристические методы
6 См. Также
7 Ссылки
8 Внешние ссылки

Робототехника

В робототехнике обратная кинематика использует уравнения кинематики для определения совместных параметров, которые обеспечивают желаемую конфигурацию (положение и вращение) для каждого из рабочих органов робота. Определение движения робота таким образом, чтобы его рабочие органы перемещались от начальной конфигурации к желаемой конфигурации, известно как планирование движения. Обратная кинематика преобразует план движения в совместные траектории привода для робота. Аналогичные формулы определяют положения скелета анимированного персонажа, который должен двигаться определенным образом в фильме, или транспортного средства, такого как автомобиль или лодка, содержащего камеру, которая снимает сцену фильм. Как только движения транспортного средства известны, их можно использовать для определения постоянно меняющейся точки обзора для компьютерных изображений объектов ландшафта, таких как здания, так что эти объекты меняются в перспективе, но сами не кажутся двигайтесь, когда бортовая камера проезжает мимо них.

Движение кинематической цепи, будь то робот или анимированный персонаж, моделируется уравнениями кинематики цепи. Эти уравнения определяют конфигурацию цепи с точки зрения ее совместных параметров. Прямая кинематика использует параметры соединения для вычисления конфигурации цепи, а обратная кинематика меняет этот расчет на противоположное, чтобы определить параметры соединения, которые достигают желаемой конфигурации.

Кинематический анализ

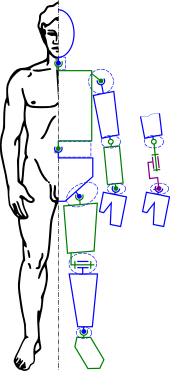Модель человеческого скелета в виде кинематической цепи позволяет позиционировать его с использованием обратной кинематики.

Кинематический анализ - один из первых шагов в проектировании большинства промышленных роботов. Кинематический анализ позволяет проектировщику получать информацию о положении каждого компонента в механической системе. Эта информация необходима для последующего динамического анализа вместе с путями управления.

Обратная кинематика - это пример кинематического анализа системы твердых тел со связями или кинематической цепи. кинематические уравнения робота могут использоваться для определения петлевых уравнений сложной шарнирной системы. Эти петлевые уравнения являются нелинейными ограничениями на параметры конфигурации системы. Независимые параметры в этих уравнениях известны как степени свободы системы.

Хотя аналитические решения проблемы обратной кинематики существуют для широкого диапазона кинематических цепочек, инструменты компьютерного моделирования и анимации часто используют метод Ньютона для решения уравнений нелинейной кинематики.

К другим приложениям алгоритмов обратной кинематики относятся и предотвращение столкновений.

Обратная кинематика и 3D-анимация

Обратная кинематика важна для программирования игр и 3D-анимация, где она используется для соединения игровых персонажей физически с миром, например, когда ноги твердо приземляются на поверхность (см. Подробный обзор методов обратной кинематики, используемых в Компьютерная графика ).

Анимированная фигура моделируется каркасом из жестких сегментов, соединенных шарнирами, который называется кинематической цепочкой. Уравнения кинематики фигуры определяют соотношение между углами сочленения фигуры и ее позой или конфигурацией. Задача прямой кинематической анимации использует уравнения кинематики для определения позы с учетом углов сочленения. В задаче обратной кинематики вычисляются углы суставов для желаемой позы фигуры.

Компьютерным дизайнерам, художникам и аниматорам часто проще определить пространственную конфигурацию сборки или фигуры с помощью движущихся частей или рук и ног, чем напрямую манипулировать углами суставов. Следовательно, обратная кинематика используется в системах автоматизированного проектирования для анимации сборок, а компьютерные художники и аниматоры - для позиционирования фигур и персонажей.

Сборка моделируется как жесткие звенья, соединенные соединениями, которые определены как сопряжения или геометрические зависимости. Перемещение одного элемента требует вычисления углов сочленения для других элементов, чтобы сохранить ограничения стыка . Например, обратная кинематика позволяет художнику перемещать руку трехмерной модели человека в желаемое положение и ориентацию и иметь алгоритм, выбирающий правильные углы суставов запястья, локтя и плеча. Успешная реализация компьютерной анимации обычно также требует, чтобы фигура двигалась в разумных антропоморфных пределах.

Метод сравнения прямой и обратной кинематики для анимации персонажа может определяться преимуществами, присущими каждому из них. Например, блокирующая анимация, в которой используются большие дуги движения, часто более выгодна в прямой кинематике. Однако более тонкая анимация и позиционирование целевого рабочего органа по отношению к другим моделям может быть проще при использовании инвертированной кинематики. Современные пакеты цифрового создания (DCC) предлагают методы для применения к моделям как прямой, так и обратной кинематики.

Аналитические решения обратной кинематики

В некоторых случаях, но не во всех, существуют аналитические решения обратной кинематической задачи. Одним из таких примеров является робот с 6 степенями свободы (например, 6 поворотных шарниров), движущийся в трехмерном пространстве (с 3 степенями свободы положения и 3 степенями свободы вращения). Если степени свободы робота превышают степени свободы рабочего органа, например, у робота с 7 степенями свободы и 7 поворотными шарнирами, то существует бесконечно много решений проблемы IK, и аналитического решения не существует. Расширяя этот пример, можно исправить одно соединение и аналитически решить для других соединений, но, возможно, лучшее решение предлагают численные методы (следующий раздел), которые вместо этого могут оптимизировать решение с учетом дополнительных предпочтений (затраты в задаче оптимизации).

Аналитическое решение задачи обратной кинематики - это выражение в замкнутой форме, которое принимает позу рабочего органа в качестве входных данных и дает положения суставов в качестве выходных данных, $q = f (x) {\ displaystyle q = f (x)}$ ${\ displaystyle q = f (x)}$ . Аналитические решатели обратной кинематики могут быть значительно быстрее, чем численные решатели, и предоставлять более одного решения, но только конечное число решений для данной позы рабочего органа.

Программа с открытым исходным кодом IKFast может находить полные аналитические решения для большинства распространенных роботов-манипуляторов и генерировать для них код C ++. Сгенерированные решатели охватывают большинство вырожденных случаев и могут завершиться за микросекунды на современных компьютерах. Одна проблема с этими решателями заключается в том, что они, как известно, не обязательно дают локально гладкие решения между двумя соседними конфигурациями, что может вызвать нестабильность, если итерационные решения для обратной кинематики требуются, например, если IK решается внутри высокоскоростного контура управления.

Численное решение задач ИК

Существует множество методов моделирования и решения задач обратной кинематики. Наиболее гибкий из этих методов обычно полагается на итеративную оптимизацию для поиска приближенного решения из-за сложности обращения уравнения прямой кинематики и возможности пустого пространства решений. Основная идея, лежащая в основе некоторых из этих методов, заключается в моделировании уравнения прямой кинематики с использованием разложения ряда Тейлора, которое может быть проще инвертировать и решать, чем исходную систему.

Обратный метод Якоби

Обратный метод Якобиана - простой, но эффективный способ реализации обратной кинематики. Пусть есть переменные $m {\ displaystyle m}$ $m$ , которые управляют уравнением прямой кинематики, то есть функцией положения. Эти переменные могут быть углами соединения, длиной или другими произвольными действительными значениями. Если система ИК живет в трехмерном пространстве, функцию положения можно рассматривать как отображение $p (x): ℜ m → ℜ 3 {\ displaystyle p (x): \ Re ^ {m} \ rightarrow \ Re ^ {3}}$ $p (x): \ Re ^ {m} \ rightarrow \ Re ^ {3}$ . Пусть $p 0 = p (x 0) {\ displaystyle p_ {0} = p (x_ {0})}$ $p_ {0} = p (x_ {0})$ задает начальное положение системы, а

p 1 = p (x 0 + Δ x) {\ displaystyle p_ {1} = p (x_ {0} + \ Delta x)}

p_ {1} = p (x_ {0} + \ Delta x)

- целевое положение системы. Метод обратного Якоби итеративно вычисляет оценку $Δ x {\ displaystyle \ Delta x}$ $\ Delta x$ , которая минимизирует ошибку, задаваемую $| | п (х 0 + Δ х е с т я м а т е) - п 1 | | {\ displaystyle || p (x_ {0} + \ Delta x_ {оценка}) - p_ {1} ||}$ ${\ displaystyle || p (x_ {0} + \ Delta x_ {оценка}) - p_ {1} ||}$ .

для малых $Δ x {\ displaystyle \ Delta x}$ $\ Delta x$ -векторы, разложение функции положения в ряд дает

p (x 1) ≈ p (x 0) + J p (x 0) Δ x {\ displaystyle p (x_ {1}) \ приблизительно p (x_ { 0}) + J_ {p} (x_ {0}) \ Delta x}

{\ displaystyle p (x_ {1}) \ приблизительно p (x_ {0}) + J_ {p} (x_ {0}) \ Дельта x}

где $J p (x 0) {\ displaystyle J_ {p} (x_ {0})}$ $J_ {p} (x_ {0})$ - (3 × m) матрица Якоби функции положения в $x 0 {\ displaystyle x_ {0}}$ $x_ {0}$ .

Обратите внимание, что (i, k) -й элемент Матрица Якоби может быть аппроксимирована численно

∂ pi ∂ xk ≈ pi (x 0, k + h) - pi (x 0) h {\ displaystyle {\ frac {\ partial p_ {i}} {\ partial x_ {k }}} \ приблизительно {\ frac {p_ {i} (x_ {0, k} + h) -p_ {i} (x_ {0})} {h}}}

{ \ frac {\ partial p_ {i}} {\ partial x_ {k}}} \ приблизительно {\ frac {p_ {i} (x _ {{0, k}} + h) -p_ {i} (x_ {0 })} {h}}

где $pi (x) {\ displaystyle p_ {i} (x)}$ $p_ {i} ( х)$ дает i-й компонент функции положения, $x 0, k + h {\ displaystyle x_ {0, k} + h}$ $x _ {{ 0, k}} + h$ - это просто $x 0 {\ displaystyle x_ {0}}$ $x_ {0}$ с небольшой дельтой, добавленной к его k-му компоненту, и $h {\ displaystyle h}$ $h$ это реа разумно небольшое положительное значение.

Взяв псевдообратную матрицу Мура-Пенроуза для якобиана (вычисляемую с использованием разложения по сингулярным числам ) и переупорядочивая члены, получаем

Δ x ≈ J p + (x 0) Δ p {\ displaystyle \ Delta x \ приблизительно J_ {p} ^ {+} (x_ {0}) \ Delta p}

\ Delta x \ приблизительно J_ {p} ^ {+} (x_ {0}) \ Delta p

где $Δ p = p (x 0 + Δ x) - p (x 0) {\ displaystyle \ Delta p = p (x_ {0} + \ Delta x) -p (x_ {0})}$ $\ Delta p = p (x_ {0} + \ Delta x) -p (x_ {0})$ .

Применение метода обратного якобиана один раз приведет к очень приблизительной оценке искомого $Δ x {\ displaystyle \ Delta x}$ $\ Delta x$ -вектора. Для масштабирования этого $Δ x {\ displaystyle \ Delta x}$ $\ Delta x$ до приемлемого значения следует использовать поиск по строке. Оценка для $Δ x {\ displaystyle \ Delta x}$ $\ Delta x$ может быть улучшена с помощью следующего алгоритма (известного как метод Ньютона-Рафсона ):

Δ xk + 1 = J p + (xk) Δ pk {\ displaystyle \ Delta x_ {k + 1} = J_ {p} ^ {+} (x_ {k}) \ Delta p_ {k}}

\ Delta x _ {{k + 1}} = J_ {p} ^ {+} (x_ {k}) \ Delta p_ {k}

Однажды $Δ x {\ displaystyle \ Delta x}$ $\ Delta x$ - вектор привел к тому, что ошибка упала близко к нулю, алгоритм должен завершиться. Существующие методы, основанные на матрице Гессе системы, как сообщалось, сходятся к желаемым значениям $Δ x {\ displaystyle \ Delta x}$ $\ Delta x$ с использованием меньшего количества итераций, хотя в некоторых случаях больше вычислительных ресурсов.

Эвристические методы

Задача обратной кинематики также может быть аппроксимирована с помощью эвристических методов. Эти методы выполняют простые итерационные операции, постепенно приводящие к приближению решения. Эвристические алгоритмы имеют низкую вычислительную стоимость (очень быстро возвращают окончательную позу) и обычно поддерживают совместные ограничения. Наиболее популярные эвристические алгоритмы: (CCD) и Прямая и обратная обратная кинематика (FABRIK).

См. Также

Физический портал

Ссылки

Внешние ссылки

Прямая и обратная обратная кинематика (FABRIK)
Робототехника и 3D-анимация в FreeBasic (на испанском языке)
Аналитический решатель обратной кинематики - по описанию кинематики робота OpenRAVE генерирует файл C ++, который аналитически решает полную IK.
Алгоритмы обратной кинематики
Обратное решение робота для общей геометрии роботов
Статья HowStuffWorks.com Как движутся персонажи в видеоиграх так плавно? с объяснением обратной кинематики
3D-анимация расчета геометрической обратной кинематики промышленного робота
3D Theory Kinematics
Protein Inverse Kinematics
Пример простой обратной кинематики с исходный код с использованием якобиана
Подробное описание решений Якобиана и ПЗС для обратной кинематики
Autodesk HumanIK
Трехмерная визуализация аналитического решения промышленного робота