Интеграл

Операция в исчислении Определенный интеграл функции может быть представлен в виде области со знаком области, ограниченной ее графиком.

В математике, интеграл присваивает числа функциям таким образом, чтобы можно было описать смещение, площадь, объем и другие понятия, возникающие в результате объединения бесконечно малых данных.. Интегрирование - одна из двух основных операций исчисления ; его обратная операция, дифференцирование, является другим. Учитывая функцию f вещественной переменной x и интервал [a, b] вещественной линии, определенный интеграл

$\int \; abf\; (x)\; dx\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; f\; (x)\; \backslash ,\; dx\}$

может неформально интерпретироваться как знаковый область области в плоскости xy, которая ограничена графиком f, осью x и вертикальными линиями x = a и x = b. Область над осью x добавляет к сумме, а область под осью x вычитается из суммы.

Операция интегрирования с точностью до аддитивной константы является обратной операцией дифференцирования. По этой причине термин «интеграл» может также относиться к связанному с ним понятию первообразной , функции F, производной которой является заданная функция f. В этом случае он называется неопределенным интегралом и записывается:

$F\; (x)\; =\; \int \; f\; (x)\; d\; x.\; \{\backslash \; displaystyle\; F\; (x)\; =\; \backslash \; int\; f\; (x)\; \backslash ,\; dx.\}$

Интегралы, обсуждаемые в этой статье, называются определенными интегралами. Это основная теорема исчисления, которая связывает дифференцирование с определенным интегралом: если f - непрерывная функция с действительными значениями, определенная на отрезке [a, b], то, однажды известна первообразная F функции f, определенный интеграл функции f на этом интервале равен

$\int \; abf\; (x)\; dx\; =\; [F\; (x)]\; ab\; =\; F\; (b)\; -\; F\; (a).\; \{\backslash \; Displaystyle\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; \backslash ,\; f\; (x)\; dx\; =\; \backslash \; left\; [F\; (x)\; \backslash \; right]\; \_\; \{a\}\; ^\; \{b\}\; =\; F\; (b)\; -F\; (a)\; \backslash ,.\}$

Принципы интеграции были независимо сформулированы Исааком Ньютоном и Готфридом Вильгельмом Лейбницем в конце 17 века, которые считали интеграл бесконечной суммой прямоугольников бесконечно малая ширина. Бернхард Риман дал строгое математическое определение интегралов. Он основан на процедуре ограничения, которая аппроксимирует площадь криволинейной области , разбивая область на тонкие вертикальные пластины. Начиная с XIX века, стали появляться более сложные понятия интегралов, в которых были обобщены тип функции, а также область , по которой выполняется интегрирование. Линейный интеграл определяется для функций двух или более переменных, а интервал интегрирования [a, b] заменяется кривой кривой, соединяющей две конечные точки. В интеграле поверхности кривая заменяется фрагментом поверхности в трехмерном пространстве.

Содержание

• 1 История
  • 1.1 Предварительные требования интеграция исчисления
  • 1.2 Лейбниц и Ньютон
  • 1.3 Формализация
  • 1.4 Историческая нотация
  • 1.5 Первое использование термина
• 2 Приложения
• 3 Терминология и обозначения
  • 3.1 Стандарт
  • 3.2 Значение символа dx
  • 3.3 Варианты
• 4 Интерпретация интеграла
• 5 Формальные определения
  • 5.1 Интеграл Римана
  • 5.2 Интеграл Лебега
  • 5.3 Другие интегралы
• 6 Свойства
  • 6.1 Линейность
  • 6.2 Неравенства
  • 6.3 Соглашения
• 7 Фундаментальная теорема исчисления
  • 7.1 Формулировки теорем
    • 7.1.1 Основная теорема исчисления
    • 7.1.2 Вторая основная теорема исчисления
  • 7.2 Вычисление интегралов
• 8 Расширения
  • 8.1 Несобственные интегралы
  • 8.2 Многократное интегрирование
  • 8.3 Линейные интегралы
  • 8.4 Поверхностные интегралы
  • 8.5 Контурные интегралы
  • 8.6 Интегралы от дифференциальных форм
  • 8.7 Суммирование
• 9 Вычисление
  • 9.1 Аналитический
  • 9.2 Символьный
  • 9.3 Числовой
  • 9.4 Механический
  • 9.5 Геометрический
• 10 См. Также
• 11 Ссылки
• 12 Библиография
• 13 Внешние ссылки
  • 13.1 Электронные книги

История

Интеграция до исчисления

Первым задокументированным систематическим методом, способным определять интегралы, является метод исчерпания древнегреческого астронома Евдокса (ок. 370 г. до н.э.), который стремился найти области и объемы, разбивая их на бесконечное количество частей, для которых была известна площадь или объем. Этот метод был развит и применен Архимедом в 3 веке до нашей эры и использовался для вычисления площади круга, площади поверхности и объема. сферы , площадь эллипса, площадь под параболой, объем сегмента параболоида вращения, объем сегмента гиперболоида вращения и площадь спирали.

. Подобный метод был независимо разработан в Китае примерно в 3 веке нашей эры Лю Хуэй, который использовал его, чтобы найти площадь круга. Позже этот метод был использован в V веке китайскими математиками, отцом и сыном Цзу Чунчжи и Цзу Гэн, чтобы найти объем сферы (Shea 2007 ; Кац 2004, стр. 125–126).

На Ближнем Востоке Хасан Ибн аль-Хайтам, латинизированный как Альхазен (ок. 965 - ок. 1040 г. н.э.), вывел формулу для суммы четвертых степеней. Он использовал результаты, чтобы выполнить то, что теперь называется интегрированием этой функции, где формулы для сумм целых квадратов и четвертых степеней позволили ему вычислить объем параболоида.

. Интегральное исчисление появилось только в 17 веке. В это время работа Кавальери с его методом Неделимых и работа Ферма начали закладывать основы современного исчисления, а Кавальери вычислил интегралы от x до степени n = 9 в квадратурной формуле Кавальери. Дальнейшие шаги были предприняты в начале 17 века Барроу и Торричелли, которые дали первые намеки на связь между интеграцией и дифференциацией. Барроу представил первое доказательство основной теоремы исчисления. Уоллис обобщил метод Кавальери, вычисляя интегралы от x до общей степени, включая отрицательные степени и дробные степени.

Лейбниц и Ньютон

Главный прорыв в интеграции произошел в 17 веке с независимым открытием фундаментальной теоремы исчисления Лейбницем и Ньютон. Лейбниц опубликовал свою работу по исчислению до Ньютона. Теорема демонстрирует связь между интегрированием и дифференцированием. Эта связь в сочетании со сравнительной простотой дифференцирования может быть использована для вычисления интегралов. В частности, основная теорема исчисления позволяет решать гораздо более широкий класс задач. Не менее важна исчерпывающая математическая основа, разработанная Лейбницем и Ньютоном. Получив название исчисление бесконечно малых, оно позволило проводить точный анализ функций в непрерывных областях. Эта структура в конечном итоге превратилась в современное исчисление, обозначение интегралов которого взято непосредственно из работ Лейбница.

Формализация

Хотя Ньютон и Лейбниц предложили систематический подход к интеграции, их работе не хватало степени строгости. Епископ Беркли незабываемо атаковал исчезающие приращения, используемые Ньютоном, назвав их «призраками умерших количеств ». Исчисление приобрело более прочную основу с развитием пределов. Впервые интегрирование было строго формализовано с использованием пределов Риманом. Хотя все ограниченные кусочно-непрерывные функции интегрируемы по Риману на ограниченном интервале, впоследствии были рассмотрены более общие функции - особенно в контексте анализа Фурье - к которому определение Римана не применимо, и Лебег сформулировал другое определение интеграла, основанное на теории меры (подполе реального анализа ). Были предложены другие определения интеграла, расширяющие подходы Римана и Лебега. Эти подходы, основанные на системе действительных чисел, являются наиболее распространенными сегодня, но существуют альтернативные подходы, такие как определение интеграла как стандартной части бесконечной суммы Римана, основанной на гиперреальном числе. система.

Историческое обозначение

Обозначение для неопределенного интеграла было введено Готфридом Вильгельмом Лейбницем в 1675 году (Бертон 1988, стр. 359 ошибка harvnb: нет цели: CITEREFBurton1988 (help ); Leibniz 1899, p. 154). Он адаптировал интегральный символ , ∫из буквы ſ (long s ), обозначающей сумму (написанную как ſumma; латинское слово означает «сумма» или «итог»). Современные обозначения для определенного интеграла с пределами выше и ниже знака интеграла были впервые использованы Жозефом Фурье в воспоминаниях Французской академии около 1819–1820 годов, перепечатанных в его книге 1822 года (Cajori 1929, стр. 249–250; Фурье 1822, §231).

Исаак Ньютон использовал небольшую вертикальную черту над переменной для обозначения интегрирования или поместил переменную в рамку. Вертикальную черту легко спутать с . x или x ', которые используются для обозначения дифференциации, а нотацию прямоугольников было трудно воспроизвести принтерам, поэтому эти обозначения не получили широкого распространения.

Первое использование термина

Термин был впервые напечатан на латыни в 1690 году: «Ergo et horum Integralia aequantur» (Бернулли, Opera 1744, Vol. 1, стр.423).

Этот термин используется в легком для понимания абзаце из Гийома де л'Опиталя в 1696 году:

Dans tout cela il n'y a бис que la premiere partie du Calcul de М. Лейбниц, laquelle consiste à origin des grandeurs entiéres à leur différences infiniment petites, et à comparer entr'eux ces infiniment petits de quelque genre qu'ils soient: c'est ce qu'on appel Calcul différentiel. Pour l'autre partie, qu'on appelle Calcul intégral, et qui consiste à remonter de ces infiniment petits aux grandeurs или aux touts dont ils sont les différences, c'est-à-dire à en Trouver les sommes, j'avois aussi dessein de le donner. Mais M. Leibniz m'ayant écrit qu'il y travailloit dans un Traité qu'il intitule De Scientia infiniti, je n'ay eu garde de prive le public d'un si bel Ouvrage qui doit renfermer tout ce qu'il ya de plus curieux pour la Méthode inverse des Tangentes...

"Из всего этого осталась только первая часть исчисления М. Лейбница, состоящая в понижении от целых величин до их бесконечно малых разностей, и при сравнении между собой этих бесконечно малых величин любого возможного вида: это то, что называется дифференциальным исчислением. Что касается другой части, это называется интегральным исчислением и заключается в возвращении назад от этих бесконечно малых величин. малых количеств или полных частей, в которых они являются различиями, то есть найти их суммы, я также имел намерение раскрыть это. Но учитывая, что М. Лейбниц написал мне, что он работал над этим в книгу, которую он называет De Scientia infiniti, я позаботился о том, чтобы не лишить публику такой прекрасной ork, который должен содержать все самое любопытное в обратном методе касательных... "(курсив добавлен)

Приложения

Интегралы также широко используются во многих областях математики как и во многих других областях, основанных на математике.

Например, в теории вероятностей интегралы используются для определения вероятности попадания некоторой случайной величины в определенный диапазон. Более того, интеграл от всей функции плотности вероятности должен быть равен 1, что обеспечивает проверку того, может ли функция без отрицательных значений быть функцией плотности или нет.

Интегралы могут использоваться для вычисления площади двумерной области с изогнутой границей, а также вычисления объема трехмерного объекта. с изогнутой границей. Площадь двумерной области может быть вычислена с использованием указанного выше определенного интеграла.

Объем трехмерного объекта, такого как диск или шайба, как указано в разделе Интегрирование диска, может быть вычислен с использованием уравнения для объема цилиндра, $\pi \; r\; 2\; h\; \{\backslash \; displaystyle\; \backslash \; pi\; r\; ^\; \{2\}\; h\}$, где $r\; \{\backslash \; displaystyle\; r\}$- радиус, который в данном случае будет расстоянием от кривую функции относительно линии, вокруг которой она вращается. Для простого диска радиус будет равен уравнению функции минус заданное значение $x\; \{\backslash \; displaystyle\; x\}$или $y\; \{\backslash \; displaystyle\; y\}$-значение строки. Например, радиус диска, созданный вращением квадратичной $y\; =\; -\; x\; 2\; +\; 4\; \{\backslash \; displaystyle\; y\; =\; -x\; ^\; \{2\}\; +4\}$вокруг линии $y\; =\; -\; 1\; \{\backslash \; displaystyle\; y\; =\; -1\}$будет задано выражением $-\; x\; 2\; +\; 4\; -\; (-\; 1)\; \{\backslash \; displaystyle\; -x\; ^\; \{2\}\; +4\; -\; (-\; 1)\}$или $-\; x\; 2\; +\; 5\; \{\backslash \; displaystyle\; -x\; ^\; \{2\}\; +5\}$. Чтобы найти объем той же формы, интеграл с такими границами $a\; \{\backslash \; displaystyle\; a\}$и $b\; \{\backslash \; displaystyle\; b\}$, что $a\; \{\backslash \; displaystyle\; a\}$и $b\; \{\backslash \; displaystyle\; b\}$являются пересечениями прямой $y\; =\; -\; x\; 2\; +\; 4\; \{\backslash \; displaystyle\; y\; =\; -\; x\; ^\; \{2\}\; +4\}$и $y\; =\; -\; 1\; \{\backslash \; displaystyle\; y\; =\; -1\}$будут использоваться следующим образом:

$\pi \; \int \; ab\; (-\; x\; 2\; +\; 5)\; 2\; dx\; \{\backslash \; displaystyle\; \backslash \; pi\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; (-\; x\; ^\; \{2\}\; +5)\; ^\; \{2\}\; \backslash ,\; dx\}$Компоненты вышеуказанного интеграла представляют переменные в уравнении для объема цилиндра, $\pi \; r\; 2\; h\; \{\backslash \; displaystyle\; \backslash \; pi\; r\; ^\; \{2\}\; h\}$. Константа пи вычитается, а радиус $-\; x\; 2\; +\; 5\; \{\backslash \; displaystyle\; -x\; ^\; \{2\}\; +5\}$возводится в квадрат внутри интеграла. Высота, представленная в формуле объема как $h\; \{\backslash \; displaystyle\; h\}$, задается в этом интеграле бесконечно малым (чтобы приблизить объем с максимально возможной точностью) членом $dx\; \{\backslash \; displaystyle\; dx\}$.

Интегралы также используются в физике в таких областях, как кинематика, для нахождения таких величин, как смещение, время и <674.>скорость. Например, при прямолинейном движении смещение объекта за интервал времени $[a,\; b]\; \{\backslash \; displaystyle\; [a,\; b]\}$определяется как:

$x\; (b)\; -\; Икс\; (а)\; знак\; равно\; \int \; abv\; (t)\; dt,\; \{\backslash \; displaystyle\; x\; (b)\; -x\; (a)\; =\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; v\; (t)\; \backslash ,\; dt,\}$

где $v\; (t)\; \{\backslash \; displaystyle\; v\; (t)\}$- скорость, выраженная как функция времени. Работа, совершаемая силой $F\; (x)\; \{\backslash \; displaystyle\; F\; (x)\}$(заданная как функция положения) из исходного положения $A\; \{\backslash \; displaystyle\; A\}$до конечной позиции $B\; \{\backslash \; displaystyle\; B\}$:

$WA\; \to \; B\; =\; \int \; ABF\; (x)\; dx.\; \{\backslash \; displaystyle\; W\_\; \{A\; \backslash \; rightarrow\; B\}\; =\; \backslash \; int\; \_\; \{A\}\; ^\; \{B\}\; F\; (x)\; \backslash ,\; dx.\}$

Интегралы также используются в термодинамике, где термодинамическое интегрирование используется для вычисления разницы в свободной энергии между двумя заданными состояниями.

Терминология и обозначения

Стандарт

Интеграл по x действительной функции f действительной переменной x на интервале [ a, b] записывается как

$abf\; (x)\; dx.\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; f\; (x)\; \backslash ,\; dx.\}$

Знак интеграла ∫ обозначает интегрирование. Символ dx, называемый дифференциалом переменной x, указывает, что переменной интегрирования является x. Интегрируемая функция f (x) называется подынтегральным выражением. Символ dx отделяется от подынтегрального выражения пробелом (как показано). Функция называется интегрируемой, если интеграл функции по области определения конечен. Точки a и b называются пределами интеграла. Интеграл, в котором указаны пределы, называется определенным интегралом. Говорят, что интеграл лежит по интервалу [a, b].

Если интеграл переходит от конечного значения a до верхнего предела бесконечности, интеграл выражает предел интеграла от a до значения b, когда b стремится к бесконечности. Если значение интеграла становится все ближе и ближе к конечному значению, говорят, что интеграл сходится к этому значению. В противном случае говорят, что интеграл расходится.

Если пределы опущены, как в

$\int \; f\; (x)\; dx,\; \{\backslash \; displaystyle\; \backslash \; int\; f\; (x)\; \backslash ,\; dx,\}$

, интеграл называется неопределенным интегралом, который представляет класс функций (первообразная ), производная которых является подынтегральной функцией. Основная теорема исчисления связывает вычисление определенных интегралов с неопределенными интегралами. Иногда пределы интегрирования опускаются для определенных интегралов, когда одни и те же пределы повторяются повторно в конкретном контексте. Обычно автор разъясняет это соглашение в начале соответствующего текста.

Существует несколько расширений обозначения интегралов для охвата интегрирования в неограниченных областях и / или в нескольких измерениях (см. Последующие разделы этой статьи).

Значение символа dx

Исторически символ dx представлял бесконечно малый «кусок» независимой переменной x, который нужно умножить на подынтегральное выражение и суммируется в бесконечном смысле. Хотя это понятие все еще полезно с эвристической точки зрения, более поздние математики сочли бесконечно малые величины несостоятельными с точки зрения действительной системы счисления. Поэтому во вводном исчислении выражению dx не придается самостоятельного значения; вместо этого он рассматривается как часть символа интеграции и служит его разделителем в правой части интегрируемого выражения.

В более сложных контекстах dx может иметь собственное значение, значение которого зависит от конкретной обсуждаемой области математики. При использовании одним из этих способов исходная нотация Лейбница кооптирована для применения к обобщению исходного определения интеграла. Некоторые распространенные интерпретации dx включают: функцию интегратора в интегрировании Римана-Стилтьеса (в целом обозначается dα (x)), мера в теории Лебега (в целом обозначается dμ), или дифференциальная форма во внешнем исчислении (обозначается $dxi\; 1\; \wedge \; \cdots \; \wedge \; dxik\; \{\backslash \; displaystyle\; dx\; ^\; \{i\_\; \{1\}\}\; \backslash \; wedge\; \backslash \; cdots\; \backslash \; wedge\; dx\; ^\; \{i\_\; \{k\}\; \}\}$в целом). В последнем случае даже буква d имеет самостоятельное значение - как оператор внешней производной на дифференциальных формах.

И наоборот, в расширенных настройках нередко пропускать dx, когда используется только простой интеграл Римана или точный тип интеграла не имеет значения. Например, можно написать $\int \; ab\; (c\; 1\; f\; +\; c\; 2\; g)\; =\; c\; 1\; \int \; abf\; +\; c\; 2\; \int \; abg\; \{\backslash \; textstyle\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; (c\_\; \{1\}\; f\; +\; c\_\; \{2\}\; g)\; =\; c\_\; \{1\}\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; f\; +\; c\_\; \{2\}\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; g\}$для выражения линейности интеграл, свойство, разделяемое интегралом Римана и всеми его обобщениями.

Варианты

В современной арабской математической нотации вместо символа ∫ используется отраженный интегральный символ , поскольку арабский шрифт и математические выражения идут прямо к left.

Некоторые авторы, особенно европейского происхождения, используют вертикальную букву «d» для обозначения переменной интеграции (т.е. dx вместо dx), поскольку, собственно говоря, «d» не является переменной.

Символ dx не всегда ставится после f (x), как, например, в

$\int \; 0\; 1\; 3\; dxx\; 2\; +\; 1\; или\; \int \; 0\; 1\; dx\; \int \; 0\; 1\; dye\; -\; (x\; 2\; +\; y\; 2).\; \{\backslash \; displaystyle\; \backslash \; int\; \backslash \; limits\; \_\; \{0\}\; ^\; \{1\}\; \{\backslash \; frac\; \{3\; \backslash \; dx\}\; \{x\; ^\; \{2\}\; +1\}\}\; \backslash \; quad\; \{\backslash \; text\; \{or\}\}\; \backslash \; quad\; \backslash \; int\; \_\; \{0\}\; ^\; \{1\}\; dx\; \backslash \; int\; \_\; \{0\}\; ^\; \{1\}\; dy\; \backslash \; e\; ^\; \{-\; (x\; ^\; \{2\}\; +\; y\; ^\; \{2\})\}.\}$

В первом выражении дифференциал как бесконечно малый «мультипликативный» множитель, формально следующий за «коммутативным своим» множитель при «умножении» в выражении 3 / (x + 1). Во втором выражении, показывающем дифференциалы, сначала демонстрируются и разъясняются переменные, которые интегрируются по отношению к популярной практике, особенно среди физиков.

Интерпретации интеграла

Интегралы во многих практических ситуациях. Площадь его поверхности (чтобы покрыть его) и длина его края (чтобы закрепить его).. Но если она овальная с закругленным дном, все эти величины требуют интегралов. Для таких тривиальных примеров может быть достаточно практических приближений, но точная инженерия (любых дисциплин) требует точных и строгих значений для этих элементов.

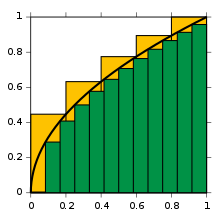Аппроксимация интеграла √x от 0 до 1, с 5 ■ (желтыми) разделами правой конечной точки и 12 ■ (зеленым) разделами левой конечной точки

Для начала рассмотрим кривую y = f (x) между x = 0 и x = 1 с f (x) = √x (см. Рисунок). Мы спрашиваем:

Какова площадь под функцию в интервале от 0 до 1?

и называем эту (пока неизвестную) область (определенным) интегралом от ф. Обозначение для этого интеграла будет

$\int \; 0\; 1\; x\; d\; x.\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{0\}\; ^\; \{1\}\; \{\backslash \; sqrt\; \{x\}\}\; \backslash \; dx.\}$

В первом приближении посмотрите на единичный квадрат, заданные стороны от x = 0 до x = 1 и y = f ( 0) = 0 и y = f (1) = 1. Его площадь ровно 1. На самом деле истинное значение интеграла должно быть несколько меньше 1. Уменьшение ширины прямоугольников аппроксимации и увеличение количества прямоугольники дают лучший результат; поэтому пересеките интервал за пять шагов, используя точки аппроксимации 0, 1/5, 2/5 и так далее до 1. Установите прямоугольник для каждого шага, используя правую конечную высоту участка кривой, таким образом √1 / 5, √2 / 5, и так далее до √1 = 1. Суммируя площади этих прямоугольников, мы получаем лучшее приближение для искомого интеграла, а именно

$1\; 5\; (1\; 5\; -\; 0)\; +\; 2\; 5\; (2\; 5\; -\; 1\; 5)\; +\; \cdots \; +\; 5\; 5\; (5\; 5\; -\; 4\; 5)\; \approx \; 0,7497.\; \{\backslash \; displaystyle\; \backslash \; textstyle\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{1\}\; \{5\}\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{1\}\; \{5\}\}\; -\; 0\; \backslash \; right)\; +\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{2\}\; \{5\}\; \}\}\; \backslash \; left\; (\{\backslash \; frac\; \{2\}\; \{5\}\}\; -\; \{\backslash \; frac\; \{1\}\; \{5\}\}\; \backslash \; right)\; +\; \backslash \; cdots\; +\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{5\}\; \{5\}\}\}\; \backslash \; left\; (\; \{\backslash \; frac\; \{5\}\; \{5\}\}\; -\; \{\backslash \; frac\; \{4\}\; \{5\}\}\; \backslash \; right)\; \backslash \; приблизительно\; 0,7497.\}$

Мы берем сумму конечного числа значений функции f, умноженную на разности две последующие точки приближения. Нетрудно заметить, что приближение все еще слишком велико. Использование большего количества шагов дает более точное приближение, но всегда будет слишком большим и никогда не будет точным. В качестве альтернативы, заменяя эти подынтервалы на единицу с высотой левого края каждой части, мы получим слишком низкое приближение: например, с двенадцатой такими подинтервалами мы получим приблизительное значение для области 0,6203.

Ключевая идея заключается в переходе от добавления конечного числа разностей точек аппроксимации, умноженных на их значения функций, к использованию бесконечно большого количества мелких или бесконечно малых шагов. Когда этот переход завершен в приведенном выше примере, оказывается, что площадь под кривой в указанных границах составляет 2/3.

Обозначение

$\int \; f\; (x)\; dx\; \{\backslash \; displaystyle\; \backslash \; int\; f\; (x)\; \backslash \; dx\}$

рассматривает интеграл как взвешенную сумму, обозначенную удлиненную буквой s, значения функции, f (x), умноженное на бесконечно малую ширину шага, так называемые дифференциалы, обозначаемые dx.

Исторически сложилось так, что после провала первая попытка строго интерпретировать бесконечно малые величины, Риман формально определил интегралы как предел взвешенных сумм, так что dx предполагал предел разницы (а именно, ширина интервала). Недостатки зависимости от интервалов и непрерывности использовали новые определения, особенно интеграл Лебега, который основан на способности расширять идею «меры» более гибкими способами. Таким образом, запись

$\int \; A\; f\; (x)\; d\; \mu \; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{A\}\; f\; (x)\; \backslash \; d\; \backslash \; mu\}$

относится к взвешенной сумме, в которой значения функции разделены, причем μ измерение веса, который будет указан каждому значению. Здесь A обозначает область интеграции.

Суммы Дарбу Верхние суммы Дарбу функции y = x Нижние суммы Дарбу функции y = x

Формальные определения

Сходящие суммы Римана

Существует много способов формального определения интеграл, не все из которых эквивалентны. Различия в основном для различных частных случаев, которые не могут быть объединены в соответствии с другими определениями, но также иногда по педагогическим причинам. Наиболее часто используемые интеграла - это интегралы Римана и интегралы Лебега.

Интеграл Римана

Интеграл Римана определяет терминах сумм Римана функций относительно тегированных разбиений интервала. Пусть [a, b] будет отрезком действительной прямой; тогда тегированный раздел [a, b] представляет собой конечную последовательность

$a\; =\; x\; 0\; \le \; t\; 1\; \le \; x\; 1\; \le \; t\; 2\; \le \; x\; 2\; \le \; \cdots \; \le \; x\; n\; -\; 1\; \le \; t\; n\; \le \; x\; n\; =\; b.\; \{\backslash \; displaystyle\; a\; =\; x\_\; \{0\}\; \backslash \; leq\; t\_\; \{1\}\; \backslash \; leq\; x\_\; \{1\}\; \backslash \; leq\; t\_\; \{2\}\; \backslash \; leq\; x\_\; \{2\}\; \backslash \; leq\; \backslash \; cdots\; \backslash \; leq\; x\_\; \{n-1\}\; \backslash \; leq\; t\_\; \{n\; \}\; \backslash \; leq\; x\_\; \{n\}\; =\; б.\; \backslash ,\; \backslash !\}$

Это разбивает интервал [a, b] на n подинтервалов [x i - 1, x i ], индексированный i, каждую из которых «помечена» выделенной точкой t i ∈ [x i-1, x i ]. Сумма Римана функции f относительно такого помеченного разбиения определяется как

$\sum \; i\; =\; 1\; n\; f\; (t\; i)\; \Delta \; i;\; \{\backslash \; displaystyle\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{n\}\; f\; (t\_\; \{i\})\; \backslash ,\; \backslash \; Delta\; \_\; \{i\};\}$

таким образом, каждый член суммы представляет собой площадь прямоугольника с высотой, равной к значению функции в выделенной точке данной подинтервала, а ширина такая же, как ширина подинтервала. Пусть Δ i = x i−xi-1 будет шириной подинтервала i; тогда сетка такого помеченного раздела представляет собой ширину самого большого подинтервала, образованного разделом, max i = 1... n Δi. Интеграл Римана функции f на интервале [a, b] равен S, если:

Для всех ε>0 существует такое δ>0, что для любого помеченного разбиения [a, b] с сеткой меньше, чем δ имеем

Когда выбранные теги дают максимальное (соответственно минимальное) значение каждого интервала, сумма Римана становится (верхней) (верхней) суммой Дарбу, предполагаемая тесная связь между интегралом Римана и Интеграл Дарбу.

Интеграл Лебега

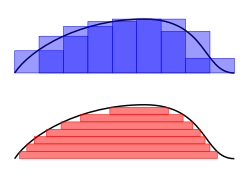Интегрирование Римана - Дарбу (вверху) и интегрирование Лебега (внизу)

Как в теории, так и в приложениях часто представляет возможность перехода к пределу при интеграл. Например, часто можно использовать схему системы, которая в подходящем смысле приближает решение проблемы. Тогда интеграл от функции решения должен быть предел интегралов приближений. Некоторые функции, которые могут быть выполнены как пределы, не интегрируются по Риману, и поэтому такие предельные теоремы не верны с интегралом Римана. Следовательно, очень важное определение интеграла позволяет интегрировать более широкий класс функций (Рудин 1987).

Таким интегралом является интеграл Лебега, который использует следующий факт для расширения класса интегрируемых функций. Так, Анри Лебег ввел интеграл, носящий его имя, объясняя этот интеграл таким образом в письме к Полу Монтелю :

. Я должен заплатить определенную сумму, которую я собрал в своем кармане. Я вынимаю из кармана банкноты и отдаю их кредитору в том порядке, в котором я их нахожу, пока не наберу общую сумму. Это интеграл Римана. Но я могу поступить иначе. После того, как я вынул все деньги из кармана, я заказываю банкноты и монеты по идентичной стоимости, а затем я плачу несколько куч один за другим кредитору. Это мой интеграл.

— Зигмунд-Шульце (2008)

Как пишет Folland (1984, стр. 56): «Чтобы вычислить интеграл Римана от f, нужно разбить область [a, b] на подинтервалы», тогда как в интеграле Лебега «фактически разбивается диапазон значений f». Таким образом, определение интеграла Лебега начинается с меры , μ. В простейшем случае мера Лебега μ (A) интервала A = [a, b] является его шириной, b - a, так что интеграл Лебега согласуется с (собственным) интегралом Римана, когда оба существуют. В более сложных случаях наборы могут быть сильно фрагментированными, без непрерывности и не похожими на интервалы.

Используя философию «разделения диапазона f», интеграл неотрицательной функции f: R→ Rдолжен быть суммой по t площадей между тонкой горизонтальной полосой между y = t и y. = т + дт. Эта область равна μ {x: f (x)>t} dt. Пусть f (t) = μ {x: f (x)>t}. Тогда интеграл Лебега f определяется как (Lieb Loss 2001)

$\int \; f\; =\; \int \; 0\; \infty \; f\; \ast \; (t)\; dt\; \{\backslash \; displaystyle\; \backslash \; int\; f\; =\; \backslash \; int\; \_\; \{0\}\; ^\; \{\backslash \; infty\}\; f\; ^\; \{\; *\}\; (t)\; \backslash ,\; dt\}$

где интеграл справа является обычным несобственным интегралом Римана (f - строго убывающая положительная функция и, следовательно, имеет хорошо известный несобственный Интеграл Римана). измеримые функции ) это определяет интеграл Лебега.

Общая измеримая функция является интегрируемой по Лебегу, если сумма абсолютных значений площади области между графиком f и осью x конечны:

В этом случае интеграл, как и в римановом случае, равенство между площадью над осью x и областью под осью x:

$\int \; E\; fd\; \mu \; =\; \int \; E\; f\; +\; d\; \mu \; -\; \int \; E\; f\; -\; d\; \mu \; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{E\}\; е\; \backslash ,\; d\; \backslash \; mu\; =\; \backslash \; int\; \_\; \{E\}\; f\; ^\; \{+\}\; \backslash ,\; d\; \backslash \; mu\; -\; \backslash \; int\; \_\; \{E\}\; f\; ^\; \{-\}\; \backslash ,\; d\; \backslash \; mu\; \}$

где

Другие интегралы

Хотя интегралы Римана и Лебега наиболее широко используемыми определениями интеграла, существуют ряды, в том числе:

• интеграл Дарбу, который определен Дарбу сумм (ограниченные суммы Римана), но эквивалент интегралу Римана - функция интегрируемой по Дарбу тогда и только тогда, когда она интегрируется по Риману. Интегралы Дарбу имеют то преимущество, что их легче определить, чем интегралы Римана.
• Интеграл Римана – Стилтьеса, расширение интеграла Римана, который интегрируется по функции, а не по переменной.
• Интеграл Лебега – Стилтьеса, развитый Иоганном Радоном, который обобщает как интегралы Римана – Стилтьеса, так и интегралы Лебега.
• интеграл Даниэля, который включает интеграл Лебега и интеграл Лебега – Стилтьеса без зависимости от мер.
• интеграл Хаара, используемый для интегрирования на локально компактных топологические группы, введенные Альфредом Хааром в 1933 году.
• Интеграл Хенстока – Курцвейла, по-разному определяемый Арно Данжуа, Оскаром Перрон и (наиболее элегантно, как калибровочный интеграл) Ярослав Курцвейл, разработанный Ральфом Хенстоком.
• интеграл Ито и интеграл Стратоновича, которые определяют интегрирование по семимартингалам, таким как Броуновское движение.
• Интеграл Юнга, который является своего рода интегралом Римана – Стилтьеса относительно некоторых функций от неограниченное изменение.
• Интеграл грубого пути, который определен для функций, снабженных некоторой дополнительной структурой «грубого пути» и обобщает стохастическое интегрирование как для семимартингалов, так и для таких процессов, как 291>дробное броуновское движение.
• интеграл Шоке, субаддитивный или супераддитивный интеграл, созданный французским математиком Гюставом Шоке в 1953 году.

Свойства

Линейность

Набор функций, интегрируемых по Риману на отрезке [a, b], образует векторное пространство с помощью операций поточечного сложения и умножения на скаляр, а также операции интегрирования

$f\; \mapsto \; \int \; abf\; (x)\; dx\; \{\backslash \; displaystyle\; f\; \backslash \; mapsto\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; f\; (x)\; \backslash ;\; dx\}$

- это линейная функция onal на этом векторном пространстве. Таким образом, во-первых, набор интегрируемых функций замыкается относительно взятия линейных комбинаций ; и, во-вторых, интеграл линейной комбинации - это линейная комбинация интегралов,

$\int \; ab\; (\alpha \; f\; +\; \beta \; g)\; (x)\; dx\; =\; \alpha \; \int \; abf\; (x)\; dx\; +\; \beta \; \int \; abg\; (x)\; dx.\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; (\backslash \; alpha\; f\; +\; \backslash \; beta\; g)\; (x)\; \backslash ,\; dx\; =\; \backslash \; alpha\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; f\; (x)\; \backslash ,\; dx\; +\; \backslash \; beta\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; g\; (x)\; \backslash ,\; dx.\; \backslash ,\}$

Аналогично, набор вещественных -значных интегрируемых по Лебегу функций на заданном пространстве с мерой E с мерой μ замкнут относительно взятия линейных комбинаций и, следовательно, образуют векторное пространство, а интеграл Лебега

$f\; \mapsto \; \int \; E\; fd\; \mu \; \{\backslash \; displaystyle\; f\; \backslash \; mapsto\; \backslash \; int\; \_\; \{E\}\; f\; \backslash ,\; d\; \backslash \; mu\; \}$

является линейным функционалом в этом векторном пространстве, так что

$\int \; E\; (\alpha \; f\; +\; \beta \; g)\; d\; \mu \; =\; \alpha \; \int \; E\; fd\; \mu \; +\; \beta \; \int \; E\; gd\; \mu .\; \{\backslash \; Displaystyle\; \backslash \; int\; \_\; \{E\}\; (\backslash \; альфа\; е\; +\; \backslash \; бета\; г)\; \backslash ,\; d\; \backslash \; му\; =\; \backslash \; альфа\; \backslash \; int\; \_\; \{E\}\; f\; \backslash ,\; d\; \backslash \; му\; +\; \backslash \; бета\; \backslash \; int\; \_\; \{E\}\; g\; \backslash ,\; d\; \backslash \; mu.\}$

В более общем плане рассмотрим векторное пространство всех измеримых функций на пространстве с мерой (E, μ), принимающих значения в локально компактном полном топологическое векторное пространство V над локально компактным топологическим полем K, f: E → V. Тогда можно определить абстрактную карту интегрирования, присваивая каждой функции f элемент из V или символ ∞,

$f\; \mapsto \; \int \; E\; fd\; \mu ,\; \{\backslash \; displaystyle\; f\; \backslash \; mapsto\; \backslash \; int\; \_\; \{E\}\; f\; \backslash ,\; d\; \backslash \; mu,\; \backslash ,\}$

, который совместим с линейными комбинациями. В этой ситуации линейность сохраняется для подпространства функций, интеграл которых является элементом V (т.е. «конечным»). Наиболее важные частные случаи возникают, когда K равно R, Cили конечное расширение поля Qpиз p-адических чисел, и V - конечномерное векторное пространство над K, и когда K = C и V представляет собой сложное гильбертово пространство.

Линейность вместе с некоторыми естественными свойствами непрерывности и нормализацией для определенного класса «простых» функций может использоваться, чтобы дать альтернативное определение интеграл. Это подход Даниэля для случая вещественнозначных функций на множестве X, обобщенный Николасом Бурбаки на функции со значениями в локально компактном топологическом векторном пространстве. См. (Hildebrandt 1953) для аксиоматической характеристики интеграла.

Неравенства

Ряд общих неравенств сохраняется для Riem ann-интегрируемые функции, верх на замкнутом и ограниченном интервале [a, b] и могут быть обобщены другие понятия интегрального (Лебег и Даниэль).

• Верхняя и нижняя границы. Интегрируемая функция f на [a, b] обязательно ограничена на этом интервале. Таким образом существует вещественных чисел m и M, так что m ≤ f (x) ≤ M для всех x в [a, b]. Нижняя первая и верхняя сумма f по [a, b] ограничены соответственно m (b - a) и M (b - a), то

$m\; (b\; -\; a)\; \le \; \int \; abf\; (x)\; dx\; \le \; M\; (b\; -\; а).\; \{\backslash \; displaystyle\; m\; (b-a)\; \backslash \; leq\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; f\; (x)\; \backslash ,\; dx\; \backslash \; leq\; M\; (b-a).\}$

• Неравенства между функциями. Если f (x) ≤ g (x) для каждого x в [a, b], то каждая из верхней и нижней сумм f ограничена сверху и верхней нижней суммой, соответственно, g. Таким образом,

$\int \; a\; b\; f\; (x)\; d\; x\; \le \; \int \; a\; b\; g\; (x)\; d\; x.\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; f\; (x)\; \backslash ,\; dx\; \backslash \; leq\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; g\; (x)\; \backslash ,\; dx.\}$

Это обобщение выше неравенства, так как M (b - a) является интегралом постоянной функции со значением M по [a, b].

Кроме того, если неравенство между функциями строго, то неравенство между интегралами тоже строгий. То есть, если f (x) < g(x) for each x in [a, b], then

• Подынтервалы. Если [c, d] является подинтервалом [a, b] и f (x) неотрицательно для всех x, то

$\int \; c\; d\; f\; (x)\; d\; x\; \le \; \int \; a\; b\; f\; (x)\; d\; x.\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{c\}\; ^\; \{d\}\; f\; (x)\; \backslash ,\; dx\; \backslash \; leq\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; f\; (x)\; \backslash ,\; dx.\}$

• Произведения и абсолютные значения функций. Если f и g - две функции, то мы можем рассматривать их точечные произведения и мощность, а также абсолютные значения :

$(fg)\; (x)\; =\; f\; (x)\; g\; (x),\; f\; 2\; (x)\; =\; (f\; (x))\; 2,\; |\; f\; |\; (x)\; =\; |\; f\; (x)\; |.\; \{\backslash \; Displaystyle\; (fg)\; (х)\; =\; е\; (х)\; г\; (х),\; \backslash ;\; е\; ^\; \{2\}\; (х)\; =\; (е\; (х))\; ^\; \{2\},\; \backslash ;\; |\; е\; |\; (х)\; =\; |\; f\; (x)\; |,\; \backslash ,\}$

Если f интегрируем по Риману на [a, b], то то же самое верно и для | f |, и

$|\; \int \; a\; b\; f\; (x)\; d\; x\; |\; \le \; \int \; a\; b\; |\; f\; (x)\; |\; d\; x.\; \{\backslash \; displaystyle\; \backslash \; left\; |\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; f\; (x)\; \backslash ,\; dx\; \backslash \; right\; |\; \backslash \; leq\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; |\; f\; (x)\; |\; \backslash ,\; dx.\}$

Более того, если f и g интегрируются по Риману, то fg также интегрируем по Риману и

$(\int \; ab\; (fg)\; (x)\; dx)\; 2\; \le \; (\int \; abf\; (x)\; 2\; dx)\; (\int \; abg\; (x)\; 2\; dx).\; \{\backslash \; displaystyle\; \backslash \; left\; (\backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; (fg)\; (x)\; \backslash ,\; dx\; \backslash \; right)\; ^\; \{2\}\; \backslash \; leq\; \backslash \; left\; (\backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; f\; (x)\; ^\; \{2\}\; \backslash ,\; dx\; \backslash \; right)\; \backslash \; left\; (\backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; g\; (x)\; ^\; \{2\}\; \backslash ,\; dx\; \backslash \; right).\}$

Это неравенство, известное как Неравенство Коши-Шварца играет важную роль в теории гильбертова, где левая часть интерпретируется как внутреннее произведение двух интегрируемых с квадратом функции f и g на интервале [а, б].

• Неравенство Гёльдера. Предположим, что p и q - два действительных числа, 1 ≤ p, q ≤ ∞, причем 1 / p + 1 / q = 1, а f и g - две интегрируемые по Риману функции. Тогда функции | f | и | г | также интегрируются и выполняется следующее неравенство Гёльдера :

$|\; \int \; f\; (x)\; g\; (x)\; d\; x\; |\; \le \; (\int \; |\; f\; (x)\; |\; p\; d\; x)\; 1\; /\; p\; (\int \; |\; g\; (x)\; |\; q\; d\; x)\; 1\; /\; q.\; \{\backslash \; Displaystyle\; \backslash \; влево\; |\; \backslash \; int\; е\; (х)\; г\; (х)\; \backslash ,\; dx\; \backslash \; вправо\; |\; \backslash \; leq\; \backslash \; влево\; (\backslash \; int\; \backslash \; влево\; |\; е\; (х)\; \backslash \; вправо\; |\; ^\; \{p\}\; \backslash ,\; dx\; \backslash \; вправо)\; ^\; \{1\; /\; p\}\; \backslash \; left\; (\backslash \; int\; \backslash \; left\; |\; g\; (x)\; \backslash \; right\; |\; ^\; \{\; q\}\; \backslash ,\; dx\; \backslash \; right)\; ^\; \{1\; /\; q\}.\}$

Для p = q = 2 неравенство Гёльдера переходит в неравенство Коши - Шварца.

• Неравенство Минковского. Предположим, что p ≥ 1 - действительное число, а f и g - функции, интегрируемые по Риману. Тогда | f |, | г | и | f + g | также интегрируемы по Риману и выполняются следующие неравенство Миненствоковского :

$(\int \; |\; f\; (x)\; +\; g\; (x)\; |\; pdx)\; 1\; /\; p\; \le \; (\int \; |\; f\; (x)\; |\; pdx)\; 1\; /\; р\; +\; (\int \; |\; g\; (x)\; |\; pdx)\; 1\; /\; р.\; \{\backslash \; Displaystyle\; \backslash \; left\; (\backslash \; int\; \backslash \; left\; |\; е\; (х)\; +\; g\; (x)\; \backslash \; right\; |\; ^\; \{p\}\; \backslash ,\; dx\; \backslash \; right)\; ^\; \{1\; /\; p\}\; \backslash \; leq\; \backslash \; left\; (\backslash \; int\; \backslash \; left\; |\; f\; (x)\; \backslash \; right\; |\; ^\; \{p\}\; \backslash ,\; dx\; \backslash \; right)\; ^\; \{1\; /\; p\}\; +\; \backslash \; left\; (\backslash \; int\; \backslash \; left\; |\; g\; (x)\; \backslash \; right\; |\; ^\; \{p\}\; \backslash ,\; dx\; \backslash \; right)\; ^\; \{\; 1\; /\; p\}.\}$

Аналог этого неравенства для интеграла Лебега используется при построении L пространств.

Условные обозначения

В этом разделе f является вещественным Интегрируемая по Риману <250 функция>. Интеграл

$\int \; abf\; (x)\; dx\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; f\; (x)\; \backslash ,\; dx\}$

на интервале [a, b] определен, если a < b. This means that the upper and lower sums of the function f are evaluated on a partition a = x0 ≤ x 1 ≤... ≤ x n = b, значения которого x i увеличиваются. Геометрически это означает, что интегрирование происходит «слева направо», оценка f в пределах интервалов [x i, x i +1 ], где интервал с более высоким индексом лежит справа. одного с более низким индексом. Значения a и b, конечные точки интервала , называются интегрирования f. Интегралы также могут быть, если a>b:

• Обратные пределы интегрирования. Если a>b, то определим

$\int \; a\; b\; f\; (x)\; d\; x\; =\; -\; \int \; b\; a\; f\; (x)\; d\; x.\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; f\; (x)\; \backslash ,\; dx\; =\; -\; \backslash \; int\; \_\; \{b\}\; ^\; \{a\}\; f\; (x)\; \backslash ,\; dx.\}$

Это с a = b, означает:

• Интегралы по интервалам нулевой длины. Если a действительное число, то

$\int \; aaf\; (x)\; dx\; =\; 0.\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{a\}\; ^\; \{a\}\; f\; (x)\; \backslash ,\; dx\; =\; 0.\}$

Первое соглашение необходимо при рассмотрении интегралов по подотрезкам [a, b]; второй говорит, что интеграл, взятый по вырожденному интервалу, или точке, должен быть нулем. Одна из причин первого соглашения состоит в том, что интегрируемость f на интервале [a, b] подразумевает, что f интегрируемо на любом подынтервале [c, d], но, в частности, интегралы обладают следующим свойством:

• Аддитивность интегрирования на интервалы. Если c - любой элемент из [a, b], то

$\int \; a\; b\; f\; (x)\; d\; x\; =\; \int \; a\; c\; f\; (x)\; d\; x\; +\; \int \; c\; b\; f\; (x)\; d\; x.\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; f\; (x)\; \backslash ,\; dx\; =\; \backslash \; int\; \_\; \{a\}\; ^\; \{c\}\; f\; (x)\; \backslash ,\; dx\; +\; \backslash \; int\; \_\; \{c\}\; ^\; \{b\}\; f\; (\; x)\; \backslash ,\; dx.\}$

Согласно первому соглашению, результирующее отношение

$\int \; acf\; (x)\; dx\; =\; \int \; abf\; (x)\; dx\; -\; \int \; cbf\; (x)\; dx\; =\; \int \; abf\; (x)\; dx\; +\; \int \; bcf\; (x)\; dx\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; int\; \_\; \{a\}\; ^\; \{c\}\; f\; (x)\; \backslash ,\; dx\; \{\}\; =\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; f\; (x)\; \backslash ,\; dx-\; \backslash \; int\; \_\; \{c\}\; ^\; \{b\}\; f\; (x)\; \backslash ,\; dx\; \backslash \backslash \; \{\}\; =\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; f\; (x)\; \backslash ,\; dx\; +\; \backslash \; int\; \_\; \{b\}\; ^\; \{\; c\}\; f\; (x)\; \backslash ,\; dx\; \backslash \; end\; \{выравнивание\}\}\}$

тогда хорошо определено для любой циклической перестановки a, b и c.

Основная теорема исчисления

Основная теорема исчисления - это утверждение, что дифференцирование и интегрирование являются обратными операциями: если непрерывная функция является первой После интеграции и дифференцирования восстанавливается исходная функция. Важное следствие, которое иногда называют второй фундаментальной теоремой исчисления, позволяет вычислять интегралы, используя первообразную интегрируемой функции.

Формулировки теорем

Основная теорема исчисления

Пусть f - непрерывная функция с действительными значениями, определенная на закрытом интервале [a, b]. Пусть F - функция, определенная для всех x в [a, b] формулой

$F\; (x)\; =\; \int \; a\; x\; f\; (t)\; d\; t.\; \{\backslash \; displaystyle\; F\; (x)\; =\; \backslash \; int\; \_\; \{a\}\; ^\; \{x\}\; f\; (t)\; \backslash ,\; dt.\}$

Тогда F непрерывна на [a, b], дифференцируема на открытом интервале (a, b) и

$F\; \prime \; (x)\; =\; f\; (x)\; \{\backslash \; displaystyle\; F\; \text{'}(x)\; =\; f\; (x)\}$

для всех x в (a, b).

Вторая фундаментальная теорема исчисления

Пусть f - функция с действительными значениями, определенная на закрытом интервале [a, b], который допускает первообразную F на [a, b]. То есть f и F являются такими функциями, что для всех x в [a, b]

$f\; (x)\; =\; F\; \prime \; (x).\; \{\backslash \; displaystyle\; f\; (x)\; =\; F\; \text{'}(x).\}$

Если f интегрируемо на [a, b], то

$\int \; a\; b\; f\; (x)\; d\; x\; =\; F\; (b)\; -\; F\; (a).\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; f\; (x)\; \backslash ,\; dx\; =\; F\; (b)\; -F\; (a).\}$

Вычисление интегралов

Вторая фундаментальная теорема допускает множество интегралов рассчитываться явно. Например, чтобы вычислить интеграл

$\int \; 0\; 1\; x\; 1/2\; dx,\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{0\}\; ^\; \{1\}\; x\; ^\; \{1/2\}\; \backslash ,\; dx,\}$

квадрата корневая функция f (x) = x между 0 и 1, достаточно найти первообразную, то есть функцию F (x), производная которой равна f (x):

$F\; \prime \; (x)\; =\; f\; (x).\; \{\backslash \; displaystyle\; F\; \text{'}(x)\; =\; f\; (x).\}$

Одна из таких функций: $F\; (x)\; =\; 2\; 3\; x\; 3/2\; \{\backslash \; displaystyle\; F\; (x)\; =\; \{\backslash \; tfrac\; \{2\}\; \{3\}\}\; x\; ^\; \{3/2\}\}$. Тогда значение рассматриваемого интеграла

$\int \; 0\; 1\; x\; 1/2\; dx\; =\; F\; (1)\; -\; F\; (0)\; =\; 2\; 3\; (1)\; 3/2\; -\; 2\; 3\; (0)\; 3/2\; =\; 2\; 3.\; \{\backslash \; Displaystyle\; \backslash \; int\; \_\; \{0\}\; ^\; \{1\}\; х\; ^\; \{1/2\}\; \backslash ,\; dx\; \backslash \; =\; \backslash \; F\; (1)\; -F\; (0)\; \backslash \; =\; \backslash \; \{\backslash \; tfrac\; \{2\}\; \{3\}\}\; (1)\; ^\; \{3/2\}\; -\; \{\backslash \; tfrac\; \{2\}\; \{3\}\}\; (0)\; ^\; \{3/2\}\; \backslash \; =\; \backslash \; \{\backslash \; tfrac\; \{2\}\; \{3\}\}.\}$

Это случай общее правило: для $f\; (x)\; =\; xq\; \{\backslash \; displaystyle\; f\; (x)\; =\; x\; ^\; \{q\}\}$с $q\; \ne \; -\; 1\; \{\backslash \; displaystyle\; q\; \backslash \; neq\; -1\}$, первообразная - это $F\; (x)\; =\; 1\; q\; +\; 1\; xq\; +\; 1\; \{\backslash \; displaystyle\; F\; (x)\; =\; \{\backslash \; tfrac\; \{1\}\; \{q\; +\; 1\}\}\; x\; ^\; \{q\; +\; 1\}\}$. Таблицы этой и подобных первообразных могут использоваться для явного вычисления интегралов, почти так же, как производные могут быть получены из таблиц.

Расширения

Неправильные интегралы

Несобственный интеграл. $\int \; 0\; \infty \; dx\; (x\; +\; 1)\; x\; =\; \pi \; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{0\}\; ^\; \{\; \backslash \; infty\}\; \{\backslash \; frac\; \{dx\}\; \{(x\; +\; 1)\; \{\backslash \; sqrt\; \{x\}\}\}\}\; =\; \backslash \; pi\}$. имеет неограниченные интервалы как для домена, так и для диапазона.

«Правильный» интеграл Римана предполагает подынтегральная функция определена и конечна на замкнутом и ограниченном интервале, заключенном в скобки пределами интегрирования. Несобственный интеграл возникает, когда одно или несколько из этих условий не выполняются. В некоторых случаях такие интегралы могут быть определены путем рассмотрения предела последовательности правильных интегралов Римана на постепенно увеличивающихся интервалах.

Если интервал неограничен, например, на его верхнем конце, то неправильный интеграл является пределом, поскольку эта конечная точка уходит в бесконечность.

$\int \; a\; \infty \; е\; (Икс)\; dx\; =\; lim\; b\; \to \; \infty \; \int \; abf\; (x)\; dx\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{a\}\; ^\; \{\backslash \; infty\}\; f\; (x)\; \backslash ,\; dx\; =\; \backslash \; lim\; \_\; \{b\; \backslash \; to\; \backslash \; infty\}\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; f\; (x)\; \backslash ,\; dx\}$

Если подынтегральная функция определена или конечна только на полуоткрытом интервале, например (a, b], то снова предел может дать конечный результат.

$\int \; abf\; (x)\; dx\; =\; lim\; \epsilon \; \to \; 0\; \int \; a\; +\; ϵ\; bf\; (x)\; dx\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; f\; (x)\; \backslash ,\; dx\; =\; \backslash \; lim\; \_\; \{\backslash \; varepsilon\; \backslash \; to\; 0\}\; \backslash \; int\; \_\; \{a\; +\; \backslash \; epsilon\}\; ^\; \{b\}\; f\; (x)\; \backslash ,\; dx\}$

То есть, неправильный интеграл - это предел собственных интегралов, когда одна конечная точка интервала интегрирования приближается либо к заданному действительному числу, либо к ∞, либо к −∞. В более сложных случаях требуются пределы на обеих конечных точках или во внутренних точках.

Множественное интегрирование

Двойной интеграл вычисляет объем под поверхностью $z\; =\; f\; (x,\; y)\; \{\backslash \; displaystyle\; z\; =\; f\; (x,\; y)\}$

Так же, как определенный интеграл от положительного Функция одной переменной представляет собой область области между графиком функции и На оси абсцисс двойной интеграл от положительной функции двух переменных представляет собой объем области между поверхностью, определяемой функцией, и плоскостью, содержащей ее область. Например, функция в двух измерениях зависит от двух вещественных переменных, x и y, и интеграла функции f по прямоугольнику R, заданному как декартово произведение двух интервалов $R\; =\; [a,\; b]\; \times \; [c,\; d]\; \{\backslash \; displaystyle\; R\; =\; [a,\; b]\; \backslash \; times\; [c,\; d]\}$может быть записано

$\int \; R\; f\; (x,\; y)\; d\; A\; \{\; \backslash \; displaystyle\; \backslash \; int\; \_\; \{R\}\; f\; (x,\; y)\; \backslash ,\; dA\}$

где дифференциал dA указывает, что интегрирование производится по площади. Этот двойной интеграл может быть определен с помощью сумм Римана и представляет (подписанный) объем под графиком z = f (x, y) в области R. При подходящих условиях ( например, если f непрерывна), теорема Фубини утверждает, что этот интеграл может быть выражен как эквивалентный повторный интеграл

$\int \; ab\; [\int \; cdf\; (x,\; y)\; dy]\; dx.\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; \backslash \; left\; [\backslash \; int\; \_\; \{c\}\; ^\; \{d\}\; f\; (x,\; y)\; \backslash ,\; dy\; \backslash \; right]\; \backslash ,\; dx.\}$

Это уменьшает проблему вычисления двойного интеграла к вычислению одномерных интегралов. По этой причине в другом обозначении интеграла по R используется знак двойного интеграла:

$\iint \; R\; f\; (x,\; y)\; d\; A.\; \{\backslash \; displaystyle\; \backslash \; iint\; \_\; \{R\}\; f\; (x,\; y)\; \backslash ,\; dA.\}$

Возможна интеграция по более общим областям. Интеграл функции f по объему по n-мерной области D из $R\; n\; \{\backslash \; displaystyle\; \backslash \; mathbb\; \{R\}\; ^\; \{n\}\}$обозначается такими символами, как :

$\int \; D\; f\; (x)\; dnx\; =\; \int \; D\; fd\; V.\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{D\}\; f\; (\backslash \; mathbf\; \{x\})\; d\; ^\; \{n\}\; \backslash \; mathbf\; \{x\}\; \backslash \; =\; \backslash \; int\; \_\; \{D\}\; f\; \backslash ,\; dV.\}$

Линейные интегралы

A линейный интеграл суммирует элементы вдоль кривой.

Концепция интеграла может быть расширена на более общие области интегрирования, такие как кривые линии и поверхности внутри пространств более высокой размерности. Такие интегралы известны как линейные интегралы и поверхностные интегралы соответственно. У них есть важные приложения в физике, например, при работе с векторными полями .

линейный интеграл (иногда называемый интегралом по путям) - это интеграл, в котором интегрируемая функция вычисляется по кривая. Используются различные линейные интегралы. В случае замкнутой кривой он также называется контурным интегралом.

Интегрируемая функция может быть скалярным полем или векторным полем . Значение линейного интеграла представляет собой сумму значений поля во всех точках кривой, взвешенных некоторой скалярной функцией на кривой (обычно длина дуги или, для векторного поля, скалярное произведение векторного поля с вектором дифференциалом на кривой). Это взвешивание отличает линейный интеграл от более простых интегралов, определенных на интервалах. Многие простые формулы в физике имеют естественные непрерывные аналоги в терминах линейных интегралов; например, тот факт, что работа равна сила, F, умноженная на смещение, s, может быть выражено (в терминах векторных величин) как:

$W\; =\; F\; \cdot \; s.\; \{\backslash \; displaystyle\; W\; =\; \backslash \; mathbf\; \{F\}\; \backslash \; cdot\; \backslash \; mathbf\; \{s\}.\}$

Для объекта, движущегося по пути C в векторном поле F, таком как электрическое поле или гравитационное поле, общая работа, выполняемая полем над объектом, получается путем суммирования дифференциальной работы, совершенной при перемещении от s к s + d с . Это дает линейный интеграл

$W\; =\; \int \; C\; F\; \cdot \; d\; s.\; \{\backslash \; displaystyle\; W\; =\; \backslash \; int\; \_\; \{C\}\; \backslash \; mathbf\; \{F\}\; \backslash \; cdot\; d\; \backslash \; mathbf\; \{s\}.\}$

Поверхностные интегралы

Определение поверхностного интеграла основывается на разделении поверхности на небольшие элементы поверхности.

Поверхностный интеграл обобщает двойные интегралы для интегрирования по поверхности (которая может быть криволинейным набором в пространстве ); его можно рассматривать как двойной интеграл аналог линейного интеграла . Интегрируемая функция может быть скалярным полем или векторным полем. Величина поверхностного интеграла представляет собой сумму поля во всех точках на поверхности. Это может быть достигнуто путем разбиения поверхности на элементы поверхности, которые обеспечивают разбиение для сумм Римана.

В качестве примера применения поверхностных интегралов рассмотрим векторное поле v на поверхности S; то есть для каждой точки x в S, v (x) является вектором. Представьте, что у нас есть жидкость, протекающая через S, так что v (x) определяет скорость жидкости в точке x. поток определяется как количество жидкости, протекающей через S в единицу времени. Чтобы найти поток, нам нужно взять скалярное произведение из v с единицей нормали поверхности к S в каждой точке, что даст нам скалярное поле, которые интегрируем по поверхности:

$\int \; S\; v\; \cdot \; d\; S.\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{S\}\; \{\backslash \; mathbf\; \{v\}\}\; \backslash \; cdot\; \backslash ,\; d\; \{\backslash \; mathbf\; \{S\}\}.\}$

Поток жидкости в этом примере может исходить от физической жидкости, такой как вода или воздух., или от электрического или магнитного потока. Таким образом, поверхностные интегралы имеют приложения в физике, в частности, в классической теории электромагнетизма.

Контурные интегралы

В комплексном анализе подынтегральное выражение - это комплексная функция комплексной переменной z вместо действительной функции действительной переменной x. Когда комплексная функция интегрируется по кривой $\gamma \; \{\backslash \; displaystyle\; \backslash \; gamma\}$в комплексной плоскости, интеграл обозначается следующим образом:

$\int \; \gamma \; f\; (z)\; d\; z.\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{\backslash \; gamma\}\; f\; (z)\; \backslash ,\; dz.\}$

Это известно как контурный интеграл.

Интегралы дифференциальных форм

A дифференциальная форма является математическим понятие в полях исчисления с несколькими переменными, дифференциальной топологии и тензоров. Дифференциальные формы организованы по степени. Например, единичная форма - это взвешенная сумма дифференциалов координат, например:

$E\; (x,\; y,\; z)\; dx\; +\; F\; (x,\; y,\; z)\; dy\; +\; G\; (x,\; y,\; z)\; dz\; \{\backslash \; displaystyle\; E\; (x,\; y,\; z)\; \backslash ,\; dx\; +\; F\; (x,\; y,\; z)\; \backslash ,\; dy\; +\; G\; (x,\; y,\; z)\; \backslash ,\; dz\}$

где E, F, G - это функции в трех измерениях. Дифференциальная одна форма может быть интегрирована по ориентированному пути, и полученный интеграл - это просто еще один способ записи линейного интеграла. Здесь основные дифференциалы dx, dy, dz измеряют бесконечно малые ориентированные длины, параллельные трем координатным осям.

Дифференциальная двойная форма - это сумма вида

$G\; (x,\; y,\; z)\; dx\; \wedge \; dy\; +\; E\; (x,\; y,\; z)\; dy\; \wedge \; dz\; +\; F\; (x,\; y,\; г)\; dz\; \wedge \; dx.\; \{\backslash \; Displaystyle\; G\; (x,\; y,\; z)\; \backslash ,\; dx\; \backslash \; клин\; dy\; +\; E\; (x,\; y,\; z)\; \backslash ,\; dy\; \backslash \; wedge\; dz\; +\; F\; (x,\; y,\; z)\; \backslash ,\; dz\; \backslash \; wedge\; dx.\}$

Здесь основные две формы $dx\; \wedge \; dy,\; dz\; \wedge \; dx,\; dy\; \wedge \; dz\; \{\backslash \; displaystyle\; dx\; \backslash \; wedge\; dy,\; dz\; \backslash \; wedge\; dx,\; dy\; \backslash \; wedge\; dz\}$измеряют параллельные ориентированные области в координатные двухплоскости. Символ $\wedge \; \{\backslash \; displaystyle\; \backslash \; wedge\}$обозначает произведение клина, которое аналогично перекрестному произведению в том смысле, что произведение клина две формы, представляющие ориентированные длины, представляют собой ориентированную область. Две формы могут быть интегрированы по ориентированной поверхности, и полученный интеграл эквивалентен поверхностному интегралу, дающему поток $E\; i\; +\; F\; j\; +\; G\; k\; \{\backslash \; displaystyle\; E\; \backslash \; mathbf\; \{i\}\; +\; F\; \backslash \; mathbf\; \{j\}\; +\; G\; \backslash \; mathbf\; \{k\}\}$.

В отличие от векторного произведения и трехмерного векторного исчисления, произведение клина и исчисление дифференциальных форм имеет смысл в произвольной размерности и на более общих многообразиях (кривые, поверхности, и их многомерные аналоги). внешняя производная играет роль градиента и curl векторного исчисления, а теорема Стокса одновременно обобщает три теоремы вектора исчисление: теорема о расходимости, теорема Грина и теорема Кельвина-Стокса.

Суммирование

Дискретный эквивалент интегрирования - суммирование. Суммирования и интегралы могут быть положены на один и тот же фундамент, используя теорию интегралов Лебега или исчисление временной шкалы.

Вычисление

Аналитический

Самый простой метод для вычисления определенных интегралов одной действительной переменной основан на фундаментальной теореме исчисления. Пусть f (x) - функция от x, которую нужно проинтегрировать на заданном интервале [a, b]. Затем найдите первообразную f; то есть функция F такая, что F ′ = f на интервале. Если подынтегральное выражение и интеграл не имеют особенностей на пути интегрирования, по основной теореме исчисления

$\int \; a\; b\; f\; (x)\; d\; x\; =\; F\; (b)\; -\; F\; (a).\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; f\; (x)\; \backslash ,\; dx\; =\; F\; (b)\; -F\; (a).\}$

Интеграл на самом деле не первообразная, но фундаментальная теорема предоставляет способ использовать первообразные для вычисления определенных интегралов.

Самый сложный шаг - обычно найти первообразную f. Редко бывает возможно взглянуть на функцию и записать ее первообразную. Чаще всего необходимо использовать один из многих методов, которые были разработаны для вычисления интегралов. Большинство этих методов переписывают один интеграл как другой, что, надеюсь, более поддается обработке. Методы включают:

• Интегрирование с помощью замены
• Интегрирование по частям
• Интегрирование с обратной функцией
• Изменение порядка интегрирования
• Интегрирование с помощью тригонометрической подстановки
• Подстановка касательного половинного угла
• Интегрирование по частям дроби
• Интегрирование по формулам редукции
• Интегрирование с использованием параметрических производных
• Интегрирование с использованием формулы Эйлера
• Замена Эйлера
• Дифференциация под знаком интеграла
• Контурное интегрирование

Существуют альтернативные методы вычисления более сложных интегралы. Многие неэлементарные интегралы могут быть разложены в ряд Тейлора и интегрированы почленно. Иногда полученный бесконечный ряд можно суммировать аналитически. Также можно использовать метод свертки с использованием G-функций Мейера, предполагая, что подынтегральное выражение может быть записано как произведение G-функций Мейера. Есть также много менее распространенных способов вычисления определенных интегралов; например, идентификатор Парсеваля может использоваться для преобразования интеграла по прямоугольной области в бесконечную сумму. Иногда интеграл можно вычислить с помощью уловки; в качестве примера см. Интеграл Гаусса.

Вычисления объемов тел вращения обычно можно выполнить с помощью интеграции диска или интеграции оболочки.

Конкретные результаты, полученные с помощью различных методов, собраны в списке интегралов.

Символьные

Многие задачи в математике, физике и технике связаны с интегрированием, когда требуется явная формула для интеграла.. С этой целью на протяжении многих лет были составлены и опубликованы обширные таблицы интегралов. С распространением компьютеров многие профессионалы, преподаватели и студенты обратились к системам компьютерной алгебры, специально разработанным для выполнения сложных или утомительных задач, включая интеграцию. Символическая интеграция была одной из мотиваций для разработки первых таких систем, таких как Macsyma и Maple.

. Основная математическая трудность при символической интеграции заключается в том, что во многих случаях закрытая формула для первообразной довольно простой на вид функции не существует. Например, известно, что первообразные функций exp (x), x и (sin x) / x не могут быть выражены в замкнутой форме, включая только рациональные и экспоненциальные функции., логарифм, тригонометрические функции и обратные тригонометрические функции, а также операции умножения и композиции; другими словами, ни одна из трех данных функций не интегрируема в элементарных функциях, которые могут быть построены из рациональных функций, корней многочлена, логарифма и экспоненциальных функций.. Алгоритм Риша обеспечивает общий критерий для определения, является ли первообразная элементарной функции элементарной, и, если это так, для ее вычисления. К сожалению, оказывается, что функции с замкнутыми выражениями первообразных являются скорее исключением, чем правилом. Следовательно, компьютеризированные системы алгебры не имеют никакой надежды найти первообразную для случайно построенной элементарной функции. С положительной стороны, если «строительные блоки» первообразных фиксированы заранее, все еще может быть возможно решить, может ли первообразное данной функции быть выражено с помощью этих блоков и операций умножения и композиции, а также найти символическое ответьте, когда он существует. Алгоритм Риша, реализованный в Mathematica, Maple и других системах компьютерной алгебры, делает именно это для функций и первообразных, построенных из рациональных функций., радикалы, логарифм и экспоненциальные функции.

Некоторые особые подынтегральные выражения встречаются достаточно часто, чтобы требовать специального изучения. В частности, может быть полезно иметь в наборе первообразных специальные функции (такие как функции Лежандра, гипергеометрическая функция, гамма-функция, неполная гамма-функция и т. д. - см. Символьная интеграция для более подробной информации). Расширение алгоритма Риша для включениятаких функций возможно, но является сложной сложной задачей, являющейся предметом активных исследований.

Совсем недавно появился новый подход, использующий D-конечные функции, которые являются решениями линейных дифференциальных уравнений с полиномиальными коэффициентами. Большинство элементарных и специальных функций являются D-конечными функциями, а интеграл от D-конечной функции также является D-конечной функцией. Это алгоритм для выражения первообразной D-конечной функции решения дифференциального уравнения.

Эта теория также позволяет вычислить интеграл D-функции как сумму ряда, заданного первыми коэффициентами, и алгоритм для вычисления любого коэффициента.

Числовой

Некоторые интегралы, встречающиеся в реальных приложениях, могут быть вычислены с помощью первообразных в замкнутой форме. Другие не так любезны. Некоторые первообразные не имеют закрытых форм, некоторые закрытые формы требуют специальных функций, которые сами по себе сложно вычислить, что поиск точного ответа происходит слишком медленно. Это мотивирует изучение и применение численных приближений интегралов. Этот предмет, называемый численным интегрированием или числовой квадратурой, возник на раннем этапе изучения интегрирования с целью проведения ручных вычислений. Развитие компьютеров общего назначения сделало численное интегрирование более практичное и вызвало улучшений. Целями численного интегрирования являются точность, надежность, эффективность и универсальность, сложные современные методы могут значительно превзойти наивные методы по всем параметрам параметрам (Dahlquist Björck 2008 ; Kahaner, Moler Nash 1989 ; Stoer Bulirsch 2002).

Рассмотрим, например, интеграл

$-\; 2\; 2\; 1\; 5\; (1\; 100\; (322\; +\; 3\; x\; (98\; +\; x\; (37\; +\; x)))\; -\; 24\; x\; 1\; +\; x\; 2)\; dx\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{-\; 2\}\; ^\; \{2\}\; \{\backslash \; tfrac\; \{1\}\; \{5\}\}\; \backslash \; left\; (\{\backslash \; tfrac\; \{1\}\; \{100\}\}\; (322\; +\; 3x\; (98\; +\; x\; (37\; +\; x)))\; -\; 24\; \{\backslash \; frac\; \{x\}\; \{1\; +\; x\; ^\; \{2\}\}\}\; \backslash \; right)\; dx\}$

, что дает точный ответ 94/25 = 3,76. (В обычной практике заранее неизвестен, поэтому важная задача - не рассматриваемая здесь - в том, чтобы решить, когда приближение достаточно хорошее.) Подход «книги расчетов» делит диапазон интегрирования, скажем, на 16 равных частей., и вычисляет значения функции.

Разнесенные значения функции

x	−2,00		−1,50		−1,00		−0,50		0, 00		0,50		1,00		1,50		2,00
f (x)	2,22800		2,45663		2,67200		2,32475		0,64400		-0,92575		-0,94000		-0,16963		0,83600
x		-1,75		-1,25		-0,75		-0,25		0,25		0,75		1,25		1, 75
f (x)		2.33041		2.58562		2.62934		1.64019		−0,32444		-1,09159		−0,60387		0,31734

Методы численных квадратур: ■ Прямоугольник, ■ Трапеция, ■ Ромберг, ■ Гаусс

Используя левый конец каждой части, метод прямоугольника суммирует 16 значений функции и умножается на ширину h, здесь 0,25, чтобы получить приблизительное значение 3,94325 для интеграла. Точность не впечатляет, но в исчислении формально используются куски бесконечно малой ширины, поэтому поначалу может показаться небольшое поводом для беспокойства. Действительно, многократное удвоение количества шагов в итоге дает приближение 3,76001. Однако требуются 2 части, большие вычислительные затраты при такой небольшой точности; а достижение большей точности делает шаги малой прочности.

В лучшем подходе прямоугольники, используемые в сумме Римана, заменяются трапециями. Правило трапеций почти так же легко вычислить; он суммирует все 17 значений функций, но весит первое и последнее на половину и снова умножается на ширинуа. Это сразу улучшает приближение до 3,76925, что заметно точнее. Кроме того, для достижения 3,76000 требуется всего 2 элемента, что значительно меньше вычислений, чем метод прямоугольника для сопоставимой точности. Идея, лежащая в основе правил трапеций, более точные приближения к функциям дают лучшие прибли к интегралу, может быть продолжена. Правило Симпсона приближает подынтегральное выражение кусочно-квадратичной функции. Суммы Римана, правило трапеций и правило Симпсона набора примерами семейства квадратурных правил, называемых формулами Ньютона - Котеса. Квадратурное правило Ньютона - Котеса степени n приближает многочлен на каждом подынтервале полиномом степени n. Этот полином выбран для интерполяции значений функции на интервале. Аппроксимации Ньютона-Котеса более высокой степени могут быть более точными, но они требуют большего количества вычислений функций (уже правило Симпсона требует вдвое больше функциональных вычислений, чем правило трапеций), и они могут страдать от числовой неточности из-за Рунге. Одним из решений этой проблемы является квадратура Кленшоу - Кертиса, в которой подынтегральное выражение аппроксимируется путем разложения его в терминах многочленов Чебышева. Это дает приближение, значения которого не отклоняются далеко от исходной функции.

Метод Ромберга основывается на методе трапеций с большим эффектом. Во-первых, длина шага постепенно уменьшается вдвое, что дает приближение трапеции, обозначаемое T (h 0), T (h 1) и т. Д., Где h k + 1 - половина h k. Для каждого нового размера шага необходимо вычислить только половину новых значений функции; остальные перенесены из предыдущего размера (как показано в таблице выше). Но действительно сильная идея состоит в том, чтобы интерполировать полином с помощью приближений и экстраполировать на T (0). При использовании этого метода для точного числового ответа требуется всего четыре части (пять значений функции). Многочлен Лагранжа, интерполирующий {h k, T (h k)}k = 0... 2 = {(4.00,6.128), (2.00,4.352), (1.00,3.908)} составляет 3,76 + 0,148h, что дает экстраполированное значение 3,76 при h = 0.

Квадратура Гаусса часто требует заметно меньше работы для достижения большей точности. Объяснение такого впечатляющего успеха заключается в выборе точек. В отличие от правил Ньютона-Котеса, которые интерполируют подынтегральное выражение с четырьмя точками, они интерполируют каждое значение и просуммируйте, чтобы получить числовой точный ответ. Интервалом точек, квадратура Гаусса вычисляет функцию в корнях набора ортогональных многочленов. Метод Гаусса с n точками точен для многочленов степени до 2n - 1. Функция в этом классе имеет степень 3 многочлен плюс член, который отменяется, потому что выбранные конечные точки симметричны относительно нуля. етоду Ромберга.)

На практике каждый метод должен использовать e xtra оценки, чтобы предотвратить, что ошибка с неизвестной функцией; это имеет тенденцию нивелировать некоторые преимущества метода Гаусса и мотивирует популярные квадратурные формулы Гаусса - Кронрода. В более широком смысле, адаптивная квадратура разделяет диапазон на части на основе свойств функции, так что точки данных концентрируются там, где они больше всего нужны.

При вычислении многомерных интегралов (например, объемные вычисления) важно использовать такие альтернативы, как интегрирование Монте-Карло.

Текст расчета не заменяет численный анализ, но наоборот. тоже правда. Даже самый лучший адаптивный числовой код иногда требует от пользователя помощи с более требовательными интегралами. Например, неправильные интегралы могут потребовать изменения переменной или методов, которые могут избежать бесконечных значений функции, а известные свойства, такие как симметрия и периодичность, могут обеспечить критическое преимущество. Например, интеграл $\int \; 0\; 1\; x\; -\; 1/2\; e\; -\; xdx\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{0\}\; ^\; \{1\}\; x\; ^\; \{-\; 1/2\}\; e\; ^\; \{-\; x\}\; \backslash ,\; dx\}$сложно вычислить численно, потому что оно бесконечно при x = 0. Однако подстановка u = √x преобразует интеграл в $2\; \int \; 0\; 1\; e\; -\; u\; 2\; du\; \{\backslash \; displaystyle\; 2\; \backslash \; int\; \_\; \{0\}\; ^\; \{1\}\; e\; ^\; \{-\; u\; ^\; \{2\}\}\; \backslash ,\; du\}$, у которого вообще нет особенностей.

Механический

Площадь произвольной двумерной формы может быть определена с помощью измерительного прибора, называемого планиметром. Объем объектов неправильной формы можно точно измерить по жидкости , перемещаемой по мере того, как объект погружается в воду.

Геометрическая

Площадь иногда может быть определена с помощью геометрических построений циркуля и линейки эквивалентного квадрата.

См. Также

• Портал математики

• Интегральное уравнение
• Интегральный символ

Ссылки

Библиография

Внешние ссылки

В Викиучебнике есть книга по теме: Исчисление

• , Энциклопедия математики, EMS Press, 2001 [1994]
• Онлайн-калькулятор интегралов, Wolfram Alpha.

Интернет-книги

• Кейслер, Х. Джером, Элементарное исчисление: подход, использующий бесконечно малые, Университет Висконсина
• Строян, К.Д., Краткое введение в исчисление бесконечно малых, Университет Айовы
• Mauch, Sean, Sean's Applied Math Book, CIT, онлайн-учебник, включающий полное введение в исчисление
• Crowell, Benjamin, Calculus, Fullerton Колледж, онлайн-учебник
• Гарретт, Пол, Заметки по расчету на первом году обучения s
• Хуссейн, Фараз, Понимание исчисления, онлайн-учебник
• Джонсон, Уильям Вулси (1909) Элементарный трактат по интегральному исчислению, ссылка с HathiTrust.
• Ковальк, В.П., Теория интеграции, Ольденбургский университет. Новая концепция к старой проблеме. Онлайн-учебник
• Слаутер, Дэн, Разностные уравнения для дифференциальных уравнений, введение в исчисление
• Численные методы интегрирования в Институте целостных численных методов
• P. С. Ван, Оценка определенных интегралов с помощью символической манипуляции (1972) - поваренная книга методов определенного интеграла