Идеальная цепь

Идеальная цепь (или свободно соединенная цепь ) - это простейшая модель для описывают полимеры, такие как нуклеиновые кислоты и белки. Он предполагает только полимер как случайное блуждание и не учитывает любые взаимодействия между мономерами. Хотя он прост, его общность дает представление о физике полимеров.

В этой модели мономеры представляют собой жесткие стержни фиксированной длины l, и их ориентация полностью не зависит от ориентации и положения соседних мономеров в той степени, в которой два мономера могут сосуществовать в одном месте. В некоторых случаях мономер имеет физическую интерпретацию, например, аминокислота в полипептиде. В других случаях мономер - это просто сегмент полимера, который можно моделировать как дискретную, свободно соединенную единицу. Если это так, l - это длина Куна. Например, хроматин моделируется как полимер, в котором каждый мономер представляет собой сегмент длиной примерно 14-46 т.п.н.

• 1 Модель
• 2 Общность модели
• 3 Энтропийная эластичность идеальной цепи
  • 3.1 Идеальная цепь при ограничении длины
  • 3.2 Идеальная длина обмена полимера с резервуаром
  • 3.3 Идеальная цепь при ограничении постоянной силы - расчет
• 4 См. Также
• 5 Внешние ссылки
• 6 Ссылки

N мер образуют полимер, общая развернутая длина которого составляет:

$L\; =\; N\; l\; \{\backslash \; displaystyle\; L\; =\; N\; \backslash ,\; l\}$, где N - количество меров.

В этом очень простом подходе, где взаимодействия между мерами не рассматриваются, энергия полимера считается независимой от его формы, что означает, что при термодинамических равновесие, все его конфигурации формы с одинаковой вероятностью возникнут, поскольку полимер колеблется во времени, в соответствии с распределением Максвелла – Больцмана.

. Позвольте нам называть $R\; \to \; \{\backslash \; displayst\; yle\; \{\backslash \; vec\; \{R\}\}\}$полный сквозной вектор идеальной цепи и $r\; \to \; 1,\dots ,\; r\; \to \; N\; \{\backslash \; displaystyle\; \{\backslash \; vec\; \{r\}\}\; \_\; \{\; 1\},\; \backslash \; ldots,\; \{\backslash \; vec\; \{r\}\}\; \_\; \{N\}\}$векторы, соответствующие отдельным мерам. Эти случайные векторы имеют компоненты в трех направлениях пространства. Большинство выражений, приведенных в этой статье, предполагают, что количество мер N велико, поэтому применяется центральная предельная теорема . На рисунке ниже показан эскиз (короткой) идеальной цепи.

Два конца цепочки не совпадают, но они колеблются вокруг друг друга, так что, конечно же:

$⟨R\; \to ⟩\; =\; \Sigma \; i\; =\; 1\; N\; ⟨r\; \to \; i⟩\; =\; 0\; \to \; \{\backslash \; displaystyle\; \backslash \; langle\; \{\backslash \; vec\; \{R\}\}\; \backslash \; rangle\; =\; \backslash \; Sigma\; \_\; \{i\; =\; 1\}\; ^\; \{N\}\; \backslash \; langle\; \{\backslash \; vec\; \{r\}\}\; \_\; \{i\}\; \backslash \; rangle\; =\; \{\backslash \; vec\; \{0\}\}\; ~\}$

На протяжении всей статьи скобки $⟨⟩\; \{\backslash \; displaystyle\; \backslash \; langle\; \backslash \; rangle\}$будут использоваться для обозначения среднего (значений, взятых с течением времени) случайной величины или случайный вектор, как указано выше.

Поскольку $r\; \to \; 1,\dots ,\; r\; \to \; N\; \{\backslash \; displaystyle\; \{\backslash \; vec\; \{r\}\}\; \_\; \{1\},\; \backslash \; ldots,\; \{\backslash \; vec\; \{r\}\}\; \_\; \{N\}\}$независимы, из Центральной предельной теоремы следует, что $R\; \to \; \{\backslash \; displaystyle\; \{\backslash \; vec\; \{R\}\}\}$распределяется согласно нормальному распределению (или гауссовскому распределению): точно, в 3D, $R\; x,\; R\; y,\; \{\backslash \; displaystyle\; R\_\; \{x\},\; R\_\; \{y\},\}$и $R\; z\; \{\backslash \; displaystyle\; R\_\; \{z\}\}$распределяются согласно нормальному распределению из среднего 0 и дисперсия :

$\sigma \; 2\; знак\; равно\; ⟨р\; Икс\; 2⟩\; -\; ⟨р\; Икс⟩\; 2\; =\; ⟨р\; Икс\; 2⟩\; -\; 0\; \{\backslash \; displaystyle\; \backslash \; sigma\; ^\; \{2\}\; =\; \backslash \; langle\; R\_\; \{x\}\; ^\; \{2\}\; \backslash \; rangle\; -\; \backslash \; langle\; R\_\; \{x\}\; \backslash \; rangle\; ^\; \{2\}\; =\; \backslash \; langle\; R\_\; \{x\}\; ^\; \{2\}\; \backslash \; rangle\; -0\}$

$⟨R\; x\; 2⟩\; =\; ⟨R\; y\; 2⟩\; =\; ⟨R\; z\; 2⟩\; =\; N\; l\; 2\; 3\; \{\backslash \; displaystyle\; \backslash \; langle\; R\_\; \{x\}\; ^\; \{2\}\; \backslash \; rangle\; =\; \backslash \; langle\; R\_\; \{y\}\; ^\; \{2\}\; \backslash \; rangle\; =\; \backslash \; langle\; R\_\; \{z\}\; ^\; \{2\}\; \backslash \; rangle\; =\; N\; \backslash ,\; \{\backslash \; frac\; \{l\; ^\; \{2\}\}\; \{3\}\}\}$

Итак, $⟨R\; 2\; \to ⟩\; =\; N\; l\; 2\; =\; L\; l\; \{\backslash \; displaystyle\; \backslash \; langle\; \{\backslash \; vec\; \{R\; ^\; \{2\}\}\}\; \backslash \; rangle\; =\; N\; \backslash ,\; l\; ^\; \{2\}\; =\; L\; \backslash ,\; l\; ~\}$. Сквозной вектор цепочки распределяется согласно следующей функции плотности вероятности :

$P\; (R\; \to )\; =\; (3\; 2\; \pi \; N\; l\; 2)\; 3/2\; e\; -\; 3\; R\; \to \; 2\; 2\; N\; l\; 2\; \{\backslash \; Displaystyle\; P\; (\{\backslash \; vec\; \{R\}\})\; =\; \backslash \; left\; (\{\backslash \; frac\; \{3\}\; \{2\; \backslash \; pi\; Nl\; ^\; \{2\}\}\}\; \backslash \; right)\; ^\; \{3/2\}\; e\; ^\; \{-\; \{\backslash \; frac\; \{3\; \{\backslash \; vec\; \{R\}\}\; ^\; \{2\}\}\; \{2Nl\; ^\; \{2\}\}\}\}\}$

Среднее расстояние от конца до конца полимера:

$⟨R\; 2\; \to ⟩\; =\; N\; l\; =\; L\; l\; \{\backslash \; displaystyle\; \{\backslash \; sqrt\; \{\backslash \; langle\; \{\backslash \; vec\; \{R\; ^\; \{2\}\}\}\; \backslash \; rangle\}\}\; =\; \{\backslash \; sqrt\; \{N\}\}\; \backslash ,\; l\; =\; \{\backslash \; sqrt\; \{L\; \backslash ,\; l\}\}\; ~\}$

В физике полимеров часто используется величина радиус инерции :

$RG\; =\; N\; l\; 6\; \{\backslash \; displaystyle\; \{\backslash \; mathit\; \{R\}\}\; \_\; \{G\}\; =\; \{\backslash \; frac\; \{\{\backslash \; sqrt\; \{N\}\}\; \backslash ,\; l\}\; \{\{\backslash \; sqrt\; \{6\}\}\; \backslash \}\}\}$

Следует отметить, что указанное выше среднее расстояние от конца до конца, которое в случае этой простой модели также является типичным амплитуда колебаний системы становится незначительной по сравнению с общей развернутой длиной полимера $N\; l\; \{\backslash \; displaystyle\; N\; \backslash ,\; l\}$при термодинамическом пределе. Этот результат является общим свойством статистических систем.

Математическое замечание: строгая демонстрация выражения плотности вероятности $P\; (R\; \to )\; \{\backslash \; displaystyle\; P\; (\{\backslash \; vec\; \{R\}\})\}$не является так же прямо, как показано выше: из применения обычной (1D) центральной предельной теоремы можно вывести, что $R\; x\; \{\backslash \; displaystyle\; R\_\; \{x\}\}$, $R\; y\; \{\backslash \; displaystyle\; R\_\; \{y\}\}$и $R\; z\; \{\backslash \; displaystyle\; R\_\; \{z\}\}$распределяются согласно центрированному нормальному распределению дисперсии $N\; l\; 2/3\; \{\backslash \; Displaystyle\; N\; \backslash ,\; l\; ^\; \{2\}\; /\; 3\}$. Тогда приведенное выше выражение для $P\; (R\; \to )\; \{\backslash \; displaystyle\; P\; (\{\backslash \; vec\; \{R\}\})\}$не единственное, которое совместимо с таким распределением для $R\; x\; \{\backslash \; displaystyle\; R\_\; \{x\}\}$, $R\; y\; \{\backslash \; displaystyle\; R\_\; \{y\}\}$и $R\; z\; \{\backslash \; displaystyle\; R\_\; \{z\}\}$. Однако, поскольку компоненты векторов $r\; \to \; 1,\dots ,\; r\; \to \; N\; \{\backslash \; displaystyle\; \{\backslash \; vec\; \{r\}\}\; \_\; \{1\},\; \backslash \; ldots,\; \{\backslash \; vec\; \{r\}\}\; \_\; \{N\}\}$некоррелированы для рассматриваемого нами случайного блуждания, из этого следует, что $R\; x\; \{\backslash \; displaystyle\; R\_\; \{x\}\}$, $R\; y\; \{\backslash \; displaystyle\; R\_\; \{y\}\; \}$и $R\; z\; \{\backslash \; displaystyle\; R\_\; \{z\}\}$также некоррелированы. Это дополнительное условие может быть выполнено, только если $R\; \to \; \{\backslash \; displaystyle\; \{\backslash \; vec\; \{R\}\}\}$распределено согласно $P\; (R\; \to )\; \{\backslash \; displaystyle\; P\; (\{\backslash \; vec\; \{R\}\})\}$. В качестве альтернативы, этот результат также может быть продемонстрирован путем применения многомерного обобщения центральной предельной теоремы или с помощью аргументов симметрии.

Хотя описанная выше элементарная модель полностью не адаптирована к описанию реальных полимеров в микроскопическом масштабе, она действительно демонстрирует некоторую актуальность в макроскопическом масштабе в случае полимера в растворе, мономеры которого образуют идеальную смесь с растворителем (в этом случае взаимодействия между мономером и мономером, молекулой растворителя и молекулой растворителя, а также между мономером и растворителем идентичны, и энергия системы может считаться постоянной, что подтверждает гипотезы модели).

Однако актуальность модели ограничена даже в макроскопическом масштабе тем фактом, что она не учитывает какой-либо исключенный объем для мономеров (или, говоря химическими терминами, пренебрегает) стерические эффекты ).

Другие модели флуктуирующего полимера, которые не учитывают взаимодействие между мономерами и исключенный объем, такие как модель червеобразной цепи, все асимптотически сходятся к этой модели на термодинамическом пределе. Для целей этой аналогии вводится сегмент Куна, соответствующий эквивалентной длине мономера, который следует рассматривать в аналогичной идеальной цепи. Количество сегментов Куна, которые следует учитывать в аналогичной идеальной цепи, равно общей длине развернутого полимера, деленной на длину сегмента Куна.

Если два свободных конца идеальной цепи прикреплены к какому-либо микроманипуляционному устройству, то это устройство испытывает силу, оказываемую полимером. Энергия идеальной цепи постоянна, и, следовательно, ее среднее по времени, внутренняя энергия, также постоянна, что означает, что эта сила обязательно проистекает из чисто энтропийного эффекта.

Эта энтропийная сила очень похожа на давление, испытываемое стенками коробки, содержащей идеальный газ. внутренняя энергия идеального газа зависит только от его температуры, а не от объема контейнера, в котором он находится, поэтому это не эффект энергии, который имеет тенденцию чтобы увеличить объем коробки, как это делает газ давление. Это означает, что давление идеального газа имеет чисто энтропийное происхождение.

Каково микроскопическое происхождение такой энтропийной силы или давления? Самый общий ответ состоит в том, что эффект тепловых флуктуаций имеет тенденцию приближать термодинамическую систему к макроскопическому состоянию, которое соответствует максимуму в количестве микроскопических состояний (или микросостояний), совместимых с этим макроскопическим состоянием. Другими словами, тепловые флуктуации приводят систему к макроскопическому состоянию максимальной энтропии.

. Что это означает в случае идеальной цепи? Во-первых, для нашей идеальной цепи микроскопическое состояние характеризуется суперпозицией состояний $r\; \to \; i\; \{\backslash \; displaystyle\; \{\backslash \; vec\; \{r\}\}\; \_\; \{i\}\}$каждого индивидуального мономера ( где i изменяется от 1 до N). В своем растворителе идеальная цепь постоянно подвергается ударам от движущихся молекул растворителя, и каждый из этих ударов переводит систему из ее текущего микроскопического состояния в другое, очень похожее микроскопическое состояние. Для идеального полимера, как будет показано ниже, существует больше микроскопических состояний, совместимых с коротким сквозным расстоянием, чем есть микроскопических состояний, совместимых с большим сквозным расстоянием. Таким образом, для идеальной цепи максимизация ее энтропии означает уменьшение расстояния между двумя ее свободными концами. Следовательно, сила, которая стремится разрушить цепь, действует идеальная цепь между двумя ее свободными концами.

В этом разделе будет выведено среднее значение этой силы. Затем будет обсуждаться общность выражения, полученного при термодинамическом пределе.

Идеальная цепь при ограничении длины

В этом подразделе будет рассмотрен случай идеальной цепи, два конца которой прикреплены к фиксированным точкам. Вектор $R\; \to \; \{\backslash \; displaystyle\; \{\backslash \; vec\; \{R\}\}\}$, соединяющий эти две точки, характеризует макроскопическое состояние (или макросостояние) идеальной цепи. Каждому макросостоянию соответствует определенное количество микросостояний, которые мы будем называть $\Omega \; (R\; \to )\; \{\backslash \; displaystyle\; \backslash \; Omega\; (\{\backslash \; vec\; \{R\}\})\}$(микросостояния определены во введении к этому разделу). Поскольку энергия идеальной цепи постоянна, каждое из этих микросостояний имеет равную вероятность возникновения. энтропия, связанная с макросостоянием, таким образом, равна:

$S\; (R\; \to )\; =\; k\; B\; log\; \; (\Omega \; (R\; \to ))\; \{\backslash \; displaystyle\; S\; (\{\backslash \; vec\; \{R\}\; \})\; =\; k\_\; \{B\}\; \backslash \; log\; (\backslash \; Omega\; (\{\backslash \; vec\; \{R\}\}))\}$, где $k\; B\; \{\backslash \; displaystyle\; k\_\; \{B\}\}$равно константа Больцмана

Вышеприведенное выражение дает абсолютную (квантовую) энтропию системы. Для точного определения $\Omega \; (R\; \to )\; \{\backslash \; displaystyle\; \backslash \; Omega\; (\{\backslash \; vec\; \{R\}\})\}$потребуется квантовая модель для идеальной цепи, что выходит за рамки данной статья. Однако мы уже вычислили плотность вероятности $P\; (R\; \to )\; \{\backslash \; displaystyle\; P\; (\{\backslash \; vec\; \{R\}\})\}$, связанную со сквозным вектором безусловного идеала. цепь, выше. Поскольку вероятность возникновения всех микросостояний идеальной цепочки одинакова, $P\; (R\; \to )\; \{\backslash \; displaystyle\; P\; (\{\backslash \; vec\; \{R\}\})\}$пропорционально $\Omega \; (R\; \to )\; \{\backslash \; Displaystyle\; \backslash \; Omega\; (\{\backslash \; vec\; \{R\}\})\}$. Это приводит к следующему выражению для классической (относительной) энтропии идеальной цепи:

$S\; (R\; \to )\; =\; k\; B\; log\; \; (P\; (R\; \to ))\; +\; C\; st\; \{\backslash \; displaystyle\; S\; (\{\backslash \; vec\; \{R\}\})\; =\; k\_\; \{B\}\; \backslash \; log\; (P\; (\{\backslash \; vec\; \{R\}\}))\; +\; C\_\; \{st\}\}$,

где $C\; st\; \{\backslash \; displaystyle\; C\_\; \{st\; \}\}$- фиксированная константа. Назовем $F\; \to \; \{\backslash \; displaystyle\; \{\backslash \; vec\; \{F\}\}\}$силу, прилагаемую цепью к точке, к которой прикреплен ее конец. Из приведенного выше выражения энтропии мы можем вывести выражение этой силы. Предположим, что положение двух концов идеальной цепочки теперь не фиксируется, а контролируется оператором. Оператор управляет эволюцией сквозного вектора $R\; \to \; \{\backslash \; displaystyle\; \{\backslash \; vec\; \{R\}\}\}$. Если оператор меняет $R\; \to \; \{\backslash \; displaystyle\; \{\backslash \; vec\; \{R\}\}\}$на крошечную величину $d\; R\; \to \; \{\backslash \; displaystyle\; \{\backslash \; vec\; \{dR\}\}\}$, тогда изменение внутренней энергии цепочки равно нулю, поскольку энергия цепочки постоянна. Это условие можно записать как:

$0\; =\; d\; U\; =\; \delta \; W\; +\; \delta \; Q\; \{\backslash \; displaystyle\; 0\; =\; dU\; =\; \backslash \; delta\; W\; +\; \backslash \; delta\; Q\; ~\}$

$\delta \; W\; \{\backslash \; displaystyle\; \backslash \; delta\; W\}$определяется как элементарное количество механической работы, переданное оператором идеальной цепочке, а $\delta \; Q\; \{\backslash \; displaystyle\; \backslash \; delta\; Q\}$определяется как элементарное количество тепла, передаваемое растворителем идеальной цепи. Теперь, если мы предположим, что преобразование, наложенное оператором на систему, является квазистатическим (т. Е. Бесконечно медленным), то преобразование системы будет обратимым во времени, и мы можем предположить, что во время ее перехода из макросостояния $R\; \to \; \{\backslash \; displaystyle\; \{\backslash \; vec\; \{R\}\}\}$в макросостояние $R\; \to \; +\; d\; R\; \to \; \{\backslash \; displaystyle\; \{\backslash \; vec\; \{R\}\}\; +\; \{\backslash \; vec\; \{dR\}\}\}$, система проходит через серию термодинамического равновесия макросостояний. Это имеет два следствия:

• во-первых, количество тепла, полученного системой во время преобразования, может быть связано с изменением ее энтропии :

$\delta \; Q\; =\; T\; d\; S\; \{\backslash \; displaystyle\; \backslash \; delta\; Q\; =\; TdS\; ~\}$, где T - температура цепи.

• секунд, чтобы преобразование оставалось бесконечно медленным, среднее усилие, прилагаемое оператор на конечных точках цепи должен уравновесить среднее усилие, оказываемое цепью на ее конечные точки. Вызов $f\; \to \; op\; \{\backslash \; displaystyle\; \{\backslash \; vec\; \{f\}\}\; \_\; \{op\}\}$силы со стороны оператора и $f\; \to \; \{\backslash \; displaystyle\; \{\backslash \; vec\; \{f\}\}\; \}$сила, действующая со стороны цепи, мы имеем:

$\delta \; W\; =\; ⟨f\; \to \; op⟩\; \cdot \; d\; R\; \to \; =\; -\; ⟨f\; \to ⟩\; \cdot \; d\; R\; \to \; \{\backslash \; displaystyle\; \backslash \; delta\; W\; =\; \backslash \; langle\; \{\backslash \; vec\; \{f\}\}\; \_\; \{op\}\; \backslash \; rangle\; \backslash \; cdot\; \{\backslash \; vec\; \{dR\}\}\; =\; -\; \backslash \; langle\; \{\backslash \; vec\; \{f\}\}\; \backslash \; rangle\; \backslash \; cdot\; \{\backslash \; vec\; \{dR\}\}\; ~\}$

Таким образом, мы приходим к:

$⟨е\; \to ⟩\; =\; T\; d\; S\; d\; R\; \to \; =\; k\; BTP\; (R\; \to )\; d\; P\; (R\; \to )\; d\; R\; \to \; \{\backslash \; displaystyle\; \backslash \; langle\; \{\backslash \; vec\; \{f\}\}\; \backslash \; rangle\; =\; T\; \{\backslash \; frac\; \{dS\}\; \{\backslash \; vec\; \{dR\}\}\}\; =\; \{\backslash \; frac\; \{k\_\; \{B\}\; T\}\; \{P\; (\{\backslash \; vec\; \{R\}\})\}\}\; \{\backslash \; frac\; \{dP\; (\{\backslash \; vec\; \{\; R\}\})\}\; \{\backslash \; vec\; \{dR\}\}\}\; ~\}$

$⟨е\; \to ⟩\; =\; -\; k\; BT\; 3\; R\; \to \; N\; l\; 2\; \{\backslash \; displaystyle\; \backslash \; langle\; \{\backslash \; vec\; \{f\}\}\; \backslash \; rangle\; =\; -k\_\; \{\; B\}\; T\; \{\backslash \; frac\; \{3\; \{\backslash \; vec\; \{R\}\}\}\; \{Nl\; ^\; \{2\}\}\}\; ~\}$

Вышеприведенное уравнение является уравнением состояния идеальной цепи. Поскольку выражение зависит от центральной предельной теоремы , оно является точным только в пределах полимеров, содержащих большое количество мономеров (то есть термодинамический предел ). Это также справедливо только для небольших расстояний от конца до конца по отношению к общей длине контура полимера, где поведение похоже на пружину. Поведение в более широких диапазонах сил можно смоделировать, используя канонический ансамбль, идентичный намагничиванию парамагнитных спинов. Для произвольных сил зависимость силы растяжения будет выражаться функцией Ланжевена $L\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{L\}\}\}$:

$RN\; l\; =\; coth\; \; (flk\; BT)\; -\; k\; BT\; fl\; =\; L\; (flk\; BT),\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{R\}\; \{Nl\}\}\; =\; \backslash \; coth\; \backslash \; left\; (\{\backslash \; frac\; \{fl\}\; \{k\_\; \{B\}\; T\}\}\; \backslash \; right)\; -\; \{\backslash \; frac\; \{\; k\_\; \{B\}\; T\}\; \{fl\}\}\; =\; \{\backslash \; mathcal\; \{L\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{fl\}\; \{k\_\; \{B\}\; T\}\}\; \backslash \; right),\}$

где расширение равно $R\; =\; |\; R\; \to \; |\; \{\backslash \; displaystyle\; R\; =\; |\; \{\backslash \; vec\; \{R\}\}\; |\}$.

Для произвольных расширений зависимость сила-расширение может быть аппроксимирована следующим образом:

$flk\; BT\; =\; L\; -\; 1\; (RN\; l)\; \approx \; 3\; RN\; l\; +\; 1\; 5\; (RN\; l)\; 2\; грех\; \; (7\; R\; 2\; N\; l)\; +\; (RN\; l)\; 3\; 1\; -\; RN\; l\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{fl\}\; \{k\_\; \{B\}\; T\}\}\; =\; \{\backslash \; mathcal\; \{L\}\; \}\; ^\; \{-\; 1\}\; \backslash \; left\; (\{\backslash \; frac\; \{R\}\; \{Nl\}\}\; \backslash \; right)\; \backslash \; приблизительно\; 3\; \{\backslash \; frac\; \{R\}\; \{Nl\}\}\; +\; \{\backslash \; frac\; \{1\}\; \{5\}\}\; \backslash \; left\; (\{\; \backslash \; frac\; \{R\}\; \{Nl\}\}\; \backslash \; right)\; ^\; \{2\}\; \backslash \; sin\; \backslash \; left\; (\{\backslash \; frac\; \{7R\}\; \{2Nl\}\}\; \backslash \; right)\; +\; \{\backslash \; frac\; \{\backslash \; left\; (\{\backslash \; frac\; \{R\}\; \{Nl\; \}\}\; \backslash \; right)\; ^\; \{3\}\}\; \{1\; -\; \{\backslash \; frac\; \{R\}\; \{Nl\}\}\}\}\}$,

где $L\; -\; 1\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{L\}\}\; ^\; \{-\; 1\; \}\}$- это обратная функция Ланжевена, N - количество связей в молекуле (поэтому, если в молекуле есть N связей, она имеет N + 1 мономеров, составляющих молекулу.).

Наконец, модель может быть расширена до еще более широких диапазонов сил путем включения модуля упругости по длине контура полимера. То есть, позволяя длине каждого звена цепи упруго реагировать на приложенную силу.

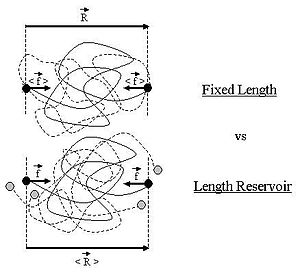
Идеальная длина замены полимера с резервуаром

В этом подразделе, как и в предыдущем, два конца полимера прикреплены к устройству для микроманипуляции. Однако на этот раз устройство не поддерживает два конца идеальной цепи в фиксированном положении, а поддерживает постоянную тянущую силу $f\; \to \; op\; \{\backslash \; displaystyle\; \{\backslash \; vec\; \{f\}\}\; \_\; \{op\}\; \}$на идеальной цепочке. В этом случае два конца полимера колеблются около среднего положения $⟨R\; \to ⟩\; \{\backslash \; displaystyle\; \backslash \; langle\; \{\backslash \; vec\; \{R\}\}\; \backslash \; rangle\}$. Идеальная цепь реагирует с постоянной противоположной силой $f\; \to \; =\; -\; f\; \to \; op\; \{\backslash \; displaystyle\; \{\backslash \; vec\; \{f\}\}\; =\; -\; \{\backslash \; vec\; \{f\}\}\; \_\; \{op\}\}$

Для идеальной цепи меняя длину с резервуаром, макросостояние системы характеризуется вектором $f\; \to \; \{\backslash \; displaystyle\; \{\backslash \; vec\; \{f\}\}\}$.

Переход между идеальной цепью фиксированной длины и идеальной цепью в контакте с резервуаром длины очень похоже на изменение между микроканоническим ансамблем и каноническим ансамблем (см. статью Статистическая механика об этом). Переход от состояния, в котором фиксированное значение накладывается на определенный параметр, к состоянию, в котором система может обмениваться этим параметром с внешним миром. Рассматриваемый параметр - это энергия для микроканонического и канонического описаний, тогда как в случае идеальной цепи параметром является длина идеальной цепи.

Как и в микроканоническом и каноническом ансамблях, два описания идеальной цепи различаются только тем, как они трактуют колебания системы. Таким образом, они эквивалентны при термодинамическом пределе. Уравнение состояния идеальной цепи остается прежним, за исключением того, что $R\; \to \; \{\backslash \; displaystyle\; \{\backslash \; vec\; \{R\}\}\}$теперь подвержено колебаниям:

$е\; \to \; =\; -\; к\; BT\; 3\; ⟨R\; \to ⟩\; N\; l\; 2\; \{\backslash \; displaystyle\; \{\backslash \; vec\; \{f\}\}\; =\; -\; k\_\; \{B\}\; T\; \{\backslash \; frac\; \{3\; \backslash \; langle\; \{\backslash \; vec\; \{R\}\}\; \backslash \; rangle\}\; \{\; Nl\; ^\; \{2\}\}\}\; ~\}$.

Идеальная цепь при ограничении постоянной силы - расчет

Схема идеальной цепи, ограниченной постоянной силой.

Рассмотрим свободно соединенную цепь из N связей длины $l\; \{\backslash \; displaystyle\; l\}$, подверженный постоянной силе удлинения f, приложенной к его концам вдоль оси z, и температуре окружающей среды $T\; \{\backslash \; displaystyle\; T\}$. Примером может служить цепь с двумя противоположными зарядами + q и -q на концах в постоянном электрическом поле $E\; \to \; \{\backslash \; displaystyle\; \{\backslash \; vec\; \{E\}\}\}$применяется вдоль оси $z\; \{\backslash \; displaystyle\; z\}$, как показано на рисунке справа. Если прямое кулоновское взаимодействие между зарядами игнорируется, то на двух концах существует постоянная сила $f\; \to \; \{\backslash \; displaystyle\; \{\backslash \; vec\; \{f\}\}\}$.

Различные конформации цепи не равновероятны, потому что они соответствуют разной энергии цепи во внешнем электрическом поле.

$U\; =\; -\; q\; E\; \to \; \cdot \; R\; \to \; =\; -\; f\; \to \; \cdot \; R\; \to \; =\; -\; f\; R\; z\; \{\backslash \; displaystyle\; U\; =\; -q\; \{\backslash \; vec\; \{E\}\}\; \backslash \; cdot\; \{\backslash \; vec\; \{R\}\}\; =\; -\; \{\; \backslash \; vec\; \{f\}\}\; \backslash \; cdot\; \{\backslash \; vec\; \{R\}\}\; =\; -\; fR\_\; \{z\}\}$

Таким образом, разные конформации цепи имеют разные статистические факторы Больцмана $exp\; (-\; U\; /\; k\; BT)\; \{\backslash \; displaystyle\; exp\; (-U\; /\; k\_\; \{B\}\; T)\}$.

функция распределения :

$Z\; =\; \sum \; statesexp\; (-\; U\; /\; k\; BT)\; =\; \sum \; statesexp\; (f\; R\; zk\; BT)\; \{\backslash \; Displaystyle\; Z\; =\; \backslash \; сумма\; \_\; \{состояния\}\; ехр\; (-U\; /\; k\_\; \{B\}\; T)\; =\; \backslash \; sum\; \_\; \{состояния\}\; ехр\; (\{fR\_\; \{z\}\; \backslash \; над\; k\_\; \{B\}\; T\})\}$

Каждое соединение мономера в цепочке характеризуется вектором $ri\; \to \; \{\backslash \; displaystyle\; \{\backslash \; vec\; \{r\_\; \{i\}\}\}\}$длины $l\; \{\backslash \; displaystyle\; l\}$и углы $\theta \; i,\; \phi \; i\; \{\backslash \; displaystyle\; \backslash \; theta\; \_\; \{i\},\; \backslash \; varphi\; \_\; \{i\}\}$в сферическая система координат. Сквозной вектор может быть представлен как: $R\; z\; =\; \sum \; i\; =\; 1\; N\; l\; cos\; \; \theta \; i\; \{\backslash \; displaystyle\; R\_\; \{z\}\; =\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{N\}\; l\; \{\; \backslash \; text\; \{\}\}\; \backslash \; cos\; \backslash \; theta\; \_\; \{i\}\}$. Следовательно:

$Z\; =\; \int \; exp\; \; (flk\; BT\; \sum \; i\; =\; 1\; N\; cos\; \; \theta \; i)\; \prod \; i\; =\; 1\; N\; sin\; \; \theta \; id\; \theta \; id\; \phi \; i\; =\; [\int \; 0\; \pi \; 2\; \pi \; sin\; \; \theta \; i\; exp\; \; (\; flk\; BT\; cos\; \; \theta \; i)\; d\; \theta \; i]\; N\; =\; [2\; \pi \; fl\; /\; (k\; BT)\; [exp\; \; (flk\; BT)\; -\; exp\; \; (-\; flk\; BT)]]\; N\; =\; [4\; \pi \; sinh\; \; (fl\; /\; (\; KBT))\; fl\; /\; (к\; BT)]\; N\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; Z\; =\; \backslash \; int\; \backslash \; exp\; (\{fl\; \backslash \; over\; k\_\; \{B\}\; T\}\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{N\}\; \backslash \; cos\; \backslash \; theta\; \_\; \{i\})\; \backslash \; prod\; \_\; \{i\; =\; 1\}\; ^\; \{N\}\; \backslash \; sin\; \backslash \; theta\; \_\; \{i\}\; d\; \backslash \; theta\; \_\; \{i\}\; d\; \backslash \; varphi\; \_\; \{i\}\; =\; \backslash \backslash \; \backslash \; left\; [\; \backslash \; int\; \_\; \{0\}\; ^\; \{\backslash \; pi\}\; 2\; \backslash \; pi\; \{\backslash \; text\; \{\}\}\; \backslash \; sin\; \backslash \; theta\; \_\; \{i\}\; \{\backslash \; text\; \{\}\}\; \backslash \; exp\; (\{fl\; \backslash \; over\; k\_\; \{B\}\; T\}\; \backslash \; cos\; \backslash \; theta\; \_\; \{i\})\; d\; \backslash \; theta\; \_\; \{i\}\; \backslash \; right]\; ^\; \{N\}\; =\; \backslash \backslash \; \backslash \; left\; [\{2\; \backslash \; pi\; \backslash \; over\; fl\; /\; (k\_\; \{B\}\; T)\}\; [\backslash \; exp\; (\{fl\; \backslash \; над\; k\_\; \{B\}\; T\})\; -\; \backslash \; exp\; (-\; \{fl\; \backslash \; over\; k\_\; \{B\}\; T\})]\; \backslash \; right]\; ^\; \{N\}\; =\; \backslash \backslash \; \backslash \; left\; [\{4\; \backslash \; pi\; \{\backslash \; text\; \{\}\}\; \backslash \; sinh\; (fl\; /\; (K\_\; \{B\}\; T))\; \backslash \; over\; fl\; /\; (k\_\; \{B\}\; T)\}\; \backslash \; right]\; ^\; \{N\}\; \backslash \; end\; \{align\}\}\}$

Свободная энергия Гиббса G можно напрямую вычислить из статистической суммы:

$G\; (T,\; f,\; N)\; =\; -\; k\; BT\; ln\; Z\; (T,\; f,\; N)\; =\; -\; N\; k\; BT\; [ln\; (4\; \pi \; sinh\; (flk\; BT))\; -\; пер\; (flk\; BT)]\; \{\backslash \; displaystyle\; G\; (T,\; f,\; N)\; =\; -\; k\_\; \{B\}\; T\; \{\; \backslash \; text\; \{\}\}\; ln\; \{\backslash \; text\; \{\}\}\; Z\; (T,\; f,\; N)\; =\; -\; Nk\_\; \{B\}\; T\; [ln\; (4\; \backslash \; pi\; \{\backslash \; text\; \{\}\}\; sinh\; (\{fl\; \backslash \; over\; k\_\; \{B\}\; T\; \}))\; -\; ln\; (\{fl\; \backslash \; over\; k\_\; \{B\}\; T\})]\}$

Здесь используется свободная энергия Гиббса, потому что ансамбль цепочек соответствует постоянной температуре $T\; \{\backslash \; displaystyle\; T\}$и постоянная сила $f\; \{\backslash \; displaystyle\; f\}$(аналог изотермино-изобарического ансамбля, который имеет постоянные температура и давление).

Среднее расстояние от конца до конца, соответствующее данной силе, можно получить как производную от свободной энергии:

Это выражение является функцией Ланжевена $L\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{L\}\}\}$, также упомянутой в предыдущих абзацах:

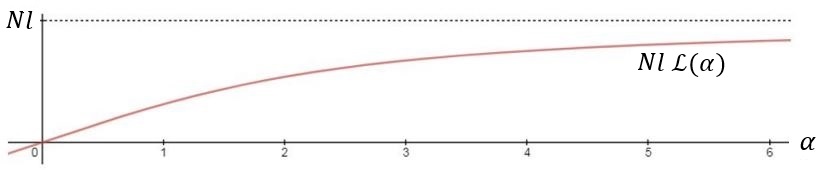
среднее расстояние $⟨R\; \to ⟩\; \{\backslash \; displaystyle\; \backslash \; left\; \backslash \; langle\; \{\backslash \; vec\; \{R\}\}\; \backslash \; right\; \backslash \; rangle\}$цепи как функция от $\alpha \; \{\backslash \; displaystyle\; \backslash \; alpha\; \}$.

$L\; (\alpha )\; =\; coth\; (\alpha )\; -\; 1\; \alpha \; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{L\}\}\; (\backslash \; alpha)\; =\; coth\; (\backslash \; alpha)\; -\; \{1\; \backslash \; over\; \backslash \; alpha\}\}$где, $\alpha \; =\; flk\; BT\; \{\backslash \; display\; style\; \backslash \; alpha\; =\; \{fl\; \backslash \; over\; k\_\; \{B\}\; T\}\}$.

Для малых относительных удлинений ($⟨R⟩\; \ll \; R\; max\; =\; l\; N\; \{\backslash \; displaystyle\; \backslash \; left\; \backslash \; langle\; R\; \backslash \; right\; \backslash \; rangle\; \backslash \; ll\; R\_\; \{max\}\; =\; lN\}$) зависимость приблизительно линейна,

$L\; (\alpha )\; \cong \; \alpha \; 3\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{L\}\}\; (\backslash \; alpha)\; \backslash \; cong\; \{\backslash \; alpha\; \backslash \; over\; 3\}\}$для $\alpha \; \ll \; 1\; \{\backslash \; displaystyle\; \backslash \; alpha\; \backslash \; ll\; 1\}$

и следует закону Гука, как показано в предыдущих абзацах:

$f\; \to \; =\; KBT\; 3\; ⟨R\; \to ⟩\; N\; l\; 2\; \{\backslash \; displaystyle\; \{\backslash \; vec\; \{f\}\}\; =\; K\_\; \{B\}\; T\; \{3\; \backslash \; left\; \backslash \; langle\; \{\backslash \; vec\; \{R\}\}\; \backslash \; right\; \backslash \; rangle\; \backslash \; over\; Nl\; ^\; \{2\}\}\; \}$.

• Полимер
• Червеобразная цепь, более сложная модель полимера
• Длина Куна
• Переход спираль-глобула