Среднее Херона

В математике Среднее Херона H двух неотрицательных действительных чисел A а B определяется по формуле:

$H\; =\; 1\; 3\; (A\; +\; AB\; +\; B).\; \{\backslash \; displaystyle\; H\; =\; \{\backslash \; frac\; \{1\}\; \{3\}\}\; \backslash \; left\; (A\; +\; \{\backslash \; sqrt\; \{AB\}\}\; +\; B\; \backslash \; right).\}$

Назван в честь героя Александрии.

• 1 Применение в твердотельной геометрии
• 2 Связь с другими средствами
• 3 Ссылки
• 4 Внешние ссылки

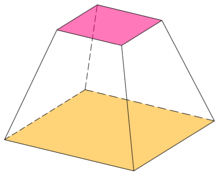Квадратная усеченная пирамида, объем которой равен высоте, умноженной на высоту Герона среднее значение квадратов

Среднее значение Герона может быть использовано при нахождении объема усеченной вершины пирамиды или конуса. Объем равен произведению высоты усеченной вершины и среднего Герона площадей противоположных параллельных граней.

Среднее по Герону чисел A и B является средневзвешенным их арифметических и геометрических средних :

$H\; =\; 2\; 3\; \cdot \; A\; +\; B\; 2\; +\; 1\; 3\; AB.\; \{\backslash \; displaystyle\; H\; =\; \{\backslash \; frac\; \{2\}\; \{3\}\}\; \backslash \; cdot\; \{\backslash \; frac\; \{A\; +\; B\}\; \{2\}\}\; +\; \{\backslash \; frac\; \{1\}\; \{3\}\}\; \backslash \; cdot\; \{\backslash \; sqrt\; \{AB\}\}.\; \}$

• Bullen, PS (2003), Справочник по средствам и их неравенствам, математике и ее приложениям (2-е изд.), Берлин, Нью-Йорк: Springer Science + Business Media, ISBN 978- 1-4020-1522-9
• Ивс, Ховард Уитли (1980), Великие моменты в математике (до 1650 года), Математическая ассоциация Америки, ISBN 978-0-88385-310-8

• Средние трапеции Геометрическое сравнение некоторых математических средств