Большой канонический ансамбль

Статистический ансамбль частиц в термодинамическом равновесии

В статистической механике, a большой канонический ансамбль (также известный как макроканонический ансамбль) - это статистический ансамбль, который используется для представления состояний механической системы частиц, находящихся в термодинамическом равновесии (термический и химический) с резервуаром. Система называется открытой в том смысле, что система может обмениваться энергией и частями с резервуаром, так что различные возможные состояния системы различаться как по их полной энергии, так и по общему количеству частиц. Объем, форма и другие внешние координаты системы остаются неизменными во всех состояниях системы.

Термодинамические переменные большого канонического ансамбля: химический потенциал (символ: µ) и абсолютная температура (символ: T). Ансамбль также зависит от механических чисел, таких как объем (символ: V), которые влияют на внутренние характерные состояния системы. Поэтому этот ансамбль иногда называют ансамблем µVT, поскольку каждое из этих трех величин является константами ансамбля.

• 1 Основы
• 2 Применимость
• 3 Свойства
• 4 Большой потенциал, средние по ансамблю и точные дифференциалы
• 5 Примеры ансамблей
  • 5.1 Статистика невзаимодействующих частиц
    • 5.1. 1 Бозоны и фермионы (квантовые)
    • 5.1.2 Неразличные классические частицы
  • 5.2 Ионизация изолированного атома
• 6 Значение химического, обобщенное «число частиц»
• 7 Точные выражения для ансамбля
  • 7.1 Квантовая механика
  • 7.2 Классическая механика
    • 7.2.1 Поправка на перерасчет
• 8 Примечания
• 9 Ссылки

Проще говоря, большой канонический ансамбль присваивает вероятность P каждому отдельному микросостоянию, заданному следующей экспонентой:

$P\; =\; e\; \Omega \; +\; \mu \; N\; -\; E\; k\; T,\; \{\backslash \; displaystyle\; P\; =\; e\; ^\; \{\backslash \; frac\; \{\backslash \; Omega\; +\; \backslash \; mu\; NE\}\; \{kT\}\},\}$

где N - количество частиц в микросостоянии, а E - полная энергия микросостояния. k - постоянная Больцмана.

Число Ω известно как большой потенциал и является постоянным для ансамбля. Коэффициенты распределения вероятностей (вероятности по полному набору микросостояний в сумме равняться единице); и многие важные средние по ансамблю могут быть непосредственно вычислены из функций Ω (µ, V, T).

В случае, когда разрешено количество частиц более одного типа, выражение вероятности обобщается до

$P\; =\; e\; \Omega \; +\; \mu \; 1\; N\; 1\; +\; \mu \; 2\; N\; 2\; +\dots \; +\; \mu \; s\; N\; s\; -\; Е\; К\; T,\; \{\backslash \; Displaystyle\; P\; =\; е\; ^\; \{\backslash \; гидроразрыва\; \{\backslash \; Omega\; +\; \backslash \; mu\; \_\; \{1\}\; N\_\; \{1\}\; +\; \backslash \; mu\; \_\; \{2\}\; N\_\; \{2\}\; +\; \backslash \; ldots\; +\; \backslash \; mu\; \_\; \{s\}\; N\_\; \{s\}\; -E\}\; \{kT\}\},\}$

где µ 1 - химический потенциал для частиц первого типа, N 1 - количество частиц такого типа в микросостоянии, µ 2 - это химический потенциал для второго типа частиц и так далее (s - количество различных частиц). Однако эти числа следует определять осторожно (см. Примечание о сохранении числа частиц ниже).

Большие ансамбли подходят для использования при описании таких систем, как электроны в проводнике или фотоны в резонаторе, где форма зафиксирована, но энергия и количество частиц может колебаться из-за контакта с резервуаром (например, в этих случаях с заземлением или темной поверхностью ). Большой канонический ансамбль обеспечивает естественную среду для точного вывода статистики Ферми - Дирака или Бозе - Эйнштейна для системы невзаимодействующих квантовых частиц (см. Примеры ниже).

Примечание к формулировке

Альтернативная формулировка для той же концепции вероятность записывается как $P\; =\; 1\; Z\; e\; (\mu \; N\; -\; E)\; /\; (k\; T)\; \{\backslash \; displaystyle\; \backslash \; textstyle\; P\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; mathcal\; \{Z\}\}\}\; e\; ^\; \{(\backslash \; mu\; NE)\; /\; (kT)\}\}$, используя функцию большого раздела $Z\; =\; е\; -\; \Omega \; /\; (k\; T)\; \{\backslash \; displaystyle\; \backslash \; textstyle\; \{\backslash \; mathcal\; \{Z\}\}\; =\; e\; ^\; \{-\; \backslash \; Omega\; /\; (kT)\}\}$, а не большой потенциал. Уравнения в статье (в терминах большого количества) могут быть переформулированы в терминах большой статистической суммы с помощью простых математических манипуляций.

Большой канонический ансамбль - это ансамбль, который находится в тепловом и химическом равновесии с резервуаром (вывод происходит по аналогии с выводом термостата нормального канонического ансамбля , и его можно найти в Reif). Большой канонический ансамбль применим к системам любого размера, маленького или большого; необходимо только предположить, что резервуар, который он контактирует, намного больше (т. е. принять макроскопический предел ).

Условие изолированности системы необходимо для того, чтобы гибкость, что она имеет четко термодинамические значения и эволюцию. Однако на практике желательно использовать большой канонический ансамбль для описания систем, которые используются в непосредственном контакте с резервуаром, поскольку именно этот контакт обеспечивает равновесие. Использование канонического ансамбля в этих случаях обычно оправдывается либо 1) предположение, что контакт является частью соединения резервуара в анализируемую систему, так что влияние соединения на область правильно смоделирован интерес. В качестве альтернативы можно использовать теоретические подходы для моделирования связи, что дает открытый статистический ансамбль.

Другой случай, в котором появляется большой канонический ансамбль, - это рассмотрение большой и термодинамической системы (система, которая находится в равновесии сама с собой). Даже если точные условия системы фактически не допускаются вариации энергии или числа частиц, большие канонический ансамбль можно использовать для упрощения вычислений некоторых термодинамических свойств. Причина этого в том, что различные термодинамические ансамбли (микроканонический, канонический ) становятся в некоторых аспектах эквивалентными большому каноническому ансамблю, когда система становится очень большой. Конечно, для небольших систем разные ансамбли больше не эквивалентны даже в среднем. В результате большой ансамбль может быть очень неточным при использовании к небольшим системам с фиксированным размером частиц, таким как атомные ядра.

• Уникальность: Большой канонический ансамбль однозначно определяется для данной системы при заданной температуре и заданном химическом потенциале и не зависит от произвольного выбора, такого как выбор системы координат (классическая механика) или основы (квантовая механика).
• Статистическое равновесие (устойчивое состояние): большой канонический ансамбль действительно не эволюционируют с течением времени, несмотря на то, что основная система находится в постоянном движении. На самом деле, ансамбль является только функцией сохраняющихся количеств (энергии и самого числа частиц).
• Тепловое и химическое равновесие с другими системами: две системы, каждая из которых описывается большим каноническим ансамблем равных температур и химические потенциалы, приведенные в термический и химический контакт, останутся неизменными, и результирующая комбинированная система будет объединенным большим ансамблем тех же температурных и химических потенциалов.
• Максимальная энтропия: для заданных механических параметров (фиксированных V), большое каноническое ансамблевое среднее логарифма вероятности - (также называемое «энтропией») является максимально возможным для любого ансамбля (то есть есть распределения вероятностей P) с тем же , и т. Д.
• Минимальный потенциал: для заданных механических параметров (фиксированное V) и заданных значений T, μ 1,…, μ s, среднее по ансамблю - наименьшее возможное значение из любого ансамбля.

Частные производные функции Ω (µ 1,…, µ s, V, T) дают средние величины большого канонического ансамбля:

• средние числа частиц

  $⟨N\; 1⟩\; =\; -\; \partial \; \Omega \; \partial \; \mu \; 1,\dots \; ⟨N\; s⟩\; =\; -\; \partial \; \Omega \; \partial \; \mu \; s,\; \{\backslash \; displaystyle\; \backslash \; langle\; N\_\; \{1\}\; \backslash \; rangle\; =\; -\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; Omega\}\; \{\backslash \; partial\; \backslash \; mu\; \_\; \{1\}\}\},\; \backslash \; quad\; \backslash \; ldots\; \backslash \; quad\; \backslash \; langle\; N\_\; \{s\}\; \backslash \; rangle\; =\; -\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; Omega\}\; \{\; \backslash \; partial\; \backslash \; mu\; \_\; \{s\}\}\},\}$

• среднее давление
  $⟨p⟩\; =\; -\; \partial \; \Omega \; \partial \; V,\; \{\backslash \; displaystyle\; \backslash \; langle\; p\; \backslash \; rangle\; =\; -\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; Omega\}\; \{\backslash \; частичное\; V\}\},\}$
• энтропия Гиббса
  $S\; =\; -\; k\; ⟨log\; \; P⟩\; =\; -\; \partial \; \Omega \; \partial \; T,\; \{\backslash \; displaystyle\; S\; =\; -k\; \backslash \; langle\; \backslash \; log\; P\; \backslash \; rangle\; =\; -\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; Omega\}\; \{\backslash \; partial\; T\}\},\}$
• и средняя энергия
  $⟨E⟩\; =\; \Omega \; +\; ⟨N\; 1⟩\; \mu \; 1\dots \; +\; ⟨N\; s⟩\; \mu \; s\; +\; СТ.\; \{\backslash \; displaystyle\; \backslash \; langle\; E\; \backslash \; rangle\; =\; \backslash \; Omega\; +\; \backslash \; langle\; N\_\; \{1\}\; \backslash \; rangle\; \backslash \; mu\; \_\; \{1\}\; \backslash \; ldots\; +\; \backslash \; langle\; N\_\; \{s\}\; \backslash \; rangle\; \backslash \; mu\; \_\; \{s\}\; +\; ST.\}$

Точный дифференциал: Из приведенных выше выражений видно, что функция Ω имеет точный дифференциал

$d\; \Omega \; =\; -\; S\; d\; T\; -\; ⟨N\; 1⟩\; d\; \mu \; 1\dots \; -\; ⟨N\; s⟩\; d\; \mu \; s\; -\; p⟩\; d\; V.\; \{\backslash \; displaystyle\; d\; \backslash \; Omega\; =\; -SdT-\; \backslash \; langle\; N\_\; \{1\}\; \backslash \; rangle\; d\; \backslash \; mu\; \_\; \{1\}\; \backslash \; ldots\; -\; \backslash \; langle\; N\_\; \{s\}\; \backslash \; rangle\; d\; \backslash \; mu\; \_\; \{s\}\; -\; \backslash \; langle\; p\; \backslash \; rangle\; dV.\}$

Первый закон термодинамики: Подставить указанное выше соотношение для E⟩ в точный дифференциал Ω, можно найти уравнение, подобное первому закону термодинамики, за исключением, что в некоторых из величин:

$d\; ⟨E⟩\; знак\; равно\; T\; d\; S\; +\; \mu \; 1\; d\; ⟨N\; 1⟩\dots \; +\; \mu \; sd\; ⟨N\; s⟩\; -\; ⟨p⟩\; d\; V.\; \{\backslash \; displaystyle\; d\; \backslash \; langle\; E\; \backslash \; rangle\; =\; TdS\; +\; \backslash \; mu\; \_\; \{1\}\; d\; \backslash \; langle\; N\_\; \{1\}\; \backslash \; rangle\; \backslash \; ldots\; +\; \backslash \; mu\; \_\; \{s\}\; d\; \backslash \; langle\; N\_\; \{s\}\; \backslash \; rangle\; -\; \backslash \; langle\; p\; \backslash \; rangle\; dV.\}$

Термодинамические флуктуации : отклонения энергия и числа частиц равны

$⟨E\; 2⟩\; -\; ⟨E⟩\; 2\; знак\; равно\; К\; T\; 2\; \partial \; ⟨E⟩\; \partial \; T\; +\; К\; T\; \mu \; 1\; \partial \; ⟨E⟩\; \partial \; \mu \; 1\; +\; К\; T\; \mu \; 2\; \partial \; ⟨E⟩\; \partial \; \mu \; 2\; +\dots ,\; \{\backslash \; displaystyle\; \backslash \; langle\; E\; ^\; \{2\}\; \backslash \; rangle\; -\; \backslash \; langle\; E\; \backslash \; rangle\; ^\; \{2\}\; =\; kT\; ^\; \{2\}\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; langle\; E\; \backslash \; rangle\}\; \{\backslash \; partial\; T\}\}\; +\; kT\; \backslash \; mu\; \_\; \{1\}\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; langle\; E\; \backslash \; rangle\}\; \{\backslash \; partial\; \backslash \; mu\; \_\; \{1\}\}\}\; +\; kT\; \backslash \; mu\; \_\; \{2\}\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; langle\; E\; \backslash \; rangle\}\; \{\backslash \; partial\; \backslash \; mu\; \_\; \{2\}\}\}\; +\; \backslash \; ldots,\}$

$⟨N\; 1\; 2⟩\; -\; ⟨N\; 1⟩\; 2\; знак\; равно\; к\; Т\; \partial \; ⟨N\; 1⟩\; \partial \; \mu \; 1.\; \{\backslash \; displaystyle\; \backslash \; langle\; N\_\; \{1\}\; ^\; \{2\}\; \backslash \; rangle\; -\; \backslash \; langle\; N\_\; \{1\}\; \backslash \; rangle\; ^\; \{2\}\; =\; kT\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; langle\; N\_\; \{1\}\; \backslash \; rangle\}\; \{\backslash \; partial\; \backslash \; mu\; \_\; \{1\}\}\}.\}$

Корреляции флуктуаций: ковариации чисел и энергии частиц равны

$⟨N\; 1\; N\; 2⟩\; -\; ⟨N\; 1⟩\; ⟨N\; 2⟩\; =\; k\; T\; \partial \; ⟨N\; 2⟩\; \partial \; \mu \; 1\; знак\; равно\; k\; T\; \partial \; ⟨N\; 1⟩\; \partial \; \mu \; 2.\; \{\backslash \; displaystyle\; \backslash \; langle\; N\_\; \{1\}\; N\_\; \{2\}\; \backslash \; rangle\; -\; \backslash \; langle\; N\_\; \{1\}\; \backslash \; rangle\; \backslash \; langle\; N\_\; \{2\}\; \backslash \; rangle\; =\; kT\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; langle\; N\_\; \{2\}\; \backslash \; rangle\}\; \{\backslash \; partial\; \backslash \; mu\; \_\; \{1\}\}\}\; =\; kT\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; langle\; N\_\; \{1\}\; \backslash \; rangle\}\; \{\backslash \; partial\; \backslash \; mu\; \_\; \{2\}\}\}.\}$

$⟨\; N\; 1\; E⟩\; -\; ⟨N\; 1⟩\; ⟨E⟩\; знак\; равно\; К\; T\; \partial \; ⟨E⟩\; \partial \; \mu \; 1,\; \{\backslash \; displaystyle\; \backslash \; langle\; N\_\; \{1\}\; E\; \backslash \; rangle\; -\; \backslash \; langle\; N\_\; \{1\}\; \backslash \; rangle\; \backslash \; langle\; E\; \backslash \; rangle\; =\; kT\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; langle\; E\; \backslash \; rangle\}\; \{\backslash \; partial\; \backslash \; mu\; \_\; \{1\}\}\},\}$

Полезность большого канонического ансамбля проиллюстрирована в примерах ниже. В каждом случае великий потенциал рассчитывается на основе соотношения

$\Omega \; =\; -\; k\; T\; ln\; \; (\sum \; микросостояния\; e\; \mu \; N\; -\; E\; k\; T)\; \{\backslash \; displaystyle\; \backslash \; Omega\; =\; -kT\; \backslash \; ln\; \backslash \; left\; (\backslash \; sum\; \_\; \{\backslash \; text\; \{\; микросостояния\}\}\; e\; ^\; \{\backslash \; frac\; \{\backslash \; mu\; NE\}\; \{kT\}\}\; \backslash \; right)\}$

, который требуется для того, чтобы вероятности микросостояний в сумме составили 1.

Статистика невзаимодействующих частиц

Бозоны и фермионы (квантовые)

В частном случае квантовой системы из многих невзаимодействующих частиц термодинамику просто вычислить. Они могут быть распределены по серию одночастичных стационарных состояний, которые представляют собой отдельные части, которые могут быть включены в общее квантовое состояние. А пока давайте назовем эти одночастичные стационарные состояния орбиталями (чтобы не путать эти состояния "с общим состоянием многих тел) с условием, что возможное свойство внутренних частиц (спин или считается поляризация ) отдельной орбиталью. Каждая орбиталь может быть занята частицами (или частями) или может быть пустой.

Устройство может взаимодействовать друг с другом, что орбиталь может взаимодействовать друг с другом, что орбиталь образует отдельную термодинамическую систему. Таким образом, каждая орбиталь сама по себе представляет собой грандиозный канонический ансамбль, настолько простой, что его статистика может быть выведена здесь. Сосредоточившись только на одном орбитали, обозначенной i, полная энергия для микросостояния из N частиц на этом орбитали будет Nϵ i, где ϵ i - характерная энергия этого уровня орбиты. Большой потенциал для орбитали основан на одной из двух форм, в зависимости от того, является ли орбиталь бозонной или фермионной:

• Для фермионов принцип исключения Паули допускает только два микросостояния для орбитали (заполнение 0 или 1), давая двухчленный ряд

  $\Omega \; i\; =\; -\; k\; T\; ln\; \; (\sum \; N\; =\; 0\; 1\; e\; N\; \mu \; -\; N\; ϵ\; ik\; T)\; =\; -\; k\; T\; ln\; \; (1\; +\; е\; \mu \; -\; ϵ\; ik\; T)\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; Omega\; \_\; \{i\}\; =\; -\; kT\; \backslash \; ln\; \{\backslash \; Big\; (\}\; \backslash \; sum\; \_\; \{N\; =\; 0\}\; ^\; \{1\}\; e\; ^\; \{\backslash \; frac\; \{N\; \backslash \; mu\; -N\; \backslash \; epsilon\; \_\; \{i\}\}\; \{kT\}\}\; \{\backslash \; Big)\}\; \backslash \backslash \; =\; -\; kT\; \backslash \; ln\; \{\backslash \; Big\; (\}\; 1\; +\; e\; ^\; \{\backslash \; frac\; \{\backslash \; mu\; -\; \backslash \; epsilon\; \_\; \{i\}\}\; \{kT\}\}\; \{\backslash \; Big)\}\; \backslash \; end\; \{align\}\}\}$

• Для бозонов N может быть любым неотрицательным целым числом, и каждое значение N считается одним микросостоянием из-за неотличимость частиц, приводящая к геометрическому ряду :
  $\Omega \; i\; =\; -\; k\; T\; ln\; \; (\sum \; N\; =\; 0\; \infty \; e\; N\; \mu \; -\; N\; ϵ\; ik\; T)\; =\; +\; k\; T\; ln\; \; (1\; -\; e\; \mu \; -\; ϵ\; ik\; T).\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; Omega\; \_\; \{i\}\; =\; -\; kT\; \backslash \; ln\; \{\backslash \; Big\; (\}\; \backslash \; sum\; \_\; \{N\; =\; 0\}\; ^\; \{\backslash \; infty\}\; e\; ^\; \{\backslash \; frac\; \{N\; \backslash \; mu\; -N\; \backslash \; epsilon\; \_\; \{i\}\}\; \{kT\}\}\; \{\backslash \; Big)\}\; \backslash \backslash \; =\; +\; kT\; \backslash \; ln\; \{\backslash \; Big\; (\}\; 1-e\; ^\; \{\backslash \; frac\; \{\backslash \; mu\; -\; \backslash \; epsilon\; \_\; \{i\}\}\; \{kT\}\; \}\; \{\backslash \; Big)\}.\; \backslash \; End\; \{align\}\}\}$

В каждом случае значение $⟨N\; i⟩\; =\; -\; \partial \; \Omega \; i\; \partial \; \mu \; \{\backslash \; displaystyle\; \backslash \; scriptstyle\; \backslash \; langle\; N\_\; \{i\}\; \backslash \; rangle\; =\; -\; \{\backslash \; tfrac\; \{\backslash \; partial\; \backslash \; Omega\; \_\; \{i\}\}\; \{\backslash \; partial\; \backslash \; mu\}\}\}$дает термодинамическое среднее число частиц на орбитали: распределение Ферми - Дирака для фермионов и распределение Бозе - Эйнштейна для бозонов. Рассматривая снова всю систему, общий большой путь путем сложения Ω i для всех орбиталей.

Неразличимые классические частицы

В классической механике также можно рассматривать неразличимые частицы (фактически, неразличимость обнаруживаемых для определения химического согласованным образом; все частицы данного вида должны быть взаимозаменяемыми). Мы снова рассматриваем возможность помещения нескольких частиц одного вида в одно и то же микросостояние одночастичное фазовое пространство, которое мы снова называем «орбитальным». По сравнению с квантовой механикой классический случай усложняется тем фактом, что микросостояние в классической механике относится не к одной точке в фазовом пространстве, а к расширенной области в фазовом пространстве: одно микросостояние содержит бесконечное количество состояний, все разные, похожего характера. В результате того, когда несколько частиц перемещаются на одну и ту же орбиталь, набор частиц (в системном общем пространстве) считается не одним целым микросостояниями, поскольку идентичные состояния (образованные перестановкой одинаковых частиц) не считаются. Поправочный коэффициент перерасчета - это факториал количества частиц.

Статистика в этом случае принимает форму экспоненциального степенного ряда

$\Omega \; orb\; =\; -\; k\; T\; ln\; \; (\sum \; N\; =\; 0\; \infty \; 1\; N!\; EN\; \mu \; -\; N\; ϵ\; orbk\; T)\; =\; -\; К\; T\; ln\; \; (\; ее\; \mu \; -\; ϵ\; orbk\; T)\; =\; -\; К\; T\; e\; \mu \; -\; ϵ\; orbk\; T,\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; Omega\; \_\; \{\backslash \; rm\; \{orb\}\}\; =\; -\; kT\; \backslash \; ln\; \{\backslash \; Большой\; (\}\; \backslash \; sum\; \_\; \{N\; =\; 0\}\; ^\; \{\backslash \; infty\}\; \{\backslash \; frac\; \{1\}\; \{N!\}\}\; E\; ^\; \{\backslash \; frac\; \{N\; \backslash \; mu\; -N\; \backslash \; epsilon\; \_\; \{\backslash \; rm\; \{orb\}\}\}\; \{kT\}\}\; \{\backslash \; Big)\}\; \backslash \backslash \; =\; -\; kT\; \backslash \; ln\; \{\backslash \; Big\; (\}\; e\; ^\; \{e\; ^\; \{\backslash \; frac\; \{\backslash \; mu\; -\; \backslash \; epsilon\; \_\; \{\backslash \; rm\; \{orb\}\}\}\; \{kT\}\}\}\; \{\backslash \; Big)\}\; \backslash \; \backslash \; =\; -\; kTe\; ^\; \{\backslash \; frac\; \{\backslash \; mu\; -\; \backslash \; epsilon\; \_\; \{\backslash \; rm\; \{orb\}\}\}\; \{kT\}\},\; \backslash \; end\; \{align\}\}\}$

значение $⟨N\; orb⟩\; знак\; равно\; -\; \partial \; \Omega \; сфера\; \partial \; \mu \; \{\backslash \; Displaystyle\; \backslash \; scriptstyle\; \backslash \; langle\; N\; \_\; \{\backslash \; rm\; \{orb\}\}\; \backslash \; rangle\; =\; -\; \{\backslash \; tfrac\; \{\backslash \; partial\; \backslash \; Omega\; \_\; \{\backslash \; rm\; \{orb\}\}\}\; \{\backslash \; partial\; \backslash \; mu\}\}\}$соответствует статистике Максвелла - Больцмана.

Ионизация изолированного атома

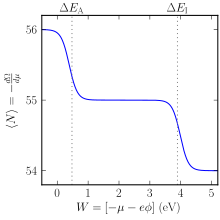Эффект поверхностной ионизации в испаренном атоме цезия при 1500 К, рассчитанный с использованием метода в этом разделе (включаявырождение ). Ось Y: среднее количество электронов; атом нейтрален, когда в нем 55 электронов. Ось X: переменная энергия, которая соответствует поверхности работа выхода.

Большой канонический ансамбль может быть, чтобы предсказать, предпочитает ли атом находиться в нейтральном состоянии или в ионизированном состоянии. Атом может существовать в ионизированном состоянии с большим или меньшим электронов по сравнению с нейтральным. Как показано ниже, ионизированные состояния могут быть термодинамически предпочтительными в зависимости от окружающей среды. Рассмотрим упрощенную модель, в которой можно находиться в одном из двух ионизированных состояний (подробный расчет также включает факторы вырождения состояний):

• нейтральное состояние с N 0 электронов и энергия E 0.
• в окисленном состоянии (N 0 - 1 электронов) с энергией E 0 + ΔE I + qϕ
• a восстановленное состояние (N 0 + 1 электронов) с энергией E 0 - ΔE A - qϕ

Здесь ΔE I и ΔE A - энергия ионизации и сродство к электрону атома, соответственно; ϕ - локальный электростатический потенциал в вакууме рядом с атомом, а −q - заряд электрона.

Таким образом, большой потенциал в этом случае определяется как

$\Omega \; =\; -\; k\; T\; ln\; \; (\; е\; \mu \; N\; 0\; -\; E\; 0\; k\; T\; +\; e\; \mu \; N\; 0\; -\; \mu \; -\; E\; 0\; -\; \Delta \; EI\; -\; q\; \varphi \; k\; T\; +\; e\; \mu \; N\; 0\; +\; \mu \; -\; E\; 0\; +\; \Delta \; EA\; +\; q\; \varphi \; k\; T).\; =\; E\; 0\; -\; \mu \; N\; 0\; -\; k\; T\; ln\; \; (1\; +\; e\; -\; \mu \; -\; \Delta \; E\; I\; -\; q\; \varphi \; k\; T\; +\; e\; \mu \; +\; \Delta \; E\; A\; +\; q\; \varphi \; k\; T).\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; Omega\; =\; -\; kT\; \backslash \; ln\; \{\backslash \; Big\; (\}\; e\; ^\; \{\backslash \; frac\; \{\backslash \; mu\; N\_\; \{0\}\; -E\_\; \{0\}\}\; \{kT\}\}\; +\; e\; ^\; \{\backslash \; frac)\; \{\backslash \; mu\; N\_\; \{0\}\; -\; \backslash \; mu\; -E\_\; \{0\}\; -\; \backslash \; Delta\; E\; \_\; \{\backslash \; rm\; \{I\}\}\; -\; q\; \backslash \; phi\}\; \{kT\}\}\; +\; e\; ^\; \{\backslash \; frac\; \{\backslash \; mu\; N\_\; \{0\}\; +\; \backslash \; mu\; -E\_\; \{0\}\; +\; \backslash \; Delta\; E\; \_\; \{\backslash \; rm\; \{A\}\}\; +\; q\; \backslash \; phi\}\; \{kT\}\}\; \{\backslash \; Big)\}.\; \backslash \backslash \; =\; E\_\; \{0\}\; -\; \backslash \; mu\; N\_\; \{0\}\; -kT\; \backslash \; ln\; \{\backslash \; Big\; (\}\; 1\; +\; e\; ^\; \{\backslash \; frac\; \{-\; \backslash \; mu\; -\; \backslash \; Delta\; E\; \_\; \{\backslash \; rm\; \{I\}\}\; -\; q\; \backslash \; phi\}\; \{kT\}\}\; +\; e\; ^\; \{\backslash \; frac\; \{\backslash \; mu\; +\; \backslash \; Delta\; E\_\; \{\backslash \; rm\; \{A\}\}\; +\; q\; \backslash \; phi\}\; \{kT\}\}\; \{\backslash \; Big)\}.\; \backslash \backslash \backslash \; end\; \{align\}\}\}$

Величина −qϕ - µ критична в этом случае для определения баланса между различными государствами. Это значение определяется окружающей средой вокруг атома.

Если один из этих элементов поместить в вакуумный ящик, то −qϕ - µ = W, работа выхода материала футеровки ящика. Сравнивая таблицы работы выхода для различных твердых материалов с таблицами сродства к электрону и энергии ионизации для разновидностей атомов, становится ясно, что многие комбинации приведут к нейтральный атом, однако некоторые конкретные комбинации могут привести к тому, что атом будет предпочитать ионизированное состояние: например, атом галогена в блоке иттербия или атом цезия в коробке вольфрам. При комнатной температуре эта ситуация нестабильна, поскольку атом стремится адсорбировать на открытой облицовке ящика вместо того, чтобы свободно плавать. Однако при высоких температурах атомы испаряются с поверхности в ионной форме; этот эффект спонтанной поверхностной ионизации был использован в качестве источника ионов цезия .

При комнатной температуре этот пример находит применение в полупроводниках, где ионизация атом допанта хорошо описывается этим ансамблем. В полупроводнике зона проводимости край ϵ C играет роль уровня энергии вакуума (заменяя −qϕ), а µ известен как уровень Ферми. Конечно, энергия ионизации и электронное сродство атома примеси сильно изменяются по сравнению с их вакуумными значениями. Типичная донорная легирующая примесь вкремнии, фосфор, имеет ΔE I = 45 мэВ; C - µ в собственном кремнии используется около 600 мэВ, что значение ионизации легирующей примеси. Однако значение C - µ сильно зависит от электростатики, поэтому при некоторых обстоятельствах можно деионизировать легирующую добавку.

. Оно должно сохраняться во время внутренней динамики системы, и только изменяться, когда система обменивается частями с внешним резервуаром.

Если частицы могут быть созданы из энергии во время динамики системы, то связанный член µN не должен появляться в вероятностном выражении для большого канонического ансамбля. По сути, это то же самое, требование µ = 0 для такого типа частиц. Так обстоит дело с фотонами в черной полости, количество которых регулярно меняется из-за поглощения и излучения на стенках полости. (С другой стороны, фотоны в резонаторе с высокой отражающей способностью могут сохраняться и иметь ненулевое значение µ.)

В некоторых случаях количество частиц не сохраняется, а N представляет собой более абстрактную сохраняемую величину:

• Химические реакции: химические реакции могут преобразовывать один тип молекулы в другой; если происходит реакция, то N i должно быть определено таким образом, чтобы они не менялись во время химической реакции.
• Физика частиц высоких энергий: обычные частицы могут быть порождены из чистой энергии, если соответствующая античастица создана. Если такой процесс разрешен, то не сохраняется ни количество частиц, ни количество античастиц. Вместо этого сохранения N = (число частиц - число античастиц). По мере увеличения энергии частиц появляется больше возможностей для преобразования между типами частиц, и поэтому количество действительно увеличивается. При самых высоких энергиях единственными сохраняющимися числами являются электрический заряд, слабый изоспин и барионное число - лептонное число.

.

• Закрытые отсеки: система, состоящая из нескольких отсеков, которые разделяют энергию, но не разделяют частицы, можно установить химические потенциалы отдельно для каждого отсека. Например, конденсатор состоит из двух проводников и заряжается за счет применения разницы в химическом потенциале электронов.
• Медленное уравновешивание: в некоторых квазиравновесных состояниях возможно двух различных популяции частиц одного и того же типа в одном. месте, каждой из которых уравновешена внутренне, но не друг с другом. Хотя это и не совсем равновесие, может быть назвать квазиравновесные химические потенциалы, которые могут различаться в разных популяциях. Примеры: (физика полупроводников ) квазиуровни Ферми (электронные химические потенциалы) в зоне проводимости и валентной зоне ; (спинтроника ) различные химические потенциалы вращения вверх и вниз; (криогеника ) различные химические потенциалы параводорода и ортоводорода

Точное математическое выражение для статистических ансамблей имеет отдельную форму в зависимости от типа рассматриваемой механики (квантовая или классическая), поскольку понятие «микросостояние» различается. В квантовой механике большой канонический ансамбль дает простое описание, поскольку диагонализация обеспечивает набор различных микросостояний системы, каждый с четко определенной энергией и численностью частиц. Классический механический случай более сложен, поскольку он включает не стационарные состояния, а интеграл по каноническому фазовому пространству.

Квантовая механика

Статистический ансамбль в квантовой механике представлен матрицей плотности , обозначается $\rho \; ^\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{\backslash \; rho\}\}\}$. Большой канонический ансамбль - это матрица плотности

$\rho \; ^\; =\; exp\; \; (1\; k\; T\; (\Omega \; +\; \mu \; 1\; N\; ^\; 1\; +\dots \; +\; \mu \; s\; N\; ^\; s\; -\; H\; ^)),\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{\backslash \; rho\; \}\}\; =\; \backslash \; exp\; \{\backslash \; big\; (\}\; \{\backslash \; tfrac\; \{1\}\; \{kT\}\}\; (\backslash \; Omega\; +\; \backslash \; mu\; \_\; \{1\}\; \{\backslash \; hat\; \{N\}\}\; \_\; \{1\}\; +\; \backslash \; ldots\; +\; \backslash \; mu\; \_\; \{s\; \}\; \{\backslash \; hat\; \{N\}\}\; \_\; \{s\}\; -\; \{\backslash \; hat\; \{H\}\})\; \{\backslash \; big)\},\}$

где Ĥ - оператор энергии системы (гамильтониан ), N̂ 1 - оператор общего числа частиц системы для частиц 1, N̂ 2 - оператор общего числа частиц частиц для частиц тип 2 и так далее. exp - матричный экспоненциальный оператор . Большой потенциал Ω определяется условием нормализации вероятности, что матрица плотности имеет след единицы, $T\; r\; \rho \; ^\; =\; 1\; \{\backslash \; displaystyle\; Tr\; \{\backslash \; hat\; \{\backslash \; rho\}\}\; =\; 1\}$:

$e\; -\; \Omega \; k\; T\; =\; Tr\; \; exp\; \; (1\; k\; T\; (\mu \; 1\; N\; ^\; 1\; +\dots \; +\; \mu \; s\; N\; ^\; s\; -\; H\; ^)).\; \{\backslash \; displaystyle\; e\; ^\; \{-\; \{\backslash \; frac\; \{\backslash \; Omega\}\; \{kT\}\}\}\; =\; \backslash \; operatorname\; \{Tr\}\; \backslash \; exp\; \{\backslash \; big\; (\}\; \{\backslash \; tfrac\; \{1\}\; \{kT\}\}\; (\backslash \; mu\; \_\; \{1\}\; \{\; \backslash \; hat\; \{N\}\}\; \_\; \{1\}\; +\; \backslash \; ldots\; +\; \backslash \; mu\; \_\; \{s\}\; \{\backslash \; hat\; \{N\}\}\; \_\; \{s\}\; -\; \{\backslash \; hat\; \{H\}\})\; \{\backslash \; big)\}.\}$

Обратите внимание, что для большого ансамбля базисные состояния операторов Ĥ, N̂ 1 и т. Д. Являются состояниями с множественными частями в проявлении, а матрица плотности определяется на той же основе. Энергия устанавливается по отдельности.

Большой канонический ансамбль в качестве альтернативы может быть записан в простой форме с использованием брэкет-нотации, поскольку возможно (учитывая взаимно коммутирующий характер операторов энергии и числа частиц) найти полный базис совместных собственных состояний |ψi⟩, индексированный i, где Ĥ | ψ i ⟩ = E i|ψi⟩, N̂ 1|ψi⟩ = N 1, i |ψi⟩ и так далее. При таком собственном базисе большой канонический ансамбль просто

$\rho \; ^\; =\; \sum \; i\; e\; \Omega \; +\; \mu \; 1\; N\; 1,\; i\; +\dots \; +\; \mu \; s\; N\; s,\; i\; -\; E\; i\; k\; T\; |\; \psi \; i⟩\; ⟨\psi \; i\; |\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{\backslash \; rho\}\}\; =\; \backslash \; sum\; \_\; \{i\}\; e\; ^\; \{\backslash \; frac\; \{\backslash \; Omega\; +\; \backslash \; mu\; \_\; \{1\}\; N\_\; \{1,\; i\}\; +\; \backslash \; ldots\; +\; \backslash \; mu\; \_\; \{s\}\; N\_\; \{s,\; i\}\; -E\_\; \{i\}\}\; \{kT\}\}\; |\; \backslash \; psi\; \_\; \{i\}\; \backslash \; rangle\; \backslash \; langle\; \backslash \; psi\; \_\; \{i\}\; |\}$

$e\; -\; \Omega \; k\; T\; =\; \sum \; т.е.\; \mu \; 1\; N\; 1,\; i\; +\dots \; +\; \mu \; s\; N\; s,\; i\; -\; E\; ik\; T.\; \{\; \backslash \; displaystyle\; e\; ^\; \{-\; \{\backslash \; frac\; \{\backslash \; Omega\}\; \{kT\}\}\}\; =\; \backslash \; sum\; \_\; \{i\}\; e\; ^\; \{\backslash \; frac\; \{\backslash \; mu\; \_\; \{1\}\; N\_\; \{1,\; i\}\; +\; \backslash \; ldots\; +\; \backslash \; mu\; \_\; \{s\}\; N\_\; \{s,\; i\}\; -E\_\; \{i\}\}\; \{kT\}\}.\}$

где сумма соответствует полному набору состояний с состоянием i, имеющим E i полную энергию, N 1, i частиц типа 1, N 2, i частиц типа 2 и так далее.

Классическая механика

В классической механике большой ансамбль вместо этого представлен совместной плотности плотности вероятности, большой на нескольких фазовых пространствах различных размеров, ρ (N 1,… N s, p 1,… p n, q 1,… Q n), где p 1,… p n и q 1,… q n - канонические координаты (обобщенные импульсы обобщенные координаты) внутренних степеней свободы системы. Выражение для большого канонического ансамбля несколько более тонкое, чем канонический ансамбль, поскольку:

• Число частиц и, следовательно, число координат меняется между различными фазовыми пространствами, и,
• жизненно важно учитывать, ли перестановка одинаковых электрических величин состоянием или нет.

В системе частиц количество степеней свободы n зависит от количества частиц, что зависит от физической ситуации.. Например, в трехмерном газе из моноатомов n = 3N, однако в молекулярных газах также будут вращательные колебательные степени свободы.

Функция вероятности плотности для большого канонического ансамбля:

$\rho \; =\; 1\; hn\; C\; e\; \Omega \; +\; \mu \; 1\; N\; 1\; +\dots \; +\; \mu \; s\; N\; s\; -\; E\; k\; T,\; \{\backslash \; displaystyle\; \backslash \; rho\; =\; \{\backslash \; frac\; \{1\}\; \{h\; ^\; \{n\}\; C\}\}\; e\; ^\; \{\backslash \; frac\; \{\backslash \; Omega\; +\; \backslash \; mu\; \_\; \{1\}\; N\_\; \{1\}\; +\; \backslash \; ldots\; +\; \backslash \; mu\; \_\; \{s\}\; N\_\; \{s\}\; -E\}\; \{kT\; \}\},\}$

где

• E - энергия системы, функция фазы (N 1,… N s, p 1,… p n, q 1,… q n),
• h - произвольная, но заранее определенная константа в единицах энергии × время, задающая протяженность одного микросостоянии и правильные размеры для ρ.
• C - это поправочный коэффициент при перерасчете (см. Ниже), функция N 1,… N s.

Опять же, значение Ω требуя, чтобы ρ была нормализованной плотности плотности вероятности:

$e\; -\; \Omega \; К\; T\; знак\; равно\; \sum \; N\; 1\; знак\; равно\; 0\; \infty \dots \; \sum \; N\; s\; =\; 0\; \infty \; \int \dots \; \int \; 1\; hn\; C\; e\; \mu \; 1\; N\; 1\; +\dots \; +\; \mu \; s\; N\; s\; -\; E\; К\; T\; dp\; 1\dots \; dqn\; \{\backslash \; displaystyle\; e\; ^\; \{\; -\; \{\backslash \; frac\; \{\backslash \; Omega\}\; \{kT\}\}\}\; =\; \backslash \; sum\; \_\; \{N\_\; \{1\}\; =\; 0\}\; ^\; \{\backslash \; infty\}\; \backslash \; ldots\; \backslash \; sum\; \_\; \{N\_\; \{s\}\; =\; 0\}\; ^\; \{\backslash \; infty\}\; \backslash \; int\; \backslash \; Я\; делаю\; ts\; \backslash \; int\; \{\backslash \; frac\; \{1\}\; \{h\; ^\; \{n\}\; C\}\}\; e\; ^\; \{\backslash \; frac\; \{\backslash \; mu\; \_\; \{1\}\; N\_\; \{1\}\; +\; \backslash \; ldots\; +\; \backslash \; mu\; \_\; \{s\}\; N\_\; \{s\}\; -E\; \}\; \{kT\}\}\; \backslash ,\; dp\_\; \{1\}\; \backslash \; ldots\; dq\_\; \{n\}\}$

Этот интеграл берется по всему доступному фазовое пространство для заданного числа частиц.

Поправка на завышенный счет

Хорошо известная проблема в статистической механике флюидов (газов, жидкостей, плазмы) заключается в том, как обрабатывать частицы, похожие или идентичные по природе: следует ли рассматривать их как различимы или нет? В уравнении движения системы отдельных частей всегда отслеживается как различимая сущность, и, тем не менее, есть также допустимые состояния системы, в положениях каждой частицы просто поменялись местами: состояния представлены в разных местах фазового пространства, но при этом будут кажутся эквивалентными.

Если считать, что перестановки одинаковых частных отдельных состояний, то вышеупомянутый фактор C равен просто C = 1. С этой точки зрения ансамбли включает переставленное состояние как отдельное микросостояние. Хотя сначала это кажется безобидным, это приводит к проблеме сильно неэкстенсивной энтропии в каноническом ансамбле, известной сегодня как парадокс Гиббса. В большом каноническом ансамбле еще одна несогласованность: количество различных перестановок зависит не только от количества частиц в системе, но и от того, сколько частиц находится в резервуаре (поскольку система может обмениваться частями с резервуаром). В этом случае энтропия и химический потенциал не должны иметь экстенсивные возможности, но также плохо реализуемые в зависимости от размера резервуара значения.

Для решения этих проблем необходимо, чтобы обмен двумя подобными частями (системы или между системой и резервуаром) не рассматривался как определение системы. Чтобы учесть этот факт, интегралы по-прежнему переносятся по всему фазовому пространству, но результат делится на

$C\; =\; N\; 1!\; N\; 2!\; \dots \; N\; s!,\; \{\backslash \; displaystyle\; C\; =\; N\_\; \{1\}!\; N\_\; \{2\}!\; \backslash \; ldots\; N\_\; \{s\}!,\}$

, которое представляет собой количество возможных перестановок. Деление на C аккуратно исправляет перерасчет, который происходит в интеграле по всему фазовому пространству.

Конечно, можно включить различимые типы частиц в большой канонический ансамбль - каждый различимый тип $i\; \{\backslash \; displaystyle\; i\}$отслеживается отдельным счетчиком частиц $N\; i\; \{\backslash \; displaystyle\; N\_\; \{i\}\}$и химический потенциал $\mu \; i\; \{\backslash \; displaystyle\; \backslash \; mu\; \_\; \{i\}\}$. В результате единственный последовательный способ включить «полностью различимые» частицы в большой канонический ансамбль - это рассмотреть все возможные различимые типы этих частиц и отслеживать каждый возможный тип с помощью отдельного счетчика частиц и отдельного химического потенциала.