Сканирование Грэма

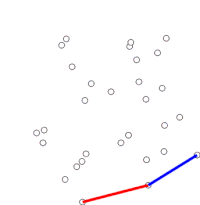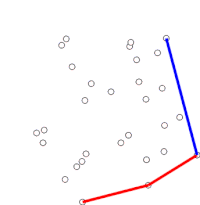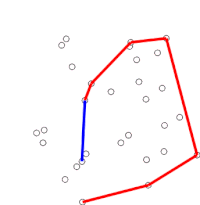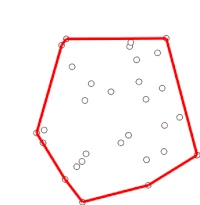
Алгоритм для вычисления выпуклой оболочки в наборе точек Демонстрация сканирования Грэма для поиска двумерной выпуклой оболочки.

Сканирование Грэма - это метод поиска выпуклой оболочки конечный набор точек на плоскости с временной сложностью O (n log n). Он назван в честь Рональда Грэма, опубликовавшего исходный алгоритм в 1972 году. Алгоритм находит все вершины выпуклой оболочки, упорядоченные вдоль ее границы. Он использует стек для эффективного обнаружения и удаления вогнутостей на границе.

• 1 Алгоритм
• 2 Временная сложность
• 3 Псевдокод
• 4 Примечания
• 5 Числовая устойчивость
• 6 См. Также
• 7 Ссылки
• 8 Дополнительная литература

Как видно, PAB и ABC идут против часовой стрелки, а BCD - нет. Алгоритм обнаруживает эту ситуацию и отбрасывает ранее выбранные сегменты до тех пор, пока не будет сделан поворот против часовой стрелки (в данном случае ABD).

Первым шагом в этом алгоритме является поиск точки с наименьшей y-координатой. Если самая низкая координата Y существует более чем в одной точке в наборе, должна быть выбрана точка с самой низкой координатой x из возможных. Назовите эту точку P. Этот шаг занимает O (n), где n - количество рассматриваемых точек.

Затем необходимо отсортировать набор точек в порядке возрастания угла, который они и точка P образуют с осью x. Для этого подходит любой универсальный алгоритм сортировки , например heapsort (который равен O (n log n)).

Сортировка по углу не требует вычисления угла. Можно использовать любую функцию угла, которая является монотонной в интервале $[0,\; \pi ]\; \{\backslash \; displaystyle\; [0,\; \backslash \; pi]\}$. Косинус легко вычисляется с использованием скалярного произведения или может использоваться наклон линии. Если на карту поставлена ​​числовая точность, функция сравнения, используемая алгоритмом сортировки, может использовать знак перекрестного произведения для определения относительных углов.

Алгоритм последовательно рассматривает каждую из точек отсортированного массива. Для каждой точки сначала определяется, составляет ли путешествие из двух точек, непосредственно предшествующих этой точке, поворот налево или направо. При повороте направо предпоследняя точка не является частью выпуклой оболочки, а лежит «внутри» ее. Затем такое же определение выполняется для набора последней точки и двух точек, которые непосредственно предшествуют точке, находящейся внутри корпуса, и повторяется до тех пор, пока не встретится набор «левый поворот», после чего алгоритм переходит к к следующей точке в наборе точек отсортированного массива за вычетом всех точек, которые были обнаружены внутри корпуса; нет необходимости снова рассматривать эти моменты. (Если на каком-либо этапе три точки коллинеарны, можно либо отбросить, либо сообщить об этом, поскольку в некоторых приложениях требуется найти все точки на границе выпуклой оболочки.)

Опять же, определение того, составляют ли три точки «левый поворот» или «правый поворот», не требует вычисления фактического угла между двумя линейными сегментами и фактически может быть достигнуто только с помощью простой арифметики. Для трех точек $P\; 1\; =\; (x\; 1,\; y\; 1)\; \{\backslash \; displaystyle\; P\_\; \{1\}\; =\; (x\_\; \{1\},\; y\_\; \{1\})\}$, $P\; 2\; =\; (x\; 2,\; y\; 2)\; \{\; \backslash \; Displaystyle\; P\_\; \{2\}\; =\; (x\_\; \{2\},\; y\_\; \{2\})\}$и $P\; 3\; =\; (x\; 3,\; y\; 3)\; \{\backslash \; displaystyle\; P\_\; \{3\}\; =\; (x\_\; \{\; 3\},\; y\_\; \{3\})\}$, вычислить координату z векторного произведения двух векторов $P\; 1\; P\; 2\; \to \; \{\; \backslash \; displaystyle\; \{\backslash \; overrightarrow\; \{P\_\; \{1\}\; P\_\; \{2\}\}\}\}$и $P\; 1\; P\; 3\; \to \; \{\backslash \; displaystyle\; \{\backslash \; overrightarrow\; \{P\_\; \{1\}\; P\_\; \{3\}\}\}\}$, которое задается выражением $(x\; 2\; -\; x\; 1)\; (y\; 3\; -\; y\; 1)\; -\; (y\; 2\; -\; y\; 1)\; (x\; 3\; -\; x\; 1)\; \{\backslash \; displaystyle\; (x\_\; \{2\}\; -x\_\; \{1\})\; (y\_\; \{3\}\; -y\_\; \{1\})\; -\; (y\_\; \{2\}\; -y\_\; \{1\})\; (x\_\; \{3\}\; -x\_\; \{1\})\}$. Если результат 0, точки коллинеарны; если он положительный, три точки образуют «левый поворот» или ориентацию против часовой стрелки, в противном случае - «правый поворот» или ориентацию по часовой стрелке (для точек, пронумерованных против часовой стрелки).

Этот процесс в конечном итоге вернется к точке, в которой он был запущен, после чего алгоритм завершен, и теперь стек содержит точки на выпуклой оболочке в порядке против часовой стрелки.

Сортировка точек имеет временную сложность O (n log n). Хотя может показаться, что временная сложность цикла равна O (n), потому что для каждой точки он возвращается, чтобы проверить, совершает ли какая-либо из предыдущих точек «поворот вправо», на самом деле это O (n), потому что каждая точка в некотором смысле считается не более двух раз. Каждая точка может появиться только один раз как точка $(x\; 2,\; y\; 2)\; \{\backslash \; displaystyle\; (x\_\; \{2\},\; y\_\; \{2\})\}$в «левом повороте» (поскольку алгоритм переходит к следующей точке $(x\; 3,\; y\; 3)\; \{\backslash \; displaystyle\; (x\_\; \{3\},\; y\_\; \{3\})\}$после этой точки), и как точка $(x\; 2,\; y\; 2)\; \{\backslash \; displaystyle\; (x\_\; \{2\},\; y\_\; \{2\})\}$в «повороте направо» (потому что точка $(x\; 2,\; y\; 2)\; \{\backslash \; displaystyle\; (x\_\; \{2\},\; y\_\; \{2\})\}$удалено). Таким образом, общая временная сложность составляет O (n log n), поскольку время сортировки преобладает над временем фактического вычисления выпуклой оболочки.

В приведенном ниже коде используется функция ccw: ccw>0, если три точки совершают поворот против часовой стрелки, по часовой стрелке, если ccw < 0, and collinear if ccw = 0. (In real applications, if the coordinates are arbitrary real numbers, the function requires exact comparison of floating-point numbers, and one has to beware of numeric singularities for "nearly" collinear points.)

Затем пусть результат будет сохранен в стек.

пусть точек будет список точек пусть stack = empty_stack () найдет самую низкую координату y и крайний левый точка, называемая P0 сортирует точки по полярному углу с помощью P0, если несколько точек имеют одинаковый полярный угол, тогда только самый дальний для точки в точках: # pop последняя точка из стека, если мы повернем по часовой стрелке, чтобы достичь этой точки, покаcount stack>1 и ccw (next_to_top (stack), top (stack), point) <= 0: pop stack push point to stack end

Теперь стек содержит выпуклую оболочку, где точки ориентированы против часовой стрелки и P0 - первая точка.

Здесь next_to_top ()- это функция для возврата элемента на одну запись ниже вершины стека, без изменения стека, и аналогично, top ()для возвращает самый верхний элемент.

Этот псевдокод адаптирован из Введение в алгоритмы.

Та же основная идея работает также, если входные данные отсортированы по координате x вместо угла, а корпус вычисляется в два этапа, производя соответственно верхнюю и нижнюю части корпуса. Эта модификация была разработана А.М. Эндрю и известна как алгоритм монотонной цепочки Эндрю. Он имеет те же основные свойства, что и сканирование Грэма.

Метод суммирования, используемый в сканировании Грэма, очень похож на метод всех ближайших меньших значений и параллельные алгоритмы для всех ближайших меньших значений может также использоваться (например, сканирование Грэма) для эффективного вычисления выпуклой оболочки отсортированных последовательностей точек.

Числовая устойчивость - это проблема, с которой приходится иметь дело в алгоритмах, использующих конечную точность компьютерная арифметика с плавающей точкой. В статье 2004 года анализировалась простая инкрементная стратегия, которую можно использовать, в частности, для реализации сканирования Грэма. Заявленная цель статьи заключалась не в конкретном анализе алгоритма, а в предоставлении учебного примера того, что и как может дать сбой из-за вычислений с плавающей запятой в вычислительной геометрии. Позже Д. Цзян и Н. Ф. Стюарт подробно остановились на этом и, используя обратный анализ ошибок, сделали два основных вывода. Во-первых, выпуклая оболочка - это хорошо обусловленная проблема, и поэтому можно ожидать, что алгоритмы будут давать ответ в пределах разумной погрешности. Во-вторых, они демонстрируют, что модификация сканирования Грэма, которую они называют Graham-Fortune (включающая идеи числовой стабильности), действительно решает проблемы конечной точности и неточных данных «в той степени, в которой это возможно».

• Алгоритмы выпуклой оболочки

• Cormen, Thomas H. ; Лейзерсон, Чарльз Э. ; Ривест, Рональд Л. ; Стейн, Клиффорд (2001) [1990]. «33.3: Нахождение выпуклой оболочки». Введение в алгоритмы (2-е изд.). MIT Press и McGraw-Hill. С. 949–955. ISBN 0-262-03293-7.