Обобщенный закон распределения

Обобщенный закон распределения (GDL) является обобщением свойства распределения что дает начало общему алгоритму передачи сообщений . Это синтез работ многих авторов в области теории информации, цифровых коммуникаций, обработки сигналов, статистики и <581.>искусственный интеллект сообщества. Закон и алгоритм были представлены в полуучебном пособии Шриниваса М. Аджи и Роберта Дж. МакЭлиса с тем же названием.

• 1 Введение
• 2 История
• 3 Задача MPF
• 4 GDL: алгоритм решения задачи MPF
  • 4.1 Алгоритм обобщенного закона распределения (GDL)
  • 4.2 Основы работы алгоритма
• 5 Планирование передачи сообщений и вычисления состояний
• 6 Построение дерева соединений
• 7 Теорема о планировании
• 8 Вычислительная сложность
• 9 Ссылки

«Закон распределения в математике - это закон, связывающий операции умножения и сложения., обозначенное символически, $a\; \ast \; (b\; +\; c)\; =\; a\; \ast \; b\; +\; a\; \ast \; c\; \{\backslash \; displaystyle\; a\; *\; (b\; +\; c)\; =\; a\; *\; b\; +\; a\; *\; c\}$; то есть, мономиальный множитель $a\; \{\backslash \; displaystyle\; a\}$распределяется или применяется отдельно к каждому члену биномиального множителя $b\; +\; c\; \{\backslash \; displaystyle\; b\; +\; c\}$, в результате получается произведение $a\; \ast \; b\; +\; a\; \ast \; c\; \{\backslash \; displaystyle\; a\; *\; b\; +\; a\; *\; c\}$"- Britannica

Как видно из определения, применение закона распределения к арифметическому выражению сокращает количество операций в нем. В предыдущем примере общее количество операций уменьшилось с трех (два умножения и сложение в $a\; \ast \; b\; +\; a\; \ast \; c\; \{\backslash \; displaystyle\; a\; *\; b\; +\; a\; *\; c\}$) до двух ( одно умножение и одно сложение в $a\; \ast \; (b\; +\; c)\; \{\backslash \; displaystyle\; a\; *\; (b\; +\; c)\}$). Обобщение закона распределения приводит к большому семейству быстрых алгоритмов. Это включает в себя БПФ и алгоритм Витерби.

Это более формально объясняется в следующем примере:

$\alpha \; (a,\; b)\; =\; def\; \sum \; c,\; d,\; e\; \in \; A\; е\; (a,\; c,\; b)\; g\; (a,\; d,\; e)\; \{\backslash \; displaystyle\; \backslash \; alpha\; (a,\; \backslash ,\; b)\; \{\backslash \; stackrel\; \{\backslash \; mathrm\; \{def\}\}\; \{=\}\}\; \backslash \; displaystyle\; \backslash \; sum\; \backslash \; limits\; \_\; \{c,\; d,\; e\; \backslash \; in\; A\}\; f\; (a,\; \backslash ,\; c,\; \backslash ,\; b)\; \backslash ,\; g\; (a,\; \backslash ,\; d,\; \backslash ,\; e)\}$где $f\; (\cdot )\; \{\backslash \; displaystyle\; f\; (\backslash \; cdot)\}$и $g\; (\cdot )\; \{\backslash \; displaystyle\; g\; (\backslash \; cdot)\}$- функции с действительным знаком, $a,\; b,\; c,\; d,\; e\; \in \; A\; \{\backslash \; displaystyle\; a,\; b,\; c,\; d,\; e\; \backslash \; in\; A\}$и $|\; А\; |\; =\; q\; \{\backslash \; displaystyle\; |\; A\; |\; =\; q\}$(например)

Здесь мы «маргинализируем» независимые переменные ($c\; \{\backslash \; displaystyle\; c\}$, $d\; \{\backslash \; displaystyle\; d\}$и $e\; \{\backslash \; displaystyle\; e\}$) для получения результата. Когда мы вычисляем вычислительную сложность, мы видим, что для каждого $q\; 2\; \{\backslash \; displaystyle\; q\; ^\; \{2\}\}$пары $(a,\; b)\; \{\backslash \; displaystyle\; (a,\; b)\}$, есть $q\; 3\; \{\backslash \; displaystyle\; q\; ^\; \{3\}\}$термины из-за тройки $(c,\; d,\; e)\; \{\backslash \; displaystyle\; (c,\; d,\; e)\}$, который должен участвовать в оценке $\alpha \; (a,\; b)\; \{\backslash \; displaystyle\; \backslash \; alpha\; (a,\; \backslash ,\; b)\}$на каждом шаге одно сложение и одно умножение. Следовательно, общее количество необходимых вычислений составляет $2\; \cdot \; q\; 2\; \cdot \; q\; 3\; =\; 2\; q\; 5\; \{\backslash \; displaystyle\; 2\; \backslash \; cdot\; q\; ^\; \{2\}\; \backslash \; cdot\; q\; ^\; \{3\}\; =\; 2q\; ^\; \{5\}\}$. Следовательно, асимптотическая сложность указанной функции равна $O\; (n\; 5)\; \{\backslash \; displaystyle\; O\; (n\; ^\; \{5\})\}$.

Если мы применим закон распределения к правой части уравнения, мы получим следующее:

$\alpha \; (a,\; b)\; знак\; равно\; def\; \sum \; c\; \in \; A\; f\; (a,\; c,\; b)\; \cdot \; \sum \; d,\; e\; \in \; A\; g\; (a,\; d,\; e)\; \{\backslash \; displaystyle\; \backslash \; alpha\; (a,\; \backslash ,\; b)\; \{\backslash \; stackrel\; \{\backslash \; mathrm\; \{def\}\}\; \{=\}\}\; \backslash \; displaystyle\; \backslash \; sum\; \backslash \; limits\; \_\; \{c\; \backslash \; in\; A\}\; f\; (a,\; \backslash ,\; c,\; \backslash ,\; b)\; \backslash \; cdot\; \backslash \; sum\; \_\; \{d,\; \backslash ,\; e\; \backslash \; in\; A\}\; g\; (a,\; \backslash ,\; d,\; \backslash ,\; e)\}$

Это означает, что $\alpha \; (a,\; b)\; \{\backslash \; displaystyle\; \backslash \; alpha\; (a,\; \backslash ,\; b)\}$можно описать как продукт $\alpha \; 1\; (a,\; b)\; \cdot \; \alpha \; 2\; (a)\; \{\backslash \; displaystyle\; \backslash \; alpha\; \_\; \{1\}\; (a,\; \backslash ,\; b)\; \backslash \; cdot\; \backslash \; alpha\; \_\; \{2\}\; (a)\; \}$где $\alpha \; 1\; (a,\; b)\; =\; def\; \sum \; c\; \in \; A\; f\; (a,\; c,\; b)\; \{\backslash \; displaystyle\; \backslash \; alpha\; \_\; \{1\}\; (a,\; b)\; \{\backslash \; stackrel\; \{\; \backslash \; mathrm\; \{def\}\}\; \{=\}\}\; \backslash \; displaystyle\; \backslash \; sum\; \backslash \; limits\; \_\; \{c\; \backslash \; in\; A\}\; f\; (a,\; \backslash ,\; c,\; \backslash ,\; b)\}$и $\alpha \; 2\; (a)\; знак\; равно\; def\; \sum \; d,\; е\; \in \; A\; g\; (a,\; d,\; e)\; \{\backslash \; displaystyle\; \backslash \; alpha\; \_\; \{2\}\; (a)\; \{\backslash \; stackrel\; \{\backslash \; mathrm\; \{def\}\}\; \{=\}\}\; \backslash \; displaystyle\; \backslash \; sum\; \backslash \; limits\; \_\; \{d,\; \backslash ,\; e\; \backslash \; in\; A\}\; g\; (a,\; \backslash ,\; d,\; \backslash ,\; e)\}$

Теперь, когда мы вычисляем t Вычислительная сложность, мы видим, что есть $q\; 3\; \{\backslash \; displaystyle\; q\; ^\; \{3\}\}$сложения в $\alpha \; 1\; (a,\; b)\; \{\backslash \; displaystyle\; \backslash \; alpha\; \_\; \{1\; \}\; (a,\; \backslash ,\; b)\}$и $\alpha \; 2\; (a)\; \{\backslash \; displaystyle\; \backslash \; alpha\; \_\; \{2\}\; (a)\}$каждый, и есть $q\; 2\; \{\backslash \; displaystyle\; q\; ^\; \{2\}\}$умножения, когда мы используем произведение $\alpha \; 1\; (a,\; b)\; \cdot \; \alpha \; 2\; (a)\; \{\backslash \; displaystyle\; \backslash \; alpha\; \_\; \{1\}\; (\; a,\; \backslash ,\; b)\; \backslash \; cdot\; \backslash \; alpha\; \_\; \{2\}\; (a)\}$для вычисления $\alpha \; (a,\; b)\; \{\backslash \; displaystyle\; \backslash \; alpha\; (a,\; \backslash ,\; b)\}$. Следовательно, общее количество необходимых вычислений равно $q\; 3\; +\; q\; 3\; +\; q\; 2\; =\; 2\; q\; 3\; +\; q\; 2\; \{\backslash \; displaystyle\; q\; ^\; \{3\}\; +\; q\; ^\; \{3\}\; +\; q\; ^\; \{2\}\; =\; 2q\; ^\; \{3\}\; +\; q\; ^\; \{2\}\}$. Следовательно, асимптотическая сложность вычисления $\alpha \; (a,\; b)\; \{\backslash \; displaystyle\; \backslash \; alpha\; (a,\; b)\}$уменьшается до $O\; (n\; 3)\; \{\backslash \; displaystyle\; O\; (n\; ^\; \{\; 3\})\}$из $O\; (n\; 5)\; \{\backslash \; displaystyle\; O\; (n\; ^\; \{5\})\}$. Это показывает на примере, что применение закона распределения снижает вычислительную сложность, что является одной из хороших черт «быстрого алгоритма».

Некоторые из проблем, для решения которых использовался закон распределения, можно сгруппировать следующим образом:

1. Алгоритмы декодирования. GDL-подобный алгоритм использовался Галлагером для декодирования кодов с низкой плотностью проверки четности. Основываясь на работе Галлагера, Таннер представил граф Таннера и выразил работу Галлагера в форме передачи сообщений. График Таннерса также помог объяснить алгоритм Витерби.

. Форни заметил, что максимальное правдоподобие Витерби при декодировании сверточных кодов также использовало алгоритмы GDL-подобной общности.

2. Алгоритм вперед-назад. Алгоритм вперед-назад помогал в качестве алгоритма отслеживания состояний в цепи Маркова. И для этого также использовался алгоритм GDL типа generality

3. Искусственный интеллект. Понятие деревьев соединений использовалось для решения многих проблем в AI. Также концепция устранения корзины использует многие концепции.

MPF или маргинализация функции произведения - это общая вычислительная проблема, которая, как частный случай, включает множество классических задач, таких как вычисление дискретного преобразования Адамара, декодирование с максимальной вероятностью линейного кода по каналу без памяти и умножение цепочки матриц. Сила GDL заключается в том, что он применяется к ситуациям, в которых сложение и умножение являются обобщенными. Коммутативное полукольцо является хорошей основой для объяснения этого поведения. Он определяется в наборе $K\; \{\backslash \; displaystyle\; K\}$с операторами «$+\; \{\backslash \; displaystyle\; +\}$» и «$.\; \{\backslash \; Displaystyle.\; \}$"где $(K,\; +)\; \{\backslash \; displaystyle\; (K,\; \backslash ,\; +)\}$и $(K,.)\; \{\backslash \; Displaystyle\; (K,\; \backslash ,.)\}$являются коммутативными моноидами и выполняется закон распределения.

Пусть $p\; 1,\dots ,\; pn\; \{\backslash \; displaystyle\; p\_\; \{1\},\; \backslash \; ldots,\; p\_\; \{n\}\}$- такие переменные, что $p\; 1\; \in \; A\; 1,\dots ,\; Pn\; \in \; A\; n\; \{\backslash \; displaystyle\; p\_\; \{1\}\; \backslash \; in\; A\_\; \{1\},\; \backslash \; ldots,\; p\_\; \{n\}\; \backslash \; in\; A\_\; \{n\}\}$где $A\; \{\backslash \; displaystyle\; A\; \}$- конечное множество и $|\; A\; i\; |\; знак\; равно\; q\; я\; \{\backslash \; displaystyle\; |\; A\_\; \{i\}\; |\; =\; q\_\; \{i\}\}$. Здесь $i\; =\; 1,\dots ,\; n\; \{\backslash \; displaystyle\; i\; =\; 1,\; \backslash \; ldots,\; n\}$. Если $S\; =\; \{i\; 1,\dots ,\; ir\}\; \{\backslash \; displaystyle\; S\; =\; \backslash \; \{i\_\; \{1\},\; \backslash \; ldots,\; i\_\; \{r\}\; \backslash \}\}$и $S\; \subset \; \{1,\dots ,\; N\}\; \{\backslash \; displaystyle\; S\; \backslash ,\; \backslash \; subset\; \backslash \; \{1,\; \backslash \; ldots,\; n\; \backslash \}\}$, пусть $AS\; =\; A\; i\; 1\; \times \; \cdots \; \times \; A\; ir\; \{\backslash \; displaystyle\; A\_\; \{\; S\}\; =\; A\_\; \{i\_\; \{1\}\}\; \backslash \; times\; \backslash \; cdots\; \backslash \; times\; A\_\; \{i\_\; \{r\}\}\}$, $p\; S\; =\; (pi\; 1,\dots ,\; pir)\; \{\backslash \; displaystyle\; p\_\; \{S\}\; =\; (p\_\; \{i\_\; \{1\}\},\; \backslash \; ldots,\; p\_\; \{i\_\; \{r\}\})\}$, $q\; S\; =\; |\; A\; S\; |\; \{\backslash \; displaystyle\; q\_\; \{S\}\; =\; |\; A\_\; \{S\}\; |\}$, $A\; =\; A\; 1\; \times \; \cdots \; \times \; A\; n\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{A\}\; =\; A\_\; \{1\}\; \backslash \; times\; \backslash \; cdots\; \backslash \; times\; A\_\; \{n\}\; \}$и $p\; =\; \{p\; 1,\dots ,\; pn\}\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{p\}\; =\; \backslash \; \{p\_\; \{1\},\; \backslash \; ldots,\; p\_\; \{n\}\; \backslash \}\}$

Пусть $S\; =\; \{S\; j\}\; j\; =\; 1\; M\; \{\backslash \; displaystyle\; S\; =\; \backslash \; \{S\_\; \{j\}\; \backslash \}\; \_\; \{j\; =\; 1\}\; ^\; \{M\}\}$где $S\; j\; \subset \; \{1,...,\; n\}\; \{\backslash \; displaystyle\; S\_\; \{j\}\; \backslash \; subset\; \backslash \; \{1,...\; \backslash ,,\; n\; \backslash \}\}$. Предположим, что функция определена как $\alpha \; i:\; AS\; i\; \to \; R\; \{\backslash \; displaystyle\; \backslash \; alpha\; \_\; \{i\}:\; A\_\; \{S\_\; \{i\}\}\; \backslash \; rightarrow\; R\}$, где $R\; \{\; \backslash \; displaystyle\; R\}$- это коммутативное полукольцо. Кроме того, $p\; S\; i\; \{\backslash \; displaystyle\; p\_\; \{S\_\; \{i\}\}\}$называются локальными доменами, а $\alpha \; i\; \{\backslash \; displaystyle\; \backslash \; alpha\; \_\; \{i\}\}$как локальные ядра.

Теперь глобальное ядро ​​$\beta :\; A\; \to \; R\; \{\backslash \; displaystyle\; \backslash \; beta:\; \backslash \; mathbf\; \{A\}\; \backslash \; rightarrow\; R\}$определяется как: $\beta \; (p\; 1,...,\; pn)\; знак\; равно\; \prod \; я\; знак\; равно\; 1\; M\; \alpha \; (п\; S\; я)\; \{\backslash \; Displaystyle\; \backslash \; бета\; (p\_\; \{1\},...\; \backslash ,,\; p\_\; \{n\})\; =\; \backslash \; prod\; \_\; \{i\; =\; 1\}\; ^\; \{M\}\; \backslash \; alpha\; (p\_\; \{S\_\; \{i\}\})\}$

Определение проблемы MPF: для одного или нескольких индексов $i\; =\; 1,...,\; M\; \{\backslash \; displaystyle\; i\; =\; 1,...\; \backslash ,,\; M\}$, вычислить таблицу значений $S\; i\; \{\backslash \; displaystyle\; S\_\; \{i\}\}$-маргинализация глобального ядра $\beta \; \{\backslash \; displaystyle\; \backslash \; beta\}$, которая является функцией $\beta \; i:\; AS\; i\; \to \; R\; \{\backslash \; displaystyle\; \backslash \; beta\; \_\; \{i\}:\; A\_\; \{S\_\; \{i\}\}\; \backslash \; rightarrow\; R\}$определяется как $\beta \; i\; (p\; S\; i)\; =\; \sum \; p\; S\; ic\; \in \; AS\; ic\; \beta \; (p)\; \{\backslash \; displaystyle\; \backslash \; beta\; \_\; \{i\}\; (p\_\; \{\; S\_\; \{i\}\})\; \backslash ,\; =\; \backslash \; displaystyle\; \backslash \; sum\; \backslash \; limits\; \_\; \{p\_\; \{S\_\; \{i\}\; ^\; \{c\}\}\; \backslash \; in\; A\_\; \{S\_\; \{i\}\; ^\; \{c\}\}\}\; \backslash \; beta\; (p)\}$

Здесь $S\; ic\; \{\backslash \; displaystyle\; S\_\; \{i\}\; ^\; \{c\}\}$является дополнением $S\; i\; \{\backslash \; displaystyle\; S\_\; \{i\}\}$с учетом на $\{1,...,\; n\}\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{\backslash \; \{\}\; 1,...\; \backslash ,,\; n\; \backslash \}\}$и $\beta \; i\; (p\; S\; i)\; \{\backslash \; displaystyle\; \backslash \; beta\; \_\; \{i\; \}\; (p\_\; \{S\_\; \{i\}\})\}$называется $i-й\; \{\backslash \; displaystyle\; i\; ^\; \{th\}\}$целевой функцией или целевой функцией в $S\; я\; \{\backslash \; Displaystyle\; S\_\; \{я\}\}$. Можно заметить, что для вычисления целевой функции $ith\; \{\backslash \; displaystyle\; i\; ^\; \{th\}\}$очевидным образом требуется $M\; q\; 1\; q\; 2\; q\; 3\; \cdots \; qn\; \{\backslash \; displaystyle\; Mq\_\; \{1\}\; q\_\; \{2\}\; q\_\; \{3\}\; \backslash \; cdots\; q\_\; \{n\}\}$операций. Это потому, что есть $q\; 1\; q\; 2\; \cdots \; qn\; \{\backslash \; displaystyle\; q\_\; \{1\}\; q\_\; \{2\}\; \backslash \; cdots\; q\_\; \{n\}\}$сложения и $(M\; -\; 1)\; q\; 1\; q\; 2...\; qn\; \{\backslash \; displaystyle\; (M-1)\; q\_\; \{1\}\; q\_\; \{2\}...\; q\_\; \{n\}\}$умножения, необходимые для вычисления $i\; th\; \{\backslash \; displaystyle\; i\; ^\; \{\backslash \; text\; \{th\}\}\}$целевая функция. Алгоритм GDL, который объясняется в следующем разделе, может уменьшить эту вычислительную сложность.

Ниже приведен пример проблемы MPF. Пусть $p\; 1,\; p\; 2,\; p\; 3,\; p\; 4,\; \{\backslash \; displaystyle\; p\_\; \{1\},\; \backslash ,\; p\_\; \{2\},\; \backslash ,\; p\_\; \{3\},\; \backslash ,\; p\_\; \{4\},\}$и $p\; 5\; \{\backslash \; displaystyle\; p\_\; \{5\}\}$быть такими переменными, что $p\; 1\; \in \; A\; 1,\; p\; 2\; \in \; A\; 2,\; p\; 3\; \in \; A\; 3,\; p\; 4\; \in \; A\; 4,\; \{\backslash \; displaystyle\; p\_\; \{1\}\; \backslash \; in\; A\_\; \{1\},\; p\_\; \{2\}\; \backslash \; in\; A\_\; \{2\},\; p\_\; \{3\}\; \backslash \; in\; A\_\; \{3\},\; p\_\; \{4\}\; \backslash \; in\; A\_\; \{4\},\; \}$и $p\; 5\; \in \; A\; 5\; \{\backslash \; displaystyle\; p\_\; \{5\}\; \backslash \; in\; A\_\; \{5\}\}$. Здесь $M\; =\; 4\; \{\backslash \; displaystyle\; M\; =\; 4\}$и $S\; =\; \{\{1,\; 2,\; 5\},\; \{2,\; 4\},\; \{1,\; 4\},\; \{2\}\; \}\; \{\backslash \; displaystyle\; S\; =\; \backslash \; \{\backslash \; \{1,2,5\; \backslash \},\; \backslash \; \{2,4\; \backslash \},\; \backslash \; \{1,4\; \backslash \},\; \backslash \; \{2\; \backslash \}\; \backslash \}\}$. Данные функции, использующие эти переменные: $f\; (p\; 1,\; p\; 2,\; p\; 5)\; \{\backslash \; displaystyle\; f\; (p\_\; \{1\},\; p\_\; \{2\},\; p\_\; \{5\})\}$и $g\; (p\; 3,\; p\; 4)\; \{\backslash \; displaystyle\; g\; (p\_\; \{3\},\; p\_\; \{4\})\}$и нам нужно вычислить $\alpha \; (p\; 1,\; p\; 4)\; \{\backslash \; displaystyle\; \backslash \; alpha\; (p\_\; \{1\},\; \backslash ,\; p\_\; \{4\})\}$и $\beta \; (p\; 2)\; \{\backslash \; displaystyle\; \backslash \; beta\; (p\_\; \{2\})\}$определяется как:

$\alpha \; (p\; 1,\; p\; 4)\; =\; \sum \; p\; 2\; \in \; A\; 2,\; p\; 3\; \in \; A\; 3,\; p\; 5\; \in \; A\; 5\; f\; (p\; 1,\; p\; 2,\; p\; 5)\; \cdot \; g\; (p\; 2,\; п\; 4)\; \{\backslash \; displaystyle\; \backslash \; alpha\; (p\_\; \{1\},\; \backslash ,\; p\_\; \{4\})\; =\; \backslash \; displaystyle\; \backslash \; sum\; \backslash \; limits\; \_\; \{p\_\; \{2\}\; \backslash \; in\; A\_\; \{2\},\; \backslash ,\; p\_\; \{3\}\; \backslash \; in\; A\_\; \{3\},\; \backslash ,\; p\_\; \{5\}\; \backslash \; in\; A\_\; \{5\}\}\; f\; (p\_\; \{1\},\; \backslash ,\; p\_\; \{2\},\; \backslash ,\; p\_\; \{5\})\; \backslash \; cdot\; g\; (p\_\; \{2\},\; \backslash ,\; p\_\; \{4\})\}$

$\beta \; (p\; 2)\; =\; \sum \; p\; 1\; \in \; A\; 1,\; p\; 3\; \in \; A\; 3,\; p\; 4\; \in \; A\; 4,\; p\; 5\; \in \; A\; 5\; f\; (p\; 1,\; p\; 2,\; p\; 5)\; \cdot \; г\; (п\; 2,\; п\; 4)\; \{\backslash \; displaystyle\; \backslash \; beta\; (p\_\; \{2\})\; =\; \backslash \; sum\; \backslash \; limits\; \_\; \{p\_\; \{1\}\; \backslash \; in\; A\_\; \{1\},\; \backslash ,\; p\_\; \{3\}\; \backslash \; in\; A\_\; \{3\},\; \backslash ,\; p\_\; \{4\}\; \backslash \; in\; A\_\; \{4\},\; \backslash ,\; p\_\; \{5\}\; \backslash \; in\; A\_\; \{5\}\}\; f\; (p\_\; \{1\},\; \backslash ,\; p\_\; \{2\},\; \backslash ,\; p\_\; \{5\})\; \backslash \; cdot\; g\; (p\_\; \{2\},\; \backslash ,\; p\_\; \{4\})\}$

Здесь локальные домены и локальные ядра определены следующим образом:

локальные домены	локальные ядра
$\{p\; 1,\; p\; 2,\; п\; 5\}\; \{\backslash \; displaystyle\; \backslash \; \{p\_\; \{1\},\; p\_\; \{2\},\; p\_\; \{5\}\; \backslash \}\}$	$(f\; (p\; 1,\; p\; 2,\; p\; 5)\; \{\backslash \; displaystyle\; (f\; (p\_\; \{\; 1\},\; p\_\; \{2\},\; p\_\; \{5\})\}$
$\{p\; 2,\; p\; 4\}\; \{\backslash \; displaystyle\; \backslash \; \{p\_\; \{2\},\; p\_\; \{4\}\; \backslash \}\}$	$g\; (p\; 2,\; p\; 4)\; \{\backslash \; displaystyle\; g\; (p\_\; \{2\},\; p\_\; \{4\})\}$
$\{p\; 1,\; p\; 4\}\; \{\backslash \; displaystyle\; \backslash \; \{p\_\; \{1\},\; p\_\; \{4\}\; \backslash \}\}$	$1\; \{\; \backslash \; displaystyle\; 1\}$
$\{p\; 2\}\; \{\backslash \; displaystyle\; \backslash \; \{p\_\; \{2\}\; \backslash \}\}$	$1\; \{\backslash \; displaystyle\; 1\}$

где $\alpha \; (p\; 1,\; p\; 4)\; \{\backslash \; displaystyle\; \backslash \; alpha\; (p\_\; \{1\},\; p\_\; \{4\})\}$- это $3-е\; \{\backslash \; displaystyle\; 3\; ^\; \{rd\}\}$целевая функция и $\beta \; (\; p\; 2)\; \{\backslash \; displaystyle\; \backslash \; beta\; (p\_\; \{2\})\}$- целевая функция $4\; th\; \{\backslash \; displaystyle\; 4\; ^\; \{th\}\}$.

Рассмотрим другой пример, где $p\; 1,\; p\; 2,\; p\; 3,\; p\; 4,\; r\; 1,\; r\; 2,\; r\; 3,\; r\; 4\; \in \; \{0,\; 1\}\; \{\backslash \; displaystyle\; p\_\; \{1\},\; p\_\; \{2\},\; p\_\; \{3\},\; p\_\; \{4\},\; r\_\; \{1\},\; r\_\; \{2\},\; r\_\; \{3\},\; r\_\; \{4\}\; \backslash \; in\; \backslash \; \{0,1\; \backslash \}\}$и $f\; (r\; 1,\; r\; 2,\; r\; 3,\; r\; 4)\; \{\backslash \; displaystyle\; f\; (r\_\; \{1\},\; r\_\; \{2\},\; r\_\; \{3\},\; r\_\; \{4\})\}$является вещественной функцией. Теперь мы рассмотрим задачу MPF, в которой коммутативное полукольцо определяется как набор действительных чисел с обычным сложением и умножением, а локальные области и локальные ядра определяются следующим образом:

локальные области	локальные ядра
$\{r\; 1,\; r\; 2,\; r\; 3,\; r\; 4\}\; \{\backslash \; displaystyle\; \backslash \; \{r\_\; \{1\},\; r\_\; \{2\},\; r\_\; \{3\},\; r\_\; \{4\}\; \backslash \}\}$	$f\; (r\; 1,\; r\; 2,\; r\; 3,\; r\; 4)\; \{\backslash \; displaystyle\; f\; (r\_\; \{1\},\; r\_\; \{2\},\; r\_\; \{3\},\; r\_\; \{4\})\}$
$\{p\; 1,\; r\; 1\}\; \{\backslash \; displaystyle\; \backslash \; \{p\_\; \{1\},\; r\_\; \{1\}\; \backslash \}\}$	$(-\; 1)\; p\; 1\; r\; 1\; \{\backslash \; displaystyle\; (-1)\; ^\; \{p\_\; \{1\}\; r\_\; \{1\}\}\}$
$\{p\; 2,\; р\; 2\}\; \{\backslash \; displaystyle\; \backslash \; \{p\_\; \{2\},\; r\_\; \{2\}\; \backslash \}\}$	$(-\; 1)\; p\; 2\; r\; 2\; \{\backslash \; displaystyle\; (-1)\; ^\; \{p\_\; \{2\}\; r\_\; \{2\}\}\}$
$\{п\; 3,\; r\; 3\}\; \{\backslash \; displaystyle\; \backslash \; \{p\_\; \{3\},\; r\_\; \{3\}\; \backslash \}\}$	$(-\; 1)\; p\; 3\; r\; 3\; \{\backslash \; displaystyle\; (-1)\; ^\; \{p\_\; \{3\; \}\; r\_\; \{3\}\}\}$
$\{p\; 4,\; r\; 4\}\; \{\backslash \; displaystyle\; \backslash \; \{p\_\; \{4\},\; r\_\; \{4\}\; \backslash \}\}$	$(-\; 1)\; p\; 4\; r\; 4\; \{\backslash \; displaystyle\; (-\; 1)\; ^\; \{p\_\; \{4\}\; r\_\; \{4\}\}\}$
$\{p\; 1,\; p\; 2,\; p\; 3,\; p\; 4\}\; \{\backslash \; displaystyle\; \backslash \; \{p\_\; \{1\},\; p\_\; \{2\},\; p\_\; \{3\},\; p\_\; \{4\}\; \backslash \}\}$	$1\; \{\backslash \; displaystyle\; 1\}$

Теперь, поскольку глобальное ядро ​​определяется как продукт loc al ядер, это

$F\; (p\; 1,\; p\; 2,\; p\; 3,\; p\; 4,\; r\; 1,\; r\; 2,\; r\; 3,\; r\; 4)\; =\; f\; (p\; 1,\; p\; 2,\; p\; 3,\; p\; 4)\; \cdot \; (-\; 1)\; п\; 1\; р\; 1\; +\; п\; 2\; р\; 2\; +\; п\; 3\; р\; 3\; +\; п\; 4\; р\; 4\; \{\backslash \; displaystyle\; F\; (p\_\; \{1\},\; p\_\; \{2\},\; p\_\; \{3\},\; p\_\; \{4\},\; r\_\; \{\; 1\},\; r\_\; \{2\},\; r\_\; \{3\},\; r\_\; \{4\})\; =\; f\; (p\_\; \{1\},\; p\_\; \{2\},\; p\_\; \{3\},\; p\_\; \{4\})\; \backslash \; cdot\; (-1)\; ^\; \{p\_\; \{1\}\; r\_\; \{1\}\; +\; p\_\; \{2\}\; r\_\; \{2\}\; +\; p\_\; \{3\}\; r\_\; \{3\}\; +\; p\_\; \{4\}\; r\_\; \{4\}\}\}$

и целевая функция в локальном домене $p\; 1,\; p\; 2,\; p\; 3,\; p\; 4\; \{\backslash \; displaystyle\; p\_\; \{1\},\; p\_\; \{2\},\; p\_\; \{3\},\; p\_\; \{4\}\}$равно

$F\; (p\; 1,\; p\; 2,\; p\; 3,\; p\; 4)\; =\; \sum \; r\; 1,\; r\; 2,\; r\; 3,\; r\; 4\; f\; (r\; 1,\; r\; 2,\; r\; 3,\; r\; 4)\; \cdot \; (-\; 1)\; p\; 1\; r\; 1\; +\; p\; 2\; r\; 2\; +\; п\; 3\; к\; 3\; +\; п\; 4\; к\; 4.\; \{\backslash \; displaystyle\; F\; (p\_\; \{1\},\; p\_\; \{2\},\; p\_\; \{3\},\; p\_\; \{4\})\; =\; \backslash \; displaystyle\; \backslash \; sum\; \backslash \; limits\; \_\; \{r\_\; \{1\},\; r\_\; \{2\},\; r\_\; \{3\},\; r\_\; \{4\}\}\; f\; (r\_\; \{1\},\; r\_\; \{2\},\; r\_\; \{3\},\; r\_\; \{4\})\; \backslash \; cdot\; (-1)\; ^\; \{p\_\; \{1\}\; r\_\; \{1\}\; +\; p\_\; \{2\}\; r\_\; \{2\; \}\; +\; p\_\; \{3\}\; r\_\; \{3\}\; +\; p\_\; \{4\}\; r\_\; \{4\}\}.\}$

Это преобразование Адамара функции $f\; (\cdot )\; \{\backslash \; displaystyle\; f\; (\backslash \; cdot)\}$. Следовательно, мы можем видеть, что вычисление преобразования Адамара является частным случаем проблемы MPF. Можно продемонстрировать и другие примеры, чтобы доказать, что проблема MPF образует частные случаи многих классических проблем, как объяснено выше, детали которых можно найти в

Если один можно найти взаимосвязь между элементами данного набора $S\; \{\backslash \; displaystyle\; S\}$, тогда можно решить проблему MPF, основываясь на понятии распространения убеждений, которое является специальное использование техники «передачи сообщений». Требуемая взаимосвязь состоит в том, что данный набор локальных доменов может быть организован в дерево соединений . Другими словами, мы создаем теоретико-графическое дерево с элементами $S\; \{\backslash \; displaystyle\; S\}$в качестве вершин tree $T\; \{\backslash \; displaystyle\; T\}$, так что для любых двух произвольных вершин говорят $vi\; \{\backslash \; displaystyle\; v\_\; \{i\}\}$и $vj\; \{\backslash \; displaystyle\; v\_\; \{j\}\}$где $я\; \ne \; j\; \{\backslash \; displaystyle\; i\; \backslash \; neq\; j\}$и между этими двумя вершинами существует ребро, то есть пересечение соответствующих меток, а именно $S\; i\; \cap \; S\; j\; \{\; \backslash \; displaystyle\; S\_\; \{i\}\; \backslash \; cap\; S\_\; \{j\}\}$, представляет собой подмножество метки на каждой вершине на уникальном пути из $vi\; \{\backslash \; displaystyle\; v\_\; \{i\}\}$на $vj\; \{\backslash \; displaystyle\; v\_\; \{j\}\}$.

Например,

Пример 1. Рассмотрим следующие девять локальных доменов:

1. $\{p\; 2\}\; \{\backslash \; displaystyle\; \backslash \; \{p\_\; \{2\}\; \backslash \}\}$
2. $\{p\; 3,\; p\; 2\}\; \{\backslash \; displaystyle\; \backslash \; \{p\_\; \{3\},\; p\_\; \{2\}\; \backslash \}\}$
3. $\{p\; 2,\; p\; 1\}\; \{\backslash \; displaystyle\; \backslash \; \{p\_\; \{\; 2\},\; p\_\; \{1\}\; \backslash \}\}$
4. $\{p\; 3,\; p\; 4\}\; \{\backslash \; displaystyle\; \backslash \; \{p\_\; \{3\},\; p\_\; \{4\}\; \backslash \}\}$
5. $\{p\; 3\}\; \{\backslash \; displaystyle\; \backslash \; \{p\_\; \{3\}\; \backslash \}\}$
6. $\{p\; 1,\; p\; 4\}\; \{\backslash \; dis\; playstyle\; \backslash \; \{p\_\; \{1\},\; p\_\; \{4\}\; \backslash \}\}$
7. $\{p\; 1\}\; \{\backslash \; displaystyle\; \backslash \; \{p\_\; \{1\}\; \backslash \}\}$
8. $\{p\; 4\}\; \{\backslash \; displaystyle\; \backslash \; \{p\_\; \{4\}\; \backslash \}\}$
9. $\{p\; 2,\; p\; 4\}\; \{\backslash \; displaystyle\; \backslash \; \{p\_\; \{2\},\; p\_\; \{4\}\; \backslash \}\}$

Для указанного выше набора локальных доменов их можно организовать в дерево соединений как показано ниже:

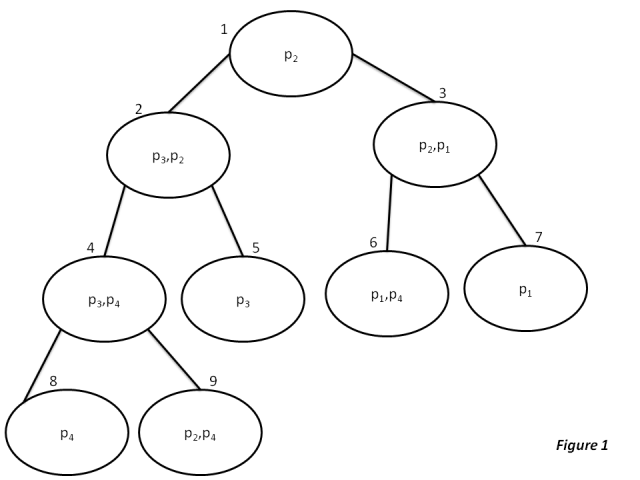
Аналогично. Если задан другой набор, подобный следующему

Пример 2: Рассмотрим следующие четыре локальных домена:

1. $\{p\; 1,\; p\; 2\}\; \{\backslash \; displaystyle\; \backslash \; \{p\_\; \{1\; \},\; p\_\; \{2\}\; \backslash \}\}$
2. $\{p\; 2,\; p\; 3\}\; \{\backslash \; displaystyle\; \backslash \; \{p\_\; \{2\},\; p\_\; \{3\}\; \backslash \}\}$
3. $\{p\; 3,\; p\; 4\}\; \{\backslash \; displaystyle\; \backslash \; \{p\_\; \{3\},\; p\_\; \{4\}\; \backslash \}\}$
4. $\{p\; 1,\; p\; 4\}\; \{\backslash \; displaystyle\; \backslash \; \{p\_\; \{1\},\; p\_\; \{4\}\; \backslash \}\}$

Затем построение дерева только с этими локальные домены невозможны, так как этот набор значений не имеет общих доменов, которые могут быть помещены между любыми двумя значениями указанного выше набора. Но, однако, если добавить два фиктивных домена, как показано ниже, то организация обновленного набора в дерево соединений станет возможной и простой.

5.$\{p\; 1,\; p\; 2\; \{\backslash \; displaystyle\; \backslash \; \{p\_\; \{1\},\; p\_\; \{2\}\}$,$p\; 4\}\; \{\backslash \; displaystyle\; p\_\; \{4\}\; \backslash \}\}$. 6.$\{p\; 2,\; p\; 3\; \{\; \backslash \; displaystyle\; \backslash \; \{p\_\; \{2\},\; p\_\; \{3\}\}$,$p\; 4\}\; \{\backslash \; displaystyle\; p\_\; \{4\}\; \backslash \}\}$

Аналогично для этого набора доменов дерево соединений выглядит так, как показано ниже:

Алгоритм обобщенного закона распределения (GDL)

Входные данные: набор локальных доменов.. Выходные данные: для заданного набора доменов вычисляется возможное минимальное количество операций, необходимых для решения проблемы.. Итак, если $vi\; \{\backslash \; displaystyle\; v\_\; \{i\}\}$и $vj\; \{\backslash \; displaystyle\; v\_\; \{j\}\}$соединены ребром в дерево соединений, то сообщение от $vi\; \{\backslash \; displaystyle\; v\_\; \{i\}\}$до $vj\; \{\backslash \; displaystyle\; v\_\; \{j\}\}$представляет собой набор / таблицу значения, задаваемые функцией: $\mu \; i,\; j\; \{\backslash \; displaystyle\; \backslash \; mu\; \_\; \{i,\; j\}\}$:$AS\; i\; \cap \; S\; j\; \to \; R\; \{\backslash \; displaystyle\; A\_\; \{S\_\; \{i\}\; \backslash \; cap\; S\_\; \{j\}\; \}\; \backslash \; rightarrow\; R\}$. Чтобы начать со всех функций, т.е. для всех комбинаций $i\; \{\backslash \; displaystyle\; i\}$и $j\; \{\backslash \; displaystyle\; j\}$в данном дереве, $\mu \; i,\; j\; \{\backslash \; displaystyle\; \backslash \; mu\; \_\; \{i,\; j\}\}$идентично $1\; \{\backslash \; displaystyle\; 1\}$, и когда конкретное сообщение обновляется, это следует уравнению, приведенному ниже.

$\mu \; я,\; J\; (п\; S\; я\; \cap \; S\; J)\; \{\backslash \; Displaystyle\; \backslash \; mu\; \_\; \{я,\; j\}\; (p\_\; \{S\_\; \{i\}\; \backslash \; cap\; S\_\; \{j\}\})\}$= $\sum \; п\; S\; я\; \setminus \; S\; J\; \in \; AS\; я\; \setminus \; S\; J\; \alpha \; я\; (п\; S\; я)\; \prod \; vk\; adj\; \; vi,\; К\; k\; J\; \mu \; К,\; J\; (п\; S\; К\; k\; S\; я)\; (1)\; \{\backslash \; Displaystyle\; \backslash \; сумма\; \_\; \{р\_\; \{S\_\; \{i\}\; \backslash \; setminus\; S\_\; \{j\}\}\; \backslash \; in\; A\_\; \{S\_\; \{i\}\; \backslash \; setminus\; S\_\; \{j\}\}\}\; \backslash \; alpha\; \_\; \{i\}\; (p\_\; \{S\_\; \{i\}\})\; \backslash \; prod\; \_\; \{\{v\_\; \{k\}\; \backslash \; имя\; оператора\; \{прил\}\; v\_\; \{i\}\},\; \{k\; \backslash \; neq\; j\}\}\; \backslash \; mu\; \_\; \{k,\; j\}\; (p\_\; \{S\_\; \{k\}\; \backslash \; cap\; S\_\; \{i\}\})\; (1)\}$

где $vk\; прил.\; \; vi\; \{\backslash \; displaystyle\; v\_\; \{k\}\; \backslash \; operatorname\; \{adj\}\; v\_\; \{i\}\}$означает, что $vk\; \{\backslash \; displaystyle\; v\_\; \{k\}\}$является дополнительной вершина с $vi\; \{\backslash \; displaystyle\; v\_\; \{i\}\}$в дереве.

Аналогичным образом каждая вершина имеет состояние, которое как таблица, содержащая значения из функций $\sigma \; i:\; AS\; i\; \to \; R\; \{\backslash \; displaystyle\; \backslash \; sigma\; \_\; \{i\}:\; A\_\; \{S\_\; \{i\}\}\; \backslash \; rightarrow\; R\}$, точно так же, как сообщения инициализируются в 1 идентично, состояние $vi\; \{\backslash \; displaystyle\; v\_\; \{i\}\}$определяется как локальное ядро ​​$\alpha \; (п\; S\; я)\; \{\backslash \; displaystyle\; \backslash \; alpha\; (p\_\; \{S\_\; \{i\}\})\}$, но всякий раз, когда $\sigma \; я\; \{\backslash \; displaystyle\; \backslash \; sigma\; \_\; \{i\}\}$обновляется, это следует к уравнению:

$\sigma \; (p\; S\; i)\; =\; \alpha \; i\; (p\; S\; i)\; \prod \; vk\; adj\; \; vi\; \mu \; k,\; j\; (p\; S\; k\; \cap \; S\; i)\; (2).\; \{\backslash \; displaystyle\; \backslash \; sigma\; (p\_\; \{S\_\; \{i\}\})\; =\; \backslash \; alpha\; \_\; \{i\}\; (p\_\; \{S\_\; \{i\}\})\; \backslash \; prod\; \_\; \{v\_\; \{k\}\; \backslash \; operatorname\; \{adj\}\; v\_\; \{i\}\}\; \backslash \; mu\; \_\; \{k,\; j\}\; (p\_\; \{S\_\; \{k\}\; \backslash \; cap\; S\_\; \{i\}\})\; (2).\}$

Основная работа алгоритма

Для заданного набора локальных доменов в входных данных, мы разработняем, либо мы можем создать дерево соединений, либо напрямую используя набор, либо добавив сначала фиктивные домены к набору, а затем создавая дерево соединений, если построение соединения невозможно, чтобы выполнить алгоритм, что нет малое количество шагов для вычислений данной задачи уравнения, но как только у нас есть дерево соединений, алгоритмы должны быть запланированы сообщения и вычислить состояния, которые могут быть выполнены, когда шаги могут быть сокращены, поэтому мы можем сообщить это ниже.

Здесь мы собираемся поговорить о двух особых случаях, а именно задаче с одной вершиной, в которой целевая функция вычисляется только на одной вершине $v\; 0\; \{\; \backslash \; displaystyle\; v\_\; \{0\}\}$, вторая - задача для всех вершин, цель которой - вычислить целевую функцию во всех вершинах.

Начнем с задачи с одной вершиной, GDL начало с направления каждого ребра к целевой вершине $v\; 0\; \{\backslash \; displaystyle\; v\_\; \{0\}\}$. Здесь сообщения отправляются только в направлении вершины. Обратите внимание, что все сообщения отправляются только один раз. Сообщения начинаются с конечных узлов (где степень равна 1) и идут вверх к вершине $v\; 0\; \{\backslash \; displaystyle\; v\_\; \{0\}\}$. Сообщение передается от листьев к своим родителям, а затем оттуда к их родителям и так далее, пока не достигнет вершины $v\; 0\; \{\backslash \; displaystyle\; v\_\; \{0\}\}$. Целевая вершина $v\; 0\; \{\backslash \; displaystyle\; v\_\; \{0\}\}$будет вычислять свое состояние только тогда, когда она получит все сообщения от всех своих соседей. Когда у нас есть состояние, мы получили ответ, и, следовательно, алгоритм завершается.

Например, давайте рассмотрим дерево соединений, приведенное выше, то есть набор из примера 1,. Теперь таблица планирования для этих доменов (где целевая вершина $п\; 2\; \{\backslash \; displaystyle\; р\_\; \{2\}\}$).

$Круглое\; сообщение\; или\; вычисление\; состояния\; \{\backslash \; displaystyle\; \{\backslash \; text\; \{Круглое\; сообщение\; или\; вычисление\; состояния\}\}\}$. $1.\; \mu \; 8,\; 4\; (п\; 4)\; знак\; равно\; \alpha \; 8\; (п\; 4)\; \{\backslash \; displaystyle\; 1.\; \backslash \; mu\; \_\; \{8,4\}\; (p\_\; \{4\})\; =\; \backslash \; alpha\; \_\; \{8\}\; (p\_\; \{4\})\}$. $2.\; \mu \; 8,\; 4\; (p\; 4)\; знак\; равно\; \Sigma \; p\; 2\; \alpha \; 9\; (p\; 2,\; p\; 4)\; \{\backslash \; displaystyle\; 2.\; \backslash \; mu\; \_\; \{8,4\}\; (p\_\; \{4\})\; =\; \backslash \; Sigma\; \_\; \{p\_\; \{2\}\; \}\; \backslash \; alpha\; \_\; \{9\}\; (p\_\; \{2\},\; p\_\; \{4\})\}$. $3.\; \mu \; 5,\; 2\; (p\; 3)\; знак\; равно\; \alpha \; 5\; (p\; 3)\; \{\backslash \; displaystyle\; 3.\; \backslash \; mu\; \_\; \{5,2\}\; (p\_\; \{3\})\; =\; \backslash \; alpha\; \_\; \{5\}\; (p\_\; \{3\})\}$. $4.\; \mu \; 6,\; 3\; (p\; 1)\; знак\; равно\; \Sigma \; p\; 4\; \alpha \; 6\; (p\; 1,\; p\; 4)\; \{\backslash \; displaystyle\; 4.\; \backslash \; mu\; \_\; \{6,3\}\; (p\_\; \{1\})\; =\; \backslash \; Sigma\; \_\; \{p\_\; \{4\}\; \}\; \backslash \; alpha\; \_\; \{6\}\; (p\_\; \{1\},\; p\_\; \{4\})\}$. $5.\; \mu \; 7,\; 3\; (п\; 1)\; знак\; равно\; \alpha \; 7\; (п\; 1)\; \{\backslash \; Displaystyle\; 5.\; \backslash \; mu\; \_\; \{7,3\}\; (p\_\; \{1\})\; =\; \backslash \; alpha\; \_\; \{7\}\; (p\_\; \{1\})\}$. $6.\; \mu \; 4,\; 2\; (p\; 3)\; =\; \Sigma \; p\; 4\; \alpha \; 4\; (p\; 3,\; p\; 4).\; \mu \; 8,\; 4\; (стр\; 4).\; \mu \; 9,\; 4\; (p\; 4)\; \{\backslash \; displaystyle\; 6.\; \backslash \; mu\; \_\; \{4,2\}\; (p\_\; \{3\})\; =\; \backslash \; Sigma\; \_\; \{p\_\; \{4\}\}\; \backslash \; alpha\; \_\; \{4\}\; (p\_\; \{3\},\; p\_\; \{4\}).\; \backslash \; Mu\; \_\; \{8,4\}\; (p\_\; \{4\}).\; \backslash \; Mu\; \_\; \{9,4\}\; (p\_\; \{4\})\}$. $7.\; \mu \; 3,\; 1\; (p\; 2)\; =\; \Sigma \; p\; 1\; \alpha \; 3\; (p\; 2,\; p\; 1).\; \mu \; 6,\; 3\; (p\; 1).\; \mu \; 7,\; 3\; (p\; 1)\; \{\backslash \; displaystyle\; 7.\; \backslash \; mu\; \_\; \{3,1\}\; (p\_\; \{2\})\; =\; \backslash \; Sigma\; \_\; \{p\_\; \{1\}\}\; \backslash \; alpha\; \_\; \{3\}\; (p\_\; \{2\},\; p\_\; \{1\}).\; \backslash \; Mu\; \_\; \{6,3\}\; (p\_\; \{1\}).\; \backslash \; Mu\; \_\; \{7,3\}\; (p\_\; \{1\})\}$. $8.\; \mu \; 2,\; 1\; (p\; 2)\; =\; \Sigma \; p\; 3\; \alpha \; 2\; (p\; 3,\; p\; 2).\; \mu \; 4,\; 2\; (п\; 3).\; \mu \; 5,\; 2\; (p\; 3)\; \{\backslash \; displaystyle\; 8.\; \backslash \; mu\; \_\; \{2,1\}\; (p\_\; \{2\})\; =\; \backslash \; Sigma\; \_\; \{p\_\; \{3\}\}\; \backslash \; alpha\; \_\; \{2\}\; (p\_\; \{3\},\; p\_\; \{2\}).\; \backslash \; Mu\; \_\; \{4,2\}\; (p\_\; \{3\}).\; \backslash \; Mu\; \_\; \{5,2\}\; (p\_\; \{3\})\}$. $9.\; \sigma \; 1\; (p\; 2)\; =\; \alpha \; 1\; (p\; 2).\; \mu \; 2,\; 1\; (p\; 2).\; \mu \; 3,\; 1\; (п\; 2)\; \{\backslash \; displaystyle\; 9.\; \backslash \; sigma\; \_\; \{1\}\; (p\_\; \{2\})\; =\; \backslash \; alpha\; \_\; \{1\}\; (p\_\; \{2\}).\; \backslash \; mu\; \_\; \{2,1\}\; (p\_\; \{2\}).\; \backslash \; Mu\; \_\; \{3,1\}\; (p\_\; \{2\})\}$

Таким образом, сложность GDL с одной вершиной может быть представлена ​​как

$\Sigma \; vd\; (v)\; |\; A\; S\; (v)\; |\; \{\backslash \; displaystyle\; \backslash \; Sigma\; \_\; \{v\}\; d\; (v)\; |\; A\_\; \{S\; \_\; \{(v)\}\}\; |\}$арифметические операции. Где (Примечание: объяснение приведенного выше уравнения объясняется позже в статье). $S\; (v)\; \{\backslash \; displaystyle\; S\; (v)\}$- это метка $v\; \{\backslash \; displaystyle\; v\}$.. $d\; (v)\; \{\backslash \; displaystyle\; d\; (v)\}$- это степень для $v\; \{\backslash \; displaystyle\; v\}$(т. Е. Количество вершин, связанных с v).

Чтобы решить проблему All-Vertices, мы можем запланировать GDL методы, некоторые из них включают параллельную управление, где в каждом раунде обновляется каждое состояние, и каждое сообщение вычисляется и передается. в то же время. В этом типе реализации состояния и сообщения будут стабилизироваться после количества раундов, которое не больше диаметра дерева. В этот момент все состояния вершин будут равны желаемой целевой функции.

Другой способ запланировать GDL для проблемы - последовательная реализация, аналогичная этой задаче с одной вершиной, за исключением того, что мы не останавливаем алгоритм до тех пор, пока все вершины необходимого набора не получат все сообщения от всех их соседи и вычислили их состояние.. Таким образом, количество арифметических операций, необходимых для этой реализации, не больше $\Sigma \; v\; \in \; V\; d\; (v)\; |\; A\; S\; (v)\; |\; \{\backslash \; Displaystyle\; \backslash \; Sigma\; \_\; \{v\; \backslash \; in\; V\}\; d\; (v)\; |\; A\_\; \{S\; \_\; \{(v)\}\}\; |\}$арифметические операции.

Ключ к построению соединений в локальном графе домена $GLD\; \{\backslash \; displaystyle\; G\_\; \{LD\}\}$, является взвешенным полным графом с $M\; \{\backslash \; displaystyle\; M\}$вершинами $v\; 1,\; v\; 2,\; v\; 3,\dots ,\; v\; M\; \{\backslash \; displaystyle\; v\_\; \{1\},\; v\_\; \{2\},\; v\_\; \{3\},\; \backslash \; ldots,\; v\_\; \{M\}\}$т.е. по одному для каждого локального домена, имеющего вес ребра $ei,\; j:\; vi\; \leftrightarrow \; vj\; \{\backslash \; displaystyle\; e\_\; \{i,\; j\}:\; v\_\; \{i\}\; \backslash \; leftrightarrow\; v\_\; \{j\}\}$имеет значение на. $\omega \; i,\; j\; =\; |\; S\; i\; \cap \; S\; j\; |\; \{\backslash \; displaystyle\; \backslash \; omega\; \_\; \{i,\; j\}\; =\; |\; S\_\; \{i\}\; \backslash \; cap\; S\_\; \{j\}\; |\}$.., если $xk\; \in \; S\; i\; \cap \; S\; j\; \{\backslash \; displaystyle\; x\_\; \{k\}\; \backslash \; in\; S\_\; \{i\}\; \backslash \; cap\; S\_\; \{j\}\}$, тогда мы говорим, что $xk\; \{\backslash \; displaystyle\; x\_\; \{k\}\}$содержится в $ei,\; j\; \{\backslash \; displaystyle\; e\_\; \{i,\; j\}\}$. Обозначается $\omega \; max\; \{\backslash \; displaystyle\; \backslash \; omega\; \_\; \{max\}\}$(вес остовного дерева размера $GLD\; \{\backslash \; displaystyle\; G\_\; \{LD\}\}$), что определяется как

$\omega \; \ast \; =\; \Sigma \; i\; =\; 1\; M\; |\; S\; i\; |\; -\; п\; \{\backslash \; displaystyle\; \backslash \; omega\; ^\; \{*\}\; =\; \backslash \; Sigma\; \_\; \{i\; =\; 1\}\; ^\; \{M\}\; |\; S\_\; \{i\}\; |\; -n\}$

, где n - количество элементов в этом наборе. Для большей ясности и подробностей, пожалуйста, обратитесь к ним.

Пусть $\prime \; T\; \prime \; \{\backslash \; displaystyle\; \text{'}T\text{'}\}$будет деревом соединений с набором вершин $\prime \; V\; \prime \; \{\backslash \; displaystyle\; \text{'}\; V\; \text{'}\}$и набор ребер $\prime \; E\; \prime \; \{\backslash \; displaystyle\text{'}\; E\; \text{'}\}$. В этом алгоритме сообщения отправляются в обоих направлениях на любом ребре, поэтому мы можем сказать / рассматривать набор ребер E как набор упорядоченных пар вершин. Например, из рисунка 1 $\prime \; E\; \prime \; \{\backslash \; displaystyle\; \text{'}E\text{'}\}$можно определить следующим образом:

$E\; =\; \{(1,\; 2),\; (2,\; 1),\; (1,\; 3),\; (3,\; 1),\; (4,\; 2),\; (2,\; 4),\; (5,\; 2),\; (2,\; 5),\; (6,\; 3),\; (3,\; 6),\; (7,\; 3)),\; (3,\; 7),\; (8,\; 4),\; (4,\; 8),\; (9,\; 4),\; (4,\; 9)\}\; \{\backslash \; Displaystyle\; E\; =\; \backslash \; \{(1,2),\; (2,1),\; (1,3),\; (3,1),\; (4,2),\; (2,4),\; (5,2),\; (2,5),\; (6,3),\; (3,6),\; (\; 7,3),\; (3,7),\; (8,4),\; (4,8),\; (9,4),\; (4,9)\; \backslash \}\}$

ПРИМЕЧАНИЕ: $E\; \{\backslash \; displaystyle\; E\; \}$выше дает вам все возможные направления, по которому может перемещаться в дереве.

Расписание для GDL как конечная последовательность подмножеств $E\; \{\backslash \; displaystyle\; E\}$. Что обычно обозначается как $E\; =\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{E\}\}\; =\}${$E\; 1,\; E\; 2,\; E\; 3,\dots ,\; EN\; \{\backslash \; displaystyle\; E\_\; \{1\},\; E\_\; \{2\},\; E\_\; \{3\},\; \backslash \; ldots,\; E\_\; \{N\}\}$}, где $EN\; \{\backslash \; displaystyle\; E\_\; \{N\}\}$- это набор сообщений, обновленных в течение $N-й\; \{\backslash \; displaystyle\; N\; ^\; \{th\}\}$раунд запуска алгоритма.

Определив / просмотрев некоторые обозначения, мы увидим, что в теореме говорится: «Когда нам дано расписание» $E\; =\; \{E\; 1,\; E\; 2,\; E\; 3,\dots ,\; EN\}\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{E\}\}\; =\; \backslash \; \{E\_\; \{1\},\; E\_\; \{2\},\; E\_\; \{3\},\; \backslash \; ldots,\; E\_\; \{N\}\; \backslash \}\}$, соответствующая решетка сообщений как конечный ориентированный граф с набором вершин $V\; \times \; \{0,\; 1,\; 2,\; 3,\dots ,\; N\}\; \{\backslash \; displaystyle\; V\; \backslash \; times\; \backslash \; \{0,1,2,3,\; \backslash \; ldots,\; N\; \backslash \}\}$, в котором типичный элемент обозначается $vi\; (t)\; \{\backslash \; displaystyle\; v\_\; \{i\}\; (t)\}$для $t\; \in \; \{0,\; 1,\; 2,\; 3,\dots ,\; N\}\; \{\backslash \; displaystyle\; t\; \backslash \; in\; \backslash \; \{0,1,2,3,\; \backslash \; ldots,\; N\; \backslash \}\}$, после завершения передачи сообщения состояние в вершине $vj\; \{\backslash \; displaystyle\; v\_\; \{j\; \}\}$будет $j\; th\; \{\backslash \; displaystyle\; j\; ^\; \{\backslash \; text\; \{th\}\}\}$целью, предназначенным для

$\sigma \; (п\; S\; я)\; знак\; равно\; \alpha \; я\; (п\; S\; я)\; \prod \; vk\; прил\; \; vi\; \mu \; К,\; J\; (п\; S\; К\; \cap \; S\; я)\; \{\backslash \; Displaystyle\; \backslash \; sigma\; (p\_\; \{S\_\; \{i\}\})\; =\; \backslash \; альфа\; \_\; \{i\}\; (p\_\; \{S\_\; \{i\}\; \})\; \backslash \; prod\; \_\; \{v\_\; \{k\}\; \backslash \; operatorname\; \{adj\}\; v\_\; \{i\}\}\; \backslash \; mu\; \_\; \{k,\; j\}\; (p\_\; \{S\_\; \{k\}\; \backslash \; cap\; S\_\; \{i\}\})\}$

и если только там - путь от $vi\; (0)\; \{\backslash \; displaystyle\; v\_\; \{i\}\; (0)\}$до $vj\; (N)\; \{\backslash \; displaystyle\; v\_\; \{j\}\; (N)\}$

Здесь мы пытаемся объяснить сложность решения задачи MPF с точки зрения количества математических операций, необходимые для вычислений. т.е. Мы сравнили количество операций, требуемых при вычислении с использованием обычного метода, мы используем методы, которые не используют передачу сообщений или соединения в коротких методах, которые не используют GDL) и количество операций, использующих обобщенный распределительный закон.

Пример: рассмотрим простейший случай, когда нам нужно вычислить следующее выражение $a\; b\; +\; a\; c\; \{\backslash \; displaystyle\; ab\; +\; ac\}$.

Для вычислений этого выражения наивно требуется два умножения и одно сложение. Выражение, выраженное с использованием закона распределения, может быть записано $a\; (b\; +\; c)\; \{\backslash \; displaystyle\; a\; (b\; +\; c)\}$простая оптимизация, которая сокращает количество операций до одного добавления и одно умножение.

Подобно объясненному выше, мы будем выражать уравнения в различных формах, чтобы выполнить как можно меньше с помощью операций GDL.

Как объяснялось в предыдущих разделах, мы решаем проблему, используя концепцию соединений деревьев. Оптимизация, полученная с помощью этих деревьев, сравнима с оптимизацией, полученной путем полугрупповой задачи на деревьях. Например, чтобы найти минимум группы чисел, мы можем заметить, что если у нас есть дерево, и все элементы находятся в нижней части дерева, то мы можем сравнить минимум два элемента последовательно. Когда этот процесс распространяется по дереву, минимум элементов будет находиться в корне.

Ниже описана сложность решений соединений с использованием передачи сообщений

Мы перепишем формулу, используем ранее, в следующую форму. Это уравнение для отправки сообщения из вершины v в w

$\mu \; v,\; w\; (pv\; \cap \; w)\; =\; \sum \; pv\; \setminus \; w\; \in \; AS\; (v)\; \setminus \; S\; (w)\; \alpha \; v\; (pv)\; \prod \; uadjvu\; \ne \; v\; \mu \; U,\; v\; (пу\; \cap \; v)\; \{\backslash \; displaystyle\; \backslash \; mu\; \_\; \{v,\; w\}\; (p\_\; \{v\; \backslash \; cap\; w\})\; =\; \backslash \; sum\; \_\; \{p\_\; \{v\; \backslash \; setminus\; w\}\; \backslash \; in\; A\_\; \{S\; (v)\; \backslash \; setminus\; S\; (w)\}\}\; \backslash \; alpha\; \_\; \{v\}\; (p\_\; \{v\})\; \backslash \; prod\; \_\; \{uadjv\_\; \{u\; \backslash \; neq\; v\}\}\; \backslash \; mu\; \_\; \{u,\; v\}\; (p\_\; \{u\; \backslash \; cap\; v\})\}$---- уравнение сообщения

Аналогичным образом мы перепишем уравнение для расчета состояния вершины v следующим образом:

$\sigma \; v\; (pv)\; =\; \alpha \; v\; (pv)\; \prod \; u\; adj\; \; v\; \mu \; v\; вес\; (pv\; \cap \; вес)\; \{\backslash \; displaystyle\; \backslash \; sigma\; \_\; \{v\}\; (p\_\; \{v\})\; =\; \backslash \; alpha\; \_\; \{v\}\; (p\_\; \{v\})\; \backslash \; prod\; \_\; \{u\; \backslash \; operatorname\; \{adj\}\; v\}\; \backslash \; mu\; \_\; \{v,\; w\}\; (p\_\; \{v\; \backslash \; cap\; w\})\}$

Сначала мы проанализируем задачу с одной вершиной и предположим, что целевая вершина равна $v\; 0\; \{\backslash \; displaystyle\; v\_\; \{0\}\}$и, следовательно, у нас есть одно ребро от $v\; \{\backslash \; displaystyle\; v\}$до $v\; 0\; \{\backslash \; displaystyle\; v\_\; \{0\}\}$. Предположим, у нас есть край $(v,\; w)\; \{\backslash \; displaystyle\; (v,\; w)\}$, мы вычисляем сообщение, используя уравнение сообщения. Для вычисления $pu\; \cap \; v\; \{\backslash \; displaystyle\; p\_\; \{u\; \backslash \; cap\; v\}\}$требуется

$qv\; \setminus \; w\; -\; 1\; \{\backslash \; displaystyle\; q\_\; \{v\; \backslash \; setminus\; w\}\; -1\}$

сложения и

$qv\; \setminus \; w\; (d\; (v)\; -\; 1)\; \{\backslash \; displaystyle\; q\_\; \{v\; \backslash \; setminus\; w\}\; (d\; (v)\; -1)\}$

умножения.

(Мы представляем $|\; AS\; (v)\; S\; (w)\; |\; \{\backslash \; displaystyle\; |\; A\_\; \{S\; (v)\; \backslash \; S\; (w)\}\; |\}$как $qv\; \setminus \; вес\; \{\backslash \; displaystyle\; q\_\; \{v\; \backslash \; setminus\; w\}\}$.)

Но будет много возможностей для $xv\; \cap \; w\; \{\backslash \; displaystyle\; x\_\; \{v\; \backslash \; cap\; w\}\}$, следовательно,. $qv\; \cap \; w\; =\; def\; |\; A\; S\; (v)\; \cap \; S\; (w)\; |\; \{\backslash \; displaystyle\; q\_\; \{v\; \backslash \; cap\; w\}\; \{\backslash \; stackrel\; \{\backslash \; mathrm\; \{def\}\}\; \{=\}\}\; |\; A\_\; \{S\; (v)\; \backslash \; cap\; S\; (w)\}\; |\}$возможностей для $пв\; \cap \; вес\; \{\backslash \; displaystyle\; p\_\; \{v\; \backslash \; cap\; w\}\}$. Таким образом, для всего сообщения потребуется

$(qv\; \cap \; w)\; (qv\; \setminus \; w\; -\; 1)\; =\; qv\; -\; qv\; \cap \; w\; \{\backslash \; displaystyle\; (q\_\; \{v\; \backslash \; cap\; w\})\; (q\_\; \{v\; \backslash \; setminus\; w\}\; -1)\; =\; q\_\; \{v\}\; -q\_\; \{v\; \backslash \; cap\; w\}\}$

сложения и

$(qv\; \cap \; w)\; qv\; \setminus \; w.\; (d\; (v)\; -\; 1)\; знак\; равно\; (d\; (v)\; -\; 1)\; qv\; \{\backslash \; displaystyle\; (q\_\; \{v\; \backslash \; cap\; w\})\; q\_\; \{v\; \backslash \; setminus\; w\}.\; (d\; (v)\; -1)\; =\; (d\; (\; v)\; -1)\; q\_\; \{v\}\}$

умножения

Общее количество арифметических операций, необходимых для отправки сообщения по направлению $v\; 0\; \{\backslash \; displaystyle\; v\_\; \{0\}\}$по краям дерева будет

$\sum \; v\; \ne \; v\; 0\; (qv\; -\; qv\; \cap \; w)\; \{\backslash \; displaystyle\; \backslash \; sum\; \_\; \{v\; \backslash \; neq\; v0\}\; (q\_\; \{v\}\; -q\_\; \{v\; \backslash \; cap\; w\})\}$

сложения и

$\sum \; v\; \ne \; v\; 0\; (d\; (v)\; -\; 1)\; qv\; \{\backslash \; displaystyle\; \backslash \; sum\; \_\; \{v\; \backslash \; neq\; v0\}\; (d\; (v)\; -1)\; q\_\; \{v\}\}$

умножения.

После того, как все сообщения были переданы, алгоритм завершается вычислением состояния в $v\; 0\; \{\backslash \; displaystyle\; v\_\; \{0\}\}$Для вычисления состояния требуется $d\; (\; v\; 0)\; q\; 0\; \{\backslash \; displaystyle\; d\; (v\_\; \{0\})\; q\_\; \{0\}\}$больше умножений. Таким образом, количество вычислений, необходимых для вычисления состояния, указано ниже:

$\sum \; v\; \ne \; v\; 0\; (qv\; -\; qv\; \cap \; w)\; \{\backslash \; displaystyle\; \backslash \; sum\; \_\; \{v\; \backslash \; neq\; v\_\; \{0\}\}\; (q\_\; \{v\}\; -q\_\; \{v\; \backslash \; cap\; w\})\}$

сложения и

$\sum \; v\; \ne \; v\; 0\; (d\; (v)\; -\; 1)\; qv\; +\; d\; (v\; 0)\; qv\; 0\; \{\backslash \; displaystyle\; \backslash \; sum\; \_\; \{v\; \backslash \; neq\; v\_\; \{\; 0\}\}\; (d\; (v)\; -1)\; q\_\; \{v\}\; +\; d\; (v\_\; \{0\})\; q\_\; \{v\_\; \{0\}\}\}$

умножения

Таким образом, общая сумма количества вычислений равно

$\chi \; (T)\; =\; \sum \; v\; \in \; V\; d\; (v)\; qv\; -\; \sum \; e\; \in \; E\; qe\; \{\backslash \; displaystyle\; \backslash \; chi\; (T)\; =\; \backslash \; sum\; \_\; \{v\; \backslash \; in\; V\}\; d\; (v)\; q\_\; \{v\}\; -\; \backslash \; sum\; \_\; \{е\; \backslash \; in\; E\}\; q\_\; \{e\}\}$---- $(1)\; \{\backslash \; displaystyle\; (1)\}$

где $e\; =\; (v,\; w)\; \{\backslash \; displaystyle\; e\; =\; (v,\; w)\}$является ребром, и его размер определяется как $qv\; \cap \; w\; \{\backslash \; displaystyle\; q\_\; \{v\; \backslash \; cap\; w\}\}$

Формула выше дает нам верхнюю границу.

Если мы определим сложность ребра $e\; =\; (v,\; w)\; \{\backslash \; displaystyle\; e\; =\; (v,\; w)\}$как

$\chi \; (e)\; =\; qv\; +\; qw\; -\; qv\; \cap \; вес\; \{\backslash \; displaystyle\; \backslash \; chi\; (e)\; =\; q\_\; \{v\}\; +\; q\_\; \{w\}\; -q\_\; \{v\; \backslash \; cap\; w\}\}$

Следовательно, $(1)\; \{\backslash \; displaystyle\; (1)\}$можно записать как

$\chi \; (T)\; =\; \sum \; e\; \in \; E\; \chi \; (e)\; \{\backslash \; displaystyle\; \backslash \; chi\; (T)\; =\; \backslash \; sum\; \_\; \{e\; \backslash \; in\; E\}\; \backslash \; chi\; (e)\}$

Теперь вычислим сложность ребра для задачи, определенной на рисунке 1, следующим образом:

$\chi \; (1,\; 2)\; =\; q\; 2\; +\; q\; 2\; q\; 3\; -\; q\; 2\; \{\backslash \; displaystyle\; \backslash \; chi\; (1,2)\; знак\; равно\; q\_\; \{2\}\; +\; q\_\; \{2\}\; q\_\; \{3\}\; -q\_\; \{2\}\}$

$\chi \; (2,\; 4)\; =\; q\; 3\; q\; 4\; +\; q\; 2\; q\; 3\; -\; q\; 3\; \{\backslash \; displaystyle\; \backslash \; chi\; (2,\; 4)\; =\; q\_\; \{3\}\; q\_\; \{4\}\; +\; q\_\; \{2\}\; q\_\; \{3\}\; -q\_\; \{3\}\}$

$\chi \; (2,\; 5)\; =\; q\; 3\; +\; q\; 2\; q\; 3\; -\; q\; 3\; \{\backslash \; displaystyle\; \backslash \; хи\; (2,5)\; знак\; равно\; q\_\; \{3\}\; +\; q\_\; \{2\}\; q\_\; \{3\}\; -q\_\; \{3\}\}$

$\chi \; (4,\; 8)\; =\; q\; 4\; +\; q\; 3\; q\; 4\; -\; q\; 4\; \{\backslash \; displaystyle\; \backslash \; chi\; (4,8)\; =\; q\_\; \{4\}\; +\; q\_\; \{3\}\; q\_\; \{4\}\; -q\_\; \{4\}\}$

$\chi \; (4,\; 9)\; =\; q\; 2\; q\; 4\; +\; q\; 3\; q\; 4\; -\; q\; 4\; \{\backslash \; displaystyle\; \backslash \; chi\; (4,9)\; =\; q\_\; \{2\}\; q\_\; \{4\}\; +\; q\_\; \{3\}\; q\_\; \{4\}\; -q\_\; \{4\}\}$

$\chi \; (1,\; 3)\; =\; q\; 2\; +\; q\; 2\; q\; 1\; -\; q\; 2\; \{\backslash \; displaystyle\; \backslash \; chi\; (1,3)\; знак\; равно\; q\_\; \{2\}\; +\; q\_\; \{2\}\; q\_\; \{1\}\; -q\_\; \{\; 2\}\}$

$\chi \; (3,\; 7)\; =\; q\; 1\; +\; q\; 1\; q\; 2\; -\; q\; 1\; \{\backslash \; displaystyle\; \backslash \; chi\; (3,7)\; знак\; равно\; q\_\; \{1\}\; +\; q\_\; \{1\}\; q\_\; \{2\}\; -q\_\; \{1\}\}$

$\chi \; (3,\; 6)\; =\; q\; 1\; q\; 4\; +\; q\; 1\; q\; 2\; -\; q\; 1\; \{\backslash \; displaystyle\; \backslash \; chi\; (3,\; 6)\; =\; q\_\; \{1\}\; q\_\; \{4\}\; +\; q\_\; \{1\}\; q\_\; \{2\}\; -q\_\; \{1\}\}$

Общая сложность будет $3\; q\; 2\; q\; 3\; +\; 3\; q\; 3\; q\; 4\; +\; 3\; q\; 1\; q\; 2\; +\; q\; 2\; q\; 4\; +\; q\; 1\; q\; 4\; -\; q\; 1\; -\; q\; 3\; -\; q\; 4\; \{\backslash \; displaystyle\; 3q\_\; \{2\}\; q\_\; \{3\}\; +\; 3q\_\; \{3\}\; q\_\; \{4\}\; +\; 3q\_\; \{1\}\; q\_\; \{2\}\; +\; q\_\; \{2\}\; q\_\; \{4\}\; +\; q\_\; \{1\}\; q\_\; \{\; 4\}\; -q\_\; ниже\; \{1\}\; -q\_\; \{3\}\; -q\_\; \{4\}\}$, что значительно по сравнению с прямым методом. (Здесь под методом мы подразумеваем методы, которые используют методы использования передачи сообщений. Время, затрачиваемое на использование методов прямого вычисления, будет эквивалентно вычислению для вычислений состояний каждого из узлов.)

всех вершин, в сообщении должно быть отправлено в обоих направлениях, а состояние должно быть вычислено в обоих вершинах. Для этого потребуется $O\; (\sum \; vd\; (v)\; d\; (v)\; qv)\; \{\backslash \; displaystyle\; O\; (\backslash \; sum\; \_\; \{v\}\; d\; (v)\; d\; (v)\; q\_\; \{v\})\}$но с помощью предварительных вычислений мы можем уменьшить количество умножений до $3\; (d\; -\; 2)\; \{\backslash \; displaystyle\; 3\; (d-2)\}$. Здесь $d\; \{\backslash \; displaystyle\; d\}$- степень вершины. Пример: Если есть набор $(a\; 1,\dots ,\; ad)\; \{\backslash \; displaystyle\; (a\_\; \{1\},\; \backslash \; ldots,\; a\_\; \{d\})\}$с $d\; \{\backslash \; displaystyle\; d\}$числа. Можно вычислить все d произведений $d\; -\; 1\; \{\backslash \; displaystyle\; d-1\}$из $ai\; \{\backslash \; displaystyle\; a\_\; \{i\}\}$с помощью не более $3\; (d\; -\; 2)\; \{\backslash \; displaystyle\; 3\; (d-2)\}$умножения вместо очевидного $d\; (d\; -\; 2)\; \{\backslash \; displaystyle\; d\; (d-2)\}$. Выполним это, вычисляя величину $b\; 1\; =\; a\; 1,\; b\; 2\; =\; b\; 1\; \cdot \; a\; 2\; =\; a\; 1\; \cdot \; a\; 2,\; bd\; -\; 1\; =\; bd\; -\; 2\; \cdot \; ad\; -\; 1\; =\; a\; 1\; a\; 2\; \cdots \; ad\; -\; 1\; \{\backslash \; displaystyle\; b\_\; \{1\}\; =\; a\_\; \{1\},\; b\_\; \{2\}\; =\; b\_\; \{1\}\; \backslash \; cdot\; a\_\; \{2\}\; =\; a\_\; \{1\}\; \backslash \; cdot\; a\_\; \{2\},\; b\_\; \{d-1\}\; =\; b\_\; \{\; d-2\}\; \backslash \; cdot\; a\_\; \{d-1\}\; =\; a\_\; \{1\}\; a\_\; \{2\}\; \backslash \; cdots\; a\_\; \{d-1\}\}$и $cd\; =\; ad,\; cd\; -\; 1\; =\; ad\; -\; 1\; cd\; =\; ad\; -\; 1\; \cdot \; ad,\dots ,\; c\; 2\; =\; a\; 2\; \cdot \; c\; 3\; =\; a\; 2\; a\; 3\; \cdots \; ad\; \{\backslash \; displaystyle\; c\_\; \{d\}\; =\; a\_\; \{d\},\; c\_\; \{d-1\}\; =\; a\_\; \{d-\; 1\}\; c\_\; \{d\}\; =\; a\_\; \{d-1\}\; \backslash \; cdot\; a\_\; \{d\},\; \backslash \; ldots,\; c\_\; \{2\}\; =\; a\_\; \{2\}\; \backslash \; cdot\; c\_\; \{3\}\; =\; a\_\; \{2\}\; a\_\; \{3\}\; \backslash \; cdots\; a\_\; \{d\}\}$для этого требуется $2\; (d\; -\; 2)\; \{\backslash \; displaystyle\; 2\; (d-2)\}$умножений. Тогда, если $mj\; \{\backslash \; displaystyle\; m\_\; \{j\}\}$обозначает произведение всех $ai\; \{\backslash \; displaystyle\; a\_\; \{i\}\}$кроме $aj\; \{\backslash \; displaystyle\; a\_\; \{j\}\}$имеем $m\; 1\; =\; c\; 2,\; m\; 2\; =\; b\; 1\; \cdot \; c\; 3\; \{\backslash \; displaystyle\; m\_\; \{1\}\; =\; c\_\; \{2\},\; m\_\; \{2\}\; =\; b\_\; \{1\; \}\; \backslash \; cdot\; c\_\; \{3\}\}$и т. д. потребуются еще $d\; -\; 2\; \{\backslash \; displaystyle\; d-2\}$умножения, в результате чего в сумме получится $3\; (d\; -\; 2)\; \{\backslash \; displaystyle\; 3\; (d-2)\}$

Когда доходит до построения соединений, мы должны выбрать остовное дерево с наименьшим значением $\chi \; (T)\; \{\backslash \; displaystyle\; \backslash \; chi\; (T)\}$, иногда это может означать добавление локального домена для снижения сложности дерева соединений.

Может показаться, что GDL верен только тогда, когда локальные домены могут быть представлены в виде дерева соединений. Но даже в случаях, когда есть циклы и количество итераций. Эксперименты с алгоритмом Галлагера - Таннера - Виберга для кодов с низкой плотностью проверки на четность подтвердили это утверждение.

1. ^ Aji, S.M.; МакЭлис, Р.Дж. (Март 2000 г.). «Обобщенный распределительный закон» (PDF). IEEE Transactions по теории информации. 46 (2): 325–343. doi : 10.1109 / 18.825794.
2. ^"закон о распределении доходов". Encyclopdia Britannica. Энциклопедия Britannica Online. Encyclopdia Britannica Inc. Проверено 1 мая 2012 г.
3. ^«Архивная копия» (PDF). Архивировано из оригинального (PDF) 19 марта 2015 года. Проверено 19 марта 2015. CS1 maint: заархивированная копия как заголовок (ссылка ) Алгоритмы дерева соединений
4. ^http://www-anw.cs.umass.edu/ ~ cs691t / SS02 / lectures / week7.PDF Архивировано 26 мая 2012 г. на Wayback Machine Алгоритм дерева соединений