Основная теорема исчисления

Основная теорема исчисления является теоремой, которая связывает понятие дифференциации в функции (вычисления градиента) с концепцией интегрирования функции (расчет площади под кривым). Эти две операции противоположны друг другу, за исключением постоянного значения, которое зависит от того, где начинается вычисление площади.

Первая часть теоремы, иногда называемая первой фундаментальной теоремой исчисления, утверждает, что одна из первообразных (также известная как неопределенный интеграл), скажем F, некоторой функции f может быть получена как интеграл от f с переменной оценкой интеграции. Отсюда следует существование первообразных для непрерывных функций.

И наоборот, вторая часть теоремы, иногда называемая второй фундаментальной теоремой исчисления, утверждает, что интеграл функции f на некотором интервале может быть вычислен с использованием любой одной, скажем F, ее бесконечного числа первообразных. Эта часть теоремы имеет ключевые практические приложения, поскольку явное нахождение первообразной функции посредством символьного интегрирования позволяет избежать численного интегрирования для вычисления интегралов.

• 1 История
• 2 Геометрическое значение
• 3 Физическая интуиция
• 4 Официальные заявления
  • 4.1 Первая часть
  • 4.2 Следствие
  • 4.3 Вторая часть
• 5 Доказательство первой части
• 6 Доказательство следствия
• 7 Доказательство второй части
• 8 Примеры
• 9 Обобщения
• 10 См. Также
• 11 Примечания
• 12 Ссылки
  • 12.1 Библиография
• 13 Дальнейшее чтение
• 14 Внешние ссылки

Смотрите также: История исчисления

Основная теорема исчисления связывает дифференцирование и интегрирование, показывая, что эти две операции по существу противоположны друг другу. До открытия этой теоремы не было признано, что эти две операции связаны. Древнегреческие математики знали, как вычислить площадь через бесконечно малые величины, и эту операцию мы теперь назвали бы интеграцией. Истоки дифференцирования также на сотни лет предшествовали фундаментальной теореме исчисления; например, в четырнадцатом веке понятия непрерывности функций и движения изучались оксфордскими калькуляторами и другими учеными. Историческая значимость фундаментальной теоремы исчисления заключается не в способности вычислять эти операции, а в осознании того, что две, казалось бы, разные операции (вычисление геометрических площадей и вычисление градиентов) на самом деле тесно связаны.

Первое опубликованное утверждение и доказательство элементарной формы фундаментальной теоремы, строго геометрического по своему характеру, было сделано Джеймсом Грегори (1638–1675). Исаак Барроу (1630–1677) доказал более обобщенную версию теоремы, а его ученик Исаак Ньютон (1642–1727) завершил развитие окружающей математической теории. Готфрид Лейбниц (1646–1716) систематизировал полученные знания в исчисление бесконечно малых величин и ввел обозначения, используемые сегодня.

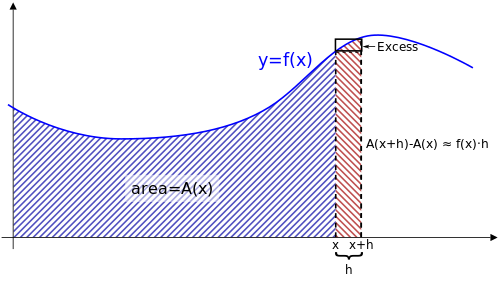Область, заштрихованная красными полосами, близка к h, умноженному на f ( x). В качестве альтернативы, если бы функция A ( x) была известна, эта область была бы точно A ( x + h) - A ( x). Эти два значения примерно равны, особенно для малых h.

Для непрерывной функции y = f ( x), график которой построен как кривая, каждое значение x имеет соответствующую функцию площади A ( x), представляющую площадь под кривой между 0 и x. Функция A ( x) может быть неизвестна, но предполагается, что она представляет площадь под кривой.

Площадь под кривой между x и x + h можно вычислить, найдя площадь между 0 и x + h, а затем вычтя площадь между 0 и x. Другими словами, площадь этой «полосы» будет A ( x + h) - A ( x).

Есть еще один способ оценить площадь этой же полосы. Как показано на прилагаемом рисунке, h умножается на f ( x), чтобы найти площадь прямоугольника примерно такого же размера, как эта полоса. Так:

${\ Displaystyle А (х + ч) -А (х) \ приблизительно е (х) \ CDOT ч}$

Фактически, эта оценка становится идеальным равенством, если мы добавим красную часть «лишней» области, показанной на диаграмме. Так:

${\ displaystyle A (x + h) -A (x) = f (x) \ cdot h + ({\ text {Red Excess}})}$

Изменение условий:

${\ displaystyle f (x) = {\ frac {A (x + h) -A (x)} {h}} - {\ frac {\ text {Red Excess}} {h}}}$.

Когда h приближается к 0 в пределе, можно показать, что последняя дробь стремится к нулю. Это верно, потому что площадь красной части лишней области меньше или равна площади крошечного прямоугольника с черной рамкой. Точнее,

${\ displaystyle \ left | f (x) - {\ frac {A (x + h) -A (x)} {h}} \ right | = {\ frac {| {\ text {Red Excess}} |} {h}} \ leq {\ frac {h (f (x + h_ {1}) - f (x + h_ {2}))} {h}} = f (x + h_ {1}) - f ( x + h_ {2}),}$

где и - точки, в которых f достигает своего максимума и минимума соответственно в интервале [ x, x + h ]. По непрерывности f последнее выражение стремится к нулю, как и h. Следовательно, левая часть стремится к нулю, как и h, что означает ${\ displaystyle x + h_ {1}}$${\ displaystyle x + h_ {2}}$

${\ displaystyle f (x) = \ lim _ {h \ to 0} {\ frac {A (x + h) -A (x)} {h}}.}$

Отсюда следует, что f ( x) = A ′ ( x). То есть производная функции площади A ( x) существует и является исходной функцией f ( x); Итак, функция площади - это просто первообразная исходной функции. Вычисление производной функции и нахождение площади под ее кривой - «противоположные» операции. В этом суть фундаментальной теоремы исчисления.

Интуитивно теорема утверждает, что сумма бесконечно малых изменений величины во времени (или по некоторой другой переменной) складывается в чистое изменение количества.

Представьте себе, например, использование секундомера для отметки крошечных отрезков времени, когда машина едет по шоссе. Представьте себе также, что вы смотрите на спидометр автомобиля во время его движения, чтобы в любой момент узнать скорость автомобиля. Чтобы понять силу этой теоремы, представьте также, что вам не разрешается смотреть в окно автомобиля, так что у вас нет прямых доказательств того, как далеко проехал автомобиль.

Для любого крошечного промежутка времени в автомобиле вы можете рассчитать, как далеко автомобиль проехал за этот промежуток, умножив текущую скорость автомобиля на длину этого крошечного промежутка времени. (Это потому, что расстояние = скорость и время.) ${\ displaystyle \ times}$

А теперь представьте, что вы делаете это мгновение за мгновением, чтобы за каждый крошечный промежуток времени вы знали, как далеко проехала машина. В принципе, вы могли бы затем рассчитать общее расстояние, пройденное в машине (даже если вы никогда не смотрели в окно), суммируя все эти крошечные расстояния.

пройденное расстояние = скорость в любой момент крошечный промежуток времени${\ displaystyle \ sum}$${\ displaystyle \ times}$

Другими словами,

пройденное расстояние = ${\ Displaystyle \ сумма v (t) \ раз \ Delta t}$

В правой части этого уравнения, когда становится бесконечно малым, операция «суммирования» соответствует интегрированию. Итак, мы показали, что интеграл от функции скорости можно использовать для вычисления того, как далеко проехал автомобиль. ${\ displaystyle \ Delta t}$

Теперь помните, что функция скорости является производной функции положения. Итак, что мы действительно показали, так это то, что интегрирование скорости восстанавливает исходную функцию положения. Это основная идея теоремы: интегрирование и дифференцирование - это тесно связанные операции, каждая из которых по сути является противоположностью другой.

Другими словами, с точки зрения своей физической интуиции, то теорема утверждает, что сумма изменений в количестве в течение долгого времени (например, положение, рассчитанная путем умножения скорости раз время) добавляет к общей чистой изменения количества. Или, говоря более широко:

• Учитывая количество, которое изменяется по некоторой переменной, и${\ displaystyle x}$${\ displaystyle t}$
• Учитывая скорость, с которой эта величина изменяется по этой переменной${\ Displaystyle v (т)}$

тогда идея о том, что «расстояние равно скорости, умноженной на время», соответствует утверждению

${\ Displaystyle dx = v (t) dt}$

Это означает, что можно восстановить исходную функцию, интегрировав ее производную, скорость, по. ${\ Displaystyle х (т)}$${\ Displaystyle v (т)}$${\ displaystyle t}$

Теорема состоит из двух частей. В первой части рассматривается производная первообразной, а во второй части рассматривается связь между первообразными и определенными интегралами.

Первая часть

Эту часть иногда называют первой фундаментальной теоремой исчисления.

Пусть f - непрерывная вещественнозначная функция, определенная на отрезке [ a, b ]. Пусть F - функция, определенная для всех x в [ a, b ] формулой

${\ Displaystyle F (x) = \ int _ {a} ^ {x} f (t) \, dt.}$

Тогда Р является равномерно непрерывной на [ с, Ь ] и дифференцируема на открытом интервале (, б), и

${\ Displaystyle F '(х) = е (х)}$

для всех x в ( a, b).

Следствие

Основная теорема исчисления (анимация)

Основная теорема часто используется для вычисления определенного интеграла функции, для которой известна первообразная. В частности, если является вещественнозначной непрерывной функцией на и является первообразной от in, то ${\ displaystyle f}$${\ displaystyle F}$${\ displaystyle f}$${\ Displaystyle [а, б]}$${\ displaystyle F}$${\ displaystyle f}$${\ Displaystyle [а, б]}$

${\ Displaystyle \ int _ {a} ^ {b} f (t) \, dt = F (b) -F (a).}$

Следствие предполагает непрерывность на всем интервале. Этот результат немного усиливается в следующей части теоремы.

Вторая часть

Эту часть иногда называют второй фундаментальной теоремой исчисления или аксиомой Ньютона – Лейбница.

Пусть - действительная функция на отрезке и первообразная от in: ${\ displaystyle f}$ ${\ Displaystyle [а, б]}$${\ displaystyle F}$${\ displaystyle f}$${\ Displaystyle (а, б)}$

${\ displaystyle F '(x) = f (x).}$

Если это Риман на то ${\ displaystyle f}$ ${\ Displaystyle [а, б]}$

${\ displaystyle \ int _ {a} ^ {b} f (x) \, dx = F (b) -F (a).}$

Вторая часть несколько сильнее следствия, поскольку не предполагает, что оно является непрерывным. ${\ displaystyle f}$

Когда существует первообразная, тогда существует бесконечно много первообразных для, получаемых добавлением произвольной константы к. Кроме того, согласно первой части теоремы первообразные всегда существуют, когда непрерывно. ${\ displaystyle F}$${\ displaystyle f}$${\ displaystyle F}$${\ displaystyle f}$${\ displaystyle f}$

Для данного f ( t) определим функцию F ( x) как

${\ Displaystyle F (x) = \ int _ {a} ^ {x} f (t) \, dt.}$

Для любых двух чисел x 1 и x 1 + ∆ x в [ a, b ] имеем

${\ Displaystyle F (x_ {1}) = \ int _ {a} ^ {x_ {1}} f (t) \, dt}$

и

${\ Displaystyle F (x_ {1} + \ Delta x) = \ int _ {a} ^ {x_ {1} + \ Delta x} f (t) \, dt.}$

Вычитание двух равенств дает

${\ Displaystyle F (x_ {1} + \ Delta x) -F (x_ {1}) = \ int _ {a} ^ {x_ {1} + \ Delta x} f (t) \, dt- \ int _ {а} ^ {x_ {1}} f (t) \, dt. \ qquad (1)}$

Можно показать, что

${\ Displaystyle \ int _ {a} ^ {x_ {1}} f (t) \, dt + \ int _ {x_ {1}} ^ {x_ {1} + \ Delta x} f (t) \, dt = \ int _ {a} ^ {x_ {1} + \ Delta x} f (t) \, dt.}$

(Сумма площадей двух соседних регионов равна площади обоих регионов вместе взятых.)

Манипулирование этим уравнением дает

${\ Displaystyle \ int _ {a} ^ {x_ {1} + \ Delta x} f (t) \, dt- \ int _ {a} ^ {x_ {1}} f (t) \, dt = \ int _ {x_ {1}} ^ {x_ {1} + \ Delta x} f (t) \, dt.}$

Подстановка вышеуказанного в (1) приводит к

${\ Displaystyle F (x_ {1} + \ Delta x) -F (x_ {1}) = \ int _ {x_ {1}} ^ {x_ {1} + \ Delta x} f (t) \, dt. \ qquad (2)}$

Согласно теореме о среднем значении для интегрирования существует действительное число такое, что ${\ displaystyle c \ in [x_ {1}, x_ {1} + \ Delta x]}$

${\ displaystyle \ int _ {x_ {1}} ^ {x_ {1} + \ Delta x} f (t) \, dt = f (c) \ cdot \ Delta x.}$

Чтобы не усложнять обозначения, мы пишем просто, но следует иметь в виду, что для данной функции значение зависит от и от, но всегда ограничено интервалом. Подставляя приведенное выше в (2), получаем ${\ displaystyle c}$${\ displaystyle f}$${\ displaystyle c}$${\ displaystyle x_ {1}}$${\ displaystyle \ Delta x,}$${\ displaystyle [x_ {1}, x_ {1} + \ Delta x]}$

${\ Displaystyle F (x_ {1} + \ Delta x) -F (x_ {1}) = f (c) \ cdot \ Delta x.}$

Разделив обе стороны на дает ${\ displaystyle \ Delta x}$

${\ displaystyle {\ frac {F (x_ {1} + \ Delta x) -F (x_ {1})} {\ Delta x}} = f (c).}$

Выражение в левой части уравнения представляет собой разностное отношение Ньютона для F при x 1.

Возьмем предел при → 0 с обеих сторон уравнения. ${\ displaystyle \ Delta x}$

${\ displaystyle \ lim _ {\ Delta x \ to 0} {\ frac {F (x_ {1} + \ Delta x) -F (x_ {1})} {\ Delta x}} = \ lim _ {\ Дельта x \ к 0} f (c).}$

Выражение в левой части уравнения - это определение производной от F в точке x 1.

${\ Displaystyle F '(x_ {1}) = \ lim _ {\ Delta x \ to 0} f (c). \ qquad (3)}$

Чтобы найти другой предел, воспользуемся теоремой сжатия. Число c находится в интервале [ x 1, x 1  + Δ x ], поэтому x 1 ≤ c ≤ x 1  + Δ x.

Также и${\ displaystyle \ lim _ {\ Delta x \ to 0} x_ {1} = x_ {1}}$${\ displaystyle \ lim _ {\ Delta x \ to 0} x_ {1} + \ Delta x = x_ {1}.}$

Следовательно, согласно теореме сжатия,

${\ displaystyle \ lim _ {\ Delta x \ to 0} c = x_ {1}.}$

Функция f непрерывна в точке x 1, предел можно взять внутри функции:

${\ displaystyle \ lim _ {\ Delta x \ to 0} f (c) = f (x_ {1}).}$

Подставляя в (3), получаем

${\ displaystyle F '(x_ {1}) = f (x_ {1}).}$

что завершает доказательство.

Предположим, что F - первообразная f, причем f непрерывна на [ a, b ]. Позволять

${\ Displaystyle G (x) = \ int _ {a} ^ {x} f (t) \, dt}$.

По первой части теоремы мы знаем, что G также является первообразной f. Поскольку F ′ - G ′ = 0, из теоремы о среднем значении следует, что F - G является постоянной функцией, то есть существует такое число c, что G ( x) = F ( x) +  c для всех x в [ a, б ]. Полагая x  =  a, имеем

${\ Displaystyle F (a) + c = G (a) = \ int _ {a} ^ {a} f (t) \, dt = 0,}$

что означает c = - F ( a). Другими словами, G ( x) = F ( x) - F ( a), и поэтому

${\ Displaystyle \ int _ {a} ^ {b} f (x) \, dx = G (b) = F (b) -F (a).}$

Это предельное доказательство с помощью сумм Римана. Пусть f (по Риману) интегрируема на отрезке [ a, b ], и пусть f допускает первообразную F на [ a, b ]. Начнем с количества F ( b) - F ( a). Пусть существуют числа x 1,..., x n такие, что

${\ displaystyle a = x_ {0} lt;x_ {1} lt;x_ {2} lt;\ cdots lt;x_ {n-1} lt;x_ {n} = b.}$

Это следует из того

${\ Displaystyle F (b) -F (a) = F (x_ {n}) - F (x_ {0}).}$

Теперь мы добавляем каждый F ( x i) вместе с его аддитивным обратным, так что результирующая величина равна:

${\ Displaystyle {\ begin {align} F (b) -F (a) amp; = F (x_ {n}) + [- F (x_ {n-1}) + F (x_ {n-1})] + \ cdots + [- F (x_ {1}) + F (x_ {1})] - F (x_ {0}) \\ amp; = [F (x_ {n}) - F (x_ {n-1 })] + [F (x_ {n-1}) - F (x_ {n-2})] + \ cdots + [F (x_ {2}) - F (x_ {1})] + [F ( x_ {1}) - F (x_ {0})]. \ end {выравнивается}}}$

Вышеуказанное количество можно записать в виде следующей суммы:

${\ Displaystyle F (b) -F (a) = \ sum _ {i = 1} ^ {n} [F (x_ {i}) - F (x_ {i-1})]. \ qquad (1) }$

Далее воспользуемся теоремой о среднем значении. Вкратце сказано,

Пусть F непрерывна на отрезке [ a, b ] и дифференцируема на открытом отрезке ( a, b). Тогда существует такое c в ( a, b), что

${\ displaystyle F '(c) = {\ frac {F (b) -F (a)} {ba}}.}$

Это следует из того

${\ Displaystyle F '(c) (ba) = F (b) -F (a).}$

Функция F дифференцируема на отрезке [ a, b ]; следовательно, он также дифференцируем и непрерывен на каждом интервале [ x i −1, x i ]. Согласно теореме о среднем значении (см. Выше),

${\ Displaystyle F (x_ {i}) - F (x_ {i-1}) = F '(c_ {i}) (x_ {i} -x_ {i-1}).}$

Подставляя приведенное выше в (1), получаем

${\ Displaystyle F (b) -F (a) = \ sum _ {i = 1} ^ {n} [F '(c_ {i}) (x_ {i} -x_ {i-1})].}$

Предположение также подразумевает, что может быть выражено как разделение. ${\ displaystyle F '(c_ {i}) = f (c_ {i}).}$${\ displaystyle x_ {i} -x_ {i-1}}$${\ displaystyle \ Delta x}$${\ displaystyle i}$

${\ Displaystyle F (b) -F (a) = \ sum _ {i = 1} ^ {n} [f (c_ {i}) (\ Delta x_ {i})]. \ qquad (2)}$

Сходящаяся последовательность сумм Римана. Число в левом верхнем углу - это общая площадь синих прямоугольников. Они сходятся к определенному интегралу функции.

Мы описываем площадь прямоугольника, умножая ширину на высоту, и складываем области вместе. Каждый прямоугольник, в силу теоремы о среднем значении, описывает аппроксимацию участка кривой, на котором он нарисован. Также не обязательно должно быть одинаковым для всех значений i, или, другими словами, ширина прямоугольников может отличаться. Нам нужно аппроксимировать кривую n прямоугольников. Теперь, когда размер перегородок становится меньше, а n увеличивается, в результате чего больше перегородок покрывает пространство, мы приближаемся к фактической площади кривой. ${\ displaystyle \ Delta x_ {i}}$

Взяв предел выражения, когда норма разбиений приближается к нулю, мы приходим к интегралу Римана. Мы знаем, что этот предел существует, потому что предполагалось, что f интегрируема. То есть мы принимаем предел, так как самый большой из разделов приближается к нулю по размеру, так что все остальные разделы меньше, а количество разделов приближается к бесконечности.

Итак, мы берем предел с обеих сторон (2). Это дает нам

${\ Displaystyle \ lim _ {\ | \ Delta x_ {i} \ | \ to 0} F (b) -F (a) = \ lim _ {\ | \ Delta x_ {i} \ | \ to 0} \ сумма _ {i = 1} ^ {n} [f (c_ {i}) (\ Delta x_ {i})].}$

Ни F ( b), ни F ( a) не зависят от, поэтому предел в левой части остается F ( b) - F ( a).${\ displaystyle \ | \ Delta x_ {i} \ |}$

${\ Displaystyle F (b) -F (a) = \ lim _ {\ | \ Delta x_ {i} \ | \ to 0} \ sum _ {i = 1} ^ {n} [f (c_ {i}) (\ Delta x_ {i})].}$

Выражение в правой части уравнения определяет интеграл по f от a до b. Следовательно, получаем

${\ Displaystyle F (b) -F (a) = \ int _ {a} ^ {b} f (x) \, dx,}$

что завершает доказательство.

Похоже, что первая часть теоремы непосредственно следует из второй. То есть предположим, что G - первообразная от f. Тогда по второй теореме. Теперь предположим. Тогда F имеет ту же производную, что и G, и поэтому F ′ = f. Однако этот аргумент работает только в том случае, если мы уже знаем, что f имеет первообразную, и единственный способ узнать, что все непрерывные функции имеют первообразные, - это первая часть фундаментальной теоремы. Например, если f ( x) = e ^-x2, то f имеет первообразную, а именно ${\ Displaystyle G (x) -G (a) = \ int _ {a} ^ {x} f (t) \, dt}$${\ Displaystyle F (x) = \ int _ {a} ^ {x} f (t) \, dt = G (x) -G (a)}$

${\ Displaystyle G (x) = \ int _ {0} ^ {x} f (t) \, dt}$

и нет более простого выражения для этой функции. Поэтому важно не интерпретировать вторую часть теоремы как определение интеграла. В самом деле, есть много функций, которые интегрируемы, но не имеют элементарных первообразных, а прерывистые функции могут быть интегрируемыми, но вообще лишены каких-либо первообразных. И наоборот, многие функции, имеющие первообразные, не интегрируемы по Риману (см . Функцию Вольтерра ).

В качестве примера предположим, что необходимо вычислить следующее:

${\ displaystyle \ int _ {2} ^ {5} x ^ {2} \, dx.}$

Здесь и мы можем использовать как первообразную. Следовательно: ${\ Displaystyle е (х) = х ^ {2}}$${\ Displaystyle F (х) = {\ гидроразрыва {х ^ {3}} {3}}}$

${\ displaystyle \ int _ {2} ^ {5} x ^ {2} \, dx = F (5) -F (2) = {\ frac {5 ^ {3}} {3}} - {\ frac {2 ^ {3}} {3}} = {\ frac {125} {3}} - {\ frac {8} {3}} = {\ frac {117} {3}} = 39.}$

Или, в более общем смысле, предположим, что

${\ displaystyle {\ frac {d} {dx}} \ int _ {0} ^ {x} t ^ {3} \, dt}$

подлежит расчету. Здесь и можно использовать как первообразную. Следовательно: ${\ Displaystyle е (т) = т ^ {3}}$${\ Displaystyle F (т) = {\ гидроразрыва {т ^ {4}} {4}}}$

${\ displaystyle {\ frac {d} {dx}} \ int _ {0} ^ {x} t ^ {3} \, dt = {\ frac {d} {dx}} F (x) - {\ frac {d} {dx}} F (0) = {\ frac {d} {dx}} {\ frac {x ^ {4}} {4}} = x ^ {3}.}$

Или, что то же самое,

${\ displaystyle {\ frac {d} {dx}} \ int _ {0} ^ {x} t ^ {3} \, dt = f (x) {\ frac {dx} {dx}} - f (0) {\ frac {d0} {dx}} = x ^ {3}.}$

В качестве теоретического примера теорему можно использовать для доказательства того, что

${\ displaystyle \ int _ {a} ^ {b} е (х) dx = \ int _ {a} ^ {c} f (x) dx + \ int _ {c} ^ {b} f (x) dx. }$

С,

${\ displaystyle {\ begin {align} \ int _ {a} ^ {b} f (x) dx amp; = F (b) -F (a), \\\ int _ {a} ^ {c} f (x) dx amp; = F (c) -F (a), {\ text {and}} \\\ int _ {c} ^ {b} f (x) dx amp; = F (b) -F (c), \ end {выровнено}}}$

результат следует из,

${\ Displaystyle F (b) -F (a) = F (c) -F (a) + F (b) -F (c).}$

Функция f не обязательно должна быть непрерывной на всем интервале. Тогда часть I теоремы гласит: если f - любая интегрируемая по Лебегу функция на [ a, b ] и x 0 - такое число в [ a, b ], что f непрерывна в x 0, то

${\ Displaystyle F (x) = \ int _ {a} ^ {x} f (t) \, dt}$

дифференцируема при x = x 0 с F ′ ( x 0) = f ( x 0). Мы можем еще больше ослабить условия на f и предположить, что оно просто локально интегрируемо. В этом случае можно заключить, что функция F дифференцируема почти всюду и F ′ ( x) = f ( x) почти всюду. На прямой это утверждение эквивалентно теореме Лебега о дифференцировании. Эти результаты остаются верными для интеграла Хенстока – Курцвейла, который допускает более широкий класс интегрируемых функций.

В более высоких измерениях теорема дифференцирования Лебега обобщает Фундаментальную теорему исчисления, утверждая, что почти для каждого x среднее значение функции f по шару радиуса r с центром в x стремится к f ( x), когда r стремится к 0.

Часть II теоремы верна для любой интегрируемой по Лебегу функции f, которая имеет первообразную F (хотя не все интегрируемые функции имеют). Другими словами, если вещественная функция F на [ a, b ] допускает производную f ( x) в каждой точке x из [ a, b ] и если эта производная f интегрируема по Лебегу на [ a, b ], то

${\ Displaystyle F (b) -F (a) = \ int _ {a} ^ {b} f (t) \, dt.}$

Этот результат может быть неверным для непрерывных функций F, которые допускают производную f ( x) почти в каждой точке x, как показывает пример функции Кантора. Однако, если Р является абсолютно непрерывным, она допускает производную F ' ( х) почти в каждой точке х, и, кроме того Р' интегрируем с F ( б) - F () равно интегралом от F ' на [ а, б ]. И наоборот, если f - любая интегрируемая функция, то F, как указано в первой формуле, будет абсолютно непрерывным с F ′ = f ae

Условия этой теоремы можно снова ослабить, если рассматривать интегралы как интегралы Хенстока – Курцвейла. В частности, если непрерывная функция F ( x) допускает производную f ( x) во всех точках, кроме счетного, то функция f ( x) интегрируема по Хенстоку – Курцвейлу и F ( b) - F ( a) равна интегралу от f на [ a, b ]. Разница здесь в том, что не нужно предполагать интегрируемость f.

Версия теоремы Тейлора, которая выражает ошибку как интеграл, может рассматриваться как обобщение основной теоремы.

Существует версия теоремы для сложных функций: пусть U является открытым множеством в C и F  : U → C есть функция, которая имеет голоморфную первообразную F на U. Тогда для каждой кривой у: [, Ь ] → U, интегральная кривая может быть вычислена как

${\ Displaystyle \ int _ {\ gamma} f (z) \, dz = F (\ gamma (b)) - F (\ gamma (a)).}$

Основная теорема может быть обобщена на кривые и поверхностные интегралы в более высоких измерениях и на многообразиях. Одним из таких обобщений, предлагаемых исчислением движущихся поверхностей, является временная эволюция интегралов. Наиболее известными расширениями фундаментальной теоремы исчисления в высших измерениях являются теорема о расходимости и градиентная теорема.

Один из самых мощных обобщений в этом направлении Стокс теоремы (иногда известный как основная теорема многофакторного исчисления): Пусть М ориентированное кусочна - гладкой коллектор из размерности п и пусть гладкая с компактным носителем ( п  - 1) -форма на M. Если ∂ М обозначает границу из М с учетом ее индуцированной ориентацией, то ${\ displaystyle \ omega}$

${\ displaystyle \ int _ {M} d \ omega = \ int _ {\ partial M} \ omega.}$

Здесь d - внешняя производная, которая определяется только с использованием структуры многообразия.

Теорема часто используется в ситуациях, когда M - вложенное ориентированное подмногообразие некоторого большего многообразия (например, R ^k), на котором определена форма. ${\ displaystyle \ omega}$

Основная теорема исчисления позволяет нам представить определенный интеграл как обыкновенное дифференциальное уравнение первого порядка.

${\ displaystyle \ int _ {a} ^ {b} f (x) \, dx}$

можно представить как

${\ Displaystyle {\ гидроразрыва {dy} {dx}} = е (х), \; \; у (а) = 0}$

с как значение интеграла. ${\ Displaystyle у (б)}$

• Дифференцирование под знаком интеграла
• Телескопическая серия

Список используемой литературы

• Апостол, Том М. (1967), Calculus, Vol. 1: Исчисление с одной переменной с введением в линейную алгебру (2-е изд.), Нью-Йорк: John Wiley amp; Sons, ISBN   978-0-471-00005-1.
• Бартл, Роберт (2001), Современная теория интеграции, AMS, ISBN   0-8218-0845-1.
• Лейтолд, Л. (1996), Исчисление одной переменной (6-е изд.), Нью-Йорк: издательство HarperCollins College Publishers.
• Рудин, Уолтер (1987), Реальный и комплексный анализ (третье изд.), Нью-Йорк: McGraw-Hill Book Co., ISBN   0-07-054234-1

• Курант, Ричард; Джон, Фриц (1965), Введение в исчисление и анализ, Springer.
• Ларсон, Рон; Эдвардс, Брюс Х.; Хейд, Дэвид Э. (2002), Исчисление одной переменной (7-е изд.), Бостон: Houghton Mifflin Company, ISBN   978-0-618-14916-2.
• Malet А., Исследования по Джеймс Gregorie (1638-1675) (диссертация, Принстон, 1989).
• Эрнандес Родригес, О.А.; Лопес Фернандес, JM. " Обучение фундаментальной теореме исчисления: историческое отражение ", Loci: Convergence ( MAA ), январь 2012 г.
• Стюарт, Дж. (2003), «Фундаментальная теорема исчисления», « Исчисление: ранние трансцендентальные», Бельмонт, Калифорния: Thomson / Brooks / Cole.
• Тернбулл, HW, изд. (1939), Том 300-летия Джеймса Грегори, Лондон.

• "Основная теорема исчисления", Энциклопедия математики, EMS Press, 2001 [1994]
• Евклидово доказательство основной теоремы исчисления при сходимости Джеймса Грегори
• Доказательство Исаака Барроу основной теоремы исчисления
• Фундаментальная теорема исчисления на imomath.com
• Альтернативное доказательство основной теоремы исчисления
• Фундаментальная теорема исчисления MIT.
• Фундаментальная теорема исчисления Mathworld.