Функция нескольких сложных переменных

Теория функций нескольких комплексных переменных - раздел математики, имеющий дело с комплексными функциями. Название поля, имеющего дело со свойствами функции нескольких сложных переменных, называется несколькими комплексными переменными (и аналитическим пространством ), что стало общим названием для всей этой области исследования, а классификация предметов математики имеет в качестве заголовка верхнего уровня. Функция является п -наборов комплексных чисел, классический изучена на комплексной координату пространства. ${\ displaystyle f: (z_ {1}, z_ {2}, \ ldots, z_ {n}) \ rightarrow f (z_ {1}, z_ {2}, \ ldots, z_ {n})}$ ${\ displaystyle \ mathbb {C} ^ {n}}$

Как и в случае комплексного анализа функций одной переменной, который имеет место n = 1, изучаемые функции являются голоморфными или комплексно-аналитическими, так что локально они являются степенными рядами по переменным z i. Эквивалентно, они локально равномерные пределы из многочленов ; или локальные решения n- мерных уравнений Коши – Римана. Для одной комплексной переменной каждая область () является областью голоморфности некоторой функции, другими словами, каждая область имеет функцию, для которой она является областью голоморфности. Для нескольких сложных переменных это не так; существуют области (), которые не являются областью голоморфности какой-либо функции, и поэтому не всегда являются областью голоморфности, поэтому область голоморфности является одной из тем в этой области. Исправление локальных данных мероморфных функций, то есть проблема создания глобальной мероморфной функции из нулей и полюсов, называется проблемой Кузена. Кроме того, интересные явления, которые происходят с несколькими комплексными переменными, фундаментально важны для изучения компактных комплексных многообразий и комплексных проективных многообразий () и имеют иной оттенок, чем комплексная аналитическая геометрия в многообразиях Штейна или на них. ${\ Displaystyle D \ подмножество \ mathbb {C}}$ ${\ Displaystyle D \ подмножество \ mathbb {C} ^ {n}, \ n \ geq 2}$ ${\ Displaystyle \ mathbb {CP} ^ {п}}$${\ displaystyle \ mathbb {C} ^ {n}}$

• 1 Историческая перспектива
• 2 Комплексное координатное пространство
  • 2.1 Связанное пространство
  • 2.2 Компактный
• 3 голоморфные функции
  • 3.1 Определение
  • 3.2 Уравнения Коши – Римана
  • 3.3 Интегральная формула Коши
    • 3.3.1 Формула оценки Коши
    • 3.3.2 Разложение голоморфных функций в степенной ряд на полидиске
    • 3.3.3 Радиус сходимости степенного ряда
    • 3.3.4 Расширение серии Лорана
  • 3.4 Формула Бохнера – Мартинелли
  • 3.5 Теорема тождества
  • 3.6 Биголоморфизм
    • 3.6.1 Теорема об отображении Римана неверна.
  • 3.7 Аналитическое продолжение
• 4 домен Рейнхардта
  • 4.1 Логарифмически-выпуклый
  • 4.2 Некоторые результаты
    • 4.2.1 Теорема Хартогса о продолжении и феномен Хартогса
    • 4.2.2 Классические результаты Таллена
    • 4.2.3 Результаты Сунады
• 5 Естественная область голоморфной функции (область голоморфности)
  • 5.1 Область голоморфности
    • 5.1.1 Свойства области голоморфности
  • 5.2 Голоморфно выпуклая оболочка
  • 5.3 Выпуклость по Леви (аппроксимация изнутри на аналитической многогранной области)
  • 5.4 Псевдовыпуклая
    • 5.4.1 Определение плюрисубгармонической функции
      • 5.4.1.1 Строго плюрисубгармоническая функция
    • 5.4.2 (Слабо) псевдовыпуклый (p-псевдовыпуклый)
    • 5.4.3 Сильно (строго) псевдовыпуклый
    • 5.4.4 (Слабо) псевдовыпуклость Леви (–Кшоски)
      • 5.4.4.1 Сильно псевдовыпуклая (–Krzoska) псевдовыпуклость (Сильно псевдовыпуклая)
      • 5.4.4.2 Общая псевдовыпуклая форма Леви
    • 5.4.5 Ока псевдовыпуклая
      • 5.4.5.1 Семейство дисков Оки
      • 5.4.5.2 Определение
    • 5.4.6 Локально псевдовыпуклые (локально Штейна, псевдовыпуклые Картана, локально свойство Леви)
  • 5.5 Условия, эквивалентные области голоморфности
• 6 связок
  • 6.1 Idéal de domaines indéterminés (предшественник понятия когерентности (пучка))
  • 6.2 Когерентный пучок
    • 6.2.1 Определение
    • 6.2.2 Когерентная теорема Оки
    • 6.2.3 Идеальная связка
  • 6.3 проблема кузена
    • 6.3.1 Проблема двоюродного брата
      • 6.3.1.1 Определение без слов когомологий пучка
      • 6.3.1.2 Определение с использованием слов когомологий пучков
    • 6.3.2 Проблема троюродного брата
      • 6.3.2.1 Определение без слов когомологий пучка
      • 6.3.2.2 Определение с использованием слов когомологий пучков
• 7 многообразий с несколькими комплексными переменными
  • 7.1 Многообразие Штейна (некомпактное многообразие)
    • 7.1.1 Определение
    • 7.1.2 Все некомпактные (открытые) римановы поверхности являются многообразием Штейна.
    • 7.1.3 Проблемы Леви
      • 7.1.3.1 K- Complete
    • 7.1.4 Свойства и примеры многообразий Штейна
  • 7.2 Комплексные проективные многообразия (компактное многообразие)
• 8 См. Также
• 9 Аннотация
• 10 Ссылки
  • 10.1 Встроенные цитаты
  • 10.2 Учебники
  • 10.3 Энциклопедия математики
  • 10.4 Планетарная математика
• 11 Дальнейшее чтение
• 12 Внешние ссылки

Многие примеры таких функций были известны в математике девятнадцатого века; абелевы функции, тета-функции и некоторые гипергеометрические ряды. Естественно, кандидатом является та же функция одной переменной, которая зависит от некоторого сложного параметра. Однако теория за долгие годы не стала полноценной областью математического анализа, так как не были раскрыты ее характерные явления. Теорема Вейерштрасса препарат теперь будет классифицироваться как коммутативной алгебры ; он действительно оправдал локальную картину, разветвленность, которая обращается к обобщению точек ветвления теории римановой поверхности.

С работами Фридриха Хартогса и Киёси Ока в 1930-х годах начала появляться общая теория; в то время в этом районе работали Генрих Бенке, Питер Таллен и Карл Штайн. Гартогс доказал некоторые основные результаты, такие, как любой изолированной особенности является съемным, для каждой аналитической функции

${\ displaystyle f: \ mathbb {C} ^ {n} \ to \ mathbb {C}}$

всякий раз, когда n gt; 1. Естественно, что с аналогами контурных интегралов будет труднее работать; когда n = 2, интеграл, окружающий точку, должен быть по трехмерному многообразию (поскольку мы находимся в четырех реальных измерениях), в то время как повторяющиеся контурные (линейные) интегралы по двум отдельным комплексным переменным должны приводить к двойному интегралу по двумерному поверхность. Это означает, что исчисление вычетов должно будет принять совсем другой характер.

После 1945 года важная работа во Франции, на семинаре Анри Картана, и в Германии с Гансом Грауэртом и Райнхольдом Реммертом, быстро изменила картину теории. Был прояснен ряд вопросов, в частности аналитического продолжения. Здесь основное различие очевидно из теории одной переменной; в то время как для каждого открытого связного множества D в in мы можем найти функцию, которая нигде не будет аналитически продолжаться через границу, чего нельзя сказать для n gt; 1. На самом деле D такого типа довольно специфичны по своей природе (особенно в комплексных координатных пространствах и многообразиях Штейна, удовлетворяющих условию, называемому псевдовыпуклостью). Естественные области определения функций, продолженные до предела, называются многообразиями Штейна, и их природа заключалась в том, чтобы обращать в нуль группы когомологий пучков. что многообразие Ходжа проективно. Фактически, именно необходимость поставить (в частности) работу Оки на более ясную основу, быстро привела к последовательному использованию пучков для формулировки теории (что имело серьезные последствия для алгебраической геометрии, в частности, из работ Грауэрта). ${\ Displaystyle \ mathbb {C}}$${\ displaystyle \ mathbb {C} ^ {n}}$

С этого момента существовала фундаментальная теория, которую можно было применять к аналитической геометрии, автоморфным формам нескольких переменных и уравнениям в частных производных. Теория деформации сложных структур и комплексных многообразий в общих чертах описана Кунихико Кодаира и Д.К. Спенсером. Знаменитая газета GAGA of Serre зафиксировала переход от géometrie analytique к géometrie algébrique.

Слышали, как К.Л. Сигель жаловался, что новая теория функций нескольких комплексных переменных содержит мало функций, а это означает, что специальная функциональная сторона теории подчинена пучкам. Интерес для теории чисел, конечно, вызывают конкретные обобщения модулярных форм. Классические кандидаты являются модульными формами Гильберта и Siegel модульных форм. В наши дни они ассоциированы с алгебраическими группами (соответственно, ограничение Вейля из поля вполне вещественных чисел в GL (2) и симплектическая группа ), для которых случается, что автоморфные представления могут быть получены из аналитических функций. В некотором смысле это не противоречит Зигелю; современная теория имеет свои, разные направления.

Последующие разработки включали теорию гиперфункций и теорему о краю клина, обе из которых были в некоторой степени вдохновлены квантовой теорией поля. Есть ряд других областей, таких как теория банаховой алгебры, которые используют несколько комплексных переменных.

Комплекс координатного пространства является декартово произведением из п копий, а когда является областью голоморфности, можно рассматривать как многообразия Штейна и более обобщенного Stein пространство. также считается комплексным проективным многообразием, кэлеровым многообразием и т. д. Это также n -мерное векторное пространство над комплексными числами, которое дает его размерность 2 n над. Следовательно, как набор и как топологическое пространство, его можно отождествить с реальным координатным пространством, и его топологическая размерность, таким образом, равна 2 n. ${\ displaystyle \ mathbb {C} ^ {n}}$ ${\ Displaystyle \ mathbb {C}}$${\ displaystyle \ mathbb {C} ^ {n}}$${\ displaystyle \ mathbb {C} ^ {n}}$ ${\ displaystyle \ mathbb {C} ^ {n}}$ ${\ Displaystyle \ mathbb {R}}$ ${\ displaystyle \ mathbb {C} ^ {n}}$ ${\ Displaystyle \ mathbb {R} ^ {2n}}$

На безкоординатном языке любое векторное пространство над комплексными числами можно рассматривать как реальное векторное пространство с вдвое большим числом измерений, где сложная структура задается линейным оператором J (таким, что J ² = - I ), который определяет умножение на мнимую единицу i.

Любое такое пространство, как реальное, ориентировано. На комплексной плоскости, рассматриваемой как декартова плоскость, умножение на комплексное число w = u + iv может быть представлено вещественной матрицей

${\ displaystyle {\ begin {pmatrix} u amp; -v \\ v amp; u \ end {pmatrix}},}$

с определителем

${\ displaystyle u ^ {2} + v ^ {2} = | w | ^ {2}.}$

Аналогичным образом, если выразить любой конечномерный комплексный линейный оператор как вещественную матрицу (которая будет составлена ​​из блоков 2 × 2 вышеупомянутой формы), то его определитель равен квадрату модуля соответствующего комплексного определителя. Это неотрицательное число, которое означает, что (реальная) ориентация пространства никогда не меняется на противоположную с помощью сложного оператора. То же самое относится и к якобианам из голоморфных функций от до. ${\ displaystyle \ mathbb {C} ^ {n}}$${\ displaystyle \ mathbb {C} ^ {n}}$

Подключенное пространство

Каждое произведение семейства связных (соответственно линейно связных) пространств связно (соответственно линейно связно).

Компактный

По теореме Тихонова пространство, отображаемое декартовым произведением, состоящим из любой комбинации компактных пространств, является компактным пространством.

Определение

Когда функция F, определенная на области D является комплексно-дифференцируема в каждой точке D, F называется голоморфная на D. Когда функция f, определенная в области D, удовлетворяет следующим условиям, она является комплексно-дифференцируемой в точке на D ; ${\ displaystyle z ^ {0}}$

Пусть,${\ displaystyle | zz ^ {0} | = | z_ {1} -z_ {1} ^ {0} | + | z_ {2} -z_ {2} ^ {0} | + \ cdots + | z_ {n } -z_ {n} ^ {0} |, \ varepsilon (z, z ^ {0}) = f (z) -f (z ^ {0}) - \ sum _ {\ nu = 1} ^ {n } \ alpha _ {\ nu} (z _ {\ nu} -z _ {\ nu} ^ {0}) \ (\ alpha _ {\ nu} \ in \ mathbb {C})}$

${\ displaystyle \ lim _ {z \ to z ^ {0}} {\ frac {\ varepsilon (z, z ^ {0})} {| zz ^ {0} |}} = 0}$, поскольку они определены однозначно, они называются коэффициентами в частных производных функции f, и каждый записывается как${\ displaystyle \ alpha _ {1}, \ dots, \ alpha _ {n}}$${\ displaystyle {\ frac {\ partial f} {\ partial {\ overline {z}} _ {1}}} (z ^ {0}), \ dots, {\ frac {\ partial f} {\ partial { \ overline {z}} _ {n}}} (z ^ {0})}$

Следовательно, функция f, определенная в области, называется голоморфной, если f удовлетворяет следующим двум условиям. ${\ Displaystyle D \ подмножество \ mathbb {C} ^ {n}}$

1. f непрерывна на D
2. Для каждой переменной, е голоморфен, а именно, ${\ displaystyle z _ {\ nu}}$

   ${\ displaystyle {\ frac {\ partial f} {\ partial {\ overline {z}} _ {\ nu}}} = 0}$

   эти условия называются леммой Осгуда.

Уравнения Коши – Римана

Пусть для каждого индекса ν

${\ displaystyle z _ {\ nu} = x _ {\ nu} + iy _ {\ nu}, \ quad f (z_ {1}, \ dots, z_ {n}) = u (x_ {1}, \ dots, x_ {n}, y_ {1}, \ dots, y_ {n}) + iv (x_ {1}, \ dots, x_ {n}, y_ {1}, \ dots y_ {n}),}$

и обобщив обычное уравнение Коши – Римана для одной переменной для каждого индекса ν, получим

${\ displaystyle {\ frac {\ partial u} {\ partial x _ {\ nu}}} = {\ frac {\ partial v} {\ partial y _ {\ nu}}}, \ \ \ \ {\ frac {\ partial u} {\ partial y _ {\ nu}}} = - {\ frac {\ partial v} {\ partial x _ {\ nu}}}.}.$

Позволять

${\ displaystyle {\ begin {align} dz _ {\ nu} amp;: = dx _ {\ nu} + i \, dy _ {\ nu}, amp; d {\ bar {z}} _ {\ nu} amp;: = dx_ { \ nu} -i \, dy _ {\ nu} \\ {\ frac {\ partial} {\ partial z _ {\ nu}}} amp;: = {\ frac {1} {2}} \ left ({\ frac {\ partial} {\ partial x _ {\ nu}}} - i {\ frac {\ partial} {\ partial y _ {\ nu}}} \ right), amp; {\ frac {\ partial} {\ partial {\ bar {z}} _ {\ nu}}} amp;: = {\ frac {1} {2}} \ left ({\ frac {\ partial} {\ partial x _ {\ nu}}} + i {\ frac {\ partial} {\ partial y _ {\ nu}}} \ right) \ end {align}}}$( Производная Виртингера )

через, пусть будет дельта Кронекера, то есть и если. Затем, как и ожидалось, ${\ displaystyle \ delta _ {\ nu} ^ {\ lambda}}$ ${\ Displaystyle \ дельта _ {\ ню} ^ {\ ню} = 1}$${\ displaystyle \ delta _ {\ nu} ^ {\ lambda} = 0}$${\ displaystyle \ nu \ neq \ lambda}$

${\ displaystyle dz _ {\ nu} \ left ({\ frac {\ partial} {\ partial z _ {\ lambda}}} \ right) = \ delta _ {\ nu} ^ {\ lambda}, dz _ {\ nu} \ left ({\ frac {\ partial} {\ partial {\ bar {z}} _ {\ lambda}}} \ right) = 0, d {\ bar {z}} _ {\ nu} \ left ({ \ frac {\ partial} {\ partial z _ {\ lambda}}} \ right) = 0, d {\ bar {z}} _ {\ nu} \ left ({\ frac {\ partial} {\ partial {\ bar {z}} _ {\ lambda}}} \ right) = \ delta _ {\ nu} ^ {\ lambda}}$

следовательно,

${\ displaystyle {\ frac {\ partial f} {\ partial {\ overline {z}} _ {\ nu}}} = 0 \ (\ nu = 1, \ dots, n)}$

Интегральная формула Коши

е удовлетворяет условиям быть непрерывным и отдельно homorphic на области D. Каждый диск имеет спрямляемую кривую, имеет кусочную гладкость, класс жордановой замкнутой кривой. () Позвольте быть область, окруженная каждым. Декартово закрытие продукта является. Также возьмите полидиск, чтобы он стал. ( и пусть будет центром каждого диска.) Повторно используя интегральную формулу Коши для одной переменной, ${\ displaystyle \ gamma}$${\ displaystyle \ gamma _ {\ nu}}$ ${\ Displaystyle {\ mathcal {C}} ^ {1}}$${\ displaystyle \ nu = 1,2, \ ldots, n}$${\ displaystyle D _ {\ nu}}$${\ displaystyle \ gamma _ {\ nu}}$${\ displaystyle {\ overline {D_ {1} \ times D_ {2} \ times \ cdots \ times D_ {n}}}}$${\ displaystyle {\ overline {D_ {1} \ times D_ {2} \ times \ cdots \ times D_ {n}}} \ in D}$ ${\ displaystyle {\ overline {\ Delta}}}$${\ displaystyle {\ overline {\ Delta}} \ subset {D_ {1} \ times D_ {2} \ times \ cdots \ times D_ {n}}}$${\ displaystyle {\ overline {\ Delta}} (z, r) = \ left \ {\ zeta = (\ zeta _ {1}, \ zeta _ {2}, \ dots, \ zeta _ {n}) \ в \ mathbb {C} ^ {n}; \ left | \ zeta _ {\ nu} -z _ {\ nu} \ right | \ leq r _ {\ nu} {\ text {для всех}} \ nu = 1, \ точки, п \ вправо \}}$${\ Displaystyle \ {г \} _ {\ ню = 1} ^ {п}}$

${\ displaystyle {\ begin {align} f (z_ {1}, \ ldots, z_ {n}) amp; = {\ frac {1} {2 \ pi i}} \ int _ {\ partial D_ {1}} {\ frac {f (\ zeta _ {1}, z_ {2}, \ ldots, z_ {n})} {\ zeta _ {1} -z_ {1}}} \, d \ zeta _ {1} \\ [6pt] amp; = {\ frac {1} {(2 \ pi i) ^ {2}}} \ int _ {\ partial D_ {2}} \, d \ zeta _ {2} \ int _ { \ partial D_ {1}} {\ frac {f (\ zeta _ {1}, \ zeta _ {2}, z_ {3}, \ ldots, z_ {n})} {(\ zeta _ {1} - z_ {1}) (\ zeta _ {2} -z_ {2})}} \, d \ zeta _ {1} \\ [6pt] amp; = {\ frac {1} {(2 \ pi i) ^ {n}}} \ int _ {\ partial D_ {n}} \, d \ zeta _ {n} \ cdots \ int _ {\ partial D_ {2}} \, d \ zeta _ {2} \ int _ {\ partial D_ {1}} {\ frac {f (\ zeta _ {1}, \ zeta _ {2}, \ ldots, \ zeta _ {n})} {(\ zeta _ {1} -z_ { 1}) (\ zeta _ {2} -z_ {2}) \ cdots (\ zeta _ {n} -z_ {n})}} \, d \ zeta _ {1} \ end {align}}}$

Поскольку это спрямляемая иорданова замкнутая кривая, а f является непрерывным, можно поменять порядок произведений и сумм, чтобы повторный интеграл можно было вычислить как кратный интеграл. Следовательно, ${\ displaystyle \ partial D}$

${\ displaystyle f (z_ {1}, \ dots, z_ {n}) = {\ frac {1} {(2 \ pi i) ^ {n}}} \ int _ {\ partial D_ {1}} \ cdots \ int _ {\ partial D_ {n}} {\ frac {f (\ zeta _ {1}, \ dots, \ zeta _ {n})} {(\ zeta _ {1} -z_ {1}) \ cdots (\ zeta _ {n} -z_ {n})}} \, d \ zeta _ {1} \ cdots d \ zeta _ {n}}$

( 1)

Формула оценки Коши

Поскольку порядок произведений и сумм взаимозаменяем, из ( 1) получаем

${\ displaystyle {\ frac {\ partial ^ {k_ {1} + \ cdots + k_ {n}} f (\ zeta _ {1}, \ zeta _ {2}, \ ldots, \ zeta _ {n}) } {\ partial {z_ {1}} ^ {k_ {1}} \ cdots \ partial {z_ {n}} ^ {k_ {n}}}} = {\ frac {k_ {1} \ cdots k_ {n }!} {(2 \ pi i) ^ {n}}} \ int _ {\ partial D_ {1}} \ cdots \ int _ {\ partial D_ {n}} {\ frac {f (\ zeta _ { 1}, \ dots, \ zeta _ {n})} {(\ zeta _ {1} -z_ {1}) ^ {k_ {1} +1} \ cdots (\ zeta _ {n} -z_ {n }) ^ {k_ {n} +1}}} \, d \ zeta _ {1} \ cdots d \ zeta _ {n}.}$

( 2)

f - класс- функция. ${\ Displaystyle {\ mathcal {C}} ^ {\ infty}}$

Из (2), если f голоморфна, на полидиске и получается следующее уравнение оценки. ${\ displaystyle \ left \ {\ zeta = (\ zeta _ {1}, \ zeta _ {2}, \ dots, \ zeta _ {n}) \ in \ mathbb {C} ^ {n}; | \ zeta _ {\ nu} -z _ {\ nu} | \ leq r _ {\ nu}, {\ text {для всех}} \ nu = 1, \ dots, n \ right \}}$${\ Displaystyle | е | \ leq {M}}$

${\ displaystyle \ left | {\ frac {\ partial ^ {k_ {1} + \ cdots + k_ {n}} f (\ zeta _ {1}, \ zeta _ {2}, \ ldots, \ zeta _ { n})} {{\ partial z_ {1}} ^ {k_ {1}} \ cdots \ partial {z_ {n}} ^ {k_ {n}}}} \ right | \ leq {\ frac {Mk_ { 1} \ cdots k_ {n}!} {{R_ {1}} ^ {k_ {1}} \ cdots {r_ {n}} ^ {k_ {n}}}}}$

Следовательно, теорема Лиувилля верна.

Разложение голоморфных функций в степенной ряд на полидиске

Если функция f голоморфна на полидиске из интегральной формулы Коши, мы видим, что ее можно однозначно разложить до следующего степенного ряда. ${\ displaystyle \ {z = (z_ {1}, z_ {2}, \ dots, z_ {n}) \ in \ mathbb {C} ^ {n}; | z _ {\ nu} -a _ {\ nu} | lt;r _ {\ nu}, {\ text {для всех}} \ nu = 1, \ dots, n \}}$

${\ displaystyle {\ begin {align} amp; f (z) = \ sum _ {k_ {1}, \ dots, k_ {n} = 0} ^ {\ infty} c_ {k_ {1}, \ dots, k_ { n}} (z_ {1} -a_ {1}) ^ {k_ {1}} \ cdots (z_ {n} -a_ {n}) ^ {k_ {n}} \, \\ amp; c_ {k_ {1 } \ cdots k_ {n}} = {\ frac {1} {(2 \ pi i) ^ {n}}} \ int _ {\ partial D_ {1}} \ cdots \ int _ {\ partial D_ {n }} {\ frac {f (\ zeta _ {1}, \ dots, \ zeta _ {n})} {(\ zeta _ {1} -a_ {1}) ^ {k_ {1} +1} \ cdots (\ zeta _ {n} -a_ {n}) ^ {k_ {n} +1}}} \, d \ zeta _ {1} \ cdots d \ zeta _ {n} \ end {выровнено}}}$

Кроме того, функция f, удовлетворяющая следующим условиям, называется аналитической функцией.

Для каждой точки, выражается в виде разложения в ряд, который сходится на D  : ${\ displaystyle a = (a_ {1}, \ dots, a_ {n}) \ in D \ subset \ mathbb {C} ^ {n}}$${\ displaystyle f (z)}$

${\ displaystyle f (z) = \ sum _ {k_ {1}, \ dots, k_ {n} = 0} ^ {\ infty} c_ {k_ {1}, \ dots, k_ {n}} (z_ { 1} -a_ {1}) ^ {k_ {1}} \ cdots (z_ {n} -a_ {n}) ^ {k_ {n}} \,}$

Мы уже объясняли, что голоморфные функции на полидиске аналитичны. Кроме того, из теоремы, полученной Вейерштрассом, мы можем видеть, что аналитическая функция на полидиске (сходящийся степенной ряд) голоморфна.

Если последовательность функций, которая сходится равномерно на компактах внутри области D, предельная функция F из также равномерно на компактах внутри области D. Кроме того, соответствующая частная производная функции также компактно сходится в области D к соответствующей производной функции f.${\ displaystyle f_ {1}, \ ldots, f_ {n}}$${\ displaystyle f_ {v}}$${\ displaystyle f_ {v}}$

${\ displaystyle {\ frac {\ partial ^ {k_ {1} + \ cdots + k_ {n}} f} {\ partial {z_ {1}} ^ {k_ {1}} \ cdots \ partial {z_ {n) }} ^ {k_ {n}}}} = \ sum _ {v = 1} ^ {\ infty} {\ frac {\ partial ^ {k_ {1} + \ cdots + k_ {n}} f_ {v} } {\ partial {z_ {1}} ^ {k_ {1}} \ cdots \ partial {z_ {n}} ^ {k_ {n}}}}}$

Радиус сходимости степенного ряда

Можно определить комбинацию положительных действительных чисел так, чтобы степенной ряд сходился равномерно в точке и не сходился равномерно в точке. ${\ Displaystyle \ {г _ {\ ню} \ (\ ню = 1, \ точки, п) \}}$${\ textstyle \ sum _ {k_ {1}, \ dots, k_ {n} = 0} ^ {\ infty} c_ {k_ {1}, \ dots, k_ {n}} (z_ {1} -a_ { 1}) ^ {k_ {1}} \ cdots (z_ {n} -a_ {n}) ^ {k_ {n}} \}$${\ displaystyle \ left \ {z = (z_ {1}, z_ {2}, \ dots, z_ {n}) \ in \ mathbb {C} ^ {n}; | z _ {\ nu} -a _ {\ nu} | lt;r _ {\ nu}, {\ text {для всех}} \ nu = 1, \ dots, n \ right \}}$${\ displaystyle \ left \ {z = (z_ {1}, z_ {2}, \ dots, z_ {n}) \ in \ mathbb {C} ^ {n}; | z _ {\ nu} -a _ {\ nu} |gt; r _ {\ nu}, {\ text {для всех}} \ nu = 1, \ dots, n \ right \}}$

Таким образом, можно получить аналогичную комбинацию радиуса сходимости для одной комплексной переменной. Эта комбинация, как правило, не уникальна, и существует бесконечное количество комбинаций.

Расширение серии Laurent

Пусть голоморфны в кольце и непрерывны на своей окружности, тогда существует следующее разложение; ${\ Displaystyle \ omega (г)}$ ${\ displaystyle \ left \ {z = (z_ {1}, z_ {2}, \ dots, z_ {n}) \ in \ mathbb {C} ^ {n}; r _ {\ nu} lt;| z | lt; R _ {\ nu}, {\ text {для всех}} \ nu +1, \ dots, n \ right \}}$

${\ displaystyle \ omega (z) = \ sum _ {k = 0} ^ {\ infty} {\ frac {1} {k!}} {\ frac {1} {(2 \ pi i) ^ {n} }} \ int _ {| \ zeta _ {\ nu} | = R _ {\ nu}} \ cdots \ int \ omega (\ zeta) \ times \ left [{\ frac {d ^ {k}} {dz ^ {k}}} {\ frac {1} {\ zeta -z}} \ right] _ {z = 0} df _ {\ zeta} \ cdot z ^ {k} + \ sum _ {k = 1} ^ { \ infty} {\ frac {1} {k!}} {\ frac {1} {2 \ pi i}} \ int _ {| \ zeta _ {\ nu} | = r _ {\ nu}} \ cdots \ int \ omega (\ zeta) \ times \ left (0, \ cdots, {\ sqrt {\ frac {k!} {\ alpha _ {1}! \ cdots \ alpha _ {n}!}}} \ cdot \ zeta _ {n} ^ {\ alpha _ {1} -1} \ cdots \ zeta _ {n} ^ {\ alpha _ {n} -1}, \ cdots 0 \ right) df _ {\ zeta} \ cdot { \ frac {1} {z ^ {k}}} \ (\ alpha _ {1} + \ cdots + \ alpha _ {n} = k)}$

Интеграл во втором члене правой части выполняется так, чтобы слева был виден нуль в каждой плоскости, также этот интегрированный ряд равномерно сходится в кольце, где и, поэтому можно проинтегрировать член. ${\ displaystyle r '_ {\ nu} lt;| z | lt;R' _ {\ nu}}$${\ displaystyle r '_ {\ nu}gt; r _ {\ nu}}$${\ Displaystyle R '_ {\ nu} lt;R _ {\ nu}}$

Формула Бохнера – Мартинелли

Интегральная формула Коши верна только для полидисков, а в области нескольких комплексных переменных полидиски являются лишь одной из многих областей, поэтому мы вводим формулу Бохнера – Мартинелли.

Предположим, что f - непрерывно дифференцируемая функция на замыкании области D на кусочно-гладкой границе. Тогда формула состояния Бохнеру Martinelli, что если г находится в области D, то для, г в ядре Бохнера-Мартинелли является дифференциальная форма в бистепени определяется ${\ displaystyle \ mathbb {C} ^ {n}}$${\ displaystyle \ partial D}$${\ displaystyle \ zeta}$${\ displaystyle \ mathbb {C} ^ {n}}$${\ Displaystyle \ омега (\ дзета, г)}$ ${\ displaystyle \ zeta}$${\ Displaystyle (п, п-1)}$

${\ displaystyle \ omega (\ zeta, z) = {\ frac {(n-1)!} {(2 \ pi i) ^ {n}}} {\ frac {1} {| z- \ zeta | ^ {2n}}} \ sum _ {1 \ leq j \ leq n} ({\ overline {\ zeta}} _ {j} - {\ overline {z}} _ {j}) \, d {\ overline { \ zeta}} _ {1} \ land d \ zeta _ {1} \ land \ cdots \ land d \ zeta _ {j} \ land \ cdots \ land d {\ overline {\ zeta}} _ {n} \ земля d \ zeta _ {n}}$

${\ Displaystyle \ Displaystyle е (z) = \ int _ {\ partial D} f (\ zeta) \ omega (\ zeta, z) - \ int _ {D} {\ overline {\ partial}} f (\ zeta) \ земля \ omega (\ zeta, z).}$

В частности, если f голоморфна, второй член обращается в нуль, поэтому

${\ displaystyle \ displaystyle f (z) = \ int _ {\ partial D} f (\ zeta) \ omega (\ zeta, z).}$

Теорема тождества

Когда функция f, g аналитична в области D, даже для нескольких комплексных переменных, теорема тождества верна в области D, поскольку она имеет степенное разложение в окрестности точки аналитики. Следовательно, выполняется принцип максимума. Кроме того, теорема об обратной функции и теорема о неявной функции удержания.

Биголоморфизм

Из утверждения теоремы об обратной функции можно определить следующее отображение.

Для области U, V n- мерного комплексного пространства биективная голоморфная функция и обратное отображение также голоморфны. В это время, называемый также биголоморфизмом U, V, мы говорим, что U и V биголоморфно эквивалентны или что они биголоморфны. ${\ displaystyle \ mathbb {C} ^ {n}}$${\ displaystyle \ phi: V \ to U}$${\ displaystyle \ phi ^ {- 1}: от V \ до U}$${\ displaystyle \ phi}$

Теорема Римана об отображении не выполняется

Когда открытые шары и открытые полидиски не биголоморфно эквивалентны, то есть между ними нет биголоморфного отображения. Это было доказано Пуанкаре в 1907 году, показав, что их группы автоморфизмов имеют разные размерности, как группы Ли. ${\ displaystyle ngt; 1}$

Аналитическое продолжение

Пусть U, V - область на, и. Предположим, что и является компонентой связности из. Если тогда говорят, что f связана с V, а g называется аналитическим продолжением f. Из теоремы тождества, если g существует, для каждого способа выбора w он единственен. Следует рассмотреть вопрос о том, правильно ли определено определение этого аналитического продолжения, можно ли определить области U, V и W произвольно. Некоторые комплексные переменные имеют ограничения на эту область, и в зависимости от формы области все аналитические функции g, принадлежащие V, связаны с, и может не существовать функция g с естественной границей. Другими словами, V нельзя определить произвольно. Это называется феноменом Хартогов. Таким образом, исследование того, когда границы домена становятся естественными границами, стало одной из основных тем исследования нескольких сложных переменных. Кроме того, в общем измерении между U и V может быть несколько пересечений. То есть f связана не как однозначная голоморфная функция, а как многозначная аналитическая функция. Это означает, что W не уникален и имеет другие свойства в окрестности точки ветвления, чем в случае одной переменной. ${\ displaystyle \ mathbb {C} ^ {n}}$${\ displaystyle f \ in {\ mathcal {O}} (U)}$${\ displaystyle g \ in {\ mathcal {O}} (V)}$${\ Displaystyle U, V, U \ cap V \ neq \ varnothing}$${\ displaystyle W}$ ${\ Displaystyle U \ cap V}$${\ displaystyle f | _ {W} = g | _ {W}}$${\ Displaystyle V \ подмножество D}$${\ displaystyle \ partial V}$

В полидисках и области Рейнхардта выполняется интегральная формула Коши и определено разложение голоморфных функций в степенной ряд, но уникальный радиус сходимости не определен для каждой переменной. Кроме того, поскольку теорема об отображении Римана не выполняется, полидиски и открытые единичные шары не являются биголоморфными отображениями. Следовательно, область сходимости степенного ряда не так проста, как случай одной переменной, но она удовлетворяет свойству, называемому логарифмически-выпуклым. Существуют различные выпуклости области сходимости нескольких комплексных переменных.

Домен D в комплексе координатного пространства, с центром в точке, со следующим свойством; Вместе с каждой точкой в домен также входит множество ${\ displaystyle \ mathbb {C} ^ {n}}$${\ Displaystyle п \ geq 1}$${\ displaystyle a = (a_ {1}, \ dots, a_ {n}) \ in \ mathbb {C} ^ {n}}$${\ displaystyle z ^ {0} = (z_ {1} ^ {0}, \ dots, z_ {n} ^ {0}) \ in D}$

${\ displaystyle \ left \ {z = (z_ {1}, \ dots, z_ {n}); \ left | z _ {\ nu} -a _ {\ nu} \ right | = \ left | z _ {\ nu} ^ {0} -a _ {\ nu} \ right |, \ \ nu = 1, \ dots, n \ right \}.}$

Реинхардт домен D с инвариантен относительно преобразований,,. Домены Рейнхардта составляют подкласс доменов Хартогса и подкласс круговых доменов, которые определяются следующим условием; Вместе со всеми точками область содержит множество ${\ displaystyle a = 0}$${\ displaystyle \ left \ {z ^ {0} \ right \} \ to \ left \ {z _ {\ nu} ^ {0} e ^ {я \ theta _ {\ nu}} \ right \}}$${\ Displaystyle 0 \ Leq \ theta _ {\ nu} lt;2 \ pi}$${\ Displaystyle \ Nu = 1, \ точки, п}$${\ displaystyle z ^ {0} \ in D}$

${\ displaystyle \ left \ {z = (z_ {1}, \ dots, z_ {n}); z = a + \ left (z ^ {0} -a \ right) e ^ {i \ theta}, \ 0 \ leq \ theta lt;2 \ pi \ right \},}$

т.е. все точки окружности с центром и радиусом, лежащие на комплексной прямой, проходящей через и. ${\ displaystyle a}$${\ textstyle \ left | z ^ {0} -a \ right | = \ left (\ sum _ {\ nu = 1} ^ {n} \ left | z _ {\ nu} ^ {0} -a _ {\ nu } \ right | ^ {2} \ right) ^ {\ frac {1} {2}}}$${\ displaystyle a}$${\ displaystyle z ^ {0}}$

Область Рейнхардта D называется полной областью Рейнхардта, если вместе со всей точкой она также содержит полидиск ${\ displaystyle z ^ {0} \ in D}$

${\ displaystyle \ left \ {z = (z_ {1}, \ dots, z_ {n}); \ left | z _ {\ nu} -a _ {\ nu} \ right | \ leq \ left | z _ {\ nu } ^ {0} -a _ {\ nu} \ right |, \ \ nu = 1, \ dots, n \ right \}.}$

Полная область Рейнхардта звездообразна относительно своего центра a. Следовательно, полная область Рейнхардта односвязна, также, когда полная область Рейнхардта является граничной линией, есть способ доказать интегральную теорему Коши без использования теоремы Жордана.

Логарифмически-выпуклый

Область Рейнхардта D называется логарифмически выпуклой, если образ множества ${\ displaystyle \ lambda (D ^ {*})}$

${\ displaystyle D ^ {*} = \ {z = (z_ {1}, \ dots, z_ {n}) \ in D; z_ {1}, \ dots, z_ {n} \ neq 0 \}}$

под отображением

${\ displaystyle \ lambda; z \ rightarrow \ lambda (z) = (\ ln | z_ {1} |, \ точки, \ ln | z_ {n} |)}$

является выпуклым множеством в вещественном координатном пространстве. ${\ Displaystyle \ mathbb {R} ^ {п}}$

Каждая такая область в является внутренней частью множества точек абсолютной сходимости (т. Е. Области сходимости) некоторого степенного ряда в, и наоборот; Область сходимости каждого степенного ряда в является логарифмически выпуклой областью Рейнхардта с центром. ${\ displaystyle \ mathbb {C} ^ {n}}$${\ textstyle \ sum _ {k_ {1}, \ dots, k_ {n} = 0} ^ {\ infty} c_ {k_ {1}, \ dots, k_ {n}} (z_ {1} -a_ { 1}) ^ {k_ {1}} \ cdots (z_ {n} -a_ {n}) ^ {k_ {n}} \}$${\ displaystyle z_ {1}, \ dots, z_ {n}}$${\ displaystyle a = 0}$

Некоторые результаты

Теорема Хартогса о продолжении и феномен Хартогса

Изучая область сходимости в области Рейнхардта, Хартогс обнаружил феномен Хартогса, в котором все голоморфные функции в некоторой области в области связаны с большей областью. ${\ displaystyle \ mathbb {C} ^ {n}}$

На полидиске, состоящем из двух дисков, когда.${\ Displaystyle \ Delta ^ {2} = \ {z \ in \ mathbb {C} ^ {2}; | z_ {1} | lt;1, | z_ {2} | lt;1 \}}$${\ Displaystyle 0 lt;\ varepsilon lt;1}$

Внутренний домен ${\ Displaystyle H _ {\ varepsilon} = \ {z = (z_ {1}, z_ {2}) \ in \ Delta ^ {2}; | z_ {1} | lt;\ varepsilon \ \ cup \ 1- \ varepsilon lt;| z_ {2} | \} \ (0 lt;\ varepsilon lt;1)}$

Теорема Хартогса о продолжении (1906 г.); Пусть F быть голоморфная функция на множестве G  \  K, где G представляет собой ограниченную (окруженный замкнутой спрямляемой жордановой кривой) на домен ( п ≥ 2) и К представляет собой компактное подмножество G. Если дополнение G  \  K связно, то любая голоморфная функция F независимо от того, как она может быть выбрана каждым распространяются на уникальную голоморфную функцию на G.${\ displaystyle \ mathbb {C} ^ {n}}$

Ее также называют теоремой Осгуда – Брауна, заключающейся в том, что для голоморфных функций нескольких комплексных переменных особенность является точкой накопления, а не изолированной точкой. Это означает, что различные свойства, которые выполняются для голоморфных функций комплексных переменных одной переменной, не выполняются для голоморфных функций нескольких комплексных переменных. Природа этих особенностей также выводится из подготовительной теоремы Вейерштрасса. Обобщение этой теоремы с использованием того же метода, что и Хартогс, было доказано в 2007 году.

Согласно теореме Хартогса о расширении область сходимости простирается от до. Если посмотреть на это с точки зрения области Рейнхардта, это область Рейнхардта, содержащая центр z = 0, а область сходимости была расширена до наименьшей полной области Рейнхардта, содержащей. ${\ displaystyle H _ {\ varepsilon}}$${\ displaystyle \ Delta ^ {2}}$${\ displaystyle H _ {\ varepsilon}}$${\ displaystyle H _ {\ varepsilon}}$${\ displaystyle \ Delta ^ {2}}$${\ displaystyle H _ {\ varepsilon}}$

Классические результаты Таллена

Классический результат Таллена гласит, что двумерная ограниченная область Рейнхарда, содержащая начало координат, является биголоморфной одной из следующих областей при условии, что орбита начала координат группы автоморфизмов имеет положительную размерность:

1. ${\ displaystyle \ {(z, w) \ in \ mathbb {C} ^ {2}; ~ | z | lt;1, ~ | w | lt;1 \}}$ (полидиск);
2. ${\ displaystyle \ {(z, w) \ in \ mathbb {C} ^ {2}; ~ | z | ^ {2} + | w | ^ {2} lt;1 \}}$ (единичный шар);
3. ${\ displaystyle \ {(z, w) \ in \ mathbb {C} ^ {2}; ~ | z | ^ {2} + | w | ^ {\ frac {2} {p}} lt;1 \} ( pgt; 0, \ neq 1)}$ (Домен Таллен).

Результаты Сунады

Тошиказу Сунада (1978) обобщил результат Таллена:

Две n -мерные ограниченные области Рейнхардта и взаимно биголоморфны тогда и только тогда, когда существует преобразование, заданное формулой, являющееся перестановкой индексов), такое что.${\ displaystyle G_ {1}}$${\ displaystyle G_ {2}}$${\ displaystyle \ varphi: \ mathbb {C} ^ {n} \ to \ mathbb {C} ^ {n}}$${\ Displaystyle z_ {я} \ mapsto r_ {i} z _ {\ sigma (i)} (r_ {i}gt; 0)}$${\ displaystyle \ sigma}$${\ Displaystyle \ varphi (G_ {1}) = G_ {2}}$

При переходе от теории одной комплексной переменной к теории нескольких комплексных переменных, в зависимости от диапазона области, может оказаться невозможным определить голоморфную функцию так, чтобы граница области стала естественной границей. Рассматривая домен, где границы области являются естественными границами (в комплексном пространстве координат вызова области голоморфности), первым результатом области голоморфности была голоморфная выпуклость H. Картан и Таллен. Проблема Леви показывает, что псевдовыпуклая область была областью голоморфности. (Первая для позже продлены до.) Киосите Око понятия «х idéal де Domaines indéterminés интерпретируются пучок когомологий с помощью H. Картан. В когомологиях пучков область голоморфности стала интерпретироваться как теория многообразий Штейна. Понятие области голоморфности также рассматривается в других комплексных многообразиях, кроме того, также в комплексном аналитическом пространстве, которое является его обобщением. ${\ displaystyle \ mathbb {C} ^ {n}}$${\ Displaystyle \ mathbb {C} ^ {2}}$${\ displaystyle \ mathbb {C} ^ {n}}$

Область голоморфности

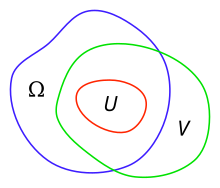
Наборы в определении. Примечание: в этом разделе заменить на рисунке буквой D.${\ displaystyle \ Omega}$

Когда функция f голоморфна в области и не может напрямую соединиться с областью вне D, включая точку границы области, область D называется областью голоморфности f, а граница называется естественной границей f. Другими словами, область голоморфности D - это верхняя грань области, в которой голоморфная функция f голоморфна, а область D, которая голоморфна, больше не может быть расширена. Для нескольких сложных переменных, то есть области, границы могут не быть естественными границами. Теорема Хартогса о расширении дает пример области, где границы не являются естественными границами. ${\ Displaystyle D \ подмножество \ mathbb {C} ^ {n}}$${\ displaystyle \ partial D}$${\ Displaystyle D \ подмножество \ mathbb {C} ^ {n} \ (п \ geq 2)}$

Формально, область D в п - мерном комплексном пространстве координат называется областью голоморфности, если не существует непустой домен и, и таким образом, что для каждой голоморфной функции F на D существует голоморфная функция г на V с на U. ${\ displaystyle \ mathbb {C} ^ {n}}$${\ Displaystyle U \ подмножество D}$${\ Displaystyle V \ подмножество \ mathbb {C} ^ {n}}$${\ Displaystyle V \ not \ subset D}$${\ Displaystyle U \ подмножество D \ cap V}$${\ displaystyle f = g}$

В этом случае каждая область () была областью голоморфности; мы можем определить голоморфную функцию с нулями, накапливающимися повсюду на границе области, которая в таком случае должна быть естественной границей для области определения ее обратной величины. ${\ displaystyle n = 1}$${\ Displaystyle D \ подмножество \ mathbb {C}}$

Свойства области голоморфности

• Если - области голоморфности, то их пересечение также является областью голоморфности.${\ displaystyle D_ {1}, \ dots, D_ {n}}$${\ textstyle D = \ bigcap _ {\ nu = 1} ^ {n} D _ {\ nu}}$
• Если - возрастающая последовательность областей голоморфности, то их объединение также является областью голоморфности (см. Теорему Бенке – Стейна ).${\ Displaystyle D_ {1} \ substeq D_ {2} \ substeq \ cdots}$${\ textstyle D = \ bigcup _ {n = 1} ^ {\ infty} D_ {n}}$
• Если и - области голоморфности, то - область голоморфности.${\ displaystyle D_ {1}}$${\ displaystyle D_ {2}}$${\ displaystyle D_ {1} \ times D_ {2}}$
• Первая проблема Кузена всегда разрешима в области голоморфности, также Картан показал, что обратное к этому результату неверно для. это также верно, с дополнительными топологическими предположениями, для троюродной проблемы.${\ Displaystyle п \ geq 3}$

Голоморфно выпуклая оболочка

Позвольте быть областью, или, альтернативно, для более общего определения, пусть будет размерным комплексным аналитическим многообразием. Пусть, далее обозначим множество голоморфных функций на G. Для компакта, то голоморфно выпуклая оболочка из K является ${\ Displaystyle G \ подмножество \ mathbb {C} ^ {n}}$${\ displaystyle G}$${\ displaystyle n}$ ${\ Displaystyle {\ mathcal {O}} (G)}$${\ Displaystyle K \ подмножество G}$

${\ displaystyle {\ hat {K}} _ {G}: = \ left \ {z \ in G; | f (z) | \ leq \ sup _ {w \ in K} | f (w) | {\ text {для всех}} f \ in {\ mathcal {O}} (G). \ right \}.}$

Получает понятие более узкое из полиномиально выпуклой оболочки, взяв вместо того, чтобы быть множество комплекснозначных полиномиальных функций на G. Полиномиально выпуклая оболочка содержит голоморфно выпуклую оболочку. ${\ Displaystyle {\ mathcal {O}} (G)}$

Домен называется голоморфно выпуклым, если для любого компакта также компактно в G. Иногда это сокращенно называют голоморфно-выпуклым. ${\ displaystyle G}$${\ displaystyle K, {\ hat {K}} _ {G}}$

Когда, каждая область является голоморфно выпуклой, поскольку тогда является объединением K с относительно компактными компонентами. ${\ displaystyle n = 1}$${\ displaystyle G}$${\ displaystyle {\ hat {K}} _ {G}}$${\ displaystyle G \ setminus K \ subset G}$

Когда, если f удовлетворяет указанной выше голоморфно выпуклости на D, она обладает следующими свойствами. для любого компакта K в D, где обозначает расстояние между K и. Кроме того, в это время D является областью голоморфности. Следовательно, любая выпуклая область является областью голоморфности. ${\ Displaystyle п \ geq 1}$${\ displaystyle {\ text {dist}} (K, D ^ {c}) = {\ text {dist}} ({\ hat {K}} _ {D}, D ^ {c})}$${\ displaystyle {\ text {dist}} (K, D ^ {c})}$${\ Displaystyle D ^ {c} = \ mathbb {C} ^ {n} \ setminus D}$${\ Displaystyle (D \ подмножество \ mathbb {C} ^ {n})}$

Выпуклый Леви (аппроксимация изнутри на аналитической многогранной области)

${\ textstyle \ bigcup _ {n = 1} ^ {\ infty} S_ {n} \ substeq D}$есть объединение возрастающей последовательности аналитических компактных поверхностей с паракомпактными и голоморфно выпуклыми свойствами такими, что. т.е. аппроксимировать изнутри аналитическим многогранником. ${\ textstyle \ bigcup _ {n = 1} ^ {\ infty} S_ {n} \ rightarrow D, S_ {n} \ подмножество S_ {n + 1}}$

Псевдовыпуклый

Псевдовыпуклый Хартогс показал, что это субгармонично для радиуса сходимости в ряду Хартогса, когда ряд Хартогса является одной переменной. Если такое соотношение выполняется в области голоморфности нескольких комплексных переменных, оно выглядит более управляемым условием, чем голоморфно выпуклое. В субгармонической функции выглядит как вид выпуклой функции, поэтому он был назван Леви как домен псевдовыпуклого. Псевдовыпуклые области важны, поскольку они позволяют классифицировать области голоморфности. ${\ displaystyle - \ log R}$${\ displaystyle R (z)}$${\ Displaystyle е (г, \ омега), \ \ омега = 0}$

Определение плюрисубгармонической функции

Функция

${\ Displaystyle е \ двоеточие D \ к {\ mathbb {R}} \ чашка \ {- \ infty \},}$

с доменом ${\ Displaystyle D \ подмножество {\ mathbb {C}} ^ {п}}$

называется плюрисубгармонической, если она полунепрерывна сверху, и для каждой комплексной прямой

${\ displaystyle \ {a + bz; z \ in \ mathbb {C} \} \ subset \ mathbb {C} ^ {n}}$ с участием ${\ displaystyle a, b \ in \ mathbb {C} ^ {n}}$

функция является субгармонической функцией на множестве${\ displaystyle z \ mapsto f (a + bz)}$

${\ displaystyle \ {z \ in \ mathbb {C}; a + bz \ in D \}.}$

В полной общности это понятие может быть определено на произвольном комплексном многообразии или даже на комплексном аналитическом пространстве следующим образом. Полунепрерывная сверху функция ${\ displaystyle X}$

${\ displaystyle f \ двоеточие X \ to \ mathbb {R} \ cup \ {- \ infty \}}$

называется плюрисубгармоническим тогда и только тогда, когда для любого голоморфного отображения

${\ Displaystyle \ varphi \ двоеточие \ Delta \ to X}$ функция

${\ displaystyle f \ circ \ varphi \ двоеточие \ Delta \ to \ mathbb {R} \ cup \ {- \ infty \}}$

является субгармоническим, где обозначает единичный круг. ${\ displaystyle \ Delta \ subset \ mathbb {C}}$

В одной комплексной переменной необходимым и достаточным условием субгармоничности вещественной функции, которая может быть дифференцируемой второго порядка по z по z одной комплексной функции, является. Следовательно, если имеет класс, то плюрисубгармонична тогда и только тогда, когда эрмитова матрица положительно полуопределенная. ${\ Displaystyle и = и (г)}$${\ displaystyle \ Delta = 4 \ left ({\ frac {\ partial ^ {2} u} {\ partial z \, \ partial {\ overline {z}}}} \ right) \ geq 0}$${\ displaystyle u}$${\ Displaystyle {\ mathcal {C}} ^ {2}}$${\ displaystyle u}$ ${\ displaystyle H_ {u} = (\ lambda _ {ij}), \ lambda _ {ij} = {\ frac {\ partial ^ {2} u} {\ partial z_ {i} \, \ partial {\ bar {z}} _ {j}}}}$

Эквивалентно, -функция u является плюрисубгармонической тогда и только тогда, когда является положительной (1,1) -формой. ${\ displaystyle C ^ {2}}$${\ displaystyle {\ sqrt {-1}} \ partial {\ bar {\ partial}} f}$

Строго плюрисубгармоническая функция

Когда эрмитова матрица u положительно определена и классна, мы называем u строгой плюрисубгармонической функцией. ${\ Displaystyle {\ mathcal {C}} ^ {2}}$

(Слабо) псевдовыпуклый (p-псевдовыпуклый)

Слабая псевдовыпуклая определяется как: Позвольте быть доменом. Один говорит, что X является псевдовыпукла, если существует непрерывная плюрисубгармоническая функция на X такая, что множество является относительно компактным подмножеством X для всех действительных чисел х. т.е. существует гладкая плюрисубгармоническая функция исчерпания. Часто здесь используется определение псевдовыпукла, которое записывается как; Пусть X - комплексное n -мерное многообразие. Тогда называется слабовыпуклой, существует гладкая плюрисубгармоническая функция исчерпания. ${\ Displaystyle X \ подмножество {\ mathbb {C}} ^ {n}}$ ${\ displaystyle \ varphi}$${\ Displaystyle \ {г \ в Икс; \ varphi (г) \ leq \ sup х \}}$ ${\ displaystyle \ psi \ in {\ text {Psh}} (X) \ cap {\ mathcal {C}} ^ {\ infty} (X)}$${\ displaystyle \ psi \ in {\ text {Psh}} (X) \ cap {\ mathcal {C}} ^ {\ infty} (X)}$

Сильно (строго) псевдовыпуклые

Пусть X - комплексное n -мерное многообразие. Сильно псевдовыпуклая, если существует гладкая строго плюрисубгармоническая функция исчерпания, т. Е. Положительно определена в каждой точке. Сильно псевдовыпуклый домен - это псевдовыпуклый домен. Сильная псевдовыпуклая область Леви называется просто сильной псевдовыпуклой и часто называется строго псевдовыпуклой, чтобы прояснить, что она имеет строго плюрисубгармоническую функцию исчерпания в связи с тем фактом, что она может не иметь строго плюрисубгармонической функции исчерпания. ${\ displaystyle \ psi \ in {\ text {Psh}} (X) \ cap {\ mathcal {C}} ^ {\ infty} (X)}$${\ displaystyle H \ psi}$

(Слабо) псевдовыпуклость Леви (–Кшоски)

Если граница, можно показать, что D имеет определяющую функцию; то есть, что существует что так, что и. Теперь D псевдовыпукло тогда и только тогда, когда для каждого и в комплексном касательном пространстве в точке p, то есть ${\ Displaystyle {\ mathcal {C}} ^ {2}}$${\ displaystyle \ rho: \ mathbb {C} ^ {n} \ to \ mathbb {R}}$${\ Displaystyle {\ mathcal {C}} ^ {2}}$${\ Displaystyle D = \ {\ rho lt;0 \}}$${\ displaystyle \ partial D = \ {\ rho = 0 \}}$${\ displaystyle p \ in \ partial D}$${\ displaystyle w}$

${\ displaystyle \ nabla \ rho (p) w = \ sum _ {i = 1} ^ {n} {\ frac {\ partial \ rho (p)} {\ partial z_ {j}}} w_ {j} = 0}$, у нас есть

${\ Displaystyle H (\ rho) = \ sum _ {i, j = 1} ^ {n} {\ frac {\ partial ^ {2} \ rho (p)} {\ partial z_ {i} \, \ partial {\ bar {z_ {j}}}}} w_ {i} {\ bar {w_ {j}}} \ geq 0.}$

Для произвольного комплексного многообразия псевдовыпуклость Леви (–Кшоски) не всегда имеет плюрисубгармоническую функцию исчерпания, т.е. не обязательно имеет (p-) псевдовыпуклую область.

Если D не имеет границы, может быть полезен следующий результат аппроксимации. ${\ Displaystyle {\ mathcal {C}} ^ {2}}$

Предложение 1 Если D псевдовыпукло, то существуют ограниченные, сильно псевдовыпуклые области Леви с -границей классов, относительно компактные в${\ displaystyle D_ {k} \ subset D}$${\ Displaystyle {\ mathcal {C}} ^ {\ infty}}$ D, такие, что

${\ displaystyle D = \ bigcup _ {k = 1} ^ {\ infty} D_ {k}.}$

Это связано с тем, что, имея as в определении, мы фактически можем найти функцию исчерпания. ${\ displaystyle \ varphi}$${\ Displaystyle {\ mathcal {C}} ^ {\ infty}}$

Сильно псевдовыпуклая (–Krzoska) псевдовыпуклость (Сильно псевдовыпуклая)

Когда форма Леви (–Krzoska) положительно определена, ее называют сильно псевдовыпуклой формой Леви (–Krzoska) или просто сильно псевдовыпуклой.

Леви тотальная псевдовыпуклая

Если для каждой граничной точки из D, существует аналитическое многообразие прохождения, которое лежит полностью вне D в некоторых окрестностях вокруг, кроме точки самого. Область D, удовлетворяющая этим условиям, называется псевдовыпуклой тотальной Леви. ${\ displaystyle \ rho}$ ${\ displaystyle {\ mathcal {B}}}$${\ displaystyle \ rho}$${\ displaystyle \ rho}$${\ displaystyle \ rho}$

Ока псевдовыпуклая

Семейство диска Оки

Пусть n -функции непрерывны на, голоморфны в, когда параметр t фиксирован в [0, 1], и предположим, что не все равны нулю в любой точке на. Тогда множество называется аналитическим диском, зависящим от параметра t, и называется его оболочкой. Если и, Q (t) называется семейством диска Оки. ${\ displaystyle \ varphi: z_ {j} = \ varphi _ {j} (u, t)}$${\ Displaystyle \ Delta: | U | \ leq 1,0 \ leq t \ leq 1}$${\ displaystyle | u | lt;1}$${\ displaystyle {\ frac {\ partial \ varphi _ {j}} {\ partial u}}}$${\ displaystyle \ Delta}$${\ Displaystyle Q (t): = \ {Z_ {j} = \ varphi _ {j} (u, t); | u | \ leq 1 \}}$${\ Displaystyle B (t): = \ {Z_ {j} = \ varphi _ {j} (u, t); | u | = 1 \}}$${\ Displaystyle Q (t) \ подмножество D \ (0 lt;t)}$${\ Displaystyle В (0) \ подмножество D}$

Определение

Когда держится на любом семействе диска Оки, D называется псевдовыпуклой Ока. Доказательство Ока проблемы Леви заключалось в том, что, когда неразветвленная риманова область была областью голоморфности (голоморфно выпуклой), было доказано, что было необходимо и достаточно, чтобы каждая граничная точка области голоморфности была псевдовыпуклой Ока. ${\ Displaystyle Q (0) \ подмножество D}$

Локально псевдовыпуклые (локально Штейна, псевдовыпуклые Картана, локально свойство Леви)

Для каждой точки существует окрестность U от й и ф голоморфно. (т. е. быть голоморфно выпуклым.) такая, что f не может быть продолжена ни в какую окрестность x. т.е. голоморфное отображение будет называться локально псевдовыпуклым, если каждая точка имеет такую ​​окрестность U, которая является штейновой (слабо 1-полной). В этой ситуации мы также будем говорить, что X является локально псевдовыпуклым над Y. Это также называлось локально Штейном, а классически - псевдовыпуклым Картаном. В клокалли псевдовыпуклый домен сам по себе является псевдовыпуклым доменом и является областью голоморфности. ${\ Displaystyle х \ в \ частичном D}$${\ Displaystyle U \ cap D}$${\ displaystyle \ psi: от X \ до Y}$${\ displaystyle y \ in Y}$${\ Displaystyle \ psi ^ {- 1} (U)}$${\ displaystyle \ mathbb {C} ^ {n}}$

Условия, эквивалентные области голоморфности

Для домена следующие условия эквивалентны: ${\ Displaystyle D \ подмножество \ mathbb {C} ^ {n}}$

1. D - область голоморфности.
2. D голоморфно выпукло.
3. D выпукло по Леви.
4. D - псевдовыпуклая.
5. D локально псевдовыпуклый.

Последствия, и являются стандартными результатами. Доказательство, т. Е. Построение глобальной голоморфной функции, не допускающей продолжения из нерасширяемых функций, определенных только локально. Это называется проблемой Леви (в честь Е.Е. Леви ) и сначала была решена Киёши Ока, а затем Ларсом Хёрмандером с использованием методов функционального анализа и уравнений в частных производных (следствие -проблемы). ${\ displaystyle 1 \ Leftrightarrow 2 \ Leftrightarrow 3}$${\ displaystyle 1 \ Rightarrow 4}$${\ Displaystyle 4 \ Rightarrow 5}$${\ displaystyle 5 \ Rightarrow 1}$ ${\ displaystyle {\ bar {\ partial}}}$

Idéal de domaines indéterminés (Предшественник понятия связного (связки))

Ока ввел понятие, которое он назвал «idéal de domaines indéterminés» или «идеалом неопределенных областей». В частности, это набор пар, голоморфных на непустом открытом множестве, таких что ${\ displaystyle (I)}$${\ Displaystyle (е, \ дельта)}$${\ displaystyle f}$${\ displaystyle \ delta}$

1. Если и произвольно, то.${\ Displaystyle (е, \ дельта) \ в (I)}$${\ Displaystyle (а, \ дельта ')}$${\ displaystyle (af, \ delta \ cap \ delta ') \ in (I)}$
2. Для каждого тогда${\ Displaystyle (е, \ дельта), (е ', \ дельта') \ в (я)}$${\ displaystyle (f + f ', \ delta \ cap \ delta') \ in (I).}$

Происхождение неопределенных доменов связано с тем, что домены меняются в зависимости от пары. Картан перевел это понятие в понятие когерентности ( пучка ) в когомологиях пучка. Это название происходит от Х. Картана. Понятие связности помогло решить проблемы с несколькими сложными переменными. ${\ Displaystyle (е, \ дельта)}$

Связный пучок

Определение

Определение когерентного пучка следующее.

Когерентный пучок на кольчатой пространстве является пучком, удовлетворяющий следующим двум свойствам: ${\ displaystyle (X, {\ mathcal {O}} _ {X})}$${\ Displaystyle {\ mathcal {F}}}$

1. ${\ Displaystyle {\ mathcal {F}}}$имеет конечный тип над, то есть каждая точка из имеет открытую окрестность в такой, что существует сюръективный морфизм для некоторого натурального числа ;${\ displaystyle {\ mathcal {O}} _ {X}}$${\ displaystyle X}$ ${\ displaystyle U}$${\ displaystyle X}$${\ displaystyle {\ mathcal {O}} _ {X} ^ {n} | _ {U} \ to {\ mathcal {F}} | _ {U}}$${\ displaystyle n}$
2. для произвольного открытого множества, произвольного натурального числа, и любой морфизма из -модулей, ядро конечного типа.${\ Displaystyle U \ substeq X}$${\ displaystyle n}$${\ displaystyle \ varphi: {\ mathcal {O}} _ {X} ^ {n} | _ {U} \ to {\ mathcal {F}} | _ {U}}$${\ displaystyle {\ mathcal {O}} _ {X}}$${\ displaystyle \ varphi}$

Морфизмы между (квази) когерентными пучками такие же, как морфизмы пучков -модулей. ${\ displaystyle {\ mathcal {O}} _ {X}}$

Кроме того, Жан-Пьер Серр (1955) доказывает, что

Если в точной последовательности пучков -модулей два из трех пучков когерентны, то третий также когерентен.${\ displaystyle 0 \ to {\ mathcal {F}} _ {1} | _ {U} \ to {\ mathcal {F}} _ {2} | _ {U} \ to {\ mathcal {F}} _ {3} | _ {U} \ to 0}$${\ displaystyle {\ mathcal {O}}}$${\ displaystyle {\ mathcal {F}} _ {j}}$

Квази-когерентный пучок на кольчатой пространстве является пучком из - модулей, который имеет локальное представление, то есть, каждая точка имеет открытую окрестность, в которой существует точная последовательность ${\ displaystyle (X, {\ mathcal {O}} _ {X})}$${\ Displaystyle {\ mathcal {F}}}$${\ displaystyle {\ mathcal {O}} _ {X}}$ ${\ displaystyle X}$${\ displaystyle U}$

${\ displaystyle {\ mathcal {O}} _ {X} ^ {\ oplus I} | _ {U} \ to {\ mathcal {O}} _ {X} ^ {\ oplus J} | _ {U} \ в {\ mathcal {F}} | _ {U} \ в 0}$

для некоторых (возможно, бесконечных) множеств и. ${\ displaystyle I}$${\ displaystyle J}$

Когерентная теорема Оки

Когерентная теорема Оки гласит, что каждый пучок, удовлетворяющий следующим условиям, является когерентным.

1. пучок из ростков голоморфных функций на или комплексное подмногообразие${\ displaystyle {\ mathcal {O}}: = {\ mathcal {O}} _ {\ mathbb {C} _ {n}}}$ ${\ displaystyle \ mathbb {C} _ {n}}$
2. идеальный пучок аналитического подмножества A открытого подмножества${\ displaystyle {\ mathcal {I}} \ langle A \ rangle}$${\ displaystyle \ mathbb {C} _ {n}}$
3. нормализация структурного пучка комплексного аналитического пространства

Из теоремы выше Серра (1955), является когерентным пучком, и (я) используется для доказательства теоремы Картана А и В. ${\ displaystyle {\ mathcal {O}} ^ {p}}$

Идеальная связка

Если - замкнутая подсхема локально нётеровой схемы, пучок всех регулярных функций, обращающихся в нуль, когерентен. Аналогично, если является замкнутым аналитическим подпространством комплексного аналитического пространства, пучок идеалов когерентен. ${\ displaystyle Z}$${\ displaystyle X}$${\ displaystyle {\ mathcal {I}} _ {Z / X}}$${\ displaystyle Z}$${\ displaystyle Z}$${\ displaystyle X}$ ${\ displaystyle {\ mathcal {I}} _ {Z / X}}$

Проблема кузена

В случае комплексных функций с одной переменной теорема Миттаг-Леффлера смогла создать глобальную мероморфную функцию из заданного полюса, а теорема факторизации Вейерштрасса смогла создать глобальную мероморфную функцию из заданного нуля. Однако эти теоремы не выполняются, поскольку особенности аналитической функции от нескольких комплексных переменных не являются изолированными точками; эта проблема называется проблемой Кузена и формулируется в терминах когомологий пучков. Они были введены в частных случаях Пьером Кузеном в 1895 году. Именно Киёси Ока показал условия решения проблемы двоюродного брата относительно области голоморфности в комплексном координатном пространстве, а также относительно проблемы троюродных братьев, если это область голоморфности на комплексном координатном пространстве, проблема Кузена - это проблема, связанная с аналитическими свойствами комплексных многообразий, но условие ее решения - только топологическое свойство, и Я.П. Серр назвал это принципом Ока. Они теперь корректны, и решить, для любого комплексного многообразия М, в терминах условий на М. M, удовлетворяющий этим условиям, является одним из способов определения многообразия Штейна.

Проблема двоюродного брата

Определение без слов когомологий пучка

Каждое различие является голоморфной функцией, где оно определено. Он запрашивает мероморфную функцию F на М таким образом, что является голоморфным на U я ; другими словами, f разделяет сингулярное поведение данной локальной функции. ${\ displaystyle f_ {i} -f_ {j}}$${\ displaystyle f-f_ {i}}$

Определение с использованием слов когомологий пучка

Пусть K пучок мероморфных функций и вывода пучка голоморфных функций на М. Если следующая карта сюръективна, первая проблема Кузена может быть решена.

${\ displaystyle H ^ {0} (M, \ mathbf {K}) {\ xrightarrow {\ phi}} H ^ {0} (M, \ mathbf {K} / \ mathbf {O}).}$

По длинной точной последовательности когомологий,

${\ displaystyle H ^ {0} (M, \ mathbf {K}) {\ xrightarrow {\ phi}} H ^ {0} (M, \ mathbf {K} / \ mathbf {O}) \ to H ^ { 1} (M, \ mathbf {O})}$

является точным, поэтому первая проблема Кузена всегда разрешима при условии, что первая группа когомологий H ¹ ( M, O) обращается в нуль. В частности, по теореме Картана B проблема Кузена всегда разрешима, если M - многообразие Штейна.

Проблема троюродного брата

Определение без слов когомологий пучка

Каждое отношение является ненулевой голоморфной функцией, где оно определено. Он запрашивает мероморфную функцию f на M, голоморфную и отличную от нуля. ${\ displaystyle f_ {i} / f_ {j}}$${\ displaystyle f / f_ {i}}$

Определение с использованием слов когомологий пучка

пусть - пучок голоморфных функций, нигде не обращающихся в нуль, и пучок мероморфных функций, не равных тождественно нулю. Тогда оба являются пучками абелевых групп, и фактор-пучок определен корректно. Если следующая карта сюръективна, то проблема троюродных братьев может быть решена. ${\ displaystyle \ mathbf {O} ^ {*}}$${\ displaystyle \ mathbf {K} ^ {*}}$ ${\ Displaystyle \ mathbf {K} ^ {*} / \ mathbf {O} ^ {*}}$${\ displaystyle \ phi}$

${\ displaystyle H ^ {0} (M, \ mathbf {K} ^ {*}) {\ xrightarrow {\ phi}} H ^ {0} (M, \ mathbf {K} ^ {*} / \ mathbf { O} ^ {*}).}$

Длинная последовательность когомологий точного пучка, связанная с фактором, есть

${\ displaystyle H ^ {0} (M, \ mathbf {K} ^ {*}) {\ xrightarrow {\ phi}} H ^ {0} (M, \ mathbf {K} ^ {*} / \ mathbf { O} ^ {*}) \ to H ^ {1} (M, \ mathbf {O} ^ {*})}$

так что проблема троюродного брата разрешима во всех случаях при условии, что ${\ displaystyle H ^ {1} (M, \ mathbf {O} ^ {*}) = 0.}$

Группу когомологий для мультипликативной структуры на можно сравнить с группой когомологий с ее аддитивной структурой путем логарифмирования. То есть существует точная последовательность пучков ${\ Displaystyle Н ^ {1} (М, \ mathbf {O} ^ {*}),}$${\ displaystyle \ mathbf {O} ^ {*}}$${\ Displaystyle Н ^ {1} (М, \ mathbf {O})}$

${\ displaystyle 0 \ to 2 \ pi i \ mathbb {Z} \ to \ mathbf {O} {\ xrightarrow {\ exp}} \ mathbf {O} ^ {*} \ to 0}$

где крайний левый пучок - локально постоянный пучок со слоем. Препятствие к определению логарифма на уровне H ¹ связано с длинной точной последовательностью когомологий ${\ Displaystyle 2 \ пи я \ mathbb {Z}}$${\ Displaystyle Н ^ {2} (М, \ mathbb {Z})}$

${\ displaystyle H ^ {1} (M, \ mathbf {O}) \ to H ^ {1} (M, \ mathbf {O} ^ {*}) \ to 2 \ pi iH ^ {2} (M, \ mathbb {Z}) \ to H ^ {2} (M, \ mathbf {O}).}$

Когда М является многообразием Штейна, средняя стрелкой является изоморфизмом, так как для так, что необходимое и достаточное условие в этом случае для второй задачи кузена быть всегда разрешимо в том, что (Это условие называется принципом Ока.) ${\ Displaystyle Н ^ {д} (М, \ mathbf {O}) = 0}$${\ displaystyle qgt; 0}$${\ displaystyle H ^ {2} (M, \ mathbb {Z}) = 0.}$

Многообразие Штейна (некомпактное многообразие)

Поскольку открытая риманова поверхность всегда имеет непостоянную однозначную голоморфную функцию и удовлетворяет второй аксиоме счетности, открытая риманова поверхность может считаться комплексным многообразием, имеющим голоморфное вложение в одномерную комплексную плоскость. Теорема вложения Уитни говорит нам, что каждое гладкое n -мерное многообразие может быть вложено как гладкое подмногообразие в, в то время как комплексное многообразие «редко» имеет голоморфное вложение в. Рассмотрим, например, произвольное компактное связное комплексное многообразие X: каждая голоморфная функция на нем постоянна по теореме Лиувилля. Теперь, когда мы знаем, что для нескольких комплексных переменных комплексные многообразия не всегда имеют голоморфные функции, которые не являются константами, рассмотрим условия, которые имеют голоморфные функции. Теперь, если бы у нас было голоморфное вложение X в, то координатные функции из ограничились бы непостоянными голоморфными функциями на X, что противоречит компактности, за исключением случая, когда X является просто точкой. Комплексные многообразия, в которые можно голоморфно вложить, называются многообразиями Штейна. Также многообразия Штейна удовлетворяют второй аксиоме счетности. ${\ Displaystyle \ mathbb {C}}$ ${\ Displaystyle \ mathbb {R} ^ {2n}}$${\ displaystyle \ mathbb {C} ^ {n}}$${\ displaystyle \ mathbb {C} ^ {n}}$${\ displaystyle \ mathbb {C} ^ {n}}$${\ displaystyle \ mathbb {C} ^ {n}}$

Многообразие Штейна является комплексным подмногообразием в векторном пространстве из п комплексных измерений. Они были введены и названы в честь Карла Штейна (1951). Пространство Штейна похоже на многообразие Штейна, но разрешено иметь особенности. Пространства Штейна являются аналогами аффинных многообразий или аффинных схем в алгебраической геометрии. Если однолистная область на соединена с многообразием, может рассматриваться как комплексное многообразие и удовлетворяет условию разделения, описанному ниже, условием превращения в многообразие Штейна является удовлетворение голоморфной выпуклости. Следовательно, многообразие Штейна - это свойства области определения (максимального) аналитического продолжения аналитической функции. ${\ displaystyle \ mathbb {C} ^ {n}}$

Определение

Пусть X является паракомпактные комплексные многообразия комплексной размерности и пусть обозначает кольцо голоморфных функций на X. Мы называем X многообразием Штейна, если выполняются следующие условия: ${\ displaystyle n}$${\ Displaystyle {\ mathcal {O}} (X)}$

• X голоморфно выпуклый, то есть для любого компактного подмножества, так называемый голоморфно выпуклая оболочкой,${\ Displaystyle K \ подмножество X}$

${\ displaystyle {\ bar {K}} = \ left \ {z \ in X; | f (z) | \ leq \ sup _ {w \ in K} | f (w) | \ \ forall f \ in { \ mathcal {O}} (X) \ right \},}$

также компактное подмножество X.

• X является голоморфно отделимо, т.е. если две точки в X, то существует такое, что${\ displaystyle x \ neq y}$${\ displaystyle f \ in {\ mathcal {O}} (X)}$${\ Displaystyle f (x) \ neq f (y).}$
• Открытая окрестность каждой точки на многообразии имеет голоморфную диаграмму к.${\ Displaystyle {\ mathcal {O}} (X)}$

Все некомпактные (открытые) римановы поверхности являются многообразием Штейна.

Пусть X - связная некомпактная (открытая) риманова поверхность. Глубокая теорема (1939) Генриха Бенке и Штейна (1948) утверждает, что X - многообразие Штейна.

Другой результат, приписанный Гансу Грауэрту и Гельмуту Рёрлю (1956), утверждает, что каждое голоморфное векторное расслоение на X тривиально. В частности, каждое линейное расслоение тривиально, поэтому. Последовательность экспоненциального пучка приводит к следующей точной последовательности: ${\ displaystyle H ^ {1} (X, {\ mathcal {O}} _ {X} ^ {*}) = 0}$

${\ displaystyle H ^ {1} (X, {\ mathcal {O}} _ {X}) \ longrightarrow H ^ {1} (X, {\ mathcal {O}} _ {X} ^ {*}) \ longrightarrow H ^ {2} (X, \ mathbb {Z}) \ longrightarrow H ^ {2} (X, {\ mathcal {O}} _ {X})}$

В настоящее время теоремы B Картанен показывает, что, таким образом. ${\ displaystyle H ^ {1} (X, {\ mathcal {O}} _ {X}) = H ^ {2} (X, {\ mathcal {O}} _ {X}) = 0}$${\ Displaystyle Н ^ {2} (Х, \ mathbb {Z}) = 0}$

Это связано с решением второй (мультипликативной) проблемы кузена.

Леви проблемы

Картан распространил проблему Леви на многообразия Штейна.

Если относительное компактное открытое подмножество многообразия Штейна X является локально псевдовыпуклым, то D является многообразием Штейна, и, наоборот, если D является локально псевдовыпуклым, то X является многообразием Штейна. т.е. Тогда X является многообразием Штейна тогда и только тогда, когда D локально является многообразием Штейна.${\ Displaystyle D \ подмножество X}$

Это было доказано Бремерманом, вложив его в достаточно высокую размерность и сведя к результату Оки. ${\ displaystyle \ mathbb {C} ^ {m}}$

Кроме того, Грауэрт доказана для произвольных комплексных многообразий M.

Если относительное компактное подмножество произвольного комплексного многообразия M является сильно псевдовыпуклым на M, то M является голоморфно выпуклым (т. Е. Многообразием Штейна). Кроме того, D само является многообразием Штейна.${\ displaystyle D \ subset M}$

И Нарасимхан распространил проблему Леви на комплексное аналитическое пространство, обобщенное на особый случай комплексных многообразий.

Комплексное аналитическое пространство, допускающее непрерывную строго плюрисубгармоническую функцию исчерпания (сильно псевдовыпуклое), называется пространством Штейна.

Проблема Леви остается нерешенной в следующих случаях;

Предположим, что X является особой пространство Штейна,. Предположим, что для всех существует открытая окрестность, т.е. пространство Штейна. Является ли D сам Stein?${\ Displaystyle D \ подмножество \ подмножество X}$${\ displaystyle p \ in \ partial D}$${\ Displaystyle U (p)}$${\ Displaystyle U \ cap D}$

более обобщенный

Предположим, что N - пространство Штейна, а f - инъективная, а также неразветвленная область Римана, такая, что отображение f является локально псевдовыпуклым отображением (т. Е. Морфизмом Штейна). Тогда М - это сама Штейн?${\ displaystyle f: M \ to N}$

а также,

Предположим, что X - пространство Штейна и возрастающее объединение открытых множеств Штейна. Тогда D - это сам Штейн?${\ Displaystyle D = \ bigcup _ {п \ in \ mathbb {N}} D_ {п}}$

Это означает, что теорема Бенке – Штейна, верная для многообразий Штейна, не нашла условий, которые должны быть установлены в пространстве Штейна.

K-полный

Грауэрт ввел понятие K-полного при доказательстве проблемы Леви.

Пусть X есть комплексное многообразие, X является K-полным, если для каждой точки, существует конечного число голоморфного отображения из X в, таким образом, что является изолированной точкой множества. Эта концепция также применима к сложному аналитическому пространству. ${\ displaystyle x_ {0} \ in X}$${\ displaystyle f_ {1}, \ dots, f_ {k}}$${\ Displaystyle \ mathbb {C} ^ {p}}$${\ displaystyle p = p (x_ {0})}$${\ displaystyle x_ {0}}$${\ displaystyle A = \ {x \ in X; f ^ {- 1} f (x_ {0}) \ (v = 1, \ dots, k) \}}$

Свойства и примеры многообразий Штейна

• Стандартное комплексное пространство - это многообразие Штейна.${\ displaystyle \ mathbb {C} ^ {n}}$
• Каждая область голоморфности в является многообразием Штейна.${\ displaystyle \ mathbb {C} ^ {n}}$
• Достаточно легко показать, что всякое замкнутое комплексное подмногообразие в многообразии Штейна также является многообразием Штейна.
• Теорема вложения многообразий Штейна утверждает следующее: Каждый Stein многообразия X комплексной размерности п может быть встроена в по биголоморфной правильной карте. ${\ Displaystyle \ mathbb {C} ^ {2n + 1}}$

Из этих фактов следует, что многообразие Штейна является замкнутым комплексным подмногообразием комплексного пространства, комплексная структура которого является структурой объемлющего пространства (поскольку вложение биголоморфно).

• Каждое многообразие Штейна (комплексной) размерности n имеет гомотопический тип n -мерного CW-комплекса.
• В одном комплексном измерении условие Штейна можно упростить: связная риманова поверхность является многообразием Штейна тогда и только тогда, когда она некомпактна. Это можно доказать, используя версию теоремы Рунге для римановых поверхностей, принадлежащую Бенке и Стейну.
• Каждое многообразие Штейна X голоморфно распространяемо, т.е. для каждой точки существует n голоморфных функций, определенных на всем X, которые образуют локальную систему координат при ограничении на некоторую открытую окрестность x.${\ displaystyle x \ in X}$
• Первую проблему Кузена всегда можно решить на многообразии Штейна.
• Многообразие Штейна эквивалентно (комплексному) сильно псевдовыпуклому многообразию. Последнее означает, что он имеет сильно псевдовыпуклую (или плюрисубгармоническую ) исчерпывающую функцию, т. Е. Гладкую вещественную функцию на X (которую можно считать функцией Морса ) с, такую, что подмножества компактны в X для любого действительного числа c. Это решение так называемой проблемы Леви, названной в честь Е.Е. Леви (1911). Функция предлагает обобщение многообразия Штейна до идеи соответствующего класса компактных комплексных многообразий с краем, называемого областью Штейна. Домен Штейна - это прообраз. Поэтому некоторые авторы называют такие многообразия строго псевдовыпуклыми многообразиями.${\ displaystyle \ psi}$ ${\ displaystyle i \ partial {\ bar {\ partial}} \ psigt; 0}$${\ Displaystyle \ {г \ в Икс \ середина \ фунт / кв. дюйм (г) \ Leq с \}}$ ${\ displaystyle \ psi}$${\ displaystyle \ {z \ mid - \ infty \ leq \ psi (z) \ leq c \}}$
• В связи с предыдущим пунктом другое эквивалентное и более топологическое определение в комплексной размерности 2 следующее: поверхность Штейна - это комплексная поверхность X с вещественной функцией Морса f на X, такая, что вдали от критических точек f поверхность поле комплексных касаний к прообразу является контактной структурой, которая индуцирует ориентацию на X с согласования с обычной ориентацией, как граница То есть, является Штейн заполнением из X с.${\ Displaystyle X_ {c} = е ^ {- 1} (с)}$ ${\ displaystyle f ^ {- 1} (- \ infty, c).}$${\ displaystyle f ^ {- 1} (- \ infty, c)}$

Существуют многочисленные дополнительные характеристики таких многообразий, в частности, улавливающие свойство их наличия «многих» голоморфных функций, принимающих значения в комплексных числах. См., Например , теоремы Картана A и B, касающиеся когомологий пучков.

В GAGA множестве аналогий, многообразия Штейна соответствуют аффинным.

Многообразия Штейна в некотором смысле двойственны эллиптическим многообразиям в комплексном анализе, которые допускают «множество» голоморфных функций комплексных чисел в себя. Известно, что многообразие Штейна эллиптично тогда и только тогда, когда оно расслоено в смысле так называемой «голоморфной теории гомотопий».

Комплексные проективные многообразия (компактное многообразие)

Мероморфные функции в комплексных функциях с одной переменной изучались на замкнутой римановой поверхности, поскольку компактная риманова поверхность имела непостоянную однозначную мероморфную функцию. Компактное одномерное комплексное многообразие было сферой Римана. Однако для компактных комплексных многообразий большой размерности (несколько комплексных переменных) существование мероморфных функций нелегко указать, поскольку особенность не является изолированной точкой. Фактически, Хопф нашел класс компактных комплексных многообразий без непостоянных мероморфных функций. Рассмотрим расширение замкнутой (компактной) римановой поверхности до более высокой размерности, то есть рассмотрим компактификацию, например, голоморфное вложение близкого комплексного подмногообразия M в комплексное проективное пространство (особенно комплексные проективные алгебраические многообразия ), Комплексные проективные многообразия в многомерном пространстве. В комплексных многообразиях происходит явление исчезновения группы когомологий пучка, и именно теорема об исчезновении Кодаиры и ее обобщающая теорема об исчезновении Накано и т. д. задают условия для возникновения этого явления. Теорема вложения Кодаиры дает комплексное кэлерово многообразие M с метрикой Ходжа достаточно большой размерности N в комплексное проективное пространство, а также теорема Чоу показывает, что аналитическое подпространство замкнутого комплексного проективного пространства является алгебраическим многообразием, и в сочетании с результатом Кодаиры M вкладывается как алгебраическое многообразие. Они дают пример вложения в многообразия с мероморфными функциями. Сходства в задачах Леви на комплексном проективном пространстве были доказаны на некоторых образцах, например, Такеучи. В общем, принцип GAGA говорит, что геометрия проективных комплексных аналитических пространств (или многообразий) эквивалентна геометрии проективных комплексных многообразий. Комбинация аналитических и алгебраических методов для сложных проективных многообразий приводит к таким областям, как теория Ходжа. ${\ Displaystyle {\ шляпа {\ mathbb {C}}} \ cong \ mathbb {CP} ^ {1}}$${\ displaystyle \ mathbb {C} ^ {n}}$${\ Displaystyle \ mathbb {CP} ^ {п}}$ ${\ Displaystyle \ mathbb {CP} ^ {п}}$

• Сложная геометрия
• CR-коллектор
• Гармонические карты
• Гармонические морфизмы
• Бесконечномерная голоморфность
• Теорема Ока – Вейля.

Встроенные цитаты

Учебники

• Behnke, H.; Thullen, P. (1934). Theorie der Funktionen mehrerer komplexer Veränderlichen. DOI : 10.1007 / 978-3-642-99659-7. ISBN   978-3-642-98844-8.
• Bochner, S.; Мартин, WT (1948). Несколько сложных переменных. Принстонский математический ряд. Издательство Принстонского университета. ISBN   978-0-598-34865-4.
• Форстер, Отто (1981). Лекции о римановых поверхностях. Выпускной текст по математике. 81. Нью-Йорк: Springer Verlag. ISBN   0-387-90617-7.
• Грауэрт, Ганс; Реммерт, Райнхольд (1979), Теория пространств Штейна, Grundlehren der Mathematischen Wissenschaften, 236, Берлин-Нью-Йорк: Springer-Verlag, ISBN   3-540-90388-7, Руководство по ремонту   0580152
• Б. В. Шабат, Введение в комплексный анализ, 1–2, Москва (1985).
  • Борис Владимирович Шабат, Введение в комплексный анализ, АМС, 1992
  • Введение в комплексный анализ. Часть II. Функции нескольких переменных. Переводы математических монографий. 110. 1992. DOI : 10,1090 / mmono / 110. ISBN   9780821819753.
• В. С. Владимиров, Методы теории функций многих комплексных переменных, Массачусетский технологический институт (1966).
• Ларс Хёрмандер (1990) [1966], Введение в комплексный анализ нескольких переменных (3-е изд.), Северная Голландия, ISBN   978-1-493-30273-4
• Картан, Анри; Такахаши, Рейджи (1992). Theorie élémentaire des fonctions analytiques d'une ou plusieurs, комплексы переменных (на французском языке) (6é. Ed., Nouv. Tir ed.). Пэрис: Германн. п. 231. ISBN.   9782705652159.
  • Элементарная теория аналитических функций одной или нескольких комплексных переменных, Dover 1995 (английский перевод)
• Кранц, Стивен Г. (1992). Теория функций нескольких комплексных переменных (второе изд.). AMS Chelsea Publishing. п. 340. DOI : 10,1090 / чел / 340. ISBN   978-0-8218-2724-6.
• Р. Майкл Рейндж, Голоморфные функции и интегральные представления от нескольких комплексных переменных, Springer 1986, 1998
• Фолькер Шайдеманн, Введение в комплексный анализ нескольких переменных, Birkhäuser, 2005, ISBN   3-7643-7490-X
• Ногучи, Дзюнджиро (2016). Аналитическая теория функций нескольких переменных Элементы когерентности Оки. п. XVIII, 397. DOI : 10.1007 / 978-981-10-0291-5. ISBN   978-981-10-0289-2.

Энциклопедия математики

• Гончар А.А.; Шабат, Б.В. (2001) [1994], "Аналитическая функция", Энциклопедия математики, EMS Press
• Соломенцев, Е.Д. (2001) [1994], "Силовые ряды", Энциклопедия математики, EMS Press
• Соломенцев, Е.Д. (2001) [1994], "Биголоморфное отображение", Энциклопедия математики, EMS Press
• Соломенцев, Е.Д. (2001) [1994], "Область Рейнхардта", Энциклопедия математики, EMS Press
• Чирка, EM (2001) [1994], "Теорема Хартогса", Энциклопедия математики, EMS Press
• Гончар А.А.; Владимиров, В.С. (2001) [1994], "Область голоморфности", Энциклопедия математики, EMS Press
• Онищик, А.Л. (2001) [1994], "Псевдовыпуклые и псевдовогнутые", Энциклопедия математики, EMS Press
• Соломенцев, Е.Д. (2001) [1994], "Плюрисубгармоническая функция", Энциклопедия математики, EMS Press
• Онищик А.Л. (2001) [1994], "Когерентный пучок", Энциклопедия математики, EMS Press
• Чирка, Е.М. (2001) [1994], "Теоремы Оки", Энциклопедия математики, EMS Press
• Чирка, EM (2001) [1994], "Задачи кузена", Энциклопедия математики, EMS Press
• Онищик А.Л. (2001) [1994], "Многообразие Штейна", Энциклопедия математики, EMS Press

ПланетаМатематика

• Эта статья содержит материал из следующих PlanetMath статей, которые лицензируются в соответствии с лицензией Creative Commons Attribution / Share-Alike Лицензии : доменное Reinhardt, Голоморфны выпуклая, голоморфность, Polydisc, биголоморфно эквивалент, Левите псевдовыпуклую, Псевдовыпуклая, функцию исчерпания.

• Кранц, Стивен Г. (1987), "Что такое нескольких комплексных переменных?", Американский Математический Месячный, 94 (3): 236-256, DOI : 10,2307 / 2323391, JSTOR   2323391
• Oka, Kiyoshi (1984), Remmert, R. (ed.), Collected Papers, Springer-Verlag Berlin Heidelberg, p. XIV, 226, ISBN   978-3-662-43412-3

• Книга с открытым исходным кодом « Вкусные кусочки нескольких сложных переменных» от Йиржи Лебля
• Комплексная аналитическая и дифференциальная геометрия ( книга OpenContent см. B2 )
• Виктор Гийемен. 18.117 Темы в нескольких комплексных переменных. Весна 2005 г. Массачусетский технологический институт: MIT OpenCourseWare, https://ocw.mit.edu. Лицензия: Creative Commons BY-NC-SA.