распределение вероятностей
Функция плотности вероятности 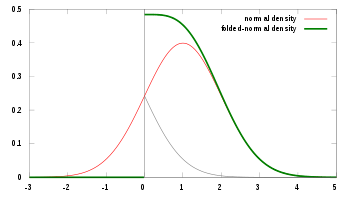 . μ = 1, σ = 1 . μ = 1, σ = 1 |
Кумулятивная функция распределения 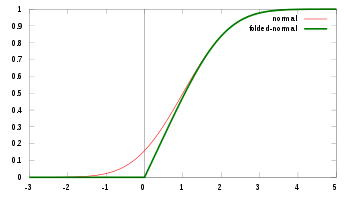 . μ = 1, σ = 1 . μ = 1, σ = 1 |
| Параметры | μ ∈ R(местоположение ). σ>0 (масштаб ) |
|---|
| Поддержка | x ∈ [0, ∞) |
|---|
| PDF |  |
|---|
| CDF | ![{\ frac {1} {2}} \ left [{\ t_dv {erf}} \ left ({\ frac {x + \ mu} {\ sigma {\ sqrt {2}}) }} \ right) + {\ t_dv {erf}} \ left ({\ frac {x- \ mu} {\ sigma {\ sqrt {2}}}} \ right) \ right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad88ca4e426758e5b8472945b7562acc5db7d03b) |
|---|
| Среднее |  |
|---|
| Дисперсия |  |
|---|
сложенное нормальное распределение - это распределение вероятностей, связанное с нормальным распределением. Для нормально распределенной случайной величины X с средним μ и дисперсией σ, случайная величина Y = | X | имеет сложенное нормальное распределение. Такой случай может возникнуть, если записана только величина некоторой переменной, но не ее знак. Распределение называется «свернутым», потому что вероятностная масса слева от x = 0 свернута, принимая абсолютное значение. В физике теплопроводности сложенное нормальное распределение является фундаментальным решением уравнения теплопроводности на полупространстве; это соответствует наличию идеального изолятора на гиперплоскости через начало координат.
Содержание
- 1 Определения
- 2 Свойства
- 2.1 Режим
- 2.2 Характеристическая функция и другие связанные функции
- 3 Связанные распределения
- 4 Статистический вывод
- 5 См. Также
- 6 Ссылки
- 7 Внешние ссылки
Определения
Плотность
функция плотности вероятности (PDF) определяется выражением

для x ≥ 0 и 0 для всех остальных. Альтернативная формулировка дается следующим образом:
 ,
,
где cosh - косинус Гиперболическая функция. Отсюда следует, что кумулятивная функция распределения (CDF) определяется как:
![{\ displaystyle F_ {Y} (x; \ mu, \ sigma ^ {2}) = {\ frac {1} {2}} \ left [{\ t_dv {erf}} \ left ({\ frac {x + \ mu} {\ sqrt {2 \ sigma ^ {2}}}}} \ right) + {\ t_dv {erf}} \ left ({\ frac {x- \ mu} {\ sqrt {2 \ sigma ^ {2}}}} \ right) \ right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bbf74023157cbecf10c9340dd9a0bfe09e3f4f1b)
для x ≥ 0, где erf () - это функция ошибок. Это выражение сводится к CDF полунормального распределения, когда μ = 0.
Среднее значение сложенного распределения тогда

или
![{\ displaystyle \ mu _ {Y} = {\ sqrt {\ frac {2} {\ pi}}} \ sigma e ^ {- {\ frac {\ mu ^ {2}} { 2 \ sigma ^ {2}}}} + \ mu \ left [1-2 \ Phi \ left (- {\ frac {\ mu} {\ sigma}} \ right) \ right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd5bfcd3dc54605d03817a06f63bebc3a87ca556)
где  - это функция нормального кумулятивного распределения :
- это функция нормального кумулятивного распределения :
![{\ displaystyle \ Phi (x) \; = \; {\ frac {1} {2}} \ left [1+ \ operatorname {erf} \ left ({\ frac {x} {\ sqrt {2}}} \ right) \ right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d4a69ed96ae507f5766a6d5b8a23da4eeec1109)
Тогда дисперсия легко выражается через среднее значение:

И среднее (μ), и дисперсию (σ) X в исходном нормальном распределении можно интерпретировать как параметры положения и масштаба Y в сложенном распределении.
Свойства
Режим
Режим распределения - это значение  , для которого плотность максимальна. Чтобы найти это значение, мы берем первую производную плотности по
, для которого плотность максимальна. Чтобы найти это значение, мы берем первую производную плотности по  и устанавливаем ее равной нулю. К сожалению, закрытой формы нет. Однако мы можем записать производную лучше и в итоге получить нелинейное уравнение
и устанавливаем ее равной нулю. К сожалению, закрытой формы нет. Однако мы можем записать производную лучше и в итоге получить нелинейное уравнение

![{\ displaystyle x \ left [e ^ {- { \ frac {1} {2}} {\ frac {\ left (x- \ mu \ right) ^ {2}} {\ sigma ^ {2}}}} + e ^ {- {\ frac {1} { 2}} {\ frac {\ left (x + \ mu \ right) ^ {2}} {\ sigma ^ {2}}}} \ right] - \ mu \ left [e ^ {- {\ frac {1} {2}} {\ frac {\ left (x- \ mu \ right) ^ {2}} {\ sigma ^ {2}}}} - e ^ {- {\ frac {1} {2}} {\ гидроразрыв {\ влево (х + \ му \ вправо) ^ {2}} {\ sigma ^ {2}}}} \ right] = 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/69f19ceec33ed5147ed745256c7244c5cb468364)


 .
.
Цагрис и др. (2014) из численного исследования показал, что когда  , максимум достигается, когда
, максимум достигается, когда  , и когда
, и когда  становится больше, чем
становится больше, чем  , максимум приближается к
, максимум приближается к  . Конечно, этого следовало ожидать, поскольку в этом случае свернутая нормаль сходится к нормальному распределению. Чтобы избежать проблем с отрицательными отклонениями, предлагается возведение параметра в степень. В качестве альтернативы вы можете добавить ограничение, например, если оптимизатор выберет отрицательную дисперсию, значение логарифмической вероятности будет NA или что-то очень маленькое.
. Конечно, этого следовало ожидать, поскольку в этом случае свернутая нормаль сходится к нормальному распределению. Чтобы избежать проблем с отрицательными отклонениями, предлагается возведение параметра в степень. В качестве альтернативы вы можете добавить ограничение, например, если оптимизатор выберет отрицательную дисперсию, значение логарифмической вероятности будет NA или что-то очень маленькое.
Характеристическая функция и другие связанные функции
- Характеристическая функция определяется как
 .
.
- Производящая функция момента определяется выражением
 .
.
- Кумулянтная производящая функция определяется как
![{\ displaystyle K_ {x} \ left (t \ right) = \ log {M_ {x} \ left (t \ right)} = \ left ({\ frac {\ sigma ^ {2} t ^ {2}) } {2}} + \ mu t \ right) + \ log {\ left \ lbrace 1- \ Phi \ left (- {\ frac {\ mu} {\ sigma}} - \ sigma t \ right) + e ^ {{\ frac {\ sigma ^ {2} t ^ {2}} {2}} - \ mu t} \ left [1- \ Phi \ left ({\ frac {\ mu} {\ sigma}} - \ сигма т \ право) \ право] \ право \ rbrace}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/18260983046f5c9d546d518542872acee9d90678) .
.
- Преобразование Лапласа задается формулой
![{\ displaystyle E \ left (e ^ {- tx} \ right) = e ^ {{\ frac {\ sigma ^ {2} t ^ {2}} {2}} - \ mu t} \ left [1- \ Phi \ left ( - {\ frac {\ mu} {\ sigma}} + \ sigma t \ right) \ right] + e ^ {{\ frac {\ sigma ^ {2} t ^ {2}} {2}} + \ mu t} \ left [1- \ Phi \ left ({\ frac {\ mu} {\ sigma}} + \ sigma t \ right) \ right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bcf88b418505cfad95c727604e731d1801bfa53d) .
.
- Преобразование Фурье задается формулой
![{\ displaystyle {\ hat {f}} \ left (t \ right) = \ phi _ {x} \ left (-2 \ pi t \ right) = e ^ {{\ frac {-4 \ pi ^ {2} \ sigma ^ {2} t ^ { 2}} {2}} - i2 \ pi \ mu t} \ left [1- \ Phi \ left (- {\ frac {\ mu} {\ sigma}} - i2 \ pi \ sigma t \ right) \ right ] + e ^ {- {\ frac {4 \ pi ^ {2} \ sigma ^ {2} t ^ {2}} {2}} + i2 \ pi \ mu t} \ left [1- \ Phi \ left ({\ гидроразрыва {\ mu} {\ sigma}} - i2 \ pi \ sigma t \ right) \ right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea9915664db6c8d360efec8ee9b94e9d45e8408c) .
.
Связанные распределения
- Когда μ = 0, распределение Y является полунормальным распределением.
- Случайная величина (Y / σ) имеет нецентральное распределение хи-квадрат с 1 степенью свободы и нецентральность равна (μ / σ).
- Сложенное нормальное распределение также можно рассматривать как предел сложенного нестандартизованного t-распределения, когда степени свободы стремятся к бесконечности.
- Существует двумерная версия, разработанная Псаракисом и Панаретосом (2001), а также многомерная версия, разработанная Чакраборти и Мутуши (2013).
- Распределение риса является многомерное обобщение свернутого нормального распределения.
Статистический вывод
Оценка параметров
Есть е несколько способов оценки параметров свернутой нормали. Все они, по сути, являются процедурой оценки максимального правдоподобия, но в некоторых случаях выполняется численная максимизация, в то время как в других случаях выполняется поиск корня уравнения. Логарифмическая вероятность свернутой нормали, когда доступна выборка  размером
размером  , может быть записывается следующим образом
, может быть записывается следующим образом
![{ \ displaystyle l = - {\ frac {n} {2}} \ log {2 \ pi \ sigma ^ {2}} + \ sum _ {i = 1} ^ {n} \ log {\ left [e ^ { - {\ frac {\ left (x_ {i} - \ mu \ right) ^ {2}} {2 \ sigma ^ {2}}}} + e ^ {- {\ frac {\ left (x_ {i}) + \ mu \ right) ^ {2}} {2 \ sigma ^ {2}}}} \ right]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/38356615fcbbd3459fa6208500c4f7510f58abc3)
![{\ displaystyle l = - {\ frac {n} {2}} \ log {2 \ pi \ sigma ^ {2}} + \ sum _ {i = 1} ^ {n} \ log {\ left [e ^ {- {\ frac {\ left (x_ {i} - \ mu \ right) ^ {2}} {2 \ sigma ^ {2}}}} \ left (1 + e ^ {- {\ frac {\ left (x_ {i} + \ mu \ right) ^ {2}} {2 \ sigma ^ {2}) }}} e ^ {\ frac {\ left (x_ {i} - \ mu \ right) ^ {2}} {2 \ sigma ^ {2}}} \ right) \ right]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e73ea6fa7d9c0d187340912c1cb8aeb4f5ac8676)

В R (язык программирования) с использованием пакета Rfast можно получить MLE очень быстро (команда foldnorm.mle). В качестве альтернативы этому распределению подойдет команда optim или nlm. Максимизировать легко, поскольку задействованы два параметра ( и
и  ). Обратите внимание, что как положительные, так и отрицательные значения для
). Обратите внимание, что как положительные, так и отрицательные значения для  приемлемы, поскольку
приемлемы, поскольку  принадлежит реальной линии. чисел, следовательно, знак не важен, потому что распределение симметрично относительно него. Следующий код записывается в R
принадлежит реальной линии. чисел, следовательно, знак не важен, потому что распределение симметрично относительно него. Следующий код записывается в R
свернутом <- function(y) { ## y is a vector with positive data n <- length(y) ## sample size sy2 <- sum(y^2) sam <- function(para, n, sy2) { me <- para[1] ; se <- exp( para[2]) f <- - n/2 * log(2/pi/se) + n * me^2 / 2 / se + sy2 / 2 / se - sum( log( cosh( me * y/se))) f } mod <- optim( c( mean(y), sd(y)), n = n, sy2 = sy2, sam, control = list(maxit = 2000)) mod <- optim( mod$par, sam, n = n, sy2 = sy2, control = list(maxit = 20000)) result <- c( -mod$value, mod$par[1], exp(mod$par[2])) names(result) <- c("log-likelihood", "mu", "sigma squared") result }. Частные производные логарифмической вероятности записываются как



 .
.
Приравнивая первую частную производную логарифмического правдоподобия нулю, мы получаем хорошее соотношение
 .
.
Обратите внимание, что у приведенного выше уравнения есть три решения, одно равное нулю и еще два с противоположным знаком. Подставляя указанное выше уравнение в частную производную логарифма правдоподобия по  и приравнивая ее к нулю, мы получаем следующее выражение для дисперсия
и приравнивая ее к нулю, мы получаем следующее выражение для дисперсия
 ,
,
, которая является той же формулой, что и в нормальном распределении. Основное различие здесь заключается в том, что  и
и  не являются статистически независимыми. Вышеупомянутые отношения могут использоваться для получения оценок максимального правдоподобия эффективным рекурсивным способом. Начнем с начального значения для
не являются статистически независимыми. Вышеупомянутые отношения могут использоваться для получения оценок максимального правдоподобия эффективным рекурсивным способом. Начнем с начального значения для  и находим положительный корень (
и находим положительный корень ( ) последнего уравнения. Затем мы получаем обновленное значение
) последнего уравнения. Затем мы получаем обновленное значение  . Процедура повторяется до тех пор, пока изменение значения логарифмической вероятности не станет незначительным. Другой более простой и эффективный способ - выполнить алгоритм поиска. Запишем последнее уравнение более элегантно
. Процедура повторяется до тех пор, пока изменение значения логарифмической вероятности не станет незначительным. Другой более простой и эффективный способ - выполнить алгоритм поиска. Запишем последнее уравнение более элегантно

 .
.
Становится ясно, что оптимизация логарифмической вероятности по двум параметрам превратилась в корневой поиск функции. Это, конечно, идентично предыдущему корневому поиску. Цагрис и др. (2014) обнаружили, что у этого уравнения есть три корня для  , т.е. есть три возможных значения
, т.е. есть три возможных значения  , удовлетворяющие этому уравнению.
, удовлетворяющие этому уравнению.  и
и  , которые представляют собой оценки максимального правдоподобия, и 0, что соответствует до минимальной логарифмической вероятности.
, которые представляют собой оценки максимального правдоподобия, и 0, что соответствует до минимальной логарифмической вероятности.
См. Также
Ссылки
- Tsagris, M.; Beneki, C.; Хассани, Х. (2014). «О сложенном нормальном распределении». Математика. 2 (1): 12–28. arXiv : 1402.3559.
- Леоне ФК, Ноттингем, РБ, Нельсон Л.С. (1961). «Свернутое нормальное распределение». Технометрика. 3 (4): 543–550. DOI : 10.2307 / 1266560. HDL : 2027 / mdp.39015095248541. JSTOR 1266560.
- Джонсон Н.Л. (1962). «Сложенное нормальное распределение: точность оценки по максимальному правдоподобию». Технометрика. 4 (2): 249–256. doi : 10.2307 / 1266622. JSTOR 1266622.
- Нельсон Л.С. (1980). «Свернутое нормальное распределение». J Qual Technol. 12 (4): 236–238.
- Эландт Р.К. (1961). «Сложенное нормальное распределение: два метода оценки параметров по моментам». Технометрика. 3 (4): 551–562. DOI : 10.2307 / 1266561. JSTOR 1266561.
- Лин ПК (2005). «Применение обобщенного складчато-нормального распределения к мерам возможностей процесса». Int J Adv Manuf Technol. 26 (7–8): 825–830. doi : 10.1007 / s00170-003-2043-x.
- Psarakis, S.; Панаретос, Дж. (1990). «Свернутое t-распределение». Коммуникации в статистике - теория и методы. 19 (7): 2717–2734.
- Psarakis, S.; Панаретос, Дж. (2001). «О некоторых двумерных расширениях свернутого нормального и свернутого t-распределений». Журнал прикладной статистической науки. 10 (2): 119–136.
- Чакраборти, А.К.; Мутуши, К. (2013). «О многомерном сложенном нормальном распределении». Санкхья Б. 75 (1): 1–15.
Внешние ссылки
 . μ = 1, σ = 1
. μ = 1, σ = 1 . μ = 1, σ = 1
. μ = 1, σ = 1
![{\ frac {1} {2}} \ left [{\ t_dv {erf}} \ left ({\ frac {x + \ mu} {\ sigma {\ sqrt {2}}) }} \ right) + {\ t_dv {erf}} \ left ({\ frac {x- \ mu} {\ sigma {\ sqrt {2}}}} \ right) \ right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad88ca4e426758e5b8472945b7562acc5db7d03b)



 ,
,![{\ displaystyle F_ {Y} (x; \ mu, \ sigma ^ {2}) = {\ frac {1} {2}} \ left [{\ t_dv {erf}} \ left ({\ frac {x + \ mu} {\ sqrt {2 \ sigma ^ {2}}}}} \ right) + {\ t_dv {erf}} \ left ({\ frac {x- \ mu} {\ sqrt {2 \ sigma ^ {2}}}} \ right) \ right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bbf74023157cbecf10c9340dd9a0bfe09e3f4f1b)

![{\ displaystyle \ mu _ {Y} = {\ sqrt {\ frac {2} {\ pi}}} \ sigma e ^ {- {\ frac {\ mu ^ {2}} { 2 \ sigma ^ {2}}}} + \ mu \ left [1-2 \ Phi \ left (- {\ frac {\ mu} {\ sigma}} \ right) \ right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd5bfcd3dc54605d03817a06f63bebc3a87ca556)

![{\ displaystyle \ Phi (x) \; = \; {\ frac {1} {2}} \ left [1+ \ operatorname {erf} \ left ({\ frac {x} {\ sqrt {2}}} \ right) \ right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d4a69ed96ae507f5766a6d5b8a23da4eeec1109)











![{\ displaystyle K_ {x} \ left (t \ right) = \ log {M_ {x} \ left (t \ right)} = \ left ({\ frac {\ sigma ^ {2} t ^ {2}) } {2}} + \ mu t \ right) + \ log {\ left \ lbrace 1- \ Phi \ left (- {\ frac {\ mu} {\ sigma}} - \ sigma t \ right) + e ^ {{\ frac {\ sigma ^ {2} t ^ {2}} {2}} - \ mu t} \ left [1- \ Phi \ left ({\ frac {\ mu} {\ sigma}} - \ сигма т \ право) \ право] \ право \ rbrace}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/18260983046f5c9d546d518542872acee9d90678)
![{\ displaystyle E \ left (e ^ {- tx} \ right) = e ^ {{\ frac {\ sigma ^ {2} t ^ {2}} {2}} - \ mu t} \ left [1- \ Phi \ left ( - {\ frac {\ mu} {\ sigma}} + \ sigma t \ right) \ right] + e ^ {{\ frac {\ sigma ^ {2} t ^ {2}} {2}} + \ mu t} \ left [1- \ Phi \ left ({\ frac {\ mu} {\ sigma}} + \ sigma t \ right) \ right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bcf88b418505cfad95c727604e731d1801bfa53d)
![{\ displaystyle {\ hat {f}} \ left (t \ right) = \ phi _ {x} \ left (-2 \ pi t \ right) = e ^ {{\ frac {-4 \ pi ^ {2} \ sigma ^ {2} t ^ { 2}} {2}} - i2 \ pi \ mu t} \ left [1- \ Phi \ left (- {\ frac {\ mu} {\ sigma}} - i2 \ pi \ sigma t \ right) \ right ] + e ^ {- {\ frac {4 \ pi ^ {2} \ sigma ^ {2} t ^ {2}} {2}} + i2 \ pi \ mu t} \ left [1- \ Phi \ left ({\ гидроразрыва {\ mu} {\ sigma}} - i2 \ pi \ sigma t \ right) \ right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea9915664db6c8d360efec8ee9b94e9d45e8408c)



















