| Граф свернутого куба | |
|---|---|
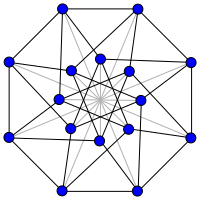 Граф свернутого куба порядка 5 (т. Е. граф Клебша ). Граф свернутого куба порядка 5 (т. Е. граф Клебша ). | |
| Вершины | 2 |
| Ребра | 2n |
| Диаметр | этаж (n / 2) |
| Хроматическое число | 2 (для четных n) или 4 (если нечетное). |
| Свойства | Регулярный граф. Гамильтониан. Дистанционно-транзитивный. |
| Таблица графиков и параметров | |
В теории графов, свернутый граф куба - это неориентированный граф, сформированный из графа гиперкуба путем добавления к нему идеального соответствия, соединяющего противоположные пары гиперкуба вершины.
Сложенный куб-граф порядка k (содержащий 2 вершины es) может быть образован путем добавления ребер между противоположными парами вершин в графе гиперкуба порядка k - 1. (В гиперкубе с двумя вершинами пары вершин противоположны, если кратчайший путь между ними имеет длину n.), эквивалентно, быть сформированным из графа гиперкуба (также) порядка k, который имеет вдвое больше вершин, посредством идентификации вместе (или сжатия) каждой противоположной пары вершин.
Граф свернутого куба порядка k является k- регулярным с 2 вершинами и 2k ребрами.
хроматическое число графа свернутого куба порядка k равно двум, когда k четное (то есть в данном случае граф двудольный ) и четыре когда k нечетное. Нечетный обхват свернутого куба нечетного порядка равен k, поэтому для нечетных k больше трех графы свернутого куба обеспечивают класс графов без треугольников с хроматическим числом четыре и произвольно большой лишний обхват. Как дистанционно регулярный граф с нечетным обхватом k и диаметром (k - 1) / 2, свернутые кубы нечетного порядка являются примерами обобщенных нечетных графов.
Когда k нечетно, двудольное двойное покрытие свернутого куба порядка k - это куб порядка k, из которого оно образовано. Однако, когда k четно, куб порядка k является двойным покрытием, но не двудольным двойным покрытием. В этом случае свернутый куб уже сам двудольный. Сложенные кубические графы наследуют от своих подграфов гиперкубов свойство иметь гамильтонов цикл, а от гиперкубов, которые их дважды покрывают, свойство быть дистанционно-транзитивным графом.
Когда k нечетно, свернутый куб порядка k содержит в качестве подграфа полное двоичное дерево с 2–1 узлами. Однако, когда k четно, это невозможно, потому что в этом случае свернутый куб представляет собой двудольный граф с равным числом вершин по обе стороны от двудольного раздела, что сильно отличается от отношения почти два к одному для двудольного графа. полное двоичное дерево.
В параллельных вычислениях свернутые кубические графы изучались как потенциальная топология сети в качестве альтернативы гиперкубу. По сравнению с гиперкубом свернутый куб с таким же количеством узлов имеет почти такую же степень вершины, но только половину диаметра . Известны эффективные распределенные алгоритмы (по сравнению с алгоритмами для гиперкуба) для широковещательной передачи информации в свернутом кубе.