Flux

Понятие в естествознании и математике Линии поля векторного поля Fчерез поверхности с единица нормальный n, угол от n до F равен θ. Поток - это мера того, какая часть поля проходит через данную поверхность. F разбивается на компоненты, перпендикулярные (⊥) и параллельные (‖) к n . Только параллельная составляющая вносит вклад в поток, потому что это максимальная протяженность поля, проходящего через поверхность в точке, перпендикулярная составляющая не влияет. Вверху: Три силовые линии через плоскую поверхность, одна нормальная к поверхности, одна параллельная и одна промежуточная. Внизу: Линия поля через изогнутую поверхность, показывающая настройку единичной нормали и элемента поверхности для вычисления потока. 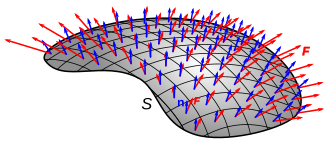Для вычисления потока векторного поля $F\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{F\}\}$(красные стрелки) через поверхность $S\; \{\backslash \; displaystyle\; S\}$поверхность разделена на небольшие участки $d\; S\; \{\; \backslash \; Displaystyle\; dS\}$. Поток через каждый участок равен нормальному (перпендикулярному) компоненту поля, точечному произведению из $F\; (x)\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{F\}\; (\backslash \; mathbf\; \{x\})\; \}$с единичным вектором нормали $n\; (x)\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{n\}\; (\backslash \; mathbf\; \{x\})\}$(синие стрелки) в точке $x\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{x\}\}$, умноженное на площадь $d\; S\; \{\backslash \; displaystyle\; dS\}$. Сумма $F\; \cdot \; nd\; S\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{F\}\; \backslash \; cdot\; \backslash \; mathbf\; \{n\}\; dS\}$для каждого фрагмента на поверхности - это поток через поверхность

Flux описывает любой эффект, который кажется проходящим или перемещающимся (независимо от того, движется он на самом деле или нет) через поверхность или вещество. Поток - это концепция в прикладной математике и векторном исчислении, которая имеет множество приложений в физике. Для явлений переноса поток - это векторная величина, описывающая величину и направление потока вещества или свойства. В векторном исчислении поток - это скалярная величина, определяемая как поверхностный интеграл перпендикулярной компоненты векторного поля над поверхностью.

Содержание

• 1 Терминология
• 2 Поток как расход на единицу площади
  • 2.1 Общее математическое определение (транспорт)
    • 2.1.1 Свойства
  • 2.2 Транспортные потоки
    • 2.2.1 Химические вещества диффузия
  • 2.3 Квантовая механика
• 3 Поток как поверхностный интеграл
  • 3.1 Общее математическое определение (поверхностный интеграл)
  • 3.2 Электромагнетизм
    • 3.2.1 Электрический поток
    • 3.2.2 Магнитный поток
    • 3.2.3 Поток Пойнтинга
• 4 единицы радиометрии в СИ
• 5 См. Также
• 6 Примечания
• 7 Дополнительная литература
• 8 Внешние ссылки

Терминология

Слово «поток» от на латыни : fluxus означает «течь», а fluere - «течь». Как поток, этот термин был введен в дифференциальное исчисление Исааком Ньютоном.

Концепция теплового потока была ключевым вкладом Джозефа Фурье, при анализе явлений теплообмена. Его основополагающий трактат Théorie analytique de la chaleur (Аналитическая теория тепла) определяет флюсию как центральную величину и продолжает выводить теперь хорошо известные выражения потока в терминах разницы температур на плите, а затем в более общем плане в терминах температурные градиенты или перепады температур в других геометрических формах. Можно утверждать, основываясь на работе Джеймса Клерка Максвелла, что определение переноса предшествует определению потока , используемому в электромагнетизме. Конкретная цитата Максвелла:

В случае потоков мы должны взять интеграл по поверхности от потока через каждый элемент поверхности. Результат этой операции называется поверхностным интегралом магнитного потока. Он представляет количество, которое проходит через поверхность.

— Джеймс Клерк Максвелл

Согласно определению переноса, поток может быть одним вектором или векторным полем / функцией положения. В последнем случае поток можно легко интегрировать по поверхности. Напротив, согласно определению электромагнетизма, поток - это интеграл по поверхности; нет смысла интегрировать поток второго определения, так как один будет интегрировать по поверхности дважды. Таким образом, цитата Максвелла имеет смысл только в том случае, если «поток» используется в соответствии с определением транспорта (и, кроме того, это векторное поле, а не одиночный вектор). Это иронично, потому что Максвелл был одним из главных разработчиков того, что мы теперь называем «электрическим потоком» и «магнитным потоком» согласно определению электромагнетизма. Их имена в соответствии с цитатой (и определением переноса) будут «поверхностный интеграл электрического потока» и «поверхностный интеграл магнитного потока», и в этом случае «электрический поток» вместо этого будет определяться как «электрическое поле» и «магнитный поток». «определяется как« магнитное поле ». Это означает, что Максвелл воспринимал эти поля как потоки / потоки некоего вида.

Учитывая магнитный поток согласно определению электромагнетизма, соответствующая плотность потока, если используется этот термин, относится к его производной вдоль поверхности, которая была интегрирована. Согласно Фундаментальной теореме исчисления соответствующая плотность потока представляет собой поток согласно определению переноса. Учитывая ток, такой как электрический ток - заряд за время, плотность тока также будет потоком в соответствии с определением переноса - заряд за время на площадь. Из-за противоречивых определений потока и взаимозаменяемости потоков, потока и тока в нетехническом английском языке все термины, используемые в этом параграфе, иногда используются взаимозаменяемо и неоднозначно. Конкретные флюсы в остальной части этой статьи будут использоваться в соответствии с их широким признанием в литературе, независимо от того, какому определению флюса соответствует этот термин.

Поток как расход на единицу площади

В явлениях переноса (теплопередача, массоперенос и гидродинамика ), поток определяется как скорость потока свойства на единицу площади, которая имеет размеры [количество] · [время] · [площадь]. Площадь - это поверхность, «через которую» проходит собственность. Например, величина речного течения, то есть количество воды, протекающей через поперечное сечение реки каждую секунду, или количество солнечной энергии, попадающей на участок земли каждую секунду, являются разновидностями потока.

Общее математическое определение (транспорт)

Вот 3 определения в порядке возрастания сложности. Каждый из них является частным случаем следующего. Во всех случаях частый символ j (или J) ​​используется для потока, q для физической величины, которая течет, t для времени и A для площади. Эти идентификаторы будут выделены жирным шрифтом только тогда, когда они являются векторами.

Во-первых, поток как (одиночный) скаляр:

$j\; =\; IA\; \{\backslash \; displaystyle\; j\; =\; \{\backslash \; frac\; \{I\}\; \{A\}\}\}$

где:

$I\; =\; lim\; \Delta \; t\; \to \; 0\; \Delta \; q\; \Delta \; t\; =\; dqdt\; \{\backslash \; displaystyle\; I\; =\; \backslash \; lim\; \backslash \; limits\; \_\; \{\backslash \; Delta\; t\; \backslash \; rightarrow\; 0\}\; \{\backslash \; frac\; \{\backslash \; Delta\; q\}\; \{\backslash \; Delta\; t\}\}\; =\; \{\backslash \; frac\; \{\backslash \; mathrm\; \{d\; \}\; q\}\; \{\backslash \; mathrm\; \{d\}\; t\}\}\}$

В этом случае поверхность, на которой измеряется поток, является фиксированной и имеет площадь A. Поверхность считается плоской, а поток считается равным везде постоянна относительно положения и перпендикулярна поверхности.

Во-вторых, поток как скалярное поле, определенное вдоль поверхности, то есть функция точек на поверхности:

$j\; (p)\; =\; \partial \; I\; \partial \; A\; (p)\; \{\backslash \; displaystyle\; j\; (\backslash \; mathbf\; \{p\})\; =\; \{\backslash \; frac\; \{\backslash \; partial\; I\}\; \{\backslash \; partial\; A\}\}\; (\backslash \; mathbf\; \{p\})\}$

$I\; (A,\; p)\; =\; dqdt\; (A,\; p)\; \{\backslash \; displaystyle\; I\; (A,\; \backslash \; mathbf\; \{p\})\; =\; \{\backslash \; frac\; \{\backslash \; mathrm\; \{d\}\; q\}\; \{\backslash \; mathrm\; \{d\}\; t\}\}\; (A,\; \backslash \; mathbf\; \{p\})\}$

Как и раньше, поверхность считается плоским, а течение всюду перпендикулярно ему. Однако поток не обязательно должен быть постоянным. q теперь является функцией p, точки на поверхности, и A, площади. Вместо того, чтобы измерять общий поток через поверхность, q измеряет поток через диск с площадью A с центром в точке p вдоль поверхности.

Наконец, поток как векторное поле :

$j\; (p)\; =\; \partial \; I\; \partial \; A\; (p)\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{j\}\; (\backslash \; mathbf\; \{p\})\; =\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; mathbf\; \{I\}\}\; \{\backslash \; partial\; A\}\}\; (\backslash \; mathbf\; \{p\})\}$

$I\; (A,\; p)\; =\; argmaxn\; ^\; n\; ^\; pdqdt\; (A,\; p,\; n\; ^)\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{I\}\; (A,\; \backslash \; mathbf\; \{p\})\; =\; \{\backslash \; underset\; \{\backslash \; mathbf\; \{\backslash \; hat\; \{n\}\}\}\; \{\backslash \; operatorname\; \{arg\; \backslash ,\; max\}\}\}\; \backslash ,\; \backslash \; mathbf\; \{\backslash \; hat\; \{n\}\}\; \_\; \{\backslash \; mathbf\; \{p\}\}\; \{\backslash \; frac\; \{\backslash \; mathrm\; \{d\}\; q\}\; \{\backslash \; mathrm\; \{d\}\; t\}\}\; (A,\; \backslash \; mathbf\; \{p\},\; \backslash \; mathbf\; \{\backslash \; hat\; \{n\}\})\}$

В этом случае нет фиксированной поверхности, над которой мы проводим измерения. q является функцией точки, площади и направления (заданного единичным вектором, $n\; ^\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{\backslash \; hat\; \{n\}\}\}$) и измеряет поток через диск площади А перпендикулярно этому единичному вектору. I определяется выбором единичного вектора, который максимизирует поток вокруг точки, потому что истинный поток максимизируется через диск, который перпендикулярен ему. Таким образом, единичный вектор однозначно максимизирует функцию, когда он указывает в «истинном направлении» потока. [Строго говоря, это злоупотребление нотацией, потому что «arg max» не может напрямую сравнивать векторы; вместо этого мы берем вектор с наибольшей нормой.]

Свойства

Эти прямые определения, особенно последнее, довольно громоздки. Например, конструкция argmax является искусственной с точки зрения эмпирических измерений, когда с помощью флюгера или аналогичного можно легко определить направление потока в точке. Вместо того, чтобы напрямую определять векторный поток, часто бывает более интуитивно понятно указать некоторые его свойства. Кроме того, по этим свойствам в любом случае можно однозначно определить поток.

Если поток j проходит через область под углом θ к нормали области $n\; ^\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{\backslash \; hat\; \{n\}\}\}$, затем

$j\; \cdot \; N\; ^\; =\; j\; cos\; \; \theta \; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{j\}\; \backslash \; cdot\; \backslash \; mathbf\; \{\backslash \; hat\; \{n\}\}\; =\; j\; \backslash \; cos\; \backslash \; theta\}$

где · - это скалярное произведение единичных векторов. Таким образом, составляющая потока, проходящего через поверхность (т.е. нормальная к ней), равна j cos θ, в то время как составляющая потока, проходящего по касательной к области, равна j sin θ, но поток, фактически проходящий через область в касательной направление. Единственная составляющая потока, проходящего по нормали к площади, - это косинусная составляющая.

Для векторного потока поверхностный интеграл от j по поверхности S дает правильное течение в единицу времени через поверхность.

$dqdt\; =\; \iint \; S\; J\; \cdot \; N\; ^\; d\; A\; =\; \iint \; S\; J\; \cdot \; d\; A\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; mathrm\; \{d\}\; q\}\; \{\backslash \; mathrm\; \{d\}\; t\}\}\; =\; \backslash \; iint\; \_\; \{S\}\; \backslash \; mathbf\; \{j\}\; \backslash \; cdot\; \backslash \; mathbf\; \{\backslash \; hat\; \{n\}\}\; \backslash ,\; \{\backslash \; rm\; \{d\}\}\; A\; \backslash \; =\; \backslash \; iint\; \_\; \{S\}\; \backslash \; mathbf\; \{j\}\; \backslash \; cdot\; \{\backslash \; rm\; \{d\}\}\; \backslash \; mathbf\; \{A\}\}$

A(и его бесконечно малая величина) - это векторная область, комбинация величины области, через которую проходит свойство, A, и единичного вектора, нормального к площадь, $n\; ^\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{\backslash \; hat\; \{n\}\}\}$. Отношение следующее: $A\; =\; A\; n\; ^\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{A\}\; =\; A\; \backslash \; mathbf\; \{\backslash \; hat\; \{n\}\}\}$. В отличие от второй системы уравнений, здесь поверхность не обязательно должна быть плоской.

Наконец, мы можем снова интегрировать в течение промежутка времени от t 1 до t 2, получая общий объем свойства, протекающего через поверхность за это время (t 2 - t 1):

$q\; =\; \int \; t\; 1\; t\; 2\; \iint \; S\; j\; \cdot \; d\; A\; dt\; \{\backslash \; displaystyle\; q\; =\; \backslash \; int\; \_\; \{t\_\; \{1\}\}\; ^\; \{t\_\; \{2\}\}\; \backslash \; iint\; \_\; \{S\}\; \backslash \; mathbf\; \{j\}\; \backslash \; cdot\; \{\backslash \; rm\; \{d\}\}\; \{\backslash \; mathbf\; \{A\}\}\; \backslash ,\; \{\backslash \; rm\; \{d\}\}\; t\}$

Транспортные потоки

Восемь наиболее распространенных форм потока из литературы по явлениям переноса определены следующим образом:

1. Поток импульса, скорость передачи импульса через единицу площади (N ·смс). (Закон вязкости Ньютона )
2. Тепловой поток, скорость теплового потока через единицу площади (Дж · м · с). (Закон проводимости Фурье ) (Это определение теплового потока соответствует первоначальному определению Максвелла.)
3. Диффузионный поток, скорость движения молекул через единицу площади (моль · м · с). (Закон диффузии Фика )
4. Объемный поток, скорость объемного потока через единицу площади (м · м · с). (Закон Дарси потока грунтовых вод )
5. Поток массы, скорость потока массы через единицу площади (кг · м · с) (либо альтернативная форма закона Фика, которая включает молекулярную массу, либо альтернативную форму закона Дарси, которая включает плотность)
6. Поток излучения, количество энергии, переданное в виде фотонов на определенном расстоянии от источника на единицу площади в секунду (Дж · м · с). Используется в астрономии для определения звездная величина и спектральный класс звезды. Также действует как обобщение теплового потока, который равен радиационному f люкс при ограничении электромагнитным спектром.
7. Поток энергии, скорость передачи энергии через единицу площади (Дж · м · с). Поток излучения и тепловой поток являются частными случаями потока энергии.
8. , скорость переноса частиц через единицу площади ([число частиц] м · с)

Эти потоки являются векторами в каждой точке. в космосе и имеют определенную величину и направление. Кроме того, можно использовать расхождение любого из этих потоков, чтобы определить скорость накопления количества в контрольном объеме вокруг данной точки пространства. Для несжимаемого потока расхождение объемного потока равно нулю.

Химическая диффузия

Как упоминалось выше, химический молярный поток компонента A в изотермической, изобарной системе равен определено в законе диффузии Фика как:

$JA\; =\; -\; DAB\; \nabla \; c\; A\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{J\}\; \_\; \{A\}\; =\; -\; D\_\; \{AB\}\; \backslash \; nabla\; c\_\; \{A\}\}$

, где символ набла ∇ обозначает оператор градиента, D AB - коэффициент диффузии (м · с) компонента A, диффундирующего через компонент B, c A - концентрация (моль / м) компонента A.

Этот поток имеет единицы моль · м · с и соответствует Первоначальное определение потока Максвелла.

Для разреженных газов кинетическая молекулярная теория связывает коэффициент диффузии D с плотностью частиц n = N / V, молекулярной массой m, сечением столкновения $\sigma \; \{\backslash \; displaystyle\; \backslash \; sigma\}$, а абсолютная температура T на

$D\; =\; 2\; 3\; n\; \sigma \; k\; T\; \pi \; m\; \{\backslash \; displaystyle\; D\; =\; \{\backslash \; frac\; \{\; 2\}\; \{3n\; \backslash \; sigma\}\}\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{kT\}\; \{\backslash \; pi\; m\}\}\}\}$

где второй факт r - это средний свободный пробег, а квадратный корень (с постоянной Больцмана k) - это средняя скорость частиц.

В турбулентных потоках перенос за счет вихревого движения можно выразить как сильно увеличенный коэффициент диффузии.

Квантовая механика

В квантовой механике частицы массы m в квантовом состоянии ψ(r, t) имеют плотность вероятности определяется как

$\rho \; =\; \psi \; \ast \; \psi \; =\; |\; \psi \; |\; 2.\; \{\backslash \; displaystyle\; \backslash \; rho\; =\; \backslash \; psi\; ^\; \{*\}\; \backslash \; psi\; =\; |\; \backslash \; psi\; |\; ^\; \{2\}.\; \backslash ,\}$

Таким образом, вероятность нахождения частицы в дифференциальном элементе объема drравна

$d\; P\; =\; |\; \psi \; |\; 2\; д\; 3\; р.\; \{\backslash \; displaystyle\; \{\backslash \; rm\; \{d\}\}\; P\; =\; |\; \backslash \; psi\; |\; ^\; \{2\}\; \{\backslash \; rm\; \{d\}\}\; ^\; \{3\}\; \backslash \; mathbf\; \{r\}.\; \backslash ,\}$

Тогда количество частиц, проходящих перпендикулярно через единицу площади поперечного сечения в единицу времени - поток вероятности;

$J\; =\; i\; \hslash \; 2\; m\; (\psi \; \nabla \; \psi \; \ast \; -\; \psi \; \ast \; \nabla \; \psi ).\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{J\}\; =\; \{\backslash \; frac\; \{i\; \backslash \; hbar\}\; \{2m\}\}\; \backslash \; left\; (\backslash \; psi\; \backslash \; nabla\; \backslash \; psi\; ^\; \{*\}\; -\; \backslash \; psi\; ^\; \{*\}\; \backslash \; nabla\; \backslash \; psi\; \backslash \; right).\; \backslash ,\}$

Иногда это называют током вероятности или плотностью тока, или плотностью потока вероятности.

Поток как интеграл поверхности

Визуализируемый поток. Кольца показывают границы поверхности. Красные стрелки обозначают поток зарядов, жидких частиц, субатомных частиц, фотонов и т. Д. Число стрелок, которые проходят через каждое кольцо, и есть поток.

Общее математическое определение (интеграл по поверхности)

Как математическая концепция, поток представлен интегралом поверхности векторного поля,

$\Phi \; F\; =\; \iint \; AF\; \cdot \; d\; A\; \{\backslash \; displaystyle\; \backslash \; Phi\; \_\; \{F\}\; =\; \backslash \; iint\; \_\; \{A\}\; \backslash \; mathbf\; \{F\}\; \backslash \; cdot\; \backslash \; mathrm\; \{d\}\; \backslash \; mathbf\; \{A\}\}$

$\Phi \; F\; =\; \iint \; AF\; \cdot \; nd\; A\; \{\backslash \; displaystyle\; \backslash \; Phi\; \_\; \{F\}\; =\; \backslash \; iint\; \_\; \{A\}\; \backslash \; mathbf\; \{F\}\; \backslash \; cdot\; \backslash \; mathbf\; \{\; n\}\; \backslash \; mathrm\; \{d\}\; A\}$

где F - это векторное поле, а dA - это векторная область поверхности A, направленная как нормаль к поверхности . Для второго n - направленный наружу единичный вектор нормали к поверхности.

Поверхность должна быть ориентируемой, т. Е. Можно различать две стороны: поверхность не загибается сама на себя. Кроме того, поверхность должна быть действительно ориентирована, то есть мы используем соглашение о том, какое направление считается положительным; обратный поток считается отрицательным.

Нормаль к поверхности обычно направляется правилом правой руки.

И наоборот, можно рассматривать поток как более фундаментальную величину и называть векторное поле плотностью потока.

Часто векторное поле рисуется кривыми (линиями поля), следующими за «потоком»; величина векторного поля - это плотность линий, а поток через поверхность - это количество линий. Линии берут начало в областях положительной дивергенции (источники) и заканчиваются в областях отрицательной дивергенции (опускания).

См. Также изображение справа: количество красных стрелок, проходящих через единицу площади, - это плотность потока, кривая , окружающая красные стрелки, обозначает границу поверхности и ориентацию стрелок относительно поверхности обозначает знак внутреннего произведения векторного поля с нормалями поверхности.

Если поверхность охватывает трехмерную область, обычно поверхность ориентирована так, что приток считается положительным; противоположным является исходящий поток .

Теорема дивергенции утверждает, что чистый исходящий поток через замкнутую поверхность, другими словами чистый исходящий поток из трехмерной области, находится путем добавления локального чистого исходящего потока из каждая точка в регионе (что выражается расхождением ).

Если поверхность не замкнута, она имеет ориентированную кривую в качестве границы. Теорема Стокса утверждает, что поток ротора векторного поля является линейным интегралом векторного поля над этой границей. Этот интеграл по траекториям также называется циркуляцией, особенно в гидродинамике. Таким образом, завиток - это плотность циркуляции.

Мы можем применить поток и эти теоремы ко многим дисциплинам, в которых мы видим токи, силы и т. Д., Приложенные через области.

Электромагнетизм

Один из способов лучше понять концепцию магнитного потока в электромагнетизме - это сравнить его с сеткой для бабочек. Количество воздуха, проходящего через сеть в любой момент времени, и есть поток. Если скорость ветра высока, то поток через сеть велик. Если сеть сделать больше, то поток будет больше, даже если скорость ветра такая же. Чтобы через сетку проходила большая часть воздуха, отверстие в сети должно быть обращено в сторону ветра. Если сетка параллельна ветру, то ветер не будет двигаться через сетку. Самый простой способ представить себе поток - это «сколько воздуха проходит через сеть», где воздух - это поле скорости, а сеть - это граница воображаемой поверхности.

Электрический поток

Электрический «заряд», такой как одиночный электрон в космосе, имеет величину, определенную в кулонах. Такой заряд окружает электрическое поле. В графической форме электрическое поле показано в виде точки, излучающей «линии потока», называемые линиями Гаусса. Плотность электрического потока - это количество электрического потока, количество «линий», проходящих через данную область. Единицы измерения: Гаусс / квадратный метр.

Используются две формы электрического потока, одна для поля E :

$\Phi \; E\; =\; \{\backslash \; displaystyle\; \backslash \; Phi\; \_\; \{E\}\; =\}$$A\; \{\backslash \; displaystyle\; \{\backslash \; scriptstyle\; A\}\}$$E\; \cdot \; d\; A\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{E\}\; \backslash \; cdot\; \{\backslash \; rm\; \{d\}\}\; \backslash \; mathbf\; \{A\}\}$

и один для поля D (называемого электрическим смещением ):

$\Phi \; D\; =\; \{\backslash \; displaystyle\; \backslash \; Phi\; \_\; \{D\}\; =\}$$A\; \{\backslash \; displaystyle\; \{\backslash \; scriptstyle\; A\}\}$$D\; \cdot \; d\; A\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{D\}\; \backslash \; cdot\; \{\backslash \; rm\; \{d\}\}\; \backslash \; mathbf\; \{A\}\}$

Это количество возникает в законе Гаусса, который гласит, что поток электрического поля Eиз замкнутой поверхности пропорционален электрическому заряду QAвнутри на поверхности (независимо от того, как этот заряд распределяется), интегральная форма имеет вид:

$A\; \{\backslash \; displaystyle\; \{\backslash \; scriptstyle\; A\}\}$$E\; \cdot \; d\; A\; =\; QA\; \epsilon \; 0\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{E\}\; \backslash \; cdot\; \{\backslash \; rm\; \{d\}\}\; \backslash \; mathbf\; \{A\}\; =\; \{\backslash \; frac\; \{Q\_\; \{A\}\}\; \{\backslash \; varepsilon\; \_\; \{0\}\}\}\}$

где ε 0 - диэлектрическая проницаемость свободного пространства.

Если рассматривать поток вектора электрического поля, E, для трубки около точечного заряда в поле заряда, но не содержащей его со сторонами, образованными касательными к полю линиями, поток для сторон равен нулю, и на обоих концах трубки имеется равный и противоположный поток. Это следствие закона Гаусса, примененного к полю обратных квадратов. Флюс для любой поверхности поперечного сечения трубки будет одинаковым. Общий поток для любой поверхности, окружающей заряд q, равен q / ε 0.

В свободном пространстве электрическое смещение задается определяющим соотношением D= ε 0E, поэтому для любого ограничивающей поверхности поток поля D равен заряду Q A внутри нее. Здесь выражение «поток» указывает на математическую операцию, и, как можно видеть, результат не обязательно является «потоком», поскольку на самом деле ничто не течет вдоль силовых линий электрического поля.

Магнитный поток

Плотность магнитного потока (магнитное поле ), имеющая единицы Вт / м (Тесла ), обозначается B, а магнитный поток определяется аналогично:

$\Phi \; B\; =\; \{\backslash \; displaystyle\; \backslash \; Phi\; \_\; \{B\}\; =\}$$A\; \{\backslash \; displaystyle\; \{\backslash \; scriptstyle\; A\}\}$$B\; \cdot \; d\; A\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{B\}\; \backslash \; cdot\; \{\backslash \; rm\; \{d\}\}\; \backslash \; mathbf\; \{A\}\}$

с тем же обозначением, указанным выше. Величина возникает в законе индукции Фарадея, где магнитный поток зависит от времени либо потому, что граница зависит от времени, либо потому, что магнитное поле зависит от времени. В интегральной форме:

$-\; d\; \Phi \; B\; dt\; =\; \oint \; \partial \; AE\; \cdot \; d\; \ell \; \{\backslash \; displaystyle\; -\; \{\backslash \; frac\; \{\{\backslash \; rm\; \{d\}\}\; \backslash \; Phi\; \_\; \{B\}\}\; \{\{\backslash \; rm\; \{d\}\}\; t\; \}\}\; =\; \backslash \; oint\; \_\; \{\backslash \; partial\; A\}\; \backslash \; mathbf\; \{E\}\; \backslash \; cdot\; d\; \{\backslash \; boldsymbol\; \{\backslash \; ell\}\}\}$

где d ℓ - бесконечно малый вектор линейный элемент замкнутой кривой $\partial \; A\; \{\backslash \; displaystyle\; \backslash \; partial\; A\}$, с величиной , равной длине бесконечно малой линейный элемент и направление, заданное касательной к кривой $\partial \; A\; \{\backslash \; displaystyle\; \backslash \; partial\; A\}$, причем знак определяется направлением интегрирования.

Скорость изменения магнитного потока через проволочную петлю составляет минус электродвижущая сила, созданная в этом проводе. Направление таково, что если позволить току проходить через провод, электродвижущая сила вызовет ток, который «противодействует» изменению магнитного поля, создавая магнитное поле, противоположное изменению. Это основа для индукторов и многих электрических генераторов.

Поток Пойнтинга

Используя это определение, поток вектора Пойнтинга Sнад заданной поверхностью - скорость, с которой электромагнитная энергия проходит через эту поверхность, определенная так же, как и раньше:

$\Phi \; S\; =\; \{\backslash \; displaystyle\; \backslash \; Phi\; \_\; \{S\}\; =\}$$A\; \{\backslash \; displaystyle\; \{\backslash \; scriptstyle\; A\}\}$$S\; \cdot \; d\; A\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{S\}\; \backslash \; cdot\; \{\backslash \; rm\; \{d\}\}\; \backslash \; mathbf\; \{A\}\}$

Поток вектора Пойнтинга через поверхность является электромагнитным мощность или энергия на единицу времени, проходящую через эту поверхность. Это обычно используется при анализе электромагнитного излучения, но также применяется к другим электромагнитным системам.

Как ни странно, вектор Пойнтинга иногда называют потоком мощности, что является примером первого использования потока, описанного выше. Он имеет единицы измерения ватт на квадратный метр (Вт / м).

Радиометрические единицы SI

Радиометрические единицы SI

• v
• t

Количество		Единица		Размер	Примечания
Имя	Символ	Название	Символ	Символ
Лучистая энергия	Qe	джоуль	J	M⋅L⋅T	Энергия электромагнитного излучения.
Плотность лучистой энергии	we	джоуль на кубический метр	Дж / м	M⋅L⋅T	Лучистая энергия на единицу объема.
Лучистый поток	Φe	ватт	W = Дж / с	M⋅L⋅T	Излучаемая, отраженная, переданная или полученная энергия излучения за единицу времени. Иногда это также называют «сияющей силой».
Спектральный поток	Φe, ν	ватт на герц	W/Hz	M⋅L⋅T	Лучистый поток на единицу частоты или длины волны. Последний обычно измеряется в W⋅nm.
	Φe, λ	ватт на метр	Вт / м	M⋅L⋅T
Сила излучения	Ie, Ом	ватт на стерадиан	W/sr	M⋅L⋅T	Излучаемый, отраженный поток излучения, переданные или принятые на единицу телесного угла. Это направленная величина.
Спектральная интенсивность	Ie, Ом, ν	ватт на стерадиан на герц	Вт⋅ср⋅Гц	M⋅L⋅T	Интенсивность излучения на единицу частоты или длины волны. Последний обычно измеряется в W⋅sr⋅nm. Это направленная величина.
	Ie, Ом, λ	ватт на стерадиан на метр	Вт⋅см	M⋅L⋅T
Сияние	Le, Ом	ватт на стерадиан на квадратный метр	W⋅sr⋅m	M⋅T	Поток излучения, излучаемый, отраженный, передаваемый или принимаемый поверхностью, на единицу телесного угла на единицу площади проекции. Это направленная величина. Иногда это также ошибочно называют «интенсивностью».
Спектральная яркость	Lе, Ом, ν	ватт на стерадиан на квадратный метр на герц	Вт⋅ср⋅м⋅Гц	M⋅T	Светимость поверхности на единицу частоты или длины волны. Последний обычно измеряется в W⋅sr⋅m⋅nm. Это направленная величина. Иногда это также неправильно называют «спектральной интенсивностью».
	Le, Ом, λ	ватт на стерадиан на квадратный метр, на метр	Вт⋅см	M⋅L⋅T
Энергия излучения. Плотность потока	Ee	ватт на квадратный метр	Вт / м	M⋅T	Поток излучения, принимаемый поверхностью на единицу площади. Иногда это также ошибочно называют «интенсивностью».
Спектральная освещенность. Спектральная плотность потока	Ee, ν	ватт на квадратный метр на герц	Вт · м · Гц	M⋅T	Энергия излучения поверхности на единицу частоты или длины волны. Иногда это также ошибочно называют «спектральной интенсивностью». Единицы измерения спектральной плотности потока, не входящие в систему СИ, включают jansky (1 Ян = 10 Вт⋅м⋅Гц) и единицу солнечного потока (1 sfu = 10 Вт⋅мГц = 10 Ян.).
	Ee, λ	ватт на квадратный метр на метр	Вт / м	M⋅L⋅T
Излучение	Je	ватт на квадратный метр	Вт / м	M⋅T	Лучистый поток оставляя (излучаемый, отраженный и проходящий) поверхность на единицу площади. Иногда это также ошибочно называют «интенсивностью».
Спектральная светимость	Jе, ν	ватт на квадратный метр на герц	Вт⋅м⋅Гц	M⋅T	Светимость поверхности на единицу частоты или длины волны. Последний обычно измеряется в Вт⋅мнм. Иногда это также ошибочно называют «спектральной интенсивностью».
	Je, λ	ватт на квадратный метр на метр	Вт / м	M⋅L⋅T
Коэффициент излучения	Me	ватт на квадратный метр	Вт / м	M⋅T	излучающий поток, излучаемый поверхностью на единицу площади. Это излучаемая составляющая излучения. «Излучение» - это старый термин для обозначения этой величины. Иногда это также ошибочно называют «интенсивностью».
Спектральная светимость	Mе, ν	ватт на квадратный метр на герц	Вт⋅м⋅Гц	M⋅T	Световая светимость поверхности на единицу частоты или длины волны. Последний обычно измеряется в Вт⋅мнм. «Спектральный коэффициент излучения» - старый термин для обозначения этой величины. Иногда это также неправильно называют «спектральной интенсивностью».
	Me, λ	ватт на квадратный метр на метр	Вт / м	M⋅L⋅T
Излучение	He	джоуль на квадратный метр	Дж / м	M⋅T	излучающее энергия, получаемая поверхностью на единицу площади, или, что эквивалентно, освещенность поверхности, интегрированная во времени облучения. Иногда это также называют «сияющим флюенсом».
Спектральная экспозиция	Hе, ν	джоуль на квадратный метр на герц	Дж⋅м⋅Гц	M⋅T	Радиационная экспозиция поверхности на единицу частоты или длины волны. Последний обычно измеряется в Дж⋅мнм. Иногда это также называют «спектральной плотностью энергии».
	He, λ	джоуль на квадратный метр, на метр	Дж / м	M⋅L⋅T
Коэффициент излучения в полусфере	ε	Н / Д		1	Коэффициент излучения поверхности, деленный на черное тело при той же температуре, что и эта поверхность.
Спектральная полусферическая излучательная способность	εν. or. ελ	Неприменимо		1	Спектральная светимость поверхности, деленная на светимость черного тела при той же температуре, что и эта поверхность.
Направленная излучательная способность	εΩ	Н / Д		1	Сияние, излучаемое поверхностью, деленное на излучаемое черным телом при той же температуре, что и эта поверхность.
Спектральная направленная излучательная способность	εОм, ν. or. εОм, λ	Н / Д		1	Спектральная яркость, излучаемая поверхностью, деленная на яркость черного тела при той же температуре, что и эта поверхность.
Полусферическое поглощение	A	Н / Д		1	Лучистый поток, поглощаемый поверхностью, деленный на поток, принимаемый этой поверхностью. Не следует путать с «оптической плотностью ».
Спектральное полусферическое поглощение	Aν. or. Aλ	Н / Д		1	Спектральный поток, поглощаемый поверхностью, деленный на поток, принимаемый этой поверхностью. Это не следует путать с «спектральным поглощением ».
Направленное поглощение	AΩ	Нет данных		1	Излучение, поглощаемое поверхностью, деленное на яркость, падающую на эту поверхность. Не следует путать с «оптической плотностью ».
Спектральное направленное поглощение	AОм, ν. or. AОм, λ	Н / Д		1	Спектральная яркость, поглощаемая поверхностью, деленная на спектральную яркость, падающую на эту поверхность. Это не следует путать с «спектральным поглощением ».
Коэффициент отражения полусферы	R	Н / Д		1	Излучаемый поток, отраженный поверхностью, деленный на поток, принимаемый этой поверхностью.
Спектральный полусферический коэффициент отражения	Rν. or. Rλ	Н / Д		1	Спектральный поток, отраженный поверхностью, деленный на поток, принимаемый этой поверхностью.
Направленное отражение	RΩ	Н / Д		1	Сияние, отраженное поверхностью, деленное на получаемое этой поверхностью.
Спектральная отражательная способность	RΩ, ν. or. RΩ, λ	N / A		1	Спектральная яркость, отраженная поверхностью, деленная на яркость, полученную этой поверхностью.
Полусферический коэффициент пропускания	T	Н / Д		1	Излучаемый поток, передаваемый поверхностью, деленный на поток, принимаемый этой поверхностью.
Спектральный полусферический коэффициент пропускания	Tν. or. Tλ	Неприменимо		1	Спектральный поток, передаваемый поверхностью, деленный на поток, принимаемый этой поверхностью.
Направленный коэффициент пропускания	TΩ	Н / П		1	Сияние, передаваемое поверхностью, деленное на получаемое этой поверхностью.
Спектральный коэффициент направленного пропускания	TОм, ν. or. TОм, λ	Н / Д		1	Спектральная яркость, передаваемая поверхностью, деленная на яркость, принимаемую этой поверхностью.
Коэффициент затухания в полусфере	μ	обратный метр	m	L	Поток излучения, поглощаемый и рассеиваемый объемом на единицу длины, деленный на полученный этим объемом.
Spectral hemispherical attenuation coefficient	μν. or. μλ	reciprocal metre	m	L	Spectral radiant flux absorbed and scattered by a volume per unit length, divided by that received by that volume.
Directional attenuation coefficient	μΩ	reciprocal metre	m	L	Radiance absorbed and scattered by a volume per unit length, divided by that received by that volume.
Spectral directional attenuation coefficient	μΩ,ν. or. μΩ,λ	reciprocal metre	m	L	Spectral radiance absorbed and scattered by a volume per unit length, divided by that received by that volume.
See also: SI ·Radiometry ·Photometry

See also

AB magnitude Explosively pumped flux compression generator Eddy covariance flux (aka, eddy correlation, eddy flux) Fast Flux Test Facility Fluence (flux of the first sort for particle beams) Fluid dynamics Flux footprint Flux pinning Flux quantization Gauss's law Inverse-square law

Mathematics portal Jansky (non SI unit of spectral flux density) Latent heat flux Luminous flux Magnetic flux Magnetic flux quantum Neutron flux Poynting flux Poynting theorem Radiant flux Rapid single flux quantum Sound energy flux Volumetric flux (flux of the first sort for fluids) Volumetric flow rate (flux of the second sort for fluids)

Notes

• Browne, Michael, PhD (2010). Physics for Engineering and Science, 2nd Edition. Schaum Outlines. New York, Toronto: McGraw-Hill Publishing. ISBN 978-0-0716-1399-6.
• Purcell, Edward, PhD (2013). Electricity and Magnetism, 3rd Edition. Cambridge, UK: Cambridge University Press. ISBN 978110-7014022.

Further reading

• Stauffer, P.H. (2006). "Flux Flummoxed: A Proposal for Consistent Usage". Ground Water. 44(2): 125–128. doi :10.1111/j.1745-6584.2006.00197.x. PMID 16556188.

External links

• The dictionary definition of flux at Wiktionary