Автоэлектронная эмиссия

Эмиссия электронов, индуцированная электростатическим полем

Полевая электронная эмиссия, также известная как полевая эмиссия (FE) и полевая эмиссия электронов, это эмиссия электронов, индуцированная электростатическим полем. Наиболее распространенный контекст - это автоэлектронная эмиссия с твердой поверхности в вакуум. Автоэлектронная эмиссия может происходить с твердыми или жидкими поверхностями, в вакууме, жидкость (например, воздух ) или любые непроводящие или слабопроводящий диэлектрик. Вызванное полем продвижение электронов из валентной в зоны проводимости полупроводников (эффект Зинера ) также можно рассматривать как форму автоэлектронной эмиссии. Терминология является исторической, поскольку связаны поверхностным фотоэффекта, терморонной эмиссии (или эффект Ричардсона - Душмана ) и «холодной электронной эмиссии», то есть есть эмиссии электронов в сильной статике (или квазиизлуч). -статические) электрические поля были открыты и изучены независимо с 1880-х по 1930-е годы. Когда автоэлектронная эмиссия используется без квалификаторов, это обычно означает «холодная эмиссия».

Автоэлектронная эмиссия в чистых металлах происходит в сильных электрических полях : градиенты обычно превышают 1 гигавольт на метр и сильно зависят от работы выхода. В то время как источники электронов, основанные на автоэлектронной эмиссии, используют ряд применений, автоэлектронная эмиссия чаще всего дополнительным первичным источником вакуумного пробоя и электрического разряда, которые инженеры стараются предотвратить. Примеры применений для поверхностной полевой эмиссии включают создание источников ярких электронов для электронных микроскопов с высоким разрешением или индуцированных зарядов с космического корабля. Устройства, которые устраняют индуцированные заряды, называются нейтрализаторами заряда.

Полевая эмиссия была объяснена квантовым туннелированием электронов в конце 1920-х годов. Это был один из триумфов зарождающейся квантовой механики. Теория автоэлектронной эмиссии из массивных металлов была предложена Ральфом Х. Фаулером и Лотаром Вольфгангом Нордхеймом. Семейство приближенных уравнений, уравнения Фаулера - Нордгейма, названо в их честь. Строго говоря, уравнения Фаулера - Нордхейма применимы только к автоэлектронной эмиссии массивных металлов и с использованием модификаций к другим объемным кристаллическим твердым телам, но они часто используются - в качестве грубого приближения - для описания полевой эмиссии от других материалов..

• 1 Терминология и условные обозначения
• 2 Ранняя история полевой электронной эмиссии
• 3 Практические применения: прошлое и настоящее
  • 3.1 Полевая электронная микроскопия и связанные с ней основы
  • 3.2 Полевая электронная спектроскопия (электронная энергетический анализ)
  • 3.3 Полевые электронные эмиттеры как электронные пушки
  • 3.4 Атомно-острые эмиттеры
  • 3.5 Полевые источники эмиссии большой площади: вакуумная наноэлектроника
    • 3.5.1 Материальные аспекты
    • 3.5.2 Применения
  • 3.6 Пробой вакуума и явление электрического разряда
  • 3.7 Внутренний перенос электронов в мобильных устройствах
• 4 Туннелирование Фаулера - Нордхейма
  • 4.1 Введение
  • 4.2 Движущая энергия
  • 4.3 Вероятность выхода
  • 4.4 Корректировка коэффициент для барьера Шоттки-Нордхейма
  • 4,5 Ширина распада
  • 4,6 Комментарии
• 5 Распределение по полной энергии
• 6 Эмиссия электронов в холодном поле
  • 6,1 Уравнения типа Фаулера-Но рдгейма
    • 6.1.1 Введение
    • 6.1.2 Форма с нулевой температурой
    • 6.1.3 Ненулевые температуры
    • 6.1.4 Физически соответствие уравнение типа Фаулера - Нордхейма
    • 6.1.5 Рекомендуемая форма для простых вычислений типа Фаулера - Нордхейма
    • 6.1.6 Комментарии
  • 6.2 Теоретические уравнения CFE
  • 6.3 Модифицированные уравнения для излучателей большой площади
  • 6.4 Модифицированные уравнения для нанометрических излучателей
  • 6.5 Эмпирическое уравнение CFE i - V
• 7 Графики Фаулера-Нордхейма и Милликена-Лауритсена
• 8 Дополнительная теоретическая информация
• 9 См. Также
• 10 Ссылки
• 11 Дополнительная литература

Автоэлектронная эмиссия, автоэлектронная эмиссия, автоэлектронная эмиссия и автоэлектронная эмиссия - общие названия этого экспериментального явления и его теории. Здесь используется первое имя.

Туннелирование Фаулера-Нордхейма - это волново-механическое туннелирование электронов через округлый треугольный барьер, создаваемый на поверхности электронного проводника путем приложения очень сильного электрического поля. Отдельные электроны могут ускользать через туннелирование Фаулера-Нордхейма из многих материалов в различных условиях.

Холодная полевая электронная эмиссия (CFE) - это название, данное определенному режиму статистической эмиссии, в котором электроны в эмиттере изначально находятся во внутреннем термодинамическом равновесии и в большинстве излучаемых электронов выход за счет туннелирования Фаулера-Нордхейма из электронных состояний, близких к эмиттерному уровень Ферми. (Напротив, в режиме эмиссии Шоттки большая часть электронов выходит за пределы ограничения с уменьшенным полем из состояний, значительно превышающих уровень Ферми.) Многие твердые и жидкие материалы могут испускать электроны в режиме CFE. если приложено электрическое поле соответствующего размера.

Уравнения типа Фаулера - Нордхейма представьте собой семейство приближенных уравнений, выведенных для описания CFE из внутренних электронных состояний в массивных металлах. Различные члены семьи представляют разные степени приближения к реальности. Приближенные уравнения необходимы, потому что для физически реалистичных моделей туннельного барьера математически невозможно в принципе решить уравнение Шредингера точно каким-либо простым способом. Нет теоретических основанийать, что уравнения типа Фаулера-Нордхейма достоверно показывают полевую эмиссию материалов, отличных от объемных твердых описательных твердых тел.

Для металлов режим CFE распространяется до температур, превышающих комнатную. Существуют другие режимы эмиссии электронов (как «тепловая электронная эмиссия » и «эмиссия Шоттки »), которые требуют значительного внешнего источника эмиттера. Существуют также режимы эмиссии, в которых внутренние электроны не находятся в термодинамическом равновесии, а ток эмиссии, частично или полностью, определяется подачей электронов в излучающую область. Неравновесный процесс эмиссии такого типа можно назвать полевой (электронной) эмиссией, если большая часть электронов ускользает за счет туннелирования, но строго это не CFE и не точно описывается уравнением типа Фаулера-Нордхейма.

Необходима осторожность, потому что в некоторых контекстах (например, в космической технике) название «полевая эмиссия» используется к полевой эмиссии первой (полевой ионной эмиссии), а не электронов, и потому что некоторых в теоретических контекстах «полевая эмиссия» эмиссия »используется как общее название, охватывающее как полевую электронную эмиссию, так и полевую эмиссию первая.

Исторически явление автоэлектронной эмиссии было известно под разными названиями, включая «аэоны», «автоэлектронная эмиссия», «холодная эмиссия», «эмиссия с холодным катодом», «автоэлектронная эмиссия»., «Автоэлектронная эмиссия» и «Автоэлектронная эмиссия».

Уравнения в этой статье написаны с использованием Международной системы количеств (ISQ). Это современная (после 1970-х годов) международная система, основанная на системе килограмм рационализированный метр -ограмм-секунда (rmks), которая используется для определения СИ. В более старой литературе по автоэлектронной эмиссии (и статьях, которые напрямую копируют уравнения из старой литературы) используются некоторые уравнения с использованием более старой системы уравнений, в которой не используется величина ε0. В этой статье все такие уравнения были преобразованы в современную международную форму. Для наглядности это нужно делать всегда.

работа выхода обычно указывается в электронвольтах (эВ), и часто удобно измерять поля вольтах на нанометр (В / нм), значения универсальных констант, представленных здесь в единицах, включающих эВ, V и нм. Все чаще это нормальная практика в исследованиях полевых выбросов. Однако все уравнения здесь используются уравнениями, согласованными с ISQ, и остаются согласованными по размерам, как требует современная международная система. Для обозначения их числовые значения универсальных констант до семи значащих цифр. Значения получены с использованием значений фундаментальных констант за 2006 год.

Автоэлектронная эмиссия имеет долгую, сложную и запутанную историю. Этот раздел охватывает раннюю историю типа, вплоть до ввода уравнения Фаулера-Нордхейма в 1928 году.

Оглядываясь назад, кажется вероятным, что электрические разряды, которые сообщили Винклер в 1744 году, были начаты CFE с его проволочным электродом. Однако значимое расследование пришлось отложить до тех пор, пока после Дж. Дж. Томсон идентифицировал электрон в 1897 году, и до тех пор, пока не стало понятно - из работ термоэмиссия и фотоэмиссия - что электроны могут испускаться изнутри металлов (а не от молекулы газа, адсорбированных на поверхности ), и что в отсутствие приложенных полей электроны, вылетающие из металлов, должны преодолеть барьер работы выхода.

По крайней мере еще в 1913 году предполагалось, что индуцированная полем эмиссия представляет собой отдельный физический эффект. Однако методы вакуумирования и очистки были значительно улучшены, это стало прочно обоснованным. Лилиенфельд (который в первую очередь интересовался этим источником электронов для медицинских рентгеновских приложений) опубликовал в 1922 году первое четкое описание на английском языке экспериментальной феноменологии эффект, он назвал «автоэлектронной эмиссией». ". Он работал над темой в Лейпциге примерно с 1910 года. Кляйнт этой этой и другие ранние работы.

После 1922 года экспериментальный интерес, в группах, сообществ Милликеном в Калифорнийский технологический институт (Caltech) в Пасадене, Калифорния, и Госслинг в General Electric Company в Лондоне. Попытки понять автоэлектронную эмиссию включали построение экспериментальных вольт-амперных данных (IV) разными способами, чтобы найти прямолинейную Шоттки предположил в 1923 году, что этот эффект может быть вызван термически индуцированной эмиссией через барьер, зависимость увеличивался от формованного напряжения, чем линейно, но графики типа log (i) в зависимости от V не были прямыми. Если это так, то графики log (i) от √V должны быть прямыми, но это не так, как экспериментальным наблюдением лишь очень слабой температурной зависимости в CFE - мо. мент, который изначально упускался из виду.

Прорыв произошел, когда Лауритсен (и Оппенгеймер независимо друг от друга) обнаружил, что графики зависимости log (i) от 1 / V дают хорошие прямые линии. Этот результат, опубликованный Милликеном и Лауритсеном в начале 1928 года, был известен Фаулеру и Нордхейму.

Оппенгеймеру, который предсказал индуцированное полем туннелирование электронов из состояния (эффект теперь называется полевой ионизацией), существует эта зависимость i (V), существует эта зависимость в опубликованных экспериментальных результатах полевой эмиссии Милликена и Эйринга и предположил, что CFE возникает из-за индуцированного полема туннелирования электронов от атомоподобных орбиталей в поверхностных атомах металла. Альтернативная теория Фаулера-Нордхейма объяснила как открытие Милликена-Лауритсена, так и очень слабую зависимость тока от температуры. Теория Фаулера-Нордхейма предсказывала, что оба они будут следствием, если CFE будет происходить из-за индуцированного полем туннелирования из состояний типа свободных электронов в то, что мы теперь назвали бы металлической области проводимости, с электронными состояниями, занятые в соответствии со статистикой Ферми-Дирака .

У Оппенгеймера математические детали своей теории были серьезно неверны. Также была небольшая числовая ошибка в окончательном уравнении теории Фаулера-Нордхейма для CFE плотности тока : это было исправлено в статье 1929 года (Stern, Gossling Fowler 1929).

Строго говоря, если барьер поле в теории Фаулера-Нордхайма 1928 года точно пропорционально приложенному напряжению, и если площадь излучения не зависит от напряжения, согласно теории Фаулера-Нордхайма 1928 года предсказывает, что графики (log (i / V) vs. 1 / V) должны быть точными прямыми линиями. Однако современные экспериментальные методы были недостаточно хороши, чтобы различать теоретический результат Фаулера-Нордхейма и экспериментальный результат Милликена-Лауритсена.

Таким образом, к 1928 г. о происхождении CFE из массивных металлов было получено, и было получено исходное уравнение типа Фаулера-Нордхейма.

В литературе часто представленной работы Фаулера-Нордхейма как доказательство существования электрона туннелирование, как предсказывает волновая межа ханика. Если это верно, то к 1928 году волновая механика была в степени признана. Более важная роль статьи Фаулера-Нордхейма заключалась в том, что это был убедительный экспериментальный аргумент, который статистика Ферми-Дирака применяла поведение электронов в металлах, как было предложено Зоммерфельдом в 1927 году. Успех теории Фаулера - Нордхейма во многом подтвердил правильность идей Зоммерфельда и во многом помог в создании современной теории электронного зонда. В частности, исходное уравнение типа Фаулера-Нордхейма было одним из первых, которое включило статистико-механические следствия существования электронного спина в теорию экспериментального конденсированного состояния. эффект. В статье Фаулера-Нордхейма также была заложена физическая основа для единой индуцированной полем и термической эмиссии электронов. До 1928 года была выдвинута гипотеза, что в металлах существуют два типа электронов, «термоэлектроны» и «электроны проводимости», и что термически испускаемые электронные токи были вызваны испусканием термоэлементов, но что токи, испускаемые полем, были обусловлены испусканием электронов проводимости. В работе Фаулера-Нордхейма 1928 г. было высказано предположение, что термионы не должны существовать как отдельный класс внутренних электронов: электроны могут исходить из единственной зоны , занятой в соответствии со статистикой Ферми-Дирака, но испускаться статистически разными способами в разных условиях температуры и приложенного поля.

Идеи Оппенгей, Фаулера и Нордхейма также были важными стимулом для развития, по Гамову, и Герни и Кондон, позднее в 1928 году, теории радиоактивного распада ядер (посредством туннелирования альфа-частиц ). 478>

Полевая электронная микроскопия и связанные с ней основы

Как уже указывалось, первые экспериментальные работы по полевой электронной эмиссии (1910–1920) были продиктованы Желание Лилиенфельда прибор миниатюрные рентгеновские трубки для медицинских приложений. Однако преуспевать этой технологии было еще рано.

После теоретических работ Фаулера-Нордхейма в 1928 году значительный прорыв произошел с разработкой в ​​1937 году Эрвином В. Мюллером полевого электронного микроскопа сферической геометрии (FEM) (также называемый «автоэмиссионным микроскопом»). В этом приборе эмиттер электронов представляет собой заостренную проволоку с радиусом при вершине r. На расстоянии R. В микроскопе отображается изображение распределения плотности тока J на ​​вершине эмиттера с изображением изображения (R / R), обычно от 10 до 10. При исследованиях методом МКЭ радиус вершины обычно составляет от 100 нм до 1 мкм. Кончик заостренного провода, когда его называют физическим объектом, был назван «полым эмиттером», «острием» или (недавно) «эмиттером Мюллера».

Когда поверхность эмиттера чистая, это изображение МКЭ характерно для: (а) материала, из которого изготовлен эмиттер: (б) ориентации относительно оси игла / материала проволока; и (c) до некоторой формы концевой части эмиттера. На изображении МКЭ темные области соответствуют областям, где локальная работа выхода φ относительно высока и / или локальное барьерное поле F относительно низкое, поэтому J относительно низкое; светлые области соответствуют областям, где φ относительно низок и / или F относительно высок, поэтому J относительно высокое. Это предсказывается показателем степени уравнений типа Фаулера-Нордхейма [см. (30) ниже].

Адсорбция слоев атомов газа (например, кислорода) на поверхности эмиттера или ее части может создавать поверхностные электрические диполи, которые изменяют локальную работу функция этой части поверхности. Это влияет на изображение МКЭ; Кроме того, изменение работы выхода можно измерить с помощью графика Фаулера-Нордхейма (см. ниже). Таким образом, FEM стал одним из первых наблюдательных инструментов науки о поверхности. Например, в 1960-х годах результаты МКЭ внесли значительный вклад в дискуссии о гетерогенном катализе. МКЭ также использовался для исследования диффузии поверхностных атомов. Однако сейчас МКЭ почти полностью вытеснен новыми методами исследования поверхности.

Следствием разработки МКЭ и последующих экспериментов стало то, что стало возможным идентифицировать (по проверке изображения МКЭ), когда излучатель был "чистым" и, следовательно, проявлял свою работу выхода с чистой поверхностью, как установлено другие техники. Это было важно в экспериментах, направленных на проверку правильности стандартного уравнения типа Фаулера-Нордхейма. В этих экспериментах было получено значение коэффициента преобразования β из напряжения в барьерное поле из графика Фаулера-Нордхейма (см. Ниже), предполагая значение φ для чистой поверхности для вольфрама, и сравнивалось это значение со значениями, полученными из электронно- микроскоп наблюдения за формой излучателя и электростатическое моделирование. Достигнута договоренность с точностью до 10%. Лишь совсем недавно появилась возможность провести сравнение в обратном направлении, поднеся хорошо подготовленный зонд так близко к хорошо подготовленной поверхности, что можно предположить приблизительную геометрию параллельных пластин, а коэффициент преобразования можно принять равным 1 / W, где W - измеренное расстояние между зондом и эмиттером. Анализ полученного графика Фаулера-Нордхейма дает значение работы выхода, близкое к независимо известной работе выхода эмиттера.

Полевая электронная спектроскопия (анализ энергии электронов)

Измерения распределения энергии полевых электронов были впервые опубликованы в 1939 году. В 1959 году это было теоретически реализовано Янгом и подтверждено экспериментально Янгом и Мюллером. что величина, измеренная в сферической геометрии, была распределением полной энергии испущенного электрона (его «распределением полной энергии»). Это связано с тем, что в сферической геометрии электроны движутся таким образом, что угловой момент относительно точки в эмиттере почти сохраняется. Следовательно, любая кинетическая энергия , которая при излучении находится в направлении, параллельном поверхности излучателя, преобразует энергию, связанную с радиальным направлением движения. Таким образом, анализатор энергии измеряет полную энергию при излучении.

С развитием в 1960-х годах чувствительных электронных анализаторов энергии стало возможным измерять мельчайшие детали распределения полной энергии. Они отражают мельчайшие детали физики поверхности, и техника полевой электронной спектроскопии некоторое время процветала, прежде чем ее вытеснили более новые методы исследования поверхности.

Полевые электронные эмиттеры как электронная пушка источников

Для достижения высокого разрешения в электронных микроскопах и других электронно-лучевых приборах (например, тех, которые используются для электронно -лучевой литографии ), начать с небольшого, оптически и стабильного источника электронов. Источники, основанные на геометрии излучения Мюллера, хорошо подходят по первому критерию. Первое наблюдение отдельного атома с помощью электронного микроскопа (ЭМ) было выполнено Крю, Уоллом и Лэнгмором в 1970 году с использованием растрового электронного микроскопа, оснащенного ранней автоэмиссионной пушкой.

с 1950-х годов, большие усилия были использованы на средствах полевой эмиссии для электронных пушках. [например, DD53] Были разработаны методы генерации осевых лучей либо для расчета нарастания эмиттера под действием поля, либо путем избирательного осаждения адсорбата с низкой работой выхода (обычно циркония оксида - ZrO) вершину эмиттера с ориентацией (100) вольфрам.

Источники, работающие при температуре, обладают тем недостатком, что они быстро покрываются молекулами адсорбата , которые поступают из вакуумных стенок системы, и эмиттер необходимо время от времени очищать путем «прошивки» до высокой температуры. В настоящее время более распространено использование источников излучения Мюллера, которые работают при повышенных температурах, либо в режиме эмиссии Шоттки, либо в так называемом промежуточном режиме температурного поля. Многие современные электронные микроскопы высокого разрешения и электронно-лучевые приборы используют или иной вид источника электронов на основе эмиттера Мюллера. В настоящее время предпринимаются попытки эксперимента углеродные нанотрубки (УНТ) в качестве источников полевой эмиссии электронных пушек.

Использование источников полевой эмиссии в электронно-оптических приборах потребовало соответствующих теорий. оптики заряженных частиц и разработки соответствующего моделирования. Для эмиттеров Мюллера были опробованы различные модели формы; Лучшей кажется модель «Сфера на ортогональном конусе» (SOC), представленная Дайком, Троланом. Долан и Барнс в 1953 году. Важное моделирование, включающее отслеживание траектории с использованием модели излучателя SOC, было выполнено Визенером и Эверхартом. В настоящее время средство для моделирования полевой эмиссии эмиттеров Мюллера часто включается в коммерческие программы электронной оптики, используемые для разработки электронно-лучевых приборов. Создание эффективных современных автоэмиссионных электронных пушек требует высокоспециализированных знаний.

Атомно-острые эмиттеры

В настоящее время можно изготовить очень острые эмиттеры, включая эмиттеры, которые заканчиваются на один атом. В этом случае электронная эмиссия исходит из области, примерно вдвое превышающей кристаллографический размер одиночного атома. Это было осуществлено путем сравнения изображений с помощью FEM и полевого ионного микроскопа (FIM). Излучатели Мюллера с одним атомом на вершине также имеют отношение к сканирующей зондовой микроскопии и сканирующей ионной микроскопии гелия (He SIM). Методы их приготовления изучаются в течение многих лет. Связанным с этим важным недавним достижением стала разработка автоматизированного метода восстановления трехатомного («тримерного») апекса в его исходном состоянии, если тример разрушается.

Источники автоэмиссии большой площади: вакуумная наноэлектроника

Материальные аспекты

Источники автоэмиссии большой площади вызывают интерес с 1970-х годов. В этих устройствах высокая плотность отдельных участков автоэмиссии создается на подложке. Это направление стало сначала известно как «вакуумная микроэлектроника», а теперь как «вакуумная наноэлектроника».

Один из двух исходных типов устройств, «массив Spindt », использовал методы изготовления кремниевых интегральных схем (IC) для изготовления регулярных массивов, в которых молибденовые конусы осаждались в небольших цилиндрических пустотах в оксидной пленке, причем пустоты закрывались противоэлектродом с центральным круглым отверстием. Эта общая геометрия также использовалась с углеродными нанотрубками, выращенными в пустоте.

Другим оригинальным типом устройства был "излучатель Latham". Это были MIMIV (металл-изолятор-металл-изолятор-вакуум) или, в более общем смысле, CDCDV (проводник-диэлектрик-проводник-диэлектрик-вакуум) - устройства, которые содержат проводящие частицы в диэлектрической пленке. Устройство излучает поле, потому что его микроструктура / наноструктура обладает улучшающими свойствами поле. Этот материал потенциальное производственное преимущество, так как его можно было наносить в виде «чернил», поэтому не было необходимости в технологиях изготовления ИС. Однако на практике оказалось сложно изготовить неизменно надежные устройства.

Продвинулись исследования по поиску других материалов, которые можно было бы осаждать / выращивать в виде тонких пленок с подходящими полевыми свойствами. В конфигурации с параллельными пластинами "макроскопическое" поле F M между пластинами определяется выражением F M = V / W, где W - расстояние между пластинами, а V - приложенное вольтаж. Если на одной пластине создается острый объект, то локальное поле F на его вершине больше F M и может быть связано с F M созданием

$F\; =\; \gamma \; FM..\; \{\backslash \; displaystyle\; F\; =\; \backslash \; gamma\; F\; \_\; \{\backslash \; mathrm\; \{M\}\}.\}$

Параметр γ называется «коэффициентом усиления поля» и в основном определяется набором объекта. Характеристики полевой эмиссии определяется локальным полем F, чем выше значение γ объекта, тем ниже значение F M, при котором происходит значительная эмиссия. Следовательно, для данного значения W, чем ниже приложенное напряжение V, при котором происходит значительная эмиссия.

В течение примерно десяти лет с середины 1990-х годов был большой интерес к автоэлектронной эмиссии из осажденных плазмой пленок аморфного и «алмазоподобного» углерода. Однако увеличился интерес увеличился, частично из-за появлений факторов CNT, частично из-за того, что появились доказательства того, что выбросов углерода, созданными неизвестным образом в процессе осаждения : это говорит о том, что контроль качества производственного процесса в промышленных масштабах может быть проблематичным.

Внедрение полевых эмиттеров CNT, как в «матовой» форме, так и в форме «выращенного массива», было значительным шагом. Системные обширные исследования как их физические характеристики. Что касается автоэлектронной эмиссии, то преимущество УНТ в том, что благодаря своей форме и высокому формату они являются «естественными объектами, усиливающими полями».

В последние годы также наблюдается значительный рост интереса к разработке других форм тонкопленочных эмиттеров, основанных как на других формах углерода (например, «углеродные наностенки»), так и на различных формах широких слоев. -зонный полупроводник. Конкретной целью является разработка наноструктур с высоким коэффициентом γ с высокой плотностью отдельных эмиссионных участков. Тонкие пленки из нанотрубок в виде полотен нанотрубок также используются для разработки автоэмиссионных электродов. Показано, что путем точной настройки параметров исполнения эти полотна достигаются оптимальной плотности отдельных участков излучения. Двухслойные электроды, полученные путем осаждения двух слоев, эти полотенце с перпендикулярным выравниванием по отношению друг к другу, могут электрическое поле, для достижения необходимого тока эмиссии 10 мкА / см, до 0,3 В / мкм и обеспечение стабильных характеристик полевой эмиссии.

Общие проблемы со всеми полевыми эмиссионными устройствами, особенно теми, которые работают в «промышленных условиях вакуума», заключаются в том, что характеристики излучения плохие из-за адсорбции выбросов газа, поступающих из других систем, а форма эмиттера В принципе, может быть изменена пагубно с помощью множества дополнительных процессов, таких как бомбардировка ионами, создаваемая ударами испускаемых электронов на атомы газовой фазы и / или на поверхности противоэлектродов. Таким образом, важным промышленным требованием является «надежность в условиях плохого вакуума»; это необходимо при исследовании новых эмиттерных материалов.

На момент написания наиболее многообещающими формами источников автоэлектронной эмиссии большой площади представлялись массивы Spindt и различные источники формы на основе УНТ.

Приложения

Развитие источников полевой эмиссии с большой площадью используется было вызвано желанием создать новые, более эффективные электронные формы информационного дисплея. Они известны как «автоэмиссионные дисплеи » или «наноэмиссионные дисплеи». Хотя было установлено несколько прототипов, таких дисплеев в надежных коммерческих продуктах, препятствующих использованию различных проблем промышленного производства, не связанных напрямую с характеристиками источника [En08].

Другие предлагаемые применения источников полевой эмиссии с большой площадью включают генерацию микроволн, нейтрализацию космических аппаратов, генерацию рентгеновского излучения и (для массивных источников) множественные электронно- лучевая литография. Также в последнее время предпринимаются попытки экспериментов большой площади на гибких подложках в соответствии с более широкими тенденциями в направлении «пластиковой электроники ».

Разработка таких приложений - миссия вакуумной наноэлектроники. Однако полевые эмиттеры лучше всего работают в условиях хорошего сверхвысокого вакуума. Их наиболее успешное применение на сегодняшний день (пистолеты FEM, FES и EM) приходятся на эти условия. Печальный факт остается фактом: полевые эмиттеры и условия вакуума плохо сочетаются друг с другом, и связанные с этим проблемы надежного обеспечения хорошей «вакуумной устойчивости» системы автоэмиссии, используемые в таких условиях, все еще ждут лучшие решения (возможно, более умных материалов), чем мы в настоящее время иметь.

Вакуумный пробой и явление электрического разряда

Как уже указывалось, сейчас считается, что самыми ранними проявлениями полевой электронной эмиссии были вызванные ею электрические разряды. После работы Фаулера-Нордхейма стало понятно, что CFE была одной из основных причин пробоя вакуума и электрического разряда. (Подробные механизмы и задействованные пути могут быть очень сложными, и не существуют единой универсальной причины). Если известно, что пробой вакуума вызван эмиссией электронов с катодами, то это первоначальное представление заключалось в том, что механизм CFE от проводящей иглы. как выступы на поверхности. Процедуры использовались (и использовались) для округления и сглаживания поверхностей электродов, которые генерируют нежелательные токи полевой электронной эмиссии. Однако работы Латама и других показали, что эмиссия также может быть присутствует с присутствием полупроводниковых на гладких поверхностях. Физика генерации излучения до сих пор полностью не изучена, но есть подозрения, что могут иметь место так называемые «эффекты тройного перехода». Дополнительную информацию можно найти в книге Лэтэма и в онлайн-библиографии.

Внутренний перенос электронов в электронных устройствах

В некоторых электронных устройствах перенос электронов от одного материала к другому или (в случай наклонных полос) от одной полосы к другой («туннелирование Зинера ») происходит в результате индуцированного полем процесса туннелирования, который можно рассматривать как форму туннелирования Фаулера-Нордхейма. Например, в книге Родерика обсуждается теория, относящаяся к контактам металл-полупроводник.

Введение

Следующая часть этой статьи посвящена с основами теории холодной автоэлектронной эмиссии из массивных металлов. Лучше всего это рассматривать на четырех основных этапах, связанных с теорией, связанной с: (1) выводом формулы для «вероятности ухода » с учетом туннелирования электронов через округлый треугольный барьер; (2) интегрирование по внутренним электронным состояниям для получения «распределения полной энергии»; (3) второе интегрирование для получения плотности тока эмиссии как функции локального барьерного поля и локальной работы выхода; (4) преобразование этого в формулу для тока как функции приложенного напряжения. Отдельно рассматриваются модифицированные уравнения, необходимые для излучателей большой площади, и вопросы анализа экспериментальных данных.

Туннелирование Фаулера-Нордхейма - это волново-механическое туннелирование электрона через точный или округлый треугольный барьер. Различают две основные ситуации: (1) когда электрон изначально находится в локализованном состоянии ; (2) когда электрон изначально не сильно локализован и лучше всего представлен бегущей волной . Излучение из объемного металла в зоне проводимости представляет собой ситуацию второго типа, и обсуждение здесь относится к этому случаю. Также предполагается, что t Барьер является одномерным (то есть не имеет структурных структур) и не имеет мелкомасштабной структуры, который вызывает эффекты «рассеяния » или «резонанса». Эти предположения необходимы, чтобы сделать это объяснение туннелирования Фаулера-Нордхейма простого; но атомная структура материи фактически не принимается во внимание.

Движущая энергия

Для электрона одномерное уравнение Шредингера можно записать в виде

$\hslash \; 2\; 2\; md\; 2\; \Psi \; (x)\; dx\; 2\; Знак\; равно\; [U\; (x)\; -\; E\; n]\; \Psi \; (x)\; знак\; равно\; M\; (x)\; \Psi \; (x),\; (1)\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; hbar\; ^\; \{2\}\}\; \{2m\}\}\; \{\backslash \; frac\; \{\backslash \; mathrm\; \{d\}\; ^\; \{\; 2\}\; \backslash \; Psi\; (x)\}\; \{\backslash \; mathrm\; \{d\}\; x\; ^\; \{2\}\}\}\; =\; \backslash \; left\; [U\; (x)\; -E\; \_\; \{\backslash \; mathrm\; \{n\}\}\; \backslash \; right]\; \backslash \; Psi\; (x)\; =\; M\; (\; x)\; \backslash \; Psi\; (x),\; \backslash \; qquad\; \backslash \; qquad\; (1)\}$

где Ψ (x) - волновая функция электрона , выраженная функция измеренного расстояния x от электрической поверхности эмиттера, ħ - приведенная постоянная Планка, m - масса электрона, U (x) - потенциальная энергия электрона, E n - полная энергия электрона, связанная с движением в x-направлении, и M (x) = [U (x) - E n ], называется движущейся энергией электрона. M (x) можно интерпретировать как отрицательное значение энергии электрона, с движением гипотетического классического точечного электрона в направлении x, и положительное значение в барьере.

Форма туннельного барьера определяется тем, как M (x) изменяется в зависимости от положения в области, где M (x)>0. Две модели имеют особый статус в теории автоэмиссии: точный треугольный (ET) барьер и барьер Шоттки - Нордхейма (SN). Они задаются уравнениями (2) и (3) соответственно:

$MET\; (x)\; =\; h\; -\; e\; F\; x\; (2)\; \{\backslash \; displaystyle\; M\; ^\; \{\backslash \; mathrm\; \{ET\}\}\; (x)\; =\; h-eFx\; \backslash \; qquad\; \backslash \; qquad\; \backslash \; qquad\; \backslash \; qquad\; \backslash \; qquad\; \backslash ;\; \backslash ;\; \backslash ;\; (2)\}$

$MSN\; (x)\; =\; час\; -\; e\; F\; x\; -\; e\; 2\; /\; (16\; \pi \; \epsilon \; 0\; x),\; (3)\; \{\backslash \; displaystyle\; M\; ^\; \{\backslash \; rm\; \{SN\}\}\; (x)\; =\; h-\; eFx-e\; ^\; \{2\}\; /\; (16\; \backslash \; pi\; \backslash \; varepsilon\; \_\; \{0\}\; x),\; \backslash \; qquad\; \backslash \; qquad\; (3)\}$

Здесь h - высота нулевого поля (или неуменьшенная высота) барьера, e - элементарный положительный заряд, F - поле барьера, а ε 0 - электрическая постоянная . По соглашению F считается положительным, даже если классическое электростатическое поле будет отрицательным. Уравнение SN использует классическую потенциальную энергию изображения для физического эффекта «корреляция и обмен».

Вероятность выхода

Для электрона, приближающегося к заданному барьеру изнутри, вероятность ухода (или «коэффициент передачи » или «коэффициент проникновения») является функцией h и F, и обозначается D (h, F). Основная цель теории туннелирования - вычислить D (h, F). Для физически реалистичных моделей барьеров, таких как барьер Шоттки-Нордхейма, уравнение Шредингера не может быть решено точно каким-либо простым способом. Можно использовать следующий так называемый «полуклассический» подход. Параметр G (h, F) может быть определен интегралом JWKB (Джеффриса-Вентцеля-Крамерса-Бриллюэна) :

$G\; (h,\; F)\; =\; g\; \int \; M\; 1/2\; dx,\; (4)\; \{\; \backslash \; displaystyle\; G\; (h,\; F)\; =\; g\; \backslash \; int\; M\; ^\; \{1/2\}\; \{\backslash \; t\_dv\; \{d\}\}\; x,\; \backslash \; qquad\; \backslash \; qquad\; (4)\}$

где интеграл берется через барьер (т. е. в.. области, где M>0), параметр g является универсальной константой, задаваемой как

$g\; =\; 2\; 2\; м\; /\; \hslash \; \approx \; 10,24624\; э\; В\; -\; 1/2\; нм\; -\; 1.\; (5)\; \{\backslash \; displaystyle\; g\; \backslash ,\; =\; 2\; \{\backslash \; sqrt\; \{2m\}\}\; /\; \backslash \; hbar\; \backslash \; приблизительно\; 10.24624\; \backslash ;\; \{\backslash \; rm\; \{эВ\}\}\; ^\; \{-\; 1/2\}\; \backslash ;\; \{\backslash \; rm\; \{nm\}\}\; ^\; \{-1\}.\; \backslash \; Qquad\; \backslash \; qquad\; (5)\}$

Форбс переработал результат, доказанный Фрёманом и Фрёманом, чтобы показать, что формально - при одномерном рассмотрении - точное решение для D может быть записано

$D\; =\; п\; е\; -\; G\; 1\; +\; п\; е\; -\; G,\; (6)\; \{\backslash \; displaystyle\; \backslash ,\; D\; =\; \{\backslash \; frac\; \{P\; \backslash \; mathrm\; \{e\}\; ^\; \{-\; G\}\}\; \{1\; +\; P\; \backslash \; mathrm\; \{e\}\; ^\; \{-\; G\}\}\},\; \backslash \; qquad\; \backslash \; qquad\; (6)\}$

где предварительный фактор туннелирования P в принципе может быть оценен путем сложных итерационных интеграций вдоль пути в комплексном пространстве. В режиме CFE мы имеем (по определению) G 1. Кроме того, для простых моделей P ≈ 1. Таким образом, ур. (6) сводится к так называемой простой формуле JWKB :

$D\; \approx \; P\; e\; -\; G\; \approx \; e\; -\; G.\; (7)\; \{\backslash \; Displaystyle\; D\; \backslash \; приблизительно\; P\; \backslash \; mathrm\; \{e\}\; ^\; \{-\; G\; \}\; \backslash \; приблизительно\; \backslash \; mathrm\; \{e\}\; ^\; \{-\; G\}.\; \backslash \; Qquad\; \backslash \; qquad\; (7)\}$

Для точного треугольного барьера ставить экв. (2) в ур. (4) дает G = bh / F, где

$b\; =\; 2\; g\; 3\; e\; =\; 4\; 2\; м\; 3\; e\; \hslash \; \approx \; 6,830890\; e\; V\; -\; 3/2\; V\; нм\; -\; 1.\; (8)\; \{\backslash \; displaystyle\; b\; =\; \{\backslash \; frac\; \{2g\}\; \{3e\}\}\; =\; \{\backslash \; frac\; \{4\; \{\backslash \; sqrt\; \{2m\}\}\}\; \{3e\; \backslash \; hbar\}\}\; \backslash \; приблизительно\; 6.830890\; \backslash ;\; \{\backslash \; mathrm\; \{eV\}\}\; ^\; \{-\; 3/2\}\; \backslash ;\; \backslash \; mathrm\; \{V\}\; \backslash ;\; \{\backslash \; mathrm\; \{nm\}\}\; ^\; \{-\; 1\}.\; \backslash \; Qquad\; \backslash \; qquad\; (8)\}$

Этот параметр b - универсальная константа, которую иногда называют второй Фаулера - Нордхейма. Для барьеров другой формы мы пишем

$G\; (h,\; F)\; =\; \nu \; (h,\; F)\; GET\; =\; \nu \; (h,\; F)\; bh\; 3/2\; /\; F,\; (9)\; \{\backslash \; displaystyle\; G\; (h,\; F)\; =\; \backslash \; nu\; (h,\; F)\; G\; ^\; \{\backslash \; mathrm\; \{ET\}\}\; =\; \backslash \; nu\; (h,\; F)\; bh\; ^\; \{3/2\}\; /\; F,\; \backslash \; qquad\; \backslash \; qquad\; (9)\}$

где ν (h, F) - это поправочный коэффициент, который, как правило, должен учитываться интегрированным интегрированным с использованием ур. (4).

Поправочный усиленный коэффициент для барьера Шоттки-Нордхейма

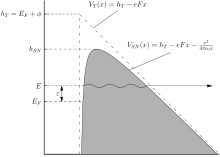барьер Шоттки-Нордхайма для полевой эмиссии Фаулера-Нордхейма (и усиленная термоэлектронная эмиссия ).

Барьер Шоттки-Нордхейма, который обеспечивает вывод данного стандартного барьера В этом случае известно, что поправочный коэффициент $\nu \; \{\backslash \; displaystyle\; \{\backslash \; it\; \{\backslash \; nu\}\}\}$равен функции одной переменной f h <396, уравнения типа Фаулера-Нордхейма является частным случаем.>, определяемая как f h = F / F h, где F h - поле необходимого для уменьшения высоты барьера Шоттки - Нордхейма с h до 0. Это поле определяется как

$F\; h\; =\; (4\; \pi \; ϵ\; 0\; /\; e\; 3)\; h\; 2\; =\; (0,6944617\; ·\; нм\; -\; 1)\; (h\; /\; e\; V)\; 2.\; (10)\; \{\backslash \; displaystyle\; \backslash ,\; F\_\; \{h\}\; =\; (4\; \backslash \; pi\; \backslash \; epsilon\; \_\; \{0\}\; /\; e\; ^\; \{3\})\; h\; ^\; \{2\}\; =\; (0,6944617\; \backslash ;\; \backslash \; mathrm\; \{V\}\; \backslash ;\; \{\backslash \; mathrm\; \{nm\}\}\; ^\; \{-\; 1\})\; (h\; /\; \{\backslash \; rm\; \{eV\}\})\; ^\; \{2\}.\; \backslash \; qquad\; \backslash \; qquad\; (10)\}$

Параметр f h изменяется от 0 до 1 и может называться масштабированным полем барьером ера для барьера Шоттки-Нордхейма с нулевой высотой поля h.

Для барьера Шоттки - Нордхейма ν (h, F) задается частным значением ν (f h) функции ν (ℓ ′). Последняя является самостоятельной функцией математической физики и была названа главной барьерной функцией Шоттки - Нордхейма. Явное разложение в ряд для ν (ℓ ′) получено в статье Дж. Дина в 2008 году. Было найдено следующее хорошее простое приближение для ν (f h):

$v\; (f\; h)\; \approx \; 1\; -\; f\; h\; +\; 1\; 6\; f\; h\; ln\; \; f\; h...........\; (11)\; \{\backslash \; displaystyle\; v\; (f\_\; \{h\})\; \backslash \; приблизительно\; 1-f\_\; \{h\}\; +\; \{\backslash \; tfrac\; \{1\}\; \{6\}\}\; f\_\; \{h\}\; \backslash \; ln\; f\_\; \{h\}...........\; \{\backslash \; rm\; \{(11)\}\}\}$

Ширина распада

Ширина затухания (в энергии), d h, измеряет, насколько быстро вероятность выхода D разрушает высоту барьера h; d h определяется как:

$1\; d\; h\; =\; -\; d\; (ln\; \; D)\; d\; h.\; (12)\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{d\_\; \{h\}\}\}\; =\; -\; \{\backslash \; frac\; \{\backslash \; mathrm\; \{d\}\; (\backslash \; ln\; D)\}\; \{\backslash \; mathrm\; \{d\}\; h\}\}.\; \backslash \; Qquad\; \backslash \; qquad\; (12)\}$

Когда h увеличивается на d h, тогда вероятность ухода D уменьшается в раз, близкий к e (≈ 2,718282). Для элементарной модели, основанной на точном треугольном барьере, где мы положили ν = 1 и P ≈ 1, мы получаем

$d\; h\; (e\; l)\; =\; 2\; F\; 3\; b\; h\; =\; e\; F\; g\; h.\; \{\backslash \; displaystyle\; d\_\; \{h\}\; ^\; \{\backslash \; mathrm\; \{(el)\}\}\; =\; \{\backslash \; frac\; \{2F\}\; \{3b\; \{\backslash \; sqrt\; \{h\}\}\}\}\; =\; \{\backslash \; frac\; \{eF\}\; \{g\; \{\backslash \; sqrt\; \{h\}\; \}\}\}.\}$

Ширина затухания d h, полученная из более общего выражения (12), отличается от этого «поправочным коэффициентом ширины затухания» λ d, поэтому:

$dh\; =\; \lambda \; ddh\; (el)\; =\; \lambda \; de\; F\; gh.\; (13)\; \{\backslash \; displaystyle\; d\_\; \{h\}\; =\; \backslash \; lambda\; \_\; \{d\}\; d\_\; \{h\}\; ^\; \{\backslash \; mathrm\; \{(el)\}\}\; =\; \{\backslash \; frac\; \{\backslash \; lambda\; \_\; \{d\}\; eF\}\; \{g\; \{\backslash \; sqrt\; \{\; час\}\}\}\}.\; \backslash \; qquad\; \backslash \; qquad\; (13)\}$

Обычно поправочный коэффициент может быть равным единице.

Ширина затухания d F для барьера с h, равным условиям работы выхода φ, представляет особый интерес. Численно это означает, как:

$d\; F\; =\; \lambda \; de\; F\; g\; \varphi \; \approx \; e\; F\; g\; \varphi \; \approx \; 0,09759678\; e\; V\; \cdot \; 1\; e\; V\; \varphi \; \cdot \; F\; 1\; V\; нм\; -\; 1.\; (14)\; \{\backslash \; displaystyle\; d\; \_\; \{\backslash \; mathrm\; \{F\}\}\; =\; \{\backslash \; frac\; \{\backslash \; lambda\; \_\; \{d\}\; eF\}\; \{g\; \{\backslash \; sqrt\; \{\backslash \; phi\}\}\}\}\; \backslash \; приблизительно\; \{\backslash \; frac\; \{eF\}\; \{g\; \{\backslash \; sqrt\; \{\backslash \; phi\}\}\}\}\; \backslash \; примерно\; 0,09759678\; \backslash ;\; \backslash \; mathrm\; \{eV\}\; \backslash ,\; \backslash \; cdot\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{1\; \backslash \; \backslash \; mathrm\; \{eV\}\}\; \{\backslash \; phi\}\}\}\; \backslash \; cdot\; \{\backslash \; frac\; \{F\}\; \{1\; \backslash \; \backslash \; mathrm\; \{V\}\; \backslash \; \backslash \; mathrm\; \{\; нм\}\; ^\; \{-\; 1\}\}\}.\; \backslash \; Qquad\; \backslash \; qquad\; (14)\}$

Для металлов значение d F обычно порядка 0,2 эВ, но изменяется в зависимости от барьерного поля F.

Комментарии

Необходима историческая справка. Идея о том, что барьер Шоттки-Нордхейма нуждается в поправочном корпусенте, как в ур. (9), был введен Нордгеймом в 1928 году, но его математический анализ фактора был неверным. Новая (правильная) функция была введена Берджессом, Кремером и Хьюстоном в 1953 году, а ее математика была развита Мерфи и Гудом в 1956 году. Эта исправленная функция, иногда известная как «специальная эллиптическая функция автоэмиссии», была выражена как функция математической функции y, известный как "параметр Нордхейма". Только недавно (с 2006 по 2008 год) стало понятно, что математически намного лучше использовать переменную ℓ ′ (= y). И только недавно удалось завершить завершение ν (ℓ ′), разработав и доказав способность разложения в точный ряд функций (на основе известных частных решений гипергеометрического дифференциального уравнения Гаусса ). (11) было найдено совсем недавно. Приближение (11) превосходит все более старые приближения эквивалентной сложности и, вероятно, в конечном итоге вытеснит их.>

сводка объединяет эти результаты. сть ухода D (h, F) формально определяется как:

$D\; (h,\; F)\; \approx \; P\; exp\; \; [-\; \nu \; (h,\; F))\; bh\; 3/2\; F],\; (15)\; \{\backslash \; displaystyle\; D\; (h,\; F)\; \backslash \; приблизительно\; P\; \backslash \; exp\; \backslash \; left\; [-\; \{\backslash \; frac\; \{\backslash \; nu\; (h,\; F)\; bh\; ^\; \{3/2\}\}\; \{F\}\}\; \backslash \; right],\; \backslash \; qquad\; \backslash \; qquad\; (15)\}$

где ν (h, F) - поправочный коэффициент, который обычно определяется интегрированным. Для частного случая барьера Шоттки-Нордхейма существует аналитический результат, и ν (h, F) задается как ν (f h), как обсуждалось выше; приближения (11) для ν (f h) более чем достаточно для всех технологических целей. Предварительный фактор P также в принципе является функцией h и (возможно) F, но для обсуждаемых здесь простых физических моделей достаточно приближения P = 1. Точный треугольный барьер - это частный случай, когда Уравнение Шредингера можно решить точно, как это было сделано Фаулером и Нордхеймом; для этого физически нереалистичного случая ν (f h) = 1, и аналитическое приближение для P существует.

Описанный здесь подход был использован для описания туннелирования Фаулера - Нордхейма из гладких, классически плоских, плоских излучающих поверхностей. Он подходит для гладких, классических изогнутых поверхностей с радиусом от 10 до 20 нм. Его можно адаптировать к поверхностям с более острым радиусом, но такие величины, как ν и D, становятся важными функциями (ов), используемыми для описания кривизны поверхности. Когда эмиттер настолько резкий, что нельзя пренебречь деталями на атомном уровне, и / или туннельный барьер толще, чем размеры вершины эмиттера, тогда желателен более сложный подход.

Как отмечалось в начале, эффекты простых структур материалов не принимаются во внимание в относительно трактовках автоэлектронной эмиссии, обсуждаемых здесь. Правильный учет атомной структуры - очень трудная проблема, и достигнут лишь ограниченный прогресс. Кажется вероятным, что основное влияние на теорию туннелирования Фаулера-Нордхейма (по сути) будет заключаться в изменении значений P и ν в уравнении. (15), суммы, которые в настоящее время трудно оценить.

Все эти замечания в принципе применимы к туннелированию Фаулером-Нордхеймом из любого проводника, где (до туннелирования) электроны можно рассматривать как в состояниях бегущей волны. Подход может быть адаптирован для применения (приблизительно) к ситуации, когда электроны находятся в локализованных состояний на или очень близко внутри излучающей поверхности, но это выходит за рамки данной статьи.

Распределение используемых испускаемых электронов важно для научных экспериментов, в использовании распределения энергии испускаемых электронов для исследования излучения излучателя физика поверхности и источников автоэлектронной эмиссии, используются в электронно-лучевых приборах, таких как электронные микроскопы. В последнем случае «ширина» (по энергии) влияет на то, насколько точно может быть сфокусирован луч.

Теоретическое объяснение следует подходу Forbes. Если ε обозначает полную энергию электрона относительно уровня Ферми эмиттера, а K p обозначает кинетическую энергию электрона, параллельную поверхность эмиттера, то нормальная энергия электрона ε n (иногда называемая его «прямой энергией») определяется как

$ϵ\; n\; =\; ϵ\; -\; K\; p...........\; (16)\; \{\backslash \; Displaystyle\; \backslash ;\; \backslash \; epsilon\; \_\; \{\backslash \; mathrm\; \{n\}\}\; =\; \backslash \; epsilon\; -K\; \_\; \{\backslash \; mathrm\; \{p\}\}...........\; (16)\}$.

Два типа теоретического распределения энергии распознаются: распределение нормальной энергии энергия (NED), которое показывает, как энергия ε n распределяется сразу после излучения (т. е. сразу за туннельным барьером); и распределение полной энергии, которое показывает, как распределяется полная энергия ε. Когда эмиттер уровень Ферми используется в качестве опорного уровня нулевой, как ε и ε п может быть либо положительным, либо отрицательным.

Эксперименты по энергетическому анализу полевых эмиттеров проводились с 1930-х годов. Однако только в конце 1950-х годов стало (Юнгом и Мюллером [, YM58]), что в этих понятных экспериментах всегда измерялось распределение энергии, которое теперь обычно обозначается j (ε). Это также верно (или почти верно), когда излучение исходит из небольшого выступа, усиливающего поле, на плоской поверхности.

Чтобы увидеть, как можно рассчитать распределение энергии в рамках Зоммерфельда модель типа свободных электронов, посмотрите на диаграмму энергетического пространства PT (PT = "параллельное-общее").

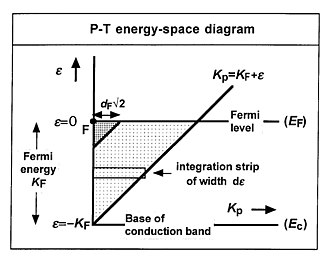PT диаграмма энергетического пространства, показывающая область в PT энергетическом пространстве, где существуют состояния бегущей волны электронов.

Здесь используется "параллельная кинетическая энергия " K p на по горизонтальной оси и полная энергия ε по вертикальной оси. Электрон внутри массивного металла обычно имеет значения K p и ε, которые лежат в пределах слегка заштрихованной области. Можно показать, что каждый элемент dεdK p этого энергетического пространства вносит свой вклад $z\; S\; f\; FD\; d\; ϵ\; d\; K\; p\; \{\backslash \; displaystyle\; z\; \_\; \{\backslash \; mathrm\; \{S\}\}\; f\; \_\; \{\backslash \; mathrm\; \{\; FD\}\}\; \backslash \; mathrm\; \{d\}\; \{\backslash \; it\; \{\backslash \; epsilon\}\}\; \backslash \; mathrm\; \{d\}\; K\; \_\; \{\backslash \; mathrm\; \{p\}\}\}$к плотности электронного тока, падающего на внутреннюю часть границы эмиттера. Здесь z S - универсальная константа (называемая здесь плотностью предложения Зоммерфельда ):

$z\; S\; =\; 4\; \pi \; em\; /\; h\; P\; 3\; =\; 1,618311\; \times \; 10\; 14\; А\; ·\; м\; -\; 2\; е\; В\; -\; 2,...........\; (17)\; \{\backslash \; displaystyle\; z\; \_\; \{\backslash \; mathrm\; \{S\}\}\; =\; 4\; \backslash \; mathrm\; \{\backslash \; pi\}\; em\; /\; h\; \_\; \{\backslash \; mathrm\; \{P\}\}\; ^\; \{3\}\; =\; 1,618311\; \backslash \; times\; 10\; ^\; \{14\}\; \backslash ,\; \{\backslash \; rm\; \{\{A\}\; \backslash ,\; m\; ^\; \{-\; 2\}\; \backslash ,\; эВ\; ^\; \{-\; 2\},...........\; (17)\}\}\}$

и $f\; FD\; \{\backslash \; displaystyle\; f\; \_\; \{\backslash \; mathrm\; \{FD\}\}\}$- это функция распределения Ферми-Дирака :

$f\; FD\; (ϵ)\; =\; 1\; /\; [1\; +\; exp\; (ϵ\; /\; k\; BT)],...........\; (18)\; \{\backslash \; displaystyle\; \backslash ,\; е\; \_\; \{\backslash \; mathrm\; \{FD\}\}\; (\backslash \; epsilon)\; =\; 1\; /\; [1+\; \backslash \; mathrm\; \{exp\}\; (\backslash \; epsilon\; /\; k\; \_\; \{\backslash \; mathrm\; \{B\}\}\; T)],...........\; (18)\}$

где T - термодинамическая температура, а k B - постоянная Больцмана.

Этот элемент плотности падающего тока видит барьер высотой h, определяемой как:

$h\; =\; \varphi \; -\; ϵ\; +\; K\; p...........\; (19\; a)\; \{\backslash \; displaystyle\; \backslash ,\; h\; =\; \backslash \; phi\; -\; \backslash \; epsilon\; +\; K\; \_\; \{\backslash \; mathrm\; \{p\}\}...........\; (19a)\}$

Соответствующая вероятность побега - это D (h, F): это может быть расширено (приблизительно) в виде

$D\; (h,\; F)\; \approx \; DF\; exp\; (ϵ\; /\; d\; F)\; exp\; (-\; K\; p\; /\; d\; F)..........\; (19\; б),\; \{\backslash \; Displaystyle\; D\; (ч,\; F)\; \backslash \; приблизительно\; D\; \_\; \{\backslash \; mathrm\; \{F\}\}\; \backslash ;\; \backslash \; mathrm\; \{exp\}\; (\backslash \; epsilon\; /\; d\; \_\; \{\backslash \; mathrm\; \{F\}\})\; \backslash ;\; \backslash \; mathrm\; \{exp\}\; (-K\; \_\; \{\backslash \; mathrm\; \{p\}\}\; /\; d\; \_\; \{\backslash \; mathrm\; \{F\}\})..........\; (19b),\}$

где D F - это вероятность выхода для барьера с неуменьшенной высотой, равной локальной работе выхода φ. Следовательно, элемент dεdK p вносит вклад $z\; S\; f\; FDD\; d\; ϵ\; d\; K\; p\; \{\backslash \; displaystyle\; z\; \_\; \{\backslash \; mathrm\; \{S\}\}\; f\; \_\; \{\backslash \; mathrm\; \{FD\}\}\; D\; \backslash \; mathrm\; \{\; d\}\; \{\backslash \; it\; \{\backslash \; epsilon\}\}\; \backslash \; mathrm\; \{d\}\; K\; \_\; \{\backslash \; mathrm\; \{p\}\}\}$в плотности тока эмиссии и общих вкладдающих электронов с энергиями в элементарном диапазоне dε, таким образом,

$j\; (ϵ)\; d\; ϵ\; =\; z\; S\; f\; FD\; [\int \; D\; d\; K\; p]\; d\; ϵ\; =\; z\; S\; f\; FDDF\; exp\; (ϵ\; /\; d\; F)\; [\int \; 0\; \infty \; exp\; (-\; K\; p\; /\; d\; F)\; d\; K\; p]\; d\; ϵ...........\; (20)\; \{\backslash \; Displaystyle\; J\; (\backslash \; epsilon)\; \backslash \; mathrm\; \{d\}\; \backslash \; epsilon\; =\; z\; \_\; \{\backslash \; mathrm\; \{S\}\}\; f\; \_\; \{\backslash \; mathrm\; \{FD\}\}\; \backslash \; left\; [\backslash \; int\; D\; \backslash \; mathrm\; \{d\}\; K\; \_\; \{\backslash \; mathrm\; \{p\}\}\; \backslash \; right]\; \backslash \; mathrm\; \{d\}\; \backslash \; epsilon\; =\; z\; \_\; \{\backslash \; mathrm\; \{S\}\}\; f\; \_\; \{\backslash \; mathrm\; \{FD\}\}\; D\; \_\; \{\backslash \; mathrm\; \{F\}\}\; \backslash \; mathrm\; \{exp\}\; (\backslash \; epsilon\; /\; d\_\; \{\backslash \; mathrm\; \{F\}\})\; \backslash \; left\; [\backslash \; int\; \_\; \{0\}\; ^\; \{\backslash \; infty\}\; \backslash \; mathrm\; \{exp\}\; (-K\; \_\; \{\backslash \; mathrm\; \{p\}\}\; /\; d\; \_\; \{\backslash \; mathrm\; \{\; F\}\})\; \backslash ;\; \backslash \; mathrm\; \{d\}\; K\; \_\; \{\backslash \; mathrm\; \{p\}\}\; \backslash \; right]\; \backslash \; mathrm\; \{d\}\; \backslash \; epsilon...........\; (20)\}$,

где интеграл в принципе берется по показанной полосе на диаграмме, но на практике может быть увеличено до ∞, когда ширина распада F намного меньше, чем энергия Ферми KF(что всегда имеет место для металла). Результат интегрирования можно записать:

$j\; (ϵ)\; =\; z\; S\; d\; F\; D\; F\; f\; F\; F\; D\; (ϵ)\; e\; x\; p\; (ϵ\; /\; d\; F)\; =\; j\; F\; f\; F\; D\; (ϵ)\; e\; x\; p\; (ϵ\; /\; d\; F),...........\; (21)\; \{\backslash \; displaystyle\; \backslash ,\; j\; (\backslash \; epsilon)\; =\; z\; \_\; \{\backslash \; mathrm\; \{S\}\}\; d\; \_\; \{\backslash \; mathrm\; \{F\}\}\; D\; \_\; \{\backslash \; mathrm\; \{F\}\}\; f\; \_\; \{\backslash \; mathrm\; \{FD\}\}\; (\backslash \; epsilon)\; \backslash \; mathrm\; \{exp\}\; (\backslash \; epsilon\; /\; d\; \_\; \{\backslash \; mathrm\; \{F\}\})\; =\; j\; \_\; \{\backslash \; mathrm\; \{F\}\}\; f\; \_\; \{\backslash \; mathrm\; \{FD\}\}\; (\backslash \; epsilon)\; \backslash \; mathrm\; \{exp\; \}\; (\backslash \; epsilon\; /\; d\_\; \{\backslash \; mathrm\; \{F\}\}),...........\; (21)\}$

где $d\; F\; \{\backslash \; displaystyle\; d\; \_\; \{\backslash \; mathrm\; \{F\}\; \}\}$и $DF\; \{\backslash \; displaystyle\; D\; \_\; \{\backslash \; mathrm\; \{F\}\}\}$- значения, соответствующие барьеру с неуменьшенной высотой h, равной локальной работе выхода φ, и $J\; F\; [=\; Z\; S\; d\; FDF]\; \{\backslash \; Displaystyle\; J\; \_\; \{\backslash \; mathrm\; \{F\}\}\; [\backslash ,\; =\; z\; \_\; \{\backslash \; mathrm\; \{S\}\}\; d\; \_\; \{\backslash \; mathrm\; \{F\}\}\; D\; \_\; \{\backslash \; mathrm\; \{F\}\}]\}$определяется этим уравнением.

Для данного эмиттера с заданным полем, примененным к нему, $j\; F\; \{\backslash \; displaystyle\; j\; \_\; \{\backslash \; mathrm\; \{F\}\}\}$не зависит от F, поэтому уравнение. (21) показывает, что форма распределения (когда ε увеличивается от отрицательного значения значительно ниже уровня Ферми) представляет собой возрастную экспоненту, умноженную на функцию распределения FD. Это генерирует знакомую форму распределения, впервые предсказанную Янгом. При низких температурах $f\; FD\; (ϵ)\; \{\backslash \; displaystyle\; f\; \_\; \{\backslash \; mathrm\; \{FD\}\}\; (\backslash \; epsilon)\}$резко меняется от 1 до 0 вблизи уровня Ферми, а FWHM распределения определяется как:

$FWHM\; =\; d\; F\; ln\; (2)\; \approx \; 0,693\; d\; F..........\; (22)\; \{\backslash \; displaystyle\; \backslash \; mathrm\; \{FWHM\}\; \backslash ,\; =\; d\; \_\; \{\backslash \; mathrm\; \{F\}\}\; \backslash \; mathrm\; \{ln\}\; (2)\; \backslash \; приблизительно\; 0,693\; \backslash ,\; d\; \_\; \{\backslash \; mathrm\; \{F\}\}...........\; (22)\}$

Тот, что экспериментальные базовые распределения полной энергии CFE имеют эту базовую форму экспериментального подтверждения того, что электроны в металлах подчиняются статистике Ферми - Дирака.

Уравнения типа Фаулера-Нордхейма

Введение

Уравнения типа Фаулера-Нордхейма в форме JF представляют собой (приближенные) теоретические уравнения, полученные для описания плотности тока J, испускаемого из внутренних электронных состояний в зона проводимости массивного металла. Плотность эмиссионного тока (ECD) J для некоторой небольшой однородной области излучающей поверхности обычно выражается функция J (φ, F) от локального барьерного поля φ, которая характеризует небольшой регион. Для описания кривизны поверхности, также может зависеть от программы (ов), используемой для описания кривизны поверхности.

Из-за физических допущений, сделанных в исходном выводе, термин «уравнение типа Фаулера-Нордхейма» долгое время использовалось только для уравнений, которые описывают ECD при нулевой температуре. Однако лучше позволить этому названию включать слегка модифицированные уравнения (обсуждаемые ниже), которые действительны для конечных температур в режиме эмиссии CFE.

Форма с нулевой температурой

Плотность тока лучше всего измерять в А / м. Полная плотность тока, излучаемого из небольшой однородной области, может быть получена путем интегрирования распределения полной энергии j (ε) по отношению к полной энергии электронов ε. При нулевой температуре функция распределения Ферми – Дирака fFD= 1 при ε <0, and fFD= 0 при ε>0. Таким образом, ECD при 0 K, J 0, дается из ур. (18) по

$J\; 0\; =\; z\; S\; d\; F\; D\; F\; \int \; -\; \infty \; 0\; e\; x\; p\; (ϵ\; /\; d\; F)\; d\; ϵ\; =\; z\; S\; d\; F\; 2\; D\; F\; =\; Z\; F\; D\; F,..........\; (23)\; \{\backslash \; displaystyle\; J\_\; \{0\}\; =\; z\; \_\; \{\backslash \; mathrm\; \{S\}\}\; d\; \_\; \{\backslash \; mathrm\; \{F\}\}\; D\; \_\; \{\backslash \; mathrm\; \{F\}\}\; \backslash \; int\; \_\; \{-\; \backslash \; infty\}\; ^\; \{0\}\; \backslash \; mathrm\; \{\; exp\}\; (\backslash \; epsilon\; /\; d\; \_\; \{\backslash \; mathrm\; \{F\}\})\; \backslash ;\; \backslash \; mathrm\; \{d\}\; \backslash \; epsilon\; \backslash ;\; =\; \backslash ;\; z\; \_\; \{\backslash \; mathrm\; \{S\}\}\; \{d\; \_\; \{\backslash \; mathrm\; \{F\}\}\}\; ^\; \{2\; \}\; D\; \_\; \{\backslash \; mathrm\; \{F\}\}\; \backslash ;\; =\; \backslash ;\; Z\; \_\; \{\backslash \; mathrm\; \{F\}\}\; D\; \_\; \{\backslash \; mathrm\; \{F\}\},..........\; (23)\}$

где $ZF\; [=\; z\; S\; d\; F\; 2]\; \{\backslash \; displaystyle\; Z\; \_\; \{\backslash \; mathrm\; \{F\}\}\; \backslash ;\; [=\; z\; \_\; \{\backslash \; mathrm\; \{S\}\}\; \{d\; \_\; \{\backslash \; mathrm\; \{F\}\}\}\; ^\; \{2\}]\}$- эффективное питание для состояния F и определяется этим уравнением. Строго говоря, нижний предел интеграла должен быть –K F, где K F - энергия Ферми ; но если d F намного меньше, чем K F (что всегда имеет место для металла), тогда не будет значительного вклада в интеграл от энергий ниже K F, и формально его можно продолжить до –∞.

Результату (23) можно дать простую и полезную физическую интерпретацию, обратившись к рис. 1. Состояние электрона в точке «F» на диаграмме («состояние F») - это «состояние движения вперед в уровень Ферми »(т. е. он описывает электрон уровня Ферми, движущийся по нормали к поверхности эмиттера и по направлению к ней). При 0 K электрон в этом состоянии видит барьер неуменьшенной высоты φ и имеет вероятность выхода D F, которая выше, чем для любого другого занятого электронного состояния. Поэтому удобно записать J 0 как Z FDF, где «эффективное питание» Z F - это плотность тока, которая должна переноситься состоянием F внутри металла. если вся эмиссия вышла из состояния F.

На практике плотность тока в основном возникает из группы состояний, близких по энергии к состоянию F, большая часть которых находится в сильно заштрихованной области энергии диаграмма пространства. Поскольку для модели свободных электронов вклад в плотность тока прямо пропорционален площади в энергетическом пространстве (с плотностью питания Зоммерфельда z S как константу пропорциональности), полезно думать о ECD как о взятом из электронных состояний в области размером d F (измеряется в эВ) на диаграмме энергия-пространство. То есть, полезно представить себе ECD как полученное из состояний в сильно заштрихованной области на рис. 1. (Это приближение медленно ухудшается с увеличением температуры.)

ZFтакже можно записать в форме:

$ZF\; =\; z\; S\; d\; F\; 2\; =\; \lambda \; d\; 2\; (z\; S\; e\; 2\; g\; -\; 2)\; \varphi \; -\; 1\; F\; 2\; =\; \lambda \; d\; 2\; a\; \varphi \; -\; 1\; F\; 2,..........\; (24)\; \{\backslash \; Displaystyle\; Z\; \_\; \{\backslash \; mathrm\; \{F\}\}\; =\; z\; \_\; \{\backslash \; mathrm\; \{S\}\}\; \{d\; \_\; \{\backslash \; mathrm\; \{F\}\}\}\; ^\; \{2\}\; =\; \{\backslash \; lambda\; \_\; \{d\}\}\; ^\; \{2\}\; (z\; \_\; \{\backslash \; mathrm\; \{S\}\}\; e\; ^\; \{2\}\; g\; ^\; \{-\; 2\})\; \backslash \; phi\; ^\; \{-\; 1\}\; F\; ^\; \{2\}\; =\; \{\backslash \; lambda\; \_\; \{d\}\}\; ^\; \{2\}\; a\; \backslash \; phi\; ^\; \{-1\}\; F\; ^\; \{2\},..........\; (24)\}$

где универсальная константа a, иногда называемая Первой константой Фаулера – Нордхейма, задается как

$a\; =\; z\; S\; e\; 2\; g\; -\; 2\; =\; e\; 3/8\; \pi \; h\; P\; \approx \; 1,541434\; \times \; 10\; -\; 6\; A\; e\; VV\; -\; 2...........\; (25)\; \{\backslash \; displaystyle\; a\; =\; z\; \_\; \{\backslash \; mathrm\; \{S\}\}\; e\; ^\; \{2\}\; g\; ^\; \{-\; 2\}\; =\; e\; ^\; \{3\}\; /\; 8\; \backslash \; pi\; h\; \_\; \{\backslash \; mathrm\; \{P\}\}\; \backslash \; приблизительно\; \backslash ;\; 1.541434\; \backslash \; times\; 10\; ^\; \{-\; 6\}\; \backslash ;\; \backslash \; mathrm\; \{A\; \backslash ;\; eV\}\; \backslash ;\; \{\backslash \; mathrm\; \{V\}\}\; ^\; \{-\; 2\}...........\; (25)\}$

Это ясно показывает, что предэкспоненциальный множитель a φF, который появляется в уравнениях типа Фаулера-Нордхейма, относится к эффективному притоку электронов к поверхности эмиттера в модели свободных электронов.

Ненулевые температуры

Чтобы получить результат, действительный для ненулевой температуры, мы отметим из ур. (23) что z SdFDF= J 0/dF. Итак, когда эк. (21) интегрируется при ненулевой температуре, затем - после этой замены и вставки явного вида функции распределения Ферми – Дирака - ECD J можно записать в виде:

$J\; =\; J\; 0\; \int \; -\; \infty \; \infty \; ехр\; (ϵ\; /\; d\; F)\; 1\; +\; ехр\; [(ϵ\; /\; d\; F)\; (d\; F\; /\; k\; BT)]\; d\; (ϵ\; /\; d\; F)\; =\; \lambda \; TJ\; 0,..........\; (26)\; \{\backslash \; Displaystyle\; J\; =\; J\_\; \{0\}\; \backslash \; int\; \_\; \{-\; \backslash \; infty\}\; ^\; \{\backslash \; infty\}\; \{\backslash \; frac\; \{\backslash \; mathrm\; \{exp\}\; (\backslash \; epsilon\; /\; d\; \_\; \{\backslash \; mathrm\; \{F\}\})\}\; \{1\; +\; \backslash \; mathrm\; \{exp\}\; [(\backslash \; epsilon\; /\; d\; \_\; \{\backslash \; mathrm\; \{F\}\})\; (d\; \_\; \{\backslash \; mathrm\; \{F\}\}\; /\; k\; \_\; \{\backslash \; mathrm\; \{B\}\}\; T)]\}\}\; \backslash \; mathrm\; \{d\}\; (\backslash \; epsilon\; /\; d\; \_\; \{\backslash \; mathrm\; \{F\}\})\; =\; \backslash \; lambda\; \_\; \{T\}\; J\_\; \{0\},..........\; (26)\}$

где λ T - коэффициент температурной поправки, определяемый интегралом. Интеграл можнопреобразовать, записав $w\; =\; d\; F\; /\; k\; BT\; \{\backslash \; displaystyle\; w\; =\; d\; \_\; \{\backslash \; mathrm\; \{F\}\}\; /\; k\; \_\; \{\backslash \; mathrm\; \{B\}\}\; T\}$и $Икс\; =\; ϵ\; /\; d\; F\; \{\backslash \; displaystyle\; x\; =\; \backslash \; epsilon\; /\; d\; \_\; \{\backslash \; mathrm\; \{F\}\}\}$, а затем $u\; =\; exp\; (x)\; \{\backslash \; displaystyle\; u\; =\; \backslash \; mathrm\; \{exp\}\; (x)\}$, в стандартный результат:

$\int \; -\; \infty \; \infty \; ex\; 1\; +\; ewxdx\; =\; \int \; 0\; \infty \; du\; 1\; +\; uw\; =\; \pi \; wsin\; (\pi \; /\; w)...........\; (27)\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{-\; \backslash \; infty\}\; ^\; \{\backslash \; infty\}\; \{\backslash \; frac\; \{\{\backslash \; mathrm\; \{e\}\}\; ^\; \{x\}\}\; \{1\; +\; \{\backslash \; mathrm\; \{e\}\}\; ^\; \{wx\}\}\; \}\; \backslash \; mathrm\; \{d\}\; x\; =\; \backslash \; int\; \_\; \{0\}\; ^\; \{\backslash \; infty\}\; \{\backslash \; frac\; \{\backslash \; mathrm\; \{d\}\; u\}\; \{1\; +\; u\; ^\; \{w\}\}\}\; =\; \{\backslash \; frac\; \{\backslash \; pi\}\; \{w\; \backslash \; mathrm\; \{sin\}\; (\backslash \; pi\; /w)\}\}...........(27)\}$

Это верно для w>1 (т. е. d F/kBT>1). Следовательно - для таких температур, что k BT

$\lambda \; T\; =\; \pi \; k\; B\; T\; /\; d\; F\; s\; i\; n\; (\pi \; k\; B\; T\; /\; d\; F)\; \approx \; 1\; +\; 1\; 6\; \pi \; k\; B\; T\; d\; F\; 2,..........\; (28)\; \{\backslash \; displaystyle\; \backslash \; lambda\; \_\; \{T\}\; =\; \{\backslash \; frac\; \{\backslash \; pi\; k\; \_\; \{\backslash \; mathrm\; \{B\}\}\; T\; /\; d\; \_\; \{\backslash \; mathrm\; \{F\}\}\}\; \{\backslash \; mathrm\; \{sin\}\; (\backslash \; pi\; k\; \_\; \{\backslash \; mathrm\; \{B\}\}\; T\; /\; d\; \_\; \{\backslash \; mathrm\; \{F\}\})\}\}\; \backslash \; приблизительно\; 1\; +\; \{\backslash \; frac\; \{1\}\; \{6\}\}\; \{\backslash \; frac\; \{\backslash \; pi\; k\; \_\; \{\backslash \; mathrm\; \{B\}\}\; T\}\; \{d\_\; \{\backslash \; mathrm\; \{F\}\}\}\}\; ^\; \{2\},..........\; (28)\}$

где расширение допустимо, только если (πk B T / d F) << 1. An example value (for φ= 4.5 eV, F= 5 V/nm, T= 300 K) is λT= 1,024. Нормальным считается, что в режиме CFE λ T всегда мало по сравнению с другими неопределенностями, и что обычно нет необходимости явно включать его в формулы для плотности тока. при комнатной температуре.

Режимы излучения металлов на практике определяются диапазонами барьерного поля F и температуры T, для которых данное семейство уравнений излучения математически адекватно. Когда барьерное поле F равно достаточно высок, чтобы режим CFE работал для эмиссии металлов при 0 K, тогда условие k BT

Обратите внимание, что результат (28) здесь применим для барьера любой формы (хотя d F будет отличаться для разных барьеров).

Физически полное уравнение типа Фаулера – Нордхейма

Результат (23) также приводит к некоторому пониманию того, что происходит, когда принимаются во внимание эффекты атомного уровня и зонная структура больше не похож на свободный электрон. Из-за наличия атомных ионных остовов поверхностный барьер, а также волновые функции электрона на поверхности будут другими. Это повлияет на значения поправочного коэффициента $\nu \; \{\backslash \; displaystyle\; \backslash \; nu\}$, префактора P и (в ограниченной степени) поправочного коэффициента λ d. Эти изменения, в свою очередь, повлияют на значения параметра D F и (в ограниченной степени) параметра d F. Для настоящего металла плотность подачи будет изменяться в зависимости от положения в энергетическом пространстве, а значение в точке «F» может отличаться от плотности подачи по Зоммерфельду. Мы можем учесть этот эффект, введя поправочный коэффициент для электронной зонной структуры λ B в ур. (23). Модинос обсуждал, как можно рассчитать этот коэффициент: он оценивает, что он, скорее всего, будет между 0,1 и 1; он может выходить за эти пределы, но маловероятно, что он выйдет за пределы диапазона 0,01 <λB<10.

. Определив общий поправочный коэффициент предложения λ Z равным λ TλBλdи комбинируя приведенные выше уравнения, мы достигаем - физически полное уравнение типа Фаулера-Нордхейма:

$J\; =\; \lambda \; Z\; a\; \varphi \; -\; 1\; F\; 2\; PF\; exp\; [-\; \nu \; F\; b\; \varphi \; 3/2\; /\; F],..........\; (29)\; \{\backslash \; Displaystyle\; J\; \backslash ;\; =\; \backslash \; lambda\; \_\; \{Z\}\; a\; \backslash \; phi\; ^\; \{-\; 1\}\; F\; ^\; \{2\}\; P\; \_\; \{\backslash \; mathrm\; \{F\}\}\; \backslash \; mathrm\; \{exp\}\; [-\; \backslash \; nu\; \_\; \{\backslash \; mathrm\; \{F\}\}\; b\; \backslash \; phi\; ^\; \{3/2\}\; /\; F],..........\; (29)\}$

где $\nu \; F\; \{\backslash \; displaystyle\; \{\backslash \; nu\}\; \_\; \{\backslash \; mathrm\; \{F\}\}\}$[=$\nu \; F\; \{\backslash \; displaystyle\; \{\backslash \; nu\}\; \_\; \{\backslash \; mathrm\; \{F\}\}\}$(φ, F)] - коэффициент поправки экспоненты для барьера неуменьшенной высоты. φ. Это наиболее общее уравнение типа Фаулера – Нордгейма. Другие уравнения в семействе получаются заменой конкретных выражений для трех поправочных коэффициентов $\nu \; F\; \{\backslash \; displaystyle\; \{\backslash \; nu\}\; \_\; \{\backslash \; mathrm\; \{F\}\}\}$, P F и λ Z он содержит. Так называемое элементарное уравнение типа Фаулера-Нордхейма, которое появляется в школьных учебниках по полевой эмиссии, получается, если положить λ Z → 1, P F → 1, $\nu \; F\; \{\backslash \; Displaystyle\; \{\backslash \; Nu\}\; \_\; \{\backslash \; mathrm\; \{F\}\}\}$→ 1; это не дает хороших количественных предсказаний, потому что делает барьер сильнее, чем он есть в физической реальности. Так называемое стандартное уравнение типа Фаулера-Нордхейма, первоначально разработанное Мерфи и Гудом и часто используемое в прошлой литературе, получается, если положить λ Z→tF, P F → 1, $\nu \; F\; \{\backslash \; displaystyle\; \{\backslash \; nu\}\; \_\; \{\backslash \; mathrm\; \{F\}\}\}$→vF, где v F - это v (f), где f - значение f h полученный, если положить h = φ, и t F является связанным параметром (со значением, близким к единице).

В рамках более полной теории, описанной здесь, коэффициент t F является составной частью поправочного коэффициента λ d [см. И обратите внимание, что λ d здесь обозначено λ D ]. Продолжение отдельной идентификации t F не имеет особого значения. Вероятно, при нынешнем уровне знаний наилучшее приближение для моделирования CFE из металлов на основе простого уравнения Фаулера-Нордхейма получается, если положить λ Z → 1, P F → 1, $\nu \; F\; \{\backslash \; displaystyle\; \{\backslash \; nu\}\; \_\; \{\backslash \; mathrm\; \{F\}\}\}$→ v (f). Это воссоздает уравнение типа Фаулера-Нордхейма, использованное Дайком и Доланом в 1956 году, и может быть названо «упрощенным стандартным уравнением типа Фаулера-Нордхейма».

Рекомендуемая форма для простых вычислений типа Фаулера-Нордхейма

В явном виде это рекомендуемое упрощенное стандартное уравнение типа Фаулера-Нордхейма и связанные формулы:

$J\; =\; a\; \varphi \; -\; 1\; F\; 2\; ехр\; [-\; v\; (f)\; b\; \varphi \; 3/2\; /\; F],..........\; (30\; a)\; \{\backslash \; displaystyle\; J\; =\; \backslash ;\; a\; \{\backslash \; phi\; ^\; \{-\; 1\}\}\; F\; ^\; \{2\}\; \backslash \; mathrm\; \{exp\}\; [-v\; (f)\; \backslash ;\; b\; \backslash \; phi\; ^\; \{3/2\}\; /\; F\; ],..........\; (30a)\}$

$a\; \approx \; 1,541434\; \times \; 10\; -\; 6\; А\; э\; ВВ\; -\; 2;\; b\; \approx \; 6.830890\; э\; В\; -\; 3/2\; В\; ·\; м\; -\; 1,..........\; (30\; б)\; \{\backslash \; displaystyle\; a\; \backslash \; приблизительно\; \backslash ;\; 1.541434\; \backslash \; times\; 10\; ^\; \{-\; 6\}\; \backslash ;\; \backslash \; mathrm\; \{A\; \backslash ;\; eV\}\; \backslash ;\; \{\backslash \; mathrm\; \{V\}\}\; ^\; \{-\; 2\};\; \backslash ;\; \backslash ;\; \backslash ;\; \backslash ;\; \backslash ;\; b\; \backslash \; приблизительно\; 6.830890\; \backslash ;\; \{\backslash \; mathrm\; \{eV\}\}\; ^\; \{-\; 3/2\}\; \backslash ;\; \backslash \; mathrm\; \{V\}\; \backslash ;\; \{\backslash \; mathrm\; \{nm\}\}\; ^\; \{-\; 1\},..........\; (30b)\}$

$v\; (f)\; \approx \; 1\; -\; f\; +\; (1/6)\; flnf..........\; (30\; с)\; \{\backslash \; displaystyle\; v\; (f)\; \backslash \; приблизительно\; 1-f\; +\; (1/6)\; f\; \backslash \; mathrm\; \{ln\}\; f..........\; (30c)\}$

$f\; =\; F\; /\; F\; \varphi \; =\; (e\; 3/4\; \pi \; ϵ\; 0)\; (F\; /\; \varphi \; 2)\; =\; (1,439964\; e\; V\; 2\; V\; -\; 1\; нм)\; (F\; /\; \varphi \; 2)...........\; (30\; d)\; \{\backslash \; displaystyle\; f\; =\; \backslash ;\; F\; /\; F\; \_\; \{\backslash \; phi\}\; =\; (e\; ^\; \{3\}\; /\; 4\; \backslash \; pi\; \backslash \; epsilon\; \_\; \{0\})\; (F\; /\; \{\backslash \; phi\}\; ^\; \{2\})\; =\; (\; 1.439964\; \backslash ;\; \{\backslash \; mathrm\; \{eV\}\}\; ^\; \{2\}\; \backslash ;\; \{\backslash \; mathrm\; \{V\}\}\; ^\; \{-\; 1\}\; \backslash ;\; \backslash \; mathrm\; \{nm\})\; (F\; /\; \{\backslash \; phi\}\; ^\; \{2\})...........\; (30d)\}$

где F φ здесь - поле, необходимое для уменьшения до нуля барьера Шоттки-Нордхейма неуменьшенной высоты, равного локальной работе -функция φ, а f - масштабированное барьерное поле для барьера Шоттки-Нордхейма нередуцированной высоты φ. [Эту величину f можно было бы более точно записать как f φ, но она делает это уравнение типа Фаулера-Нордхейма менее загроможденным, если принять соглашение, что простое f означает величину, обозначенную f φ дюйм, ур. (2.16).] Для примера (φ = 4,5 эВ, F = 5 В / нм), f ≈ 0,36 и v (f) ≈ 0,58; практические диапазоны для этих параметров обсуждаются далее в.

Обратите внимание, что переменная f (масштабируемое барьерное поле) не то же самое, что переменная y (параметр Нордхейма), широко использовавшаяся в прошлой литературе по полевой эмиссии, и «v (f)» НЕ имеет того же математического значения и значений, что и величина «v (y)», которая встречается в литературе по автоэлектронной эмиссии. В контексте описанной здесь пересмотренной теории формулы для v (y) и таблицы значений для v (y) следует игнорировать или рассматривать как значения v (f). Если требуются более точные значения для v (f), то предоставляются формулы, которые дают значения для v (f) с абсолютной математической точностью лучше 8 × 10. Однако приведенная выше формула аппроксимации (30c), которая дает значения, верные с точностью до абсолютной математической точности лучше 0,0025, должна давать значения, достаточно точные для всех технологических целей.

Комментарии

Историческая справка по методов вывода уравнений типа Фаулера-Нордхейма. Существует несколько возможных подходов к выводу этих уравнений с использованием теории свободных электронов. The approach used here was introduced by Forbes in 2004 and may be described as "integrating via the total energy distribution, using the parallel kinetic energy Kpas the first variable of integration". Basically, it is a free-electron equivalent of the Modinos procedure (in a more advanced quantum-mechanical treatment) of "integrating over the Поверхностная зона Бриллюэна ». Напротив, обработка CFE свободными электронами Янга в 1959 г., Гадзука и Пламмера в 1973 г. и Модиноса в 1984 г. также интегрирует через распределение полной энергии, но использует нормальную энергию ε n (или связанная величина) в качестве первой переменной интегрирования.

Существует также более старый подход, основанный на основополагающей статье Нордхейма в 1928 году, который формулирует проблему по-другому, а затем использует сначала K p, а затем ε n (или связанная величина) в качестве переменных интегрирования: это известно как «интегрирование через распределение нормальной энергии». Этот подход продолжает использоваться некоторыми авторами. Хотя он имеет некоторые преимущества, особенно при обсуждении резонансных явлений, он требует интегрирования функции распределения Ферми – Дирака на первом этапе интегрирования: для электронных зонных структур, подобных свободным электронам, это может привести к очень сложным и ошибочным результатам. склонная математика (как в работе Страттона полупроводники ). Кроме того, интегрирование через распределение нормальной энергии не дает экспериментально измеренных распределений энергии электронов.

В целом используемый здесь подход кажется более легким для понимания и приводит к более простой математике.

Это также в принципе ближе к более сложным подходам, используемым при работе с реальными объемными кристаллическими твердыми телами, где первым шагом является либо интегрирование вкладов в ECD по поверхностям постоянной энергии в волновой вектор пространство (k -пространство) или для интегрирования вкладов по соответствующей зоне Бриллюэна на поверхности. Подход Forbes эквивалентен интегрированию по сферической поверхности в k -пространстве с использованием переменной K p для определения кольцевого элемента интегрирования, имеющего цилиндрическую симметрию относительно оси в направление, нормальное к излучающей поверхности, или к интегрированию по (протяженной) поверхности зоны Бриллюэна с использованием элементов кругового кольца.

Теоретические уравнения CFE

В предыдущем разделе объясняется, как вывести уравнения типа Фаулера-Нордхейма. Строго, эти уравнения применимы только к CFE из массивных металлов. Идеи, изложенные в следующих разделах, применимы к ДОВСЕ в более общем плане, но ур. (30) будет использоваться для их иллюстрации.

Для CFE основные теоретические подходы обеспечивают взаимосвязь между локальной плотностью тока эмиссии J и локальным полем барьера F в локальном положении на излучающей поверхности. Эксперименты измеряют эмиссионный ток i из некоторой определенной части эмиссионной поверхности как функцию напряжения V, приложенного к некоторому противоэлектроду. Чтобы связать эти переменные с J и F, используются вспомогательные уравнения.

Коэффициент преобразования напряжения β в барьерное поле определяется как:

$F\; =\; \beta \; V,..........\; (31)\; \{\backslash \; displaystyle\; F\; =\; \backslash ;\; \backslash \; beta\; V,..........\; (31)\}$

Значение F меняется от позиции к позиции на поверхности эмиттера, а значение β соответственно меняется.

Для металлического эмиттера значение β для данного положения будет постоянным (независимо от напряжения) при следующих условиях: (1) устройство представляет собой «диодную» конструкцию, в которой присутствуют только электроды. эмиттер и набор «окружения», все части которого находятся под одинаковым напряжением; (2) отсутствует значительный излучаемый полем вакуум объемный заряд (FEVSC) (это будет верно, за исключением очень высоких плотностей тока эмиссии, около 10 А / м или выше); (3) не существует значимых «полей исправлений» из-за неоднородностей в локальной работе выхода (обычно предполагается, что это правда, но может не быть в некоторых обстоятельствах). Для неметаллов физические эффекты, называемые «проникновение поля» и «изгиб полосы » [M084], могут сделать β функцией приложенного напряжения, хотя, что удивительно, исследований этого эффекта мало.

Плотность эмиссионного тока J меняется от позиции к позиции по поверхности эмиттера. Полный ток эмиссии i из специальной части эмиттера путем интегрирования J по этой части. Чтобы получить простое уравнение для i (V), используется следующая процедура. Контрольная точка «r» выбирается в этой части поверхности эмиттера (часто точка, в которой плотность тока самая высокая), и плотность тока в контрольной точке обозначается как J r. Параметр A r, называемый условной излучением (относительно точки «r»), затем определяется следующим образом:

$i\; =\; A\; r\; J\; r\; =\; \int \; J\; d\; A,..........\; (32)\; \{\backslash \; displaystyle\; i\; =\; A\; \_\; \{\backslash \; mathrm\; \{r\}\}\; J\; \_\; \{\backslash \; mathrm\; \{r\}\}\; =\; \backslash \; int\; J\; \backslash \; mathrm\; \{d\}\; A,..........\; (32)\; \}$

, где интеграл берется по интересующей части эмиттера.

Этот параметр A r был введен в теорию CFE Стерном, Госслингом и Фаулером в 1929 году (которыевали его «средневзвешенной площадью»). Для практических датчиков плотности тока эмиссии, используемая в уравнениях типа Фаулера-Нордхейма, всегда является плотностью тока в некоторой контрольной точке (хотя обычно это не указывается). Давно установленное обозначение обозначает эту эталонную плотность тока основным символом J, соответствующее локальное поле и коэффициент преобразования - простыми символами F и β без нижнего индекса «r», использованного выше; в дальнейшем используется это соглашение.

Условная площадь излучения A r часто используется функция эталонного местного поля (и, следовательно, напряжение), в некоторых случаях может быть функция температуры.

A r имеет математическое определение, оно не обязательно соответствует области, из которой наблюдается эмиссия от одноточечного эмиттера в полевом электроне (эмиссия) микроскоп. С эмиттером большой площади, который содержит много отдельных участков излучения, A r почти всегда будет намного меньше, чем "макроскопическая" геометрическая площадь (A M) эмиттера. как видно визуально (см. ниже).

Включение этих вспомогательных свойств в ур. (30a) дает

$i\; =\; A\; r\; a\; \varphi \; -\; 1\; \beta \; 2\; V\; 2\; e\; x\; p\; [-\; v\; (f)\; b\; \varphi \; 3/2\; /\; \beta \; V],..........\; (33)\; \{\backslash \; Displaystyle\; я\; =\; \backslash ;\; A\; \_\; \{\backslash \; mathrm\; \{r\}\}\; a\; \{\backslash \; phi\; ^\; \{-\; 1\}\}\; \{\backslash \; beta\}\; ^\; \{2\}\; V\; ^\; \{2\}\; \backslash \; mathrm\; \{exp\}\; [-v\; (f)\; \backslash ;\; b\; \backslash \; phi\; ^\; \{3/2\}\; /\; \backslash \; beta\; V],..........\; (33)\}$

Это упрощенное стандартное уравнение типа Фаулера-Нордхейма в iV форма. Соответствующее «физически полное» уравнение получается путем умножения на λ ZPF.

Модифицированные уравнения для излучателей большой площади

Уравнения в разделе применимы ко всем полевым излучателям, работающим в режиме CFE. Однако дальнейшие разработки полезны для излучения с большой площадью, которые содержат много отдельных выбросов металлов.

Для таких излучателей условная площадь излучения почти всегда будет намного меньше, чем кажущаяся «макроскопическая» геометрическая площадь (A M) физического излучателя, наблюдаемая визуально. Безразмерный параметр α r, площадь излучения, может быть определен как

$A\; r\; =\; \alpha \; r\; A\; M...........\; (34)\; \{\backslash \; Displaystyle\; A\; \_\; \{\backslash \; mathrm\; \{r\}\}\; =\; \backslash ;\; \backslash \; alpha\; \_\; \{\backslash \; mathrm\; \{r\}\}\; A\; \_\; \{\backslash \; mathrm\; \{M\}\}...........\; (34)\}$

Также может быть определена "макроскопическая" (или "средняя") плотность тока эмиссии J M (усредненная по геометрической площади A M эмиттера) и связанная к эталонной плотности тока J r, использованная выше, на

$JM\; =\; i\; /\; AM\; =\; \alpha \; r\; (i\; /\; A\; r)\; =\; \alpha \; r\; J\; r...........\; (35)\; \{\backslash \; Displaystyle\; J\; \_\; \{\backslash \; mathrm\; \{M\}\}\; =\; \backslash ;\; я\; /\; A\; \_\; \{\backslash \; mathrm\; \{M\}\}\; =\; \backslash \; alpha\; \_\; \{\backslash \; mathrm\; \{r\}\}\; (я\; /\; A\; \_\; \{\backslash \; mathrm\; \{r\}\})\; =\; \backslash \; alpha\; \_\; \{\backslash \; mathrm\; \{r\}\}\; J\; \_\; \{\backslash \; mathrm\; \{r\}\}...........\; (35)\}$

Это приводит к следующей "версиим большой площади" упрощенное стандартное уравнение типа Фаулера-Нордхейма:

$JM\; =\; \alpha \; ra\; \varphi \; -\; 1\; F\; 2\; ехр\; [-\; v\; (f)\; b\; \varphi \; 3/2\; /\; F],..........\; (36)\; \{\backslash \; displaystyle\; J\; \_\; \{\backslash \; mathrm\; \{M\}\}\; =\; \backslash \; alpha\; \_\; \{\backslash \; mathrm\; \{r\}\}\; a\; \{\backslash \; phi\; ^\; \{-\; 1\}\}\; F\; ^\; \{2\}\; \backslash \; mathrm\; \{exp\}\; [-v\; (\; е)\; \backslash ;\; b\; \backslash \; phi\; ^\; \{3/2\}\; /\; F],..........\; (36)\}$

$i\; =\; \alpha \; r\; AM\; a\; \varphi \; -\; 1\; \beta \; 2\; V\; 2\; exp\; [-\; v\; (е)\; b\; \varphi \; 3/2\; /\; \beta \; V],..........\; (37)\; \{\backslash \; Displaystyle\; я\; =\; \backslash ;\; \backslash \; альфа\; \_\; \{\backslash \; mathrm\; \{r\}\}\; A\; \_\; \{\backslash \; mathrm\; \{M\}\}\; а\; \{\backslash \; phi\; ^\; \{-\; 1\}\}\; \{\backslash \; beta\}\; ^\; \{2\}\; V\; ^\; \{2\}\; \backslash \; mathrm\; \{exp\}\; [-v\; (е)\; \backslash ;\; b\; \backslash \; phi\; ^\; \{3/2\}\; /\; \backslash \; beta\; V],..........\; (37)\}$

Оба эти уравнения содержат площадь эффективности излучения α r. Для любого данного эмиттера этот параметр имеет значение, которое обычно малоизвестно. В общем, α r сильно различируется как между разными материалами излучателя, так и между разными образцами одного и того же материала, приготовленными и обработанными по-разному. Вероятны значения в диапазоне от 10 до 10, а значения вне этого диапазона - возможны.

Наличие α r в ур. (36) учитывает разницу между макроскопическими плотностями тока, часто цитируемыми в литературе (10 А / м для многих форм эмиттеров с большой площадью, кроме обычно массивов шпиндтов ) и локальными плотностями тока при фактических места эмиссии, которые могут сильно различаться, но обычно считаются порядком 10 А / м или, возможно, немного меньше.

В части технической литературы по эмиттерам большой площади не проводится четких различий между местами макроскопической плотностей тока или условной излучения A r и макроскопической площадью A M, и / или исключает параметр α r из процитированных соотношений. Необходима осторожность, чтобы избежать ошибок интерпретации.

Также удобно иногда разделить коэффициент преобразования β r на «макроскопическую часть», которая относится к общей геометрии излучателя и его окружения, и «локальная часть», которая относится к способности очень структуры поверхности эмиттера усиливать электрическое поле. Обычно это делается путем определения «макроскопического поля» F M, которое представляет собой присутствие в месте отсутствия локальной структуры, вызывающее усиление. Это поле F M связано с приложенным напряжением «коэффициентом преобразования напряжения в макроскопическое поле» β M, определяемым как:

$F\; M\; =\; \beta \; M\; V...........\; (38)\; \{\backslash \; Displaystyle\; F\; \_\; \{\backslash \; mathrm\; \{M\}\}\; =\; \backslash ;\; \backslash \; beta\; \_\; \{\backslash \; mathrm\; \{M\}\}\; V...........\; (38)\}$

В общем случае системы, состоящей из двух параллельных пластин, разделенных расстояний W, с излучающими наноструктурами, созданными на одна из них, β M = 1 / W.

Затем определяется «коэффициент расширения поля» γ и соотносится со значениями β r и β M посредством

$\gamma \; =\; F\; r\; /\; FM\; =\; \beta \; r\; /\; \beta \; M...........\; (39)\; \{\backslash \; Displaystyle\; \backslash \; гамма\; =\backslash ;\; F\; \_\; \{\backslash \; mathrm\; \{r\}\}\; /\; F\; \_\; \{\backslash \; mathrm\; \{M\}\}\; =\; \backslash \; beta\; \_\; \{\backslash \; mathrm\; \{r\}\}\; /\; \backslash \; beta\; \_\; \{\backslash \; mathrm\; \{M\}\}...........\; (39)\}$

С ур. (31), это дает следующие формулы:

$F\; =\; \gamma \; F\; M\; =\; \beta \; V..........\; (40);\; \beta \; =\; \beta \; M\; \gamma ..........\; (41);\; \{\backslash \; Displaystyle\; F\; =\; \backslash ;\; \backslash \; гамма\; F\; \_\; \{\backslash \; mathrm\; \{M\}\}\; =\; \backslash \; бета\; V..........\; (40);\; \backslash ;\; \backslash ;\; \backslash ;\; \backslash ;\; \backslash ;\; \backslash ;\; \backslash ;\; \backslash ;\; \backslash ;\; \backslash \; beta\; =\; \backslash ;\; \backslash \; beta\; \_\; \{\backslash \; mathrm\; \{M\}\}\; \backslash \; gamma..........\; (41);\}$

где, в соответствии с обычным соглашением, суффикс "r" теперь исключен из параметров, относящихся к контрольной точке. Существуют формулы для оценки γ с использованием классической электростатики для различных форм излучателя, в частности «полусферы на столбе».

Уравнение (40) подразумевает, что версия Фаулера -Уравнения типа Нордхейма могут записаны, где либо F, либо βV везде заменены на $\gamma \; FM\; \{\backslash \; displaystyle\; \backslash \; gamma\; F\; \_\; \{\backslash \; mathrm\; \{M\}\; \}\}$. Это часто делается в технологических приложениях, где основной интерес добавляет улучшенные свойства наноструктуры с локальным эмиттером. Однако в некоторых прошлых работах неспособность провести четкое различие между барьерным полем F и макроскопическим полем F M приводило к путанице или ошибку.

В более общем плане, цели технологического развития полевых эмиттеров большие площади заключаются в повышении однородности излучения за счет увеличения значения площади излучения излучения α r и уменьшения «начальное» напряжение, при котором происходит значительная эмиссия, за счет увеличения значения β. Уравнение (41) показывает, что это может быть сделано двумя способами: либо путем разработки наноструктур с «высокой геометрией», либо путем изменения общей системы так, что β M увеличивается. Существуют различные компромиссы и ограничения.

На практике, использованное выше определение макроскопического поля, используется наиболее распространенным в литературе другие (источники) тип макроскопического поля и коэффициент усиления поля, особенно в связи с использованием зондов для исследовать характеристики отдельных излучателей.

В технологических контекстах данные полевой эмиссии часто строятся с использованием (конкретного определения) F M или 1 / F M как координата x. Однако для научного анализа необработанные экспериментальные данные, а также напрямую строить необработанные измеренные данные i-V. Значения технологических параметров, таких как (различные формы) γ, могут быть получены из подобранных параметров i-V (см. Ниже) с использованием соответствующих определений.

Модифицированные уравнения для нанометрических излучателей

Большинство теоретических выводов теории автоэмиссии сделано в предположении, что барьер принимает форму Шоттки-Нордхейма ур. (3). Однако такая форма барьера не действительна для излучения с радиусами кривизны $R\; \{\backslash \; displaystyle\; R\}$, сравнимыми с длиной туннельного барьера. Последнее зависит от работы выхода и поля, но в случаях представляющих практический интерес, приближение барьера SN можно считать допустимым для излучения с радиусом $R>20\; нм\; \{\backslash \; displaystyle\; R>20\; \{\backslash \; text\; \{нм\}\}\}$, как объясняется в следующем абзаце.

Основное предположение приближения барьера SN в том, что член электростатического принимает линейную форму $\Phi \; =\; F\; x\; \{\backslash \; displaystyle\; \backslash \; Phi\; =\; Fx\}$в области туннелирования. Было доказано, что последнее выполнено, только если $x\; \ll \; R\; \{\backslash \; displaystyle\; x\; \backslash \; ll\; R\}$. Следовательно, если туннелирование области имеет длину $L\; \{\backslash \; displaystyle\; L\}$, для всех $x\; \{\backslash \; displaystyle\; x\}$, определяющих процесс туннелирования; таким образом, если $L\; \ll \; R\; \{\backslash \; displaystyle\; L\; \backslash \; ll\; R\}$уравнение (1) выполнено, и приближение SN-барьера действительно. Наблюдаемость достаточно высока для достижения измеримой полевой эмиссии, L не более 1-2 нм. Следовательно, барьер SN систем излучения с помощью порядка нескольких десятков нм.

современные излучатели намного острее этого, с радиусами порядка нескольких нм. Следовательно, стандартное уравнение FN или любая его версия, предполагающая барьер SN, приводит к значительным ошибкам для таких резких излучателей. Это было доказано теоретически и подтверждено экспериментально.

Вышеупомянутая проблема была рассмотрена в исх. Барьер SN был обобщен с учетом кривизны излучателя. Можно доказать, что электростатический потенциал на любой металлической поверхности с радиусом кривизны $R\; \{\backslash \; displaystyle\; R\}$может быть астотически расширен как

$\Phi \; (x)\; =\; F\; x\; [\; 1\; -\; x\; R\; +\; O\; (x\; R)\; 2]\; для\; x\; \ll \; R...........\; (42)\; \{\backslash \; displaystyle\; \backslash \; Phi\; (x)\; =\; Fx\; \backslash \; left\; [1\; -\; \{\backslash \; frac\; \{x\}\; \{R\}\}\; +\; O\; \backslash \; left\; (\{\backslash \; frac\; \{x\}\; \{R\}\}\; \backslash \; right)\; ^\; \{2\}\; \backslash \; right]\; \{\backslash \; text\; \{,\; for\}\}\; x\; \backslash \; ll\; R\; \{\backslash \; text\; \{.\}\}..........\; (42)\}$

Кроме того, возможности изображения для резкого эмиттера лучше представлен не плоской, а сферической металлической поверхности. После пренебрежения всеми членами $O\; (x\; /\; R)\; 2\; \{\backslash \; displaystyle\; O\; (x\; /\; R)\; ^\; \{2\}\}$общий потенциальный барьер принимает форму, найденную Кирицакисом и Ксантакисом

$MKX\; (x)\; знак\; равно\; h\; -\; e\; F\; x\; (1\; -\; x\; R)\; -\; e\; 2\; 16\; \pi \; ϵ\; 0\; x\; (1\; +\; x\; /\; 2\; R)..........\; (43)\; \{\backslash \; displaystyle\; M\; ^\; \{KX\}\; (x)\; =\; h-eFx\; \backslash \; left\; (1\; -\; \{\backslash \; frac\; \{x\}\; \{R\}\}\; \backslash \; right)\; -\; \{\backslash \; frac\; \{e\; ^\; \{2\}\}\; \{16\; \backslash \; pi\; \backslash \; epsilon\; \_\; \{0\}\; x\; (1\; +\; x\; /\; 2R)\}\}..........\; (43)\}$

Если аппроксимация JWKB (4) используется для этого барьера, показатель Гамова принимает форму, которая обобщает ур. (5)

$G\; (h,\; F,\; R)\; =\; b\; h\; 3/2\; F\; (v\; (f)\; +\; \omega \; (f)\; h\; e\; F\; R)..........\; (44)\; \{\backslash \; displaystyle\; G\; (h,\; F,\; R)\; =\; \{\backslash \; frac\; \{bh\; ^\; \{3/2\}\}\; \{F\}\}\; \backslash \; left\; (v\; (f)\; +\; \backslash \; omega\; (f)\; \{\backslash \; frac\; \{h\}))\; \{eFR\}\}\; \backslash \; right)..........\; (44)\}$

где $f\; \{\backslash \; displaystyle\; f\}$определяется как (30d), $v\; (е)\; \{\backslash \; displaystyle\; v\; (f)\}$определяется выражением (30c) и $\omega \; (f)\; \{\backslash \; displaystyle\; \backslash \; omega\; (f)\}$является новой функцией, которая может быть аппроксимирована аналогично (30c) (здесь есть типовые ошибки, исправленные здесь):

$\omega \; (f)\; \approx \; 4\; 5-7\; 40\; f\; +\; 1\; 200\; log\; \; (f)...........\; (45)\; \{\backslash \; displaystyle\; \backslash \; omega\; (f)\; \backslash \; приблизительно\; \{\backslash \; frac\; \{4\}\; \{5\}\}\; -\; \{\backslash \; frac\; \{7\}\; \{40\}\}\; f\; +\; \{\backslash \; frac\; \{1\}\; \{200\}\}\; \backslash \; log\; (f)\; \{\backslash \; text\; \{.\}\}..........\; (45)\}$

Дано выражение для показателя Гамова как функции высоты барьера без полей $h\; \{\backslash \; displaystyle\; h\}$, плотность излучаемого тока для эмиссии холодного поля может быть получена из ур. (23). Отсюда получаем

$J\; =\; a\; F\; 2\; \varphi \; (1\; \lambda \; d\; (f)\; +\; \varphi \; e\; FR\; \psi \; (f))\; -\; 2\; exp\; \; [-\; b\; \varphi \; 3/2\; F\; (v\; (f)\; +\; \omega \; (f)\; \varphi \; e\; FR)]..........\; (46)\; \{\backslash \; displaystyle\; J\; =\; a\; \{\backslash \; frac\; \{F\; ^\; \{2\}\}\; \{\backslash \; phi\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{1\}\; \{\backslash \; lambda\; \_\; \{d\}\; (f)\}\}\; +\; \{\backslash \; frac\; \{\; \backslash \; phi\}\; \{eFR\}\}\; \backslash \; psi\; (f)\; \backslash \; right)\; ^\; \{-\; 2\}\; \backslash \; exp\; \backslash \; left\; [-\; \{\backslash \; frac\; \{b\; \backslash \; phi\; ^\; \{3/2\}\}\; \{F\}\}\; \backslash \; left\; (v\; (f)\; +\; \backslash \; omega\; (f)\; \{\backslash \; frac\; \{\backslash \; phi\}\; \{eFR\}\}\; \backslash \; right)\; \backslash \; right]..........\; (46)\}$

где функции $\lambda \; d\; (е)\; \{\backslash \; displaystyle\; \backslash \; lambda\; \_\; \{d\}\; (f)\}$и $\psi \; (f)\; \{\backslash \; displaystyle\; \backslash \; psi\; (f)\}$как

$1\; \lambda \; d\; (f)\; \equiv \; v\; (f)\; -\; 4\; 3\; f\; \partial \; v\; \partial \; f\; \approx \; 1\; +\; f\; 9\; -\; f\; журнал\; \; (f)\; 22..........\; (47\; а)\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{\backslash \; lambda\; \_\; \{d\}\; (f)\}\}\; \backslash \; Equiv\; v\; (f)\; -\; \{\backslash \; frac\; \{4\}\; \{3\}\}\; f\; \{\backslash \; frac\; \{\backslash \; partial\; v\; \}\; \{\backslash \; partial\; f\}\}\; \backslash \; приблизительно\; 1\; +\; \{\backslash \; frac\; \{f\}\; \{9\}\}\; -\; \{\backslash \; frac\; \{f\; \backslash \; log\; (f)\}\; \{22\}\}..........\; (47a)\; \}$

и

$\psi \; (f)\; \equiv \; 5\; 3\; \omega \; (f)\; -\; 4\; 3\; f\; \partial \; \omega \; \partial \; f\; \approx \; 4\; 3\; -\; f\; 15\; -\; f\; log\; \; (f)\; 1200..........\; (47\; б)\; \{\backslash \; Displaystyle\; \backslash \; psi\; (е)\; \backslash \; экв\; \{\backslash \; гидроразрыва\; \{5\}\; \{3\}\}\; \backslash \; omega\; (f)\; -\; \{\backslash \; frac\; \{4\}\; \{3\}\}\; f\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; omega\}\; \{\backslash \; partial\; f\}\}\; \backslash \; приблизительно\; \{\backslash \; frac\; \{4\}\; \{3\}\}\; -\; \{\backslash \; frac\; \{f\}\; \{15\}\}\; -\; \{\backslash \; frac\; \{f\; \backslash \; log\; (f)\}\; \{1200\}\}..........\; (47b)\}$

В уравнении (46) для целей полноты, $\lambda \; d\; \{\backslash \; displaystyle\; \backslash \; lambda\; \_\; \{d\}\}$не аппроксимируется единицей, как в (29) и (30a), хотя для практических случаев это очень хорошее приближение. Помимо этого, уравнения (43), (44) и (46) совпадают с уравнениями стандартной теории Фаулера-Нордгейма (3), (9) и (30a) в пределе $R\; \to \; \infty \; \{\backslash \; Displaystyle\; R\; \backslash \; rightarrow\; \backslash \; infty\}$; это ожидается, поскольку первые уравнения обобщают последние.

Наконец, обратите внимание, что приведенный выше анализ является асимптотическим в пределе $L\; \ll \; R\; \{\backslash \; displaystyle\; L\; \backslash \; ll\; R\}$, аналогично стандартной теории Фаулера-Нордхейма с использованием барьера SN. Однако добавление квадратичных делает его значительно более точным для излучения с радиусами кривизны в диапазоне ~ 5-20 нм. Для более острых эмиттеров нет общего приближения для плотности тока. Чтобы получить плотность тока, можно вычислить электростатический потенциал и определить интеграл JWKB численно. Для этого были разработаны программы программного обеспечения для научных вычислений.

Эмпирическое уравнение CFE i - V

На современном этапе развития теории CFE важно различать теоретические уравнения CFE и эмпирическое уравнение CFE. Первые происходят из физики конденсированного состояния (хотя и в контекстах, где их детальное развитие затруднительно). С другой стороны, эмпирическое уравнение CFE просто пытается представить фактическую экспериментальную форму зависимости тока от напряжения V.

В 1920-х годах эмпирические уравнения использовались для определения появившейся степени V в показателе степени полулогарифмического уравнения, предполагаемого для описания экспериментальных результатов ДОВСЕ. В 1928 году теория и эксперимент были объединены, чтобы показать, что (за исключением, возможно, очень острых излучателей) эта мощность равна V. Недавно было высказано предположение, что теперь следует провести эксперименты CFE, чтобы попытаться найти мощность (κ) V в предэкспоненте следующего эмпирического уравнения CFE:

$i\; =\; CV\; \kappa \; exp\; [-\; B\; /\; V],..........\; (48)\; \{\backslash \; Displaystyle\; я\; =\; \backslash ;\; CV\; ^\; \{\backslash \; kappa\}\; \backslash \; mathrm\; \{exp\}\; [-B\; /\; V],..........\; (48)\}$

где B, C и κ рассматривает как константы.

Из ур. (42) легко показать, что

$-\; d\; l\; n\; i\; /\; d\; (1\; /\; V)\; =\; \kappa \; V\; +\; B,..........\; (49)\; \{\backslash \; Displaystyle\; -\; \backslash \; mathrm\; \{dln\}\; я\; /\; \backslash \; mathrm\; \{d\}\; (1\; /\; V)\; =\; \backslash ;\; \backslash \; kappa\; V\; +\; B,..........\; (49)\}$

В 1920-х годах экспериментальные методы не могли различить результаты κ = 0 (предполагалось Милликеном и Лортисеном) и κ = 2 (прогнозировалось исходным уравнением типа Фаулера-Нордхейма). Однако теперь должна быть возможность проводить достаточно точные измерения dlni / d (1 / V) (при необходимости, используя синхронизирующий усилитель / методы фазочувствительного обнаружения и оборудование с компьютерным управлением), и для получения κ из наклона соответствующего графика данных.

После открытия приближения (30b) теперь очень ясно, что даже для CFE из массивных металлов значение κ = 2 не ожидается. Это можно показать следующим образом. Используя ур. (30c) выше, безразмерный параметр η может быть определен как

$\eta \; =\; b\; \varphi \; 3/2\; /\; F\; \varphi \; =\; (быть\; 3/4\; \pi \; ϵ\; 0)\; \varphi \; -\; 1/2\; \approx \; 9,836239\; (e\; V\; /\; \varphi )\; 1\; /\; 2...........\; (50)\; \{\backslash \; displaystyle\; \backslash \; eta\; =\; b\; \backslash \; phi\; ^\; \{3/2\}\; /\; F\; \_\; \{\backslash \; phi\}\; =\; \backslash ;\; (be\; ^\; \{3\}\; /\; 4\; \backslash \; pi\; \backslash \; epsilon\; \_\; \{0\})\; \{\backslash \; phi\}\; ^\; \{\; -1/2\}\; \backslash \; приблизительно\; 9,836239\; \backslash ;\; \backslash ;\; (\backslash \; mathrm\; \{eV\}\; /\; \backslash \; phi)\; ^\; \{1/2\}...........\; (50)\}$

Для φ = 4,50 эВ этот параметр имеет значение η = 4,64. Поскольку f = F / F φ и v (f) задается уравнением (30b), показатель степени в упрощенном стандартном уравнении типа Фаулера-Нордхейма (30) можно записать в альтернативной форме, а затем расширяется следующим образом:

$exp\; [-\; v\; (f)\; b\; \varphi \; 3/2\; /\; F]\; =\; exp\; [-\; v\; (f)\; \eta \; /\; f]\; \approx \; e\; \eta \; f\; -\; \eta \; /\; 6\; exp\; [-\; \eta \; /\; f]\; =\; e\; \eta \; f\; -\; \eta \; /\; 6\; ехр\; [-\; b\; \varphi \; 3/2\; /\; F]...........\; (51)\; \{\backslash \; Displaystyle\; \backslash \; mathrm\; \{exp\}\; [-v\; (f)\; \backslash ;\; b\; \{\backslash \; phi\}\; ^\; \{3/2\}\; /\; F]\; \backslash ;\; =\; \backslash ;\; \backslash \; mathrm\; \{exp\}\; [-v\; (f)\; \backslash \; ;\; \backslash \; eta\; /\; f]\; \backslash ;\; \backslash \; приблизительно\; \backslash ;\; \{\backslash \; mathrm\; \{e\}\}\; ^\; \{\backslash \; eta\}\; f\; ^\; \{-\; \backslash \; eta\; /\; 6\}\; \backslash \; mathrm\; \{exp\}\; [-\; \backslash \; eta\; /\; f]\; \backslash ;\; =\; \backslash ;\; \{\backslash \; mathrm\; \{e\}\}\; ^\; \{\backslash \; eta\}\; f\; ^\; \{-\; \backslash \; eta\; /\; 6\}\; \backslash \; mathrm\; \{exp\}\; [-b\; \{\backslash \; phi\}\; ^\; \{3/2\}\; /\; F]...........\; (51)\}$

При условии, что коэффициент преобразования β не зависит от напряжения, параметр f имеет альтернативное определение f = V / V φ, где V φ - напряжение, необходимое в конкретной экспериментальной системе для уменьшения высоты барьера Шоттки-Нордхейма с φ до нуля. Таким образом, ясно, что множитель v (f) в показателе экспоненты теоретического уравнения (30) вызывает дополнительную V-зависимость в предэкспоненте эмпирического уравнения. Таким образом (для эффектов, связанных с барьером Шоттки-Нордхейма и для эмиттера с φ = 4,5 эВ) мы получаем прогноз:

$\kappa \; \approx \; 2\; -\; \eta \; /\; 6\; =\; 2\; -\; 0,77\; =\; 1,23...........\; (52)\; \{\backslash \; displaystyle\; \backslash \; kappa\; \backslash \; приблизительно\; 2-\; \backslash \; eta\; /6=2-0.77=1.23...........(52)\}$

Поскольку также может быть зависимость напряжения от других факторов в уравнении типа Фаулера-Нордхейма, в частности, в условной области выбросов A r и в локальной работе выхода, не обязательно ожидать, что κ для CFE из металла локальная работа выхода 4,5 эВ должна иметь значение κ = 1,23, но, конечно, нет никаких оснований ожидать, что она будет иметь исходное значение Фаулера-Нордхейма κ = 2.

Первая экспериментальная проверка этого предложения был проведен Кирком, который использовал несколько более сложную форму анализа данных, чтобы найти значение 1,36 для своего параметра κ. Его параметр κ очень похож, но не совсем такой же, как параметр κ, используемый здесь, но, тем не менее, его результаты, похоже, подтверждают потенциальную полезность этой формы анализа.

Использование эмпирического уравнения CFE (42) и измерение κ могут быть особенно полезны для неметаллов. Строго говоря, уравнения типа Фаулера-Нордхейма применимы только к излучению из зоны проводимости объемных кристаллических твердых тел. Однако эмпирические уравнения вида (42) должны применяться ко всем материалам (хотя, вероятно, для очень острых излучателей может потребоваться модификация). Кажется весьма вероятным, что один из способов, которым уравнения CFE для новых материалов могут отличаться от уравнений типа Фаулера-Нордхейма, заключается в том, что эти уравнения CFE могут иметь различную степень F (или V) в их предэкспонентах. Измерения κ могут дать некоторые экспериментальные свидетельства этого.

Исходное теоретическое уравнение, выведенное Фаулером и Нордхеймом, за последние 80 лет повлияло на способ построения и анализа экспериментальных данных CFE. В очень широко используемом графике Фаулера-Нордхейма, представленном Stern et al. в 1929 году величина ln {i / V} нанесена на график зависимости от 1 / V. Первоначальное мышление заключалось в том, что (как предсказывалось исходным или элементарным уравнением типа Фаулера-Нордхейма) это будет генерировать точную прямую линию наклона S FN. S FN будет связано с параметрами, которые появляются в показателе степени уравнения типа Фаулера-Нордхейма формы i-V следующим образом:

$S\; F\; N\; =\; -\; b\; \varphi \; 3/2\; /\; \beta ...........\; (47)\; \{\backslash \; displaystyle\; S\; \_\; \{\backslash \; mathrm\; \{FN\}\}\; =\; \backslash ;\; -\; b\; \{\backslash \; phi\}\; ^\; \{3/2\}\; /\; \backslash \; beta...........\; (47)\}$

Следовательно, знание φ позволит определить β или наоборот.

[В принципе, в геометриях системы, где присутствует локальная усиливающая поле наноструктура и может быть определен макроскопический коэффициент преобразования β M, знание β затем позволяет значение эмиттера эффективный коэффициент усиления поля γ определяется по формуле γ = β / β M. В обычном случае пленочного эмиттера, созданного на одной пластине двух пластин с разделением пластин W (так что β M = 1 / W), тогда

$\gamma \; =\; \beta \; W...........\; (48)\; \{\backslash \; displaystyle\; \backslash \; gamma\; =\; \backslash ;\; \backslash \; beta\; W...........\; (48)\}$

В настоящее время это одно из наиболее вероятных применений графиков Фаулера-Нордхейма.]

Впоследствии стало ясно, что исходное мышление, приведенное выше, строго верно только для физически нереалистичной ситуации с плоским излучателем и точным треугольным барьером. Для реальных излучателей и реальных барьеров необходимо ввести «поправочный коэффициент наклона» σ FN, что дает пересмотренную формулу

$S\; F\; N\; =\; -\; \sigma \; F\; N\; b\; \varphi \; 3/2\; /\; \beta ...........\; (49)\; \{\backslash \; displaystyle\; S\; \_\; \{\backslash \; mathrm\; \{FN\}\}\; =\; \backslash ;\; -\; \backslash \; sigma\; \_\; \{\backslash \; mathrm\; \{FN\}\}\; b\; \{\backslash \; phi\}\; ^\; \{3/2\}\; /\; \backslash \; beta...........\; (49)\}$

На значение σ FN, в принципе, будет влиять любой параметр в физически полном уравнении типа Фаулера-Нордхейма для i (V), который имеет напряжение зависимость.

В настоящее время единственным параметром, который считается важным, является поправочный коэффициент $\nu \; F\; \{\backslash \; displaystyle\; \backslash \; nu\; \_\; \{\backslash \; mathrm\; \{F\}\}\}$, относящийся к форме барьера., и единственный барьер, для которого существует какая-либо хорошо обоснованная подробная теория, - это барьер Шоттки-Нордхейма. В этом случае σ FN задается математической функцией, называемой s. Эта функция s была впервые правильно представлена ​​в таблице (как функция параметра Нордхейма y) Берджессом, Кремером и Хьюстоном в 1953 году; и современная трактовка, которая дает s как функцию масштабированного барьерного поля f для барьера Шоттки-Нордхейма, приведена в. Однако уже давно было ясно, что для практической работы эмиттера значение s лежит в диапазоне от 0,9 до 1..

На практике из-за дополнительной сложности, связанной с подробным учетом поправочного коэффициента наклона, многие авторы (фактически) помещают σ FN = 1 в уравнение. (49), тем самым создавая систематическую ошибку в их оценочных значениях β и / или γ, обычно составляющую около 5%.

Однако эмпирическое уравнение (42), которое в принципе является более общим, чем уравнения типа Фаулера-Нордхейма, приносит с собой возможные новые способы анализа данных i-V автоэлектронной эмиссии. В общем, можно предположить, что параметр B в эмпирическом уравнении связан с нередуцированной высотой H некоторого характерного барьера, видимого туннелирующими электронами, как

$B\; =\; b\; H\; 3/2\; /\; \beta ...........\; (50)\; \{\backslash \; displaystyle\; B\; =\; \backslash ;\; bH\; ^\; \{3/2\}\; /\; \backslash \; beta...........\; (50)\}$

(В большинстве случаев, но не обязательно во всех, H будет быть равным локальной работе выхода; это, конечно, верно для металлов.) Проблема в том, как определить значение B экспериментально. Есть два очевидных пути. (1) Предположим, что ур. (43) можно использовать для определения достаточно точного экспериментального значения κ по наклону графика формы [–dln {i} / d (1 / V) vs. V]. В этом случае второй график зависимости ln (i) / V от 1 / V должен быть точной прямой линией наклона –B. Этот подход должен быть наиболее точным способом определения B.

(2) В качестве альтернативы, если значение κ точно не известно и не может быть точно измерено, но может быть оценено или угадано, тогда значение для B может быть получен из графика формы [ln {i} vs. 1 / V]. Это форма графика, использованная Милликеном и Лауритсеном в 1928 году. (43) дает

$B\; =\; -\; d\; l\; n\; (i)\; /\; d\; (1\; /\; V)\; -\; \kappa \; (1\; /\; V)...........\; (51)\; \{\backslash \; displaystyle\; B\; =\; \backslash ;\; -\; \backslash \; mathrm\; \{dln\}\; (i)\; /\; \backslash \; mathrm\; \{d\}\; (1\; /\; V)\; -\; \backslash \; kappa\; (1\; /\; V)...........\; (\; 51)\}$

Таким образом, B может быть определено с хорошей степенью приближения путем определения среднего наклона графика Милликена-Лауритсена в некотором диапазоне значений 1 / V и применения коррекции с использованием значения 1 / V в средней точке диапазона и предполагаемое значение κ.

Основные преимущества использования графика Милликена-Лауритсена и этой формы процедуры коррекции, а не графика Фаулера-Нордхейма и коэффициента коррекции наклона, заключаются в следующем. (1) Процедура построения несколько проще. (2) Коррекция включает физический параметр (V), который является измеряемой величиной, а не физический параметр (f), который должен быть вычислен [для того, чтобы затем вычислить значение s (f) или, в более общем плане, σ FN (f)]. (3) И сам параметр κ,и процедура коррекции более прозрачны (и легче понимаются), чем эквиваленты графика Фаулера-Нордхейма. (4) Эта процедура учитывает все физические эффекты, которые влияют на значение κ, тогда как процедура коррекции графика Фаулера-Нордхейма (в том виде, в котором она проводилась в течение последних 50 лет) учитывает только эти эффекты связаны с формой барьера - предполагая, кроме того, что эта форма является формой барьера Шоттки-Нордхейма. (5) Существует более четкое разделение теоретических и технологических проблем: теоретики будут заинтересованы в установлении, какую информацию любые измеренные значения κ предоставляют о теории CFE; но экспериментаторы могут просто использовать измеренные значения κ, чтобы сделать более точные оценки (при необходимости) коэффициентов усиления поля.

Эту процедуру коррекции для графиков Милликена-Лауритсена станет проще применять, когда будет проведено достаточное количество измерений κ были сделаны, и есть лучшее представление о том, каковы на самом деле типичные значения. В настоящее время кажется вероятным, что для большинства материалов κ будет лежать в диапазоне -1 <κ<3.

Разработать приближенную теорию CFE из металлов, указанных выше, сравнительно легко по следующим причинам. (1) Теория свободных электронов Зоммерфельда с ее частными предположениями о распределении внутренних электронных состояний по энергиям в первом приближении адекватно применима ко многим металлам. (2) В большинстве случаев металлы не имеют поверхностных состояний и (во многих случаях) металлические волновые функции не имеют значимых «поверхностных резонансов ». (3) Металлы имеют высокую плотность состояний на уровне Ферми, поэтому заряд, который генерирует / экранирует внешние электрические поля, лежит в основном за пределами верхнего атомного слоя, и никакого значимого «проникновения поля» не происходит.. (4) Металлы обладают высокой электропроводностью : внутри металлических эмиттеров не происходит значительных падений напряжения: это означает, что нет факторов, препятствующих подаче электронов на излучающую поверхность, и что электроны в этой области могут быть как в эффективное локальное термодинамического равновесия и в эффективном термодинамическом равновесии с электронами в опорной конструкции металла, на которых установлен излучатель. (5) Эффекты на атомном уровне не принимаются во внимание.

Развитие «простых» теорий полевой электронной эмиссии и, в частности, разработка уравнений типа Фаулера-Нордхейма, опирается на то, что все пять из перечисленных выше факторов являются правда. Для материалов, отличных от металлов (и для металлических эмиттеров с атомарной остротой), один или несколько из вышеперечисленных факторов будут неверными. Например, кристаллические полупроводники не имеют зонной структуры, подобной свободным электронам, имеют поверхностные состояния, подвержены проникновению поля и искривлению зон, и может демонстрировать как внутренние падения напряжения, так и статистическую развязку распределения электронов в поверхностных состояниях от распределения электронов в поверхностной области объемной зонной структуры (эта развязка известна как «эффект Модиноса»).

На практике теория фактического туннельного процесса Фаулера-Нордхейма во многом одинакова для всех материалов (хотя детали формы барьера могут отличаться, и модифицированная теория должна быть разработана для начальных состояний, которые локализованы, а не подобны бегущей волне ). Однако, несмотря на такие различия, можно ожидать (для ситуаций термодинамического равновесия ), что все уравнения CFE будут иметь показатели, которые в целом ведут себя аналогичным образом. Вот почему применение уравнений типа Фаулера-Нордхейма к материалам, выходящим за рамки приведенных здесь выводов, часто работает. Если интерес представляют только параметры (такие как коэффициент усиления поля), которые относятся к наклону графиков Фаулера-Нордхайма или Милликена-Лауритсена и к показателю уравнения уравнения CFE, теория типа Фаулера-Нордхейма часто дает разумные оценки. Однако получить значимые значения плотности тока обычно или всегда терпят неудачу.

Обратите внимание, что прямая линия на графике Фаулера-Нордхейма или Милликена-Лауритсена не означает, что излучение из соответствующего подчиняется типу Фаулера-Нордхейма: это указывает только на то, что механизм отдельных электронов представляет собой вероятно туннелирование Фаулера-Нордхейма.

Различные материалы радикального распределения энергии внутренних электронных состояний, такие как интегрированные средства распределения тока по внутренним электронным состояниям. В частности, барьерного поля в предэкспоненте может отличаться от мощности исходного значения Фаулера-Нордхейма «2». Исследование эффектов такого рода - активная тема для исследований. Эффекты "резонанса" и "рассеяния " на атомном уровне, если они возникают, также изменят теорию.

Там, где материалы подвержены проникновению силовых лент, необходимо иметь хорошие теории таких эффектов (для каждого отдельного класса материалов), прежде чем можно будет разработать детальные теории CFE. Когда возникают эффекты падения напряжения, теория эмиссионного тока может в большей или меньшей степени стать теорией, которая включает в себя эффекты внутреннего переноса, и может стать очень сложной.

• Автоэмиссионный микроскоп
• Автоэмиссионные зонды
• Матрица полевых эмиттеров
• Автоэмиссионный дисплей
• Эффект Франца – Келдыша

Общая информация

• W. Чжу, изд. (2001). Вакуумная микроэлектроника. Уайли, Нью-Йорк.
• Г.Н. Ферси (2005). Полевая эмиссия в вакуумной микроэлектронике. Kluwer Academic, Нью-Йорк. ISBN 0-306-47450-6.

Проникновение в поле и изгиб полосы (полупроводники)

• Сейватц, Рут; Грин, Мино (1958). «Расчеты космического заряда полупроводников». Журнал прикладной физики. 29 (7): 1034. Bibcode : 1958JAP.... 29.1034S. doi : 10,1063 / 1,1723358.
• А. Многие, Ю. Гольдштейн и Н. Гровер, Поверхности полупроводников (Северная Голландия, Амстердам, 1965).
• W. Менш, Полупроводниковые поверхности и интерфейсы (Springer, Берлин, 1995).
• Пэн, Джи; Ли, Чжибин; Он, Чуньшань; Чен, Гуйхуа; Ван, Вэйлян; Дэн, Шаочжи; Сюй, Ниншэн; Чжэн, Сяо; Чен, Гуаньхуа; Edgcombe, Крис Дж.; Форбс, Ричард Г. (2008). «Роль вершинных диполей и проникновения поля в физике заряженных, излучающих поле, однослойных углеродных нанотрубок». Журнал прикладной физики. Издательство AIP. 104 (1): 014310. arXiv : cond-mat / 0612600. doi : 10.1063 / 1.2946449. ISSN 0021-8979.

Полевой вакуум пространственный заряд

• Barbour, J.P.; Dolan, W. W.; Trolan, J. K.; Martin, E. E.; Дайк, У. П. (1953). «Эффекты пространственного заряда в полевой эмиссии». Физический обзор. 92 (1): 45–51. Полномочный код : 1953PhRv... 92... 45B. doi : 10.1103 / PhysRev.92.45.

Автоэлектронная эмиссия при высоких температурах и фото-полевая эмиссия

• Дженсен, Кевин (2007). Физика электронной эмиссии. Достижения в области визуализации и электронной физики. 149 . Сан-Диего: Academic Press. ISBN 978-0-12-374207-0. OCLC 647688316.

индуцированная полем взрывная электронная эмиссия

• G.A. Месяц, Взрывная электронная эмиссия (УРО Пресс, Екатеринбург, 1998),