(Математическое) разложение в произведение
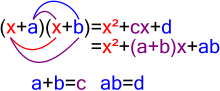
Многочлен x + cx + d, где a + b = c и ab = d, может быть разложено на (x + a) (x + b).
В математике, факторизация (или факторизация, см. английский орфографические различия ) или факторинг состоит из записи числа или другого математического объекта как произведения нескольких факторов, обычно меньших или более простых же объектов типа. Например, 3 × 5 - это факторизация целого числа 15, а (x - 2) (x + 2) - факторизация полинома x - 4.
Факторизация обычно не считается значимым в системе счисления, имеющим деление, как большие или комплексные числа, поскольку  можно тривиально записать как
можно тривиально записать как  всякий раз, когда
всякий раз, когда  не равно нулю. Значимая факторизация для рационального числа или рациональной функции может быть получена путем выполнения его младших членов и раздельной факторизации числителя и знаменателя.
не равно нулю. Значимая факторизация для рационального числа или рациональной функции может быть получена путем выполнения его младших членов и раздельной факторизации числителя и знаменателя.
Факторизация была впервые рассмотрена древнегреческими математиками в случае целых чисел. Они доказали фундаментальные теорему арифметики, которая утверждает, что каждое положительное число может быть разложено на произведение простые числа, которые не могут быть дополнительно разложены на целые числа больше 1. Более того, это факторизация уникальна от до порядка факторов. Хотя целочисленная факторизация является своим обратным умножением, это намного сложнее алгоритмически, который используется в криптосистеме RSA для реализации криптография с открытым ключом.
Полиномиальная факторизация также изучалась веками. В элементарной алгебре разложение многочлена на множители сводит проблему поиска его корней к поиску корней множителей. Полиномы с коэффициентами в целых числах или в поле обладают своей уникальной факторизации, версией теоремы основнойоремы арифметики с заменой простых чисел на неприводимые многочлены. В частности, одномерный многочлен с комплексными допускаются уникальное (с помощью до порядка) факторизация в линейные многочлены : это версия фундаментального Теорема алгебры. В этом случае факторизация может быть выполнена с помощью алгоритмов поиска корня. Случай полиномов с целыми коэффициентами является фундаментальным для компьютерной алгебры. Существуют эффективные компьютерные алгоритмы для вычислений (полных) факторизаций внутри кольца многочленов с рациональными числовыми коэффициентами (см. факторизация многочленов ).
A коммутативное кольцо, обладающее своим уникальной факторизации, называется областью уникальной факторизации. Существуют системы счисления, такие как электрические кольца алгебраических целых чисел, которые не являются уникальными областями факторизации. Однако кольца алгебраических целых удовлетворяют более слабому свойству дедекиндовских областей : идеалы однозначно множатся в простые идеалы.
Факторизация может также относиться к более общим разложениям математического объекта. в продукт меньших или более простых объектов. Например, каждая функция может быть включена в состав сюръективной функции с инъективной функцией . Матрицы обладают множеством видов матричных факторизаций. Например, каждая матрица имеет уникальную факторизацию LUP как произведение матрицы нижнего треугольника L со всеми диагональными элементами, равными едиными, верхней треугольной матрицы U и матрицу перестановок P; это матричная формулировка исключения Гаусса.
Содержание
- 1 Целые числа
- 2 Выражения
- 2.1 История факторизации выражений
- 2.2 Общие методы
- 2.2. 1 Общий множитель
- 2.2.2 Группировка
- 2.2.3 Сложение и вычитание членов
- 2.3 Узнаваемые шаблоны
- 3 Полиномы
- 3.1 Факторизация примитивной части и содержимого
- 3.2 Использование теоремы о множителях
- 3.3 Рациональные корни
- 3.4 Использование формул для полиномиальных корней
- 3.5 Использование отношений между корнями
- 4 Уникальные области факторизации
- 5 Идеалы
- 6 Матрицы
- 7 См. Также
- 8 Примечания
- 9 Ссылки
- 10 Внешние ссылки
Целые числа
По основной теореме арифметики, каждое целое число больше 1 имеет уникальную (до порядка множителей) факторизацию на простые числа, которые предоставляют собой те целые числа, которые не могут быть разложены на целых чисел больше один.
Для вычислений факторизации целого числа n необходим алгоритм для нахождения делителя q числа n или того, что n является основным. Когда такой делитель найден, повторное применение этого алгоритма к факторам q и n / q дает в итоге полную факторизацию n.
Для нахождения делителя q числа n, если таковой имеется, достаточно проверить все значения q такие, что 1 < q and q ≤ n. In fact, if r is a divisor of n such that r>n, тогда q = n / r является делителем n, таким что q ≤ n.
Если проверять значения q в возрастании, первый найденный делитель обязательно является основным числом, а кофактор r = n / q не может иметь делителя меньше q. Чтобы получить полную факторизацию, алгоритм, ищу делитель r, который не меньше q и не больше √r.
Нет необходимости проверить все значения q для применения метода. В принципе, достаточно проверить только простые делители. Здесь должна быть таблица простых чисел, которую можно сгенерировать, например, с помощью сита Эратосфена. Мы не можем сразу увидеть, как они просты или нет. Обычно можно приступить к проверке 2, 3, 5 и чисел>5, последняя цифра которых равна 1, 3, 7, 9, сумма цифр не кратна 3.
Этот метод хорошо работает для факторизации малых целых чисел, но неэффективен для больших целых чисел. Например, Пьер де Ферма не смог, что 6-е число Ферма

не является основным числом. Фактически, применение метода потребовало бы более 10000 делений для числа, содержащего 10 десятичных цифр..
Существуют более эффективные алгоритмы факторизации. Однако они являются неэффективными, поскольку на современном уровне техники невозможно факторизовать, даже с более мощными компьютерами, число из 500 десятичных цифр производится двумя случайно выбранными простыми числами. Это обеспечивает безопасность криптосистемы RSA, которая широко используется для безопасной связи в Интернете.
Пример
Для разложения n = 1386 на простые числа:
- Начните с деления на 2: число четное, и n = 2 · 693. Продолжайте с 693 и 2 как первый кандидат в делитель.
- 693 нечетно (2 не является делителем), но делится на 3: у одного 693 = 3 · 231 и n = 2 · 3 · 231. Продолжайте в качестве с 231 и 3 в качестве первого кандидата в делитель.
- 231 также делится на 3: у одного 231 = 3 · 77, и, таким образом, n = 2 · 3 · 77. Продолжайте с 77 и 3 в качестве первого кандидата в делители.
- 77 не делится на 3, так как сумма его цифр равна 14, а не кратно 3. Оно также не кратно 5, потому что его последняя цифра равна 7. Следующий нечетный делитель проверено 7. У одного 77 = 7 · 11, и, таким образом, n = 2 · 3 · 7 · 11. Это показывает, что 7 простое число (легко проверить напрямую). Продолжите с 11 и 7. в качестве первого кандидата на делитель.
- Как 7>11, один закончен. Таким образом, 11 является основным числом, а факторизация на простых множителях равна
- 1386 = 2 · 3 · 7 · 11.
Выражения
Манипулирование выражениями является поставщиком алгебры. Факторизация - один из наиболее важных методов манипулирования выражениями по нескольким причинам. Если можно уравнение в факторизованной форме E⋅F = 0, тогда задача решения разбивается на две (и, как правило, более простые) задачи E = 0 и F = 0. Когда выражение может быть факторизовано, факторы часто намного проще. Например,

, имеющий 16 умножений, 4 вычитания и 3 сложения, можно разложить на более простое выражение

только с двумя умножениями и тремя вычитаниями. Более того, факторизованная форма сразу дает корни x = a, b, c многочлена от x, представленного этими выражениями.
С другой стороны, факторизация не всегда возможна, и когда это возможно, факторы не всегда проще. Например,  можно разложить на два несократимых множителя
можно разложить на два несократимых множителя  и
и  .
.
Были разработаны различные методы нахождения факторизаций; Некоторые предложения ниже.
Решение алгебраических уравнений может рассматриваться как проблема факторизации. Фактически, основную теорему алгебры можно сформулировать следующим образом. Каждый многочлен от x степени n с комплексными коэффициентами может быть разложен на n линейных множителей  для i = 1,..., n, где a i s - корни многочлена. Несмотря на то, что структура факторизации в этих случаях известна, и обычно не могут быть вычислены в терминах радикалов (n корней) по теореме Абеля - Руффини. В большинстве случаев лучшее, что можно сделать, - это вычислить приблизительные значения корней с помощью алгоритма поиска корней.
для i = 1,..., n, где a i s - корни многочлена. Несмотря на то, что структура факторизации в этих случаях известна, и обычно не могут быть вычислены в терминах радикалов (n корней) по теореме Абеля - Руффини. В большинстве случаев лучшее, что можно сделать, - это вычислить приблизительные значения корней с помощью алгоритма поиска корней.
История факторизации выражений
Систематическое использование алгебраических манипуляций для упрощения выражений (точнее, уравнения )) могут быть датированы 9 веком, с помощью книги аль-Хорезми Сборник вычислений по завершению и уравновешиванию, который озаглавлен двумя видами манипуляции. Однако даже для решения квадратный метод факторизации не использовался до работы Харриота, опубликованной в 1631 году, через десять лет после его смерти.
В его книге Artis В первом разделе Analyticae Praxis и Aequationes Algebraicas Resolvendas Харриот нарисовал таблицы для сложения, вычитания, умножения и деления одночленов, биномов и трехчленов. Затем во втором разделе, он составил уравнение aa - ba + ca = + bc и показано, что оно соответствует форме умножения, которую он ранее предоставил, давая факторизацию (a - b) (a + c).
Общие методы
Следующие методы ниже применяются к любому выражению, которое является суммой или может быть преобразовано в сумме. Таким образом, они чаще всего применяются к полиномам, хотя они также могут быть выполнены, как составные части составляют одночленами, то есть составные части произведены переменными и константами.
Общий множитель
Может случиться так, что некоторые множители являются общими для всех членов. В этом случае закон распределения позволяет вычленить этот общий множитель. Если таких факторов несколько, стоит самый большой из общих факторов. Кроме того, если есть целочисленные коэффициенты, можно вычесть самый большой общий делитель этих коэффициентов.
Например,

поскольку 2 является наибольшим общим делителем 6, 8 и 10, и  разделяет все термины.
разделяет все термины.
Группировка
Условия группировки использовать другие методы получения факторизации.
Например, чтобы разложить на множители

можно заметить, что первые два члена имеют общий множитель x, а последние два члена имеют общий множитель y. Таким образом,

Тогда простой осмотр показывает общий множитель x + 5, что приводит к факторизации

В общем, это работает для сумм из 4 членов, которые были получены как произведение двух биномы. Хотя не часто, это может работать и для более сложных примеров.
Сложение и вычитание терминов
Иногда при некоторой группировке терминов появляется часть распознаваемого шаблона. Добавочные шаблоны для завершения шаблона и вычитать их, чтобы не улучшить значения выражения.
Типичное использование этого метода - завершение метода квадрата для получения квадратной формулы.
Другой пример - факторизация  Если не действительный квадратный корень из –1, обычно обозначаемый i, то получится разность квадратов
Если не действительный квадратный корень из –1, обычно обозначаемый i, то получится разность квадратов

может потребоваться факторизация с вещественным числом коэффициенты. Складывая и вычитая  и группируя три члена вместе, можно распознать квадрат бинома :
и группируя три члена вместе, можно распознать квадрат бинома :

Вычитание и сложение  также дает факторизацию:
также дает факторизацию:

Эти факторизации работают не только с комплексными числами, но и с любым полем, где –1, 2 или –2 - это площадь. В конечное поле произведение неквадратов является квадратом; это означает, что полином  который неприводим по целым числам сводится по модулю для каждого простого числа. Например,
который неприводим по целым числам сводится по модулю для каждого простого числа. Например,

 с
с 
 с
с 
 начиная с
начиная с 
Узнаваемые шаблоны
Многие чисаторы обеспечение равенства между суммой и произведением. Вышеупомянутые методы 1 «Я» для того, чтобы найти суммеой идентичности, появиться в выражении, следовательно, может быть заменено произведением.
Приведенные ниже используются в качестве обозначения, которое обычно используется в обозначении. между двумя квадратами и двумя кубиками

- Например,

- Сумма / разность двух кубов


- Разница между четырьмя й степени

- Сумма / разность двух n-х степеней
- В следующих тождествах множители могут быть также часто разложены на множители:

- Разница, четная или нечетная экспонента

- Это представляет собой пример показывающий, что коэффициенты могут быть намного больше, ч сумма, которая разложена на множители.
- Сумма, нечетный показатель

- (получено чанги ng F на –F в предыдущей формуле)
- Если показатель степень является степенью двойки, это выражение, как правило, не может быть разложено на множители без введения комплексных чисел (если E и F содержат комплексные числа, это может быть не так). Если n имеет нечетный делитель, то есть если n = pq с нечетным p, можно использовать предыдущую формулу (в «Сумма, нечетный показатель»), примененную к

- Трехчлены и кубические формулы


Визуализация биномиального разложения до 4-й степени
- биномиальная теорема используются шаблоны, которые можно легко распознать по целым числам, которые в них
- В низкой степени:




- В общем, коэффициенты развернутых форм
 и
и  - биномиальные коэффициенты, которые появляются в n-й строке треугольника Паскаля.
- биномиальные коэффициенты, которые появляются в n-й строке треугольника Паскаля.
Корни из единицы
н-ые корни из единицы - это комплексные числа, каждое из которых является корнем полинома  Таким образом, это число
Таким образом, это число

для 
Отсюда следует, что для любых двух выражений E и F одно имеет:



Если E и F - реальные выражения, и кто-то хочет действительные факторы, необходимо заменить каждую пару комплексно сопряженных факторов на ее произведение. Комплексное сопряжение  равно
равно  и
и

одна имеет следующие действительные факторизации (одна переходит от одной к другой, заменяя k на n - k или n + 1 - k, и применяется обычные тригонометрические формулы :


косинусы, которые появляются в этих факторизации, являются алгебраическими числами и могут быть выражены в терминах радикалов (это возможно, потому что их группа Галуа циклический); однако эти радикальные выражения слишком сложны, чтобы их можно было использовать за низкие значения n. Например,



Часто требуется факторизация с рациональными коэффициентами. Такая факторизация включает циклотомических многочленов. Чтобы выразить рациональные факторизации сумм и разностей или степеней, нам потребуется обозначение для усреднения полинома : если  его гомогенизация - двумерный многочлен
его гомогенизация - двумерный многочлен  Тогда имеем
Тогда имеем


где произведения берутся по всем делителям n или всем делителям 2n, которые не делят n, и  - n- й круговой многочлен.
- n- й круговой многочлен.
Например,


так как делители 6 равны 1, 2, 3, 6, а делители 12, которые не делят 6, равны 4 и 12.
Многочлены
Для многочленов факторизация сильно связана с решением проблемы алгебраических уравнений. Алгебраическое уравнение имеет вид

где

где P (x) многочлен от x, такой, что  Решение этого уравнения (также называемое корнем из многочлен) представляет собой такое значение r из x, что
Решение этого уравнения (также называемое корнем из многочлен) представляет собой такое значение r из x, что

Если

- факторизация P как произведение двух многочленов, тогда корни P являются объединением корни Q и корни R. Таким образом, решение P сводится к более основные задачи решения Q и R.
И наоборот, теорема о множителях утверждает, что если r является корнем из P, тогда P можно разложить на множители как

где Q (x) является частным от евклидова делен ия числа P на x - r.
Если коэффициенты P являются действительными или комплексными числами, фундаментальная теорема алгебры утверждает, что P имеет действительный или комплексный корень. Используя рекурсивную теорему о факторах, получаем, что

где  являются действительные или комплексные корни P, причем некоторые из них, возможно, повторяются. Эта полная факторизация является уникальной от до порядка факторов.
являются действительные или комплексные корни P, причем некоторые из них, возможно, повторяются. Эта полная факторизация является уникальной от до порядка факторов.
Если коэффициенты P имеют действительные, обычно требуется факторизация, при которых коэффициенты действующие коэффициенты. В этом случае в полной факторизации могут быть факторы, имеющие степень два. Эта факторизация может быть легко выведена из приведенной выше полной факторизации. Фактически, если r = a + ib не является действительным корнем P, то его комплексное сопряжение s = a - ib также является корнем P. Итак, произведение

- множитель P, имеющий действительные коэффициенты. Эта группировка нереальных факторов может продолжаться до тех пор, пока не будет получена факторизация с действующими множителями, которые являются полиномами первой или второй степени.
Для выполнения этих физических или комплексных факторизаций необходимо знать корни полинома. Как правило, их нельзя вычислить точно, и можно получить только приблизительные значения корней. См. Алгоритм поиска корня для ознакомления с многочисленными эффективными алгоритмами , которые были разработаны для этой цели.
Основные алгебраические уравнения, которые практикуются, имеют целочисленные или рациональные коэффициенты, и может потребоваться факторизация с факторами того же типа. Основная теорема арифметики может быть обобщена на этот случай. То есть многочлены с целыми или рациональными элементами, имеющими свойство уникальной факторизации . Точнее, каждый полином с рациональными коэффициентами может быть разложен на множители в произведении

где q - рациональное число и  - непостоянные многочлены с целыми коэффициентами, которые являются неприводимым и примитивным ; это означает, что ни один из
- непостоянные многочлены с целыми коэффициентами, которые являются неприводимым и примитивным ; это означает, что ни один из  не может быть записан как произведение двух многочленов (с целыми коэффициентами), которые не равны ни 1, ни –1 ( целые числа как полиномы нулевой степени). Более того, эта факторизация уникальна до порядка факторов и умножения на -1 четного числа факторов.
не может быть записан как произведение двух многочленов (с целыми коэффициентами), которые не равны ни 1, ни –1 ( целые числа как полиномы нулевой степени). Более того, эта факторизация уникальна до порядка факторов и умножения на -1 четного числа факторов.
Существуют эффективные алгоритмы для вычислений этой факторизации, реализованы в большинстве систем компьютерной алгебры. См. Факторизация многочленов. К сожалению, для вычислений на бумаге и карандаше эти алгоритмы слишком сложны, чтобы их можно было использовать. Помимо общих эвристик, в этом случае доступно лишь несколько методов, которые обычно работают только для многочленов низкой степени с небольшим количеством ненулевых коэффициентов. Основные такие методы использования в следующих подразделах.
Факторизация примитивной части и содержания
Каждый многочлен с рациональными коэффициентами может быть разложен на множители уникальным способом как рационального числа и многочлена с целым числом. коэффициентов, который является примитивом (то есть наибольший общий делитель коэффициентов равенства 1) и имеет положительный ведущий коэффициент (коэффициент члена наивысшей степени). Например:


В этой факторизации рациональное число называется содержимым, а примитивный многочлен - примитивной частью. Вычисление этой факторизации может быть выполнено следующим образом: во-первых, приведите все коэффициенты к общему знаменателю, чтобы получить частное на целое число q многочлена с целыми коэффициентами. Затем делят больший общий делитель p коэффициентов этого многочлена для получения примитивной части, содержание которой составляет  Наконец, если необходимо, меняют знаки p и всех коэффициентов примитивной части.
Наконец, если необходимо, меняют знаки p и всех коэффициентов примитивной части.
Эта факторизация может привести к результату, большему, чем исходный многочлен (обычно, когда имеется много взаимно простых знаменателей), но даже в этом случае примитивная часть обычно проще манипулировать для дальнейшей факторизации.
Использование теоремы о факторах
Теорема о факторах утверждает, что если r является корнем многочлена

(то есть P (r) = 0), тогда существует факторизация

где

с  и
и

для i = 1,..., n - 1.
Это может быть полезно, когда либо путем проверки, или, используя некоторую внешнюю информацию, можно узнать корень многочлена. Для вычисления Q (x) вместо использования приведенной выше формулы можно также использовать полиномиальное деление в столбик или синтетическое деление.
. Например, для полинома  легко увидеть, что сумма его коэффициентов равна 0. Таким образом, r = 1 является корнем. Поскольку r + 0 = 1 и
легко увидеть, что сумма его коэффициентов равна 0. Таким образом, r = 1 является корнем. Поскольку r + 0 = 1 и  один имеет
один имеет

Рациональные корни
Поиск рациональных корни многочлена имеет смысл только для многочленов с рациональными коэффициентами. Примитивная факторизация частичного содержания (см. выше) сводит проблему поиска рациональных корней к случаю многочленов с целочисленными коэффициентами, такими, что наибольший общий делитель коэффициентов единице.
Если  является рациональным корнем много такойчлена
является рациональным корнем много такойчлена

теорема о факторах показывает, что имеется факторизация

где оба фактора имеют целочисленные коэффициенты (тот, что Q имеет целочисленные коэффициенты, следует из приведенной выше формулы P (x) к  ).
).
Сравнение коэффициентов степени n и постоянных коэффициентов в приведенном выше равенстве показывает, что если  является рациональный корень в сокращенной форме, тогда q является делителем
является рациональный корень в сокращенной форме, тогда q является делителем  и p является делителем
и p является делителем  Следовательно, существует конечное число возможностей для p и q, которые можно систематически исследовать.
Следовательно, существует конечное число возможностей для p и q, которые можно систематически исследовать.
Например, если многочлен

имеет рациональный корень  с q>0, тогда p должно делить 6; то есть
с q>0, тогда p должно делить 6; то есть  и q должны делить 2, то есть
и q должны делить 2, то есть  Более того, если x < 0, all terms of the polynomial are negative, and, therefore, a root cannot be negative. That is, one must have
Более того, если x < 0, all terms of the polynomial are negative, and, therefore, a root cannot be negative. That is, one must have

Прямое вычисление показывает, что  является корнем, и что другого рационального корня не существует. Применение теоремы о факторах приводит, наконец, к факторизации
является корнем, и что другого рационального корня не существует. Применение теоремы о факторах приводит, наконец, к факторизации 
AC-метод
Для квадратичных многочленов вышеуказанный метод может быть адаптирован, что приведет к так называемому ac-методу факторизации.
Рассмотрим квадратный многочлен

с целыми коэффициентами. Если он имеет рациональный корень, его знаменатель должен делиться равномерно. Таким образом, это может быть записано как возможно приводимая дробь  Согласно формулам Виета другой корень равенство
Согласно формулам Виета другой корень равенство

с  Таким образом, второй корень также является рациональным, а вторая формула Виета дает
Таким образом, второй корень также является рациональным, а вторая формула Виета дает

то есть

Проверка всех пар целых чисел, произведение равно ac, дает рациональные корни, если таковые имеются.
Например, рассмотрим квадратичный многочлен

Проверка множителей ac = 36 приводит к 4 + 9 = 13 = b, что дает два корня

и факторизация

Использование формул для корней многочлена
Любой одномерный квадратичный многочлен  можно разложить на множители, используя квадратную формулу :
можно разложить на множители, используя квадратную формулу :

где  и
и  - два корня многочлена.
- два корня многочлена.
Если a, b, c все действительны, факторы действительны тогда и только тогда, когда различающий  неотрицательно. В противном случае квадратичный многочлен не может быть разложен на непостоянные действительные множители.
неотрицательно. В противном случае квадратичный многочлен не может быть разложен на непостоянные действительные множители.
Квадратичная формула действительна, когда коэффициенты принадлежат любому полю характеристики , отличному от двух, и, в частности, для коэффициентов в конечном поле с нечетным числом элементов.
Существуют также формулы для корней полиномов кубической и , которые, в общем, слишком сложны для практического использования. использовать. Теорема Абеля - Руффини показывает, что не существует общих формул корней в терминах радикалов для многочленов пятой степени и выше.
Использование отношений между корнями
Может случиться так, что кто-то знает некоторую взаимосвязь между корнями многочлена и его коэффициентами. Использование этих знаний может помочь факторизовать многочлен и найти его корни. Теория Галуа основана на систематическом исследовании отношений между корнями и коэффициентами, включая формулы Виета.
. Здесь мы рассматриваем более простой случай, когда два корня  и
и  полинома
полинома  удовлетворяют осознанию
удовлетворяют осознанию

, где Q - многочлен.
Это означает, что  является общим корнем от
является общим корнем от  и
и  Следовательно, это корень наибольшего общего делителя этих двух многочленов. Отсюда следует, что этот самый большой общий делитель является непостоянным множителем
Следовательно, это корень наибольшего общего делителя этих двух многочленов. Отсюда следует, что этот самый большой общий делитель является непостоянным множителем  алгоритм Евклида для многочленов позволяет вычислить этот наибольший общий множитель.
алгоритм Евклида для многочленов позволяет вычислить этот наибольший общий множитель.
Например, если кто-то знает или догадывается, что:  имеет два корня, сумма которых равна нулю, можно применить алгоритм Евклида к
имеет два корня, сумма которых равна нулю, можно применить алгоритм Евклида к  и
и  Первый шаг деления состоит в добав
Первый шаг деления состоит в добав  к
к  , что дает остаток от
, что дает остаток от

Затем, разделив  на
на  дает ноль в качестве нового остатка и x - 5 в частном, что приводит к полной факторизации
дает ноль в качестве нового остатка и x - 5 в частном, что приводит к полной факторизации

Уникальные домены факторизации
Целые числа и многочлены над полем разделяют свойство уникальной факторизации, то есть каждый ненулевой элемент может быть разложен на произведение обратимого элемента (unit, ± 1 в случае целых чисел) и произведения неприводимых элементов (простых чисел в случае целых чисел), и эта факторизация уникальна до перестановки множителей и сдвига единиц среди множителей. Целые домены, которые разделяют это свойство, называются уникальными доменами факторизации (UFD).
Наибольшие общие делители существуют в UFD, и наоборот, каждая область целостности, в которой существуют самые большие общие делители, является UFD. Каждая область главного идеала является UFD.
A Евклидова область - это целостная область, которая определена евклидово деление, подобное делению целых чисел. Каждая евклидова область является областью главных идеалов и, следовательно, UFD.
В евклидовой области евклидово деление позволяет определить алгоритм Евклида для вычислений наибольших общих делителей. Однако это не подразумевает существования алгоритма факторизации. Существует явный пример поля F, такого что не может существовать какой-либо алгоритм факторизации в евклидовой области F [x] одномерных многочленов над F.
Идеалы
В теории алгебраических чисел изучение диофантовых уравнений математиков в 19 веке к введению обобщения целых чисел, называемых целыми алгебраическими числами. Первым кольцом алгебраических целых чисел, которые были рассмотрены, были целые числа Гаусса и целые числа Эйзенштейна, которые разделяют с обычными целыми числами свойство быть областями главных идеалов. и таким образом обладают своим уникальной факторизации ..
К сожалению, быстро электрически появились, что большинство колец алгебраических целых чисел не являются главными и не имеют уникальной факторизации. Самый простой пример: ![\ mathbb { Z} [{\ sqrt {-5}}],](https://wikimedia.org/api/rest_v1/media/math/render/svg/643ef2c1e3b8b8e684a0ddf73d649cb0202cc0c1) , в котором
, в котором

, и все эти факторы несводимы.
Отсутствие уникальной факторизации - главная трудность при решении диофантовых уравнений. Например, многие неверные доказательства Великой теоремы Ферма (вероятно, включая «поистине чудесное доказательство этого слишком узко, чтобы вместить») были основаны на неявном предположении уникальной факторизации.
Эту трудность разрешил Дедекинд, который доказал, что кольца алгебраических целых чисел имеют уникальную факторизацию идеалов : в этих кольцах каждый идеал является произведением простые идеалы, и эта факторизация уникальна по порядку множителей. интегральные домены, обладающие этим уникальным своим факторизации, теперь называются дедекиндовыми доменами. У них есть много хороших свойств, которые делают их фундаментальными в алгебраической теории чисел.
Матрицы
Кольца матриц некоммутативны и не имеют уникальной факторизации: как правило, много способов записать матрицу как произведение матриц. Таким образом, проблема факторизации состоит в рассмотрении факторов заданных типов. Например, разложение LU дает матрицу как произведение нижней треугольной матрицы на верхней треугольной матрицы. Обычно рассматривают «разложение LUP», имеющее матрицу перестановок в качестве фактора третьего.
См. Разложение матрицы для получения информации о наиболее распространенных типах факторизации матриц.
A логическая матрица представляет собой двоичное отношение, а матричное умножение соответствует композиции отношений. Декомпозиция отношений посредством факторизации для профилирования природы отношения, например, дифункционального отношения.
См. Также
Примечания
Ссылки
- Бернсайд, Уильям Сноу ; Пантон, Артур Уильям (1960) [1912], Теория правил с введением в теорию бинарных алгебраических форм (первый), Дувр
- Диксон, Леонард Юджин (1922), Первый курс теории уравнений, Нью-Йорк: Джон Wiley Sons
- Файт, Уильям Бенджамин (1921), College Algebra (Revised), Бостон: DC Heath Co.
- Klein, Felix (1925), Элементарная математика от Продвинутая точка зрения; Арифметика, алгебра, анализ, Довер
- Селби, Сэмюэл М., Стандартные математические таблицы CRC (18-е изд.), The Chemical Rubber Co.
Внешние ссылки
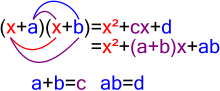 Многочлен x + cx + d, где a + b = c и ab = d, может быть разложено на (x + a) (x + b).
Многочлен x + cx + d, где a + b = c и ab = d, может быть разложено на (x + a) (x + b). 






















 с
с 
 с
с 
 начиная с
начиная с 










 Визуализация биномиального разложения до 4-й степени
Визуализация биномиального разложения до 4-й степени 



 и
и  - биномиальные коэффициенты, которые появляются в n-й строке треугольника Паскаля.
- биномиальные коэффициенты, которые появляются в n-й строке треугольника Паскаля.






















































































![\ mathbb { Z} [{\ sqrt {-5}}],](https://wikimedia.org/api/rest_v1/media/math/render/svg/643ef2c1e3b8b8e684a0ddf73d649cb0202cc0c1)
