Факторный анализ

Факторный анализ - это статистический метод, используемый для описания изменчивости наблюдаемых, коррелировали переменные с точки зрения меньшего количества ненаблюдаемых чисел, называемые факторами . Например, возможно, что вариации многомерных чисел в основном отражают вариации двух ненаблюдаемых (лежащих в основе) переменных. Факторный анализ ищет такие совместные вариации в ответ на ненаблюдаемые скрытые переменные. Наблюдаемые переменные модели изменяются как линейные комбинации дополнительных факторов плюс термины «ошибка ». Факторный анализ направлен на поиск независимых скрытых чисел.

Теория, лежащая в основе методов факторного анализа, заключается в том, что информацию, полученную о взаимозависимости между наблюдаемыми переменными, можно использовать позже, чтобы сократить набор в наборе данных. Факторный анализ обычно используется в биологии, психометрии, личностных теориях, маркетинге, продуктом, опыте операций и финансы. Это может помочь дело с набором данных, в которых имеется большое количество чисел, которые, как считается, отражают меньшее количество основных / скрытых чисел. Используется один из наиболее используемых методов взаимозависимости, когда используется набор систематических методов взаимозависимости, который используется в том, чтобы выявить скрытые факторы взаимозависимости.

Факторный анализ связан с анализом главных компонентов (PCA), но они не идентичны. В этой области существуют большие разногласия по различию между двумя методами (см. Раздел разведочный факторный анализ по с анализом компонентов ниже). PCA можно рассматривать как более базовую версию исследовательского факторного анализа (EFA), который был разработан в первые дни до появления высокоскоростных компьютеров. И PCA, и факторный анализ использования уменьшения размера набора данных, но подходы, используемые для этого, различны для этих двух методов. Факторный анализ разработан с помощью методов некоторых ненаблюдаемых факторов, тогда PCA напрямую не решает эту задачу; в лучшем случае PCA дает приближение к желаемым факторам. С точки зрения исследовательского анализа, собственные значения PCA - это завышенные нагрузки компонентов, т. Е. Загрязненные дисперсией ошибок.

• 1 Статистическая модель
  • 1.1 Определение
  • 1.2 Пример
  • 1.3 Математическая модель того же примера
  • 1.4 Геометрическая интерпретация
• 2 Практическая реализация
  • 2.1 Типы факторного анализа
    • 2.1.1 Исследовательский факторный анализ
    • 2.1.2 Подтверждающий факторный анализ
  • 2.2 Типы выделения факторов
  • 2.3 Терминология
  • 2.4 Критерии определения факторов
    • 2.4.1 Современный уровень
    • 2.4.2 Старые методы
    • 2.4.3 Байесовский метод
  • 2.5 Методы ротации
  • 2.6 Факторный анализ высшего порядка
• 3 В психометрии
  • 3.1 История
  • 3.2 Приложения в психологии
  • 3.3 Преимущества
  • 3.4 Недостатки
• 4 Исследовательский факторный анализ (EFA) по анализам основных компонентов (PCA)
  • 4.1 Параметры, противопоставляющие PCA и EFA
  • 4.2 Дисперсия против ковариации
  • 4.3 Различия в процедурах и результатах
• 5 В маркетинге
  • 5.1 Сбор информации
  • 5.2 Анализ
  • 5.3 Хорошущест ва
  • 5.4 Недостатк и
• 6 В физических и биологических науках
• 7 В анализроматриц
• 8 Реализация
• 9 См. Также
• 10 Ссылки
• 11 Дополнительная литература
• 12 Внешние ссылки

Определение

Предположим, у нас есть набор $p\; \{\backslash \; displaystyle\; p\; \}$наблюдаемые случайные величины, $x\; 1,\dots ,\; xp\; \{\backslash \; displaystyle\; x\_\; \{1\},\; \backslash \; dots,\; x\_\; \{p\}\}$со средними значениями $\mu \; 1,\dots ,\; {\rm M}\; p\; \{\backslash \; displaystyle\; \backslash \; mu\; \_\; \{1\},\; \backslash \; dots,\; \backslash \; mu\; \_\; \{p\}\}$.

Предположим, что для некоторых неизвестных констант $lij\; \{\backslash \; displaystyle\; l\_\; \{ij\}\}$и $k\; \{\backslash \; displaystyle\; k\}$ненаблюдаемые случайные величины $F\; j\; \{\backslash \; displaystyle\; F\_\; \{j\}\}$(называются «общие факторы, "потому что они на всех наблюдаемых случайных величин), где $i\; \in \; 1,\dots ,\; p\; \{\backslash \; displaystyle\; i\; \backslash \; in\; \{1,\; \backslash \; dots,\; p\}\}$и $j\; \in \; 1,\dots ,\; k,\; \{\backslash \; displaystyle\; j\; \backslash \; in\; \{1,\; \backslash \; dots,\; k\},\}$где , у нас есть, что у каждого члена случайной величины (в отличие от среднего значения этой переменной) должны быть записаны как линейная комбинац и я из общих множителей :

$xi\; -\; \mu \; i\; =\; li\; 1\; F\; 1\; +\; \cdots \; +\; lik\; F\; k\; +\; \epsilon \; i.\; \{\backslash \; displaystyle\; x\_\; \{i\}\; -\; \backslash \; mu\; \_\; \{i\}\; =\; l\_\; \{i1\}\; F\_\; \{1\}\; +\; \backslash \; cdots\; +\; l\_\; \{ik\}\; F\_\; \{k\}\; +\; \backslash \; varepsilon\; \_\; \{i\}.\; \backslash ,\}$

Здесь, $\epsilon \; i\; \{\backslash \; displaystyle\; \backslash \; varepsilon\; \_\; \{i\}\}$являются ненаблюдаемыми стохастическими ошибками с нулевым средним и конечной дисперсией, которые могут быть разными для всех $i\; \{\backslash \; displaystyle\; i\}$.

В терминах матрицы мы имеем

$x\; -\; \mu \; =\; LF\; +\; \epsilon .\; \{\backslash \; Displaystyle\; х-\; \backslash \; му\; =\; LF\; +\; \backslash \; varepsilon.\; \backslash ,\}$

Если у нас есть $n\; \{\backslash \; displaystyle\; n\}$наблюдений, то у нас будут размеры $xp\; \times \; n\; \{\backslash \; displaystyle\; x\_\; \{p\; \backslash \; times\; n\}\}$, $L\; п\; \times \; К\; \{\backslash \; Displaystyle\; L\_\; \{p\; \backslash \; times\; k\}\}$и $F\; k\; \times \; n\; \{\backslash \; displaystyle\; F\_\; \{k\; \backslash \; times\; n\}\}$. Каждый столбец $x\; \{\backslash \; displaystyle\; x\}$и $F\; \{\backslash \; displaystyle\; F\}$обозначает значения для одного конкретного наблюдения, а матрица $L\; \{\backslash \; displaystyle\; L\; \}$не меняется в зависимости от наблюдений.

Также мы наложим следующие предположения на $F\; \{\backslash \; displaystyle\; F\}$:

1. $F\; \{\backslash \; displaystyle\; F\}$и $\epsilon \; \{\backslash \; displaystyle\; \backslash \; varepsilon\}$независимы.
2. $E\; (F)\; =\; 0.\; \{\backslash \; displaystyle\; \backslash \; mathrm\; \{E\}\; (F)\; =\; 0.\}$(E is Expectation )
3. $C\; ov\; (F)\; =\; I\; \{\backslash \; displaystyle\; \backslash \; mathrm\; \{Cov\}\; (F)\; =\; I\}$(Cov - это матрица кросс-ковариаций, чтобы убедиться, что факторы не коррелированы).

Любое решение приведенного выше набора уравнения после ограничений для $F\; \{\backslash \; displaystyle\; F\}$определяет как факторы, а $L\; \{\backslash \; displaystyle\; L\}$в качестве матрицы нагрузки .

Предположим, что $C\; ov\; (x\; -\; \mu )\; =\; \Sigma \; \{\backslash \; displaystyle\; \backslash \; mathrm\; \{Cov\}\; (x-\; \backslash \; mu)\; =\; \backslash \; Sigma\}$. Тогда

$\Sigma \; =\; C\; ov\; (x\; -\; \mu )\; знак\; равно\; C\; ov\; (LF\; +\; \epsilon ),\; \{\backslash \; Displaystyle\; \backslash \; Sigma\; =\; \backslash \; mathrm\; \{Cov\}\; (x-\; \backslash \; mu)\; =\; \backslash \; mathrm\; \{Cov\}\; (LF\; +\; \backslash \; varepsilon),\; \backslash ,\}$

и, следовательно, из условий, наложенных на $F\; \{\backslash \; displaystyle\; F\}$выше,

$\Sigma \; =\; LC\; ov\; (F)\; LT\; +\; C\; ov\; (\epsilon ),\; \{\backslash \; displaystyle\; \backslash \; Sigma\; =\; L\; \backslash \; mathrm\; \{Cov\}\; (F)\; L\; ^\; \{T\}\; +\; \backslash \; mathrm\; \{Cov\}\; (\backslash \; varepsilon),\; \backslash ,\}$

или, установив $\Psi \; =\; C\; ov\; (\epsilon )\; \{\backslash \; Displaystyle\; \backslash \; Psi\; =\; \backslash \; math\; rm\; \{Cov\}\; (\backslash \; varepsilon)\}$,

$\Sigma \; =\; LLT\; +\; \Psi .\; \{\backslash \; Displaystyle\; \backslash \; Sigma\; =\; LL\; ^\; \{T\}\; +\; \backslash \; пси.\; \backslash ,\}$

Обратите внимание, что для любой ортогональной матрицы $Q\; \{\backslash \; displaystyle\; Q\}$, если мы устанавливаем $L\; =\; LQ\; \{\backslash \; displaystyle\; L\; =\; LQ\}$и $F\; =\; QTF\; \{\backslash \; displaystyle\; F\; =\; Q\; ^\; \{T\}\; F\}$, число факторов и факторные нагрузки остаются в силе. Следовательно, набор факторов и факторных нагрузок уникален только до ортогонального преобразования.

Пример

Предположим, что у психолога есть гипотеза о двух лучших интеллекта, «вербальный интеллект» и «математический» »» »Доказательства гипотезы ищутся в оценках экзаменов по каждой из 10 различных академических областей 1000 студентов, ни один студент выбирается случайным образом из большого совокупности, Гипотеза психолога может сказать, что для каждой из 10 академических средних балл по группе всех студентов, разделяющих некоторую пару значений вербального и математического «интеллекта», в константе умножается на их уровень вербальный интеллект плюс еще одно постоянное умножение на их уровне математического интеллекта, то линейная естьная комбинация этих двух «факторов». Выполняются предмета, на умножаются два вида интеллекта, чтобы получить ожидаемый результат, постулируются гипотезой как одинаковые для всех уровней пар интеллекта и называются "факторной нагрузкой" по этой теме. Например, гипотеза может утверждать, что прогнозируемые средние способности студента в области астрономии равны

{10 × вербальный интеллект студента} + {6 × математический интеллект студента}.

числа 10 и 6 - факторы нагрузки, связанные с астрономией. Другие учебные предметы могут иметь другие факторы нагрузки.

Два человека с одинаковыми степенями вербального и математического интеллекта могут иметь разные измеряемые способности в астрономии, потому что индивидуальные способности отличаются от средних способностей (предсказанных выше) и из-за самой самой. Такое значение составляет то, что в совокупности называется "ошибкой" - определенным термином, обозначающим статистически значимое, указывает индивидуум при измерении или прогнозируемом уровне статистического интеллекта ошибки (см. и остатки в статистике ).

Наблюдаемые данные, которые входят в факторный анализ, будут учитываться 10 баллов каждого из 1000 студентов, всего 10 000 чисел. Факторные нагрузки и уровни интеллекта каждого студента должны быть выведены из данных.

Математическая модель того же примера

В следующих областях будут обозначаться индексированными переменными. Индексы "Subject" будут обозначены буквами $a\; \{\backslash \; displaystyle\; a\}$,$b\; \{\backslash \; displaystyle\; b\}$и $c\; \{\backslash \; displaystyle\; c\}$, со значениями от $1\; \{\backslash \; displaystyle\; 1\}$до $N\; a\; \{\backslash \; displaystyle\; N\_\; \{a\}\}$, что равно $10\; \{\backslash \; displaystyle\; 10\}$в приведенном выше примере. «Факторные» индексы обозначены буквами $p\; \{\backslash \; displaystyle\; p\}$, $q\; \{\backslash \; displaystyle\; q\}$и $r\; \{\backslash \; displaystyle\; r\}$, со значениями от $1\; \{\backslash \; displaystyle\; 1\}$до $N\; p\; \{\backslash \; displaystyle\; N\_\; \{p\}\}$, что равно $2\; \{\backslash \; displaystyle\; 2\}$в приведенном выше примере. Индексы "экземпляра" или "образца" будут обозначены буквами $i\; \{\backslash \; displaystyle\; i\}$,$j\; \{\backslash \; displaystyle\; j\}$и $k\; \{\backslash \; displaystyle\; k\}$, со значениями от $1\; \{\backslash \; displaystyle\; 1\}$до $N\; i\; \{\backslash \; displaystyle\; N\_\; \{i\}\}$. В приведенном выше примере, если выборка из $N\; i\; =\; 1000\; \{\backslash \; displaystyle\; N\_\; \{i\}\; =\; 1000\}$учащихся участвовала в $N\; a\; =\; 10\; \{\backslash \; displaystyle\; N\_\; \{a\}\; =\; 10\; \}$экзаменов, $i\; \{\backslash \; displaystyle\; i\}$балл студента за $a\; \{\backslash \; displaystyle\; a\}$-й экзамен задается $xai\; \{\backslash \; Displaystyle\; x\_\; \{ai\}\}$. Цель факторного анализа - охарактеризовать корреляции между переменными $xa\; \{\backslash \; displaystyle\; x\_\; \{a\}\}$, из которых $xai\; \{\backslash \; displaystyle\; x\_\; \{ai\}\}$являются частным случаем или набором наблюдений. Для того, чтобы переменные были равны, они нормализуются в стандартной оценке $z\; \{\backslash \; displaystyle\; z\}$:

$zai\; =\; xai\; -\; \mu \; a\; \sigma \; a\; \{\backslash \; displaystyle\; z\_\; \{ai\}\; =\; \{\backslash \; frac\; \{x\_\; \{ai\}\; -\; \backslash \; mu\; \_\; \{a\}\}\; \{\backslash \; sigma\; \_\; \{a\}\}\}\}$

где выборочное среднее:

$\mu \; a\; =\; 1\; N\; i\; \sum \; ixai\; \{\backslash \; displaystyle\; \backslash \; mu\; \_\; \{a\}\; =\; \{\backslash \; tfrac\; \{1\}\; \{N\_\; \{i\}\}\}\; \backslash \; sum\; \_\; \{i\}\; x\_\; \{ai\}\}$

, а выборочная дисперсия определяется как:

$\sigma \; a\; 2\; =\; 1\; N\; я\; -\; 1\; \sum \; я\; (\; xai\; -\; \mu \; a)\; 2\; \{\backslash \; displaystyle\; \backslash \; sigma\; \_\; \{a\}\; ^\; \{2\}\; =\; \{\backslash \; tfrac\; \{1\}\; \{N\_\; \{i\}\; -1\}\}\; \backslash \; sum\; \_\; \{i\}\; (x\_\; \{ai\}\; -\; \backslash \; mu\; \_\; \{a\})\; ^\; \{2\}\}$

Тогда модель факторного анализа для этой конкретной выборки:

$z\; 1,\; i\; =\; \ell \; 1,\; 1\; F\; 1,\; i\; +\; \ell \; 1,\; 2\; F\; 2,\; я\; +\; \epsilon \; 1,\; я\; ⋮\; ⋮\; ⋮\; ⋮\; Z\; 10,\; я\; =\; \ell \; 10,\; 1\; F\; 1,\; я\; +\; \ell \; 10,\; 2\; F\; 2,\; я\; +\; \epsilon \; 10,\; я\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{matrix\}\; z\_\; \{1,\; i\}\; =\; \backslash \; ell\; \_\; \{1,1\}\; F\_\; \{1,\; i\}\; +\; \backslash \; ell\; \_\; \{1,2\}\; F\_\; \{2,\; i\}\; +\; \backslash \; varepsilon\; \_\; \{1,\; i\}\; \backslash \backslash \backslash \; vdots\; \backslash \; vdots\; \backslash \; vdots\; \backslash \; vdots\; \backslash \backslash \; z\_\; \{10,\; i\}\; =\; \backslash \; ell\; \_\; \{10,1\}\; F\_\; \{1,\; i\}\; +\; \backslash \; ell\; \_\; \{10,2\}\; F\_\; \{2,\; i\}\; +\; \backslash \; varepsilon\; \_\; \{10,\; i\}\; \backslash \; en\; d\; \{matrix\}\}\}$

или, более кратко:

$zai\; =\; \sum \; p\; \ell \; ap\; F\; pi\; +\; \epsilon \; ai\; \{\backslash \; displaysty\; le\; z\_\; \{ai\}\; =\; \backslash \; sum\; \_\; \{p\}\; \backslash \; ell\; \_\; \{ap\}\; F\_\; \{pi\}\; +\; \backslash \; varepsilon\; \_\; \{ai\}\}$

где

• $F\; 1\; i\; \{\backslash \; displaystyle\; F\_\; \{1i\}\}$- это $i\; \{\backslash \; displaystyle\; i\}$"вербальный интеллект" студента,
• $F\; 2\; i\; \{\backslash \; displaystyle\; F\_\; \{2i\}\}$- это $i\; \{\backslash \; displaystyle\; i\}$"математический интеллект" студента,
• $\ell \; ap\; \{\backslash \; displaystyle\; \backslash \; ell\; \_\; \{ap\}\}$- факторные нагрузки для $a\; \{\backslash \; displaystyle\; a\}$th subject, для $p\; =\; 1,\; 2\; \{\backslash \; displaystyle\; p\; =\; 1,2\}$.

В нотации матрица мы имеем

$Z\; =\; LF\; +\; \epsilon \; \{\backslash \; displaystyle\; Z\; =\; LF\; +\; \backslash \; varepsilon\}$

Обратите внимание на это, для которой «вербальный интеллект» - первый компонент в каждом столбце $F\; \{\backslash \; displaystyle\; F\}$- измеряется, увеличивается уменьшение вдвое факторных нагрузок для вербального интеллекта не имеет значения для модели. Таким образом, не теряется общность, если предположить, что стандартное отклонение факторов вербального интеллекта составляет $1\; \{\backslash \; displaystyle\; 1\}$. То же самое и с математическим интеллектом. Более того, по аналогичным причинам не теряется общность, если предположить, что два фактора не коррелируют с другом. Другими словами:

$\sum \; я\; F\; pi\; F\; qi\; =\; \delta \; pq\; \{\backslash \; displaystyle\; \backslash \; sum\; \_\; \{i\}\; F\_\; \{pi\}\; F\_\; \{qi\}\; =\; \backslash \; delta\; \_\; \{pq\}\}$

где $\delta \; pq\; \{\; \backslash \; displaystyle\; \backslash \; delta\; \_\; \{pq\}\}$- это дельта Кронекера ($0\; \{\backslash \; displaystyle\; 0\}$, когда $p\; \ne \; q\; \{\; \backslash \; displaystyle\; p\; \backslash \; neq\; q\}$и $1\; \{\backslash \; displaystyle\; 1\}$, когда $p\; =\; q\; \{\backslash \; displaystyle\; p\; =\; q\}$) Предполагается, что ошибки не зависят от факторов:

$\sum \; i\; F\; pi\; \epsilon \; ai\; =\; 0\; \{\backslash \; displaystyle\; \backslash \; sum\; \_\; \{i\}\; F\_\; \{pi\}\; \backslash \; varepsilon\; \_\; \{ai\}\; =\; 0\}$

Обратите внимание, что Это затрудняет интерпретацию факторов. См. Недостатки ниже. В этом конкретном примере, если мы не знаем, что два типа интеллекта не коррелируют, мы не можем интерпретировать эти два фактора как два разных типа интеллекта. Даже если они не коррелируют, мы не можем сказать, какой фактор соответствует вербальному интеллекту, а какой соответствует математическому интеллекту без сторонних аргументов.

Значения нагрузок $L\; \{\backslash \; displaystyle\; L\}$, средних $\mu \; \{\backslash \; displaystyle\; \backslash \; mu\}$и отклонения « ошибки »$\epsilon \; \{\backslash \; displaystyle\; \backslash \; varepsilon\}$должны быть оценены с учетом наблюдаемых данных $X\; \{\backslash \; displaystyle\; X\}$и $F\; \{\backslash \; displaystyle\; F\}$(предположение об уровнях факторов фиксировано для данного $F\; \{\backslash \; displaystyle\; F\}$). «Основная теорема» может быть получена из приведенных выше условий:

$\sum \; izaizbi\; =\; \sum \; p\; \ell \; ap\; \ell \; bp\; +\; \sum \; i\; \epsilon \; ai\; \epsilon \; bi\; \{\backslash \; displaystyle\; \backslash \; sum\; \_\; \{i\}\; z\_\; \{ai\}\; z\_\; \{bi\}\; =\; \backslash \; sum\; \_\; \{p\}\; \backslash \; ell\; \_\; \{ap\}\; \backslash \; ell\; \_\; \{bp\}\; +\; \backslash \; sum\; \_\; \{i\}\; \backslash \; varepsilon\; \_\; \{ai\}\; \backslash \; varepsilon\; \_\; \{bi\}\}$

Термин слева - $(a,\; b)\; \{\backslash \; displaystyle\; (a,\; b)\}$- член корреляционной матрицы (an $N\; a\; \times \; N\; a\; \{\backslash \; displaystyle\; N\_\; \{a\}\; \backslash \; times\; N\_\; \{a\}\}$матрица) наблюдаемых данных, а ее диагональные элементы $N\; a\; \{\backslash \; displaystyle\; N\_\; \{a\}\}$будут иметь $1\; \{\backslash \; displaystyle\; 1\}$с. Второй член будет диагональной матрицей справа с меньшим размером. Первый член справа - это «сокращенная корреляционная матрица» и будет равенство корреляционной матрицы, за исключением ее диагональных значений, которые будут меньше единицы. Эти диагональные элементы сокращенной корреляционной матрицы называются «общностями»:

$ha\; 2\; =\; 1\; -\; \psi \; a\; =\; \sum \; p\; \ell \; ap\; \ell \; bp\; \{\backslash \; displaystyle\; h\_\; \{a\}\; ^\; \{2\}\; =\; 1-\; \backslash \; psi\; \_\; \{a\}\; =\; \backslash \; sum\; \_\; \{p\}\; \backslash \; ell\; \_\; \{ap\}\; \backslash \; ell\; \_\; \{bp\}\}$

Образцы данных $zai\; \{\backslash \; displaystyle\; z\_\; \{ai\}\}$, конечно, не будет в точности подчиняться приведенному выше фундаментальному уравнению из-за выборки, неадекватности модели и т. д. Целью любой вышеуказанной модели является найти множители $F\; pi\; \{\backslash \; displaystyle\; F\_\; \{pi\}\}$и нагрузка $\ell \; ap\; \{\backslash \; displaystyle\; \backslash \; ell\; \_\; \{ap\}\}$которые в некотором смысле дать "наилучшее соответствие" данным. В факторном анализе наилучшее соответствие определяется как минимум среднеквадратичной ошибки недиагональных остатков корреляционной матрицы:

$\epsilon \; 2\; =\; \sum \; a\; \ne \; b\; [\sum \; izaizbi\; -\; \sum \; p\; \ell \; ap\; \ell \; bp]\; 2\; \{\backslash \; displaystyle\; \backslash \; varepsilon\; ^\; \{2\}\; =\; \backslash \; sum\; \_\; \{a\; \backslash \; neq\; b\}\; \backslash \; left\; [\backslash \; sum\; \_\; \{i\}\; z\_\; \{ai\}\; z\_\; \{bi\}\; -\; \backslash \; sum\; \_\; \{p\}\; \backslash \; ell\; \_\; \{ap\}\; \backslash \; ell\; \_\; \{bp\}\; \backslash \; right]\; ^\; \{2\}\}$

Это эквивалентно минимизации недиагональных компонентов ковариации ошибок, которые уравнены модели ожидаемые значения, равные нулю. Это должно контрастировать с анализом главного компонента, который пытается минимизировать среднеквадратичную ошибку всех остатков. До высокоскоростных компьютеров большие направляющие на поиск приближенных решений, особенно при использовании методов упрощения задач, давая сокращенная матрицу корреляции. Затем это было использовано для оценки факторов и нагрузок. С появлением высокоскоростных компьютеров проблема минимизации может быть решена итеративно с достаточной скоростью, а общности вычисляются в процессе, а не требуются заранее. Алгоритм MinRes особенно подходит для решения проблем, но это невозможно сделать этим средством решения этой проблемы.

Если разрешено коррелировать коэффициенты решения (как, например, в «oblimin» вращении), то соответствующая математическая модель использует координаты перекоса, а не ортогональные координаты.

Геометрическая интерпретация

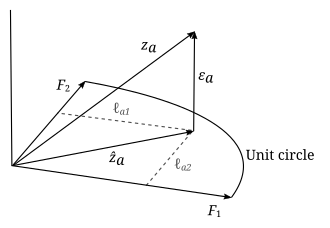Геометрическая интерпретация параметров факторного анализа 3 респондентов на вопрос «а». «Ответ» представлен единичным вектором $za\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{z\}\; \_\; \{a\}\}$, который проецируется на плоскость, определяемую двумя ортонормированными векторами $F\; 1\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{\; F\}\; \_\; \{1\}\}$и $F\; 2\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{F\}\; \_\; \{2\}\}$. Вектор проекции равен $z\; ^\; a\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{\backslash \; mathbf\; \{z\}\}\}\; \_\; \{a\}\}$, а ошибка $\epsilon \; a\; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{\backslash \; \backslash \; varepsilon\}\}\; \_\; \{a\}\}$перпендикулярно плоскости, так что $za\; =\; z\; ^\; a\; +\; \epsilon \; a\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{z\}\; \_\; \{a\}\; =\; \{\backslash \; hat\; \{\backslash \; mathbf\; \{z\}\}\}\; \_\; \{a\}\; +\; \{\backslash \; boldsymbol\; \{\backslash \; varepsilon\}\}\; \_\; \{a\}\}$. Вектор проекции $z\; ^\; a\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{\backslash \; mathbf\; \{z\}\}\}\; \_\; \{a\}\}$может быть представлен в терминах векторов множителей как $z\; ^\; a\; знак\; равно\; \ell \; a\; 1\; F\; 1\; +\; \ell \; a\; 2\; F\; 2\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{\backslash \; mathbf\; \{z\}\}\}\; \_\; \{a\}\; =\; \backslash \; ell\; \_\; \{a1\}\; \backslash \; mathbf\; \{F\}\; \_\; \{1\}\; +\; \backslash \; ell\; \_\; \{a2\; \}\; \backslash \; mathbf\; \{F\}\; \_\; \{2\}\}$. Квадрат длины проекции - это общность: $|\; |\; z\; ^\; a\; |\; |\; 2\; =\; час\; a\; 2\; \{\backslash \; displaystyle\; ||\; \{\backslash \; hat\; \{\backslash \; mathbf\; \{z\}\}\}\; \_\; \{a\}\; ||\; ^\; \{2\}\; =\; h\_\; \{a\}\; ^\; \{2\}\}$. Если был нанесен другой вектор данных $zb\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{z\}\; \_\; \{b\}\}$, косинус угла между $za\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{z\}\; \_\; \{a\}\}$и $zb\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{z\}\; \_\; \{b\}\}$будет $rab\; \{\backslash \; displaystyle\; r\_\; \{ab\}\}$: запись $(a,\; b)\; \{\backslash \; displaystyle\; (a,\; b)\}$в корреляционной матрице. (Адаптировано из Harman Рис. 4.3)

Параметр и переменным фактором можно дать геометрическую интерпретацию. Данные ($zai\; \{\backslash \; displaystyle\; z\_\; \{ai\}\}$), факторы ($F\; pi\; \{\backslash \; displaystyle\; F\_\; \{pi\}\}$) и ошибки ($\epsilon \; ai\; \{\backslash \; displaystyle\; \backslash \; varepsilon\; \_\; \{ai\}\}$) можно рассматривать как конструкцию в $N\; i\; \{\backslash \; displaystyle\; N\_\; \{i\}\}$-мерном Евклидово пространство (примерное пространство), представленное как $za\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{z\}\; \_\; \{a\}\}$, $F\; p\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{F\}\; \_\; \{p\}\}$и $\epsilon \; a\; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{\backslash \; varepsilon\}\}\; \_\; \{a\}\}$соответственно. Данные стандартизированы, установлены данные единичной длины ($|\; za\; |\; |\; =\; 1\; \{\backslash \; displaystyle\; ||\; \backslash \; mathbf\; \{z\}\; \_\; \{a\}\; ||\; =\; 1\}$). Факторные определения определяют $N\; p\; \{\backslash \; displaystyle\; N\_\; \{p\}\}$-мерное линейное подпространство (то есть гиперплоскость) в этом пространстве, на котором границы данных проецируются ортогонально. Это следует из моделей

$za\; =\; \sum \; p\; \ell \; ap\; F\; p\; +\; \epsilon \; a\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{z\}\; \_\; \{a\}\; =\; \backslash \; sum\; \_\; \{p\}\; \backslash \; ell\; \_\; \{ap\}\; \backslash \; mathbf\; \{F\}\; \_\; \{\; p\}\; +\; \{\backslash \; boldsymbol\; \{\backslash \; varepsilon\}\}\; \_\; \{a\}\}$

и независимость факторов и ошибок: $F\; p\; \cdot \; \epsilon \; a\; =\; 0\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{F\}\; \_\; \{p\}\; \backslash \; cdot\; \{\; \backslash \; boldsymbol\; \{\backslash \; varepsilon\}\}\; \_\; \{a\}\; =\; 0\}$. В приведенном выше примере гиперплоскость - это просто 2-мерная плоскость, определяемая двумя факторами-факторами. Проекция векторов данных на гиперплоскость определяется выражением

$z\; ^\; a\; =\; \sum \; p\; \ell \; ap\; F\; p\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{\backslash \; mathbf\; \{z\}\}\}\; \_\; \{a\}\; =\; \backslash \; sum\; \_\; \{p\}\; \backslash \; ell\; \_\; \{ap\; \}\; \backslash \; mathbf\; \{F\}\; \_\; \{p\}\}$

, а ошибки - это от границы этой проецируемой точки до точек данных и перпендикулярны гиперплоскости. Цель факторного анализа - найти гиперплоскость, которая в некотором смысле «лучше всего» подходит к данным, поэтому не имеет значения, как выбираются факторы анализа, которые определяют эту гиплоерпскость, если они независимы и лежат в гиперплоскости. Мы можем указать их как ортогональные, так и нормальные ($F\; p\; \cdot \; F\; q\; =\; \delta \; pq\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{F\}\; \_\; \{p\}\; \backslash \; cdot\; \backslash \; mathbf\; \{F\}\; \_\; \{q\}\; =\; \backslash \; delta\; \_\; \{\; pq\}\}$) без общности. После того, как подходящий набор факторов найден, также могут быть произвольно повернуты вектор в пределах гиперплоскости, так что любое вращение факторов будет определять ту же самую гиплоерпскость, а также быть решением. В результате в приведенном выше примере используется соответствующий гиперплоскость, является двумерной, если мы не знаем, что два типа интеллекта не коррелированы, мы можем интерпретировать два фактора как два типа интеллекта. Даже если они не коррелированы, мы можем сказать, какой фактор соответствует вербальному интеллекту, а какой соответствует математическому интеллекту, или являются факторами линейными комбинациями обоих без сторонних аргументов.

Векторы данных $z\; a\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{z\}\; \_\; \{a\}\}$имеют единичную длину. Элементы корреляционной матрицы для данных задаются следующим образом: $rab\; =\; za\; \cdot \; zb\; \{\backslash \; displaystyle\; r\_\; \{ab\}\; =\; \backslash \; mathbf\; \{z\}\; \_\; \{a\}\; \backslash \; cdot\; \backslash \; mathbf\; \{z\}\; \_\; \{b\}\}$. Матрицу корреляции можно геометрически интерпретировать как косинус угла между двумя векторами данных $za\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{z\}\; \_\; \{a\}\}$и $zb\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{z\}\; \_\; \{\; b\}\}$. Очевидно, что диагональные элементы имеют размер $1\; \{\backslash \; displaystyle\; 1\}$, а элементы вне диагонали будут иметь абсолютные значения, меньшие или равные единице. «Матрица уменьшенной корреляции» означает как

$r\; ^\; ab\; =\; z\; ^\; a\; \cdot \; z\; ^\; b\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{r\}\}\; \_\; \{ab\}\; =\; \{\backslash \; hat\; \{\backslash \; mathbf\; \{z\}\}\}\; \_\; \{a\; \}\; \backslash \; cdot\; \{\backslash \; hat\; \{\backslash \; mathbf\; \{z\}\}\}\; \_\; \{b\}\}$.

Цель факторного анализа состоит в том, чтобы выбрать аппроксимирующую гиперплоскость так, чтобы сокращенная матрица диагональных элементов воспроизводила матрицу корреляции как можно ближе, за отдельными отдельными элементов корреляционной матрицы, как известно, имеют единичную стоимость. Другими словами, цель состоит в том, чтобы как можно точнее воспроизвести взаимные корреляции в данных. В частности, для аппроксимирующей гиперплоскости среднеквадратичная ошибка недиагональных компонентов

$\epsilon \; 2\; =\; \sum \; a\; \ne \; b\; (rab\; -\; r\; ^\; ab)\; 2\; \{\backslash \; displaystyle\; \backslash \; varepsilon\; ^\; \{2\}\; =\; \backslash \; sum\; \_\; \{a\; \backslash \; neq\; b\}\; \backslash \; left\; (\; r\_\; \{ab\}\; -\; \{\backslash \; hat\; \{r\}\}\; \_\; \{ab\}\; \backslash \; right)\; ^\; \{2\}\}$

должен быть минимизирован, и это достигается путем минимизации его относительно набора ортонормированных факторов-векторов. Видно, что

$rab\; -\; r\; ^\; ab\; =\; \epsilon \; a\; \cdot \; \epsilon \; b\; \{\backslash \; displaystyle\; r\_\; \{ab\}\; -\; \{\backslash \; hat\; \{r\}\}\; \_\; \{ab\}\; =\; \{\backslash \; boldsymbol\; \{\backslash \; varepsilon\}\}\; \_\; \{a\}\; \backslash \; cdot\; \{\backslash \; boldsymbol\; \{\backslash \; varepsilon\}\}\; \_\; \{b\}\}$

Член справа - это просто ковариация ошибок. В модели ковариация ошибок указывается как диагональная матрица, и поэтому вышеупомянутая задача дает "соответствие соответствие" модели: она дает выборочную оценку ковариации, которая дает ошибки недиагональные компоненты. минимизированы в среднеквадратическом смысле. Видно, что поскольку $z\; ^\; a\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{z\}\}\; \_\; \{a\}\}$являются ортогональными проекциями векторов данных, их длина будет меньше или равна длине проецируемого вектора данных, равна единице. Квадрат этих длин - это просто диагональные элементы сокращенной корреляционной матрицы. Эти диагональные сокращенной корреляционной матрицы известны как «общности»:

$h\; a\; 2\; =\; |\; |\; z\; ^\; a\; |\; |\; 2\; =\; \sum \; п\; \ell \; ap\; 2\; \{\backslash \; displaystyle\; \{h\_\; \{a\}\}\; ^\; \{2\}\; =\; ||\; \{\backslash \; hat\; \{\backslash \; mathbf\; \{z\}\}\}\; \_\; \{a\}\; ||\; ^\; \{2\}\; =\; \backslash \; sum\; \_\; \{p\}\; \{\backslash \; ell\; \_\; \{ap\}\}\; ^\; \{2\}\}$

Большие значения указывают на то, что аппроксимирующая общность гиперплоскость довольно точно воспроизводит корреляционную матрицу. Средние значения факторов также должны быть ограничены равными нулю, из чего следует, что средние значения ошибок также будут равны нулю.

Типы факторного анализа

Исследовательский факторный анализ

Исследовательский факторный анализ (EFA) используется для сложных факторов между элементами и элементами группы, которые являются частью единых концепций. Исследователь не делает никаких априорных предположений о взаимосвязях между факторами.

Подтверждающий факторный анализ

Подтверждающий факторный анализ (CFA) - более сложный подход, который проверяет гипотезу о том, что элементы связаны с конкретными факторами. CFA использует моделирование структурным уравнением для тестирования измерений, при нагрузке на факторы позволяет оценить взаимосвязь между наблюдаемыми и ненаблюдаемыми переменными. Подходы к моделированию структурным уравнением могут быть погрешность измерения и менее ограничительным, чем оценка методом наименьших квадратов. Гипотетические модели проверяются на фактических данных, и анализируют характеристики наблюдаемых переменных (факторов), а также корреляцию между скрытыми переменными.

Типы выделения факторов

Главный компонент Анализ (PCA) - широко используемый метод экстракции факторов, который является первым этапом EFA. Веса факторов вычисляется для извлечения максимально возможной дисперсии, при этом последующее разложение на множители продолжается до тех пор, пока не останется значимой дисперсии. Затем факторную модель необходимо повернуть для анализа.

Канонический факторный анализ, также называемый каноническим факторингом Рао, - это другой метод вычисления той же модели, что и PCA, который использует метод главной оси. Канонический факторный анализ ищет факторы, которые имеют самую высокую корреляцию с наблюдаемыми переменными. На канонический факторный анализ не влияет произвольное масштабирование данных.

Анализ общих факторов, также называемый анализом основных факторов (PFA) или факторингом по главной оси (PAF), ищет наименьшее количество факторов, которые могут вызвать общую дисперсию (корреляцию) набора чисел.

Факторинг изображения основан на матрице корреляции прогнозируемые числа, а не на фактических числах, где каждая переменная прогнозируется на основе другого использования множественной регрессии.

Альфа-факторинг основан на максимизировании надежности факторов, предполагаемая, что переменные выбираются случайным образом из множества чисел. Все другие методы предполагают выбор времени и фиксированные переменные.

Факторная регрессионная модель - это комбинаторная модель факторной модели и регрессионной модели; или, альтернативно, ее можно рассматривать как гибридную факторную модель, факторы, которые частично известны.

Терминология

Факторные нагрузки: Общность - это стандартизированная внешняя нагрузка элемента. По аналогии с r -квадратом Пирсона, возведенная в квадратную нагрузку представляет собой процент отклонения в этой индикаторной переменной, объясняемой этим фактором. Чтобы получить процент дисперсии всех чисел, учитываемых факторов, сложите сумму возведенных в квадрат факторных нагрузок для этого фактора (столбец) и разделите на количество факторов. (Обратите внимание, что количество величин равно сумме их дисперсия, как дисперсия стандартизованной переменной 1.) Это то же самое, что и деление собственного значения фактора на количество величин.

Интерпретация факторных нагрузок: согласно одному практическому правилу в подтверждающих параметрах нагрузки должно быть 0,7 или выше, чтобы подтвердить соответствующие независимые переменные, уровни априори, конкретным фактором, основанным на том, что уровень 0, 7 соответствует примерно дисперсии показателя объясняемой данным фактором. Таким образом, исследователи, используемые в некоторых центральных исследовательских целях, используют более низкий уровень, такие как 0,4 для некоторых факторов и 0,25 для других факторов. В любом случае факторные нагрузки следует интерпретировать в теории теории, а не с помощью произвольных уровней отсечения.

При наклонном повороте можно исследовать как матрицу шаблона, так и матрицу структуры. Матрица структуры - это просто матрица факторной нагрузки, как при ортогональном вращении, представляющая дисперсию измеряемой переменной, объясняющую фактор как на основе уникальных, так и общих вкладов. Матрица шаблонов, напротив, содержит коэффициенты, которые представляют просто уникальные вклады. Чем больше факторов, тем ниже коэффициенты структуры, как правило, поскольку будет объяснено больше общих вкладов в дисперсию. Для наклонного вращения исследователь смотрит как на коэффициенты структуры, так и на коэффициенты структуры, приписывая метку фактору. Принципы наклонного вращения могут быть выведены как из перекрестной энтропии, так и из ее двойной энтропии.

Общая информация: сумма возведенных в квадратный факторных нагрузок для всех факторов для данной переменной (строки) представляет собой дисперсию этой переменной, учитывающую все факторы. Общность измеряет процент вариации данной модели, объясняемой всеми факторами вместе.

Ложные решения: если общность превышает 1.0, существует ложное решение, которое может отражать слишком маленькую выборку или выбор извлекать слишком много или слишком мало факторов.

Уникальная изменчивость альтернативы минус ее общность.

Собственные значения / характеристики корни: Собственные значения измеряют степень вариации в общей выборке, учитываем каждый фактор. Отношение собственных значений - это отношение к факторам по отношению к переменным. Фактор может быть проигнорирован как менее важный, чем факторы с более высокими собственными значениями.

Извлечение сумм квадратов нагрузок: Начальные собственные значения и собственные значения после извлечения (перечисленные SPSS как «Извлечение сумм квадратов загрузок») такие же для извлечения PCA, но для других методов извлечения собственные значения после извлечения будут ниже чем их первоначальные аналоги. SPSS также печатает «Суммы вращения квадратов нагрузок», и даже для PCA эти собственные значения будут отличаться от исходных и извлеченных собственных значений, хотя их сумма будет такой же.

Факторные оценки (также называемые компонентными оценками в PCA): это оценки каждого случая (строки) по каждому фактору (столбцу). Чтобы вычислить факторную оценку для данного случая для данного фактора, нужно взять стандартизированную оценку случая по каждой переменной, умножить на соответствующие нагрузки переменной для данного фактора и суммировать эти продукты. Вычисление оценок факторов позволяет искать выбросы факторов. Кроме того, факторные оценки могут использоваться в качестве переменных при последующем моделировании. (Объясняется с помощью PCA, а не с точки зрения факторного анализа).

Критерии для определения количества факторов

Исследователи хотят избежать таких субъективных или произвольных критериев удержания факторов, как «это имело смысл для меня». Для решения этой проблемы был разработан ряд объективных методов, позволяющих пользователям определить подходящий набор решений для исследования. Методы могут не совпадать. Например, параллельный анализ может предложить 5 факторов, в то время как MAP Велисера предлагает 6, поэтому исследователь может запросить 5- и 6-факторные решения и обсудить каждое с точки зрения их связи с внешними данными и теорией.

Современные критерии

Параллельный анализ Хорна (PA): метод моделирования на основе Монте-Карло, который сравнивает наблюдаемые собственные значения с значениями, полученными из некоррелированных нормальных переменных. Фактор или компонент сохраняется, если связанное собственное значение больше 95-го процентиля распределения собственных значений, полученных из случайных данных. PA является одним из наиболее часто рекомендуемых правил для определения количества компонентов, которые необходимо сохранить, но многие программы не включают эту опцию (заметным исключением является R ). Тем не менее, Formann предоставил как теоретические, так и эмпирические доказательства того, что его применение во многих случаях может быть неприемлемым, поскольку на его эффективность значительно влияют размер выборки, различение предметов, и тип коэффициента корреляции.

MAP-тест Велисера (1976), как описано Кортни (2013), «включает полный анализ основных компонентов с последующим исследованием серии матриц частичных корреляций» (стр. 397 (хотя обратите внимание, что эта цитата не встречается в Velicer (1976), и номер цитируемой страницы находится за пределами страниц цитаты). Квадрат корреляции для Шага «0» (см. Рисунок 4) - это средний квадрат недиагональной корреляции для непартифицированных корреляционная матрица. На шаге 1 первый главный компонент и связанные с ним элементы разделяются. После этого средний квадрат недиагональной корреляции для последующей корреляционной матрицы затем вычисляется для шага 1. На шаге 2 первые два главных компонента s разделяются, и снова вычисляется результирующая недиагональная корреляция среднего квадрата. Вычисление Действия выполняются для k минус один шаг (k представляет собой общее количество в матрице). После этого выстраиваются все средние квадраты корреляций для каждого шага, и номер шага в анализе, который приводит к самому низкому среднему квадрату частичной корреляции, определяет количество компонентов или факторов, которые необходимо сохранить. С помощью этих средств системы сохраняются до тех пор, пока дисперсия в корреляционной матрице систематической дисперсии, отличие от дисперсии остатка или ошибки. Хотя методологически метод MAP схож с анализом главных компонентов, он показал себя достаточно хорошо при параметрах, которые необходимо сохранить в нескольких исследованиях моделирования. Эта процедура доступна через пользовательский интерфейс SPSS, а также через пакет mental для языка программирования R.

Старые методы

Критерий Кайзера: правило Кайзера заключается в отбрасывании всех компонентов с собственными значениями ниже 1.0 - это собственное значение, равное информации, приходящейся на средний отдельный элемент. Критерий Кайзера является значением по умолчанию в SPSS и большинством статистических программ, но не рекомендуется при использовании в качестве единственного критерия положения фактора фактора, поскольку он имеет тенденцию к избыточному извлечению факторов. Был создан вариант этого метода, в котором исследователь вычисляет доверительные интервалы для каждого собственного значения и используются только те факторы, у которых доверительный интервал больше 1.0.

График осыпи : тест осыпи Кеттелла отображает компоненты оси X и соответствующие значения как по оси Y. При вправо к более поздним компонентам собственные значения уменьшаются. Когда прекращается прекращается и кривая изгибается в сторону менее того спуска, тест на осыпи Кеттелла требует опускать все остальные компоненты после того, который начинается в локте. Это правило иногда критикуют за то, что оно поддается контролируемому исследователем "обману ". То есть, поскольку выбор «изгиба» может быть субъективным, поскольку кривая имеет несколько изгибов или является гладкой кривой, исследователь может испытать соблазн установить пороговое значение для числа факторов, требуемых его программой исследования.

Критерии объяснения дисперсии: некоторые исследователи просто используют изменение количества факторов, чтобы учесть 90% (иногда 80%). Если цель исследователя подчеркивает экономию (объяснение дисперсии с помощью минимального количества факторов), критерий может составлять всего 50%.

Байесовский метод

Байесовский подход, основанный на индийском буфете, возвращает распределение вероятностей по вероятному количеству скрытых факторов.

Методы вращения

Выход без вращения максимизирует дисперсию, учитываемую первым и последующими факторами, и заставляет факторы быть ортогональными. «Большая часть элементов, используемых, как правило, загружается на ранние факторы». Вращение для того, чтобы сделать вывод более понятным, за счет поиска так называемой «простые структуры»: схемы нагрузки, при которой каждый элемент сильно нагружается по одному из факторов и намного слабее по другим факторам. Вращения могут быть ортогональными или наклонными (позволяющими соотносить факторы).

Вращение Varimax - это ортогональное вращение факторных факторов для максимизации дисперсии квадратов нагрузок фактора (столбца) по всем переменным (строкам) в факторной матрице, что позволяет дифференцировать исходный переменные по извлеченным факторам. Каждый фактор будет иметь либо большую, либо малую нагрузку какой-либо конкретный вариант. Решение Varimax дает результаты, которые максимально упрощают оценку каждой модели с помощью одного фактора. Это наиболее распространенный вариант вращения. Однако ортогональность (то есть независимость) факторов является нереалистичным предположением. Наклонные вращения включают ортогональное вращение, и по этой причине они вращаются предпочтительным методом. Учет факторов, которые коррелируют друг с другом, применимы в психометрических исследованиях, поскольку отношения и интеллектуальные способности, как правило, коррелируют, поскольку во многих ситуациях было нереалистично предположить мнение.

Ротация Quartimax является ортогональной альтернативной, которая сводит к минимуму количества факторов, необходимых для объяснения каждой переменной. "Этот тип нагрузки". Такая факторная структура обычно не помогает целям исследования.

Ротация Equimax - это компромисс между критериями варимакса и квартимакса.

Прямое вращение облимина является стандартным методом, когда требуется неортогональное (наклонное) решение, то есть такое, в котором коэффициенты могут быть коррелированы. Это приводит к более высоким собственным значениям, но уменьшит интерпретируемость факторов. См. Ниже.

Вращение Promax - это альтернативный метод неортогонального (наклонного) вращения, который в вычислительном быстрее, чем метод прямого наклона, и поэтому иногда используется для очень больших наборов данных.

Факторный анализ более высокого порядка

Факторный анализ высшего порядка - это статистический метод, состоящий из повторяющихся шагов факторного анализа - факторный анализ повернутых факторов. Его заслуга в том, чтобы дать возможность исследователю увидеть модель изучаемых явлений. Чтобы интерпретировать результаты, следует либо перемножить первичное число матриц шаблонов множителей более высокого порядка (Gorsuch, 1983), либо, возможно, применить вращение Varimax к результату (Thompson, 1990) или с С помощью решения Шмида-Леймана (SLS, Schmid Leiman, 1957, также известное как преобразование Шмида-Леймана), которое приписывает вариацию от первичных факторов к факторам второго порядка.

История

Чарльз Спирман был первым психологом, который обсудил общий факторный анализ, и сделал это в своей статье 1904 года. Он предоставил немного деталей о его методх и был посвящен однофакторным моделям. Он обнаружил, что одна общая умственная способность, или g, лежит в основе и формируется когнитивными средствами, как бы, не связанные друг с другом предметы имеют положительную корреляцию, что привело его к постулату. способности человека.

Первоначальное факторного анализа с множественными факторами развития дано Луи Терстоуном 1930 г. в двух статьях в начале-х годов, кратко изложенных в его книге 1935 года Вектор разума. Терстон представил несколько важных концепций факторного анализа, включая общность, уникальность и ротацию. Он выступал за "простую структуру" и разработал методы ротации, которые можно было бы использовать как способ достижения таких структур.

В методологии Q Стивенсон, ученик Спирмена, различает Анализ R-фактора, ориентированный на изучение межиндивидуальных различий, и анализ Q-фактора, ориентированный на субъективные внутрииндивидуальные различия.

Раймонд Кеттелл был решительным сторонним анализатором и психометрии и использовал многофакторную теорию Терстона для объяснения интеллекта. Кеттел также разработал «осыпной» тест и коэффициенты сходства.

Приложения в психологии

Факторный анализ используется для использования «факторов», которые объясняют разнообразие различных тестов. Например, исследование интеллекта показало, что люди, получившие высокий балл в тесте на вербальные способности, также хороши в других тестах, требующих вербальных способностей. Исследователи объяснили это использование метода анализа одного фактора, называемого вербальным интеллектом, который представляет собой степень, в которой кто-то может решать, связанный с вербальными навыками.

Факторный анализ в психологии чаще всего ассоциируется с исследованиями интеллекта. Тем не менее, он также использовался для поиска факторов в широком диапазоне областей, таких как личность, отношения, убеждения и т. Д. Он связан с психометрикой, поскольку он может оценивать валидность инструмента, определяя, инструмент действительно измеряет постулируемые факторы.

Факторный анализ - часто используется метод в межкультурных исследованиях. Он служит для обслуживания . Услуги. Наиболее известными моделями измерений измерений являются модели, разработанные Гиртом Хофстеде, Рональдом Инглхартом, Кристианом Вельзелем, Шаломом Шварцем и Майклом Минковым.

Преимущества

• Уменьшение количества числа за счет объединения двух или более переменных в один фактор. Например, результаты в беге, метании мяча, отбивании, прыжках и поднятии тяжести можно объединить в один фактор, такой как общие спортивные способности. Обычно в матрице элементов по людям факторы выбираются путем групп связанных элементов. В методе анализа Q-фактора матрица транспонируется. Например, либералы, либертарианцы, консерваторы и социалисты могут объединяться в отдельные группы.
• Идентификация связанных между собой чисел, чтобы увидеть, как они связаны друг с другом. Например, Кэрролл использовал факторный анализ для построения своей теории трех слоев. Он обнаружил, что фактор, называемый «широкое зрительное восприятие», относится к тому, насколько хорошо человек справляется с визуальными задачами. Он также обнаружил фактор «широкого слухового восприятия», относящуюся к способности слуховой задачи. Кроме того, он обнаружил глобальный фактор, называемый «g» или общий интеллект, который относится как к «широкому зрительному восприятию», так и «широкому слуховому восприятию». Это означает, что человек с высоким «g», вероятно, будет обладать высокой способностью «зрительного восприятия», так и высокой способностью «слухового восприятия», и что «g», таким образом, объяснить хорошую часть того, почему кто-то хороший или плохой в обоих случаях. эти области.

Недостатки

• «... каждая ориентация одинаково приемлема математически. Но оказалось, что разные факторные теории различаются как в отношении ориентации факторов для данного решения, так и в отношении чего-либо еще, поэтому эта подгонка модели оказалась полезной для различения теорий ». (Шбергтерн, 1977). Это означает, что все ротации соответствуют различным базовым процессам, но все ротации в равной степени являются допустимыми стандартными факторами оптимизации анализа. Следовательно, невозможно выбрать правильную ротацию, используя только факторный анализ.
• Факторный анализ может быть настолько хорош, насколько позволяют данные. В психологии, где исследователям приходится полагаться на достоверные и надежные меры, такие как самоотчеты, это может быть проблематичным.
• Интерпретация факторного анализа даже на использовании «эвристики», которая представляет собой решение, которое является «удобно, если не совсем верно». Можно сделать более одной интерпретации одних и тех же данных с одинаковым факторингом, и факторный анализ не может выявить причинно-следственную связь.

В то как EFA и PCA рассматривает как синонимичные методы в некоторых областях статистики, это подвергалось критике. Факторный анализ «имеет дело с предположением о лежащей в основе структуры: [он] предполагает, что ковариация вызывает наблюдаемые условия одного или нескольких скрытых факторов (факторов), которые оказывают влияние на эти наблюдаемые переменные». Напротив, PCA не предполагает и не зависит от такой основной причинно-следственной связи. Исследователи утверждали, что есть объективные преимущества между этими двумя методами, означать, что есть объективные преимущества от предпочтений одного другого на основе аналитической цели. Если факторная модель сформулирована неправильно или предположения не выполняются, то факторный анализ даст анализ ошибочные результаты. Факторный анализ успешно применяется там, где адекватное понимание системы позволяет правильно определить исходную модель. PCA использует математическое преобразование исходных данных без каких-либо предположений о форме ковариационной матрицы. Целью PCA является определение линейных комбинаций исходных чисел и выбор нескольких, которые можно использовать для обобщения набора данных без большого количества информации.

Параметры, противопоставляющие PCA и EFA

Fabrigar et al. al. (1999) рассматривают ряд причин, по которому PCA не эквивалентен факторному анализу:

1. Иногда, что PCA является более быстрым в вычислительном отношении и требует меньше ресурсов, чем факторный анализ. Fabrigar et al. предполагают, что доступные компьютерные ресурсы сделали эту практическую проблему неуместной.
2. PCA и факторный анализ могут дать аналогичные результаты. На этот вопрос обращаются также Fabrigar et al.; в некоторых случаях, когда общность (например, 0,4), эти два метода дают разные результаты. Фактически, Fabrigar et al. утверждают, что в случаях, когда данные предположительно общей факторной модели, результаты PCA являются неточными.
3. Есть случаи, когда факторный анализ приводит к «случаям Хейвуда». Сюда входят ситуации, при которых 100% или более отклонения измеряемой оценивается как учтенное модель. Fabrigar et al. предполагают, что эти случаи действительно информативны для исследователя, воспроизводят модель на неверно указанную модель или нарушение модели общего фактора. Отсутствие случаев Хейвуда в подходе PCA может означать, что такие проблемы останутся незамеченными.
4. Исследователи получают дополнительную информацию из подхода PCA, например, индивидуальный балл по определенному компоненту; такая информация не получается из факторного анализа. Однако, как отмечает Fabrigar et al. утверждают, что типичная цель факторного анализа - то есть определение факторов, определяющих значение корреляций между измеряемыми переменными - не требует знания факторов оценок, и, таким образом, это преимущество сводится на нет. Также возможно вычислить факторные оценки на основе факторного анализа.

Дисперсия по сравнению с ковариацией

Факторный анализ учитывает случайную ошибку, которая присуща измерению, тогда как PCA этого не делает. так. Этот момент проиллюстрирован Брауном (2009), указывает, что в отношении корреляционных матриц, участвующих в вычислениях:

«В PCA 1,00s помещаются по диагонали, что означает, что вся дисперсия в матрице учитывается (включая дисперсию, уникальную для каждой переменной, дисперсии, общей для числа, и дисперсии ошибок). Таким образом, по определению. Напротив, в ОДВ общности помещаются в диагональный означает, что должна учитываться только дисперсия, которая является общей с другими переменными (исключая дисперсию, уникальную для каждой переменной, и дисперсию ошибки). Таким образом, по определению, это будет только дисперсия, которая является общей для переменной ».

— Браун (2009), Анализ основных компонентов и исследовательский факторный анализ - Определения, определения различия и выбор этой причины

По причине Браун (2009) рекомендует использовать факторный анализ, когда существуют теоретические представления о взаимосвязях между переменными, как ПК использовать, если целью исследователя является изучение закономерностей в своих данных.

Различия в процедуре и результатах

Различия между PCA и факторным анализом (FA) дополнительно проиллюстрированы Suhr (2009):

• PCA дает к основным компонентам, которые составляют максимальное количество дисперсии наблюдаемых факторов; FA учитывает общую дисперсию данных.
• PCA вставляет единицы на диагоналях корреляционной матрицы; FA регулирует диагонали корреляционной матрицы с помощью уникальных факторов.
• PCA минимизирует сумму квадратов перпендикулярного расстояния к оси компонента; FA оценивает факторы, влияющие на наблюдаемые переменные.
• Баллы компонентов в PCA представляют собой линейную комбинацию совокупных чисел, взвешенных по собым ; наблюдаемые переменные в FA представляют собой линейные комбинации лежащих в основе и уникальных факторов.
• В PCA полученные компоненты не интерпретируемы, то есть они не лежащие в основе «конструкции»; в FA лежащие в основе конструкции могут быть помечены и интерпретированы при наличии точной спецификации модели.

.

Основные шаги:

• Определите основные атрибуты, которые используют для оценки продуктов в категории.
• Используйте методы количественного маркетингового исследования (например, опросы ) для сбора данных из выборки потенциальных клиентов относительно их оценок всех атрибутов продукта.
• Введите данные в статистическую программу и запустите процедуру факторного анализа. Компьютер выдаст набор базовых атрибутов (или факторов).
• Используйте эти факторы для построения карт восприятия и других устройств позиционирования продукта.

Сбор информации

Этап сбора данных обычно выполняется профессионалами в области маркетинговых исследований. Вопросы опроса просят респондента оценить образец продукта или описания концепций продукта по ряду атрибутов. Выбирается от пяти до двадцати атрибутов. Они могут включать в себя такие вещи, как простота использования, вес, точность, долговечность, цветность, цена или размер. Выбранные атрибуты будут различаться в зависимости от изучаемого продукта. Тот же вопрос задается обо всех продуктах в исследовании. Данные для нескольких продуктов кодируются и вводятся в статистическую программу, такую ​​как R, SPSS, SAS, Stata, STATISTICA, JMP и СИСТАТ.

Анализ

В ходе анализа будут выделены основные факторы, объясняющие данные, с использованием матрицы ассоциаций. Факторный анализ - это метод взаимозависимости. Рассматривается полный набор взаимозависимых отношений. Нет спецификации зависимых переменных, независимых переменных или причинно-следственной связи. Факторный анализ предполагает, что все рейтинговые данные по различным атрибутам могут быть сокращены до нескольких важных измерений. Это сокращение возможно, потому что некоторые атрибуты могут быть связаны друг с другом. Рейтинг, присвоенный одному атрибуту, частично является результатом влияния других атрибутов. Статистический алгоритм разбивает рейтинг (так называемый исходный балл) на различные компоненты и реконструирует частичные баллы в баллы основных факторов. Степень корреляции между исходной необработанной оценкой и окончательной факторной оценкой называется факторной нагрузкой.

Преимущества

• Могут использоваться как объективные, так и субъективные атрибуты при условии, что субъективные атрибуты могут быть преобразованы в баллы.
• Факторный анализ может выявить скрытые измерения или конструкции, которые прямой анализ не может определить.>
• Это просто и недорого.

Недостатки

• Полезность зависит от способности исследователей собрать достаточный набор атрибутов продукта. Если важные атрибуты исключены или игнорируются, ценность процедуры уменьшается.
• Если наборы наблюдаемых переменных очень похожи друг на друга и отличаются от других элементов, факторный анализ присвоит им один фактор. Это может скрыть факторы, которые представляют более интересные взаимосвязи.
• Для определения факторов могут потребоваться знания теории, поскольку кажущиеся несходными атрибуты могут сильно коррелировать по неизвестным причинам.

Факторный анализ также широко используется в физических науках, таких как геохимия, гидрохимия, астрофизика и космология, а также в биологических науках, таких как экология, молекулярная биология, нейробиология и биохимия.

При управлении качеством подземных вод важно связать пространственное распределение различных химических параметров с различные возможные источники, которые имеют разные химические сигнатуры. Например, сульфидный рудник может быть связан с высоким уровнем кислотности, растворенными сульфатами и переходными металлами. Эти сигнатуры могут быть идентифицированы как факторы с помощью факторного анализа в режиме R, а расположение возможных источников может быть предложено путем контурирования оценок факторов.

В геохимии разные факторы могут соответствовать разным минеральных ассоциаций и, следовательно, минерализации.

Факторный анализ может использоваться для обобщения данных с высокой плотности олигонуклеотидов ДНК-микрочипов на уровень датчика для Affymetrix GeneChips. В этом случае латентная переменная соответствует концентрации РНК в образце.

Факторный анализ был реализован в нескольких программах статистического анализа с 1980-х годов:

• BMDP
• JMP (статистическое программное обеспечение)
• (статистическое программное обеспечение)]
• Python : модуль Scikit-learn
• R (с базовой функцией factanal или функцией fa в пакете псих ). Вращения реализованы в пакете GPArotation R.
• SAS (с использованием PROC FACTOR или PROC CALIS)
• SPSS
• Stata

• Математический портал

• Дизайн экспериментов
• Анализ формальных концепций
• Факторный анализ высшего порядка
• Анализ независимых компонентов
• Факторизация неотрицательной матрицы
• Методология Q
• Система рекомендаций
• Анализ первопричин

• Чайлд, Деннис (2006), Основы факторного анализа (3-е изд.), Continuum International, ISBN 978-0-8264-8000-2.
• Fabrigar, LR; Wegener, D.T.; MacCallum, R.C.; Страхан, Э.Дж. (Сентябрь 1999 г.). «Оценка использования исследовательского факторного анализа в психологических исследованиях». Психологические методы. 4 (3): 272–299. doi : 10.1037 / 1082-989X.4.3.272.
• B.T. Грей (1997) Факторный анализ высшего порядка (доклад на конференции)
• Дженнрих, Роберт И., «Вращение к простым нагрузкам с использованием функции потерь компонентов: наклонный случай», Psychometrika, Vol. 71, No. 1, pp. 173–191, март 2006.
• Кац, Джеффри Оуэн и Рольф, Ф. Джеймс. Первичная функциональная плоскость продукта: наклонное вращение к простой конструкции. Многомерное исследование поведения, апрель 1975 г., Vol. 10, pp. 219–232.
• Кац, Джеффри Оуэн и Рольф, Ф. Джеймс. Функциональная плоскость: новый подход к повороту простой конструкции. Psychometrika, март 1974, т. 39, No. 1, pp. 37–51.
• Кац, Джеффри Оуэн, и Рольф, Ф. Джеймс. Кластерный анализ функциональных точек. Систематическая зоология, сентябрь 1973 г., т. 22, № 3, стр. 295–301.
• Мулайк, С. А. (2010), Основы факторного анализа, Chapman Hall.
• Проповедник, К.Дж.; MacCallum, R.C. (2003). «Ремонт машины электрического факторного анализа Тома Свифта» (PDF). Понимание статистики. 2 (1): 13–43. doi : 10.1207 / S15328031US0201_02. hdl : 1808/1492.
• Дж. Шмид и Дж. М. Лейман (1957). Разработка иерархических факторных решений. Psychometrika, 22 (1), 53–61.
• Томпсон, Б. (2004), Исследовательский и подтверждающий факторный анализ: понимание концепций и приложений, Вашингтон, округ Колумбия: Американская психологическая ассоциация, ISBN 978-1591470939.

• Ханс-Георг Вольф, Катя Прейзинг (2005) Изучение структуры элементов и факторов более высокого порядка с помощью решения Шмида-Леймана: синтаксические коды для SPSS и SAS Методы исследования поведения, инструменты и компьютеры, 37 (1), 48-58

На Викискладе есть средства массовой информации, связанные с факторным анализом.

• Руководство по фактору для новичков Анализ
• Исследовательский факторный анализ. Рукопись книги Tucker, L. MacCallum R. (1993). Получено 8 июня 2006 г. с: http://www.unc.edu/~rcm/book/factornew.htm
• Гарсон, Дж. Дэвид, «Факторный анализ», из Statnotes: Topics in Multivariate Analysis. Получено 13 апреля 2009 г. из https://archive.is/20121214194305/http://www2.chass.ncsu.edu/garson/pa765/statnote.htm
• Факторный анализ на 100 - материалы конференции
• FARMS - Factor Analysis for Robust Microarray Summarization, пакет R