Игра с расширенной формой

редактировать

Игра с расширенной формой - это спецификация игры в теории игр, позволяя (как следует из названия) явным образом представить ряд ключевых аспектов, таких как последовательность возможных ходов игроков, их выбор в каждой точке принятия решения, (возможно, несовершенный ) информацию о каждом игроке. имеет информацию о ходах другого игрока, когда он принимает решение, и его выплатах за все возможные исходы игры. Игры с расширенной формой также допускают представление неполной информации в форме случайных событий, смоделированных как «ходы по своей природе ».

Содержание

1 Конечные игры расширенной формы
- 1.1 Совершенная и полная информация
- 1.2 Несовершенная информация
- 1.3 Неполная информация
- 1.4 Формальное определение
2 Бесконечное пространство действий
3 См. Также
4 Ссылки
5 Дополнительная литература

Игры с расширенными формами

Некоторые авторы, особенно во вводных учебниках, первоначально определяют игру с расширенными формами как просто игру дерево с выплатами (без несовершенной или неполной информации), и добавьте другие элементы в последующих главах в качестве уточнений. В то время как остальная часть этой статьи следует этому мягкому подходу с мотивирующими примерами, мы заранее представляем конечные игры с расширенной формой, как (в конечном итоге) построенные здесь. Это общее определение было введено Гарольдом В. Куном в 1953 году, который расширил более раннее определение фон Неймана из 1928 года. После презентации Харта (1992), игра расширенной формы для n игроков, таким образом, состоит из следующего:

Конечное множество n (рациональных) игроков
A корневое дерево, называемое деревом игр
Каждый терминал (лист) узел игрового дерева имеет кортеж из n выплат, что означает, что существует одна выплата для каждого игрока в конце каждого возможного игрового
A раздела нетерминальных узлов дерево игр в n + 1 подмножествах, по одному для каждого (рационального) игрока, и со специальным подмножеством для фиктивного игрока, называемым Шанс (или Природа). Подмножество узлов каждого игрока называется «узлами игрока». (Таким образом, игра с полной информацией имеет пустой набор узлов шанса.)
Каждый узел случайного игрока имеет распределение вероятностей по его исходящим граням.
Каждый узел набор узлов рационального игрока далее разбивается на информационные наборы, которые делают определенные выборы неотличимыми для игрока при выполнении хода в том смысле, что:
- существует взаимно - одно соответствие между исходящими ребрами любых двух узлов одного и того же информационного набора - таким образом, набор всех исходящих ребер информационного набора разделен на классы эквивалентности, каждый класс представляет возможный выбор для хода игрока на некоторая точка—, и
- каждый (направленный) путь в дереве от корня до конечного узла может пересекать каждый информационный набор не более одного раза
полное описание игры, заданное вышеуказанными параметрами, имеет вид общеизвестно среди игроков

Таким образом, игра представляет собой путь через дерево от корня до конечного узла. В любом данном нетерминальном узле, принадлежащем Chance, исходящая ветвь выбирается в соответствии с распределением вероятностей. В узле любого рационального игрока игрок должен выбрать один из классов эквивалентности для ребер, который определяет ровно одно исходящее ребро, за исключением (в общем) того, что игрок не знает, за каким из них следует. (Внешний наблюдатель, знающий выбор каждого другого игрока до этого момента и реализация ходов Природы, может точно определить преимущество.) чистая стратегия для игрока, таким образом, состоит из selection - выбор ровно одного класса исходящих ребер для каждого набора информации (своего). В игре с идеальной информацией информационные наборы - это одиночки. Менее очевидно, как следует интерпретировать выплаты в играх с узлами Chance. Предполагается, что каждый игрок имеет функцию полезности фон Неймана – Моргенштерна, определенную для каждого результата игры; это предположение влечет за собой, что каждый рациональный игрок будет оценивать априори случайный результат по его ожидаемой полезности.

Приведенная выше презентация, хотя и точно определяет математическую структуру, по которой ведется игра, тем не менее опускает более техническое обсуждение формализации утверждений о том, как ведется игра, например, «игрок не может различать узлы в одной и той же информации. устанавливается при принятии решения ». Их можно уточнить с помощью эпистемической модальной логики ; подробности см. в Shoham Leyton-Brown (2009, глава 13).

A идеальная информация игра для двух игроков по дереву игр (как определено в комбинаторной теории игр и искусственном интеллекте ) может быть представлена как расширенная игра с результатами (например, победа, поражение или ничья ). Примеры таких игр включают крестики-нолики, шахматы и бесконечные шахматы. Игра по дереву expectminimax, как и игра в нарды, не имеет несовершенной информации (все информационные наборы являются одиночными), но имеет ходы случайности. Например, покер имеет как случайные ходы (раздающиеся карты), так и несовершенную информацию (карты, тайно удерживаемые другими игроками). (Binmore 2007, глава 2)

Совершенная и полная информация

Полное представление в развернутой форме определяет:

участников игры
для каждого игрока каждая возможность, которую он имеет для перемещения
, что каждый игрок может сделать на каждом своем ходу
что каждый игрок знает для каждого хода
выплаты, полученные каждый игрок для каждой возможной комбинации ходов

Игра, представленная в развернутой форме

В игре справа есть два игрока: 1 и 2. Числа у каждого нетерминального узла указывают, какому игроку принадлежит этот узел решения. Числа у каждого конечного узла представляют выплаты игрокам (например, 2,1 представляет выплату 2 игроку 1 и выплату 1 игроку 2). Метки у каждого ребра графа - это название действия, которое это ребро представляет.

Начальный узел принадлежит игроку 1, что указывает на то, что игрок 1 ходит первым. Игра по дереву выглядит следующим образом: игрок 1 выбирает между U и D; Игрок 2 наблюдает за выбором игрока 1 и затем выбирает между U 'и D'. Выплаты указаны в дереве. Четыре исхода представлены четырьмя конечными узлами дерева: (U, U '), (U, D'), (D, U ') и (D, D'). Выплаты, связанные с каждым результатом, соответственно, следующие (0,0), (2,1), (1,2) и (3,1).

Если игрок 1 играет D, игрок 2 будет играть U ', чтобы максимизировать свой выигрыш, и поэтому игрок 1 получит только 1. Однако, если игрок 1 играет U, игрок 2 максимизирует свой выигрыш, играя D' и player 1 получает 2. Игрок 1 предпочитает 2 к 1 и поэтому будет играть U, а игрок 2 - D '. Это идеальное равновесие во вспомогательной игре.

Несовершенная информация

Преимущество представления игры таким образом состоит в том, что ясно, каков порядок игры. Дерево ясно показывает, что игрок 1 ходит первым, а игрок 2 наблюдает за этим ходом. Однако в некоторых играх так не происходит. Один игрок не всегда соблюдает выбор другого (например, ходы могут быть одновременными или ход может быть скрытым). Информационный набор представляет собой набор узлов решений, такой что:

Каждый узел в наборе принадлежит одному игроку.
Когда игра достигает набора информации, игрок, который собирается двигаться, не может различать узлы в наборе информации; то есть, если набор информации содержит более одного узла, игрок, которому принадлежит этот набор, не знает, какой узел в наборе был достигнут.

В развернутой форме набор информации обозначен пунктирной линией, соединяющей все узлы в этот набор или иногда с помощью цикла, проведенного вокруг всех узлов в этом наборе.

Игра с несовершенной информацией, представленной в развернутой форме.

Если игра имеет набор информации с более чем одним участником, то говорят, что эта игра имеет несовершенную информацию. Игра с точной информацией такова, что на любой стадии игры каждый игрок точно знает, что имело место ранее в игре; т.е. каждый информационный набор представляет собой одноэлементный набор. Любая игра без точной информации содержит несовершенную информацию.

Игра справа такая же, как и вышеприведенная игра, за исключением того, что игрок 2 не знает, что делает игрок 1, когда они приходят играть. Первая описанная игра содержит точную информацию; игра справа нет. Если оба игрока рациональны и оба знают, что оба игрока рациональны, и все, что известно любому игроку, известно каждому игроку (т.е. игрок 1 знает, что игрок 2 знает, что игрок 1 рациональный, а игрок 2 знает это и т. Д.) до бесконечности), игра в первой игре будет следующей: игрок 1 знает, что если он играет U, игрок 2 будет играть D '(потому что для игрока 2 выигрыш 1 предпочтительнее выигрыша 0), и поэтому игрок 1 получит 2. Однако, если игрок 1 играет D, игрок 2 будет играть U '(потому что для игрока 2 выплата 2 лучше, чем выплата 1), а игрок 1 получит 1. Следовательно, в первой игре равновесие будет (U, D '), потому что игрок 1 предпочитает получать 2 к 1 и поэтому будет играть U, а игрок 2 будет играть D'.

Во второй игре менее ясно: игрок 2 не может наблюдать за ходом игрока 1. Игрок 1 хотел бы обмануть игрока 2, заставив его думать, что они играли в U, когда они на самом деле сыграли в D, так что игрок 2 будет играть D ', а игрок 1 получит 3. Фактически во второй игре существует идеальное байесовское равновесие. где игрок 1 играет D, а игрок 2 играет U ', а игрок 2 придерживается убеждения, что игрок 1 определенно будет играть D. В этом равновесии каждая стратегия рациональна с учетом имеющихся убеждений, и каждое убеждение согласуется с сыгранными стратегиями. Обратите внимание, как несовершенство информации меняет исход игры.

Чтобы упростить решение этой игры для равновесия Нэша, его можно преобразовать в нормальную форму. Учитывая, что это одновременная /последовательная игра, у первого и второго игрока есть по две стратегии.

Стратегии игрока 1: { U, D}
Стратегии игрока 2: {U ', D'}


Игроки 1 \ 2	Вверх '(U')	Вниз '(D ')
Вверх (U)	(0,0)	(2, 1)
Вниз (D)	(1,2)	(3, 1)

У нас будет матрица два на два с уникальной выплатой за каждую комбинацию ходов. Используя игру в нормальной форме, теперь можно решить игру и определить доминирующие стратегии для обоих игроков.

Если игрок 1 играет вверх (U), игрок 2 предпочитает играть вниз (D ') (Выплата 1>0)
Если игрок 1 играет вниз (D), игрок 2 предпочитает играть вверх ( U ') (Выплата 2>1)
Если игрок 2 играет Upn (U'), игрок 1 предпочитает играть Down (D) (Выплата 1>0)
Если игрок 2 играет Вниз (D '), игрок 1 предпочитает играть вниз (D) (3>2)

Эти предпочтения могут быть отмечены в матрице, и любое поле, в котором оба игрока имеют предпочтение, обеспечивает равновесие по Нэшу. Эта конкретная игра имеет единственное решение (D, U ’) с выигрышем (1,2).

В играх с бесконечным пространством действий и несовершенной информацией, информационные наборы, не являющиеся одноэлементными, представлены, если необходимо, путем вставки пунктирной линии, соединяющей (неузловые) конечные точки за дугой, описанной выше, или штрихом дуги сам. В описанном выше соревновании Штакельберга, если бы второй игрок не наблюдал за ходом первого игрока, игра больше не соответствовала бы модели Штакельберга; это будет соревнование Курно.

Неполная информация

Может случиться так, что игрок не знает точно, каковы выплаты в игре или какого типа его оппоненты находятся. В такого рода играх неполная информация. В развернутом виде он представлен как игра с полной, но несовершенной информацией с использованием так называемого преобразования Харшани. Это преобразование вводит в игру понятие выбора природы или выбора Бога. Представьте себе игру, в которой работодатель решает, стоит ли нанимать соискателя работы. Способности соискателя могут быть одним из двух: высокими или низкими. Уровень их способностей случайный; у них либо низкая способность с вероятностью 1/3, либо высокая способность с вероятностью 2/3. В этом случае удобно моделировать природу как своего рода игрока, который выбирает способности претендента в соответствии с этими вероятностями. Однако у природы нет вознаграждения. Выбор природы представлен в дереве игры незаполненным узлом. Края, исходящие от узла выбора природы, помечены с вероятностью наступления события, которое он представляет.

Игра с неполной и несовершенной информацией, представленной в развернутой форме

Игра справа - это игра с полной информацией (все игроки и выплаты известны всем), но с неполной информацией (работодатель не знает, что ход природы был.) Начальный узел находится в центре и он не заполнен, поэтому природа движется первой. Природа выбирает с той же вероятностью тип игрока 1 (что в этой игре равносильно выбору выигрышей в сыгранной вспомогательной игре), либо t1, либо t2. У игрока 1 для них есть отдельные наборы информации; т.е. игрок 1 знает, к какому они типу (это не обязательно). Однако игрок 2 не соблюдает выбор природы. Они не знают тип игрока 1; однако в этой игре они наблюдают за действиями игрока 1; т.е. есть идеальная информация. Действительно, теперь уместно изменить приведенное выше определение полной информации: на каждом этапе игры каждый игрок знает, во что играли другие игроки. В случае с приватной информацией каждый игрок знает, во что играла природа. Информационные наборы, как и раньше, представлены пунктирными линиями.

В этой игре, если природа выберет t1 в качестве типа игрока 1, игра будет похожа на самую первую описанную игру, за исключением того, что игрок 2 этого не знает (и сам факт того, что это прорезает их информацию устанавливает дисквалификацию из статуса подигры ). Есть одно разделяющее идеальное байесовское равновесие ; т.е. равновесие, в котором разные типы делают разные вещи.

Если оба типа играют одно и то же действие (объединение), равновесие не может быть сохранено. Если оба играют D, игрок 2 может сформировать уверенность в том, что они находятся на любом узле в информационном наборе, только с вероятностью 1/2 (потому что это шанс увидеть любой тип). Игрок 2 максимизирует свой выигрыш, играя D '. Однако, если они играют D ', тип 2 предпочтет сыграть U. Это не может быть равновесием. Если оба типа играют U, игрок 2 снова формирует уверенность в том, что они находятся в любом из узлов с вероятностью 1/2. В этом случае игрок 2 играет D ', но затем тип 1 предпочитает играть D.

Если тип 1 играет U, а тип 2 играет D, игрок 2 будет играть D', какое бы действие они ни наблюдали, но затем введите 1 предпочитает D. Таким образом, единственное равновесие происходит с типом 1, играющим D, типом 2, играющим U, и игроком 2, играющим U ', если они наблюдают D, и случайным образом, если они наблюдают U. Своими действиями игрок 1 сигнализирует о своих введите игроку 2.

Формальное определение

Формально конечная игра в развернутой форме - это структура $Γ = ⟨K, H, [(H i) i ∈ I], {A (H)} H ∈ H, a, ρ, U⟩ {\ Displaystyle \ Gamma = \ langle {\ mathcal {K}}, \ mathbf {H}, [(\ mathbf {H} _ {i}) _ {i \ in {\ mathcal {I}}}], \ {A (H) \} _ {H \ in \ mathbf {H}}, a, \ rho, u \ rangle}$ $\ Gamma = \ langle {\ mathcal {K}}, {\ mathbf {H}}, [({\ mathbf { H}} _ {i}) _ {{i \ in {\ mathcal {I}}}}], \ {A (H) \} _ {{H \ in {\ mathbf {H}}}}, а, \ rho, и \ rangle$ где:

$К = ⟨V, v 0, T, p⟩ {\ displaystyle {\ mathcal {K}} = \ langle V, v ^ {0}, T, p \ rangle}$ ${\ mathcal {K}} = \ langle V, v ^ {0}, T, p \ rangle$ конечное дерево с набором узлов $V {\ displaystyle V}$ $V$ , уникальный начальный узел $v 0 ∈ V {\ displaystyle v ^ {0} \ in V}$ $v ^ {0} \ in V$ , набор t концевые узлы $T ⊂ V {\ displaystyle T \ subset V}$ $T \ subset V$ (пусть $D = V ∖ T {\ displaystyle D = V \ setminus T}$ $D = V \ setminus T$ будет набор узлов решений) и непосредственную функцию-предшественницу $p: V → D {\ displaystyle p: V \ rightarrow D}$ $p: V \ rightarrow D$ , на которой представлены правила игры,
$H {\ displaystyle \ mathbf {H}}$ $\ mathbf {H}$ - это раздел $D {\ displaystyle D}$ $D$ , называемый информационным разделом,
$A (H) {\ displaystyle A (H)}$ $A (H)$ - набор действий, доступных для каждого информационного набора $H ∈ H {\ displaystyle H \ in \ mathbf {H}}$ $H \ in {\ mathbf {H}}$ , который формирует раздел на множестве все действия $A {\ displaystyle {\ mathcal {A}}}$ ${\ mathcal {A}}$ .
$a: V ∖ {v 0} → A {\ displaystyle a: V \ setminus \ {v ^ {0} \} \ rightarrow { \ mathcal {A}}}$ $a: V \ setminus \ {v ^ {0} \} \ rightarrow {\ mathcal {A}}$ - это раздел действий, связывающий каждый узел $v {\ displaystyle v}$ $v$ с одним действием $a (v) {\ displaystyle a (v)}$ $a (v)$ , выполнение:

$∀ H ∈ H, ∀ v ∈ H {\ displaystyle \ forall H \ in \ mathbf {H}, \ forall v \ in H}$ $\ forall H \ in {\ mathbf {H}}, \ forall v \ in H$ , ограничение $av: s (v) → A (H) {\ displaystyle a_ {v}: s (v) \ rightarrow A (H)}$ $a_ {v}: s (v) \ rightarrow A (H)$ of $a { \ displaystyle a}$ $a$ на $s (v) {\ displaystyle s (v)}$ $s (v)$ является взаимно однозначным соответствием, причем $s (v) {\ displaystyle s (v)}$ $s (v)$ набор узлов-преемников $v {\ displaystyle v}$ $v$ .

$I = {1,..., I} {\ displaystyle {\ mathcal {I}} = \ {1,..., I \}}$ ${\ mathcal {I }} = \ {1,..., I \}$ - конечный набор игроков, $0 {\ displaystyle 0}$ ${ \ displaystyle 0}$ является (называется специальным игроком) природой, и $(H i) i ∈ I ∪ {0} {\ displaystyle (\ mathbf {H} _ {i}) _ {i \ in {\ mathcal {I}} \ cup \ {0 \}}}$ ${\ displaystyle (\ mathbf {H} _ {i}) _ {i \ in {\ mathcal {I}} \ cup \ {0 \}}}$ - это раздел плеера с информационным набором $H {\ displaystyle \ mathbf {H}}$ $\ mathbf {H}$ . Пусть $ι (v) = ι (H) {\ displaystyle \ iota (v) = \ iota (H)}$ $\ iota (v) = \ iota (H)$ - один игрок, который делает ход в узле $v ∈ H. {\ Displaystyle v \ в H}$ $v \ in H$ .
$ρ = {ρ H: A (H) → [0, 1] | H ∈ H 0} {\ Displaystyle \ rho = \ {\ rho _ {H}: A (H) \ rightarrow [0,1] | H \ in \ mathbf {H} _ {0} \}}$ $\ rho = \ {\ rho _ {H}: A (H) \ rightarrow [0,1] | H \ in {\ mathbf {H}} _ {0} \ }$ - это семейство вероятностей действий природы, а
$u = (ui) i ∈ I: T → RI {\ displaystyle u = (u_ {i}) _ {i \ in {\ mathcal { I}}}: T \ rightarrow \ mathbb {R} ^ {\ mathcal {I}}}$ ${\ displaystyle u = (u_ {i}) _ {i \ in {\ mathcal {I}} }: T \ rightarrow \ mathbb {R} ^ {\ mathcal {I}}}$ - это функция профиля выплаты.

Бесконечное пространство действий

Возможно, у игрока есть бесконечное количество возможных действий на выбор в конкретном узле принятия решения. Устройство, используемое для представления этого, представляет собой дугу, соединяющую два ребра, выходящих из рассматриваемого узла решения. Если пространство действий представляет собой континуум между двумя числами, нижнее и верхнее ограничивающие числа помещаются внизу и вверху дуги соответственно, обычно с переменной, которая используется для выражения выигрышей. Бесконечное количество узлов решения, которые могут возникнуть, представлены одним узлом, помещенным в центр дуги. Аналогичное устройство используется для представления пространств действий, которые, хотя и не бесконечны, достаточно велики, чтобы их невозможно было представить с краем для каждого действия.

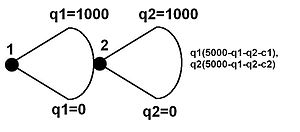Игра с бесконечными пространствами действий, представленными в развернутой форме

Дерево слева представляет такую игру, либо с бесконечными пространствами действий (любое действительное число от 0 до 5000), либо с очень большими пробелы действия (возможно, любое целое число от 0 до 5000). Это будет указано в другом месте. Здесь предполагается, что это первая и, для конкретности, предполагается, что она представляет две фирмы, участвующие в конкуренции Штакельберга. Выплаты фирмам представлены слева: $q 1 {\ displaystyle q_ {1}}$ $q_ {1}$ и $q 2 {\ displaystyle q_ {2}}$ <130.>в качестве стратегии, которую они принимают, и $c 1 {\ displaystyle c_ {1}}$ $c_ {1}$ и $c 2 {\ displaystyle c_ {2}}$ $c_ {2}$ в качестве некоторых констант ( здесь предельные издержки для каждой фирмы). Идеальное равновесие по Нэшу подигры этой игры можно найти, взяв первую частную производную каждой функции выигрыша по переменной стратегии ведомого (фирмы 2) ( $q 2 {\ displaystyle q_ {2}}$ $q_ {2}$ ) и нахождение его функции наилучшего ответа, $q 2 (q 1) = 5000 - q 1 - c 2 2 {\ displaystyle q_ {2} (q_ {1}) = {\ tfrac {5000-q_ {1} -c_ {2}} {2}}}$ ${\ displaystyle q_ {2} (q_ {1}) = {\ tfrac {5000- q_ {1} -c_ {2}} {2}}}$ . Тот же процесс может быть проделан для лидера, за исключением того, что при расчете своей прибыли он знает, что фирма 2 воспроизведет вышеуказанный ответ, и поэтому его можно заменить его задачей максимизации. Затем он может решить для $q 1 {\ displaystyle q_ {1}}$ $q_ {1}$ , взяв первую производную, что даст $q 1 ∗ = 5000 + c 2-2 c 1 2 {\ displaystyle q_ {1} ^ {*} = {\ tfrac {5000 + c_ {2} -2c_ {1}} {2}}}$ ${\ displaystyle q_ {1} ^ {*} = {\ tfrac {5000 + c_ {2} -2c_ {1}} {2}}}$ . Подавая это в функцию наилучшего отклика фирмы 2, $q 2 ∗ = 5000 + 2 c 1-3 c 2 4 {\ displaystyle q_ {2} ^ {*} = {\ tfrac {5000 + 2c_ {1} -3c_ {2}} {4}}}$ ${\ displaystyle q_ {2} ^ {*} = {\ tfrac {5000 + 2c_ {1} -3c_ {2}} {4 }}}$ и $(q 1 *, q 2 *) {\ displaystyle (q_ {1} ^ {*}, q_ {2} ^ {*}) }$ $(q_ {1} ^ {*}, q_ {2} ^ {*})$ - идеальное равновесие по Нэшу для подыгры.

См. Также

Ссылки

Харт, Серджиу (1992). «Игры в экстенсивной и стратегической формах». В Ауман, Роберт ; Харт, Серджиу (ред.). Справочник по теории игр с экономическими приложениями. 1 . Эльзевир. ISBN 978-0-444-88098-7. CS1 maint: ref = harv (ссылка )
Бинмор, Кеннет (2007). Игра по-настоящему: текст по теории игр. Oxford University Press, США. ISBN 978-0-19-530057-4. CS1 maint: ref = harv (ссылка )
Дрешер М. (1961). Математика стратегических игр: теория и приложения (Глава 4: Игры в обширной форме, стр. 74–78). Rand Corp. ISBN 0-486-64216-X
Фуденберг Д. и Тироль Дж. (1991) Теория игр (Ch3 Extensive form games, pp67–106). MIT press. ISBN 0-262-06141-4
Лейтон-Браун, Кевин; Шохам, Йоав (2008), Основы теории игр: краткое, междисциплинарное введение, Сан-Рафаэль, Калифорния: Morgan Claypool Publishers, ISBN 978-1-59829-593-1. Введение в математику на 88 страницах; см. Главы 4 и 5. Бесплатное онлайн во многих университетах.
Luce RD и Raiffa H. (1957). Игры и решения: введение и критический обзор. (Ch3: Extensive and Normal Forms, pp39–55). Wiley New York. ISBN 0-486-65943-7
Осборн М.Дж. и Рубинштейн А. 1994. Курс теории игр (Глава 6 «Обширная игра с точной информацией», стр. 89–115). Пресса MIT. ISBN 0-262-65040-1
Шохам, Йоав; Лейтон-Браун, Кевин (2009), Многоагентные системы: алгоритмические, теоретико-игровые и логические основы, Нью-Йорк: Cambridge University Press, ISBN 978-0-521-89943-7. Исчерпывающий справочник с вычислительной точки зрения; см. главу 5. Можно загрузить бесплатно онлайн.

Дополнительная литература

Хорст Херрлих (2006). Аксиома выбора. Springer. ISBN 978-3-540-30989-5., пункт 6.1, «Катастрофы в теории игр» и 7.2 «Измеримость (аксиома детерминированности)», обсуждает проблемы расширения конечного определение случая для бесконечного числа вариантов (или ходов)

Исторические статьи

Дж. Нойман (1928). "Zur Theorie der Gesellschaftsspiele". Mathematische Annalen. 100 : 295–320. doi : 10.1007 / BF01448847.
Гарольд Уильям Кун (2003). Лекции по теории игр. Издательство Принстонского университета. ISBN 978-0-691-02772-2.содержит лекции Куна в Принстоне с 1952 года (ранее официально не публиковались, но сейчас распространяются в виде фотокопий)