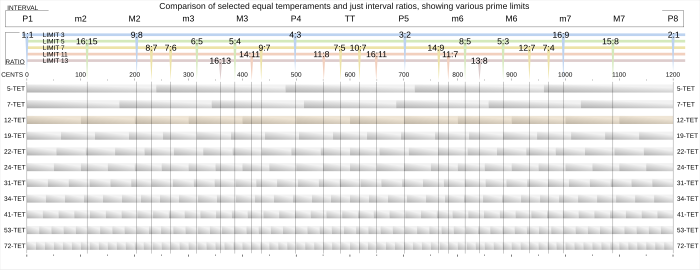
 Сравнение некоторых одинаковых темпераментов. График охватывает октаву по горизонтали (откройте изображение, чтобы просмотреть всю ширину), и каждый заштрихованный прямоугольник соответствует ширине одного шага шкалы. Отношения только интервал разделены в ряды их крайними пределами.
Сравнение некоторых одинаковых темпераментов. График охватывает октаву по горизонтали (откройте изображение, чтобы просмотреть всю ширину), и каждый заштрихованный прямоугольник соответствует ширине одного шага шкалы. Отношения только интервал разделены в ряды их крайними пределами.Равная темперация - это музыкальная темперация или система, что соответствует только интервалам на деление октавы (или другого интервала) на равные шаги. Это означает, что соотношение частот любая соседней пары нот одинаково, что дает одинаковый воспринимаемый размершага, поскольку высота воспринимается примерно как логарифм
В классической музыке и западной музыке в наиболее распространенной системе 18-го века была двенадцатонная равная темперация (также известная как 12 равных темпераментов, 12 - TET или 12-ET ; неофициально сокращенно двенадцатьных ), что делит октаву на 12 частей, все из равны в логарифмическом масштабе с производством, равным корню 12- йстепени из 2 (√2 ≈ 1,05946). Этот результирующий наименьший интервал, ⁄ 12 ширины октавы, называется полутоном или полушагом. В западных странах термин «равный темперамент» без оговорок обычно означает 12-TET.
В наше время 12-TET обычно настраивается относительно стандартного тона 440 Гц, называемого A440, что означает одну ноту, A настроен на 440 герц, все остальные известные как несколько полутонов, кроме него, либовыше, либо ниже в частот. Стандартный тон не всегда был 440 Гц. Она изменилась и в целом выросла за последние несколько сотен лет.
Другие равные темпераменты по-разному делят октаву. Например, некоторые музыкальные произведения были написаны на языках 19-TET и 31-TET, тогда как в арабской тональной системе используется 24-TET.
Вместо разделения октавы равный интервал может также разделить другой интервал, как, например, версия с равным темпомшкалы Болена - Пирса, которая разделяет только интервал октавы и пятую часть (соотношение 3: 1), называемую в этой системе «тритаве» или «псевдооктавой », на 13 равных частей.
Для систем, которые делят октаву поровну, но не используют приближения только интервалов, можно использовать термин равное деление октавы или EDO .
Неограниченные струнные ансамбли, которые могут регулировать настройку всех нот, кроме открытого струн, и вокальные группы, у нет ограничений механической настройки, иногда используют настройку гораздо ближе к , просто интонация по акустическим причинам. Другие инструменты, такие как некоторые духовые, клавишные и ладовые инструменты, часто имеют одинаковую темперацию, технические характеристики не позволяют точно настроить. Некоторые духовые инструменты, которые могут легко и быстро проверить свой тон, в первую очередь тромбоны, использоватьнастройку, аналогичную настройку струнных ансамблей и вокальных групп.
 Сравнение равных темпераментов между 10-TET и 60-TET на каждом основном интервале малых основных пределов (красный: 3/2, зеленый: 5/4, синий: 7/4, желтый: 11/8, голубой: 13 / 8). Каждый цветной график показывает, сколько ошибок происходит (в центах) в ближайшем приближении соответствующего точного интервала (черная линия в центре). Две черные кривые, окружающие график с обеих сторон, максимально возможную ошибку, а серыевнутри них указывают на ее половину.
Сравнение равных темпераментов между 10-TET и 60-TET на каждом основном интервале малых основных пределов (красный: 3/2, зеленый: 5/4, синий: 7/4, желтый: 11/8, голубой: 13 / 8). Каждый цветной график показывает, сколько ошибок происходит (в центах) в ближайшем приближении соответствующего точного интервала (черная линия в центре). Две черные кривые, окружающие график с обеих сторон, максимально возможную ошибку, а серыевнутри них указывают на ее половину. В равной степени При работе расстояния между двумя соседними ступенями шкалыравно равно равно равно интервалу. Воспринимаемая идентичность интервала зависит от его отношения, эта шкала с четными шагами представляет собой геометрическую последовательность умножений. (арифметическая последовательность интервалов не будет звучать равномерно и не позволит транспонировать к разным клавишам.) В частности, наименьший интервал в равномерно темперированной шкале - это соотношение:

![{\displaystyle r={\sqrt[{n}]{p}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b55fb394d767c50fb569ca27fd636072c72fbd7c)
где отношение r делит отношение p (обычно октава , которая составляет 2: 1) на n равных частей. (См. Двенадцатитоновая равная температура ниже.)
Шкалы часто измеряются в центах, которые делят октаву на 1200 равных интервалов (каждый называется центом). Эта логарифмическая шкала упрощает сравнение различных систем, широко используется в этзыкологии. Базовый шаг в центах для любой одинаковойтемперации можно найти, взяв ширину p выше в центах (обычно октаву, который составляет 1200 центов в ширину), называемый ниже w, и разделив ее на n частей:

В музыкальном материале, принадлежащем одинаковому темпераменту, часто дается целочисленное обозначение, что означает, что одно целое число используется для каждого шага. Это упрощает обобщение обсуждения материала высоты тона в темперации точно так же, как логарифм умножения сводит его к сложению. Кроме того, применяя модульную арифметику , где модуль представляет собой делений октавы (обычно 12), эти целые числа можно уменьшить до классов высоты тона, что устраняет различие (или признает сходство) между одноименными нотами, например c равно 0 независимо от октавного регистратора. В стандарте кодирования MIDI используются целочисленные обозначения нот.
12-тональная равная темперация, которая делит октаву на двенадцать равных интервалов, является наиболее распространенной музыкальной системой, используемой сегодня, особенно в западной музыке.
Двумя фигурами, которые часто приписывают достижение точных расчетов одинакового темперамента, являются Чжу Зайю (также латинизируется как Чу-Цайюй. Китайский: 朱 載 堉) в 1584 году и Симон Стевин в 1585 году. Согласно Фрицу А. Каттнеру,критику теории, известно, что «Чу-Цайю представил очень точный, простой и гениальный метод арифметических вычислений равного темперамента. моно-аккорды в 1584 году »и что« Саймон Стевин математическое определение равной темперации плюс несколько наименьших вычислений соответствующих числовых значений в 1585 или позже году ». Развитие происходило независимо.
Кеннет Робинсон приписывает изобретение равного темперамента Чжу Зайюй и приводит текстовые цитаты в доказательства. Цитируется ЧжуЗайюй, который сказал, что в тексте, датируемом 1584 годом: «Я основал новую систему. Я определяю одну ступню как число, из которого должны быть извлечены другие, и используя пропорции, я извлекаю их. Катнер не соглашается и отмечает, что его утверждение «не может считаться правильным без конкретных оговорок». Каттнер предполагает, что ни Чжу Зайюй, ни Саймон Стевин не достижим одинакового темперамента и что ни один из них
 Смоловые трубы равного темперамента Чжу Зайюй
Смоловые трубы равного темперамента Чжу Зайюй Вто время как Китай ранее придумал аппроксимации для 12 -TET, Чжу Зайю был первым человеком, который математически решил двенадцатитонную равную темперамент, которую он описал в его Fusion of Music and Calendar 律 暦 融通 в 1580 году и Полный сборник музыки и высоты тона (Yuelü quan shu 樂律 全書) в 1584 году, расширенный отчет также дан Джозефом Нидхэмом. получил свой результат математически, разделив длину трубы и трубы на √2 ≈ 1,059463, длина трубы на √2, так что после двенадцати делений ( октавы) длина была разделена на коэффициент 2.
Чжу Зайюй создал не сколько инструментов, настроенных на его систему, в том числе бамбуковые трубки.
Некоторые из первых европейцев, выступавших за равный темперамент, были лютнистами Винченцо Галилей, и Франческо Спиначино, каждый из которых писал на нем музыку.
Саймон Стевин был первым, кто разработал 12-TET на основе корня двенадцатой степени двойной степени, который онописан в Van De Spiegheling der singconst (около 1605 г.), опубликованном в посмертно почти трианной века спустя в 1884 году.
В течение всего столетия в Европе использовались одинаковые системы, включая 12 различных темпераментов, а также означает один темперамент и темперамент, каждый из которых можно рассматривать как приближение к первому. Щипковые музыканты (лютнисты и гитаристы) обычно предпочитают равный темперамент, в то время как другие были более разобщенными.В конце концов, победила двенадцатитоновая ровная темперация. Это позволяет использовать новые стили симметричной тональности и политональности, атональной музыки, например, написанной с помощью техники двенадцати тонов или сериализма и Джаз (по крайней мере, его фортепианная составляющая) развивался и процветал.
 Один октава из 12 тет на монохорде
Один октава из 12 тет на монохорде В двенадцатитонной равной темперации, которая делит октаву на 12 равныхчастей, ширину полутона, то есть соотношение частот интервала между двумя соседними нотами - это корень двенадцатой степени из двух :
![{\displaystyle {\sqrt[{12}]{2}}=2^{\frac {1}{12}}\approx 1.059463}](https://wikimedia.org/api/rest_v1/media/math/render/svg/232c2beab28b1c46c328080d982595d9ef196e08)
Это эквивалентно:

Этот интервал делится на 100 центов.
Чтобы найтичастоту, P n в примечании к 12-TET можно использовать следующее определение:
![{\displaystyle P_{n}=P_{a}\left({\sqrt[{12}]{2}}\right)^{( n-a)}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3381e111c79f7e16a073bbe05c6cabeaba2ff79a)
В формуле P n относится к высоте тона или частоты (обычно в герцах ), вы пытаетесь найти. Р а относится к частоте опорного поля. п и относится к номерам, присвоенный желаемая высота и опорное поле, соответственно. Эти два числа взяты из спискапоследовательных целых чисел, последовательным полутонам. Например, A 4 (эталонная высота тона) - это 49-я клавиша от левого края фортепиано (настроенная на 440 Гц ), а C 4(средняя C ) и F # 4 - это 40-я и 46-я клавиши соответственно. Эти числа можно использовать для частоты частоты C 4 и F # 4:
![{\displaystyle P_{40}=440\left({\sqrt[{12}]{2}}\right)^{(40-49)}\approx 261.626\ \mathrm {Hz} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/f16dc9af5bbe778786f73eca304c80c72584cd70)
![{\displaystyle P_{46}=440\left({\sqrt[{12}]{2}}\right)^{(46-49)}\approx 369.994\ \mathrm {Hz} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c7144b8e3148077acb97a47d384a62a1f2a5445)
Интервалы в 12-TET очень близки к некоторым интервалам в только интонации. Пятые и четвертые почти неотличимо близки к просто интервалам, а третьи и шестые находятся дальше.
В следующей таблице размеры различных интервалов сравниваются с их аналогами с равным темпом,указанными в виде отношений, а также центов.
| Имя | Точное в 12 -TET | Десятичное значение в 12-TET | Центах | Интервал только интонации | Центы только в интонации | Разница |
|---|---|---|---|---|---|---|
| Унисон (C ) | 2 = 1 | 1 | 0 | ⁄1= 1 | 0 | 0 |
| Младшая секунда (C♯ /D♭ ) | 2 = √2 | 1.059463 | 100 | ⁄15= 1.06666… | 111,73 | −11,73 |
| Большая секунда (D ) | 2 = √2 | 1,122462 | 200 | ⁄8= 1,125 | 203, 91 | −3,91 |
| Незначительная треть (D♯ /E♭ ) | 2 = √2 | 1,189207 | 300 | ⁄5= 1,2 | 315,64 | −15,64 |
| Большая третья (E ) | 2 = √2 | 1,259921 | 400 | ⁄4= 1,25 | 386,31 | +13,69 |
| Идеальная четвертая (F ) | 2 = √32 | 1,334840 | 500 | ⁄3= 1,33333… | 498,04 | +1,96 |
| Тритон (F♯ /G♭ ) | 2 = √2 | 1,414214 | 600 | ⁄5= 1,4. ⁄7= 1,4 2857... | 582,51. 617,49 | +17,49. −17,49 |
| Идеальная пятая ( G ) | 2 = √128 | 1,498307 | 700 | ⁄2= 1,5 | 701,96 | -1,96 |
| Незначительный шестой ( G♯ /A♭ ) | 2 = √4 | 1,587401 | 800 | ⁄5= 1,6 | 813,69 | −13, 69 |
| Старший шестой (A ) | 2 = √8 | 1,681793 | 900 | ⁄3= 1,66666… | 884,36 | +15, 64 |
| Младший седьмой (A♯ /B♭ ) | 2 = √32 | 1,781797 | 1000 | ⁄9= 1,77777… | 996, 09 | +3,91 |
| Большая седьмой (B ) | 2 = √2048 | 1.887749 | 1100 | ⁄8= 1,875 | 1088, 27 | +11,73 |
| Октава (C ) | 2 = 2 | 2 | 1200 | ⁄1= 2 | 1200,00 | 0 |
Скрипки, альты и виолончели настроены в идеальных квинтах (G - D - A - E для скрипок и C - G - D - A для альтов и виолончелей), что предполагает их полутоновое соотношение немного выше, чем в обычном двенадцатитонном ровном темпераменте. Идеальная квинта находится в механизме 3: 2 со своим основным тоном, и этот интервалпокрывается 7 ступенями, каждый тон находится в введении √ ⁄ 2 к следующему (100,28 цента), что обеспечивает идеальную квинту с помощью 3 : 2, но слегка расширенную октаву с помощью ≈ 517: 258 или ≈ 2.00388: 1, а не обычное соотношение 2: 1, потому что двенадцать идеальных пятых не равны семи октавам. Однако во время реальной игры скрипач выбирает высоту звука на слух, и только четыре непрерывных высоты звука гарантированно демонстрируют это соотношение 3: 2.
пяти- и семитональная одинаковая темперация (5-TET ![]() Play и 7-TET
Play и 7-TET ![]() Play ) с шагом 240
Play ) с шагом 240 ![]() Играть и 171
Играть и 171 ![]() Играть центов соответственно, довольно распространены.
Играть центов соответственно, довольно распространены.
5-TET и 7-TET обозначают конечные точки допустимого диапазона настройки синтонической темперации, как показано на рис. 1.
индонезийские гамеланы настроены на 5-TET согласно Kunst (1949), носогласно Hood (1966)) и Макфи (1966) их настройка широко рассматривается, и согласно Тензеру (2000), они содержат растянутые октавы. Сейчас общепризнано, что из двух основных систем настройки в музыке гамелана, slendro и pelog, только slendro в некоторой степени напоминает пятитональный равный темперамент, в то время как pelog весьма неравен; однако Surjodiningrat et al. (1972) проанализировал пелог как семизначную подмножестводевятитональной равной темперации (133-центовые шаги ![]() Play ).
Play ).
A Тайский ксилофон, измеренный Мортоном (1974), «выборировался только плюс-минус 5 центов» от 7-TET. Согласно Мудортону, «тайские инструменты с фиксированной высотой звука настроены на эквидистантную систему из семи высот на октаву...», как и в традиционной музыке, все высоты звуковой системы не используются в одном режиме (называемом «масштаб»); в тайской системе пять из семииспользуются в основных режимах высот в любом режиме, таким образом, установлены неэквидистантные интервалов для режима. ![]() Играть
Играть
Играть
Культура, измеренная Бойлсом (1969), характеризовалась 175-процентным семитональным равным темпераментом, который слегка растягивает октаву, как в инструментальной музыке гамелана.
В китайской музыке традиционно используется 7-TET.
 Системы обозначений Исли Блэквуда для 16 одинаковыхтемпераментов: интервалы обозначены так же, как и те, к которым приближаются. эквивалентов.
Системы обозначений Исли Блэквуда для 16 одинаковыхтемпераментов: интервалы обозначены так же, как и те, к которым приближаются. эквивалентов.  Сравнение одинаковых темпераментов от 9 до 25 (по Sethares (2005), стр.58).
Сравнение одинаковых темпераментов от 9 до 25 (по Sethares (2005), стр.58). 24 EDO, четверть тональная шкала (или 24-TET) была популярной микротональной настройкой в 20-м веке, вероятно, потому что она представляет собой удобную точку доступа для композиторов, использующих стандартную высоту звука и нотацию Western 12 EDO, которые также интересовалисьмикротональностью. звука 12 EDO, и так же новые высоты на полпути между каждой двойной парой из 12 полей EDO, они могут использовать дополнительные цвета без какой-либо тактики, доступной в 12-тональной гармонии. Тот факт, что позволил 24 кратно 12, также позволил легко достичь 24 EDO инструментально, используя два 12 EDO, специально настроенных на четверть тона, например, два фортепиано, что также позволяет исполнителю играть на другом фортепиано каждой рукой), чтобы прочитать знакомые12-тональные обозначения. Различные композиторы, в том числе Чарльз Айвз, экспериментировали с музыкой для четвертных фортепиано. 24 ОКБ очень хорошо аппроксимирует 11-ю гармонику, в отличие от 12 ОКБ.
19 ОКБ знаменито и некоторые инструменты настроены в 19 ОКБ. Он немного более плоскую идеальную пятую часть (694 цента), но ее основная шестая часть находится менее чем в одном центе от основной шестой части только интонации (884 цента). Его минорная третье также меньше цента отинтонации. Его идеальный четвертый (503 цента) всего на 5 центов резче, чем просто интонация, и на 3 цента лучше, чем у 12-тет.
23 EDO - самый крупный EDO, который может приблизить 3-ю, 5-ю, 7-ю и 11-гармон юики (3: 2, 5: 4, 7: 4, 11: 8) в пределах 20 центов, что делает его привлекательное. микротоналистам, ищим необычную территорию микротональной гармонии.
27 EDO - наименьший EDO, который однозначно представляет все интервалы, составляющие первые восемь гармоник. Онсмягчает семеричную запятую, но не синтоническую запятую..
29 ОКБ - наименьшее количество равных делений октавы, которое дает лучшую идеальную квинту, чем 12 ОКБ. Его основная третья примерно такая же неточная, как 12-TET; однако он настроен ровно на 14 центов, а не на 14 центов. Он также настраивает 7-ю, 11-ю и 13-ю гармоники примерно на одинаковую характеристику. Это означает, что такие интервалы, как 7: 5, 11: 7, 13:11 и т. Д., Очень хорошо сочетаются в 29-TET.
31ОКБ защищали Христиан Гюйгенс и Адриан Фоккер. 31 EDO имеет немного менее точную пятую часть, чем 12 EDO, но обеспечивает почти только мажорные трети и обеспечивает приличное совпадение для гармоник, по крайней мере, до 13, из которых седьмая гармоника особенно точна.
34 EDO дает несколько меньших суммарных комбинированных ошибок приближения к 5-предельным отношениям 3: 2, 5: 4, 6: 5 и их инверсии, чем 31 EDO, хотя приближение 5: 4 хуже. 34 EDO не приближаеткоэффициенты, включающие простое число 7. Он содержит тритон с концентрацией 600 центов, так как это EDO с четным номером.
41 EDO - это второе наименьшее количество равных делений, которое дает лучшую идеальную пятую часть, чем 12 EDO. Его первое третье точнее, чем 12 ОКБ и 29 ОКБ, что составляет около 6 центов. Это не означает один, поэтому он различает 10: 9 и 9: 8, в отличие от 31edo. Он более точен в 13-м лимите, чем 31edo.
46 EDO обеспечивает слегка резкую мажорную третьюи улучшает пятую часть, придавая трезвучиям характерный яркий звук. Гармоники до 11 аппроксимируются с точностью до 5 центов, при этом 10: 9 и 9: 5 составляют одну пятую цента от чистого. Это временная система с одинарным показателем, она различает 10: 9 и 9: 8.
53 EDO лучше приближает к просто созвучия, чем 12, 19 или 31 EDO, но использовалось только время от времени. Его очень хорошие идеальные квинты делают его взаимозаменяемым расширенным пифагорейским строем, но он также учитывает раскольнический темперамент и иногда используется в турецкой музыке теория. Однако это не соответствует требованиям темпераментов среднего человека, которые позволяют легко дотянуться до хорошей трети через цикл квинт. В 53 EDO самые согласные трети могли быть достигнуты вместо этого с помощью пифагорейской уменьшенной (C-F ♭), поскольку это пример раскольнического темперамента, как и 41 EDO.
72 EDO хорошо аппроксимирует многиетолько интонационные интервалы, даже в пределах 7 и 11, таких как 7: 4, 9: 7, 11: 5, 11: 6 и 11: 7. 72 EDO преподавал, писал и выполнял на практике Джо Манери и его ученики (чьи атональные наклонности обычно избегают любых ссылок на просто интонации вообще). Его можно рассматривать как расширение 12 EDO, потому что 72 кратно 12. 72 EDO имеет наименьший интервал, который в шесть раз меньше, чем наименьший интервал 12 EDO, и, следовательно, содержит шесть копий 12 EDO,начинающихся с разных шагов. Он также содержит три экземпляра 24 ОКБ и две копии 36 ОКБ, которые сами по себе кратны 12 ОКБ. 72 EDO также подвергся критике за его избыточность за счет плохих приближений, 2000 EDO, несмотря на то, что они не требовались для каких-либо нижних пределов только интонации (например, 5-предел).
96 EDO аппимирует все интервалы с точностью до 6,25 цента, что уничтожимо. Будучи восьмикратным числом, кратным 12, его можно полностью использовать как обычный 12 EDO.Его отстаивали несколько композиторов, особенно Хулиан Каррильо с 1924 по 1940-е гг.
Другие равные части октавы, которые находили время от времени, включают 15 EDO, 17 EDO, 19 EDO и 22 EDO.
2, 5, 12, 41, 53, 306, 665 и 15601 являются знаменателями первые подходящие дроби из журнала 2 (3), поэтому 2, 5, 12, 41, 53, 306, 665 и 15601 двенадцатая (и пятая), равны целому числу октав - лучшее приближение 2, 5, 12, 41,53, 306, 665 и 15601 всего двенадцатых / пятых, чем для любых одинаковых температур с меньшим тонов.
1, 2, 3, 5, 7, 12, 29, 41, 53, 200... (последовательность A060528 в OEIS ) - это последовательность делений октавы, которые обеспечивают все лучше и лучше приближения идеальной пятой части. Связанные содержат деления, аппроксимирующие другие интервалы.
Это приложение: [1] вычисляет частоты, приблизительные центы и MIDI изгибвысоты тона значения для любых системного равного деления октавы. Обратите внимание, что «скругленный» и «напольный» производят одинаковое значение изменения высоты звука MIDI.
Равномерная версия шкалы Болена - Пирса состоит из соотношения 3: 1, 1902 цента, условно идеальная квинта плюс октава (то есть есть идеальная двенадцатая), называемая в этой теории тритавой (![]() игрой ), и разделена натринадцать равных частей. Это обеспечивает очень близкое соответствие правильно настроенным отношениям, состоящим только из нечетных чисел. Каждый шаг стоит 146,3 цента (
игрой ), и разделена натринадцать равных частей. Это обеспечивает очень близкое соответствие правильно настроенным отношениям, состоящим только из нечетных чисел. Каждый шаг стоит 146,3 цента (![]() игра ), или √3.
игра ), или √3.
Венди Карлос создала три необычных одинаковых темперамента после тщательного изучения свойств темпераментов, имеющих размер шага от 30 до 120 центов. Они назывались альфа, бета и гамма. Их можно рассматривать как равные части идеальной пятой части. Каждый изних дает очень хорошее приближение нескольких интервалов. Их размер шага:
Альфа и бета могут быть услышаны в заглавном треке ее альбома 1986 года Beauty in the Beast.
В этом разделе полутон и весь тон не имеют обычных значений 12-EDO, поскольку в нем обсуждается, как онидолжны быть смягчены разными способами, чем их простые версии, для создания желаемых отношений. Пусть количество шагов в полутоне будет s, а количество шагов в тоне будет t.
Существует ровно одно семейство одинаковых темпераментов, которое фиксирует полутон для любой правильной доли целого тона, сохраняя при этом ноты в правильном порядке (что означает, например, что C, D, E, F) и F♯ находятся в порядке возрастания, если они сохраняют свои обычные отношения с C). То естьфиксация q как правильное дроби одного отношения qt = s также определяет уникальное семейство из равного темперамента и его кратных, которые соответствуют этому отношению.
, где k - целое число, 12k-EDO устанавливает q = ⁄ 2, а 19k-EDO устанавливает q = ⁄ 3. Наименьшие кратные в этих семействах (например, 12 и 19 выше) дополнительным своим не иметь не за пределами круга пятых. (В целом это неверно; в 24-EDO полу-диезы и полу-диезы не находятся в кругеквинт, начиная с C.) Крайний случай - 5k-EDO, где q = 0 и полутон становится унисон и 7k-EDO, где q = 1, а полутон и тон - это один и тот же интервал.
Как только человек знает, сколько шагов в полутоне и тоне в этой одинаковой темперации, он может найти количество шагов в октаве. Равная темперация, удовлетворяющая вышеуказанным свойствам (включая отсутствие нот вне круга квинт), делит октаву на шаги 7t - 2s, идеальную квинту - на шаги 4t - s. Если есть вне круга квинт, то это количествопредставляет собой количество, необходимое для создания всех нот (например, два в 24-EDO, шесть в 72-EDO). (Для этого нужно взять малый полутон: 19-EDO имеет два полутона, один из которых ⁄ 3 тон, а другой ⁄ 3.)
Самым маленьким из этих семейств является 12k-EDO, и в частности, 12-EDO - это наименьший равный темперамент, обладающий указанными выше свойствами. Кроме того, он также делает полутон ровно половиной целого тона. Это некоторые из причин, по которому 12-EDOстал наиболее часто используемым равным темпераментом. (Другая причина состоит в том, что 12-EDO - это наименьший равный темперамент, близкий к 5-предельной гармонии, следующий наименьший - 19-EDO.)
Каждый выбор дроби q для отношений приводит к ровно одному равному семейству темпераментов, но обратное неверно: 47-EDO имеет два разных полутона, один из которых ⁄ 7 тон, другой ⁄ 9, которые не являются дополнениями друг друга как в 19-ОКБ ( ⁄ 3 и ⁄ 3). Выбор каждого полутона дает различный выбор идеальной квинты.
 Рис. 1: обычные диатонические настройки континуум, который включает в себя множество настроек «равной темперации» (Milne 2007).
Рис. 1: обычные диатонические настройки континуум, который включает в себя множество настроек «равной темперации» (Milne 2007). Диатоническая настройка в двенадцать равных может быть обобщена на любую обычную диатоническую настройку, делящую октаву как последовательность шагов TTSTTTS (или ее вращение) со всеми T и всеми S одногоразмера, а S меньше, чем Т. В двенадцати равных S является полутоном и составляет половину размера тона T. Когда S уменьшаются до нуля, результатом становится TTTTT или пятитональная равная темперация.По мере увеличения полутонов в конечном итоге все шаги становятся одинаковыми. размер, и в результате получается семь тонов равного темперамента. Эти две конечные точки не входят в обычные диатонические настройки.
Ноты в обычном диатоническом строе соединены вместе циклом из семитемперированных квинт. Двенадцатитоновая система аналогичным образом обобщает последовательность CDCDDCDCDCDD (или ее вращение) хроматических и диатонических полутонов, соединенных вместе в цикле из двенадцати пятых. В этом случае семь равных получается в пределе, поскольку размер C стремится к нулю, и пять равных - это предел, поскольку D стремится к нулю, в то время как двенадцать равных, конечно же, в случае C = D.
Некоторые из промежуточные размеры тонов и полутонов также могут бытьсозданы в системах одинаковой темперации. Например, если диатонический полутон вдвое превышает размер хроматического полутона, то есть D = 2 * C, результат будет равен девятнадцати, с одним шагом для хроматического полутона, двумя шагами для диатонического полутона и тремя шагами для тона и общим числом. шагов 5 * T + 2 * S = 15 + 4 = 19 шагов. Получающаяся в результате двенадцатитоновая система близко приближается к исторически важной 1/3 запятой, означающей один.
Если хроматическийполутон составляет две трети диатонического полутона, то есть C = (2/3) * D, результат равен тридцать одному, с двумя шагами для хроматического полутона, тремя шагами для диатонического полутона и пять шагов для тона, где 5 * T + 2 * S = 25 + 6 = 31 шаг. Получающаяся в результате двенадцатитоновая система близко приближается к исторически важной 1/4 запятой, означающей один.
| coauthors =()