Электронная зонная структура

Описывает диапазон энергий, которые может иметь электрон в твердом теле, и диапазоны энергий, которых он может не иметь

В физике твердого тела электронная зонная структура (или просто зонная структура ) твердого тела описывает диапазон энергетические уровни, которые электроны могут иметь внутри, а также диапазоны энергии, которых они могут не иметь (называемые запрещенными зонами или запрещенными зонами).

Теория зон выводит эти зоны и запрещенные зоны, исследуя разрешенные квантово-механические волновые функции для электрона в большой периодической решетке атомов или молекул. Теория полос успешно использовалась для объяснения многих физических свойств твердых тел, таких как удельное электрическое сопротивление и оптическое поглощение, и составляет основу понимания всех твердотельных устройств. (транзисторы, солнечные элементы и т. Д.).

• 1 Почему возникают полосы и запрещенные зоны
• 2 Основные концепции
  • 2.1 Допущения и ограничения теории зонной структуры
  • 2.2 Кристаллическая симметрия и волновые векторы
    • 2.2.1 Асимметрия: зонные структуры в некристаллические твердые тела
  • 2.3 Плотность состояний
  • 2.4 Заполнение зон
    • 2.4.1 Названия зон вблизи уровня Ферми (зона проводимости, валентная зона)
• 3 Теория в кристаллах
  • 3.1 Почти приближение свободных электронов
  • 3.2 Модель сильной связи
  • 3.3 Модель KKR
  • 3.4 Теория функционала плотности
  • 3.5 Методы функций Грина и приближение ab initio GW
  • 3.6 Динамическая теория среднего поля
  • 3.7 Другое
• 4 Диаграммы полос
• 5 См. Также
• 6 Ссылки
• 7 Библиография
• 8 Дополнительная литература
• 9 Внешние ссылки

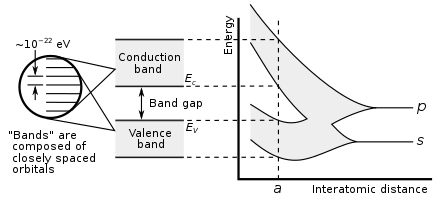Показаны электронные Зонная структура возникает на гипотетическом примере большого количества атомов углерода, соединенных вместе, чтобы сформировать кристалл алмаза. График (справа) показывает уровни энергии как функцию расстояния между атомами. Когда атомы находятся далеко друг от друга (правая часть графика), каждый атом имеет валентные атомные орбитали p и s, которые имеют одинаковую энергию. Однако, когда атомы сближаются, их орбитали начинают перекрываться. Согласно принципу исключения Паули каждая атомная орбиталь делится на N молекулярных орбиталей, каждая с разной энергией, где N - количество атомов в кристалле. Поскольку N такое большое число, соседние орбитали очень близки друг к другу по энергии, поэтому орбитали можно рассматривать как непрерывную энергетическую полосу. а - расстояние между атомами в реальном кристалле алмаза. На этом расстоянии орбитали образуют две зоны, называемые валентной зоной и зоной проводимости, с шириной запрещенной зоны 5,5 эВ между ними. Воспроизвести медиа Анимация образования зон и того, как электроны заполняют их в металле и изоляторе

Электроны одиночного изолированного атома занимают атомные орбитали, каждая из которых имеет дискретный энергетический уровень. Когда два или более атома соединяются вместе, чтобы сформировать молекулу, их атомные орбитали перекрываются. Принцип исключения Паули гласит, что никакие два электрона не могут иметь одинаковые квантовые числа в молекуле. Таким образом, если два идентичных атома объединяются, чтобы сформировать двухатомную молекулу, каждая атомная орбиталь разделяется на две молекулярные орбитали с разной энергией, позволяя электронам на прежних атомных орбиталях занять новую орбитальную структуру. без той же энергии.

Подобным образом, если большое количество N идентичных атомов объединяются, чтобы сформировать твердое тело, такое как кристаллическая решетка, атомные орбитали перекрываются. Поскольку принцип исключения Паули гласит, что никакие два электрона в твердом теле не имеют одинаковых квантовых чисел, каждая атомная орбиталь расщепляется на N дискретных молекулярных орбиталей, каждая с разной энергией. Поскольку количество атомов в макроскопическом куске твердого тела очень велико (N ~ 10), количество орбиталей очень велико, и, следовательно, они очень близко разнесены по энергии (порядка 10 эВ). Энергия соседних уровней настолько близка друг к другу, что их можно рассматривать как континуум, энергетическую полосу.

Это образование полос в основном характерно для самых удаленных электронов (валентных электронов ) в атоме, которые участвуют в химической связи и электропроводности. Внутренние электронные орбитали не перекрываются в значительной степени, поэтому их полосы очень узкие.

Запрещенные зоны - это, по существу, оставшиеся диапазоны энергии, не покрытые какой-либо зоной, в результате конечной ширины энергетических зон. Полосы имеют разную ширину, причем ширина зависит от степени перекрытия в атомных орбиталях, из которых они возникают. Две соседние полосы могут быть недостаточно широкими, чтобы полностью покрыть диапазон энергии. Например, полосы, связанные с остовными орбиталями (такими как 1s электронов ), чрезвычайно узкие из-за небольшого перекрытия между соседними атомами. В результате между основными полосами обычно образуются большие запрещенные зоны. Более высокие полосы включают в себя сравнительно большие орбитали с большим перекрытием, которые постепенно становятся шире при более высоких энергиях, так что запрещенные зоны отсутствуют при более высоких энергиях.

Допущения и ограничения теории зонной структуры

Зонная теория - это только приближение к квантовому состоянию твердого тела, которое применяется к твердым телам, состоящим из множества идентичных атомов или молекулы, связанные вместе. Это предположения, необходимые для того, чтобы теория полос была верной:

• Система бесконечного размера: для того, чтобы полосы были непрерывными, кусок материала должен состоять из большого количества атомов. Поскольку макроскопический кусок материала содержит порядка 10 атомов, это не является серьезным ограничением; Теория полос применяется даже к микроскопическим транзисторам в интегральных схемах. С изменениями концепция зонной структуры также может быть расширена на системы, которые являются «большими» только в некоторых измерениях, например, двумерные электронные системы.
• Однородная система: ленточная структура является внутренним свойством материала, что предполагает, что материал однороден. На практике это означает, что химический состав материала должен быть однородным по всей детали.
• Невзаимодействие: зонная структура описывает «одноэлектронные состояния». Существование этих состояний предполагает, что электроны движутся в статическом потенциале без динамического взаимодействия с колебаниями решетки, другими электронами, фотонами и т. Д.

Приведенные выше предположения нарушаются в В ряде важных практических ситуаций, а использование зонной структуры требует тщательного контроля за ограничениями зонной теории:

• Неоднородности и границы раздела: вблизи поверхностей, переходов и других неоднородностей нарушается объемная зонная структура. Имеются не только локальные мелкомасштабные сбои (например, поверхностные состояния или легирующие состояния внутри запрещенной зоны), но также и локальные зарядовые дисбалансы. Эти зарядовые дисбалансы имеют электростатические эффекты, которые глубоко распространяются на полупроводники, изоляторы и вакуум (см. легирование, изгиб зон ).
• В том же направлении большинство электронных эффектов (емкость, электрическая проводимость, экранирование электрического поля ) связаны с физикой прохождения электронов через поверхности и / или вблизи границ раздела. Полное описание этих эффектов в изображении зонной структуры требует по крайней мере, элементарная модель электрон-электронного взаимодействия (см. пространственный заряд, искривление зоны ).
• Малые системы: для систем, которые малы по всем измерениям (например, небольшая молекула или квантовая точка ), непрерывная зонная структура отсутствует. Переход между малыми и большими измерениями - это область мезоскопической физики.
• Сильно коррелированные материалы (например, Изоляторы Мотта ) просто нельзя понять в терминах одноэлектронных состояний. Электронная зонная структура Эти материалы плохо определены (или, по крайней мере, определены не однозначно) и могут не предоставить полезной информации об их физическом состоянии.

Кристаллическая симметрия и волновые векторы

Рис. 1. Зона Бриллюэна гранецентрированная кубическая решетка, показывающая метки для особых точек симметрии. 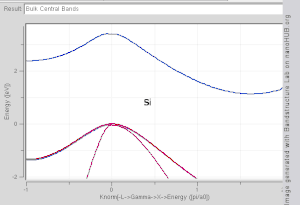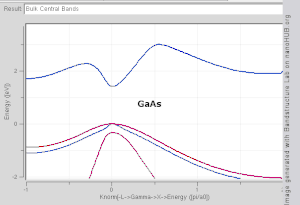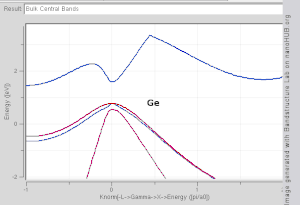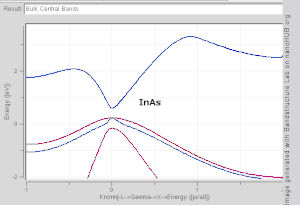Рис. 2. График зонной структуры для Si, Ge, GaAs и InAs, созданный с помощью модели сильной связи. Обратите внимание, что Si и Ge являются материалами с непрямой запрещенной зоной, в то время как GaAs и InAs - прямыми.

При расчетах зонной структуры используется периодическая природа кристаллической решетки с использованием ее симметрии. Одноэлектронное уравнение Шредингера решается для электрона в периодическом по решетке потенциале, давая электроны Блоха в качестве решений:

$\psi \; nk\; (r)\; =\; eik\; \cdot \; runk\; (r)\; \{\backslash \; displaystyle\; \backslash \; psi\; \_\; \{n\; \backslash \; mathbf\; \{k\}\}\; (\backslash \; mathbf\; \{r\})\; =\; e\; ^\; \{я\; \backslash \; mathbf\; \{k\}\; \backslash \; cdot\; \backslash \; mathbf\; \{r\}\}\; u\_\; \{n\; \backslash \; mathbf\; \{k\}\}\; (\; \backslash \; mathbf\; \{r\})\}$,

где k называется волновым вектором. Для каждого значения k существует несколько решений уравнения Шредингера, обозначенных n, индексом полосы, который просто нумерует энергетические полосы. Каждый из этих энергетических уровней плавно эволюционирует с изменением k, образуя плавную полосу состояний. Для каждой полосы мы можем определить функцию E n(k), которая является дисперсионным соотношением для электронов в этой полосе.

Волновой вектор принимает любое значение внутри зоны Бриллюэна, которая представляет собой многогранник в пространстве волнового вектора (обратная решетка ), связанном с решеткой кристалла. Волновые векторы за пределами зоны Бриллюэна просто соответствуют состояниям, которые физически идентичны этим состояниям в зоне Бриллюэна. Специальным точкам / линиям высокой симметрии в зоне Бриллюэна присваиваются такие метки, как Γ, Δ, Λ, Σ (см. Рис. 1).

Трудно визуализировать форму полосы как функцию волнового вектора, так как для этого потребуется график в четырехмерном пространстве, E относительно k x, k y, k z. В научной литературе часто можно встретить графики ленточной структуры, которые показывают значения E n(k) для значений k вдоль прямых линий, соединяющих точки симметрии, часто обозначаемых Δ, Λ, Σ или [100], [111] и [110] соответственно. Другой метод визуализации полосовой структуры состоит в построении изоповерхности постоянной энергии в пространстве волнового вектора, показывающей все состояния с энергией, равной определенному значению. Изоповерхность состояний с энергией, равной уровню Ферми, известна как поверхность Ферми.

Энергетическая запрещенная зона может быть классифицирована с использованием волновых векторов состояний, окружающих запрещенную зону:

• Прямая запрещенная зона : состояние с наименьшей энергией над запрещенной зоной имеет то же k, что и состояние с наибольшей энергией под запрещенной зоной.
• Непрямая запрещенная зона : ближайшие состояния выше и ниже запрещенной зоны не имеют одинакового значения k .

Асимметрия: полосовые структуры в некристаллических твердых телах

Хотя электронные полосные структуры обычно связаны с кристаллическими материалы, квазикристаллические и аморфные твердые вещества также могут иметь запрещенные зоны. Их несколько труднее изучать теоретически, поскольку они лишены простой симметрии кристалла, и обычно невозможно определить точное соотношение дисперсии. В результате практически все существующие теоретические работы по электронной зонной структуре твердых тел сосредоточены на кристаллических материалах.

Плотность состояний

Функция плотности состояний g (E) определяется как количество электронных состояний в единице объема, на единицу энергии для энергий электронов, близких к E.

Функция плотности состояний важна для расчетов эффектов на основе зонной теории. В Золотом правиле Ферми, вычислении скорости оптического поглощения, оно предоставляет как количество возбудимых электронов, так и количество конечных состояний электрона. Он появляется в расчетах электропроводности, где он обеспечивает количество подвижных состояний, и при вычислении скорости рассеяния электронов, где он дает количество конечных состояний после рассеяния.

Для энергий внутри зоны промежуток, g (E) = 0.

Заполнение полос

Заполнение электронных состояний в различных типах материалов при равновесии. Здесь высота - это энергия, а ширина - плотность доступных состояний для определенной энергии в указанном материале. Оттенок соответствует распределению Ферми – Дирака (черный = все состояния заполнены, белые = состояния не заполнены). В металлах и полуметаллах уровень Ферми EFнаходится внутри по крайней мере одной зоны. В изоляторах и полупроводниках уровень Ферми находится внутри запрещенной зоны ; однако в полупроводниках зоны достаточно близки к уровню Ферми, чтобы быть термически заселенными электронами или дырками.

При термодинамическом равновесии вероятность состояния энергетического состояния E, заполненный электроном, задается распределением Ферми – Дирака, термодинамическим распределением, которое учитывает принцип исключения Паули :

$f\; (E)\; =\; 1\; 1\; +\; e\; (E\; -\; \mu )\; /\; К\; BT\; \{\backslash \; Displaystyle\; f\; (E)\; =\; \{\backslash \; frac\; \{1\}\; \{1\; +\; e\; ^\; \{\{(E-\; \backslash \; mu)\}\; /\; \{k\; \_\; \{\backslash \; rm\; \{B\}\}\; T\}\}\}\}\}$

где:

• kBT - произведение постоянной Больцмана и температуры, а
• µ - общий химический потенциал электронов, или уровень Ферми (в физике полупроводников эта величина чаще обозначается E F). Уровень Ферми твердого тела напрямую связан с напряжением на нем, измеренным с помощью вольтметра. Обычно на диаграммах зонной структуры уровень Ферми принимается равным нулю энергии (произвольный выбор).

Плотность электронов в материале - это просто интеграл от распределения Ферми – Дирака, умноженный на плотность состояний:

$N\; /\; V\; знак\; равно\; \int \; -\; \infty \; \infty \; г\; (E)\; е\; (E)\; d\; E\; \{\backslash \; Displaystyle\; N\; /\; V\; =\; \backslash \; int\; \_\; \{-\; \backslash \; infty\}\; ^\; \{\backslash \; infty\}\; г\; (E)\; f\; (E)\; \backslash ,\; dE\}$

Хотя существует бесконечное количество зон и, следовательно, бесконечное количество состояний, в эти зоны можно поместить только конечное число электронов. Предпочтительное значение количества электронов является следствием электростатики: даже если поверхность материала может быть заряжена, внутренняя масса материала предпочитает иметь нейтральный заряд. Условие нейтральности заряда означает, что N / V должно соответствовать плотности протонов в материале. Чтобы это произошло, материал электростатически подстраивается, сдвигая свою зонную структуру вверх или вниз по энергии (тем самым сдвигая g (E)), пока он не достигнет правильного равновесия по отношению к уровню Ферми.

Названия зон вблизи уровня Ферми (зона проводимости, валентная зона)

Твердое тело имеет бесконечное количество разрешенных зон, так же как атом имеет бесконечное количество уровней энергии. Однако большинство полос просто имеют слишком высокую энергию и обычно не принимаются во внимание при обычных обстоятельствах. И наоборот, с остовными орбиталями связаны зоны с очень низкой энергией (такие как 1s электронов ). Эти низкоэнергетические остовные зоны также обычно не учитываются, поскольку они все время остаются заполненными электронами и поэтому инертны. Точно так же материалы имеют несколько запрещенных зон по всей их ленточной структуре.

Наиболее важные зоны и запрещенные зоны - те, которые важны для электроники и оптоэлектроники - это зоны с энергией, близкой к уровню Ферми. Зонам и запрещенным зонам вблизи уровня Ферми в зависимости от материала даются специальные названия:

• В полупроводнике или зонном изоляторе уровень Ферми окружен запрещенной зоной., называемая запрещенной зоной (чтобы отличать ее от других запрещенных зон в зонной структуре). Ближайшая зона над запрещенной зоной называется зоной проводимости, а ближайшая зона ниже запрещенной зоны называется валентной зоной. Название «валентная зона» появилось по аналогии с химией, поскольку в полупроводниках (и изоляторах) валентная зона построена из валентных орбиталей.
• . В металле или полуметалле ферми уровень находится внутри одной или нескольких разрешенных полос. В полуметаллах зоны обычно называют «зоной проводимости» или «валентной зоной» в зависимости от того, является ли перенос заряда более электронным или дырочным, по аналогии с полупроводниками. Однако во многих металлах зоны не являются ни электронными, ни дырочными, и их часто называют просто «валентной зоной», поскольку они состоят из валентных орбиталей. Запрещенные зоны в зонной структуре металла не важны для физики низких энергий, поскольку они слишком далеки от уровня Ферми.

анзац - частный случай электронных волн в периодической кристаллической решетке с использованием в общем случае динамической теории дифракции. Каждый кристалл представляет собой периодическую структуру, которая может быть охарактеризована решеткой Браве, и для каждой решетки Браве мы можем определить обратную решетку, которая инкапсулирует периодичность в набор из трех векторов обратной решетки (b1,b2,b3). Теперь любой периодический потенциал V (r ), который имеет ту же периодичность, что и прямая решетка, может быть разложен в ряд Фурье, единственными ненулевыми компонентами которого являются компоненты, связанные с обратной величиной решетки векторов. Таким образом, расширение можно записать так:

$V\; (r)\; =\; \sum \; KVK\; ei\; K\; \cdot \; r\; \{\backslash \; displaystyle\; V\; (\backslash \; mathbf\; \{r\})\; =\; \backslash \; sum\; \_\; \{\backslash \; mathbf\; \{K\}\}\; \{V\; \_\; \{\backslash \; mathbf\; \{\; K\}\}\; e\; ^\; \{i\; \backslash \; mathbf\; \{K\}\; \backslash \; cdot\; \backslash \; mathbf\; \{r\}\}\}\}$

где K = m 1b1+ m 2b2+ m 3b3для любого набор целых чисел (m 1,m2,m3).

Исходя из этой теории, можно попытаться предсказать зонную структуру конкретного материала, однако большинство неэмпирических методов расчета электронной структуры не могут предсказать наблюдаемую ширину запрещенной зоны.

Приближение почти свободных электронов

В приближении почти свободных электронов полностью игнорируются взаимодействия между электронами. Это приближение позволяет использовать теорему Блоха, которая утверждает, что электроны в периодическом потенциале имеют волновые функции и периодические по волновому вектору энергии вплоть до постоянного фазового сдвига между соседними обратной решеткой векторов. Последствия периодичности математически описываются функцией теоремы Блоха:

$\Psi \; n,\; k\; (r)\; =\; eik\; \cdot \; run\; (r)\; \{\backslash \; displaystyle\; \{\backslash \; Psi\}\; \_\; \{n,\; \backslash \; mathbf\; \{k\}\}\; (\backslash \; mathbf\; \{\; r\})\; =\; e\; ^\; \{я\; \backslash \; mathbf\; \{k\}\; \backslash \; cdot\; \backslash \; mathbf\; \{r\}\}\; u\_\; \{n\}\; (\backslash \; mathbf\; \{r\})\}$

, где функция $un\; (r)\; \{\backslash \; displaystyle\; u\_\; \{n\}\; (\backslash \; mathbf\; \{r\})\}$периодичен по кристаллической решетке, то есть

$un\; (r)\; =\; un\; (r\; -\; R)\; \{\backslash \; displaystyle\; u\_\; \{n\}\; (\backslash \; mathbf\; \{r\})\; =\; u\_\; \{n\}\; (\backslash \; mathbf\; \{rR\})\}$.

Здесь индекс n относится к n-му энергетическому диапазону, волновой вектор k связан с направлением движения электрона, r - положение в кристалле, а R - расположение атомной позиции.

Модель NFE особенно хорошо работает в таких материалах, как металлы, где расстояния между соседними атомами малы. В таких материалах перекрытие атомных орбиталей и потенциалов на соседних атомах относительно велико. В этом случае волновая функция электрона может быть аппроксимирована (модифицированной) плоской волной. Зонная структура такого металла, как алюминий, даже приближается к приближению пустой решетки.

модели сильной связи

Крайность, противоположная приближению почти свободных электронов, предполагает наличие электронов в кристалл ведет себя так же, как совокупность составляющих атомов. Эта модель сильной связи предполагает решение независимого от времени уравнения для одиночного электрона Шредингера $\Psi \; \{\backslash \; displaystyle\; \backslash \; Psi\}$хорошо аппроксимируется с помощью линейная комбинация из атомных орбиталей $\psi \; n\; (r)\; \{\backslash \; displaystyle\; \backslash \; psi\; \_\; \{n\}\; (\backslash \; mathbf\; \{r\})\}$.

$\Psi \; (r)\; =\; \sum \; n,\; р\; bn,\; р\; \psi \; N\; (г\; -\; R)\; \{\backslash \; Displaystyle\; \backslash \; Psi\; (\backslash \; mathbf\; \{r\})\; =\; \backslash \; sum\; \_\; \{n,\; \backslash \; mathbf\; \{R\}\}\; b\_\; \{n,\; \backslash \; mathbf\; \{R\}\}\; \backslash \; psi\; \_\; \{n\}\; (\backslash \; mathbf\; \{rR\})\}$,

где коэффициенты $bn,\; R\; \{\backslash \; displaystyle\; b\_\; \{n,\; \backslash \; mathbf\; \{R\}\}\}$выбираются для получения наилучшего приближенное решение такого вида. Индекс n относится к уровню атомной энергии, а R относится к атомному узлу. Более точный подход, использующий эту идею, использует функции Ванье, определяемые следующим образом:

$an\; (r\; -\; R)\; =\; VC\; (2\; \pi )\; 3\; \int \; BZ\; dke\; -\; ik\; \cdot \; (R\; -\; r)\; unk\; \{\backslash \; displaystyle\; a\_\; \{n\}\; (\backslash \; mathbf\; \{rR\})\; =\; \{\backslash \; frac\; \{V\_\; \{C\}\}\; \{(2\; \backslash \; pi)\; ^\; \{3\}\}\}\; \backslash \; int\; \backslash \; limits\; \_\; \{\backslash \; text\; \{BZ\}\}\; d\; \backslash \; mathbf\; \{\; k\}\; e\; ^\; \{-\; я\; \backslash \; mathbf\; \{k\}\; \backslash \; cdot\; (\backslash \; mathbf\; \{Rr\})\}\; u\_\; \{n\; \backslash \; mathbf\; \{k\}\}\}$;

в котором $unk\; \{\backslash \; displaystyle\; u\_\; \{n\; \backslash \; mathbf\; \{\; k\}\}\}$- периодическая часть теоремы Блоха, а интеграл берется по зоне Бриллюэна. Здесь индекс n относится к n-й энергетической зоне в кристалле. Функции Ванье локализованы около атомных узлов, как атомные орбитали, но, будучи определенными в терминах функций Блоха, они точно связаны с решениями, основанными на кристаллическом потенциале. Функции Ванье на разных атомных позициях R ортогональны. Функции Ванье можно использовать для формирования решения Шредингера для n-й энергетической зоны как:

$\Psi \; n,\; k\; (r)\; =\; \sum \; R\; e\; -\; ik\; \cdot \; (R\; -\; r)\; an\; (r\; -\; R)\; \{\backslash \; displaystyle\; \backslash \; Psi\; \_\; \{N,\; \backslash \; mathbf\; \{k\}\}\; (\backslash \; mathbf\; \{r\})\; =\; \backslash \; sum\; \_\; \{\backslash \; mathbf\; \{R\}\}\; e\; ^\; \{-\; я\; \backslash \; mathbf\; \{k\}\; \backslash \; cdot\; (\backslash \; mathbf\; \{Rr\})\; \}\; a\_\; \{n\}\; (\backslash \; mathbf\; \{rR\})\}$.

Модель TB хорошо работает в материалах с ограниченным перекрытием между атомными орбиталями и потенциалами на соседних атомах. Зонные структуры таких материалов, как Si, GaAs, SiO 2 и алмаз, например, хорошо описываются TB-гамильтонианами на основе атомных sp-орбиталей. В переходных металлах смешанная модель TB-NFE используется для описания широкой зоны проводимости NFE и узких встроенных d-полос TB. Радиальные функции атомной орбитальной части функций Ванье проще всего вычислить с помощью методов псевдопотенциала. Расчеты структуры полосы NFE, TB или комбинированного NFE-TB, иногда расширенные приближениями волновой функции на основе методов псевдопотенциала, часто используются в качестве экономической отправной точки для дальнейших расчетов.

Модель KKR

Простейшая форма этого приближения центрирует неперекрывающиеся сферы (называемые формами для маффинов) на позициях атомов. В этих областях потенциал, испытываемый электроном, аппроксимируется сферически симметричным относительно данного ядра. В оставшейся межузельной области экранированный потенциал аппроксимируется как постоянная величина. Обеспечивается непрерывность потенциала между сферами с атомным центром и межузельной областью.

Вариационная реализация была предложена Коррингой, Коном и Ростокером и часто упоминается как модель KKR.

Теория функций плотности

В современной физической литературе большая часть электронных структур и зонных диаграмм рассчитывается с использованием теории функционала плотности (DFT), которая является не моделью, а скорее теорией, т. Е. Микроскопической теорией из первых принципов. из физики конденсированного состояния, который пытается справиться с электронно-электронной проблемой многих тел путем введения члена в функционал электронной плотности. Полосы, рассчитанные методом DFT, во многих случаях согласуются с экспериментально измеренными полосами, например, с помощью фотоэмиссионной спектроскопии с угловым разрешением (ARPES). В частности, форма полосы обычно хорошо воспроизводится с помощью DFT. Но есть также систематические ошибки в полосах DFT по сравнению с результатами экспериментов. В частности, кажется, что DFT систематически занижает примерно на 30-40% ширину запрещенной зоны в изоляторах и полупроводниках.

Принято считать, что DFT - это теория для предсказания свойств основного состояния только системы (например, полная энергия, атомная структура и т. д.), и свойства этого возбужденного состояния не могут быть определены с помощью DFT. Это заблуждение. В принципе, DFT может определять любое свойство (основное состояние или возбужденное состояние) системы с учетом функционала, который отображает плотность основного состояния на это свойство. В этом суть теоремы Хоэнберга – Кона. Однако на практике не существует известного функционала, который отображает плотность основного состояния в энергии возбуждения электронов в материале. Таким образом, то, что в литературе цитируется как полосный график ДПФ, является представлением ДПФ энергий Кона – Шэма, то есть энергий фиктивной невзаимодействующей системы, системы Кона – Шэма, которая имеет никакой физической интерпретации. Электронную структуру Кона-Шэма не следует путать с реальной квазичастичной электронной структурой системы, и нет теоремы Купмана, справедливой для энергий Кона-Шэма, как для Энергии Хартри – Фока, которые действительно можно рассматривать как приближение для. Следовательно, в принципе, ДПФ, основанное на Коне – Шэме, не является зонной теорией, то есть теорией, подходящей для расчета зон и диаграмм. В принципе зависимое от времени ДПФ можно использовать для расчета истинной полосовой структуры, хотя на практике это часто бывает сложно. Популярным подходом является использование гибридных функционалов, которые включают часть точного обмена Хартри – Фока; это приводит к существенному улучшению прогнозируемой ширины запрещенной зоны полупроводников, но менее надежен для металлов и материалов с широкой запрещенной зоной.

.

Методы функции Грина и приближение ab initio GW

Для расчета зон, включая электрон-электронное взаимодействие многокомпонентные эффекты, можно прибегнуть к так называемым методам функции Грина. Действительно, знание функции Грина системы обеспечивает наблюдаемые как основное (полная энергия), так и возбужденное состояние системы. Полюсы функции Грина - это энергии квазичастиц, полосы твердого тела. Функция Грина может быть вычислена путем решения уравнения Дайсона, если известна собственная энергия системы. Для реальных систем, таких как твердые тела, собственная энергия является очень сложной величиной, и для решения проблемы обычно требуются приближения. Одним из таких приближений является приближение GW, так называемое из математической формы, которую собственная энергия принимает как произведение Σ = GW функции Грина G и динамически экранированного взаимодействия W. Этот подход более уместен при рассмотрении расчет полосовых графиков (а также количеств за их пределами, таких как спектральная функция), а также может быть сформулирован полностью ab initio способом. Приближение GW, кажется, обеспечивает ширину запрещенной зоны диэлектриков и полупроводников в соответствии с экспериментом и, следовательно, исправляет систематическое занижение DFT.

Теория динамического среднего поля

Хотя приближение почти свободных электронов способно описать многие свойства электронных зонных структур, одним из следствий этой теории является то, что она предсказывает одинаковое количество электронов в каждой ячейка. Если число электронов нечетное, мы могли бы ожидать, что в каждой элементарной ячейке есть неспаренный электрон, и, таким образом, валентная зона не полностью занята, что делает материал проводником. Однако такие материалы, как CoO, которые имеют нечетное количество электронов на элементарную ячейку, являются изоляторами, что прямо противоречит этому результату. Этот вид материала известен как изолятор Мотта и требует включения подробных электрон-электронных взаимодействий (рассматриваемых только как усредненное влияние на кристаллический потенциал в зонной теории) для объяснения несоответствия. Модель Хаббарда представляет собой приблизительную теорию, которая может включать эти взаимодействия. Его можно рассматривать непертурбативно в рамках так называемой динамической теории среднего поля, которая пытается преодолеть разрыв между приближением почти свободных электронов и атомным пределом. Однако формально в этом случае состояния не являются невзаимодействующими, и концепция зонной структуры не подходит для описания этих случаев.

Другое

Расчет зонных структур - важная тема теоретической физики твердого тела. В дополнение к моделям, упомянутым выше, другие модели включают следующее:

• Приближение пустой решетки : «зонная структура» области свободного пространства, которая была разделена на решетку.
• возмущение k · p Теория - это метод, который позволяет приблизительно описать полосовую структуру с помощью всего нескольких параметров. Этот метод обычно используется для полупроводников, а параметры в модели часто определяются экспериментально.
• Модель Кронига-Пенни, одномерная прямоугольная яма Модель полезна для иллюстрации формирования полос. Несмотря на простоту, он предсказывает многие важные явления, но не является количественным.
• Модель Хаббарда

Полосная структура была обобщена на волновые векторы, которые являются комплексными числами, что привело к так называемой сложной полосовой структуре., который представляет интерес на поверхностях и интерфейсах.

Каждая модель описывает одни типы твердых тел очень хорошо, а другие - плохо. Модель почти свободных электронов хорошо работает для металлов, но плохо для неметаллов. Модель сильного связывания чрезвычайно точна для ионных изоляторов, таких как соли галогенидов металлов (например, NaCl ).

Чтобы понять, как изменяется зонная структура относительно уровня Ферми в реальном пространстве, диаграмму зонной структуры часто сначала упрощают в виде зонной диаграммы. На ленточной диаграмме вертикальная ось - энергия, а горизонтальная ось - реальное пространство. Горизонтальные линии представляют уровни энергии, а блоки представляют энергетические диапазоны. Когда горизонтальные линии на этой диаграмме наклонены, энергия уровня или полосы изменяется с расстоянием. Схематически это изображает наличие электрического поля внутри кристаллической системы. Диаграммы полос полезны для соотнесения общих свойств структуры различных материалов друг с другом при контакте друг с другом.

На Викискладе есть материалы, связанные с Дисперсионными соотношениями электронов.

• Феликс Блох - пионер теории зонной структуры
• Алан Херис Уилсон - пионер в теории зонной структуры
• Технология запрещенной зоны - процесс изменения зонной структуры материала

• Чарльз Киттель (1996). Введение в физику твердого тела (седьмое изд.). Нью-Йорк: Вили. ISBN 978-0-471-11181-8.

1. Микроэлектроника, Джейкоб Миллман и Арвин Габриэль, ISBN 0 -07-463736-3, Tata McGraw-Hill Edition.
2. Физика твердого тела, Нил Эшкрофт и Н. Дэвид Мермин, ISBN 0- 03-083993-9
3. Элементарная физика твердого тела: принципы и приложения, М. Али Омар, ISBN 0-201-60733-6
4. Электронные и оптоэлектронные свойства of Semiconductor Structures – Chapter 2 and 3 by Jasprit Singh, ISBN 0-521-82379-X
5. Electronic Structure: Basic Theory and Practical Methods by Richard Martin, ISBN 0-521-78285-6
6. Condensed Matter Physics by Michael P. Marder, ISBN 0-471-17779-2
7. Computational Methods in Solid State Physics by VV Nemoshkalenko and NV Antonov, ISBN 90-5699-094-2
8. Elementary Electronic Structure by Walter A. Harrison, ISBN 981-238-708-0
9. Pseudopotentials in the theory of metals by Walter A. Harrison, W.A. Benjamin (New York) 1966
10. Tutorial on Bandstructure Methods by Dr. Vasileska (2008)

• Media related to Electronic band structures at Wikimedia Commons
• Animation, applications and research about quantum physics and band theory (Université Paris Sud)