Войти
Система двенадцатеричная (также известная как с основанием 12, десятичная, или, реже, унциал ) - это позиционное обозначение система счисления, использующая двенадцать в качестве основания. Число двенадцать (то есть число, записанное как "12" в системе счисления с основанием десять ) вместо этого записывается как "10" в двенадцатеричной системе счисления (что означает "1 дюжина и 0 единиц "вместо" 1 десяток и 0 единиц "), тогда как строка цифр" 12 "означает" 1 дюжина и 2 единицы "(то есть то же число, что в десятичной системе, записывается как" 14 "). Аналогичным образом, в двенадцатеричной системе «100» означает «1 брутто », «1000» означает «1 брутто », а «0,1» означает «1 двенадцатая» (вместо их десятичных значений «1 сотня», «1 тысяча» и «1 десятая»).
Число двенадцать, высшее составное число, является наименьшим числом с четырьмя нетривиальными множителями (2, 3, 4, 6) и наименьшее, чтобы включить в качестве множителей все четыре числа (от 1 до 4) в диапазоне субитизирующего и наименьшее избыточное число. В результате этой повышенной факторизации системы счисления и ее делимости на широкий диапазон самых элементарных чисел (тогда как десять имеет только два нетривиальных фактора: 2 и 5, а не 3, 4 или 6), двенадцатеричные представления легче, чем десятичные, вписываются во многие общие шаблоны, о чем свидетельствует более высокая регулярность, наблюдаемая в двенадцатеричной таблице умножения. В результате двенадцатеричная система счисления была названа оптимальной. Из его множителей 2 и 3 являются простым, что означает обратные всех 3-гладких чисел (таких как 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 27, 32, 36,...) имеют завершающее представление в двенадцатеричном формате. В частности, пять наиболее элементарных дробей (⁄ 2, ⁄ 3, ⁄ 3, ⁄ 4 и ⁄ 4) все имеют короткое завершающее представление в двенадцатеричной системе счисления (0,6, 0,4, 0,8, 0,3 и 0,9 соответственно), а двенадцать - это наименьший основание системы счисления с этой функцией (поскольку это наименее распространенный кратное из 3 и 4). Все это делает эту систему счисления более удобной для вычисления дробей, чем большинство других широко используемых систем счисления, таких как десятичная, десятичная, двоичная, восьмеричная и шестнадцатеричная системы. Хотя системы трехзначной и шестидесятеричной (где оканчиваются обратные значения всех 5-гладких чисел) в этом отношении работают даже лучше, это достигается за счет громоздкости таблицы умножения и гораздо большее количество символов для запоминания.
Для обозначения десяти и одиннадцати в двенадцатеричной системе счисления использовались различные символы; Unicode включает 
(U + 218A ↊ ПОВОРОТНУЮ ЦИФРУ ВТОРОЙ) и 
(U + 218B ↋ ПОВОРОТНУЮ ЦИФРУ ТРИ). Используя эти символы, счет от нуля до двенадцати в двенадцатеричном формате читает: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 
, 
, 10. Они были реализованы в Unicode 8.0 (2015), но по состоянию на 2019 год большинство общих шрифтов Unicode, используемых текущими операционными системами и браузерами, еще не включали их. Более распространенной альтернативой является использование A и B, как в шестнадцатеричном формате, а на этой странице используются «A» и «B».
. Языки, использующие двенадцатеричные системы счисления, встречаются редко. Языки в Нигерийском Среднем поясе, такие как Джанджи, Гбири-Нирагу (Гуре-Кахугу), Пити и диалект Нимбия в Гвандара ; и язык Chepang из Непал, как известно, используют двенадцатеричные числа.
германские языки имеют специальные слова для 11 и 12, например, одиннадцать и двенадцать в английском. Однако они происходят от протогерманских * ainlif и * twalif (означающих, соответственно, один слева и два слева), что предполагает десятичное, а не двенадцатеричное происхождение.
Исторически единиц из времени во многих цивилизациях двенадцатеричный. Есть двенадцать знаков зодиака , двенадцать месяцев в году, а у вавилонян в сутках было двенадцать часов (хотя в какой-то момент это было изменено на 24). Традиционные китайские календари, часы и компасы основаны на двенадцати земных ветвях. В имперском футе 12 дюймов, в тройском фунте 12 тройских унций, в шиллинге 12 старых британских пенсов, 24 (12 × 2) часа. в день и многие другие предметы, подсчитываемые по дюжине, брутто (144, квадрат из 12) или большой брутто (1728, куб из 12). Римляне использовали систему дробей, основанную на 12, включая uncia, которое стало одновременно английскими словами унция и дюйм. До десятичной системы, Ирландия и Соединенное Королевство использовали смешанную двенадцатерично-десятичную денежную систему (12 пенсов = 1 шиллинг, 20 шиллингов или 240 пенсов к фунт стерлингов или ирландский фунт ), и Карл Великий установил денежную систему, которая также имела смешанную основу из двенадцати и двадцати, остатки которой сохраняются во многих местах.
| Таблица единиц по базе 12 | |||||
|---|---|---|---|---|---|
| Относительное. значение | Французская единица. длины | Английская единица. длины | Английская. (тройская) единица. веса | римская единица. веса | английская единица. массы |
| 12 | пид | фут | фунт | libra | |
| 12 | pouce | inch | oz | uncia | slinch |
| 12 | ligne | line | 2 scruples | 2 scrupula | slug |
| 12 | point | point | seed | siliqua | |
Важность 12 объясняется количеством лунных циклов в году, а также тем фактом, что у людей 12 костей пальцев (фаланги ) на одной руке (по три на каждом из четырех пальцев). Можно сосчитать до 12, когда большой палец действует как указатель, по очереди касаясь каждой кости пальца. Традиционная система подсчета пальцев, которая до сих пор используется во многих регионах Азии, работает таким же образом и может помочь объяснить появление систем счисления на основе 12 и 60, помимо систем, основанных на 10, 20 и 5. В В этой системе одна (обычно правая) рука постоянно считает до 12, отображая количество итераций на другой (обычно левой), пока не заполнятся пять десятков, то есть 60.
В двенадцатеричной системе счисления двенадцать записывается как 10, но существует множество предложений о том, как записать десять и одиннадцать.
Разрешить ввод на пишущих машинках буквы, такие как A и B (как в шестнадцатеричном ), T и E (инициалы десяти и одиннадцати), X и E (X от римской цифры вместо десяти) или X и Z. Некоторые используют греческие буквы, такие как δ (от греческого δέκα 'десять') и ε (для греческого ένδεκα 'одиннадцать') или τ и ε . Фрэнк Эмерсон Эндрюс, один из первых американских защитников двенадцатеричной системы, предложил и использовал в своей книге «Новые числа» X и ℰ (сценарий E, U + 2130).
Эдна Крамер в своей книге 1951 года «Главный поток математики» использовала шестиконечную звездочку (секстиль ) ⚹и хэш (или окторп) # . Символы были выбраны потому, что они доступны на пишущих машинках; они также есть на кнопочных телефонах. Это обозначение использовалось в публикациях Общества дюжины Америки (DSA ) с 1974–2008 гг.
С 2008 по 2015 год в DSA использовались символы 
и 
, символы, разработанные Уильямом Аддисоном Двиггинсом.
. 
Общество дюжины Великобритании (DSGB ) предложил символы и . Это обозначение, полученное из арабских цифр с поворотом на 180 °, было введено сэром Исааком Питманом. В марте 2013 года было внесено предложение о включении цифровых форм для десяти и одиннадцати, распространяемых Обществами дюжины, в Стандарт Юникода. Из них британские / Pitman формы были приняты для кодирования как символы в кодовых точках U + 218A ↊ ПОВОРОТНАЯ ЦИФРА ВТОРАЯ и U + 218B ↋ ПОВОРОТНАЯ ЦИФРА ТРЕТЬЯ. Они были включены в выпуск Unicode 8.0 в июне 2015 года и доступны в LaTeX как \ textturntwoи \ textturnthree.
после цифр Pitman. были добавлены в Unicode, DSA провела голосование и затем начала публиковать контент, используя вместо этого цифры Питмана. Они по-прежнему используют буквы X и E в тексте ASCII. Поскольку символы Unicode плохо поддерживаются, на этой странице используются «A» и «B».
Другие предложения более креативны или эстетичны; например, многие не используют какие-либо арабские цифры в соответствии с принципом «отдельной идентичности».
Существуют также различные предложения о том, как различать двенадцатеричные числа число от десятичного. Они включают выделение курсивом двенадцатеричных чисел «54 = 64», добавление «точки Хамфри» (точка с запятой вместо десятичной точки ) к двенадцатеричным числам «54; 6 = 64,5» или некоторая комбинация двух. Другие используют нижний индекс или прикрепленные метки для обозначения основания, что позволяет представлять более десятичных и двенадцатеричных чисел (для отдельных букв 'z' из "do z enal" используется, поскольку 'd' будет означать десятичное) например «54 z = 64 d,« 54 12 = 64 10 »или« doz 54 = dec 64. »
Общество Дюжины Америки предложило произносить десять и одиннадцать как «дек» и «эль». Для имен степеней двенадцати есть две выдающиеся системы.
В этой системе для дробей добавляется префикс e-.
| Двенадцатеричный | Имя | Десятичное | Двенадцатеричная дробь | Имя |
|---|---|---|---|---|
| 1; | один | 1 | ||
| 10; | do | 12 | 0;1 | edo |
| 100; | gro | 144 | 0; 01 | egro |
| 1000; | mo | 1,728 | 0; 001 | эмо |
| 10,000; | до-мо | 20,736 | 0; 000,1 | эдо-мо |
| 100000; | gro-mo | 248,832 | 0; 000,01 | egro-mo |
| 1,000,000; | би-мо | 2,985,984 | 0; 000,001 | эби-мо |
| 10,000,000; | до-би-мо | 35,831,808 | 0; 0,000,001 | эдо-би-мо |
| 100000000; | гро-би-мо | 429,981,696 | 0; 00,000,001 | эгро-би-мо |
| 1 000 000 000; | три-мо | 5,159,780,352 | 0; 000,000,001 | этри-мо |
| 10,000,000,000; | до-три-мо | 61,917,364,224 | 0; 0,000,000,001 | эдо-три-мо |
| 100000000000; | гро-три-мо | 743,008,370,688 | 0; 00,000,000,001 | эгро-три-мо |
| 1 000 000 000 000; | quad-mo | 8,916,100,448,256 | 0; 000,000,000,001 | equad-mo |
| 10,000,000,000,000; | до-квад-мо | 106,993,205,379,072 | 0; 0,000,000,000,001 | эдо-квад-мо |
| 100,000,000,000,000; | гро-квад-мо | 1,283,918,464,548,864 | 0; 00,000,000,000,001 | эгро-квад-мо |
| 1,000,000,000,000,000; | пента-мо | 15 407 021 574 586 368 | 0; 000 000 000 000 001 | эпента-мо |
| 10 000 000 000 000 000; | до-пента-мо | 184,884,258,895,036,416 | 0; 0,000,000,000,000,001 | эдо-пента-мо |
| 100,000,000,000,000,000; | гро-пента-мо | 2,218,611,106,740,436,992 | 0; 00,000,000,000,000,001 | эгро-пента-мо |
| 1,000,000,000,000,000,000; | hexa-mo | 26,623,333,280,885,243,904 | 0; 000,000,000,000,000,001 | ehexa-mo |
Несколько цифр в этой серии произносятся по-разному: 12 - это "до" два"; 30 - «три до»; 100 - «gro»; BA9 - это «el gro dek do девять»; B86 - «эль гро восемь до шесть»; 8BB, 15A - «восемь гро эль до эль мо, один гро пять до дек»; и т. д.
В этой системе используется окончание -qua для положительных степеней числа 12 и окончание -cia для отрицательных степеней числа 12, и расширение имен систематических элементов IUPAC (со слогами dec и lev для двух дополнительных цифр, необходимых для двенадцатеричной системы), чтобы выразить, какая мощность имеется в виду.
| Десятичное число | Имя | Десятичное число | Десятичное число | Имя |
|---|---|---|---|---|
| 1; | один | 1 | ||
| 10; | unqua | 12 | 0; 1 | uncia |
| 100; | biqua | 144 | 0; 01 | bicia |
| 1000; | триква | 1,728 | 0; 001 | триша |
| 10,000; | квадра | 20,736 | 0; 000,1 | квадча |
| 100000; | пентква | 248,832 | 0; 000,01 | пентча |
| 1,000,000; | гексика | 2,985,984 | 0; 000,001 | гексия |
| 10,000,000; | septqua | 35,831,808 | 0; 000,000,1 | septcia |
| 100000000; | octqua | 429,981,696 | 0; 000,000,01 | octcia |
| 1,000,000,000; | эннква | 5,159,780,352 | 0; 000,000,001 | эннсия |
| 10,000,000,000; | деква | 61 917 364 224 | 0; 000 000 000,1 | децча |
| 100 000 000 000; | левква | 743,008,370,688 | 0; 000,000,000,01 | левча |
| 1 000 000 000 000; | уннильква | 8,916,100,448,256 | 0; 000,000,000,001 | уннильсия |
| 10,000,000,000,000; | ununqua | 106,993,205,379,072 | 0; 000,000,000,000,1 | ununcia |
Уильям Джеймс Сидис использовано 12 в качестве основы для его сконструированного языка Вендергуд в 1906 году, отметив, что это наименьшее число с четырьмя факторами и его преобладание в торговле.
Аргументы в пользу двенадцатеричной системы были подробно изложены в книге Фрэнка Эмерсона Эндрюса 1935 года «Новые числа: как принятие двенадцатеричного основания упростит математику». Эмерсон отметил, что из-за преобладания множителя двенадцать во многих традиционных единицах измерения веса и измерения многие вычислительные преимущества, заявленные для метрической системы, могут быть реализованы либо путем принятия весов и мер, основанных на десяти, либо путем принятия двенадцатеричная система счисления.
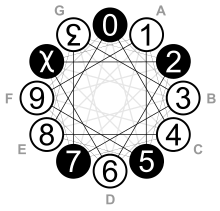Двенадцатеричный циферблат, как на логотипе Общества дюжины Америки, здесь используется для обозначения музыкальных клавиш И Общество дюжины Америки, и Общество дюжины Великобритании способствуют широкому распространению системы основания-двенадцать. Они используют слово «дюжинал» вместо «двенадцатеричной системы», чтобы избежать более явно выраженной десятичной терминологии. Однако этимология слова «дюжина» сама по себе также является выражением, основанным на терминологии десятичной системы, поскольку «дюжина» является прямым производным от французского слова douzaine, производного от французского слова «двенадцать», douze которое связано со старым французским словом doze от латинского duodecim.
По крайней мере, еще с 1945 года некоторые члены Общества дюжины Америки и Общества дюжины Великобритании высказывали предположение, что более подходящим словом будет "унциальный". Uncial является производным от латинского слова uncia, означающего «одна двенадцатая», а также аналога латинского слова decima, означающего «одна десятая», по основанию двенадцать.
Математик и мысленный калькулятор Александр Крейг Эйткен был откровенным сторонником двенадцатеричной системы:
Двенадцатеричные таблицы легко освоить, легче, чем десятичные; и в начальном обучении они были бы намного интереснее, поскольку маленькие дети нашли бы более увлекательные занятия с двенадцатью стержнями или кубиками, чем с десятью. Любой, у кого есть эти таблицы, будет выполнять эти вычисления в двенадцатеричной шкале более чем в полтора раза быстрее, чем в десятичной. Это мой опыт; Я уверен, что тем более это будет опыт других.
— А. К. Эйткен, «Двенадцать и десятки» в «Слушателе» (25 января 1962 г.)Но последнее количественное преимущество, по моему собственному опыту, таково: в разнообразных и обширных вычислениях обычного и не слишком сложного типа По прошествии многих лет я прихожу к выводу, что эффективность десятичной системы счисления может быть оценена примерно в 65 или меньше, если мы присвоим 100 двенадцатеричной системе.
— A. К. Эйткен, «Дело против десятичной системы» (1962)В американском телесериале «Маленькие двенадцать пальцев» Schoolhouse Rock! инопланетный ребенок изображен с использованием арифметики с основанием двенадцать, с использованием «dek», «el» и «doh» в качестве имен для десяти, одиннадцати и двенадцати, а также скрипта Эндрюса-X и скрипта-E для символов цифр.
Системы измерений, предложенных дюжинами, включают:
Число 12 имеет шесть факторов, которые равны 1, 2, 3, 4, 6 и 12, из которых 2 и 3 являются простым. В десятичной системе имеется только четыре множителя: 1, 2, 5 и 10, из которых 2 и 5 являются простыми. Vigesimal (с основанием 20) добавляет два множителя к десяти, а именно 4 и 20, но без дополнительного простого множителя. Хотя у двадцати есть 6 множителей, два из которых простые, как и двенадцать, это также намного большее основание, поэтому набор цифр и таблица умножения намного больше. У двоичного числа есть только два множителя: 1 и 2, причем последний является простым. Шестнадцатеричный (основание 16) имеет пять множителей, добавляя 4, 8 и 16 к значениям 2, но без дополнительных простых чисел. Тригесимальная система (основание 30) - это наименьшая система, в которой есть три различных простых множителя (все три наименьших простых числа: 2, 3 и 5), а всего восемь множителей (1, 2, 3, 5, 6, 10, 15)., и 30). Шестидесятеричный - который древние шумеры и вавилоняне на самом деле использовали среди прочих - добавляет к этому четыре удобных множителя 4, 12, 20 и 60, но без нового простого числа. факторы. Наименьшая система с четырьмя разными простыми множителями - это основание 210, и образец следует за примориалами . Во всех базовых системах существует сходство с представлением кратных чисел, которые на единицу меньше основания.
| × | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B |
| 2 | 2 | 4 | 6 | 8 | A | 10 | 12 | 14 | 16 | 18 | 1A |
| 3 | 3 | 6 | 9 | 10 | 13 | 16 | 19 | 20 | 23 | 26 | 29 |
| 4 | 4 | 8 | 10 | 14 | 18 | 20 | 24 | 28 | 30 | 34 | 38 |
| 5 | 5 | A | 13 | 18 | 21 | 26 | 2B | 34 | 39 | 42 | 47 |
| 6 | 6 | 10 | 16 | 20 | 26 | 30 | 36 | 40 | 46 | 50 | 56 |
| 7 | 7 | 12 | 19 | 24 | 2B | 36 | 41 | 48 | 53 | 5A | 65 |
| 8 | 8 | 14 | 20 | 28 | 34 | 40 | 48 | 54 | 60 | 68 | 74 |
| 9 | 9 | 16 | 23 | 30 | 39 | 46 | 53 | 60 | 69 | 76 | 83 |
| A | A | 18 | 26 | 34 | 42 | 50 | 5A | 68 | 76 | 84 | 92 |
| B | B | 1A | 29 | 38 | 47 | 56 | 65 | 74 | 83 | 92 | A1 |
Для преобразования чисел между основаниями можно использовать общий алгоритм преобразования (см. соответствующий раздел под позиционным обозначением ). В качестве альтернативы можно использовать таблицы преобразования цифр. Представленные ниже числа могут использоваться для преобразования любого двенадцатеричного числа от 0; 01 до BBB, BBB; BB в десятичное или любого десятичного числа от 0,01 до 999 999,99 в двенадцатеричное. Чтобы использовать их, данное число необходимо сначала разложить на сумму чисел, каждое из которых содержит только одну значащую цифру. Например:
Это разложение работает одинаково независимо от того, в каком основании выражено число. Просто выделите каждую ненулевую цифру, заполнение им столько нулей, сколько необходимо, чтобы сохранить их соответствующие значения мест. Если цифры в данном числе включают нули (например, 102,304,05), они, конечно, не учитываются при разложении цифр (102,304,05 = 100,000 + 2,000 + 300 + 4 + 0,05). Затем таблицы преобразования цифр можно использовать для получения эквивалентного значения в целевой базе для каждой цифры. Если заданное число находится в двенадцатеричной системе счисления, а целевая основа десятичная, мы получаем:
Теперь, поскольку слагаемые уже преобразованы в десятичную систему, обычная десятичная арифметика используется для выполнения сложить и перекомпоновать число, получив результат преобразования:
Двуодесятичный ----->Десятичный
100000 = 248 832 20000 = 41 472 3000 = 5 184 400 = 576 50 = 60 + 6 = + 6 0; 7 = 0,583333333333... 0; 08 = 0,055555555555... -------------------------------- ------------ 123,456; 78 = 296,130,638888888888...
То есть, (двенадцатеричный) 123,456,78 равняется (десятичный) 296,130,638 ≈ 296 130,64
Если заданное число является десятичным, а целевая база - двенадцатеричной, метод в основном тот же. Используя таблицы преобразования цифр:
(десятичный) 100,000 + 20,000 + 3,000 + 400 + 50 + 6 + 0,7 + 0,08 = (двенадцатеричный) 49, A54 + B, 6A8 + 1, 8A0 + 294 + 42 + 6 + 0; 849724972497249724972497... + 0; 0B62A68781B05915343A0B62...
Однако, чтобы вычислить эту сумму и пересчитать число, теперь таблицы сложения для двенадцатеричной системы должны быть Вместо таблиц сложения для десятичных чисел, с которыми большинство людей уже знакомо, потому что теперь слагаемые имеют основание двенадцать и поэтому арифметика с ними также должна быть в двенадцатеричной системе. В десятичной системе счисления 6 + 6 равно 12, а в двенадцатеричной - 10; Итак, если использовать десятичную арифметику с двенадцатеричными числами, можно получить неверный результат. Правильно выполняя арифметические действия в двенадцатеричном формате, можно получить результат:
Десятичное ----->Десятичное число
100000 = 49, A54 20000 = B, 6A8 3000 = 1,8A0 400 = 294 50 = 42 + 6 = + 6 0; 7 = 0,849724972497249724972497... 0; 08 = 0,0B62A68781B05915343A0B62... ------------------------- ------------------------------- 123,456,78 = 5B, 540.943A0B62A68781B05915343A...
То есть, (десятичное) 123,456,78 равно (двенадцатеричное) 5B, 540; 943A0B62A68781B059153... ≈ 5B, 540; 94
| Duod. | Десятичный | Duod. | Десятичный | Duod. | Дек. | Дуод. | Дек. | Дуод. | Дек. | Дуод. | Дек. | Дуод. | Дек. | Дуод. | Дек. | Дуод. | Дек. |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1,000,000 | 2,985,984 | 100,000 | 248,832 | 10,000 | 20,736 | 1,000 | 1,728 | 100 | 144 | 10 | 12 | 1 | 1 | 0; 1 | 0,083 | 0; 01 | 0,00694 |
| 2,000,000 | 5,971,968 | 200,000 | 497,664 | 20,000 | 41,472 | 2,000 | 3,456 | 200 | 288 | 20 | 24 | 2 | 2 | 0; 2 | 0,16 | 0; 02 | 0,0138 |
| 3,000,000 | 8,957,952 | 300,000 | 746,496 | 30,000 | 62,208 | 3,000 | 5,184 | 300 | 432 | 30 | 36 | 3 | 3 | 0; 3 | 0,25 | 0; 03 | 0,02083 |
| 4,000,000 | 11,943,936 | 400,000 | 995,328 | 40,000 | 82,944 | 4,000 | 6,912 | 400 | 576 | 40 | 48 | 4 | 4 | 0; 4 | 0,3 | 0 ; 04 | 0,027 |
| 5,000,000 | 14,929,920 | 500,000 | 1,244,160 | 50,000 | 103,680 | 5,000 | 8,640 | 500 | 720 | 50 | 60 | 5 | 5 | 0; 5 | 0,416 | 0; 05 | 0,03472 |
| 6,000,000 | 17,915,904 | 600,000 | 1,492,992 | 60,000 | 124,416 | 6,000 | 10,368 | 600 | 864 | 60 | 72 | 6 | 6 | 0; 6 | 0,5 | 0; 06 | 0,0416 |
| 7,000,000 | 20,901,888 | 700,000 | 1,741,824 | 70,000 | 145,152 | 7,000 | 12,096 | 700 | 1,008 | 70 | 84 | 7 | 7 | 0; 7 | 0,583 | 0; 07 | 0,04861 |
| 8,000,000 | 23,887,872 | 800,000 | 1,990,656 | 80,000 | 165,888 | 8,000 | 13,824 | 800 | 1,152 | 80 | 96 | 8 | 8 | 0; 8 | 0,6 | 0; 08 | 0,05 |
| 9,000,000 | 26,873,856 | 900,000 | 2,239,488 | 90,000 | 186,624 | 9,000 | 15,552 | 900 | 1,296 | 90 | 108 | 9 | 9 | 0; 9 | 0,75 | 0; 09 | 0,0625 |
| A, 000,000 | 29,859,840 | A00,000 | 2,488,320 | A0,000 | 207,360 | A, 000 | 17,280 | A00 | 1,440 | A0 | 120 | A | 10 | 0; A | 0,83 | 0; 0A | 0,0694 |
| B, 000,000 | 32,845,824 | B00,000 | 2,737,152 | B0,000 | 228,096 | B, 000 | 19 008 | B00 | 1,584 | B0 | 132 | B | 11 | 0; B | 0,916 | 0; 0B | 0,07638 |
| Дек. | Duod. | Дек. | Duod. | Дек. | Duod. | Дек. | Duod. | Дек. | Duod. | Декабрь | Duod. | Дек. | Duod. | Dec. | Duodecimal | Dec. | Duodecimal |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1,000,000 | 402,854 | 100,000 | 49, A54 | 10,000 | 5,954 | 1,000 | 6B4 | 100 | 84 | 10 | A | 1 | 1 | 0,1 | 0; 12497 | 0,01 | 0; 015343A0B62A68781B059 |
| 2,000,000 | 805,4A8 | 200,000 | 97,8A8 | 20,000 | B, 6A8 | 2,000 | 1,1A8 | 200 | 148 | 20 | 18 | 2 | 2 | 0,2 | 0; 2497 | 0,02 | 0; 02A68781B05915343A0B6 |
| 3,000,000 | 1,008,140 | 300,000 | 125,740 | 30,000 | 15,440 | 3,000 | 1,8A0 | 300 | 210 | 30 | 26 | 3 | 3 | 0,3 | 0; 37249 | 0,03 | 0; 043A0B62A68781B059153 |
| 4,000,000 | 1,40A, 994 | 400,000 | 173,594 | 40,000 | 1B, 194 | 4,000 | 2,394 | 400 | 294 | 40 | 34 | 4 | 4 | 0,4 | 0; 4972 | 0,04 | 0 ; 05915343A0B62A68781B |
| 5,000,000 | 1,811,628 | 500,000 | 201,428 | 50,000 | 24, B28 | 5,000 | 2, A88 | 500 | 358 | 50 | 42 | 5 | 5 | 0,5 | 0; 6 | 0,05 | 0; 07249 |
| 6,000,000 | 2,014,280 | 600,000 | 24B, 280 | 60,000 | 2A, 880 | 6000 | 3,580 | 600 | 420 | 60 | 50 | 6 | 6 | 0,6 | 0; 7249 | 0,06 | 0; 08781B05915343A0B62A6 |
| 7,000,000 | 2,416, B14 | 700,000 | 299,114 | 70,000 | 34,614 | 7,000 | 4,074 | 700 | 4A4 | 70 | 5A | 7 | 7 | 0,7 | 0; 84972 | 0,07 | 0; 0A0B62A68781B05915343 |
| 8,000,000 | 2,819,768 | 800,000 | 326, B68 | 80,000 | 3A, 368 | 8,000 | 4,768 | 800 | 568 | 80 | 68 | 8 | 8 | 0,8 | 0; 9724 | 0,08 | 0; 0B62A68781B05915343A |
| 9,000,000 | 3,020,400 | 900,000 | 374, A00 | 90,000 | 44,100 | 9,000 | 5,260 | 900 | 630 | 90 | 76 | 9 | 9 | 0,9 | 0; A9724 | 0,09 | 0; 10B62A68781B05915343A |
(В этом разделе все числа записываются в двенадцатеричном формате)
Этот раздел посвящен правилам делимости в двенадцатеричном формате.
Любое целое число делится на 1.
Если число делится на 2, то единичной цифрой этого числа будет 0, 2, 4, 6, 8 или A.
Если число делится на 3, тогда единичная цифра этого числа будет 0, 3, 6 или 9.
Если число делится на 4, то единичная цифра этого числа число будет 0, 4 или 8.
Чтобы проверить делимость на 5, удвойте цифру единиц и вычтите результат из числа, образованного остальными цифрами. Если результат делится на 5, то данное число делится на 5.
Это правило происходит из 21 (5 * 5)
Примеры:. 13правило =>| 1-2 * 3 | = 5, которое делится на 5.. 2BA5 rule =>| 2BA-2 * 5 | = 2B0 (5 * 70), который делится на 5 (или примените правило к 2B0).
OR
Чтобы проверить делимость на 5, вычтите цифру единиц и тройку результата из числа, образованного остальными цифрами. Если результат делится на 5, то данное число делится на 5.
Это правило происходит из 13 (5 * 3)
Примеры:. 13правило =>| 3-3 * 1 | = 0, который делится на 5.. 2BA5 rule =>| 5-3 * 2BA | = 8B1 (5 * 195), который делится на 5 (или примените правило к 8B1).
OR
Сформируйте чередующуюся сумму блоков двух справа налево. Если результат делится на 5, то данное число делится на 5.
Это правило происходит от 101, так как 101 = 5 * 25, поэтому это правило также можно проверить на делимость на 25.
Пример:
97,374,627 =>27-46 + 37-97 = -7B, что делится на 5.
Если число делится на 6, то цифра единицы этого числа будет 0 или 6.
Чтобы проверить делимость на 7, утроите цифру единиц и прибавьте результат к числу, образованному остальными цифрами. Если результат делится на 7, то данное число делится на 7.
Это правило происходит из 2B (7 * 5)
Примеры:. 12правило =>| 3 * 2 + 1 | = 7, которое делится на 7.. 271B rule =>| 3 * B + 271 | = 29A (7 * 4A), которое делится на 7 (или примените правило к 29A).
OR
Чтобы проверить делимость на 7, вычтите цифру единиц и удвойте результат из числа, образованного остальными цифрами. Если результат делится на 7, то данное число делится на 7.
Это правило происходит от 12 (7 * 2)
Примеры:. 12правило =>| 2-2 * 1 | = 0, который делится на 7.. 271B rule =>| B-2 * 271 | = 513 (7 * 89), которое делится на 7 (или примените правило к 513).
OR
Для проверки делимости на 7, 4 раза число единиц и вычесть результат из числа, образованного остальными цифрами. Если результат делится на 7, то данное число делится на 7.
Это правило происходит из 41 (7 * 7)
Примеры:. 12правило =>| 4 * 2-1 | = 7, которое делится на 7.. 271B rule =>| 4 * B-271 | = 235 (7 * 3B), которое делится на 7 (или примените правило к 235).
OR
Сформируйте чередующуюся сумму блоков по три справа налево. Если результат делится на 7, то данное число делится на 7.
Это правило исходит из 1001, поскольку 1001 = 7 * 11 * 17, поэтому это правило также можно проверить. для делимости на 11 и 17.
Пример:
386,967,443 =>443-967 + 386 = -168, что делится на 7.
Если двухзначное число, образованное последние 2 цифры данного числа делятся на 8, тогда данное число делится на 8.
Пример: 1B48, 4120
rule =>с 48 ( 8 * 7) делится на 8, то 1B48 делится на 8. rule =>поскольку 20 (8 * 3) делится на 8, то 4120 делится на 8.
Если 2-значное число образовано двумя последними цифр данного числа делится на 9, тогда данное число делится на 9.
Пример: 7423, 8330
rule =>с 23 (9 * 3) делится на 9, то 7423 делится на 9. rule =>поскольку 30 (9 * 4) делится на 9, то 8330 делится на 9.
Если число делится на 2 и 5, то число делится по A.
Если сумма цифр числа делится на B, тогда число делится на B (эквивалент отбрасывания девяток в десятичном виде).
Пример: 29, 61B13
rule =>2 + 9 = B, которое делится на B, тогда 29 делится на B. rule =>6 + 1 + B + 1 + 3 = 1A, который делится на B, тогда 61B13 делится на B.
Если число делится на 10, то единичная цифра этого числа будет 0.
Суммируйте альтернативные цифры и вычтите суммы. Если результат делится на 11, число делится на 11 (эквивалент делимости на одиннадцать в десятичной системе счисления).
Пример: 66, 9427
rule =>| 6-6 | = 0, который делится на 11, то 66 делится на 11. rule =>| (9 + 2) - (4 + 7) | = | A-A | = 0 which is divisible by 11, then 9427 is divisible by 11.
If the number is divisible by 2 and 7 then the number is divisible by 12.
If the number is divisible by 3 and 5 then the number is divisible by 13.
If the 2-digit number formed by the last 2 digits of the given number is divisible by 14then the given number is divisible by 14.
Example: 1468, 7394
rule =>since 68(14*5) divisible by 14, then 1468 is divisible by 14. rule =>since 94(14*7) divisible by 14, then 7394 is divisible by 14.
Duodecimal fractions may be simple:
or complicated:
| Examples in duodecimal | Decimal equivalent |
|---|---|
| 1 × (5/8) = 0;76 | 1 × (5/8) = 0;625 |
| 100 × (5/8) = 76 | 144 × (5/8) = 90 |
| 576/9 = 76 | 810/9 = 90 |
| 400/9 = 54 | 576/9 = 64 |
| 1A;6 + 7;6 = 26 | 22.5 + 7.5 = 30 |
As explained in recurring decimals, whenever an irreducible fraction is written in radix point notation in any base, the fraction can be expressed exactly (terminates) if and only if all the prime factors of its denominator are also prime factors of the base. Thus, in base-ten (= 2 × 5) system, fractions whose denominators are made up solely of multiples of 2 and 5 terminate: 1/8 = 1/(2×2×2), 1/20 = 1/(2×2×5) and 1/500 = 1/(2×2×5×5×5) can be expressed exactly as 0.125, 0.05 and 0.002 respectively. 1/3 and 1/7, however, recur (0.333... and 0.142857142857...). In the duodecimal (= 2× 2 × 3) система, 1/8 - точное значение; 1/20 и 1/500 повторяются, потому что они включают 5 как фактор; 1/3 точно; и 1/7 повторяется, как и в десятичной системе счисления.
Число знаменателей, дающих завершающие дроби в пределах заданного числа цифр, скажем n, в базе b - это количество делителей (делителей) числа b, n-й степени основания b (хотя сюда входит делитель 1, который не дает дробей при использовании в качестве знаменателя). Количество множителей b дается с использованием его разложения на простые множители.
Для десятичного числа 10 = 2 × 5. Количество делителей определяется путем прибавления единицы к каждой экспоненте каждого простого числа и умножения полученных величин вместе, так что количество делителей 10 равно (n + 1) (п + 1) = (п + 1).
Например, число 8 является множителем 10 (1000), поэтому 1/8 и другие дроби со знаминателем 8 не могут требовать более 3 десятичных знаков после запятой для завершения. 5/8 = 0,625 десять
Для двенадцатеричной системы 12 = 2 × 3. Имеет (2n + 1) (n + 1) делителей. Знаменатель выборки, равный 8, является множителем брутто (12 = 144), поэтому для завершения восьмых не может потребоваться более двух двенадцатеричных дробных знаков. 5/8 = 0; 76 двенадцать
Поскольку и десять, и двенадцать имеют два уникальных простых множителя, количество делителей b для b = 10 или 12 возрастает квадратично с показателем n (другими словами, порядок n).
Общество дюжины Америки утверждает, что множитель 3 чаще встречается в реальных задачах деления, чем множитель 5. Таким образом, в практических приложениях, то неприятность, связанная с повторением десятичных знаков, встречается реже, когда используется двенадцатеричная система записи. Сторонники двенадцатеричной системы утверждают, что это особенно верно в отношении финансовых расчетов, в которых часто используются двенадцать месяцев в году.
Однако, когда повторяющиеся дроби действительно встречаются в двенадцатеричной системе счисления, они с меньшей вероятностью будут иметь очень короткий период, чем в десятичной системе счисления, поскольку 12 (двенадцать) находится между двумя простыми числами, 11 (одиннадцать) и 13 (тринадцать), тогда как является десятичным на составной номер 9. Тем не, наличие более короткого или более длинного периода не устраняет основного неудобства, заключающегося в том, что нельзя получить конечное представление для таких дробей в заданной базе (поэтому для их обработки необходимо округление, которое вносит неточность, вычислений), и в целом более вероятно, что придется иметь дело с бесконечными различными цифрами, когда дроби выражаются в десяти выражениях, чем в двенадцатеричном виде, потому что одно из каждых трех последовательных чисел содержит простой множитель 3 в факторизации, тогда как только один из пяти содержит простой множитель 5. Все другие простые множители, кроме 2, не разделяются ни десятью, ни двенадцатью, поэтому они не влияют на относительную вероятность встретить повторяющиеся цифры (любая несократимая дробь, которая содержит любое из этих других множителей в своем знаменателе, будет повторяться в любом основании). Кроме того, простой множитель 2 появляется дважды при факторизации двенадцати и только один раз при разложении десяти; это означает, что большинство дробей, знаменатели которых имеют более степени двойки, имеют более короткое и удобное представление в двенадцатеричном виде, чем в десятичном (например, 1 / (2) = 0,25 = 0,3 двенадцать ; 1 / (2) = 0,125 десять = 0,16 двенадцать ; 1 / (2) = 0,0625 10 = 0,09 12 ; 1 / (2) = 0,03125 10 = 0,046 12 и т. Д.).
| Десятичное основание . Простые множители основания: 2, 5. Простые множители единицы ниже основания: 3. Простые множители единицы над основанием: 11. Все остальные простые числа: 7, 13, 17, 19, 23, 29, 31 | Двенадцатеричное основание . Простые множители основания: 2, 3. Простые множители единицы ниже основания: B. Простые множители единицы над основанием: 11. Все остальные простые множители: 5, 7, 15, 17, 1B, 25, 27 | ||||
| Доли | Простые множители. числа знаменатель | Позиционное представление | Позиционное представление | Простые множители. знаменателя | Дробь |
|---|---|---|---|---|---|
| 1/2 | 2 | 0,5 | 0; 6 | 2 | 1/2 |
| 1/3 | 3 | 0,3 | 0; 4 | 3 | 1/3 |
| 1/4 | 2 | 0,25 | 0; 3 | 2 | 1/4 |
| 1/5 | 5 | 0,2 | 0; 2497 | 5 | 1/5 |
| 1/6 | 2, 3 | 0,16 | 0; 2 | 2, 3 | 1/6 |
| 1/7 | 7 | 0,142857 | 0; 186A35 | 7 | 1/7 |
| 1/8 | 2 | 0,125 | 0; 16 | 2 | 1/8 |
| 1/9 | 3 | 0,1 | 0; 14 | 3 | 1/9 |
| 1/10 | 2, 5 | 0,1 | 0; 12497 | 2, 5 | 1 / A |
| 1/11 | 11 | 0,09 | 0; 1 | B | 1 / B |
| 1/12 | 2, 3 | 0,083 | 0; 1 | 2, 3 | 1/10 |
| 1/13 | 13 | 0,076923 | 0; 0B | 11 | 1/11 |
| 1/14 | 2, 7 | 0,0714285 | 0; 0A35186 | 2, 7 | 1/12 |
| 1/15 | 3, 5 | 0,06 | 0; 09724 | 3, 5 | 1/13 |
| 1/16 | 2 | 0,0625 | 0; 09 | 2 | 1/14 |
| 1/17 | 17 | 0,0588235294117647 | 0; 08579214B36429A7 | 15 | 1/15 |
| 1/18 | 2, 3 | 0,05 | 0; 08 | 2, 3 | 1/16 |
| 1/19 | 19 | 0,052631578947368421 | 0; 076B45 | 17 | 1/17 |
| 1/20 | 2, 5 | 0,05 | 0; 07249 | 2, 5 | 1/18 |
| 1/21 | 3, 7 | 0,047619 | 0; 06A3518 | 3, 7 | 1/19 |
| 1/22 | 2, 11 | 0,045 | 0; 06 | 2, B | 1 / 1A |
| 1/23 | 23 | 0,0434782608695652173913 | 0; 06316948421 | 1B | 1 / 1B |
| 1/24 | 2, 3 | 0,0416 | 0; 06 | 2, 3 | 1/20 |
| 1/25 | 5 | 0,04 | 0; 05915343A0B62A68781B | 5 | 1/21 |
| 1/26 | 2, 13 | 0,0384615 | 0; 056 | 2, 11 | 1/22 |
| 1/27 | 3 | 0,037 | 0; 054 | 3 | 1/23 |
| 1/28 | 2, 7 | 0,03571428 | 0; 05186A3 | 2, 7 | 1/24 |
| 1/29 | 29 | 0,0344827586206896551724137931 | 0; 04B7 | 25 | 1/25 |
| 1/30 | 2, 3, 5 | 0,03 | 0; 04972 | 2, 3, 5 | 1/26 |
| 1/31 | 31 | 0,032258064516129 | 0; 0478AA093598166B74311B28623A55 | 27 | 1/27 |
| 1/32 | 2 | 0,03125 | 0; 046 | 2 | 1/28 |
| 1/33 | 3, 11 | 0,03 | 0; 04 | 3, B | 1/29 |
| 1/34 | 2, 17 | 0,02941176470588235 | 0; 0429A708579214B36 | 2, 15 | 1 / 2A |
| 1/35 | 5, 7 | 0,0285714 | 0; 0414559B3931 | 5, 7 | 1 / 2B |
| 1/36 | 2, 3 | 0,027 | 0; 04 | 2, 3 | 1/30 |
Длина двенадцатеричного периода 1 / n составляет (в основе 10)
Длина двенадцатеричного периода 1 / (n-е простое число) составляет (по основанию 10)
Наименьшее простое число с двенадцатеричным периодом (по основанию 10):
Представления иррациональных чисел в любой позиционной системе счисления (включая десятичную и двенадцатеричную) ни завершение, ни повторение. В следующей таблице приведены первые цифры некоторых важных алгебраических и трансцендентных чисел в десятичном, так и в двенадцатеричном формате.
| Алгебраическое иррациональное число | В десятичном формате | В двенадцатеричном формате |
|---|---|---|
| √2 квадратный корень из 2 | 1.414213562373... | 1; 4B79170A07B8... |
φ (phi), золотое сечение =  | 1.618033988749... | 1; 74BB6772802A... |
| Трансцендентное число | В десятичном формате | В двенадцатеричном формате |
| π (пи) отношение длины окружности круга до его диаметра | 3,141592653589... | 3; 184809493B91... |
| e, основание натурального логарифма | 2,718281828459... | 2; 875236069821... |
