Диэдральная группа порядка 6

редактировать

Некоммутативная группа с 6 элементами

граф Кэли с перестановками треугольника

Цикл граф с матрицей перестановок 3 элементов. (генераторы a и b такие же, как на графике Кэли, показанном выше.)

Таблица Кэли как таблица умножения матрицы перестановок

Позиции шести элементов в таблице Кэли. Только нейтральные элементы симметричны главной диагонали, поэтому эта группа не абелева.

таблица Кэли, как общая (и специальная ) линейная группа GL (2, 2)

В математике, D3(иногда альтернативно обозначается D6) - это группа диэдра степени 3, или, другими словами, группа диэдра порядка 6. Она изоморфна симметрической группе S3степени 3. Это также наименьшая возможная неабелева группа.

Эта страница иллюстрирует многие концепции групп на примере этой группы.

Содержание

1 Группы симметрии
2 Перестановки набора из трех объектов
3 Сводка групповых операций
4 Классы сопряженности
5 Подгруппы
6 Полупрямые продукты
7 Групповое действие
- 7.1 Орбиты и стабилизаторы
8 Теория представлений
9 См. Также
10 Ссылки
11 Внешние ссылки

Группы симметрии

Группа диэдра D 3 - это группа симметрии равностороннего треугольника, то есть это набор всех преобразований, таких как отражение, вращение и их комбинации, которые оставляют форму и положение этого треугольника фиксировано. В случае D 3 каждая возможная перестановка вершин треугольника составляет такое преобразование, так что группа этих симметрий изоморфна симметричной группе S 3 всех перестановок трех различных элементов. Это не относится к группам диэдра высших порядков.

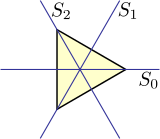
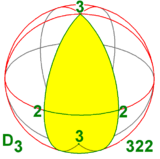
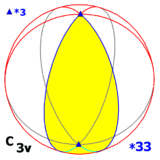
Диэдральная группа D 3 изоморфна двум другим группам симметрии в трех измерениях:

одной с 3-кратной осью вращения и перпендикулярной 2-кратной осью вращения (отсюда три из них) : D 3
один с 3-кратной осью вращения в плоскости отражения (и, следовательно, также в двух других плоскостях отражения): C 3v

Перестановки набора из трех объектов

Рассмотрим три окрашенных блоки (красный, зеленый и синий), изначально размещенные в порядке RGB. Симметричная группа S3является тогда группой всех возможных перегруппировок этих блоков. Если мы обозначим через a действие «поменять местами первые два блока», а через b действие «поменять местами последние два блока», мы можем записать все возможные перестановки в терминах этих двух действий.

В мультипликативной форме мы традиционно пишем xy для комбинированного действия «сначала сделай y, затем сделай x»; так что ab - это действие RGB ↦ RBG ↦ BRG, то есть «взять последний блок и переместить его на передний план». Если мы напишем e для «оставить блоки такими, какие они есть» (идентифицирующее действие), тогда мы можем записать шесть перестановок из набора из трех блоков как следующие действия:

e: RGB ↦ RGB или ()
a: RGB ↦ GRB или (RG)
b: RGB ↦ RBG или (GB)
ab: RGB ↦ BRG или (RBG)
ba: RGB ↦ GBR или (RGB)
aba: RGB ↦ BGR или (RB)

Обозначение в скобках - это обозначение цикла .

Обратите внимание, что действие aa имеет эффект RGB ↦ GRB ↦ RGB, оставляя блоки такими, какими они были; поэтому мы можем написать aa = e. Аналогично,

bb = e,
(aba) (aba) = e и
(ab) (ba) = (ba) (ab) = e;

поэтому каждое из вышеуказанных действий имеет обратное.

Путем проверки мы также можем определить ассоциативность и замыкание (две из необходимых аксиом группы ); обратите внимание, например, что

(ab) a = a (ba) = aba и
(ba) b = b (ab) = bab.

Группа неабелева, поскольку для Например, ab ≠ ba. Поскольку он построен из основных действий a и b, мы говорим, что набор {a, b} порождает его.

Группа имеет презентацию

⟨r, a ∣ r 3 = 1, a 2 = 1, ara = r - 1⟩ {\ displaystyle \ langle r, a \ mid r ^ { 3} = 1, a ^ {2} = 1, ara = r ^ {- 1} \ rangle}

\ langle r, a \ mid r ^ {3} = 1, a ^ {2} = 1, ara = r ^ {{- 1}} \ rangle

, также записывается

⟨r, a ∣ r 3, a 2, arar⟩ { \ Displaystyle \ langle r, a \ mid r ^ {3}, a ^ {2}, arar \ rangle}

\ langle r, a \ mid r ^ {3}, a ^ {2}, arar \ rangle

или

⟨a, b ∣ a 2 = b 2 = (ab) 3 = 1⟩ {\ displaystyle \ langle a, b \ mid a ^ {2} = b ^ {2} = (ab) ^ {3} = 1 \ rangle}

\ langle a, b \ mid a ^ {2} = b ^ {2} = (ab) ^ {3} = 1 \ rangle

, также записывается как

⟨a, b ∣ a 2, b 2, (ab) 3⟩ {\ displaystyle \ langle a, b \ mid a ^ {2}, b ^ {2}, (ab) ^ {3} \ rangle}

\ langle a, b \ mid a ^ {2}, b ^ {2}, (ab) ^ {3} \ rangle

где a и b - перестановки, а r = ab - циклическая перестановка. Обратите внимание, что второе представление означает, что группа является группой Кокстера. (Фактически, все группы диэдра и симметрии являются группами Кокстера.)

Сводка групповых операций

С помощью генераторов a и b мы определяем дополнительные сокращения c: = aba, d: = ab и f: = ba, так что a, b, c, d, e и f - все элементы этой группы. Затем мы можем суммировать групповые операции в форме таблицы Кэли :

*	e	a	b	c	d	f
e	e	a	b	c	d	f
a	a	e	d	f	b	c
b	b	f	e	d	c	a
c	c	d	f	e	a	b
d	d	c	a	b	f	e
f	f	b	c	a	e	d

. Обратите внимание, что неравные неидентичные элементы только коммутируют, если они являются обратными друг другу. Следовательно, группа не имеет центра, то есть центр группы состоит только из единичного элемента.

Классы сопряженности

Мы можем легко выделить три вида перестановок трех блоков, классы сопряженности группы:

без изменений (), группа элемент порядка 1
, меняющий местами два блока: (RG), (RB), (GB), три элемента группы порядка 2
циклическая перестановка всех трех блоков: (RGB), ( RBG), два групповых элемента порядка 3

Например, (RG) и (RB) оба имеют форму (xy); перестановка букв R, G и B (а именно (GB)) меняет обозначение (RG) на (RB). Следовательно, если мы применим (GB), затем (RB), а затем обратное к (GB), которое также является (GB), в результате перестановка будет (RG).

Обратите внимание, что элементы сопряженной группы всегда имеют один и тот же порядок, но в целом два элемента группы, которые имеют одинаковый порядок, не обязательно должны быть сопряженными.

Подгруппы

Из теоремы Лагранжа мы знаем, что любая нетривиальная подгруппа группы с 6 элементами должна иметь порядок 2 или 3. В Фактически, две циклические перестановки всех трех блоков с идентичностью образуют подгруппу порядка 3, index 2, а перестановки двух блоков, каждый с идентичностью, образуют три подгруппы порядка 2, индекс 3. Существование подгрупп порядка 2 и 3 также является следствием теоремы Коши.

Первым упомянутым является {(), (RGB), (RBG)}, чередующаяся группа A3.

Левый смежный класс и правый смежный класс A 3 совпадают (как и для любой подгруппы индекса 2) и состоят из A 3 и набор из трех свопов {(RB), (RG), (BG)}.

Левые смежные классы {(), (RG)}:

{(), (RG)}
{(RB), (RGB)}
{(GB), (RBG)}

Правые смежные классы {(RG), ()}:

{(RG), ()}
{(RBG), (RB)}
{(RGB), (GB)}

Таким образом, A 3 является нормальным, а три другие нетривиальные подгруппы не являются. Фактор-группа G / A 3 изоморфна C 2.

$G = A 3 ⋊ H {\ displaystyle G = \ mathrm {A} _ {3} \ rtimes H}$ $G = {\ mathrm {A}} _ {3} \ rtimes H$ , полупрямой продукт, где H - подгруппа из двух элементов: () и одного из трех свопов. Это разложение также является следствием (частным случаем) теоремы Шура – Цассенхауза.

В терминах перестановок два групповых элемента G / A 3 представляют собой набор четных перестановок и набор нечетных перестановок.

Если исходная группа - это группа, созданная поворотом плоскости на 120 ° вокруг точки и отражением относительно прямой, проходящей через эту точку, то фактор-группа имеет два элемента, которые можно описать как подмножества «просто повернуть (или ничего не делать)» и «сделать зеркальное отображение ».

Обратите внимание, что для группы симметрии квадрата неравномерная перестановка вершин соответствует не зеркальному отображению, а операциям, недопустимым для прямоугольников, то есть повороту на 90 ° и применению диагональной оси отражения.

Полупрямые продукты

$C 3 ⋊ φ C 2 {\ displaystyle \ mathrm {C} _ {3} \ rtimes _ {\ varphi} \ mathrm {C} _ {2}}$ ${\ mathrm {C}} _ {3} \ rtimes _ {\ varphi} {\ mathrm {C} } _ {2}$ равно $C 3 × C 2 {\ displaystyle \ mathrm {C} _ {3} \ times \ mathrm {C} _ {2}}$ ${\ mathrm {C}} _ {3} \ times {\ mathrm {C}} _ {2}$ , если и φ (0), и φ ( 1) идентичны. Полупрямое произведение изоморфно группе диэдра порядка 6, если φ (0) - тождество, а φ (1) - нетривиальный автоморфизм C 3, который инвертирует элементы.

Таким образом получаем:

(n1, 0) * (n 2, h 2) = (n 1 + n 2, h 2)

(n1, 1) * (n 2, h 2) = (n 1 - n 2, 1 + h 2)

для всех n 1, n 2 в C 3 и h 2 в C 2. Более кратко,

(n 1, h 1) ∗ (n 2, h 2) = (n 1 + (- 1) h 1 n 2, h 1 + h 2) {\ displaystyle (n_ {1}, h_ {1}) * (n_ {2}, h_ {2}) = (n_ {1} + (- 1) ^ {h_ {1}} n_ {2}, h_ {1} + h_ {2})}

{\ displaystyle (n_ {1}, h_ {1}) * (n_ {2}, h_ {2}) = (n_ {1} + (- 1) ^ {h_ {1}} n_ {2}, h_ {1} + h_ {2})}

для всех n 1, n 2 в C 3 и h 1, h 2 в C 2.

В таблице Кэли:

	00	10	20	01	11	21
00	00	10	20	01	11	21
10	10	20	00	11	21	01
20	20	00	10	21	01	11
01	01	21	11	00	20	10
11	11	01	21	10	00	20
21	21	11	01	20	10	00

Обратите внимание, что для второй цифры у нас, по сути, есть таблица 2 × 2, с 3 × 3 равными значениями для каждой из этих 4 ячеек. первая цифра в левой половине таблицы такая же, как в правой половине, но верхняя половина отличается от нижней половины.

Для прямого продукта таблица такая же, за исключением того, что первые цифры нижняя половина таблицы - это s как в верхней половине.

Групповое действие

Рассмотрим D 3 геометрическим образом, как группу симметрии из изометрий плоскости, и рассмотрим соответствующее действие группы на наборе из 30 равномерно расположенных точек на окружности, пронумерованных от 0 до 29, с 0 на одной из осей отражения.

В этом разделе показаны концепции групповых действий для этого случая.

Действие G на X называется

транзитивным, если для любых двух x, y в X существует g в G такой, что g · x = y; это не тот случай
точный (или эффективный), если для любых двух различных g, h в G существует x в X такой, что g · x ≠ h · x; это так, потому что, за исключением идентичности, группы симметрии не содержат элементов, которые "ничего не делают"
свободны, если для любых двух различных g, h в G и всех x в X мы имеем g · x ≠ h · x; это не тот случай, потому что есть отражения

Орбиты и стабилизаторы

Орбиты 30 равномерно расположенных точек на окружности под действием группы D3

Орбита точки x в X - это набор элементов X, на которые x может быть перемещен элементами G. Орбита x обозначается Gx:

G x = {g ⋅ x ∣ g ∈ G} {\ displaystyle Gx = \ left \ {g \ cdot x \ mid g \ in G \ right \}}

Gx = \ left \ {g \ cdot x \ mid g \ in G \ right \}

Орбиты: {0, 10, 20}, {1, 9, 11, 19, 21, 29}, {2, 8, 12, 18, 22, 28}, {3, 7, 13, 17, 23, 27}, {4, 6, 14, 16, 24, 26} и {5, 15, 25}. Точки на орбите «эквивалентны». Если к узору применяется группа симметрии, то внутри каждой орбиты цвет будет одинаковым.

Множество всех орбит X под действием G записывается как X / G.

Если Y является подмножеством X, мы пишем GY для положим {g · y: y ∈ Y и g ∈ G}. Мы называем подмножество Y инвариантным относительно G, если GY = Y (что эквивалентно GY ⊆ Y). В этом случае G также действует на Y. Подмножество Y называется фиксированным относительно G, если g · y = y для всех g в G и всех y в Y. Объединение, например, две орбиты инвариантны относительно G, но не фиксированы.

Для каждого x в X мы определяем подгруппу стабилизатора из x (также называемую группой изотропии или маленькой группой ) как набор всех элементов в G, которые фиксируют x:

G x = {g ∈ G ∣ g ⋅ x = x} {\ displaystyle G_ {x} = \ {g \ in G \ mid g \ cdot x = x \} }

G_ {x} = \ {g \ in G \ mid g \ cdot x = x \}

Если x является точкой отражения (0, 5, 10, 15, 20 или 25), ее стабилизатор - это группа второго порядка, содержащая идентичность и отражение в x. В остальных случаях стабилизатор - тривиальная группа.

Для фиксированного x в X рассмотрим отображение из G в X, заданное формулой g ↦ g · x. Изображение этой карты представляет собой орбиту x, а совместное изображение представляет собой набор всех левых смежных классов G x. Стандартная теорема о факторах теории множеств затем дает естественную биекцию между G / G x и Gx. В частности, биекция задается как hG x ↦ h · x. Этот результат известен как теорема о стабилизаторе орбиты . В двух случаях малой орбиты стабилизатор нетривиален.

Если два элемента x и y принадлежат одной и той же орбите, то их подгруппы стабилизаторов, G x и G y, изоморфны. Точнее: если y = g · x, то G y = gG x g. В примере это применимо, например, для 5 и 25 - обе точки отражения. Отражение около 25 соответствует повороту на 10, отражение около 5 и повороту на -10.

Результат, тесно связанный с теоремой о стабилизаторе орбиты, - это лемма Бернсайда :

| X / G | = 1 | G | ∑ g ∈ G | X г | {\ displaystyle \ left | X / G \ right | = {\ frac {1} {\ left | G \ right |}} \ sum _ {g \ in G} \ left | X ^ {g} \ right |}

\ left | X / G \ right | = {\ frac {1} {\ left | G \ right |}} \ sum _ {g \ in G} \ left | X ^ {g} \ right |

где X - множество точек, зафиксированных g. То есть количество орбит равно среднему количеству точек, зафиксированных на один элемент группы.

Для идентичности все 30 точек фиксированы, для двух вращений - нет, а для трех отражений - по две: {0, 15}, {5, 20} и {10, 25}. Таким образом, среднее число витков составляет шесть.

Теория представлений

С точностью до изоморфизма эта группа имеет три неприводимых комплексных унитарных представления, которые мы будем называть $I {\ displaystyle I}$ $I$ (тривиальное представление), $ρ 1 {\ displaystyle \ rho _ {1}}$ $\ rho _ {1}$ и $ρ 2 {\ displaystyle \ rho _ {2}}$ $\ rho _ {2}$ , где нижний индекс указывает измерение. По своему определению как группа перестановок над набором из трех элементов, группа имеет представление на $C 3 {\ displaystyle \ mathbb {C} ^ {3}}$ $\ mathbb {C} ^ {3}$ путем перестановки элементов вектор, фундаментальное представление. Это представление не является неприводимым, поскольку оно распадается как прямая сумма $I {\ displaystyle I}$ $I$ и $ρ 2 {\ displaystyle \ rho _ {2}}$ $\ rho _ {2}$ . $I { \ displaystyle I}$ $I$ отображается как подпространство векторов вида $(λ, λ, λ), λ ∈ C {\ displaystyle (\ lambda, \ lambda, \ lambda), \ lambda \ in \ mathbb {C}}$ $(\ lambda, \ lambda, \ lambda), \ lambda \ in {\ mathbb {C }}$ и $ρ 2 {\ displaystyle \ rho _ {2}}$ $\ rho _ {2}$ - это представление в его ортогональном дополнении, которые являются векторами формы $(λ 1, λ 2, - λ 1 - λ 2) {\ displaystyle (\ lambda _ {1}, \ lambda _ {2}, - \ lambda _ {1} - \ lambda _ {2})}$ $(\ lambda _ {1}, \ lambda _ {2}, - \ lambda _ {1} - \ lambda _ {2})$ . Нетривиальное одномерное представление $ρ 1 {\ displaystyle \ rho _ {1}}$ $\ rho _ {1}$ возникает через группы $Z 2 {\ displaystyle \ mathbb {Z} _ {2}}$ $\ mathbb {Z} _ {2}$ оценка: Действие - это умножение на знак перестановки элемента группы. Каждая конечная группа имеет такое представление, поскольку по своему регулярному действию она является подгруппой циклической группы. Подсчет квадратных размеров представлений ( $1 2 + 1 2 + 2 2 = 6 {\ displaystyle 1 ^ {2} + 1 ^ {2} + 2 ^ {2} = 6}$ $1 ^ {2} + 1 ^ {2} + 2 ^ {2} = 6$ , порядок группы), мы видим, что это должны быть все неприводимые представления.

2-мерное неприводимое линейное представление дает 1-мерное проективное представление (т. е. действие на проективное строка, вложение в группу Мебиуса PGL (2, C )), поскольку эллиптическое преобразование. Это может быть представлено матрицами с элементами 0 и ± 1 (здесь записано как дробно-линейные преобразования ), известными как ангармоническая группа :

порядок 1: $z {\ displaystyle z}$ $z$
порядок 2: $1 - z, 1 / z, z / (z - 1) {\ displaystyle 1-z, 1 / z, z / (z-1)}$ $1-z, 1 / z, z / (z-1)$
порядок 3: $(z - 1) / z, 1 / (1 - z) {\ displaystyle (z-1) / z, 1 / (1-z)}$ $(z-1) / z, 1 / (1-z)$

и, таким образом, опускается до представления над любым полем, которое всегда верный / инъективный (поскольку никакие два термина не отличаются только знаком). Над полем с двумя элементами проективная прямая имеет только 3 точки, и это, таким образом, исключительный изоморфизм $S 3 ≈ P G L (2, 2). {\ displaystyle S_ {3} \ приблизительно \ mathrm {PGL} (2,2).}$ $S_ {3} \ приблизительно {\ mathrm { PGL}} (2,2).$ В характеристике 3 это вложение стабилизирует точку $- 1 = [- 1: 1], { \ displaystyle -1 = [- 1: 1],}$ $-1 = [- 1: 1],$ , поскольку $2 = 1/2 = - 1 {\ displaystyle 2 = 1/2 = -1}$ $2 = 1/2 = -1$ ( в характеристике больше 3 эти точки различны и переставлены и являются орбитой гармонического поперечного отношения ). Над полем из трех элементов проективная прямая имеет 4 элемента, и поскольку PGL (2, 3) изоморфна симметрической группе из 4 элементов, S 4, результирующее вложение $S 3 ↪ S 4 {\ displaystyle \ mathrm {S} _ {3} \ hookrightarrow \ mathrm {S} _ {4}}$ ${ \ mathrm {S}} _ {3} \ hookrightarrow {\ mathrm {S}} _ {4}$ равняется стабилизатору точки $- 1 {\ displaystyle -1}$ $-1$ .

См. Также

Группа диэдра порядка 8

Ссылки

Fraleigh, John B. (1993), A First Course in Abstract Algebra (5-е изд.), Addison-Wesley, pp. 93–94, ISBN 978-0-201-53467-2

Внешние ссылки

http://mathworld.wolfram.com/DihedGroupD3.html

	00	10	20	01	11	21
00	00	10	20	01	11	21
10	10	20	00	11	21	01
20	20	00	10	21	01	11
01	01	21	11	00	20	10
11	11	01	21	10	00	20
21	21	11	01	20	10	00

	00	10	20	01	11	21
00	00	10	20	01	11	21
10	10	20	00	11	21	01
20	20	00	10	21	01	11
01	01	21	11	00	20	10
11	11	01	21	10	00	20
21	21	11	01	20	10	00

	00	10	20	01	11	21
00	00	10	20	01	11	21
10	10	20	00	11	21	01
20	20	00	10	21	01	11
01	01	21	11	00	20	10
11	11	01	21	10	00	20
21	21	11	01	20	10	00