В теории групп, дициклическая группа (обозначение Dic nили Q4n, ⟨N, 2,2⟩) - особый вид неабелевой группы порядка 4n (n>1). Это расширение циклической группы порядка 2 посредством циклической группы порядка 2n, дающее имя дициклической. В обозначениях точных последовательностей групп это расширение может быть выражено как:

В общем, для любой конечной абелевой группы с элементом порядка 2, один может определять дициклическую группу.
Для каждого целого числа n>1 дициклическая группа Dic n может быть определена как подгруппа единицы сгенерированных кватернионов по

Более абстрактно, можно определить дициклическую группу Dic n как группа со следующим представлением

Некоторые моменты, на которые следует обратить внимание, вытекающие из этого определения:
Таким образом, каждый элемент Dic n можно однозначно записать как ax, где 0 ≤ к < 2n and j = 0 or 1. The multiplication rules are given by




Отсюда следует, что Dic n имеет порядок 4n.
Когда n = 2, дициклическая группа изоморфна к кватернионной группе Q. В более общем смысле, когда n является степенью 2, дициклическая группа изоморфна обобщенной группе кватернионов.
Для каждого n>1 дициклическая группа Dic n - неабелева группа порядка 4n. (Для вырожденного случая n = 1 группа Dic 1 является циклической группой C 4, которая не считается дициклической.)
Пусть A = ⟨a ⟩ Быть подгруппой Dic n, порожденной a. Тогда A - циклическая группа порядка 2n, поэтому [Dic n : A] = 2. Как подгруппа index 2, она автоматически является нормальной подгруппой. Фактор-группа Dic n / A является циклической группой порядка 2.
Dic n разрешима ; заметим, что A нормальна и, будучи абелевой, сама разрешима.
Дициклическая группа - это бинарная полиэдральная группа - это один из классов подгрупп группы Pin Pin - (2), которая является подгруппой группы Spin Spin (3) - и в этом контексте известна как бинарная группа диэдра .
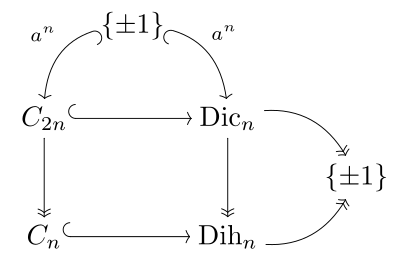
Связь с бинарная циклическая группа C2n, циклическая группа C n и диэдральная группа Dih n порядка 2n показаны на диаграмме справа и параллельны соответствующая диаграмма для группы Pin. Кокстер записывает двоичную группу диэдра как ⟨2,2, n⟩ и двоичную циклическую группу с угловыми скобками, n⟩.
Имеется внешнее сходство между дициклическими группами и диэдральными группами ; оба являются своего рода «зеркальным отражением» лежащей в основе циклической группы. Но представление группы диэдра будет иметь x = 1 вместо x = a; и это дает другую структуру. В частности, Dic n не является полупрямым произведением A и ⟨x⟩, поскольку A ∩ ⟨x⟩ нетривиально.
Дициклическая группа имеет уникальную инволюцию (т.е. элемент порядка 2), а именно x = a. Обратите внимание, что этот элемент находится в центре Dic n. Действительно, центр состоит исключительно из единицы и x. Если мы добавим отношение x = 1 к представлению Dic n, мы получим представление группы диэдра Dih 2n, поэтому фактор-группа Dic n/
Существует естественный гомоморфизм 2-к-1 от группы единичных кватернионов к 3-мерной группе вращения, описанной в кватернионах и пространственные вращения. Поскольку дициклическая группа может быть вложена внутрь единичных кватернионов, можно спросить, каков ее образ при этом гомоморфизме. Ответ прост: группа симметрии диэдра Dih n. По этой причине дициклическая группа также известна как бинарная диэдральная группа . Обратите внимание, что дициклическая группа не содержит никакой подгруппы, изоморфной Dih n.
. Аналогичная конструкция прообраза с использованием Pin + (2) вместо Pin - (2) дает другая группа диэдра, Dih 2n, а не дициклическая группа.
Пусть A будет абелевой группой, имеющей определенный элемент y в A с порядком 2. Группа G называется обобщенной дициклической группой, записанный как Dic (A, y), если он генерируется A и дополнительным элементом x, и, кроме того, мы имеем, что [G: A] = 2, x = y, и для все a в A, xax = a.
Поскольку для циклической группы четного порядка всегда существует уникальный элемент порядка 2, мы можем видеть, что дициклические группы - это просто особый тип обобщенной дициклической группы.