Выводы преобразований Лоренца

Существует множество способов получения преобразований Лоренца с использованием различных физических принципов, начиная с уравнений Максвелла до постулатов специальной теории относительности Эйнштейна и математических инструментов, начиная с элементарной алгебры и гиперболических функций, к линейной алгебре и теории групп.

В этой статье представлены некоторые из наиболее простых для использования в контексте специальной теории относительности для простейшего случая теории Лоренца. ускорение в стандартной конфигурации, т.е. две инерциальные системы, движущиеся относительно друг друга с постоянной (равномерной) относительной скоростью, меньше, чем скорость света, и с использованием Декартовы координаты так, чтобы оси x и x лежали на одной прямой.

• 1 Историческая справка
• 3 Преобразование Лоренца
• 3 Физические принципы
  • 3.1 Второй постулат
  • 3.2 Инвариантность интервала
• 4 Стандартная конфигурация
• 5 Решения
• 6 Использование геометрии пространства-времени
  • 6.1 Решение Ландау и Лифшица
  • 6.2 Гиперболическое вращение
• 7 Из физических принципов
  • 7.1 Замедление времени и длины длины
  • 7.2 Сферические волновые фронты света
  • 7.3 Галилеев и относительность Эйнштейна
    • 7.3.1 Галилеевы системы отсчета
    • 7.3.2 Использование принципа относительности
    • 7.3.3 Определение констант первого уравнения
    • 7.3.4 Определение констант второго уравнения
  • 7.4 Популярный вывод Эйнштейна
• 8 Использование теории групп
  • 8.1 На основе групповых постулатов
  • 8.2 Повышение от генераторов
• 9 На основе экспериментов
• 10 См. Также
• 11 Примечания
• 12 Ссылки

В фундаментальных разделах современной физики, а именно в общей теории относительности и ее широко применяемых сложного подмножества специальной теории относительности, а также релятивистской квантовой механики и релятивистской квантовой теории поля, преобразование Лоренца является одним из правил преобразования, согласно которому все правилаом преобразования четырехвекторы и тензоры, содержащие физические величины, преобразуются из одной системы отсчета в другую.

Яркими примерами таких четырех векторов являются четыре позиции и четыре импульса частиц, а для полей электромагнитный тензор и тензор энергии-импульса. Тот факт, что эти объекты трансформируются в соответствии с преобразованием Лоренца, математически определяет их как и тензоры; см. определение в тензор.

Данные четырех векторов или тензоров в одном кадре, «правило преобразования» позволяет определить измененные компоненты тех же четырех векторов или тензоров в другом кадре, которые могут быть увеличены или ускорены относительно к исходному кадру. «Повышение» не следует объединять с пространственным перемещением, оно скорее показывает относительной скоростью между кадрами. Само правило преобразования зависит от относительного движения кадров. В простейшем случае двух инерциальных систем относительная скорость между ними входит в правило преобразования. Для вращающихся систем отсчета или неинерциальных систем отсчета требуются дополнительные параметры, включая относительную скорость (направление и направление), ось вращения и угол поворота.

Обычная трактовка (например, оригинальная работа Альберта Эйнштейна ) основана на неизменности скорости света. Однако это не обязательно является отправной точкой: действительно (как показано, например, во втором томе Курса теоретической физики Ландау и Лифшицем ), то на самом деле речь идет о локальности ответственностьий: ответственность, что влияние, которое, скажем, одна частица оказывает на другую, не может передаваться мгновенно. Следовательно, существует теоретическая максимальная скорость передачи информации, которая должна быть инвариантной, и оказывается, что эта скорость совпадает со скоростью света в вакууме. Ньютон сам назвал идею действия на расстоянии философски «абсурдной» и считал, что гравита должна передаваться неким агентом в соответствии с определенными законами.

Майкельсон и Морли в 1887 году разработал эксперимент с использованием интерферометра и наполовину посеребренного зеркала, который был достаточно точным, чтобы поток эфира. Система зеркал отражала свет обратно в интерферометр. Если бы он имел место дрейф эфира, он вызвал бы фазовый сдвиг и изменение интерференции, которое было бы обнаружено. Однако фазового сдвига обнаружено не было. Отрицательный результат эксперимента Майкельсона-Морли оставил подрыв концепции эфира (или его дрейфа). Вследствие этого возникло недоумение относительно того, почему свет, очевидно, ведет себя как волна, без какой-либо обнаруживаемой среды, через которую может распространяться волновая активность.

В статье 1964 года Эрик Кристофер Зееман показал, что причинно-следственная связь сохраняет свойство, условие, более слабое в математическом смысле, чем неизменность скорости света., достаточно, чтобы устойчивость, преобразование координат преобразователей Лоренца. В статье Нормана Гольдштейна показан аналогичный результат с использованием инерции (временных линий).

Эйнштейн основал свою теорию относительности на двух фундаментальных постулатах.. Во-первых, все физические законы одинаковы для всех инерциальных отсчетов, независимо от их относительного системного состояния; и, во-вторых, скорость света в свободном положении одинакова во всех инерциальных системах, независимо от относительной скорости каждой системы отсчета. Преобразование Лоренца, по сути, является следствием этого второго постулата.

Второй постулат

Предположим второй постулат специальной теории относительности, утверждающий постоянство скорости света, независимо от системы отсчета, и рассмотрим набор движущихся систем отсчета. относительно друг друга с постоянной скоростью, то есть инерциальными системами, каждое из которых снабжено собственным набором декартовых координат, обозначающих точки, то есть событий -времени. Чтобы выразить инвариантность скорости света в математической форме, зафиксируйте два события в системе отсчета времени. Пусть первым событием будет излучение светового сигнала, вторым - его поглощение.

Выберите любой опорный кадр в коллекции. В его координатах первому событию были присвоены координаты , а второй $x\; 2,\; y\; 2,\; z\; 2,\; ct\; 2\; \{\backslash \; displaystyle\; x\_\; \{2\},\; y\_\; \{2\},\; z\_\; \{2\},\; ct\_\; \{2\}\}$. Пространственное расстояние между излучением и поглощением составляет $(x\; 2\; -\; x\; 1)\; 2\; +\; (y\; 2\; -\; y\; 1)\; 2\; +\; (z\; 2\; -\; z\; 1)\; 2\; \{\backslash \; displaystyle\; \{\backslash \; sqrt\; \{(x\_\; \{2\}\; -\; x\_)\; \{1\})\; ^\; \{2\}\; +\; (y\_\; \{2\}\; -y\_\; \{1\})\; ^\; \{2\}\; +\; (z\_\; \{2\}\; -z\_\; \{1\})\; ^\; \{2\}\}\}\}$, но это также расстояние $c\; (t\; 2\; -\; t\; 1)\; \{\backslash \; displaystyle\; c\; (t\_\; \{2\}\; -t\_\; \{1\})\}$, пройденное сигналом. Следовательно, можно составить уравнение

$c\; 2\; (t\; 2\; -\; t\; 1)\; 2\; -\; (x\; 2\; -\; x\; 1)\; 2\; -\; (y\; 2\; -\; y\; 1)\; 2\; -\; (z\; 2\; -\; z\; 1)\; 2\; =\; 0.\; \{\backslash \; стиль\; отображения\; c\; ^\; \{2\}\; (t\_\; \{2\}\; -t\_\; \{1\})\; ^\; \{2\}\; -\; (x\_\; \{2\}\; -x\_\; \{1\})\; ^\; \{2\}\; -\; (y\_\; \{2\}\; -y\_\; \{1\})\; ^\; \{2\}\; -\; (z\_\; \{2\}\; -z\_\; \{1\})\; ^\; \{2\}\; =\; 0.\}$

Каждая другая система координат будет записывать в своих собственных координатах то же уравнение. Это непосредственное математическое следствие неизменности скорости света. Величина слева называется пространственно-временным интервалом. Интервал для событий, разделенных световыми сигналами, одинаково (ноль) во всех системах отсчета и поэтому называется инвариантом.

Инвариантностью интервала

Для преобразования Лоренца, иметь физическое значение Реализованный по своей природе, чтобы очень важно, чтобы интервал был инвариантной мерой для любых двух событий, а не только для тех, которые разделены световыми сигналами. Чтобы установить это, рассмотрим бесконечно малый интервал,

$ds\; 2\; =\; c\; 2\; dt\; 2\; -\; dx\; 2\; -\; dy\; 2\; -\; dz\; 2,\; \{\backslash \; displaystyle\; ds\; ^\; \{2\}\; =\; c\; ^\; \{2\}\; dt\; ^\; \{2\}\; -\; dx\; ^\; \{2\}\; -dy\; ^\; \{2\}\; -dz\; ^\; \{2\},\}$

как записано в системе $K\; \{\backslash \; displaystyle\; K\}$. Пусть $K\; \prime \; \{\backslash \; displaystyle\; K\; \text{'}\}$будет другой системой, назначающей интервал $ds\; \prime \; 2\; \{\backslash \; displaystyle\; ds\text{'}\; ^\; \{2\}\}$одним и тем же двум бесконечно разделенные события. Если $ds\; 2\; =\; 0\; \{\backslash \; displaystyle\; ds\; ^\; \{2\}\; =\; 0\}$, то интервал будет равен нулю в любой другой системе (второй постулат), а поскольку $ds\; 2\; \{\; \backslash \; displaystyle\; ds\; ^\; \{2\}\}$и $ds\; \prime \; 2\; \{\backslash \; displaystyle\; ds\; \text{'}^\; \{2\}\}$- бесконечно малые величины одного порядка, они должны быть пропорциональны каждому другому,

$ds\; 2\; =\; ads\; \prime \; 2.\; \{\backslash \; displaystyle\; ds\; ^\; \{2\}\; =\; ads\; \text{'}^\; \{2\}.\}$

От чего может зависеть $a\; \{\backslash \; displaystyle\; a\}$? Это может не зависеть от положения двух событий в визуальном времени, потому что это нарушит постулируемую однородность пространства-времени. Это может зависеть от относительной скорости $V\; \prime \; \{\backslash \; displaystyle\; V\; \text{'}\}$между $K\; \{\backslash \; displaystyle\; K\}$и $K\; \prime \; \{\backslash \; displaystyle\; K\text{'}\; \}$, но только по скорости, а не по направлению, потому что последнее нарушило бы изотропию пространства.

Теперь введите системы $K\; 1\; \{\backslash \; displaystyle\; K\_\; \{1\}\}$и $K\; 2\; \{\backslash \; displaystyle\; K\_\; \{2\}\}$,

$ds\; 2\; =\; a\; (\; V\; 1)\; ds\; 1\; 2,\; ds\; 2\; =\; a\; (V\; 2)\; ds\; 2\; 2,\; ds\; 1\; 2\; =\; a\; (V\; 12)\; ds\; 2\; 2.\; \{\backslash \; displaystyle\; ds\; ^\; \{2\}\; =\; a\; (V\_\; \{1\})\; ds\_\; \{\; 1\}\; ^\; \{2\},\; \backslash \; quad\; ds\; ^\; \{2\}\; =\; a\; (V\_\; \{2\})\; ds\_\; \{2\}\; ^\; \{2\},\; \backslash \; quad\; ds\_\; \{1\}\; ^\; \{2\}\; =\; a\; (V\_\; \{12\})\; ds\_\; \{2\}\; ^\; \{2\}.\}$

Отсюда следует,

$a\; (V\; 2)\; a\; (V\; 1)\; =\; a\; (V\; 12).\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{a\; (V\_\; \{2\})\}\; \{a\; (V\_\; \{1\})\}\}\; =\; a\; (V\_\; \{12\}).\}$

Теперь можно заметить, что в правой части $V\; 12\; \{\backslash \; displaystyle\; V\_\; \{12\}\}$зависит как от $V\; 1\; \{\backslash \; displaystyle\; V\_\; \{1\}\}$, так и от $V\; 2\; \{\backslash \; displaystyle\; V\_\; \{2\}\}$; а также от угла между векторами $V\; 1\; \{\backslash \; displaystyle\; \{\backslash \; textbf\; \{V\}\}\; \_\; \{1\}\}$и $V\; 2\; \{\backslash \; displaystyle\; \{\backslash \; textbf\; \{V\}\}\; \_\; \{\; 2\}\}$. Однако можно также заметить, что левая часть не зависит от этого угла. Таким образом, единственный способ сохранить истинность уравнения - это если функция $a\; (V)\; \{\backslash \; displaystyle\; a\; (V)\}$является константой. Далее, по же уравнению эта постоянная равная единице. Таким образом,

$ds\; 2\; =\; ds\; \prime \; 2\; \{\backslash \; displaystyle\; ds\; ^\; \{2\}\; =\; ds\; \text{'}^\; \{2\}\}$

для всех систем $K\; \prime \; \{\backslash \; displaystyle\; K\text{'}\}$. Это верно для всех бесконечно малых интервалов, это верно для всех интервалов.

Большинство, если не все, выводы преобразований Лоренца принимают это как должное [Неясно, что такое "это". "Это" то, что пространственно-временные интервалы равны? Или "это" то, что верно для всех бесконечно малых интервалов, также верно для всех интервалов? ]. В этих выводах они используют только постоянство скорости света (инвариантность светоподобных отдельных событий). Этот результат гарантирует, что преобразование Лоренца является правильным преобразованием [опять же неясно, что означает «Это»].

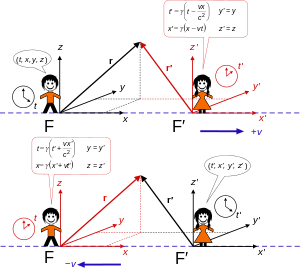
Пространственно-временные координаты событий, наблюдаемые каждым наблюдателем в их инерциальной системе отсчета (в стандартной конфигурации), показаны в речевых пузырях.. Вверху: кадр F ′ движется со скоростью v по оси x кадра F.. Внизу: кадр F движется со скоростью -v вдоль оси x ′ кадра F′.

. Можно увидеть инвариантный интервал как функция неположительно определенного промежутка времени. Набор искомых преобразователей должен оставлять это расстояние неизменным. Из-за декартовой природы системы координат системы отсчета можно сделать вывод, что, как и в евклидовом случае, возможные преобразования состоят из сдвигов и вращений, при этом для термина «вращение» следует допускать несколько более широкое.

Интервал тривиально инвариантен относительно перевода. Для поворотов есть четыре координаты. Следовательно, есть шесть плоскостей вращения. Три из них - это вращения в пространственных плоскостях. Интервал инвариантен и относительно обычных поворотов.

Осталось найти «вращение» в трех оставшихся координатных плоскостях, которое оставляет интервал инвариантным. Точно так же найти способ назначить координаты, чтобы они совпадали с координатами, системой движущейся системы отсчета.

Общая проблема состоит в том, чтобы найти такое преобразование, что

$c\; 2\; (t\; 2\; -\; t\; 1)\; 2\; -\; (x\; 2\; -\; x\; 1)\; 2\; -\; (y\; 2\; -\; y\; 1)\; 2\; -\; (z\; 2\; -\; z\; 1)\; 2\; =\; c\; 2\; (t\; 2\; \prime \; -\; t\; 1\; \prime )\; 2\; -\; (x\; 2\; \prime \; -\; x\; 1\; \prime )\; 2\; -\; (y\; 2\; \prime \; -\; y\; 1\; \prime )\; 2\; -\; (z\; 2\; \prime \; -\; z\; 1\; \text{'})\; 2.\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash ,\; \backslash ,\; \backslash ,\; \backslash ,\; \backslash ,\; \backslash ,\; \backslash ,\; \backslash ,\; c\; ^\; \{2\}\; (t\_\; \{2\}\; -t\_\; \{1\})\; ^\; \{2\; \}\; -\; (x\_\; \{2\}\; -x\_\; \{1\})\; ^\; \{2\}\; -\; (y\_\; \{2\}\; -y\_\; \{1\})\; ^\; \{2\}\; -\; (z\_\; \{2\}\; -z\_\; \{1\})\; ^\; \{2\}\; \backslash \; \backslash \; =\; c\; ^\; \{2\}\; (t\_\; \{2\}\; \text{'}-\; t\_\; \{1\}\text{'})\; ^\; \{2\}\; -\; (x\_\; \{2\}\; \text{'}-\; x\_\; \{1\}\text{'})\; ^\; \{2\}\; -\; (y\_\; \{2\}\; \text{'}\; -\; y\_\; \{1\}\; \text{'})\; ^\; \{2\}\; -\; (z\_\; \{2\}\text{'}\; -\; z\_\; \{1\}\; \text{'})\; ^\; \{2\}.\; \backslash \; End\; \{align\}\}\}$

Для решения общей проблемы можно использовать знание об инвариантности перемещений и обычных вращений, чтобы предположить, без ограничения общности, что кадры F и F 'выровнены таким образом, что оси их координат все пересекаются в t = t '= 0 и что оси x и x' выровнен, и система F 'имеет скорость V вдоль положительной оси x. Назовите это стандартной конфигурацией. Это сводит общую проблему к нахождению такого преобразования, что

$c\; 2\; (t\; 2\; -\; t\; 1)\; 2\; -\; (x\; 2\; -\; x\; 1)\; 2\; =\; c\; 2\; (t\; 2\; \prime \; -\; t\; 1\; \prime )\; 2\; -\; (x\; 2\; \prime \; -\; x\; 1\; \prime )\; 2.\; \{\backslash \; displaystyle\; c\; ^\; \{2\}\; (t\_\; \{2\}\; -t\_\; \{1\})\; ^\; \{2\}\; -\; (x\_\; \{2\}\; -x\_\; \{1\})\; ^\; \{2\}\; =\; c\; ^\; \{\; 2\}\; (t\_\; \{2\}\; \text{'}-t\_\; \{1\}\text{'})\; ^\; \{2\}\; -\; (x\_\; \{2\}\; \text{'}-\; x\_\; \{1\}\text{'})\; ^\; \{2\}.\}$

Стандартная конфигурация, используемая в большинстве примеров ниже. Линейное решение более простые задачи

$c\; 2\; t\; 2\; -\; x\; 2\; =\; c\; 2\; t\; \prime \; 2\; -\; x\; \prime \; 2\; \{\backslash \; displaystyle\; c\; ^\; \{2\}\; t\; ^\; \{2\}\; -x\; ^\; \{2\}\; =\; c\; ^\; \{2\}\; t\; \text{'}^\; \{2\}\; -x\text{'}\; ^\; \{2\}\}$

решает более общую проблему, поскольку разности координат преобразуются таким же образом. При рассмотрении этой простой проблемы в литературе обычно аргументируется линейность. Это решение не является линейным, то оно не решает исходную задачу из-за перекрестных членов, появляющихся при расширении квадратов.

Как уже упоминалось, общая проблема решается переводом в пространство-время. Они не кажутся решением более простой поставленной задачи, в отличие от бустов (а иногда и поворотов в зависимости от угла атаки). Еще больше решений существует, если настаивать только на неизменности интервала для светоподобных разделенных событий. Это нелинейные конформные («сохраняющие угол») преобразования. Имеются

преобразования Лоренца ⊂ преобразования Пуанкаре ⊂ преобразования конформных групп.

Некоторые уравнения физики конформно инвариантны, например уравнения Максвелла в пространстве, свободном от источников, но не все. Релевантность конформных преобразований в пространстве-времени в настоящее время неизвестна, но конформная группа в двух измерениях очень актуальна в конформной теории поля и статистической механике. Таким образом, именно группа Пуанкаре выделяется постулатами специальной теории относительности. Именно наличие лоренцевых бустов (для которых сложение скоростей отличается от простого сложения, которое допускает бы скорость, превышение скорости света) в отличие от обычных бустеров, которые отделяют его от галилеевского группы из относительности Галилея. Пространственные вращения, пространственные и временные инверсии и трансляции происходят в электрических источниках и теориях (законы сохранения энергии и углового момента). Не все принятые теории соблюдают симметрию относительно инверсий.

Решение Ландау и Лифшица

Три формулы формулы гиперболических функций (H1 - H3).

$1.\; cosh\; 2\; \; \Psi \; -\; sinh\; 2\; \; \Psi \; =\; 1,\; 2.\; sinh\; \; \Psi \; =\; tanh\; \; \Psi \; 1\; -\; tanh\; 2\; \; \Psi ,\; 3.\; cosh\; \; \Psi \; =\; 1\; 1\; -\; tanh\; 2\; \; \Psi ,\; \{\backslash \; displaystyle\; \{\backslash \; text\; \{1.\; \}\}\; \backslash \; cosh\; ^\; \{2\}\; \backslash \; Psi\; -\; \backslash \; sinh\; ^\; \{2\}\; \backslash \; Psi\; =\; 1,\; \backslash \; quad\; \{\backslash \; text\; \{2.\; \}\}\; \backslash \; sinh\; \backslash \; Psi\; =\; \{\backslash \; frac\; \{\backslash \; tanh\; \backslash \; Psi\}\; \{\backslash \; sqrt\; \{1-\; \backslash \; tanh\; ^\; \{2\}\; \backslash \; Psi\}\}\},\; \backslash \; quad\; \{\backslash \; text\; \{3.\; \}\}\; \backslash \; cosh\; \backslash \; Psi\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sqrt\; \{1-\; \backslash \; tanh\; ^\; \{2\}\; \backslash \; Psi\}\}\},\}$

Проблема, поставленная в стандартной конфигурации для повышения в в направлении x, где штрихованные координаты относительной движущейся системы, решаются путем нахождения линейного решения более простых задач

$c\; 2\; t\; 2\; -\; x\; 2\; =\; c\; 2\; t\; \prime \; 2\; -\; x\; \prime \; 2.\; \{\backslash \; displaystyle\; c\; ^\; \{2\}\; t\; ^\; \{2\}\; -x\; ^\; \{2\}\; =\; c\; ^\; \{2\}\; t\; \text{'}^\; \{2\}\; -x\text{'}\; ^\; \{2\}.\}$

Наиболее эффективное общее решение: можно проверить прямую заменой с помощью (H1),

$x\; =\; x\; \prime \; ch\; \; \Psi \; +\; ct\; \prime \; sinh\; \; \Psi ,\; ct\; =\; x\; \prime \; sinh\; \; \Psi \; +\; ct\; \prime \; ch\; \Psi .\; \{\backslash \; displaystyle\; x\; =\; x\; \text{'}\backslash \; cosh\; \backslash \; Psi\; +\; ct\text{'}\; \backslash \; sinh\; \backslash \; Psi,\; \backslash \; quad\; ct\; =\; x\; \text{'}\backslash \; sinh\; \backslash \; Psi\; +\; ct\text{'}\; \backslash \; cosh\; \backslash \; Psi.\}$

(1)

Чтобы найти роль Ψ в физическом окружении, запишите прогрессию происхождения F ', т.е. х '= 0, х = vt. Уравнения используются (используя сначала x '= 0),

$x\; =\; c\; t\; \prime \; sinh\; \; \Psi ,\; c\; t\; =\; c\; t\; \prime \; ch\; \Psi .\; \{\backslash \; displaystyle\; x\; =\; ct\; \text{'}\backslash \; sinh\; \backslash \; Psi,\; \backslash \; quad\; ct\; =\; ct\text{'}\; \backslash \; cosh\; \backslash \; Psi.\}$

Теперь разделите:

$xct\; =\; tanh\; \; \Psi \; =\; vc\; \Rightarrow \; sinh\; \; \Psi \; =\; vc\; 1\; -\; v\; 2\; с\; 2,\; сш\; \; \Psi \; знак\; равно\; 1\; 1\; -\; v\; 2\; с\; 2,\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{x\}\; \{ct\}\}\; =\; \backslash \; tanh\; \backslash \; Psi\; =\; \{\backslash \; frac\; \{v\}\; \{c\}\}\; \backslash \; Rightarrow\; \backslash \; quad\; \backslash \; sinh\; \backslash \; Psi\; =\; \{\backslash \; frac\; \{\backslash \; frac\; \{v\}\; \{c\}\}\; \{\backslash \; sqrt\; \{1\; -\; \{\backslash \; frac\; \{v\; ^\; \{2\}\}\; \{c\; ^\; \{2\}\}\}\}\}\},\; \backslash \; quad\; \backslash \; cosh\; \backslash \; Psi\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sqrt\; \{1\; -\; \{\backslash \; frac\; \{v\; ^\; \{2\}\}\; \{c\; ^\; \{2\}\}\}\}\}\},\}$

где x = vt использовалось на первом этапе, ( H2) и (H3) во втором, что при повторном подключении к (1)дает

$x\; =\; x\; \prime \; +\; vt\; \prime \; 1\; -\; v\; 2\; c\; 2,\; t\; знак\; равно\; t\; \text{'}+\; vc\; 2\; x\text{'}\; 1\; -\; v\; 2\; c\; 2,\; \{\backslash \; displaystyle\; x\; =\; \{\backslash \; frac\; \{x\; \text{'}+\; vt\text{'}\}\; \{\backslash \; sqrt\; \{1\; -\; \{\backslash \; frac\; \{v\; ^\; \{2\}\}\; \{c\; ^\; \{2\; \}\}\}\}\}\},\; \backslash \; quad\; t\; =\; \{\backslash \; frac\; \{t\; \text{'}+\; \{\backslash \; frac\; \{v\}\; \{c\; ^\; \{2\}\}\}\; x\text{'}\}\; \{\backslash \; sqrt\; \{1\; -\; \{\backslash \; frac\; \{v\; ^\; \{2\})\; \}\; \{c\; ^\; \{2\}\}\}\}\}\}$

или используя обычные сокращения,

$x\; =\; \gamma \; (x\; \prime \; +\; vt\; \prime ),\; t\; =\; \gamma \; (t\; \prime \; +\; vx\; \prime \; c\; 2),\; x\; \prime \; =\; \gamma \; (x\; -\; vt),\; t\; \prime \; =\; \gamma \; (t\; -\; vxc\; 2).\; \{\backslash \; displaystyle\; x\; =\; \backslash \; gamma\; (x\; \text{'}+\; vt\text{'}),\; \backslash ,\; \backslash ,\; t\; =\; \backslash \; gamma\; \backslash \; left\; (t\; \text{'}+\; \{\backslash \; frac\; \{vx\text{'}\}\; \{c\; ^\; \{2\}\}\}\; \backslash \; right),\; \backslash \; quad\; x\; \text{'}=\; \backslash \; gamma\; (x-vt),\; \backslash ,\; \backslash ,\; t\text{'}\; =\; \backslash \; gamma\; \backslash \; left\; (t\; -\; \{\backslash \; frac\; \{vx\}\; \{c\; ^\; \{2\}\}\}\; \backslash \; right).\}$

Это вычисление повторяется более подробно в разделе гиперболическое вращение.

Гиперболическое вращение

Преобразования Лоренца также могут быть получены путем простого применения постулатов специальной теории относительности и использования гиперболических тождеств..

Постулаты относительности

Начните с уравнений сферического волнового фронта светового импульса с центром в начале координат:

$(ct)\; 2\; -\; (x\; 2\; +\; y\; 2\; +\; z\; 2)\; =\; (ct\; \prime )\; 2\; -\; (x\; \prime \; 2\; +\; y\; \prime \; 2\; +\; z\; \prime \; 2)\; =\; 0\; \{\backslash \; displaystyle\; (ct)\; ^\; \{2\}\; -\; (x\; ^\; \{2\}\; +\; y\; ^\; \{2\}\; +\; z\; ^\; \{2\})\; =\; (ct\; \text{'})\; ^\; \{2\}\; -\; (x\text{'}\; ^\; \{2\}\; +\; y\; \text{'}^\; \{2\}\; +\; z\text{'}\; ^\; \{2\})\; =\; 0\}$

которые принимают одинаковую форму в обеих системах отсчета из-за постулатов специальной теории относительности. Затем рассмотрим относительное движение по осям x каждого кадра в стандартной конфигурации выше, так что y = y ′, z = z ′, что упрощается до

$(ct)\; 2\; -\; x\; 2\; =\; (ct\; \prime )\; 2\; -\; x\; \prime \; 2\; \{\backslash \; displaystyle\; (ct)\; ^\; \{2\}\; -x\; ^\; \{2\}\; =\; (ct\; \text{'})\; ^\; \{2\}\; -x\text{'}\; ^\; \{2\}\}$

Линейность

Теперь предположим, что преобразования принимают линейная форма:

$x\; \prime \; =\; A\; x\; +\; B\; ctct\; \prime \; =\; C\; x\; +\; D\; ct\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; x\; \text{'}=\; Ax\; +\; Bct\; \backslash \backslash \; ct\text{'}\; =\; Cx\; +\; Dct\; \backslash \; end\; \{\; выровнено\}\}\}$

где должны быть найдены A, B, C, D. Если бы они были нелинейными, они не принимали бы одинаковую форму для всех наблюдателей, поскольку фиктивные силы (следовательно, ускорения) возникли бы в одном кадре, дажеatrix} t '\\ x' \ end {bmatrix}} = {\ begin {bmatrix} \ gamma \ delta \\ - v \ gamma \ gamma \ end {bmatrix}} {\ begin {bmatrix} t \\ x \ end {bmatrix}}.}

Теперь рассмотрим обратный элемент группового постулата. Есть два способа перейти от системы координат K ′ к системе координат K. Первый заключается в применении обратной матрицы преобразования к координатам K ′:

$[tx]\; =\; 1\; \gamma \; 2\; +\; v\; \delta \; \gamma \; [\gamma \; -\; \delta \; v\; \gamma \; \gamma ]\; [t\; \text{'}\; Икс\; \text{'}].\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{bmatrix\}\; t\; \backslash \backslash \; x\; \backslash \; end\; \{bmatrix\}\}\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; gamma\; ^\; \{2\}\; +\; v\; \backslash \; delta\; \backslash \; gamma\}\}\; \{\backslash \; begin\; \{bmatrix\}\; \backslash \; gamma\; -\; \backslash \; delta\; \backslash \backslash \; v\; \backslash \; gamma\; \backslash \; gamma\; \backslash \; end\; \{bmatrix\}\}\; \{\backslash \; begin\; \{bmatrix\}\; t\; \text{'}\backslash \backslash \; x\text{'}\; \backslash \; end\; \{bmatrix\}\}.\}$

Второе, учитывая, что координата K 'система движется со скоростью v относительно системы координат K, система координат K должна двигаться со скоростью -v относительно системы координат K '. Замена v на −v в матрице преобразования дает:

$[tx]\; =\; [\gamma \; (-\; v)\; \delta \; (-\; v)\; v\; \gamma \; (-\; v)\; \gamma \; (-\; v)]\; [t\; \prime \; x\; \prime ],\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{bmatrix\}\; t\; \backslash \backslash \; x\; \backslash \; end\; \{bmatrix\}\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; \backslash \; gamma\; (-v)\; \backslash \; delta\; (-v)\; \backslash \backslash \; v\; \backslash \; gamma\; (-v)\; \backslash \; gamma\; (-\; v)\; \backslash \; end\; \{bmatrix\}\}\; \{\backslash \; begin\; \{bmatrix\}\; t\; \text{'}\backslash \backslash \; x\text{'}\; \backslash \; end\; \{bmatrix\}\},\}$

Теперь функция γ не может зависеть от направления v, потому что это, по-видимому, фактор который определяет релятивистское сжатие и замедление времени. Эти две (в нашем изотропном мире) не могут зависеть от направления v. Таким образом, γ (-v) = γ (v) и сравнивая две матрицы, мы получаем

$\gamma \; 2\; +\; v\; \delta \; \gamma \; =\; 1.\; \{\backslash \; displaystyle\; \backslash \; gamma\; ^\; \{2\}\; +\; v\; \backslash \; delta\; \backslash \; gamma\; =\; 1.\; \backslash ,\}$

Согласно постулату группы замыкания, композиция двух преобразований координат является также преобразованием координат, таким образом, произведением двух матриц также должна быть матрица нашей той же формы. Преобразование K в K ′ и из K ′ в K ′ ′ дает следующую матрицу преобразования для перехода от K к K ′ ′:

$[t\; ″\; x\; ″]\; =\; [\gamma \; (v\; \prime )\; \delta \; (v\; \prime )\; -\; v\; \prime \; \Gamma \; (v\; \prime )\; \gamma \; (v\; \prime )]\; [\gamma \; (v)\; \delta \; (v)\; -\; v\; \gamma \; (v)\; \gamma \; (v)]\; [tx]\; =\; [\gamma \; (v\; \prime )\; \gamma \; (v)\; -\; v\; \delta \; (v\; \prime )\; \Gamma \; (v)\; \gamma \; (v\; \prime )\; \delta \; (v)\; +\; \delta \; (v\; \prime )\; \gamma \; (v)\; -\; (v\; \prime \; +\; v)\; \gamma \; (v\; \prime )\; \gamma \; (v)\; -\; v\; \prime \; \gamma \; (v\; \prime )\; \delta \; (v)\; +\; \gamma \; (v\; \prime )\; \gamma \; (v)]\; [tx].\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \{\backslash \; begin\; \{bmatrix\}\; t\; \text{'}\text{'}\; \backslash \backslash \; x\; \text{'}\text{'}\; \backslash \; end\; \{bmatrix\}\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; \backslash \; gamma\; (v\; \text{'})\; \backslash \; delta\; (v\text{'})\; \backslash \backslash \; -\; v\; \text{'}\backslash \; gamma\; (v\text{'})\; \backslash \; gamma\; (v\; \text{'})\; \backslash \; end\; \{bmatrix\}\}\; \{\backslash \; begin\; \{bmatrix\}\; \backslash \; gamma\; (v)\; \backslash \; delta\; (v)\; \backslash \backslash \; -\; v\; \backslash \; gamma\; (v)\; \backslash \; gamma\; (v)\; \backslash \; end\; \{bmatrix\}\}\; \{\backslash \; begin\; \{bmatrix\}\; t\; \backslash \backslash \; x\; \backslash \; end\; \{bmatrix\}\}\; \backslash \backslash \; =\; \{\backslash \; begin\; \{bmatrix\}\; \backslash \; gamma\; (v\; \text{'})\; \backslash \; gamma\; (v)\; -\; v\; \backslash \; delta\; (v\; \text{'})\; \backslash \; gamma\; (v)\; \backslash \; gamma\; (v\text{'})\; \backslash \; delta\; (v)\; +\; \backslash \; delta\; (v\; \text{'})\; \backslash \; gamma\; (v)\; \backslash \backslash \; -\; (v\text{'}\; +\; v)\; \backslash \; gamma\; (v\; \text{'})\; \backslash \; gamma\; (v)\; -\; v\; \text{'}\backslash \; gamma\; (v\text{'})\; \backslash \; delta\; (v)\; +\; \backslash \; gamma\; (v\; \text{'})\; \backslash \; gamma\; (v)\; \backslash \; end\; \{bmatrix\}\}\; \{\backslash \; begin\; \{bmatrix\}\; t\; \backslash \backslash \; x\; \backslash \; конец\; \{bmatrix\}\}.\; \backslash \; end\; \{followers\}\}$

В исходной матрице преобразования обоих основных диагональных элементов равны γ, следовательно, для комбинированной матрицы преобразования должна быть такая же форма, что и исходное преобразование матрицы, главные диагональные элементы также должны быть равны. Приравнивание этих элементов и перестановка дает:

$\gamma \; (v\; \prime )\; \gamma \; (v)\; -\; v\; \delta \; (v\; \prime )\; \gamma \; (v)\; =\; -\; v\; \prime \; \gamma \; (v\; \prime )\; \delta \; (v)\; +\; \gamma \; (v\; \prime )\; \gamma \; (v)\; \{\backslash \; displaystyle\; \backslash \; gamma\; (v\; \text{'})\; \backslash \; gamma\; (v)\; -v\; \backslash \; delta\; (v\text{'})\; \backslash \; gamma\; (v)\; =\; -\; v\; \text{'}\backslash \; gamma\; (v\text{'})\; \backslash \; delta\; (v)\; +\; \backslash \; gamma\; (v\; \text{'})\; \backslash \; гамма\; (v)\; \backslash ,\}$

$v\; \delta \; (v\text{'})\; \gamma \; (v)\; =\; v\; \prime \; \gamma \; (v\; \prime )\; \delta \; (v)\; \{\backslash \; displaystyle\; v\; \backslash \; delta\; (v\; \text{'})\; \backslash \; gamma\; (v)\; =\; v\; \text{'}\backslash \; gamma\; (v\text{'})\; \backslash \; delta\; (v)\; \backslash ,\}$

$\delta \; (v)\; v\; \gamma \; (v)\; =\; \delta \; (v\; \prime )\; v\; \prime \; \gamma \; (v\; \prime ).\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; delta\; (v)\}\; \{v\; \backslash \; gamma\; (v)\}\}\; =\; \{\backslash \; frac\; \{\backslash \; delta\; (v\; \text{'})\}\; \{v\text{'}\; \backslash \; gamma\; (v\; \text{'})\}\}.\; \backslash ,\}$

Знаменатель будет ненулевым при отличном от нуля, потому что γ (v) всегда отличен от нуля;

$\gamma \; 2\; +\; v\; \delta \; \gamma \; =\; 1\; \{\backslash \; displaystyle\; \backslash \; gamma\; ^\; \{2\}\; +\; v\; \backslash \; delta\; \backslash \; gamma\; =\; 1\}$.

Если v = 0, у нас есть единичная матрица, которая совпадает с помещением v = 0 в конце концов, мы получаем окончательную матрицу других значений v, окончательную матрицу действующую для всех инерциальных систем.

Для ненулевого v эта комбинация функций должна быть универсальной константой, единицей и то же самое для всех инерциальных систем. Определим эту константу как δ (v) / v γ (v) = κ, где κ имеет размерность , равную 1 / v. Решение

$1\; =\; \gamma \; 2\; +\; v\; \delta \; \gamma \; =\; \gamma \; 2\; (1\; +\; \kappa \; v\; 2)\; \{\backslash \; displaystyle\; 1\; =\; \backslash \; gamma\; ^\; \{2\}\; +\; v\; \backslash \; delta\; \backslash \; gamma\; =\; \backslash \; gamma\; ^\; \{2\}\; (1+\; \backslash \; каппа\; v\; ^\; \{2\})\; \backslash ,\}$

в итоге получаем

$\gamma \; =\; 1/1\; +\; \kappa \; v\; 2\; \{\backslash \; displaystyle\; \backslash \; gamma\; =\; 1\; /\; \{\backslash \; sqrt\; \{1+\; \backslash \; kappa\; v\; ^\; \{2\}\}\}\}$

и, таким образом, матрица преобразования, согласованная с аксиомами группы, задается как

$[t\; \prime \; x\; \prime ]\; =\; 1\; 1\; +\; \kappa \; v\; 2\; [1\; \kappa \; v\; -\; v\; 1]\; [tx].\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{bmatrix\}\; t\; \text{'}\backslash \backslash \; x\text{'}\; \backslash \; end\; \{bmatrix\}\}\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sqrt\; \{1+\; \backslash \; kappa\; v\; ^\; \{2\}\}\}\}\; \{\backslash \; begin\; \{bmatrix\}\; 1\; \backslash \; kappa\; v\; \backslash \backslash \; -\; v\; 1\; \backslash \; end\; \{bmatrix\}\}\; \{\backslash \; begin\; \{bmatrix\}\; t\; \backslash \backslash \; x\; \backslash \; end\; \{bmatrix\}\}.\}$

Если κ>0, тогда будут преобразование (с κv ≫ 1), которые преобразуют время в пространственном координату и наоборот. Мы исключаем это по физическим причинам, потому что время может течь только в положительном направлении. Таким образом, с групповыми постулатами согласуются два типа матриц преобразования:

1. с κ = 0 и
2. с κ < 0.

преобразованиями Галилея

Если κ = 0, то мы получим галилеевы Кинематика Ньютона с преобразованием Галилея,

$[t\; \prime \; x\; \prime ]\; =\; [1\; 0\; -\; v\; 1]\; [tx],\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{bmatrix\}\; t\; \text{'}\backslash \backslash \; x\text{'}\; \backslash \; end\; \{bmatrix\}\}\; =\; \{\backslash \; begin\; \{\; bmatrix\}\; 1\; 0\; \backslash \backslash \; -\; v\; 1\; \backslash \; end\; \{bmatrix\}\}\; \{\backslash \; begin\; \{bmatrix\}\; t\; \backslash \backslash \; x\; \backslash \; end\; \{bmatrix\}\}\; \backslash ;,\}$

где время абсолютное, t ′ = t, и относительная скорость v двух инерциальных систем отсчета не ограничена.

Преобразования Лоренца

Если κ <0, то мы устанавливаем $c\; =\; 1\; /\; -\; \kappa \; \{\backslash \; displaystyle\; c\; =\; 1\; /\; \{\backslash \; sqrt\; \{-\; \backslash \; kappa\}\}\}$, которое становится инвариантная скорость, скорость света в вакууме. Это дает κ = -1 / c, и, таким образом, мы получаем специальную теорию относительности с преобразованием Лоренца

$[t\; \prime \; x\; \prime ]\; =\; 1\; 1\; -\; v\; 2\; c\; 2\; [1\; -\; vc\; 2\; -\; v\; 1]\; [tx\; ],\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{bmatrix\}\; t\; \text{'}\backslash \backslash \; x\text{'}\; \backslash \; end\; \{bmatrix\}\}\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sqrt\; \{1-\; \{v\; ^\; \{2\}\; \backslash \; over\; c\; ^\; \{2\}\}\; \}\}\}\; \{\backslash \; begin\; \{bmatrix\}\; 1\; \{-\; v\; \backslash \; over\; c\; ^\; \{2\}\}\; \backslash \backslash \; -\; v\; 1\; \backslash \; end\; \{bmatrix\}\}\; \{\backslash \; begin\; \{bmatrix\}\; t\; \backslash \backslash \; x\; \backslash \; end\; \{bmatrix\}\}\; \backslash ;,\}$

где скорость света - это конечная универсальная постоянная, максимально возможная относительная скорость между инерциальными системами отсчета.

Если v ≪ c преобразование Галилея является хорошим приближением преобразования Лоренца.

Только эксперимент может ответить на вопрос, какая из двух возможностей, κ = 0 или κ < 0, is realised in our world. The experiments measuring the speed of light, first performed by a Danish physicist Оле Рёмер, показывает, что она конечна, эксперимент Майкельсона - Морли показал, что это абсолютная скорость, и, таким образом, что κ < 0.

Повышение от генераторов

Используя скорость ϕ для параметров преобразования Лоренца, усиление в направлении x составляет

$[ct\; \prime \; x\; \prime \; y\; \prime \; z\; \prime ]\; знак\; равно\; [cosh\; \; \varphi \; -\; sinh\; \; \varphi \; 0\; 0\; -\; sinh\; \; \varphi \; cosh\; \; \varphi \; 0\; 0\; 0\; 0\; 1\; 0\; 0\; 0\; 0\; 1]\; [ctxyz],\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{bmatrix\}\; ct\; \text{'}\backslash \backslash \; x\text{'}\; \backslash \backslash \; y\; \text{'}\backslash \backslash \; z\text{'}\; \backslash \; end\; \{bmatrix\}\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; \backslash \; cosh\; \backslash \; phi\; -\; \backslash \; sh\; \backslash \; phi\; 0\; 0\; \backslash \backslash \; -\; \backslash \; sinh\; \backslash \; phi\; \backslash \; cosh\; \backslash \; phi\; 0\; 0\; \backslash \backslash \; 0\; 0\; 1\; 0\; \backslash \backslash \; 0\; 0\; 0\; 1\; \backslash \; \backslash \backslash \; end\; \{bmatrix\}\}\; \{\backslash \; begin\; \{bmatrix\}\; c\; \backslash ,\; t\; \backslash \backslash \; x\; \backslash \backslash \; y\; \backslash \backslash \; z\; \backslash \; end\; \{bmatrix\}\},\; \}$

аналогично для увеличения в направлении y

$[ct\; \prime \; x\; \prime \; y\; \prime \; z\; \prime ]\; =\; [ch\; \; \varphi \; 0\; -\; sh\; \; \; \varphi \; 0\; 0\; 1\; 0\; 0\; -\; sinh\; \; \varphi \; 0\; ch\; \; \varphi \; 0\; 0\; 0\; 0\; 1]\; [ctxyz],\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{bmatrix)\}\; ct\; \text{'}\backslash \backslash \; x\text{'}\; \backslash \backslash \; y\; \text{'}\backslash \backslash \; z\text{'}\; \backslash \; end\; \{bm\; atrix\}\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; \backslash \; ch\; \backslash \; phi\; 0\; -\; \backslash \; sh\; \backslash \; phi\; 0\; \backslash \backslash \; 0\; 1\; 0\; 0\; \backslash \backslash \; -\; \backslash \; sinh\; \backslash \; phi\; 0\; \backslash \; cosh\; \backslash \; phi\; 0\; \backslash \; \backslash \; 0\; 0\; 0\; 1\; \backslash \backslash \backslash \; end\; \{bmatrix\}\}\; \{\backslash \; begin\; \{bmatrix\}\; c\; \backslash ,\; t\; \backslash \backslash \; x\; \backslash \backslash \; y\; \backslash \backslash \; z\; \backslash \; end\; \{bmatrix\}\},\}$

и направление z

$[ct\; \prime \; x\; \prime \; Y\; \prime \; z\; \prime ]\; =\; [ch\; \; \varphi \; 0\; 0\; -\; sh\; \; \varphi \; 0\; 1\; 0\; 0\; 0\; 0\; 1\; 0\; -\; sh\; \varphi \; 0\; 0\; ch\; \varphi ]\; [ctxyz].\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{bmatrix\}\; ct\; \text{'}\backslash \backslash \; x\text{'}\; \backslash \backslash \; y\; \text{'}\backslash \backslash \; z\text{'}\; \backslash \; end\; \{bmatrix\}\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; \backslash \; cosh\; \backslash \; phi\; 0\; 0\; -\; \backslash \; sinh\; \backslash \; phi\; \backslash \backslash \; 0\; 1\; 0\; 0\; \backslash \; \backslash \; 0\; 0\; 1\; 0\; \backslash \backslash \; -\; \backslash \; sinh\; \backslash \; phi\; 0\; 0\; \backslash \; cosh\; \backslash \; phi\; \backslash \backslash \backslash \; end\; \{bmatrix\}\}\; \{\backslash \; begin\; \{bmatrix\}\; c\; \backslash ,\; t\; \backslash \backslash \; x\; \backslash \backslash \; y\; \backslash \backslash \; z\; \backslash \; end\; \{bmatrix\}\}\; \backslash ,.\; \}$

где ex, ey, ez- декартовы базисные расположение, набор взаимно перпендикулярных единичных векторов вдоль их указанного расположения. Если один кадр увеличивает со скоростью v>единичный вектор n= v/ v = β / β в направлении относительного движения.. Общее повышение:

$[ct\; \prime \; x\; \prime \; y\; \prime \; z\; \prime ]\; =\; [ch\; \; \varphi \; -\; nx\; sinh\; \; \varphi \; -\; ny\; sinh\; \; \varphi \; -\; nz\; sinh\; \; \varphi \; -\; nx\; sinh\; \; \varphi \; 1\; +\; (ch\; \; \varphi \; -\; 1)\; nx\; 2\; (ch\; \varphi \; -\; 1)\; nxny\; (ch\; \; \varphi \; -\; 1)\; nxnz\; -\; ny\; sh\; \varphi \; (ch\; \; \varphi \; -\; 1)\; nynx\; 1\; +\; (ch\; \; \varphi \; -\; 1)\; ny\; 2\; (ch\; \; \varphi \; -\; 1)\; nynz\; -\; nz\; sh\; \varphi \; (ch\; \; \varphi \; -\; 1)\; nznx\; (ch\; \; \varphi \; -\; 1)\; nzny\; 1\; +\; (ch\; \; \varphi \; -\; 1)\; nz\; 2]\; [ctxyz].\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{bmatrix\}\; c\; \backslash ,\; t\; \text{'}\backslash \backslash \; x\text{'}\; \backslash \backslash \; y\; \text{'}\backslash \backslash \; z\text{'}\; \backslash \; end\; \{bmatrix\}\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; \backslash \; cosh\; \backslash \; phi\; -n\_\; \{x\}\; \backslash \; sinh\; \backslash \; phi\; -n\_\; \{y\}\; \backslash \; sinh\; \backslash \; phi\; -n\_\; \{z\}\; \backslash \; sinh\; \backslash \; phi\; \backslash \backslash \; -\; n\_\; \{x\}\; \backslash \; sinh\; \backslash \; phi\; 1\; +\; (\backslash \; ch\; \backslash \; phi\; -1)\; n\_\; \{x\}\; ^\; \{2\}\; (\backslash \; ch\; \backslash \; phi\; -1)\; n\_\; \{x\}\; n\_\; \{y\}\; (\backslash \; ch\; \backslash \; phi\; -1)\; n\_\; \{x\}\; n\_\; \{z\}\; \backslash \backslash \; -\; n\_\; \{y\}\; \backslash \; sinh\; \backslash \; phi\; (\; \backslash \; cosh\; \backslash \; phi\; -1)\; n\_\; \{y\}\; n\_\; \{x\}\; 1\; +\; (\backslash \; ch\; \backslash \; phi\; -1)\; n\_\; \{y\}\; ^\; \{2\}\; (\backslash \; cosh\; \backslash \; phi\; -1)\; n\_\; \{y\}\; n\_\; \{z\; \}\; \backslash \backslash \; -\; n\_\; \{z\}\; \backslash \; sinh\; \backslash \; phi\; (\backslash \; ch\; \backslash \; phi\; -1)\; n\_\; \{z\}\; n\_\; \{x\}\; (\backslash \; cosh\; \backslash \; phi\; -1)\; n\_\; \{z\}\; n\_\; \{y\}\; 1\; +\; (\; \backslash \; cosh\; \backslash \; phi\; -1)\; n\_\; \{z\}\; ^\; \{2\}\; \backslash \backslash \backslash \; end\; \{bmatrix\}\}\; \{\backslash \; begin\; \{bmatrix\}\; c\; \backslash ,\; t\; \backslash \backslash \; x\; \backslash \backslash \; y\; \backslash \backslash \; z\; \backslash \; end\; \{bmatrix\}\}\; \backslash ,.\}$

Примечание матрица зависит от направления относительного движения, а также от скорости во всех трех числах (два для направления, один для скорости).

Мы можем преобразовать каждый из матриц повышения в другую форму следующим образом. Сначала рассмотрим усиление по оси x. разложение Тейлора матрицы повышения относительно ϕ = 0 равно

$B\; (e\; x,\; \varphi )\; =\; \sum \; n\; =\; 0\; \infty \; \varphi \; n\; n!\; \partial \; n\; B\; (e\; x,\; \varphi )\; \partial \; \varphi \; n\; |\; \varphi \; =\; 0\; \{\backslash \; Displaystyle\; B\; (\backslash \; mathbf\; \{e\}\; \_\; \{x\},\; \backslash \; phi)\; =\; \backslash \; sum\; \_\; \{n\; =\; 0\}\; ^\; \{\backslash \; infty\}\; \{\backslash \; frac\; \{\backslash \; phi\; ^\; \{n\}\}\; \{n!\}\; \}\; \backslash \; осталось.\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{n\}\; B\; (\backslash \; mathbf\; \{e\}\; \_\; \{x\},\; \backslash \; phi)\}\; \{\backslash \; partial\; \backslash \; phi\; ^\; \{n\}\}\}\; \backslash \; right\; |\; \_\; \{\backslash \; phi\; =\; 0\}\}$

где производные матрицы по ϕ задаются дифференцированием каждого элемента матрицы отдельно, аобозначение | ϕ = 0 указывает, что ϕ устанавливается в ноль после вычислений.. Расширение до первого порядка дает бесконечно малое преобразование

$B\; (e\; x,\; \varphi )\; =\; I\; +\; \varphi \; \partial \; B\; \partial \; \varphi \; |\; \varphi \; =\; 0\; =\; [1\; 0\; 0\; 0\; 0\; 1\; 0\; 0\; 0\; 0\; 1\; 0\; 0\; 0\; 0\; 1]\; -\; \varphi \; [0\; 1\; 0\; 0\; 1\; 0\; 0\; 0\; 0\; 0\; 0\; 0\; 0\; 0\; 0\; 0]\; \{\backslash \; displaystyle\; B\; (\backslash \; mathbf\; \{\; e\}\; \_\; \{x\},\; \backslash \; phi)\; =\; I\; +\; \backslash \; phi\; \backslash \; left.\; \{\backslash \; frac\; \{\backslash \; partial\; B\}\; \{\backslash \; partial\; \backslash \; phi\}\}\; \backslash \; right\; |\; \_\; \{\backslash \; phi\; =\; 0\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; 1\; 0\; 0\; 0\; \backslash \backslash \; 0\; 1\; 0\; 0\; \backslash \backslash \; 0\; 0\; 1\; 0\; \backslash \backslash \; 0\; 0\; 0\; 1\; \backslash \; end\; \{bmatrix\}\}\; -\; \backslash \; phi\; \{\backslash \; begin\; \{bmatrix\}\; 0\; 1\; 0\; 0\; \backslash \backslash \; 1\; 0\; 0\; 0\; \backslash \backslash \; 0\; 0\; 0\; 0\; \backslash \backslash \; 0\; 0\; 0\; 0\; \backslash \; end\; \{\; bmatrix\}\}\}$

, которое действительно небольшое (следовательно, ϕ и более высокие степени незначительны) может интерпретироваться как отсутствие повышения (первый член I представляет собой единичную матрицу 4 × 4), за которым следует небольшое повышение. Матрица

$К\; х\; =\; [0\; 1\; 0\; 0\; 1\; 0\; 0\; 0\; 0\; 0\; 0\; 0\; 0\; 0\; 0]\; \{\backslash \; displaystyle\; K\_\; \{x\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; 0\; 1\; 0\; 0\; \backslash \backslash \; 1\; 0\; 0\; 0\; \backslash \backslash \; 0\; 0\; 0\; 0\; \backslash \backslash \; 0\; 0\; 0\; 0\; \backslash \; end\; \{bmatrix\}\}\}$

- это генератор повышения в направлении x, поэтому бесконечно малое усиление равно

$B\; (ex,\; \varphi )\; =\; I\; -\; \varphi \; K\; x\; \{\backslash \; displaystyle\; B\; (\backslash \; mathbf\; \{e\}\; \_\; \{x\},\; \backslash \; phi)\; =\; I-\; \backslash \; phi\; K\_\; \{x\}\}$

Теперь ϕ мало, поэтому деление на положительное целое число N дает еще меньшее приращение скорости ϕ / N и при этом бесконечно малое усиление с быстротой ϕ,

$B\; (например,\; \varphi )\; =\; (I\; -\; \varphi \; K\; x\; N)\; N\; \{\backslash \; displaystyle\; B\; (\backslash \; mathbf\; \{e\}\; \_\; \{x\},\; \backslash \; phi)\; =\; \backslash \; left\; (I\; -\; \{\backslash \; frac\; \{\backslash \; phi\; K\_\; \{x\}\}\; \{N\}\}\; \backslash \; right)\; ^\; \{N\}\}$

В пределе бесконечного числа бесконечно малых шагов мы получить преобразование конечного ускорения

$B\; (ex,\; \varphi )\; =\; lim\; N\; \to \; \infty \; (I\; -\; \varphi \; K\; x\; N)\; N\; =\; e\; -\; \varphi \; K\; x\; \{\backslash \; displaystyle\; B\; (\backslash \; mathbf\; \{e\; \}\; \_\; \{x\},\; \backslash \; phi)\; =\; \backslash \; lim\; \_\; \{N\; \backslash \; rightarrow\; \backslash \; infty\}\; \backslash \; left\; (I\; -\; \{\backslash \; frac\; \{\backslash \; phi\; K\_\; \{x\}\}\; \{N\}\}\; \backslash \; right)\; ^\; \{\; N\}\; =\; e\; ^\; \{-\; \backslash \; phi\; K\_\; \{x\}\}\}$

, который является предельным определением ex ponential из-за Леонарда Эйлера, и теперь верно для любого ϕ.

Повторение процесса для повышения в направлениях y и z приводит к получению других генераторов

$K\; y\; =\; [0\; 0\; 1\; 0\; 0\; 0\; 0\; 0\; 1\; 0\; 0\; 0\; 0\; 0\; 0\; 0],\; K\; z\; =\; [0\; 0\; 0\; 1\; 0\; 0\; 0\; 0\; 0\; 0\; 0\; 0\; 1\; 0\; 0\; 0]\; \{\backslash \; displaystyle\; K\_\; \{y\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; 0\; 0\; 1\; 0\; \backslash \backslash \; 0\; 0\; 0\; 0\; \backslash \backslash \; 1\; 0\; 0\; 0\; \backslash \backslash \; 0\; 0\; 0\; 0\; \backslash \; end\; \{bmatrix\}\}\; \backslash ,,\; \backslash \; quad\; K\_\; \{z\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; 0\; 0\; 0\; 1\; \backslash \backslash \; 0\; 0\; 0\; 0\; \backslash \backslash \; 0\; 0\; 0\; 0\; \backslash \backslash \; 1\; 0\; 0\; 0\; \backslash \; end\; \{bmatrix\}\}\}$

и бусты

$B\; (ey,\; \varphi )\; =\; e\; -\; \varphi \; K\; y,\; B\; (\; ez,\; \varphi )\; =\; e\; -\; \varphi \; K\; z.\; \{\backslash \; Displaystyle\; B\; (\backslash \; mathbf\; \{e\}\; \_\; \{y\},\; \backslash \; phi)\; =\; e\; ^\; \{-\; \backslash \; phi\; K\_\; \{y\}\}\; \backslash ,,\; \backslash \; quad\; B\; (\backslash \; mathbf\; \{e\}\; \_\; \{z\},\; \backslash \; phi)\; =\; e\; ^\; \{-\; \backslash \; phi\; K\_\; \{z\}\}\; \backslash ,.\}$

Для любого направления бесконечно малое преобразование (малое ϕ и расширение до первого порядка)

$B\; (n,\; \varphi )\; =\; I\; +\; \varphi \; \partial \; B\; \partial \; \varphi \; |\; \varphi \; =\; 0\; знак\; равно\; [1\; 0\; 0\; 0\; 0\; 1\; 0\; 0\; 0\; 0\; 1\; 0\; 0\; 0\; 0\; 1]\; -\; \varphi \; [0\; nxnynznx\; 0\; 0\; 0\; ny\; 0\; 0\; 0\; nz\; 0\; 0\; 0]\; \{\backslash \; displaystyle\; B\; (\backslash \; mathbf\; \{n\},\; \backslash \; phi)\; =\; I\; +\; \backslash \; phi\; \backslash \; left.\; \{\backslash \; frac\; \{\backslash \; partial\; B\}\; \{\backslash \; partial\; \backslash \; phi\}\}\; \backslash \; right\; |\; \_\; \{\backslash \; phi\; =\; 0\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; 1\; 0\; 0\; 0\; \backslash \backslash \; 0\; 1\; 0\; 0\; \backslash \backslash \; 0\; 0\; 1\; 0\; \backslash \; \backslash \; 0\; 0\; 0\; 1\; \backslash \; end\; \{bmatrix\}\}\; -\; \backslash \; phi\; \{\backslash \; begin\; \{bmatrix\}\; 0\; n\_\; \{x\}\; n\_\; \{y\}\; n\_\; \{z\}\; \backslash \backslash \; n\_\; \{x\}\; 0\; 0\; 0\; \backslash \backslash \; n\_\; \{y\}\; 0\; 0\; 0\; \backslash \backslash \; n\_\; \{z\}\; 0\; 0\; 0\; \backslash \; end\; \{bmatrix\}\}\}$

где

$[0\; nxnynznx\; 0\; 0\; 0\; ny\; 0\; 0\; 0\; nz\; 0\; 0\; 0]\; =\; nx\; K\; x\; +\; ny\; К\; Y\; +\; NZ\; К\; Z\; знак\; равно\; N\; \cdot \; К\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{bmatrix\}\; 0\; n\_\; \{x\}\; n\_\; \{y\}\; n\_\; \{z\}\; \backslash \backslash \; n\_\; \{x\}\; 0\; 0\; 0\; \backslash \backslash \; n\_\; \{y\}\; 0\; 0\; 0\; \backslash \backslash \; n\_\; \{z\}\; 0\; 0\; 0\; \backslash \; end\; \{bmatrix\}\}\; =\; n\_\; \{x\}\; K\_\; \{x\}\; +\; n\_\; \{y\}\; K\_\; \{y\}\; +\; n\_\; \{z\}\; K\_\; \{z\}\; =\; \backslash \; mathbf\; \{n\}\; \backslash \; cdot\; \backslash \; mathbf\; \{K\}\}$

- генератор повышения в направлении n . Это генератор полного повышения, вектор матриц K = (K x, K y, K z), спроецированных в направлении повышения п . Бесконечно малое усиление равно

$B\; (n,\; \varphi )\; =\; I\; -\; \varphi \; (n\; \cdot \; K)\; \{\backslash \; displaystyle\; B\; (\backslash \; mathbf\; \{n\},\; \backslash \; phi)\; =\; I-\; \backslash \; phi\; (\backslash \; mathbf\; \{n\}\; \backslash \; cdot\; \backslash \; mathbf\; \{K\})\}$

Тогда в пределе бесконечного числа бесконечно малых шагов мы получаем конечное преобразование буста

$B\; (n,\; \varphi )\; =\; lim\; N\; \to \; \infty \; (I\; -\; \varphi \; (n\; \cdot \; K)\; N)\; N\; знак\; равно\; е\; -\; \varphi \; (N\; \cdot \; K)\; \{\backslash \; Displaystyle\; B\; (\backslash \; mathbf\; \{n\},\; \backslash \; phi)\; =\; \backslash \; lim\; \_\; \{N\; \backslash \; rightarrow\; \backslash \; infty\}\; \backslash \; left\; (I\; -\; \{\backslash \; frac\; \{\backslash \; phi\; (\backslash \; mathbf\; \{n\})\; \backslash \; cdot\; \backslash \; mathbf\; \{K\})\}\; \{N\}\}\; \backslash \; right)\; ^\; \{N\}\; =\; e\; ^\; \{-\; \backslash \; phi\; (\backslash \; mathbf\; \{n\}\; \backslash \; cdot\; \backslash \; mathbf\; \{K\})\}\}$

что теперь верно для любого ϕ. Разложив матричную экспоненту число −ϕ (n· K) в ее степенной ряду

$e\; -\; \varphi \; n\; \cdot \; K\; =\; \sum \; n\; =\; 0\; \infty \; 1\; n!\; (-\; \varphi \; N\; \cdot \; К)\; n\; \{\backslash \; Displaystyle\; е\; ^\; \{-\; \backslash \; phi\; \backslash \; mathbf\; \{n\}\; \backslash \; cdot\; \backslash \; mathbf\; \{K\}\}\; =\; \backslash \; sum\; \_\; \{n\; =\; 0\}\; ^\; \{\backslash \; infty\}\; \{\backslash \; frac\; \{1\}\; \{n!\}\}\; (-\; \backslash \; phi\; \backslash \; mathbf\; \{n\}\; \backslash \; cdot\; \backslash \; mathbf\; \{K\})\; ^\; \{n\}\}$

теперь нам нужны генератора мощности. Квадрат равен

$(n\; \cdot \; K)\; 2\; =\; [1\; 0\; 0\; 0\; 0\; nx\; 2\; nxnynxnz\; 0\; nynxny\; 2\; nynz\; 0\; nznxnznynz\; 2]\; \{\backslash \; displaystyle\; (\backslash \; mathbf\; \{n\}\; \backslash \; cdot\; \backslash \; mathbf\; \{K\})\; ^\; \{2\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; 1\; 0\; 0\; 0\; \backslash \backslash \; 0\; n\_\; \{x\}\; ^\; \{2\}\; n\_\; \{x\}\; n\_\; \{y\}\; n\_\; \{x\}\; n\_\; \{z\}\; \backslash \backslash \; 0\; n\_\; \{\; y\}\; n\_\; \{x\}\; n\_\; \{y\}\; ^\; \{2\}\; n\_\; \{y\}\; n\_\; \{z\}\; \backslash \backslash \; 0\; n\_\; \{z\}\; n\_\; \{x\}\; n\_\; \{z\}\; n\_\; \{y\}\; n\_\; \{z\}\; ^\; \{2\}\; \backslash \; end\; \{bmatrix\}\}\}$

но куб (n· K) возвращается к (n· K), и, как всегда, нулевая степень является тождеством 4 × 4, (n· K) = Я . В общем случае нечетные степени n = 1, 3, 5,... равны

$(n\; \cdot \; K)\; n\; =\; (n\; \cdot \; K)\; \{\backslash \; displaystyle\; (\backslash \; mathbf\; \{n\}\; \backslash \; cdot\; \backslash \; mathbf\; \{K\})\; ^\; \{n\}\; =\; (\backslash \; mathbf\; \{n\}\; \backslash \; cdot\; \backslash \; mathbf\; \{K\})\}$

, а четные степени n = 2, 4, 6,... равны

$(n\; \cdot \; K)\; n\; =\; (n\; \cdot \; К)\; 2\; \{\backslash \; displaystyle\; (\backslash \; mathbf\; \{n\}\; \backslash \; cdot\; \backslash \; mathbf\; \{K\})\; ^\; \{n\}\; =\; (\backslash \; mathbf\; \{n\}\; \backslash \; cdot\; \backslash \; mathbf\; \{K\})\; ^\; \{2\}\}$

поэтому явный вид матрицы повышения зависит только от генератора и его квадрата. Разделение степенного ряда на нечетный степенной ряд и четный степенной ряд с использованием нечетной и четной мощности генератора, а также ряд Тейлора для sinhϕ и chϕ около ϕ = 0 дает более компактную, но детализированную форму матрицы усиления

$e - ϕ n ⋅ K = - ∑ n = 1, 3, 5… ∞ 1 n! ϕ n (n ⋅ K) n + ∑ n = 0, 2, 4… ∞ 1 n! ϕ N (N ⋅ K) N = - [ϕ + ϕ 3 3! + ϕ 5 5! + ⋯] (N ⋅ K) + I + [- 1 + 1 + 1 2! ϕ 2 + 1 4! ϕ 4 + 1 6! ϕ 6 + ⋯] (N ⋅ K) 2 = - зп ⁡ ϕ (n ⋅ K) + I + (- 1 + cosh ⁡ ϕ) (n ⋅ K) 2 {\ displaystyle {\ begin {align} e ^ { - \ phi \ mathbf {n} \ cdot \ mathbf {K}} = - \ sum _ {n = 1,3,5 \ ldots} ^ {\ infty} {\ frac {1} {n!}} \ phi ^ {n} (\ mathbf {n} \ cdot \ mathbf {K}) ^ {n} + \ sum _ {n = 0,2,4 \ ldots} ^ {\ infty} {\ frac {1} { n!}} \ phi ^ {n} (\ mathbf {n} \ cdot \ mathbf {K}) ^ {n} \\ = - \ left [\ phi + {\ frac {\ phi ^ {3}} {3!}} + {\ Frac {\ phi ^ {5}} {5!}} + \ Cdots \ right] (\ mathbf {n} \ cdot \ mathbf {K}) + I + \ left [-1 + 1 + {\ frac {1} {2!}} \ Phi ^ {2} + {\ frac {1} {4!}} \ Phi ^ {4} + {\ frac {1} {6!}} \ phi ^ {6} + \ cdots \ right] (\ mathbf {n} \ cdot \ mathbf {K}) ^ {2} \\ = - \ sinh \ phi (\ mathbf {n} \ cdot \ mathbf { K}) + I + (- 1+ \ cosh \ phi) (\ mathbf {n} \ cdot \ mathbf {K}) ^ {2} \ end {align}}}$

где 0 = - 1 + 1 введено для четного степенного ряда, чтобы завершить ряд Тейлора для chϕ. Повышение похоже на формулу вращения Родригеса,

$B\; (n,\; \varphi )\; =\; e\; -\; \varphi \; n\; \cdot \; K\; =\; I\; -\; sh\; \; \varphi \; (n\; \cdot \; K)\; +\; (ch\; \; \varphi \; -\; 1)\; (n\; \cdot \; К)\; 2.\; \{\backslash \; Displaystyle\; В\; (\backslash \; mathbf\; \{n\},\; \backslash \; phi)\; =\; е\; ^\; \{-\; \backslash \; phi\; \backslash \; mathbf\; \{n\}\; \backslash \; cdot\; \backslash \; mathbf\; \{K\}\}\; =\; I-\; \backslash \; sinh\; \backslash \; phi\; (\backslash \; mathbf\; \{n\}\; \backslash \; cdot\; \backslash \; mathbf\; \{K\})\; +\; (\backslash \; cosh\; \backslash \; phi\; -1)\; (\backslash \; mathbf\; \{n\}\; \backslash \; cdot\; \backslash \; mathbf\; \{K\})\; ^\; \{2\}\; \backslash ,.\}$

Отрицание скорости в экспоненте дает матрицу обратного преобразования,

$В\; (N,\; -\; \varphi )\; знак\; равно\; e\; \varphi \; N\; \cdot \; K\; =\; I\; +\; sh\; \; \varphi \; (n\; K)\; +\; (ch\; \; \varphi \; -\; 1)\; (n\; \cdot \; K)\; 2.\; \{\backslash \; Displaystyle\; B\; (\backslash \; mathbf\; \{n\},\; -\; \backslash \; phi)\; =\; e\; ^\; \{\backslash \; phi\; \backslash \; mathbf\; \{n\}\; \backslash \; cdot\; \backslash \; mathbf\; \{K\}\}\; =\; I\; +\; \backslash \; sinh\; \backslash \; phi\; (\backslash \; mathbf\; \{n\}\; \backslash \; cdot\; \backslash \; mathbf\; \{K\})\; +\; (\backslash \; ch\; \backslash \; phi\; -1)\; (\backslash \; mathbf\; \{n\}\; \backslash \; cdot\; \backslash \; mathbf\; \{K\})\; ^\; \{2\}\; \backslash ,.\}$

В квантовой механике, релятивистская квантовая механика и квантовая теория поля, для повышающих генераторов используется другое соглашение; все генераторы повышения умножаются на множитель мнимой единицы i = √ − 1.

Говард Перси Робертсон и другие показали, что преобразование Лоренца также может быть получено эмпирическим путем. Для этого необходимо записать преобразования координат, которые включают экспериментально проверяемые параметры. Например, пусть дана единственная «предпочтительная» инерциальная система координат $X,\; Y,\; Z,\; T\; \{\backslash \; displaystyle\; X,\; Y,\; Z,\; T\}$, в которой скорость света постоянна, изотропны и не зависят от скорости источника. Также предполагается, что синхронизация Эйнштейна и синхронизация с помощью медленной передачи часов эквивалентны в этом кадре. Затем предположим, что другой кадр $x,\; y,\; z,\; t\; \{\backslash \; displaystyle\; x,\; y,\; z,\; t\}$находится в относительном движении, в котором часы и стержни имеют такое же внутреннее устройство, что и в предпочтительном кадре.. Следующие отношения, однако, остаются неопределенными:

• $a\; (v)\; \{\backslash \; displaystyle\; a\; (v)\}$разница в измерениях времени,
• $b\; (v)\; \{\backslash \; displaystyle\; b\; (v)\; \}$различия в измеренных продольных длинах,
• $d\; (v)\; \{\backslash \; displaystyle\; d\; (v)\}$разницы в измеренных поперечных длинах,
• $\epsilon \; (v)\; \{\backslash \; displaystyle\; \backslash \; varepsilon\; (v)\}$зависит от процедуры синхронизации часов в движущемся кадре,

тогда формулы преобразования (предполагаемые линейными) между этими кадрами имеют следующий вид:

$t\; =\; a\; (\; v)\; T\; +\; \epsilon \; (v)\; хх\; знак\; равно\; б\; (v)\; (X\; -\; v\; T)\; y\; =\; d\; (v)\; Y\; z\; =\; d\; (v)\; Z\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; t\; =\; a\; (v)\; T\; +\; \backslash \; varepsilon\; (v)\; x\; \backslash \backslash \; x\; =\; b\; (v)\; (X-vT)\; \backslash \backslash \; y\; =\; d\; (v)\; Y\; \backslash \backslash \; z\; =\; d\; (v)\; Z\; \backslash \; end\; \{align\}\}\}$

$\epsilon \; (v)\; \{\backslash \; displaystyle\; \backslash \; varepsilon\; (v)\}$зависит от соглашения о синхронизации и не определяется экспериментально, он получает значение $-\; v\; /\; c\; 2\; \{\backslash \; displaystyle\; -v\; /\; c\; ^\; \{2\}\; \}$с использованием синхронизации Эйнштейна в обо их кадрах. Соотношение между $b\; (v)\; \{\backslash \; displaystyle\; b\; (v)\}$и $d\; (v)\; \{\backslash \; displaystyle\; d\; (v)\}$определяется эксперимент Майкельсона – Морли, соотношение между $a\; (v)\; \{\backslash \; displaystyle\; a\; (v)\}$и $b\; (\; v)\; \{\backslash \; displaystyle\; b\; (v)\; \}$определяется с помощью эксперимента Кеннеди-Торндайка, а $a\; (v)\; \{\backslash \; displaystyle\; a\; (v)\}$определяется только Эксперимент Айвса – Стилвелла. Таким образом, они были определены с большой точностью до $1\; /\; a\; (v)\; =\; b\; (v)\; =\; \gamma \; \{\backslash \; displaystyle\; 1\; /\; a\; (v)\; =\; b\; (v)\; =\; \backslash \; gamma\}$и $d\; (v)\; =\; 1\; \{\backslash \; displaystyle\; d\; (v)\; =\; 1\}$, который преобразует вышеуказанное преобразование в преобразование Лоренца.

• Пространство гировектора
• Группа Лоренца
• Теорема Нётер
• Группа Пуанкаре
• Собственное время
• Релятивистская метрика
• Спинор

• Greiner, W. ; Бромли, Д. А. (2000). Релятивистская квантовая механика (3-е изд.). спрингер. ISBN 9783540674573. CS1 maint: ref = harv (ссылка )
• Ландау, LD ; Лифшиц, EM (2002) [1939]. Классическая теория полей. Курс теоретической физики. 2 (4-е изд.). Баттерворт-Хайнеманн. ISBN 0 -7506-2768-9. CS1 maint: ref = harv (ссылка )
• Вайнберг, С. (2002), Квантовая теория полей, 1, Кембридж University Press, ISBN 0-521-55001-7