Степень реакции

В турбомашине, Степень реакции или коэффициент реакции (R) определяется как отношение падения статического давления в роторе к падению статического давления в ступени или как отношение статической энтальпии падение ротора до падения статической энтальпии в ступени.

Степень реакции (R ) является важным фактором при проектировании лопаток турбины, компрессоров, насосов и др. турбомашины. Он также говорит об эффективности машины и используется для правильного выбора машины по назначению.

Существуют различные определения энтальпий, давлений или расхода геометрии устройства. В случае турбин , как импульсных, так и реактивных машин, Степень реакции (R) определяется как отношение передачи энергии посредством изменения статического напора к общей передаче энергии в роторе т.е.

$R\; =\; Изэнтропическое\; изменение\; энтальпии\; в\; роторе\; Изэнтропическое\; изменение\; энтальпии\; на\; стадии\; \{\backslash \; displaystyle\; R\; =\; \{\backslash \; frac\; \{\backslash \; text\; \{Изэнтропическое\; изменение\; энтальпии\; в\; роторе\}\}\; \{\backslash \; text\; \{Изэнтропическое\; изменение\; энтальпии\; в\; стадии\}\}\}\}$.

Для газовой турбины или компрессора он определяется как отношение изоэнтропического перепада тепла в движущихся лопастях (то есть в роторе) к сумме изоэнтропического тепла. капли в неподвижных лопастях (т.е. статоре) и движущихся лопастях, т.е.

$R\; =\; Изэнтропическое\; падение\; тепла\; в\; роторе\; Изэнтропическое\; падение\; тепла\; в\; стадии\; \{\backslash \; displaystyle\; R\; =\; \{\backslash \; frac\; \{\backslash \; text\; \{Изэнтропическое\; падение\; тепла\; в\; роторе\}\}\; \{\; \backslash \; text\; \{Изэнтропический\; перепад\; тепла\; в\; ступени\}\}\}\}$.

В насосах степень реакции зависит от статического и динамического напора. Степень реакции определяется как доля передачи энергии посредством изменения статического напора к общей передаче энергии в роторе, т. Е.

$R\; =\; повышение\; статического\; давления\; в\; роторе\; Общее\; повышение\; давления\; на\; стадии\; \{\backslash \; displaystyle\; R\; =\; \{\backslash \; frac\; \{\backslash \; text\; \{Повышение\; статического\; давления\; в\; роторе\}\}\; \{\backslash \; text\; \{Общее\; повышение\; давления\; в\; ступени\}\}\}\}$.

Содержание

• 1 Отношение
• 2 Выбор реакции (R) и влияние на КПД
  • 2.1 50 % реакции
  • 2.2 Реакция менее 50%
  • 2.3 Реакция более 50%
  • 2.4 Реакция = ноль
• 3 Ссылки
• 4 Дополнительная литература и работы, относящиеся к

Отношение

Большинство турбомашин в определенной степени эффективны и могут быть приближены к изоэнтропическому процессу на стадии. Следовательно, из $T\; ds\; =\; dh\; -\; dp\; \rho \; \{\backslash \; displaystyle\; Tds\; =\; dh\; -\; \{\backslash \; frac\; \{dp\}\; \{\backslash \; rho\}\}\}$,

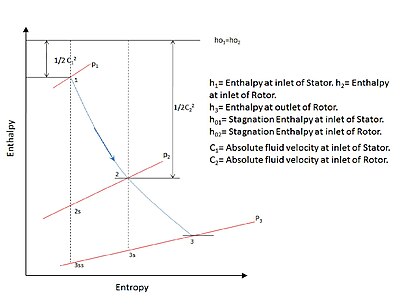Рис. 1. График зависимости энтальпии от энтропии для ступенчатого потока в турбине

легко видеть, что для изэнтропического процесса ∆H ≃ ∆P. Следовательно, это может подразумеваться

$R\; =\; \Delta \; H\; (ротор)\; \Delta \; H\; (Stage)\; \{\backslash \; displaystyle\; R\; =\; \{\backslash \; frac\; \{\backslash \; Delta\; H\; \{\backslash \; text\; \{(Rotor)\}\}\}\; \{\backslash \; Delta\; H\; \{\backslash \; text\; \{\; (Стадия)\}\}\}\}\}$

То же самое можно выразить математически следующим образом:

$R\; =\; \int \; 3\; ss\; 2\; s\; dh\; \int \; 3\; ss\; 1\; dh\; Или\; \int \; 3\; ss\; 2\; s\; dp\; \int \; 3\; ss\; 1\; dp\; \{\backslash \; displaystyle\; \backslash \; R\; =\; \{\backslash \; frac\; \{\backslash \; int\; \_\; \{3ss\}\; ^\; \{2s\}\; \{\backslash \; textrm\; \{dh\}\}\}\; \{\backslash \; int\; \_\; \{3ss\}\; ^\; \{1\}\; \{\backslash \; textrm\; \{dh\}\}\}\}\; \backslash ,\; \backslash \; \{\backslash \; textrm\; \{Or\}\}\; \backslash ,\; \backslash \; \{\backslash \; frac\; \{\backslash \; int\; \_\; \{3ss\}\; ^\; \{2s\}\; \{\backslash \; textrm\; \{dp\}\}\}\; \{\backslash \; int\; \_\; \{3ss\}\; ^\; \{1\}\; \{\backslash \; textrm\; \{dp\}\}\}\}\; \}$

Где от 1 до 3ss на рисунке 1 представляет изоэнтропический процесс, начинающийся от входа статора в точке 1 до выхода ротора в точке 3. А от 2 до 3s - изэнтропический процесс от входа ротора в точке 2 до выхода ротора в точке 3. Треугольник скорости (Рис. 2.) для процесса потока внутри ступени представляет собой изменение скорости жидкости, когда она течет сначала в статоре или неподвижных лопастях, а затем через ротор или движущиеся лопасти. Из-за изменения скоростей происходит соответствующее изменение давления.

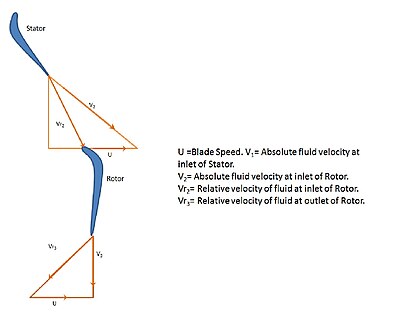Рис. 2. Треугольник скорости потока жидкости в турбине

В другом используемом часто используемом определении скорости ступеней используются как:

$h\; 2\; -\; h\; 3\; =\; 1\; 2\; (V\; r\; 3\; 2\; -\; V\; r\; 2\; 2)\; +\; 1\; 2\; (U\; 2\; 2\; -\; U\; 3\; 2)\; \{\backslash \; displaystyle\; \backslash ,\; h\_\; \{2\}\; -h\_\; \{3\}\; =\; \{1\; \backslash \; over\; \{2\}\}\; (V\_\; \{r3\}\; ^\; \{2\}\; -V\_\; \{r2\}\; ^\; \{2\; \})\; +\; \{1\; \backslash \; over\; \{2\}\}\; (U\_\; \{2\}\; ^\; \{2\}\; -U\_\; \{3\}\; ^\; \{2\})\}$

- это падение энтальпии в роторе и

$час\; 01\; -\; час\; 03\; =\; час\; 02\; -\; час\; 03\; =\; (U\; 2\; V\; вес\; 2\; -\; U\; 1\; V\; вес\; 1)\; \{\backslash \; displaystyle\; \backslash ,\; h\_\; \{01\}\; -h\_\; \{03\}\; =\; h\_\; \{02\}\; -h\_\; \{03\}\; =\; (U\_\; \{2\}\; \backslash ,\; V\_\; \{w2\}\; -U\_\; \{1\}\; \backslash ,\; V\_\; \{w1\})\}$

- полное падение энтальпии. Тогда степень реакции выражается как

$R\; =\; [1\; 2\; (V\; r\; 3\; 2\; -\; V\; r\; 2\; 2)\; +\; 1\; 2\; (U\; 2\; 2\; -\; U\; 3\; 2)]\; (U\; 2\; V\; w\; 2\; -\; U\; 1\; V\; вес\; 1)\; \{\backslash \; displaystyle\; R\; =\; \{\backslash \; frac\; \{[\{1\; \backslash \; over\; \{2\}\}\; (V\_\; \{r3\}\; ^\; \{2\}\; -V\_\; \{r2\}\; ^\; \{2\})\; +\; \{1\; \backslash \; over\; \{2\}\}\; (\; U\_\; \{2\}\; ^\; \{2\}\; -U\_\; \{3\}\; ^\; \{2\})]\}\; \{(U\_\; \{2\}\; \backslash ,\; V\_\; \{w2\}\; -U\_\; \{1\}\; \backslash ,\; V\_\; \{w1\})\}\}\}$

Для осевых станков $U\; 2\; =\; U\; 1\; =\; U\; \{\backslash \; displaystyle\; U2\; =\; U1\; =\; U\}$, тогда

$R\; =\; (V\; r\; 3\; 2\; -\; V\; r\; 2\; 2)\; 2\; U\; (V\; вес\; 3\; +\; V\; вес\; 2)\; \{\backslash \; Displaystyle\; R\; =\; \{\backslash \; frac\; \{(V\_\; \{r3\}\; ^\; \{2\}\; -V\_\; \{r2\}\; ^\; \{2\})\}\; \{2U\; (V\_\; \{w3\}\; +\; V\_\; \{w2\})\}\}\}$

Степень реакции также может быть записана в терминах геометрии турбомашины, полученной по формуле

$R\; =\; (V\; f\; 2\; U)\; (tan\; \; \beta \; 3\; -\; tan\; \; \beta \; 2)\; \{\backslash \; displaystyle\; R\; =\; (\{\backslash \; frac\; \{V\_\; \{f\}\}\; \{2U\}\})\; (\backslash \; tan\; \{\backslash \; beta\; \_\; \{3\}\}\; -\; \backslash \; tan\; \{\backslash \; beta\; \_\; \{2\}\})\}$

где $\beta \; 3\; \{\backslash \; displaystyle\; \backslash \; beta\; \_\; \{3\}\}$- угол лопатки на выходе из ротора, а $\beta \; 2\; \{\backslash \; displaystyle\; \backslash \; beta\; \_\; \{2\}\}$- угол выхода лопатки из статора. На практике $(V\; f\; 2\; U)\; \{\backslash \; displaystyle\; (\{\backslash \; frac\; \{V\_\; \{f\}\}\; \{2U\}\})\}$заменяется на ϕ и $(tan\; \; \beta \; 3\; -\; загар\; \; \beta \; 2)\; \{\backslash \; Displaystyle\; (\backslash \; загар\; \{\backslash \; бета\; \_\; \{3\}\}\; -\; \backslash \; загар\; \{\backslash \; бета\; \_\; \{2\}\})\}$как $загар\; \; \beta \; м\; \{\backslash \; Displaystyle\; \backslash \; tan\; \{\backslash \; beta\; \_\; \{m\}\}\}$, что дает $R\; =\; \varphi \; tan\; \; \beta \; m.\; \{\backslash \; displaystyle\; R\; =\; \backslash \; phi\; \backslash \; tan\; \{\backslash \; beta\; \_\; \{m\}\}.\}$Степень реакции теперь зависит только от ϕ и $tan\; \; \beta \; m\; \{\backslash \; displaystyle\; \backslash \; tan\; \{\backslash \; beta\; \_\; \{m\}\}\}$которые опять же зависят от геометрических параметров β3 и β2, то есть от углов лопаток на выходе из статора и ротора. Используя треугольники скорости, степень реакции может быть получена следующим образом:

$R\; =\; 1\; 2\; +\; V\; f\; 2\; U\; (tan\; \; \beta \; 3\; -\; tan\; \; \alpha \; 2)\; \{\backslash \; displaystyle\; R\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; +\; \{\backslash \; frac\; \{V\_\; \{f\}\}\; \{2U\}\}\; (\backslash \; tan\; \{\backslash \; beta\; \_\; \{3\}\}\; -\; \backslash \; tan\; \{\backslash \; alpha\; \_\; \{2\}\})\}$

Это соотношение снова очень полезно, когда ротор угол лопасти и угол ротора определяются для данной геометрии.

Выбор реакции (R) и влияние на эффективность

Рисунок 3. Влияние реакции на общую статическую эффективность при фиксированном значении коэффициента нагрузки ступени

На рисунке 3 рядом показано изменение полная статическая эффективность при разном коэффициенте нагрузки лопасти в зависимости от степени реакции. Основное уравнение записывается как

$R\; =\; 1\; +\; \Delta \; W\; 2\; U\; 2\; -\; C\; y\; 2\; U\; \{\backslash \; displaystyle\; R\; =\; 1\; +\; \{\backslash \; frac\; \{\backslash \; Delta\; W\}\; \{2U\; ^\; \{2\}\}\}\; -\; \{\backslash \; frac\; \{C\_\; \{y2\}\}\; \{U\}\}\}$

где $\Delta \; W\; 2\; U\; 2\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; Delta\; W\}\; \{2U\; ^\; \{2\}\}\}\}$- коэффициент загрузки сцены. Диаграмма показывает оптимизацию полного статического КПД при заданном коэффициенте нагрузки ступени путем подходящего выбора реакции. Из диаграммы видно, что при фиксированном коэффициенте нагрузки ступени существует относительно небольшое изменение общей статической эффективности для широкого диапазона конструкций.

50% реакция

Степень реакции влияет на эффективность ступени и, таким образом, используется в качестве расчетного параметра. Используются ступени со степенью реакции 50%, где перепад давления равномерно распределяется между статором и ротором для турбины .

. Рис. 4. Треугольник скорости для степени реакции = 1/2 в турбине

. Это снижает тенденцию отделения пограничного слоя от поверхности лопатки, избегая больших потерь давления торможения.

Если R = ⁄ 2, то из отношения степени реакции | C | α2 = β3 и треугольник скоростей (рис. 4.) симметричен. Ступень энтальпия равномерно распределяется по ступени (рисунок 5.). Кроме того, компоненты вихря одинаковы на входе ротора и диффузора.

. Рис. 5. График энтальпии стадии для степени реакции = 1⁄2 в турбина и насос. Рис. 6. Энтальпия стадии для реакции менее половины

Реакция менее 50%

Стадия, имеющая реакцию менее половины, предполагает, что падение давления или падение энтальпии в роторе меньше чем падение давления в статоре турбины. То же самое для насоса или компрессора, как показано на рисунке 6. Таким образом, статор вносит больший вклад в общую извлеченную или выполненную работу. Из соотношения для степени реакции | C | α2>β3.

Рисунок 7. Треугольник скорости для реакции более 50%.

Реакция более 50%

Стадия, на которой реакция превышает половину, предполагает, что падение давления или падение энтальпии в роторе больше, чем давление падение статора для турбины. То же самое для насоса или компрессора. Таким образом, в этом случае ротор имеет больший вклад в общую извлеченную или выполненную работу. Из соотношения для степени реакции | C | α2 < β3 which is also shown in corresponding Figure 7.

.

Реакция = ноль

Это особый случай, используемый для импульсной турбины, который предполагает, что полное падение давления в турбине происходит в статоре. Статор выполняет действие сопла, преобразуя напор в скоростной напор и вытягивая работу. На практике трудно добиться адиабатического расширения на импульсной стадии, то есть расширения только в сопле, из-за необратимости процесса. На рис. 8 показано соответствующее падение энтальпии для случая реакции = 0.

Рис. 8. Энтальпия стадии для степени реакции = 0 в турбине

Ссылки

Дополнительная литература и работы, относящиеся к

• Гопалакришнан, Г. и Притхви Рай, Д., Трактат о Turbomachines, Scitech, Ченнаи, Индия, 2012
• Венканна, Б.К. (Июль 2011 г.). Основы турбомашиностроения. Нью-Дели: PHI Learning Private Limited. ISBN 978-81-203-3775-6.
• Шеперд, Д.Г., Принципы турбомашин, Девятая печать, Макмиллан, 1969
• Висклиценус, Г.Ф., Гидромеханика турбомашин, McGraw-Hill, New York, 1947
• Thomson, WR, Предварительный проект газовых турбин, Emmott and CO. Ltd., Лондон, 1963
• Траупель, W., Thermische Turbomachinen, 3rd Эдн, Springer Verlag, Берлин, 1978
• Эйнли, Д.Г. и Мэтисон, GCR (1951). Метод оценки производительности осевых турбин. ARC R. and M.
• Dunham, J. and Panton, J. (1973). Опыты по конструкции малой осевой турбины. Публикация конференции 3, Инстн. Мех. Engrs.
• Хорлок, Дж. Х. (1960). Потери и КПД осевых турбин. Int. J. Mech. Sci.,
• Ким, Т. Х., Такао, М., Сетогучи, Т., Канеко, К. и Иноуэ, М. (2001). Сравнение производительности турбин для преобразования энергии волн. Int. J. Therm. Sci.,
• http://www.physicsforums.com/archive/index.php/t-243219.html
• https://www.scribd.com/doc/55453233/18/Degree-of- реакция