Уравнение Дебая - Хюккеля

Химики Питер Дебай и Эрих Хюккель Что, заметил растворы, ионные растворенные вещества, не ведут себя идеально даже при очень низких значениях. Таким образом, растворенных веществ является основополагающим для расчета динамики, они предположили, что для расчета коэффициентов активности дополнительный фактор, который они назвали гамма. Поэтому они разработали уравнение Дебая-Хюккеля и предельный закон Дебая-Хюккеля . Активность пропорциональна только концентрации и изменяется с помощью коэффициента, известного как коэффициент активности $\gamma \; \{\backslash \; displaystyle\; \backslash \; gamma\}$. Этот коэффициент учитывает эффект взаимодействия Класс в растворе.

Содержание

• 1 Предельный закон Дебая-Хюккеля
• 2 Краткое изложение первой статьи Дебая и Хюккеля по теории разбавленных электролитов
  • 2.1 Введение
  • 2.2 Основы
  • 2.3 Потенциальная энергия произвольной ионный раствор
  • 2.4 Дополнительный электрический член к термодинамическому потенциалу
• 3 Обезразмерение
• 4 Экспериментальная проверка теории
• 5 Расширения теории
• 6 См. также
• 7 Примечания
• 8 Ссылки
• 9 Внешние ссылки

Закон ограничения Дебая - Хюккеля

Для расчета активности $a\; C\; \{\backslash \; displaystyle\; a\_\; \{\; C\}\}$иона C в растворе, необходимо знать концентрацию и коэффициент активности:

$a\; C\; =\; \gamma \; [C]\; [C\; \ominus ],\; \{\backslash \; displaystyle\; a\_\; \{C\}\; =\; \backslash \; gamma\; \{\backslash \; frac\; \{[C]\}\; \{[C\; ^\; \{\backslash \; ominus\}]\}\},\}$

где

$\gamma \; \{\backslash \; displaystyle\; \backslash \; gamma\}$- коэффициент активности C,

$[C\; \ominus ]\; \{\backslash \; displaystyle\; [C\; ^\; \{\backslash \; ominus\}]\}$- это совершенство выбранного стандартного, например, 1 моль / кг, если используется моляльность,

$[C]\; \{\backslash \; displaystyle\; [C]\}$является мерой накопленной C.

Деление $[C]\; \{\backslash \; displaystyle\; [C]\}$с $[C\; \ominus ]\; \{\backslash \; displaystyle\; [C\; ^\; \{\backslash \; ominus\}]\}$дает безразмерную оценку.

Предельный закон Дебая - Хюккеля позволяет определить коэффициент иона в разбавленном растворе с известной ионной силой. Уравнение имеет вид

$ln\; \; (\gamma \; i)\; =\; -\; zi\; 2\; q\; 2\; \kappa \; 8\; \pi \; \epsilon \; r\; \epsilon \; 0\; k\; BT\; =\; -\; zi\; 2\; q\; 3\; NA\; 1/2\; 4\; \pi \; (\epsilon \; r\; \epsilon \; 0\; k\; BT)\; 3/2\; 10\; 3\; I\; 2\; =\; -\; A\; zi\; 2\; I,\; \{\backslash \; displaystyle\; \backslash \; ln\; (\backslash \; gamma\; \_\; \{i\})\; =\; -\; \{\backslash \; frac\; \{z\_\; \{i\}\; ^\; \{2\}\; q\; ^\; \{2\}\; \backslash \; kappa\}\; \{8\; \backslash \; pi\; \backslash \; varepsilon\; \_\; \{r\}\; \backslash \; varepsilon\; \_\; \{0\}\; k\; \_\; \{\backslash \; text\; \{B\}\}\; T\}\}\; =\; -\; \{\backslash \; frac\; \{z\_\; \{i\}\; ^\; \{2\}\; q\; ^\; \{3\}\; N\; \_\; \{\backslash \; text\; \{A\; \}\}\; ^\; \{1/2\}\}\; \{4\; \backslash \; pi\; (\backslash \; varepsilon\; \_\; \{r\}\; \backslash \; varepsilon\; \_\; \{0\}\; k\; \_\; \{\backslash \; text\; \{B\}\}\; T)\; ^\; \{3/2\}\}\}\; \{\backslash \; sqrt\; \{10\; ^\; \{3\}\; \{\backslash \; frac\; \{I\}\; \{2\}\}\}\}\; =\; -\; Az\_\; \{i\}\; ^\; \{2\}\; \{\backslash \; sqrt\; \{I\}\},\}$

где

$zi\; \{\backslash \; displaystyle\; z\_\; \{i\}\; \}$- это зарядовое число типа иона i,

$q\; \{\backslash \; displaystyle\; q\}$- элементарный заряд,

$\kappa \; \{\backslash \; displaystyle\; \backslash \; kappa\}$- это обратное значение экранирования по Дебаю (определено ниже),

$\epsilon \; r\; \{\backslash \; displaystyle\; \backslash \; varepsilon\; \_\; \{r\}\}$- это относительная диэлектрическая проницаемость растворителя,

$\epsilon \; 0\; \{\backslash \; displaystyle\; \backslash \; varepsilon\; \_\; \{0\}\}$- диэлектрическая проницаемость свобо дного п ространства,

$k\; B\; \{\backslash \; displaystyle\; k\_\; \{\backslash \; text\; \{B\}\}\}$- это постоянная Больцмана,

$T\; \{\backslash \; displaystyle\; T\}$- температура раствор,

$NA\; \{\backslash \; displaystyle\; N\; \_\; \{\backslash \; mathrm\; \{A\}\}\}$- постоянная Авогадро,,

$I\; \{\backslash \; displaystyle\; I\}$- ионная сила раствор (определенная ниже),

$A\; \{\backslash \; displaystyle\; A\}$- константа, которая зависит от температуры. Если $I\; \{\backslash \; displaystyle\; I\}$выражается в единицах молярности, а не молярности (как в уравнении выше и в остальной части этой статьи), то экспериментальное значение для $A\; \{\backslash \; displaystyle\; A\}$воды составляет $1,172\; моль\; -\; 1/2\; кг\; 1/2\; \{\backslash \; displaystyle\; 1.172\; \{\backslash \; text\; \{mol\}\}\; ^\; \{-\; 1/2\}\; \{\backslash \; text\; \{кг\}\}\; ^\; \{1\; /\; 2\}\}$при 25 ° C. Обычно используется десятичный логарифм, и в этом случае мы множим $ln\; \; 10\; \{\backslash \; displaystyle\; \backslash \; ln\; 10\}$, поэтому A равно $0,509\; моль\; -\; 1/2\; кг\; 1.\; /\; 2\; \{\backslash \; displaystyle\; 0.509\; \{\backslash \; text\; \{mol\}\}\; ^\; \{-\; 1/2\}\; \{\backslash \; text\; \{kg\}\}\; ^\; \{1/2\}\}$. Множитель $10\; 3\; \{\backslash \; displaystyle\; 10\; ^\; \{3\}\}$перед $I\; /\; 2\; \{\backslash \; displaystyle\; I\; /\; 2\}$в уравнении для случая, когда размеры $I\; \{\backslash \; displaystyle\; I\}$равны $моль\; /\; дм\; 3\; \{\backslash \; displaystyle\; \{\backslash \; text\; \{моль\}\}\; /\; \{\backslash \; text\; \{dm\}\}\; ^\; \{3\}\}$. Когда размеры $I\; \{\backslash \; displaystyle\; I\}$равны $моль\; /\; м\; 3\; \{\backslash \; displaystyle\; \{\backslash \; text\; \{моль\}\}\; /\; \{\backslash \; text\; \{m\}\}\; ^\; \{3\}\}$, множитель $10\; 3\; \{\backslash \; displaystyle\; 10\; ^\; \{3\}\}$должен быть исключен из уравнений.

Важно отметить, что, поскольку ионы в этом вместе, фактор активности, полученный из этого уравнения, фактически средним коэффициентом активности.

Избыточное осмотическое давление, полученное по теории Дебая - Хюккеля, выражается в единицах сгс :

$P\; ex\; =\; -\; k\; BT\; \kappa \; cgs\; 3\; 24\; \pi \; =\; -\; k\; BT\; (4\; \pi \; \sum \; jcjqj\; ϵ\; 0\; ϵ\; rk\; BT)\; 3/2\; 24\; \pi .\; \{\backslash \; displaystyle\; P\; ^\; \{\backslash \; text\; \{ex\}\}\; =\; -\; \{\backslash \; frac\; \{k\; \_\; \{\backslash \; text\; \{B\}\}\; T\; \backslash \; kappa\; \_\; \{\backslash \; text\; \{cgs\}\}\; ^\; \{3\}\}\; \{24\; \backslash \; pi\}\}\; =\; -\; \{\backslash \; frac\; \{k\; \_\; \{\backslash \; text\; \{B\}\}\; T\; \backslash \; left\; (\{\backslash \; frac\; \{4\; \backslash \; pi\; \backslash \; sum\; \_\; \{j\}\; c\_\; \{j\}\; q\_\; \{j\}\}\; \{\backslash \; epsilon\; \_\; \{0\}\; \backslash \; epsilon\; \_\; \{r\}\; k\; \_\; \{\backslash \; text\; \{B\}\}\; T\}\}\; \backslash \; right)\; ^\; \{3/2\}\}\; \{24\; \backslash \; pi\}\}.\}$

Таким образом, полное давление складывается из избыточного осмотического давления и идеального давления $P\; id\; =\; k\; BT\; \sum \; ici\; \{\backslash \; displaystyle\; P\; ^\; \{\backslash \; text\; \{id\}\}\; =\; k\; \_\; \{\backslash \; text\; \{B\}\}\; T\; \backslash \; sum\; \_\; \{i\}\; c\_\; \{i\}\}$. Осмотический коэффициент тогда определяется как

$\varphi \; =\; P\; id\; +\; P\; ex\; P\; id\; =\; 1\; +\; P\; ex\; P\; id.\; \{\backslash \; displaystyle\; \backslash \; phi\; =\; \{\backslash \; frac\; \{P\; ^\; \{\backslash \; text\; \{id\}\}\; +\; P\; ^\; \{\backslash \; text\; \{ex\}\}\}\; \{P\; ^\; \{\backslash \; text\; \{id\}\}\}\}\; =\; 1\; +\; \{\backslash \; frac\; \{P\; ^\; \{\backslash \; text\; \{ex\}\}\}\; \{P\; ^\; \{\backslash \; text\; \{id\}\}\}\}.\}$

Краткое изложение первой статьи Дебая и Хюккеля по теории разбавленных электролитов

Английское Статья название «К теории электролитов» ». I. Понижение точки замерзания и связанные с ним явления ». Первоначально он был опубликован в 1923 году в 24 томе немецкоязычного журнала Physikalische Zeitschrift. Английский перевод статьи включен в сборник статей, подаренный Дебаю «его учениками, и издателями случаю его семидесятилетия 24 марта 1954 года». Другой перевод на английский язык был завершен в 2019 году. Статья относится к воздействию ионно-индуцированных электрических полей, таким образом, она касается электростатики.

В том же году они опубликовали эту В статье Дебай и Хюккель, далее DH, также опубликовали статью, в которойывалась их первоначальная характеристикаоров под название «Теория электролитов. II. Предельный закон для электропроводности », но эта последующая статья не является (еще) здесь.

В нижеследующем резюме (пока что неполное и непроверенное) используются современные обозначения и терминология как из химии, так и из математики, во избежание путаницы. Кроме того, за некоторыми исключениями для большей ясности, разделы в этом резюме являются (очень) сокращенными версиями исходных статей.

Введение

DH обратите внимание, что формула Гульдберга - Вааге для разновидностей электролита в равновесие химической реакции в классической форме имеет вид

$\prod \; i\; =\; 1\; sxi\; \nu \; i\; Знак\; равно\; К,\; \{\backslash \; displaystyle\; \backslash \; prod\; \_\; \{i\; =\; 1\}\; ^\; \{s\}\; x\_\; \{i\}\; ^\; \{\backslash \; nu\; \_\; \{i\}\}\; =\; K,\}$

где

$\prod \; \{\backslash \; displaystyle\; \backslash \; textstyle\; \backslash \; prod\}$- это обозначение для умножения,

$i\; \{\backslash \; displaystyle\; i\}$- фиктивная переменная, указывающая вид,

$s\; \{\backslash \; displaystyle\; s\}$- количество частиц, участвующих в реакции,

$xi\; \{\backslash \; displaystyle\; x\_\; \{i\}\}$- мольная доля видов $i\; \{\; \backslash \; displaystyle\; i\}$,

$\nu \; i\; \{\backslash \; displaystyle\; \backslash \; nu\; \_\; \{i\}\}$- стехиометрический коэффициент вида $i\; \{\backslash \; displaystyle\; i\}$,

K - константа равновесия.

DH говорят, что из-за «взаимных электростатических сил между ионами» необходимо изменить уравнение Гульдберга - Вааге, заменив $K\; \{\backslash \; displaystyle\; K\}$с $\gamma \; K\; \{\backslash \; disp\; laystyl\; e\; \backslash \; gamm\; a\; K\}$, где $\gamma \; \{\backslash \; displaystyle\; \backslash \; gamma\}$- это общий коэффициент активности, а не «специальный» коэффициент активности (отдельный вид деятельности коэффициент, который используется в современной химии с 2007 года.

Связь между $\gamma \; \{\backslash \; displaystyle\; \backslash \; gamma\}$и специальными коэффициентами активности $\gamma \; я\; \{\backslash \; displaystyle\; \backslash \; gamma\; \_\; \{i\}\}$is

$журнал\; \; (\gamma )\; =\; \sum \; я\; =\; 1\; с\; \nu \; я\; журнал\; \; (\gamma \; я).\; \{\backslash \; displaystyle\; \backslash \; log\; (\backslash \; gamma)\; =\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{s\}\; \backslash \; nu\; \_\; \{i\}\; \backslash \; log\; (\backslash \; gamma\; \_\; \{i\}).\}$

Основы

DH использует свободные энтропии Гельмгольца и Гиббса $\Phi \; \{\backslash \; displaystyle\; \backslash \; Phi\}$и $\Xi \; \{\backslash \; displaystyle\; \backslash \; Xi\}$для выражения влияния электростатических сил в электролите на его термодинамическое состояние. В частности, они разделяют большую часть термодинамических потенциалов на классические и электростатические термины:

$\Phi \; =\; S\; -\; UT\; =\; -\; AT,\; \{\backslash \; displaystyle\; \backslash \; Phi\; =\; S\; -\; \{\backslash \; frac\; \{U\}\; \{T\}\; \}\; =\; -\; \{\backslash \; frac\; \{A\}\; \{T\}\},\}$

где

$\Phi \; \{\backslash \; displaystyle\; \backslash \; Phi\}$равно свободная энтропия Гельмгольца,

$S\; \{\backslash \; displaystyle\; S\; \}$- энтропия,

$U\; \{\backslash \; displaystyle\; U\}$- внутренняя энергия,

$T\; \{\backslash \; displaystyle\; T\}$- температура,

$A\; \{\backslash \; displaystyle\; A\}$is свободная энергия Гельмгольца.

DH дает общий дифференциал из $\Phi \; \{\backslash \; displaystyle\; \backslash \; Phi\}$as

$d\; \Phi \; =\; PT\; d\; V\; +\; UT\; 2\; d\; T,\; \{\backslash \; displaystyle\; d\; \backslash \; Phi\; =\; \{\backslash \; frac\; \{P\}\; \{T\}\}\; \backslash ,\; dV\; +\; \{\backslash \; frac\; \{U\}\; \{T\; ^\; \{2\}\}\}\; \backslash ,\; dT,\}$

где

$P\; \{\backslash \; displaystyle\; P\}$- давление,

$V\; \{\backslash \; displaystyle\; V\}$- объем.

По определению полного дифференциала это означает, что

$PT\; =\; \partial \; \Phi \; \partial \; V,\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{P\}\; \{T\}\}\; =\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; Phi\}\; \{\backslash \; p\; artial\; V\}\},\}$

$UT\; 2\; =\; \partial \; \Phi \; \partial \; T,\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{U\}\; \{T\; ^\; \{2\}\}\}\; =\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; Phi\}\; \{\backslash \; partial\; T\}\; \},\}$

, которые будут полезны в дальнейшем.

Как было сказано ранее, внутренняя энергия делится на две части:

$U\; =\; U\; k\; +\; U\; e\; \{\backslash \; displaystyle\; U\; =\; U\_\; \{k\}\; +\; U\_\; \{e\}\}$

где

$k\; \{\backslash \; displaystyle\; k\}$указывает на классическую часть,

$e\; \{\backslash \; displaystyle\; e\}$указывает на электрическую часть.

Аналогично, свободная энтропия Гельмгольца также делится на две части:

$\Phi \; =\; \Phi \; k\; +\; \Phi \; e.\; \{\backslash \; displaystyle\; \backslash \; Phi\; =\; \backslash \; Phi\; \_\; \{k\}\; +\; \backslash \; Phi\; \_\; \{e\}.\}$

Состояние DH без инструкций логики, что

$\Phi \; e\; =\; \int \; U\; e\; T\; 2\; d\; T.\; \{\backslash \; displaystyle\; \backslash \; Phi\; \_\; \{e\}\; =\; \backslash \; int\; \{\backslash \; frac\; \{U\_\; \{e\}\}\; \{T\; ^\; \{2\}\}\}\; \backslash ,\; dT.\}$

Может показаться, что без какого-либо обоснования

$\Phi \; е\; =\; \int \; P\; e\; T\; d\; V\; +\; \int \; U\; е\; T\; 2\; d\; T.\; \{\backslash \; displaystyle\; \backslash \; Phi\; \_\; \{e\}\; =\; \backslash \; int\; \{\backslash \; frac\; \{P\_\; \{e\}\}\; \{T\}\}\; \backslash ,\; dV\; +\; \backslash \; int\; \{\backslash \; frac\; \{U\_\; \{e\; \}\}\}\; \{T\; ^\; \{2\}\}\}\; \backslash ,\; dT.\}$

Без особого упоминания этого, DH позже дает то, что может быть требуемым (выше) обоснованием, утверждая, что $\Phi \; e\; =\; \Xi \; e\; \{\; \backslash \; displaystyle\; \backslash \; Phi\; \_\; \{e\}\; =\; \backslash \; Xi\; \_\; \{e\}\}$, предположение, что растворитель несжимаем.

Определение свободной энтропии Гиббса $\Xi \; \{\backslash \; displaystyle\; \backslash \; Xi\}$is

$\Xi \; =\; S\; -\; U\; +\; PVT\; =\; \Phi \; -\; PVT\; =\; -\; GT,\; \{\backslash \; displaystyle\; \backslash \; Xi\; =\; S\; -\; \{\backslash \; frac\; \{U\; +\; PV\}\; \{T\}\}\; =\; \backslash \; Phi\; -\; \{\backslash \; frac\; \{PV\}\; \{T\}\}\; =\; -\; \{\backslash \; frac\; \{G\}\; \{T\}\},\}$

где $G\; \{\backslash \; displaystyle\; G\}$равно свободная энергия Гиббса.

DH дает общий дифференциал $\Xi \; \{\backslash \; displaystyle\; \backslash \; Xi\}$as

$d\; \Xi \; =\; -\; VT\; d\; P\; +\; U\; +\; PVT\; 2\; d\; T.\; \{\backslash \; displaystyle\; d\; \backslash \; Xi\; =\; -\; \{\backslash \; frac\; \{V\}\; \{T\}\}\; \backslash ,\; dP\; +\; \{\backslash \; frac\; \{U\; +\; PV\}\; \{T\; ^\; \{2\}\}\}\; \backslash ,\; dT.\}$

Здесь заметка DH что для воды, содержащее 1 моль на литр хлорида калия (номинальное давление и температура не указаны), электрическое давление $P\; e\; \{\backslash \; displaystyle\; P\_\; \{e\}\}$составляет 20 атмосфер. Кроме того, они отмечают, что этот уровень давления дает относительное изменение объема на 0,001. Поэтому они пренебрегают изменением объема воды из-за электрического давления, записывая

$\Xi \; =\; \Xi \; k\; +\; \Xi \; e,\; \{\backslash \; displaystyle\; \backslash \; Xi\; =\; \backslash \; Xi\; \_\; \{k\}\; +\; \backslash \; Xi\; \_\; \{e\},\}$

и положим

$\Xi \; е\; знак\; равно\; \Phi \; е\; знак\; равно\; \int \; U\; е\; T\; 2\; d\; T.\; \{\backslash \; displaystyle\; \backslash \; Xi\; \_\; \{e\}\; =\; \backslash \; Phi\; \_\; \{e\}\; =\; \backslash \; int\; \{\backslash \; frac\; \{U\_\; \{e\}\}\; \{T\; ^\; \{2\}\}\}\; \backslash ,\; dT.\}$

DH говорят, что, согласно Планка, классическая часть свободной энтропии Гиббса равна

$\Xi \; k\; =\; \sum \; i\; =\; 0\; s\; N\; i\; (\xi \; i\; -\; k\; B\; ln\; (xi)),\; \{\backslash \; displaystyle\; \backslash \; Xi\; \_\; \{k\}\; =\; \backslash \; sum\; \_\; \{я\; =\; 0\}\; ^\; \{s\}\; N\_\; \{i\}\; (\backslash \; xi\; \_\; \{i\}\; -k\; \_\; \{\backslash \; text\; \{B\}\}\; ln\; (x\_\; \{i\; \})),\}$

где

$i\; \{\backslash \; displaystyle\; i\}$- это вид,

$s\; \{\backslash \; displaystyle\; s\}$- количество различных типов частиц в растворе,

$N\; i\; \{\backslash \; displaystyle\; N\_\; \{i\}\}$- количество частиц вида i,

$\xi \; i\; \{\backslash \; displaystyle\; \backslash \; xi\; \_\; \{i\}\}$- специфическая для частиц свободная энтропия Гиббса вида i,

$k\; B\; \{\backslash \; displaystyle\; k\; \_\; \{\backslash \; text\; \{B\}\}\}$- постоянная Больцмана,

$xi\; \{\backslash \; displaystyle\; x\_\; \{i\}\}$- мольн ая доля частиц i.

Растворителем является нулевой вид. Определение $\xi \; i\; \{\backslash \; displaystyle\; \backslash \; xi\; \_\; \{i\}\}$выглядит следующим образом, где строчные буквы обозначают специфичные для частиц версии соответствующих расширенных свойств:

$\xi \; i\; =\; si\; -\; ui\; +\; P\; vi\; T.\; \{\backslash \; displaystyle\; \backslash \; xi\; \_\; \{i\}\; =\; s\_\; \{i\}\; -\; \{\backslash \; frac\; \{u\_\; \{i\}\; +\; Pv\_\; \{i\}\}\; \{T\}\}.\}$

DH это не говорит, но функциональная форма для $\Xi \; k\; \{\backslash \; displaystyle\; \backslash \; Xi\; \_\; \{k\}\}$может быть получено из функциональной зависимости химического компонента идеальной смеси от его мольной доли.

DH обратите внимание, что внутренняя энергия $U\; \{\backslash \; displaystyle\; U\}$раствор ниже за счет электрического взаимодействия его первого, но эффект не может быть определен с использованием кристаллографического приближения для расстояний между расстояниями расстояниями разнородными атомами (кубический корень из отношения к количеству частиц в объеме). Это потому, что в жидком растворе больше теплового движения, чем в кристалле. Тепловое движение тенденцию размывать естественную решетку. Вместо этого DH вводит концепцию ионной атмосферы или облака. Подобно кристаллической решетке, каждый ион все еще пытается окружить себя противоположно заряженными ионами, но в более свободной форме; на малых расстояниях от положительного обнаружения вероятность отрицательных результатов выше.

Потенциальная энергия используется произвольно

Электронейтральная среда требует, чтобы

$\sum \; я\; знак\; равно\; 1\; s\; N\; izi\; =\; 0,\; \{\backslash \; displaystyle\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{s\}\; N\_\; \{i\}\; z\_\; \{i\}\; =\; 0,\}$

где

$N\; i\; \{\backslash \; displaystyle\; N\_\; \{i\}\}$- общее количество первого вида i в растворе,

$zi\; \{\backslash \; displaystyle\; z\_\; \{i\}\}$- зарядовое число вида i.

доставить ионного вида я изначально находящийся далеко, в точку $P\; \{\backslash \; displaystyle\; P\}$Чтобы внутри ионного облака, требуется энергия взаимодействия в размере $ziq\; \phi \; \{\backslash \; displaystyle\; z\_\; \{i\}\; q\; \backslash \; varphi\}$, где $q\; \{\backslash \; displaystyle\; q\}$- элементарный заряд, а $\phi \; \{\; \backslash \; displaystyle\; \backslash \; varphi\}$- значение поля скалярного электрического в $P\; \{\backslash \; displaystyle\; P\}$. Если бы электрические силы были единственной действующей конфигурацией, конфигурация с минимальной энергией достигнута в конфигурации решетки с плотной упаковкой. Однако ионы находятся в тепловом равновесии друг с другом и относительно свободно перемещаются. Таким образом, они подчиняются статистике Больцмана и образуют распределение Больцмана. числовая плотность всех видов $ni\; \{\backslash \; displaystyle\; n\_\; \{i\}\}$отличается от их совокупных (средних) значений $ni\; 0\; \{\backslash \; displaystyle\; n\_\; \{i\}\; ^\; \{\; 0\}\}$на соответствующий коэффициент Больцмана $e\; -\; ziq\; \phi \; k\; BT\; \{\backslash \; displaystyle\; e\; ^\; \{-\; \{\backslash \; frac\; \{z\_\; \{i\}\; q\; \backslash \; varphi)\}\; \{k\; \_\; \{\backslash \; text\; \{B\}\}\; T\}\}\}\}$, где $k\; B\; \{\backslash \; displaystyle\; k\; \_\; \{\backslash \; text\; \{B\}\}\}$- это Постоянная Больцмана, а $T\; \{\backslash \; displaystyle\; T\}$- температура. Таким образом, в каждой точке облака

$ni\; =\; N\; i\; V\; e\; -\; ziq\; \phi \; k\; BT\; =\; ni\; 0\; e\; -\; ziq\; \phi \; k\; B\; T.\; \{\backslash \; displaystyle\; n\_\; \{i\}\; =\; \{\backslash \; frac\; \{N\_\; \{i\}\}\; \{\; V\}\}\; e\; ^\; \{-\; \{\backslash \; frac\; \{z\_\; \{i\}\; q\; \backslash \; varphi\}\; \{k\; \_\; \{\backslash \; text\; \{B\}\}\; T\}\}\}\; =\; n\_\; \{i\}\; ^\; \{0\}\; e\; ^\; \{-\; \{\backslash \; frac\; \{\; z\_\; \{i\}\; q\; \backslash \; varphi\}\; \{k\; \_\; \{\backslash \; text\; \{B\}\}\; T\}\}\}.\}$

Обратите внимание, что в пределе бесконечной температуры, все ионы распределены равномерно, без учета их электростатического взаимодействия.

плотность заряда связана с числовой плотностью:

$\rho \; =\; \sum \; iziqni\; =\; \sum \; iziqni\; 0\; e\; -\; ziq\; \phi \; k\; BT.\; \{\backslash \; displaystyle\; \backslash \; rho\; =\; \backslash \; sum\; \_\; \{i\}\; z\_\; \{i\}\; qn\_\; \{i\}\; =\; \backslash \; sum\; \_\; \{i\}\; z\_\; \{i\}\; qn\_\; \{i\}\; ^\; \{0\}\; e\; ^\; \{-\; \{\backslash \; frac\; \{z\_\; \{i)))\}\; q\; \backslash \; varphi\}\; \{k\; \_\; \{\backslash \; text\; \{B\}\}\; T\}\}\}.\}$

При объединении этого результата для плотности заряда с уравнением Пуассона из электростатики, форма Уравнение Пуассона - Больцмана дает:

$2\; \phi \; =\; -\; \rho \; \epsilon \; r\; \epsilon \; 0\; =\; -\; iziqni\; 0\; \epsilon \; r\; \epsilon \; 0\; e\; -\; ziq\; \phi \; k\; BT.\; \{\backslash \; displaystyle\; \backslash \; nabla\; ^\; \{2\}\; \backslash \; varphi\; =\; -\; \{\backslash \; frac\; \{\backslash \; rho\}\; \{\backslash \; varepsilon\; \_\; \{r\}\; \backslash \; varepsilon\; \_\; \{0\}\}\}\; =\; -\; \backslash \; sum\; \_\; \{i\}\; \{\backslash \; frac\; \{z\_\; \{i\; \}\; qn\_\; \{i\}\; ^\; \{0\}\}\; \{\backslash \; varepsilon\; \_\; \{r\}\; \backslash \; varepsilon\; \_\; \{0\}\}\}\; e\; ^\; \{-\; \{\backslash \; frac\; \{z\_\; \{i\}\; q\; \backslash \; varphi\}\; \{k\; \_\; \{\backslash \; text\; \{B\}\; \}\; T\}\}\}.\}$

Это уравнение трудно решить, и оно не следует принципу линейной суперпозиции для взаимосвязи между зарядов и потенциального поля. Она была решена шведским математиком Томасом Хаконом Гронваллом и его сотрудниками, физиками-химиками В.К. Ла Мер и Карлом Сандведом в статье 1928 года из Physikalische Zeitschrift, посвященной расширениям теории Дебая - Хюккеля, которые прибегли к расширению ряда Тейлора.

Однако для достаточно низких концентраций пример можно использовать приближение разложения в ряд Тейлора первого порядка экспоненциальной функции ($ex\; \approx \; 1\; +\; x\; \{\backslash \; displaystyle\; e\; ^\; \{x\}\; \backslash \; 1\; +\; x\; \}$для ), чтобы создать линейное дифференциальное уравнение (Hamann, Hamnett, and Vielstich. Electrochemistry. Wiley-VCH. Раздел 2.4.2). DH говорят, что это приближение справедливо на больших расстояниях между ионами, что равносильно утверждению о концентрации. Наконец, без доказательств заявляет, что добавление дополнительных членов в расширение мало влияет на окончательное решение. Таким образом,

$-\; \sum \; iziqni\; 0\; \epsilon \; r\; \epsilon \; 0\; e\; -\; ziq\; \phi \; k\; BT\; \approx \; -\; \sum \; iziqni\; 0\; \epsilon \; r\; \epsilon \; 0\; (1\; -\; ziq\; \phi \; k\; BT)\; =\; -\; (\sum \; iziqni\; 0\; \epsilon \; r\; \epsilon \; 0\; -\; \sum \; izi\; 2\; q\; 2\; ni\; 0\; \phi \; \epsilon \; r\; \epsilon \; 0\; k\; BT).\; \{\backslash \; displaystyle\; -\; \backslash \; sum\; \_\; \{i\}\; \{\backslash \; frac\; \{z\_\; \{i\}\; qn\_\; \{i\}\; ^\; \{0\}\}\; \{\backslash \; varepsilon\; \_\; \{r\}\; \backslash \; varepsilon\; \_\; \{0\}\}\}\; e\; ^\; \{-\; \{\backslash \; frac\; \{\; z\_\; \{i\}\; q\; \backslash \; varphi\}\; \{k\; \_\; \{\backslash \; text\; \{B\}\}\; T\}\}\}\; \backslash \; приблизительно\; -\; \backslash \; sum\; \_\; \{i\}\; \{\backslash \; frac\; \{z\_\; \{i\}\; qn\_\; \{i\}\; ^\; \{0\}\}\; \{\backslash \; varepsilon\; \_\; \{r\}\; \backslash \; varepsilon\; \_\; \{0\}\}\}\; \backslash \; left\; (1\; -\; \{\backslash \; frac\; \{z\_\; \{i\}\; q\; \backslash \; varphi\}\; \{k\; \_\; \{\backslash \; text\; \{B\}\}\; T\}\}\; \backslash \; right)\; =\; -\; \backslash \; left\; (\backslash \; сумма\; \_\; \{i\}\; \{\backslash \; frac\; \{z\_\; \{i\}\; qn\_\; \{i\}\; ^\; \{0\}\}\; \{\backslash \; varepsilon\; \_\; \{r\}\; \backslash \; varepsilon\; \_\; \{0\}\}\}\; -\; \backslash \; sum\; \_\; \{i\}\; \{\backslash \; frac\; \{\; z\_\; \{i\}\; ^\; \{2\}\; q\; ^\; \{2\}\; n\_\; \{i\}\; ^\; \{0\}\; \backslash \; varphi\}\; \{\backslash \; varepsilon\; \_\; \{r\}\; \backslash \; varepsilon\; \_\; \{0\}\; k\; \_\; \{\backslash \; text\; \{B\}\}\; T\}\}\; \backslash \; верно).\; \}$

Уравнение Пуассона - Больцмана преобразуется в

$\nabla \; 2\; \phi \; =\; \sum \; izi\; 2\; q\; 2\; ni\; 0\; \phi \; \epsilon \; r\; \epsilon \; 0\; k\; BT,\; \{\backslash \; displaystyle\; \backslash \; nabla\; ^\; \{2\}\; \backslash \; varphi\; =\; \backslash \; sum\; \_\; \{i\}\; \{\backslash \; frac\; \{z\_\; \{i\}\; ^\; \{2\}\; q\; ^\; \{2\}\; n\_\; \{i\}\; ^\; \{0\}\; \backslash \; varphi\}\; \{\backslash \; varepsilon\; \_\; \{r\}\; \backslash \; varepsilon\; \_\; \{0\}\; k\; \_\; \{\backslash \; text\; \{B\}\}\; T\}\},\}$

, поскольку первое суммирование равно нулю из-за электронейтральности.

Вынесите скалярный потенциал за скобки и присвойте оставшиеся постоянные значения $\kappa \; 2\; \{\backslash \; displaystyle\; \backslash \; kappa\; ^\; \{2\}\}$. Кроме того, пусть $I\; \{\backslash \; displaystyle\; I\}$будет ионной силой раствор:

$\kappa \; 2\; =\; \sum \; izi\; 2\; q\; 2\; ni\; 0\; \epsilon \; r\; \epsilon \; 0\; k\; BT\; =\; 2\; Я\; Q\; 2\; \epsilon \; р\; \epsilon \; 0\; К\; BT,\; \{\backslash \; Displaystyle\; \backslash \; каппа\; ^\; \{2\}\; =\; \backslash \; sum\; \_\; \{i\}\; \{\backslash \; frac\; \{z\_\; \{i\}\; ^\; \{2\}\; q\; ^\; \{2\}\; n\_\; \{i\}\; ^\; \{\; 0\}\}\; \{\backslash \; varepsilon\; \_\; \{r\}\; \backslash \; varepsilon\; \_\; \{0\}\; k\; \_\; \{\backslash \; text\; \{B\}\}\; T\}\}\; =\; \{\backslash \; frac\; \{2Iq\; ^\; \{2\}\}\; \{\backslash \; varepsilon\; \_\; \{r\}\; \backslash \; varepsilon\; \_\; \{\; 0\}\; k\; \_\; \{\backslash \; text\; \{B\}\}\; T\}\},\}$

$I\; =\; 1\; 2\; \sum \; izi\; 2\; ni\; 0.\; \{\backslash \; displaystyle\; I\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \backslash \; sum\; \_\; \{i\}\; z\_\; \{i\}\; ^\; \{2\}\; n\_\; \{i\}\; ^\; \{0\}.\}$

Итак, уравнение сводится к уравнениям Гельмгольца :

$\nabla \; 2\; \phi \; =\; \kappa \; 2\; \phi .\; \{\backslash \; displaystyle\; \backslash \; nabla\; ^\; \{2\}\; \backslash \; varphi\; =\; \backslash \; kappa\; ^\; \{2\}\; \backslash \; varphi.\}$

Сегодня, $\kappa \; -\; 1\; \{\backslash \; displaystyle\; \backslash \; kappa\; ^\; \{-\; 1\}\}$называется длиной экранирования Дебая. DH признает этого элемента в своей статье, которая представляет собой как меру толщины ионной атмосферы, которая представляет собой двойной электрический слой типа Гуи - Чепмена.

уравнить можно выразить в сферических координатах, взяв $r\; =\; 0\; \{\backslash \; displaystyle\; r\; =\; 0\}$на некотором произвольном ионе:

$\nabla \; 2\; \phi \; =\; 1\; r\; 2\; \partial \; \partial \; r\; (r\; 2\; \partial \; \phi \; (r)\; \partial \; r)\; =\; \partial \; 2\; \phi \; (r)\; \partial \; r\; 2\; +\; 2\; r\; \partial \; \phi \; (r)\; \partial \; r\; =\; \kappa \; 2\; \phi \; (r).\; \{\backslash \; displaystyle\; \backslash \; nabla\; ^\; \{2\}\; \backslash \; varphi\; =\; \{\backslash \; frac\; \{1\}\; \{r\; ^\; \{2\}\}\}\; \{\backslash \; frac\; \{\backslash \; partial\}\; \{\backslash \; partial\; r\}\}\; \backslash \; left\; (r\; ^\; \{2\}\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; varphi\; (r)\}\; \{\backslash \; partial\; r\}\}\; \backslash \; right)\; =\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; \backslash \; varphi\; (r)\}\; \{\backslash \; partial\; r\; ^\; \{2\}\}\}\; +\; \{\backslash \; frac\; \{\; 2\}\; \{r\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; varphi\; (r)\}\; \{\backslash \; partial\; r\}\}\; =\; \backslash \; kappa\; ^\; \{2\}\; \backslash \; varphi\; (r).\}$

Уравнение имеет следующее общее решение (оставьте имея в Имеется в виду, что $\kappa \; \{\backslash \; displaystyle\; \backslash \; kappa\}$является положительной константой):

$\phi \; (r)\; =\; A\; e\; -\; \kappa \; 2\; rr\; +\; A\; \prime \; e\; \kappa \; 2\; r\; 2\; r\; \kappa \; 2\; Знак\; равно\; A\; е\; -\; \kappa \; rr\; +\; A\; ″\; e\; \kappa \; rr\; =\; A\; e\; -\; \kappa \; rr,\; \{\backslash \; displaystyle\; \backslash \; varphi\; (r)\; =\; A\; \{\backslash \; frac\; \{e\; ^\; \{-\; \{\backslash \; sqrt\; \{\backslash \; kappa\; ^\; \{2\}\}\}\; r\; \}\}\; \{r\}\}\; +\; A\; \text{'}\{\backslash \; frac\; \{e\; ^\; \{\{\backslash \; sqrt\; \{\backslash \; kappa\; ^\; \{2\}\}\}\; r\}\}\; \{2r\; \{\backslash \; sqrt\; \{\backslash \; kappa\; ^\; \{2\}\}\}\}\}\; =\; A\; \{\; \backslash \; frac\; \{e\; ^\; \{-\; \backslash \; kappa\; r\}\}\; \{r\}\}\; +\; A\; \text{'}\text{'}\; \{\backslash \; frac\; \{e\; ^\; \{\backslash \; kappa\; r\}\}\; \{r\}\}\; =\; A\; \{\backslash \; frac\; \{e\; ^\; \{-\; \backslash \; kappa\; r\}\; \}\; \{r\}\},\}$

где $A\; \{\backslash \; displaystyle\; A\}$, $A\; \prime \; \{\backslash \; displaystyle\; A\; \text{'}\}$и $A\; ″\; \{\backslash \; displaystyle\; A\text{'}\; \text{'}\}$- неопределенные конст анты

По определению электрический потенциал равенство нулю на бесконечности, поэтому $A\; ″\; \{\backslash \; displaystyle\; A\; \text{'}\text{'}\}$должен быть равенством нулю.

На следующем этапе DH предполагает, что существует определенный радиус $ai\; \{\backslash \; displaystyle\; a\_\; \{i\}\}$, за пределами никакие ионы в атмосфере могут приблизиться к (заряду) центр выделенного иона. Этот радиус может быть связан с физическим размером самого иона, размерами в облаке и любыми молекулами воды, которые окружают ионы. Математически они рассматривают выделенный ион как точечный заряд, к которому нельзя приближаться в пределах радиуса $ai\; \{\backslash \; displaystyle\; a\_\; \{i\}\}$.

Потенциал точечного заряда сам по себе равно

$\phi \; pc\; (\; r)\; =\; 1\; 4\; \pi \; \epsilon \; r\; \epsilon \; 0\; ziqr.\; \{\backslash \; displaystyle\; \backslash \; varphi\; \_\; \{\backslash \; text\; \{pc\}\}\; (r)\; =\; \{\backslash \; frac\; \{1\}\; \{4\; \backslash \; pi\; \backslash \; varepsilon\; \_\; \{r\}\; \backslash \; varepsilon\; \_\; \{0\}\}\}\; \{\backslash \; frac\; \{z\_\; \{i\}\; q\; \}\; \{r\}\}.\}$

DH говорят, что полный потенциал внутри сферы равен

$\phi \; sp\; (r)\; =\; \phi \; pc\; (r)\; +\; B\; i\; =\; 1\; 4\; \pi \; \epsilon \; r\; \epsilon \; 0\; ziqr\; +\; B\; i,\; \{\; \backslash \; displaystyle\; \backslash \; varphi\; \_\; \{\backslash \; text\; \{sp\}\}\; (r)\; =\; \backslash \; varphi\; \_\; \{\backslash \; text\; \{pc\}\}\; (r)\; +\; B\_\; \{i\}\; =\; \{\backslash \; frac\; \{1\}\; \{4\; \backslash \; pi\; \backslash \; varepsilon\; \_\; \{r\; \}\; \backslash \; varepsilon\; \_\; \{0\}\}\}\; \{\backslash \; frac\; \{z\_\; \{i\}\; q\}\; \{r\}\}\; +\; B\_\; \{i\},\}$

где $B\; i\; \{\backslash \; displaystyle\; B\_\; \{i\}\}$- постоянная, представляющая потенциал, добавляемый ионной атмосферной атмосферой. Не дается никакого обоснования того, что $B\; i\; \{\backslash \; displaystyle\; B\_\; \{i\}\}$константой. Однако можно увидеть, что это так, если учесть, что любое сферическое распределение статического заряда подчиняется математике теоремы об оболочке. Теорема оболочек гласит, что на заряженные частицы внутри сферы (с произвольным зарядом) не действует сила. Нормально-ионная атмосфера (усредненная по времени) сферически симметрична с зарядом, изменяемым в зависимости от радиуса $r\; \{\backslash \; displaystyle\; r\}$, ее можно представить как бесконечный ряд концентрических заряжать снаряды. Следовательно, внутри радиуса $a\; i\; \{\backslash \; displaystyle\; a\_\; \{i\}\}$ионная атмосфера не проявляет силы. Если сила равна нулю, то потенциал постоянен (по определению).

В сочетании модели непрерывного распределения, которая дала уравнение Пуассона - Больцмана и модель точечного заряда, что на радиусе $ai\; \{\backslash \; displaystyle\; a\_\; \{i\}\}$, существует непрерывность $\phi \; (r)\; \{\backslash \; displaystyle\; \backslash \; varphi\; (r)\}$и его первой производной. Таким образом,

$\phi \; (ai)\; =\; A\; ie\; -\; \kappa \; aiai\; =\; 1\; 4\; \pi \; \epsilon \; r\; \epsilon \; 0\; ziqai\; +\; B\; i\; =\; \phi \; sp\; (ai),\; \{\backslash \; displaystyle\; \backslash \; varphi\; (a\_\; \{i\})\; =\; A\_\; \{i\; \}\; \{\backslash \; frac\; \{e\; ^\; \{-\; \backslash \; kappa\; a\_\; \{i\}\}\}\; \{a\_\; \{i\}\}\}\; =\; \{\backslash \; frac\; \{1\}\; \{4\; \backslash \; pi\; \backslash \; varepsilon\; \_\; \{r\}\; \backslash \; varepsilon\; \_\; \{0\}\}\}\; \{\; \backslash \; frac\; \{z\_\; \{i\}\; q\}\; \{a\_\; \{i\}\}\}\; +\; B\_\; \{i\}\; =\; \backslash \; varphi\; \_\; \{\backslash \; text\; \{sp\}\}\; (a\_\; \{i\}),\}$

$\phi \; \prime \; (ai)\; =\; -\; A\; ie\; -\; \kappa \; ai\; (1\; +\; \kappa \; ai)\; ai\; 2\; =\; -\; 1\; 4\; \pi \; \epsilon \; r\; \epsilon \; 0\; ziqai\; 2\; =\; \phi \; sp\; \text{'}(ai),\; \{\backslash \; displaystyle\; \backslash \; varphi\text{'}\; (a\_\; \{i\})\; =\; -\; \{\backslash \; frac\; \{\; A\_\; \{i\}\; e\; ^\; \{-\; \backslash \; kappa\; a\_\; \{i\}\}\; (1+\; \backslash \; kappa\; a\_\; \{i\})\}\; \{a\_\; \{i\}\; ^\; \{2\}\}\}\; =\; -\; \{\backslash \; frac\; \{1\}\; \{4\; \backslash \; pi\; \backslash \; varepsilon\; \_\; \{r\}\; \backslash \; varepsilon\; \_\; \{0\}\}\}\; \{\backslash \; frac\; \{z\_\; \{i\}\; q\}\; \{a\_\; \{i\}\; ^\; \{2\}\}\}\; =\; \backslash \; varphi\; \_\; \{\backslash \; text\; \{sp\}\}\; \text{'}(a\_\; \{i\; \}),\}$

$A\; я\; знак\; равно\; ziq\; 4\; \pi \; \epsilon \; р\; \epsilon \; 0\; е\; \kappa \; ai\; 1\; +\; \kappa \; ai,\; \{\backslash \; displaystyle\; A\_\; \{i\}\; =\; \{\backslash \; frac\; \{z\_\; \{i\}\; q\}\; \{4\; \backslash \; pi\; \backslash \; varepsilon\; \_\; \{r\}\; \backslash \; varepsilon\; \_\; \{0\}\}\}\; \{\backslash \; frac\; \{e\; ^\; \{\backslash \; kappa\; a\_\; \{i\}\}\}\; \{1+\; \backslash \; kappa\; a\_\; \{i\}\}\},\}$

$B\; i\; =\; -\; ziq\; \kappa \; 4\; \pi \; \epsilon \; r\; \epsilon \; 0\; 1\; 1\; +\; \kappa \; ai.\; \{\backslash \; displaystyle\; B\_\; \{i\}\; =\; -\; \{\backslash \; frac\; \{z\_\; \{i\}\; q\; \backslash \; kappa\}\; \{4\; \backslash \; pi\; \backslash \; varepsilon\; \_\; \{r\}\; \backslash \; varepsilon\; \_\; \{0\}\}\}\; \{\backslash \; frac\; \{1\}\; \{1+\; \backslash \; kappa\; a\_\; \{i\}\}\}.\}$

По определению потенциальная энергия, потенциальная энергия, связанная с выделенным ионом в ионной атмосфере, равна

ui = ziq B i = - zi 2 q 2 κ 4 π ε r ε 0 1 1 + κ ai. {\ displaystyle u_ {i} = z_ {i} qB_ {i} = - {\ frac {z_ {i} ^ {2} q ^ {2} \ kappa} {4 \ pi \ varepsilon _ {r} \ varepsilon _ {0}}} {\ frac {1} {1+ \ kappa a_ {i}}}.}

Обратите внимание, что для этого нужно только заряд выделенного иона и всех остальных лучей..

Чтобы вычислить потенциальную энергию всего электролита, использовать многозарядное обобщение для потенциальной энергии:

$U\; e\; =\; 1\; 2\; \sum \; i\; =\; 1\; s\; N\; iui\; =\; -\; \sum \; i\; =\; 1\; с\; N\; izi\; 2\; 2\; q\; 2\; \kappa \; 4\; \pi \; \epsilon \; r\; \epsilon \; 0\; 1\; 1\; +\; \kappa \; ai.\; \{\backslash \; displaystyle\; U\_\; \{e\}\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{s\}\; N\_\; \{i\}\; u\_\; \{i\}\; =\; -\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{\; s\}\; \{\backslash \; frac\; \{N\_\; \{i\}\; z\_\; \{i\}\; ^\; \{2\}\}\; \{2\}\}\; \{\backslash \; frac\; \{q\; ^\; \{2\}\; \backslash \; kappa\}\; \{4\; \backslash \; pi\; \backslash \; varepsilon\; \_\; \{r\}\; \backslash \; varepsilon\; \_\; \{0\; \}\}\}\; \{\backslash \; frac\; \{1\}\; \{1+\; \backslash \; kappa\; a\_\; \{i\}\}\}.\}$

Дополнительный электрический член к термодинамическому потенциалу

обезразмеривание

Дифференциальное уравнение имеет вид готов к решение (как указано выше, уравнение справедливо только для низких концентраций):

$\partial \; 2\; \phi \; (r)\; \partial \; r\; 2\; +\; 2\; r\; \partial \; \phi \; (r)\; \partial \; r\; =\; I\; q\; \phi \; (r)\; \epsilon \; r\; \epsilon \; 0\; k\; BT\; =\; \kappa \; 2\; \phi \; (r).\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; \backslash \; varphi\; (r)\}\; \{\backslash \; partial\; r\; ^\; \{2\}\}\}\; +\; \{\backslash \; frac\; \{2\}\; \{r\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; varphi\; (r)\}\; \{\backslash \; partial\; r\}\}\; =\; \{\backslash \; frac\; \{Iq\; \backslash \; varphi\; (r)\}\; \{\backslash \; varepsilon\; \_\; \{r\}\; \backslash \; varepsilon\; \_\; \{0\}\; k\; \_\; \{\backslash \; text\; \{B\}\}\; T\}\}\; =\; \backslash \; kappa\; ^\; \{\; 2\}\; \backslash \; varphi\; (r).\}$

Использование π-теоремы Бакингема для этой задачи приводит к следующим безразмерным группам:

$\pi \; 1\; =\; q\; \phi \; (r)\; k\; BT\; =\; \Phi \; (R\; (\; r))\; \{\backslash \; displaystyle\; \backslash \; pi\; \_\; \{1\}\; =\; \{\backslash \; frac\; \{q\; \backslash \; varphi\; (r)\}\; \{k\; \_\; \{\backslash \; text\; \{B\}\}\; T\}\}\; =\; \backslash \; Phi\; (R\; (r))\}$

$\pi \; 2\; знак\; равно\; \epsilon \; р\; \{\backslash \; displaystyle\; \backslash \; pi\; \_\; \{2\}\; =\; \backslash \; varepsilon\; \_\; \{r\}\}$

$\pi \; 3\; =\; ak\; BT\; \epsilon \; 0\; q\; 2\; \{\backslash \; displaystyle\; \backslash \; pi\; \_\; \{3\}\; =\; \{\backslash \; frac\; \{ak\; \_\; \{\backslash \; текст\; \{B\}\}\; T\; \backslash \; varepsilon\; \_\; \{0\}\}\; \{q\; ^\; \{2\}\}\}\}$

$\pi \; 4\; =\; a\; 3\; I\; \{\backslash \; displaystyle\; \backslash \; pi\; \_\; \{4\}\; =\; a\; ^\; \{3\}\; I\; \}$

$\pi \; 5\; знак\; равно\; z\; 0\; \{\backslash \; displaystyle\; \backslash \; pi\; \_\; \{5\}\; =\; z\_\; \{0\}\}$

$\pi \; 6\; =\; ra\; =\; R\; (r).\; \{\backslash \; displaystyle\; \backslash \; pi\; \_\; \{6\}\; =\; \{\backslash \; frac\; \{r\}\; \{a\}\}\; =\; R\; (r).\}$

$\Phi \; \{\backslash \; displaystyle\; \backslash \; Phi\}$называется приведенным скалярным потенциалом. поле. $R\; \{\backslash \; displaystyle\; R\}$называется уменьшенным радиусом. Существующие группы могут быть повторно объединены для образования двух других безразмерных групп для подстановки в дифференциальное уравнение. Первый - это то, что можно назвать квадратом уменьшенной длины экранирования, $(\kappa \; a)\; 2\; \{\backslash \; displaystyle\; (\backslash \; kappa\; a)\; ^\; \{2\}\}$. Второй можно назвать уменьшенным центральным зарядом иона, $Z\; 0\; \{\backslash \; displaystyle\; Z\_\; \{0\}\}$(с большой буквы). Обратите внимание, что, хотя $z\; 0\; \{\backslash \; displaystyle\; z\_\; \{0\}\}$уже безразмерен, без подстановки, приведенной ниже, дифференциальное уравнение все равно будет размерным.

$\pi \; 4\; \pi \; 2\; \pi \; 3\; знак\; равно\; a\; 2\; q\; 2\; I\; \epsilon \; р\; \epsilon \; 0\; К\; BT\; =\; (\kappa \; a)\; 2\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; pi\; \_\; \{4\}\}\; \{\backslash \; pi\; \_\; \{2\}\; \backslash \; pi\; \_\; \{3\}\}\}\; =\; \{\backslash \; frac\; \{a\; ^\; \{2\}\; q\; ^\; \{2\}\; I\}\; \{\backslash \; varepsilon\; \_\; \{r\}\; \backslash \; varepsilon\; \_\; \{0\}\; k\; \_\; \{\backslash \; text\; \{B\}\}\; T\}\}\; =\; (\backslash \; каппа\; а)\; ^\; \{2\}\}$

$\pi \; 5\; \pi \; 2\; \pi \; 3\; =\; z\; 0\; q\; 2\; 4\; \pi \; a\; \epsilon \; р\; \epsilon \; 0\; К\; BT\; =\; Z\; 0\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; pi\; \_\; \{5\}\}\; \{\backslash \; pi\; \_\; \{2\}\; \backslash \; pi\; \_\; \{3\}\}\}\; =\; \{\backslash \; frac\; \{z\_\; \{0\}\; q\; ^\; \{2\}\}\; \{4\; \backslash \; pi\; a\; \backslash \; varepsilon\; \_\; \{r\}\; \backslash \; varepsilon\; \_\; \{0\}\; k\; \_\; \{\; \backslash \; text\; \{B\}\}\; T\}\}\; =\; Z\_\; \{0\}\}$

получить безразмерное дифференциальное уравнение и начальные условия, викоризовать группы $\pi \; \{\backslash \; displaystyle\; \backslash \; pi\}$, чтобы исключить $\phi \; (r)\; \{\backslash \; displaystyle\; \backslash \; varphi\; (r)\}$в пользу $\Phi \; (R\; (r))\; \{\backslash \; displaystyle\; \backslash \; Phi\; (R\; (r))\}$, затем удалите $R\; (r)\; \{\backslash \; displaystyle\; R\; (r)\}$в пользу $r\; \{\backslash \; displaystyle\; r\}$, выполняя правило цепочки и заменяя $R\; \text{'}(r)\; =\; a\; \{\backslash \; displaystyle\; \{R\; ^\; \{\backslash \; prime\}\}\; (r)\; =\; a\}$, затем удалите $r\; \{\backslash \; displaystyle\; r\}$в пользу $R\; \{\backslash \; displaystyle\; R\}$(правило цепочки не требуется), затем е лиминат $I\; \{\backslash \; displaystyle\; I\}$в пользу $(\kappa \; a)\; 2\; \{\; \backslash \; displaystyle\; (\backslash \; kappa\; a)\; ^\; \{2\}\}$, затем удалите $z\; 0\; \{\backslash \; displaystyle\; z\_\; \{0\}\}$в пользу $Z\; 0\; \{\backslash \; displaystyle\; Z\_\; \{0\}\}$. В результате получаются следующие уравнения:

$\partial \; \Phi \; (R)\; \partial \; R\; |\; R\; =\; 1\; =\; -\; Z\; 0\; \{\backslash \; Displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; Phi\; (R)\}\; \{\backslash \; partial\; R\}\}\; \{\backslash \; bigg\; |\}\; \_\; \{R\; =\; 1\}\; =\; -\; Z\_\; \{0\}\}$

$\Phi \; (\infty )\; знак\; равно\; 0\; \{\backslash \; Displaystyle\; \backslash \; Phi\; (\backslash \; infty)\; =\; 0\}$

$\partial \; 2\; \Phi \; (R)\; \partial \; R\; 2\; +\; 2\; R\; \partial \; \Phi \; (R)\; \partial \; R\; =\; (\kappa \; a)\; 2\; \Phi \; (R).\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; \backslash \; Phi\; (R)\}\; \{\backslash \; partial\; R\; ^\; \{2\}\}\}\; +\; \{\backslash \; frac\; \{2\}\; \{R\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; Phi\; (R)\}\; \{\backslash \; partial\; R\}\}\; =\; (\backslash \; kappa\; a)\; ^\; \{2\}\; \backslash \; Phi\; (R).\}$

Для поваренной соли в 0,01 M растворе при 25 ° C типичное значение $(\kappa \; a)\; 2\; \{\backslash \; displaystyle\; (\backslash \; kappa\; a)\; ^\; \{2\}\}$равно 0,0005636, а типичное значение $Z\; 0\; \{\backslash \; displaystyle\; Z\_\; \{0\}\}$равно 7,017, подчеркивая тот факт, что при низких уровнях х $(\kappa \; a)\; 2\; \{\backslash \; displaystyle\; (\backslash \; kappa\; a)\; ^\; \{2\}\}$является целью для приближения нулевого порядка величины, например возмущения анализ. К сожалению, из-за граничного условия на регулярное возмущение не работает. Это же граничное условие не позволяет нам найти точное решение уравнений. Однако сингулярное возмущение может работать.

Экспериментальная проверка теории

Чтобы проверить справедливость теории Дебая-Хюккеля, было испробовано множество экспериментальных способов измерения коэффициентов активности: проблема в том, что нам нужно идти в сторону очень высокие разведения. Типичными примерами являются: измерение давления пара, точки замерзания, осмотического давления (косвенные методы) и измерения электрического потенциала в ячейках (прямой метод). При переходе к разбавлению хорошие результаты были получены с использованием жидкостных мембранных ячеек, возможно исследовать водные среды 10 M, и было обнаружено, что для электролитов 1: 1 уравнение Дебая-Хюккеля полностью верно, но для электролитов 2: 2 или 3: 2 можно найти отрицательное отклонение от предельного закона Дебая - Хюккеля: это странное поведение может наблюдаться только в очень разбавленной области, а в более концентрированных областях становится положительным. Возможно, уравнение Дебая - Хюккеля не способно предвидеть такое поведение из-за линеаризации уравнения Пуассона - Больцмана, а может и нет: исследования по этому поводу были начаты только в последние годы 20-го века, потому что раньше этого не было. Невозможно исследовать область 10 миллионов, так что не исключено.

Расширения теории

Был предложен ряд подходов для расширения действия закона на диапазоны концентраций, которые обычно встречаются в химии

Один из таких расширенных подходов Дебая-Хюккеля уравнение имеет вид:

$-\; log\; 10\; \; (\gamma )\; =\; A\; |\; z\; +\; z\; -\; |\; I\; 1\; +\; B\; a\; I\; \{\backslash \; displaystyle\; \backslash \; -\; \backslash \; log\; \_\; \{10\}\; (\backslash \; gamma)\; =\; \{\backslash \; frac\; \{A\; |\; z\; \_\; \{+\}\; z\; \_\; \{-\}\; |\; \{\backslash \; sqrt\; \{I\}\}\}\; \{1\; +\; Ba\; \{\; \backslash \; sqrt\; \{I\}\}\}\; \backslash ,\}$

где $\gamma \; \{\backslash \; displaystyle\; \backslash \; \backslash \; gamma\; \backslash ,\}$как его десятичный логарифм - коэффициент активности, $z\; \{\backslash \; displaystyle\; \backslash \; z\; \backslash ,\}$- целочисленный заряд иона (1 для H, 2 для Mg и т. Д.), $I\; \{\backslash \; displaystyle\; \backslash \; I\; \backslash ,\}$- ионная сила водного раствора, а $a\; \{\backslash \; displaystyle\; \backslash \; a\; \backslash ,\}$- размер или эффективный диаметр иона в ангстрем. Эффективный гидратированный радиус иона a - это радиус иона и его тесно связанных молекул воды. Большие ионы и менее заряженные ионы менее прочно связывают воду и имеют меньший радиус гидратации, чем более мелкие и более заряженные ионы. Типичные значения составляют 3Å для таких ионов, как H, Cl, CN и HCOO. Эффективный диаметр для иона гидроксония составляет 9 Å. $A\; \{\backslash \; displaystyle\; \backslash \; A\; \backslash ,\}$и $B\; \{\backslash \; displaystyle\; \backslash \; B\; \backslash ,\}$- константы со значениями соответственно 0,5085 и 0,3281 при 25 ° C. в воде.

Расширенное уравнение Дебая – Хюккеля дает точные результаты для μ ≤ 0,1. Для растворов с большей ионной силой следует использовать уравнения Питцера. В этих растворах коэффициент активности может фактически увеличиваться с увеличением ионной силы.

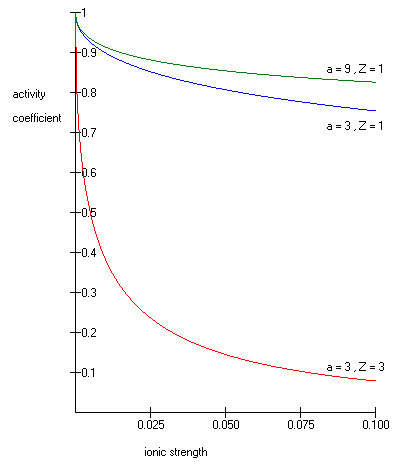
Уравнение Дебая – Хюккеля нельзя использовать в растворах поверхностно-активных веществ, где присутствие мицелл влияет на электрохимические свойства системы (даже грубая оценка дает завышенную оценку γ на ~ 50 %).

См. Также

• Сильный электролит
• Слабый электролит
• Ионная атмосфера
• Теория Дебая – Хюккеля
• Уравнение Пуассона – Больцмана

Примечания

1. ^http: // homepages. rpi.edu/~keblip/THERMO/chapters/Chapter33.pdf, стр. 9.
2. ^ Сборник статей Питера Дж. В. Дебая. Нью-Йорк, Нью-Йорк: Interscience Publishers, Inc. 1954.
3. ^П. Дебай и Э. Хюккель (1923). "Zur Theorie der Elektrolyte. I. Gefrierpunktserniedrigung und verwandte Erscheinungen". Physikalische Zeitschrift. 24: 185–206.
4. ^P. Дебай и Э. Хюккель (1923). «Теория электролитов. 1. Понижение точки замерзания и связанные с ним явления. Перевод Майкла Дж. Брауса (2020)». Physikalische Zeitschrift. 24: 185–206.
5. ^Зальцман, Уильям Р. (2001-08-21). «Смеси; частичные молярные количества; идеальные растворы». Химическая термодинамика. Университет Аризоны. Архивировано с оригинального 07.06.2007. Проверено 23 октября 2007 г.
6. ^http://www.pm a.caltech.edu/Courses/ph136/yr2006/text.html Архивировано 2007-08-28 на Wayback Machine, раздел 19.3
7. ^http: // guava.physics.uiuc.edu/~nigel/courses/569/Essays_2004/files/lu.pdf раздел 3.1)
8. ^http: / /hyperphysics.phy-astr.gsu.edu/hbase/electric/laplace.html
9. ^http://hyperphysics.phy-astr.gsu.edu/hbase/electric/potsph.html

Ссылки

• P. Дебай; Э. Хюкель (1923). "Zur Theorie der Elektrolyte. I. Gefrierpunktserniedrigung und verwandte Erscheinungen" [Теория электролитов. I. Понижение точки замерзания и связанные с ним явления] (PDF). Physikalische Zeitschrift. 24: 185–206.
• ^Хаманн, Хамнетт и Вильстих (1998). Электрохимия. Вайнхайм: Wiley-VCH Verlag GmbH. ISBN 3-527-29096-6. CS1 maint: несколько имен: список авторов (ссылка )
• ^Harris, Daniel C. (2003). Количественный химический анализ (6-е изд.). WH Freeman Company. ISBN 0-7167-4464-3.
• ^Скуг, Дуглас А. Основы аналитической химии. ISBN 0-534-41796-5.
• Ф. Малатеста, Р. Замбони. Активность и осмотические коэффициенты от ЭДС жидких мембранных клеток, VI - ZnSO4, MgSO4, CaSO4 и SrSO4 в воде при 25 C. 1997, 26, 791–815

Внешние ссылки

• Для простого расчета коэффициентов активности в (немицеллярных) ознакомьтесь с открытым проектом IUPAC Aq-solutions (бесплатное ПО) .
• Gold Book определение