Теорема Де Муавра – Лапласа

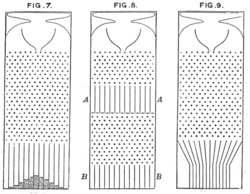
Сходимость распределения биномиального распределения к нормальному В системе, ячейки которой заполнены в соответствии с биномиальное распределение (например, Galton "bean machine ", показанное здесь), учитывая достаточное количество попыток (здесь ряды выводов, каждый из которых вызывает падение " bean, чтобы упасть влево или вправо), форма, представляющая распределение вероятностей k успехов в n испытаниях (см. нижнюю часть рис. 7), приблизительно соответствует распределению Гаусса со средним значением np и дисперсией np (1 − p), предполагая, что испытания независимы, а успех случается с вероятностью p. Рассмотрим подбрасывание набора из n монет очень большое количество раз и подсчет количества выпавших «орлов» каждый раз. Возможное количество голов при каждом броске k изменяется от 0 до n по горизонтальной оси, в то время как вертикальная ось представляет относительную частоту появления исхода k голов. Таким образом, высота каждой точки - это вероятность наблюдения k орлов при подбрасывании n монет (биномиальное распределение на основе n попыток). Согласно теореме де Муавра – Лапласа, когда n увеличивается, форма дискретного распределения сходится к непрерывной гауссовой кривой нормального распределения.

В теории вероятностей, Теорема де Муавра – Лапласа, которая является частным случаем центральной предельной теоремы , утверждает, что нормальное распределение может использоваться в качестве приближения к биномиальному распределению при определенных условиях. В частности, теорема показывает, что функция массы вероятности случайного числа «успехов», наблюдаемых в серии $n\; \{\backslash \; displaystyle\; n\}$независимых Бернулли испытания, каждое из которых имеет вероятность $p\; \{\backslash \; displaystyle\; p\}$успеха (биномиальное распределение с $n\; \{\backslash \; displaystyle\; n\}$испытаниями), сходится к функции плотности вероятности нормального распределения со средним значением $np\; \{\backslash \; displaystyle\; np\}$и стандартным отклонением $np\; (1\; -\; p)\; \{\; \backslash \; displaystyle\; \{\backslash \; sqrt\; \{np\; (1-p)\}\}\}$, поскольку $n\; \{\backslash \; displaystyle\; n\}$становится большим, предполагая, что $p\; \{\backslash \; displaystyle\; p\; \}$не $0\; \{\backslash \; displaystyle\; 0\}$или $1\; \{\backslash \; displaystyle\; 1\}$.

Теорема появилась во втором издании Доктрины. of Chances авторства Abraham de Moivre, опубликовано в 1738 году. Хотя де Муавр не использовал термин «испытания Бернулли», он писал о распределении вероятностей количества раз "головы "появляется, когда монета подбрасывается 3600 раз.

Это одно из производных от конкретной функции Гаусса, используемой в нормальном распределении.

• 1 Теорема
  • 1.1 Доказательство
  • 1.2 Альтернативное доказательство
• 2 Общая информация
• 3 См. Также
• 4 Примечания

По мере роста n, для k в окрестности np мы можем аппроксимировать

$(nk)\; pkqn\; -\; k\; \simeq \; 1\; 2\; \pi \; npqe\; -\; (k\; -\; np)\; 2\; 2\; npq,\; p\; +\; q\; =\; 1,\; p,\; q>0\; \{\backslash \; displaystyle\; \{n\; \backslash \; choose\; k\}\; \backslash ,\; p\; ^\; \{k\}\; q\; ^\; \{nk\}\; \backslash \; simeq\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sqrt\; \{2\; \backslash \; pi\; npq\}\}\}\; \backslash ,\; e\; ^\; \{-\; \{\backslash \; frac\; \{(k-np)\; ^\; \{2\}\}\; \{2npq\}\}\},\; \backslash \; qquad\; p\; +\; q\; =\; 1,\; \backslash \; p,\; q>0\}$

в том смысле, что соотношение левой и правой стороны сторона сходится к 1 при n → ∞.

Доказательство

Более строго теорему можно сформулировать следующим образом: $(X\; -\; np)\; /\; npq\; \{\backslash \; displaystyle\; \backslash \; left\; (X\; \backslash !\; \backslash ,\; -\; \backslash !\; \backslash ,\; np\; \backslash \; right)\; \backslash !\; /\; \backslash !\; \{\backslash \; sqrt\; \{npq\}\}\}$, с $X\; \{\backslash \; displaystyle\; \backslash \; textstyle\; X\}$случайная величина с биномиальным распределением, приближается к стандартной норме при $n\; \to \; \infty \; \{\backslash \; отображает\; tyle\; n\; \backslash !\; \backslash \; to\; \backslash !\; \backslash \; infty\}$, с отношением вероятностной массы $X\; \{\backslash \; displaystyle\; X\}$к предельной нормальной плотности, равной 1. Это может отображаться для произвольной ненулевой и конечной точки $c\; \{\backslash \; displaystyle\; c\}$. На немасштабированной кривой для $X\; \{\backslash \; displaystyle\; X\}$это будет точка $k\; \{\backslash \; displaystyle\; k\}$, заданная как

$k\; =\; np\; +\; cnpq\; \{\backslash \; displaystyle\; k\; =\; np\; +\; c\; \{\backslash \; sqrt\; \{npq\}\}\}$

Например, с $c\; \{\backslash \; displaystyle\; c\}$на 3, $k\; \{\backslash \; displaystyle\; k\; \}$остается на 3 стандартных отклонения от среднего значения на немасштабированной кривой.

Нормальное распределение со средним значением $\mu \; \{\backslash \; displaystyle\; \backslash \; mu\}$и стандартным отклонением $\sigma \; \{\backslash \; displaystyle\; \backslash \; sigma\}$определяется дифференциальное уравнение (DE)

$f\; \text{'}(x)\; =\; -\; x\; -\; \mu \; \sigma \; 2\; f\; (x)\; \{\backslash \; displaystyle\; f\text{'}\; \backslash !\; (x)\; \backslash !\; =\; \backslash !\; -\; \backslash !\; \backslash ,\; \{\backslash \; frac\; \{x-\; \backslash \; mu\}\; \{\backslash \; sigma\; ^\; \{2\}\}\}\; f\; (x)\}$с начальным условием, заданным аксиомой вероятности $\int \; -\; \infty \; \infty \; f\; (x)\; dx\; =\; 1\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{-\; \backslash \; infty\}\; ^\; \{\backslash \; infty\}\; \backslash !\; f\; (x)\; \backslash ,\; dx\; \backslash !\; =\; \backslash !\; 1\}$.

Предел биномиального распределения приближается к нормальному, если биномиальное удовлетворяет этому ДУ. Поскольку бином является дискретным, уравнение начинается с разностного уравнения, предел которого трансформируется в DE. В разностных уравнениях используется дискретная производная, $p\; (k\; +\; 1)\; -\; p\; (k)\; \{\backslash \; displaystyle\; \backslash \; textstyle\; p\; (k\; \backslash !\; +\; \backslash !\; 1)\; \backslash !\; -\; \backslash !\; P\; (k)\}$, изменение размера шага 1. Поскольку $n\; \to \; \infty \; \{\backslash \; displaystyle\; \backslash \; textstyle\; n\; \backslash !\; \backslash \; To\; \backslash !\; \backslash \; Infty\}$, дискретная производная становится непрерывная производная. Следовательно, доказательство необходимо показать только то, что для немасштабированного биномиального распределения

$f\; \prime \; (x)\; f\; (x)\; \cdot \; -\; \sigma \; 2\; x\; -\; \mu \; \to \; 1\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{f\; \text{'}\backslash !\; (X)\}\; \{f\; \backslash !\; (x)\}\}\; \backslash !\; \backslash \; cdot\; \backslash !\; -\; \backslash !\; \backslash ,\; \{\backslash \; frac\; \{\backslash \; sigma\; ^\; \{2\}\}\; \{x-\; \backslash \; mu\}\}\; \backslash !\; \backslash \; to\; \backslash !\; 1\}$as $n\; \to \; \infty \; \{\backslash \; displaystyle\; n\; \backslash !\; \backslash \; To\; \backslash !\; \backslash \; Infty\}$.

Требуемый результат может быть показан напрямую:

$f\; \prime \; (x)\; f\; (x)\; npqnp\; -\; k\; =\; p\; (N,\; К\; +\; 1)\; -\; п\; (N,\; К)\; п\; (N,\; К)\; npq\; -\; c\; =\; np\; -\; k\; -\; qkq\; +\; qnpq\; -\; c\; =\; -\; cnpq\; -\; qnpq\; +\; cqnpq\; +\; qnpq\; -\; c\; \to \; 1\; \{\backslash \; displaystyle\; \{\; \backslash \; begin\; \{align\}\; \{\backslash \; frac\; \{f\; \text{'}\backslash !\; (x)\}\; \{f\; \backslash !\; (x)\}\}\; \{\backslash \; frac\; \{npq\}\; \{np\; \backslash !\; \backslash ,\; -\; \backslash !\; \backslash ,\; k\}\}\; \backslash !\; =\; \{\backslash \; frac\; \{p\; \backslash \; left\; (n,\; k\; +\; 1\; \backslash \; right)\; -p\; \backslash \; left\; (n,\; k\; \backslash \; right)\}\; \{p\; \backslash \; left\; (n,\; k\; \backslash \; right)\}\}\; \{\backslash \; frac\; \{\backslash \; sqrt\; \{npq\}\; \}\; \{-\; c\}\}\; \backslash \backslash \; =\; \{\backslash \; frac\; \{np-kq\}\; \{kq\; +\; q\}\}\; \{\backslash \; frac\; \{\backslash \; sqrt\; \{npq\}\}\; \{-\; c\}\}\; \backslash \backslash \; =\; \{\backslash \; frac\; \{-c\; \{\; \backslash \; sqrt\; \{npq\}\}\; -\; q\}\; \{npq\; +\; cq\; \{\backslash \; sqrt\; \{npq\}\}\; +\; q\}\}\; \{\backslash \; frac\; \{\backslash \; sqrt\; \{npq\}\}\; \{-\; c\}\}\; \backslash \backslash \; \backslash \; to\; 1\; \backslash \; end\; \{выровнено\}\; \}\}$

Последнее верно, потому что член $-\; cnpq\; \{\backslash \; displaystyle\; -cnpq\}$доминирует как в знаменателе, так и в числителе при $n\; \to \; \infty \; \{\backslash \; displaystyle\; n\; \backslash !\; \backslash \; To\; \backslash !\; \backslash \; infty\}$.

Поскольку $k\; \{\backslash \; displaystyle\; \backslash \; textstyle\; k\}$принимает только целые значения, константа $c\; \{\backslash \; displaystyle\; \backslash \; textstyle\; c\}$подлежит округлению. ошибка. Однако максимальное значение этой ошибки, $0,5\; /\; npq\; \{\backslash \; displaystyle\; \backslash \; textstyle\; \{0,5\}\; /\; \backslash !\; \{\backslash \; Sqrt\; \{npq\}\}\}$, является исчезающим значением.

Альтернативное доказательство

Доказательство состоит в преобразовании левой части (в формулировке теоремы) в правую с помощью трех приближений.

Во-первых, согласно формуле Стирлинга факториал большого числа n можно заменить приближением

$n!\; \simeq \; n\; n\; e\; -\; n\; 2\; \pi \; n\; при\; n\; \to \; \infty .\; \{\backslash \; displaystyle\; n!\; \backslash \; simeq\; n\; ^\; \{n\}\; e\; ^\; \{-\; n\}\; \{\backslash \; sqrt\; \{2\; \backslash \; pi\; n\}\}\; \backslash \; qquad\; \{\backslash \; text\; \{as\}\}\; n\; \backslash \; to\; \backslash \; infty.\}$

Таким образом,

$(nk)\; pkqn\; -\; k\; =\; n!\; к!\; (п\; -\; к)!\; pkqn\; -\; k\; \simeq \; nne\; -\; n\; 2\; \pi \; nkke\; -\; k\; 2\; \pi \; k\; (n\; -\; k)\; n\; -\; ke\; -\; (n\; -\; k)\; 2\; \pi \; (n\; -\; k)\; pkqn\; -\; k\; =\; n\; 2\; \pi \; k\; (n\; -\; k)\; nnkk\; (N\; -\; К)\; N\; -\; KPKQN\; -\; К\; знак\; равно\; N\; 2\; \pi \; К\; (N\; -\; К)\; (NPK)\; К\; (NQN\; -\; K)\; N\; -\; К\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{Выровнено\}\; \{п\; \backslash \; выбрать\; к\}\; р\; ^\; \{\; k\}\; q\; ^\; \{nk\}\; =\; \{\backslash \; frac\; \{n!\}\; \{k!\; (nk)!\}\}\; p\; ^\; \{k\}\; q\; ^\; \{nk\}\; \backslash \backslash \; \backslash \; simeq\; \{\backslash \; frac\; \{n\; ^\; \{n\}\; e\; ^\; \{-\; n\}\; \{\backslash \; sqrt\; \{2\; \backslash \; pi\; n\}\}\}\; \{k\; ^\; \{k\}\; e\; ^\; \{-\; k\}\; \{\backslash \; sqrt\; \{2\; \backslash \; pi\; k\}\}\; (nk)\; ^\; \{nk\}\; e\; ^\; \{-\; (\; nk)\}\; \{\backslash \; sqrt\; \{2\; \backslash \; pi\; (nk)\}\}\}\}\; p\; ^\; \{k\}\; q\; ^\; \{nk\}\; \backslash \backslash \; =\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{n\}\; \{2\; \backslash \; pi\; k\; \backslash \; left\; (nk\; \backslash \; right)\}\}\}\; \{\backslash \; frac\; \{n\; ^\; \{n\}\}\; \{k\; ^\; \{k\}\; \backslash \; left\; (nk\; \backslash \; right)\; ^\; \{nk\}\}\}\; p\; ^\; \{k\}\; q\; ^\; \{nk\}\; \backslash \backslash \; =\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{n\}\; \{2\; \backslash \; pi\; k\; \backslash \; left\; (nk\; \backslash \; right)\}\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{np\}\; \{k\}\}\; \backslash \; right)\; ^\; \{k\}\; \backslash \; left\; (\{\backslash \; frac\; \{nq\; \}\; \{nk\}\}\; \backslash \; right)\; ^\; \{nk\}\; \backslash \; end\; \{align\}\}\}$

Затем приближение $kn\; \to \; p\; \{\backslash \; displaystyle\; \{\backslash \; tfrac\; \{k\}\; \{n\}\}\; \backslash \; к\; p\}$используется для сопоставления корня, указанного выше, с желаемым корнем справа.

$(nk)\; pkqn\; -\; k\; \simeq \; 1\; 2\; \pi \; nkn\; (1\; -\; kn)\; (npk)\; k\; (nqn\; -\; k)\; n\; -\; k\; \simeq \; 1\; 2\; \pi \; npq\; (npk)\; k\; (nqn\; -\; k)\; n\; -\; kp\; +\; q\; =\; 1\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \{n\; \backslash \; choose\; k\}\; p\; ^\; \{k\}\; q\; ^\; \{nk\}\; \backslash \; simeq\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{1\}\; \{2\; \backslash \; pi\; n\; \{\backslash \; frac\; \{k\}\; \{n\}\}\; \backslash \; left\; (1\; -\; \{\backslash \; frac\; \{k\}\; \{n\}\}\; \backslash \; right)\}\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{np\}\; \{k\}\}\; \backslash \; right)\; ^\; \{k\}\; \backslash \; left\; (\{\backslash \; frac\; \{nq\}\; \{nk\}\}\; \backslash \; right)\; ^\; \{nk\}\; \backslash \backslash \; \backslash \; simeq\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sqrt\; \{2\; \backslash \; pi\; npq\}\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{np\}\; \{k\}\}\; \backslash \; right)\; ^\; \{k\}\; \backslash \; left\; (\{\backslash \; frac\; \{nq\}\; \{nk\}\}\; \backslash \; right)\; ^\; \{nk\}\; \backslash \; qquad\; p\; +\; q\; =\; 1\; \backslash \backslash \backslash \; end\; \{align\}\}\}$

Наконец, выражение переписывается в виде экспоненты и используется приближение ряда Тейлора для ln (1 + x):

$ln\; \; (1\; +\; x)\; \simeq \; x\; -\; x\; 2\; 2\; +\; x\; 3\; 3\; -\; \cdots \; \{\backslash \; displaystyle\; \backslash \; ln\; \backslash \; left\; (\; 1\; +\; x\; \backslash \; right)\; \backslash \; simeq\; x\; -\; \{\backslash \; frac\; \{x\; ^\; \{2\}\}\; \{2\}\}\; +\; \{\backslash \; frac\; \{x\; ^\; \{3\}\}\; \{3\}\}\; -\; \backslash \; cdots\}$

Тогда

$(nk) pkqn - k ≃ 1 2 π npq exp ⁡ {ln ⁡ ((npk) k) + ln ⁡ ((nqn - k) n - k)} = 1 2 π npq exp ⁡ {- k ln ⁡ (knp) + (k - n) ln ⁡ (n - knq)} = 1 2 π npq exp ⁡ {- k ln ⁡ (np + xnpqnp) + (k - n) ln ⁡ (n - np - xn pqnq)} = 1 2 π npq exp ⁡ {- k ln ⁡ (1 + xqnp) + (k - n) ln ⁡ (1 - xpnq)} p + q = 1 = 1 2 π npq exp ⁡ {- k ( xqnp - x 2 q 2 np + ⋯) + (k - n) (- xpnq - x 2 p 2 nq - ⋯)} = 1 2 π npq exp ⁡ {(- np - xnpq) (xqnp - x 2 q 2 np + ⋯) + (np + xnpq - n) (- xpnq - x 2 p 2 nq - ⋯)} = 1 2 π npq exp ⁡ {(- np - xnpq) (xqnp - x 2 q 2 np + ⋯) - (nq - xnpq) (- xpnq - x 2 p 2 nq - ⋯)} = 1 2 π npq exp ⁡ {(- xnpq + 1 2 x 2 q - x 2 q + ⋯) + (xnpq + 1 2 x 2 p - x 2 p - ⋯)} = 1 2 π npq exp ⁡ {- 1 2 x 2 q - 1 2 x 2 p - ⋯} = 1 2 π npq exp ⁡ {- 1 2 x 2 (p + q) - ⋯} ≃ 1 2 π npq exp ⁡ {- 1 2 x 2} = 1 2 π npqe - (k - np) 2 2 npq {\ displaystyle {\ begin {align} {n \ select k} p ^ { k} q ^ {nk} \ simeq {\ frac {1} {\ sqrt {2 \ pi npq}}} \ exp \ left \ {\ ln \ left (\ left ({\ frac {np} {k} } \ right) ^ {k} \ right) + \ ln \ left (\ left ({\ frac {nq} {nk}} \ right) ^ {nk} \ right) \ right \} \\ = {\ frac {1} {\ sqrt {2 \ pi npq}}} \ exp \ left \ {- k \ ln \ left ({\ frac {k} {np}} \ right) + (kn) \ ln \ left ({\ frac {nk} {nq}} \ right) \ right \} \\ = {\ frac {1} {\ sqrt {2 \ pi npq}}} \ exp \ left \ {- k \ ln \ left ({\ frac {np + x {\ sqrt {npq}}} {np}} \ right) + (kn) \ ln \ left ({\ frac {n-np-x {\ sqrt {npq}}} {nq}} \ right) \ right \} \\ = {\ frac {1} {\ sqrt {2 \ pi npq}}} \ exp \ left \ {- k \ ln \ left ({1 + x {\ sqrt {\ frac {q} {np}}}} \ right) + (kn) \ ln \ слева ({1-x {\ sqrt {\ frac {p} {nq}}}} \ right) \ right \} \ qquad p + q = 1 \\ = {\ frac {1} {\ sqrt {2 \ pi npq}}} \ exp \ left \ {- k \ left ({x {\ sqrt {\ frac {q} {np}}}} - {\ frac {x ^ {2} q} {2np}}) + \ cdots \ right) + (kn) \ left ({- x {\ sqrt {\ frac {p} {nq}}} - {\ frac {x ^ {2} p} {2nq}}} - \ cdots \ right) \ right \} \\ = {\ frac {1} {\ sqrt {2 \ pi npq}}} \ exp \ left \ {\ left (-np-x {\ sqrt {npq}} \ right) \ left ({x {\ sqrt {\ frac {q} {np}}}} - {\ frac {x ^ {2} q} {2np}} + \ cdots \ right) + \ left (np + x {\ sqrt {npq}} - n \ right) \ left (-x {\ sqrt {\ frac {p} {nq}}} - {\ frac {x ^ {2} p} {2nq}} - \ cdots \ right) \ right \} \\ = {\ frac {1} {\ sqrt {2 \ pi npq}}} \ exp \ left \ {\ left (-np-x {\ sqrt {npq}} \ right) \ left (x {\ sqrt {\ frac {q} {np}}} - {\ frac {x ^ {2} q} {2np}} + \ cdots \ right) - \ left (nq-x {\ sqrt {npq}} \ right) \ left (-x {\ sqrt {\ frac {p} {nq}}} - {\ frac {x ^ {2} p} {2nq} } - \ cdots \ right) \ right \} \\ = {\ frac {1} {\ sqrt {2 \ pi npq}}} \ exp \ left \ {\ left (-x {\ sqrt {npq}} + {\ frac {1} {2}} x ^ {2} qx ^ {2} q + \ cdots \ right) + \ left (x {\ sqrt {npq}} + {\ frac {1} {2}} x ^ {2} px ^ {2} p- \ cdots \ right) \ right \} \\ = {\ frac {1} {\ sqrt {2 \ pi npq}}} \ exp \ left \ {- { \ frac {1} {2}} x ^ {2} q - {\ frac {1} {2}} x ^ {2} p- \ cdots \ right \} \\ = {\ frac {1} { \ sqrt {2 \ pi npq}}} \ exp \ left \ {- {\ frac {1} {2}} x ^ {2} (p + q) - \ cdots \ right \} \\ \ simeq { \ frac {1} {\ sqrt {2 \ pi npq}}} \ exp \ left \ {- {\ frac {1} {2}} x ^ {2} \ right \} \\ = {\ frac { 1} {\ sqrt {2 \ pi npq}}} e ^ {\ frac {- (k-np) ^ {2}} {2npq}} \\\ end {align}}}$

Каждый "$\simeq \; \{\backslash \; displaystyle\; \backslash \; simeq\}$"в приведенном выше аргументе - это утверждение, что две величины асимптотически эквивалентны при увеличении n в том же смысле, что и в исходном утверждении теоремы, т. Е. Что отношение каждой пары величин стремится к 1 при n → ∞.

• Стена - это пример телевизионного игрового шоу, в котором используется теорема Де Муавра – Лапласа.

• Распределение Пуассона - альтернативное приближение биномиального распределения для больших значений n.