Поперечное сечение (физика)

редактировать

Вероятность того, что данный процесс происходит при столкновении частиц

В физике крест секция - это мера вероятности того, что определенный процесс произойдет при столкновении двух частиц. Например, сечение Резерфорда является мерой вероятности того, что альфа-частица будет отклонена на заданный угол во время столкновения с атомным ядром. Поперечное сечение обычно обозначается σ (сигма ) и выражается в терминах поперечной площади, в которую должна попасть падающая частица, чтобы произошел данный процесс.

Когда две частицы взаимодействуют, их взаимное поперечное сечение представляет собой площадь , поперечную их относительному движению, в пределах которой они должны встретиться, чтобы рассыпаться друг от друга. Если частицы представляют собой твердые неупругие сферы, которые взаимодействуют только при контакте, их поперечное сечение рассеяния связано с их геометрическим размером. Если частицы взаимодействуют посредством некоторой силы, действующей на расстоянии, такой как электромагнетизм или гравитация, их поперечное сечение рассеяния обычно больше, чем их геометрический размер. Когда поперечное сечение задается как функция некоторой переменной конечного состояния, такой как угол частицы или энергия, оно называется дифференциальным поперечным сечением . Когда сечение интегрируется по всем углам рассеяния (и, возможно, другим переменным), оно называется полным сечением .

Сечения рассеяния могут быть определены в ядерном, атомном и физика элементарных частиц для столкновений ускоренных пучков частиц одного типа с целями (неподвижными или движущимися) частиц второго типа. Вероятность возникновения любой данной реакции пропорциональна ее поперечному сечению. Таким образом, указание сечения для данной реакции является показателем вероятности того, что данный процесс рассеяния произойдет.

Измеренная скорость реакции данного процесса сильно зависит от экспериментальных переменных, таких как плотность материала мишени, интенсивность луча, эффективность обнаружения устройства или угол настройка прибора обнаружения. Однако эти величины можно учесть, что позволяет измерить основное сечение столкновения двух частиц.

Дифференциальные и полные сечения рассеяния являются одними из наиболее важных измеряемых величин в ядерной, атомной и физике элементарных частиц.

Содержание

1 Столкновение частиц газа
2 Затухание пучка частиц
3 Дифференциальное сечение
4 Квантовое рассеяние
- 4.1 Связь с S-матрицей
5 единиц
6 Рассеяние света
- 6.1 Рассеяние света на протяженных телах
  - 6.1.1 Связь с физическими размерами
- 6.2 Метеорологическая дальность
7 Примеры
- 7.1 Пример 1: упругое столкновение двух твердых сфер
- 7.2 Пример 2: рассеяние света от двумерного круглого зеркала
- 7.3 Пример 3: рассеяние света от трехмерного сферического зеркала
8 См. также
9 Ссылки
10 Внешние ссылки

Столкновение между частицами газа

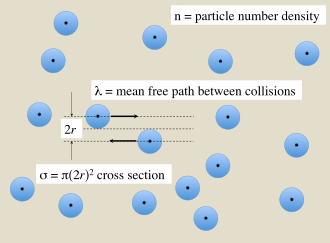Рисунок 1. В газе, состоящем из частиц индивидуального диаметра 2r, поперечное сечение σ для столкновений связано с концентрацией частиц n и средней длиной свободного пробега между столкновениями λ.

В газе частиц конечного размера происходят столкновения между частицами, которые зависят от их размера в поперечном сечении. Среднее расстояние, которое проходит частица между столкновениями, зависит от плотности частиц газа. Эти величины связаны соотношением

σ = 1 n λ, {\ displaystyle \ sigma = {\ frac {1} {n \ lambda}},}

{\ displaystyle \ sigma = {\ frac {1} {n \ lambda}},}

где

σ - поперечное сечение двухкомпонентного столкновение частиц (СИ единиц: м),

λ - средний свободный пробег между столкновениями (единицы СИ: м),

n - числовая плотность целевых частиц (единицы СИ: м).

Если частицы в газе можно рассматривать как твердые сферы радиуса r, которые взаимодействуют посредством прямого контакта, как показано на рисунке 1, тогда эффективное сечение столкновения пары равно

σ = π (2 r) 2 {\ displaystyle \ sigma = \ pi \ left (2r \ right) ^ {2}}

{\ displaystyle \ sigma = \ pi \ left (2r \ right) ^ {2}}

Если частицы в газ взаимодействует посредством силы с большим диапазоном, чем их физический размер, тогда поперечное сечение является большей эффективной площадью, которая может зависеть от множества переменных, таких как энергия частиц.

Поперечные сечения могут быть вычислены для атомных столкновений, но также используются в субатомной сфере. Например, в ядерной физике «газ» низкоэнергетических нейтронов сталкивается с ядрами в реакторе или другом ядерном устройстве с поперечным сечением , которое зависит от энергии и, следовательно, также с четко определенной средней длиной свободного пробега между столкновениями.

Затухание пучка частиц

Если пучок частиц входит в тонкий слой материала толщиной dz, поток Φ пучка будет уменьшаться на dΦ в соответствии с к

d Φ dz = - n σ Φ, {\ displaystyle {\ frac {\ mathrm {d} \ Phi} {\ mathrm {d} z}} = - n \ sigma \ Phi,}

{\ displaystyle {\ frac {\ mathrm {d} \ Phi} {\ mathrm {d} z}} = - n \ sigma \ Phi,}

где σ - полное сечение всех событий, включая рассеяние, поглощение или преобразование в другой вид. Плотность рассеивающих центров обозначена n. Решение этого уравнения показывает экспоненциальное ослабление интенсивности луча:

Φ = Φ 0 e - n σ z, {\ displaystyle \ Phi = \ Phi _ {0} e ^ {- n \ sigma z},}

{\ displaystyle \ Phi = \ Phi _ {0} e ^ {- n \ sigma z},}

где Φ 0 - начальный поток, а z - полная толщина материала. Для света это называется законом Бера – Ламберта.

Дифференциальное сечение

Рассмотрим классическое измерение, когда одна частица рассеивается от одной неподвижной целевой частицы. Обычно используется сферическая система координат , при этом цель размещается в начале координат, а ось z этой системы координат совмещена с падающим лучом. Угол θ - это угол рассеяния, измеренный между падающим лучом и рассеянным лучом, а φ - это азимутальный угол .

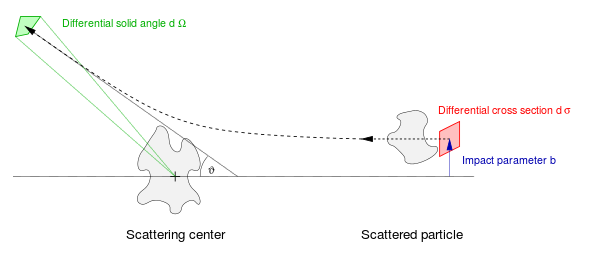
. Прицельный параметр b - перпендикуляр смещение траектории налетающей частицы, а исходящая частица вылетает под углом θ. Для данного взаимодействия (кулоновское, магнитное, гравитационное, контактное и т. Д.) Прицельный параметр и угол рассеяния имеют однозначно однозначно функциональная зависимость друг от друга. Как правило, прицельный параметр нельзя ни контролировать, ни измерять от события к событию, и предполагается, что он принимает все возможные значения при усреднении по множеству событий рассеяния. Дифференциальный размер поперечного сечения - это элемент площади в плоскости прицельного параметра, т.е. dσ = b dφ db. Дифференциальный угловой диапазон рассеянной частицы под углом θ представляет собой элемент телесного угла dΩ = sin θ dθ dφ. Дифференциальное сечение представляет собой частное этих величин dσ / dΩ.

Это функция угла рассеяния (и, следовательно, также прицельного параметра), а также других наблюдаемых величин, таких как импульс падающей частицы. Дифференциальное поперечное сечение всегда считается положительным, даже если более высокие параметры удара обычно вызывают меньший прогиб. В цилиндрически-симметричных ситуациях (относительно оси луча) азимутальный угол φ не изменяется в процессе рассеяния, и дифференциальное сечение можно записать как

d σ d (cos ⁡ θ) = ∫ 0 2 π d σ d Ω d φ {\ Displaystyle {\ frac {\ mathrm {d} \ sigma} {\ mathrm {d} (\ cos \ theta)}} = \ int _ {0} ^ {2 \ pi} {\ frac {\ mathrm {d} \ sigma} {\ mathrm {d} \ Omega}} \, \ mathrm {d} \ varphi}

{\ displaystyle {\ frac {\ mathrm {d} \ sigma} {\ mathrm {d} (\ cos \ theta)}} = \ int _ {0} ^ {2 \ pi} {\ frac {\ mathrm {d} \ sigma} {\ mathrm {d} \ Omega}} \, \ mathrm {d} \ varphi}

В ситуациях, когда процесс рассеяния не является азимутально симметричным, например когда луч или частицы мишени обладают магнитными моментами, ориентированными перпендикулярно оси луча, дифференциальное поперечное сечение также должно быть выражено как функция от азимутального угла.

Для рассеяния частиц падающего потока F inc от неподвижной мишени, состоящей из множества частиц, дифференциальное сечение dσ / dΩ под углом (θ, φ) связано с потоком детектирования рассеянных частиц F out (θ, φ) в частицах в единицу времени на

d σ d Ω (θ, φ) = 1 nt Δ Ω F out (θ, φ) F inc. {\ displaystyle {\ frac {\ mathrm {d} \ sigma} {\ mathrm {d} \ Omega}} (\ theta, \ varphi) = {\ frac {1} {nt \ Delta \ Omega}} {\ frac {F _ {\ text {out}} (\ theta, \ varphi)} {F _ {\ text {inc}}}}.}

{\ displaystyle {\ frac {\ mathrm {d} \ sigma} {\ mathrm {d} \ Omega}} (\ theta, \ varphi) = {\ frac {1} {nt \ Delta \ Omega}} {\ frac {F _ {\ text {out}} (\ theta, \ varphi)} {F _ {\ text {inc}}}}.}

Здесь ΔΩ - конечный угловой размер детектора (единицы СИ: sr ), n - числовая плотность целевых частиц (единицы СИ: м), а t - толщина неподвижной цели (единицы СИ: м). Эта формула предполагает, что цель достаточно тонкая, чтобы каждая частица луча взаимодействовала не более чем с одной частицей цели.

Полное сечение σ может быть восстановлено путем интегрирования дифференциального сечения dσ / dΩ по полному телесному углу (4π стерадиана):

σ = ∮ 4 π ⁡ d σ d Ω d Ω знак равно ∫ 0 2 π ∫ 0 π d σ d Ω sin ⁡ θ d θ d φ. {\ displaystyle \ sigma = \ oint _ {4 \ pi} {\ frac {\ mathrm {d} \ sigma} {\ mathrm {d} \ Omega}} \, \ mathrm {d} \ Omega = \ int _ { 0} ^ {2 \ pi} \ int _ {0} ^ {\ pi} {\ frac {\ mathrm {d} \ sigma} {\ mathrm {d} \ Omega}} \ sin \ theta \, \ mathrm { d} \ theta \, \ mathrm {d} \ varphi.}

{\ displaystyle \ sigma = \ oint _ {4 \ pi} {\ frac {\ mathrm {d} \ sigma} {\ mathrm {d} \ Omega}} \, \ mathrm {d} \ Omega = \ int _ {0} ^ {2 \ pi} \ int _ {0} ^ {\ pi} {\ frac {\ mathrm { d} \ sigma} {\ mathrm {d} \ Omega}} \ sin \ theta \, \ mathrm {d} \ theta \, \ mathrm {d} \ varphi.}

Обычно опускают квалификатор «дифференциал» , когда тип поперечного сечения может быть выведен из контекста. В этом случае σ можно называть интегральным поперечным сечением или полным поперечным сечением. Последний термин может сбивать с толку в контекстах, где задействовано несколько событий, поскольку «общее» также может относиться к сумме поперечных сечений по всем событиям.

Дифференциальное сечение является чрезвычайно полезной величиной во многих областях физики, поскольку его измерение может выявить большой объем информации о внутренней структуре целевых частиц. Например, дифференциальное сечение резерфордского рассеяния предоставило убедительные доказательства существования атомного ядра.

Вместо телесного угла переданный импульс может использоваться в качестве независимой переменной дифференциальных сечений.

Дифференциальные сечения неупругого рассеяния содержат резонансные пики, которые указывают на создание метастабильных состояний и содержат информацию об их энергии и времени жизни.

Квантовое рассеяние

В не зависящем от времени формализме квантового рассеяния исходная волновая функция (до рассеяния) считается плоской волной с определенным импульсом k:

ϕ - (r) ⟶ r → ∞ eikz, {\ displaystyle \ phi _ {-} (\ mathbf {r}) \; {\ stackrel {r \ to \ infty} {\ longrightarrow}} \; e ^ {ikz},}

{\ displaystyle \ phi _ {-} (\ mathbf {r}) \; {\ stackrel { г \ к \ infty} {\ longrightarrow}} \; e ^ {ikz},}

где z и r - относительные координаты между снарядом и целью. Стрелка указывает, что это описывает только асимптотическое поведение волновой функции, когда снаряд и цель находятся слишком далеко друг от друга, чтобы взаимодействие могло иметь какой-либо эффект.

После рассеяния ожидается, что волновая функция примет следующий асимптотический вид:

ϕ + (r) ⟶ r → ∞ f (θ, ϕ) eikrr, {\ displaystyle \ phi _ {+} (\ mathbf {r}) \; {\ stackrel {r \ to \ infty} {\ longrightarrow}} \; f (\ theta, \ phi) {\ frac {e ^ {ikr}} {r} },}

{\ displaystyle \ phi _ {+} (\ mathbf {r}) \; {\ stackrel {r \ to \ infty} {\ longrightarrow}} \; f (\ theta, \ phi) {\ frac {e ^ {ikr}} {r}},}

где f - некоторая функция угловых координат, известная как амплитуда рассеяния. Эта общая форма действительна для любого короткодействующего энергосберегающего взаимодействия. Это неверно для дальнодействующих взаимодействий, поэтому при работе с электромагнитными взаимодействиями возникают дополнительные сложности.

Полная волновая функция системы ведет себя асимптотически как сумма

ϕ (r) ⟶ r → ∞ ϕ - (r) + ϕ + (r). {\ displaystyle \ phi (\ mathbf {r}) \; {\ stackrel {r \ to \ infty} {\ longrightarrow}} \; \ phi _ {-} (\ mathbf {r}) + \ phi _ {+ } (\ mathbf {r}).}

{\ displaystyle \ phi (\ mathbf {r}) \; {\ stackrel {r \ to \ infty} {\ longrightarrow}} \; \ phi _ {-} (\ mathbf {r}) + \ phi _ {+} (\ mathbf {r}).}

Дифференциальное сечение связано с амплитудой рассеяния:

d σ d Ω (θ, ϕ) = | f (θ, ϕ) | 2. {\ displaystyle {\ frac {\ mathrm {d} \ sigma} {\ mathrm {d} \ Omega}} (\ theta, \ phi) = {\ bigl |} f (\ theta, \ phi) {\ bigr | } ^ {2}.}

{\ displaystyle {\ frac {\ mathrm {d} \ sigma} {\ mathrm {d} \ Omega}} (\ theta, \ phi) = {\ bigl |} f (\ theta, \ phi) {\ bigr |} ^ {2}.}

Это имеет простую интерпретацию как плотность вероятности нахождения рассеянного снаряда под заданным углом.

Таким образом, поперечное сечение является мерой эффективной площади поверхности, видимой падающим частицам, и как таковое выражается в единицах площади. Поперечное сечение двух частиц (т.е. наблюдаемое, когда две частицы сталкиваются друг с другом) является мерой события взаимодействия между двумя частицами. Сечение пропорционально вероятности того, что взаимодействие произойдет; например, в простом эксперименте по рассеянию количество частиц, рассеянных за единицу времени (ток рассеянных частиц I r) зависит только от количества падающих частиц в единицу времени (ток падающих частиц I i), характеристики цели (например, количество частиц на единицу поверхности N) и тип взаимодействия. Для Nσ ≪ 1 имеем

I r = I i N σ, σ = I r I i 1 N = вероятность взаимодействия × 1 N. {\ displaystyle {\ begin {align} I _ {\ text {r}} = I _ {\ text {i}} N \ sigma, \\\ sigma = {\ frac {I _ {\ text {r}}} {I _ {\ text {i}}}} {\ frac {1} {N}} \\ = {\ text {вероятность взаимодействия}} \ times {\ frac {1} {N}}. \ End { выровнено}}}

{\ displaystyle {\ begin {выровнено } I _ {\ text {r}} = I _ {\ text {i}} N \ sigma, \\\ sigma = {\ frac {I_ {\ text {r}}} {I _ {\ text {i}}}} {\ frac {1} {N}} \\ = {\ text {вероятность взаимодействия}} \ times {\ frac {1} {N}}. \ End {align}}}

Отношение к S-матрице

Если приведенные массы и импульсы сталкивающейся системы равны m i, piи m f, pfдо и после столкновения, соответственно, дифференциальное сечение определяется как

d σ d Ω = (2 π) 4 mimfpfpi | Т ф я | 2, {\ displaystyle {\ frac {\ mathrm {d} \ sigma} {\ mathrm {d} \ Omega}} = \ left (2 \ pi \ right) ^ {4} m_ {i} m_ {f} { \ frac {p_ {f}} {p_ {i}}} {\ bigl |} T_ {fi} {\ bigr |} ^ {2},}

{\ displaystyle {\ frac {\ mathrm {d} \ sigma} {\ mathrm {d} \ Omega}} = \ left (2 \ pi \ right) ^ {4} m_ {i} m_ {f} {\ frac {p_ {f}} {p_ {i}}} {\ bigl |} T_ {fi} {\ bigr |} ^ {2},}

где матрица T на оболочке определяется как

S фи знак равно δ фи - 2 π я δ (Е е - Е я) δ (пи - пф) Т фи {\ Displaystyle S_ {фи} = \ дельта _ {фи} -2 \ пи я \ дельта \ влево ( E_ {f} -E_ {i} \ right) \ delta \ left (\ mathbf {p} _ {i} - \ mathbf {p} _ {f} \ right) T_ {fi}}

{\ displaystyle S_ {fi} = \ delta _ {fi} -2 \ pi i \ delta \ left (E_ {f} -E_ {i} \ right) \ delta \ left (\ mathbf {p} _ {i} - \ mathbf {p} _ {f} \ right) T_ {fi}}

в терминах S-матрица. Здесь δ - дельта-функция Дирака. Вычисление S-матрицы является основной целью теории рассеяния.

Единицы

Хотя единица СИ полных сечений составляет м, на практике обычно используются устройства меньшего размера.

В ядерной физике и физике элементарных частиц условной единицей измерения является амбар b, где 1 b = 10 м = 100 фм. Также широко используются меньшие единицы с префиксом, такие как mb и μb. Соответственно, дифференциальное сечение может быть измерено в таких единицах, как мб / ср.

Когда рассеянное излучение представляет собой видимый свет, обычно длину пути измеряют в сантиметрах. Чтобы избежать необходимости в коэффициентах пересчета, сечение рассеяния выражается в см, а числовая концентрация - в см. Измерение рассеяния видимого света, известное как нефелометрия, эффективно для частиц диаметром 2–50 мкм : как таковое, оно широко используется в метеорологии. и при измерении загрязнения атмосферы.

Рассеяние рентгеновских лучей также можно описать в терминах сечений рассеяния, в этом случае квадрат Ангстрём - удобная единица измерения: 1 Å = 10 м = 10000 пм = 10 байт. Сумма сечений рассеяния, фотоэлектрического излучения и образования пар (в амбарах) отображается как «атомный коэффициент ослабления» (узкий луч) в амбарах.

Рассеяние света

Для света, как и в других настройках, сечение рассеяния обычно отличается от геометрического сечения частицы и зависит от длины волны света и диэлектрическая проницаемость, форма и размер частицы. Общее количество рассеяния в разреженной среде пропорционально произведению поперечного сечения рассеяния на количество присутствующих частиц.

С точки зрения площади, полное сечение (σ) представляет собой сумму сечений, обусловленных поглощением, рассеянием и фотолюминесценцией <146.>. Сумму сечений поглощения и рассеяния иногда называют сечением экстинкции.

σ = σ a + σ s + σ l. {\ displaystyle \ sigma = \ sigma _ {\ text {a}} + \ sigma _ {\ text {s}} + \ sigma _ {\ text {l}}.}

{\ displaystyle \ sigma = \ sigma _ {\ text {a}} + \ sigma _ {\ text {s}} + \ sigma _ {\ text {l} }.}

Общее сечение относится к поглощение интенсивности света согласно закону Бера – Ламберта, согласно которому поглощение пропорционально концентрации частиц:

A λ = C l σ, {\ displaystyle A_ { \ lambda} = Cl \ sigma,}

{\ displaystyle A_ { \ lambda} = Cl \ sigma,}

где A λ - оптическая плотность при данной длине волны λ, C - концентрация частиц в виде числовой плотности, а l - длина пути. Поглощение излучения представляет собой логарифм (декадный или, чаще, естественный ) обратной величины пропускания T:

A λ = - журнал ⁡ Т. {\ displaystyle A _ {\ lambda} = - \ log {\ mathcal {T}}.}

A _ {\ lambda} = - \ log {\ mathcal {T}}.

Рассеяние света на протяженных телах

В контексте рассеяния света на протяженных телах сечение рассеяния, σ scat, описывает вероятность рассеяния света макроскопической частицей. В общем, сечение рассеяния отличается от геометрического сечения частицы , поскольку оно зависит от длины волны света и диэлектрической проницаемости в дополнение к форме и размеру частица. Общее количество рассеяния в разреженной среде определяется произведением поперечного сечения рассеяния на количество присутствующих частиц. Что касается площади, полное сечение (σ) представляет собой сумму сечений, обусловленных поглощением, рассеянием и люминесценцией :

σ = σ a + σ s + σ l. {\ displaystyle \ sigma = \ sigma _ {\ text {a}} + \ sigma _ {\ text {s}} + \ sigma _ {\ text {l}}.}

{\ displaystyle \ sigma = \ sigma _ {\ text {a}} + \ sigma _ {\ text {s}} + \ sigma _ {\ text {l} }.}

Общее сечение относится к поглощение интенсивности света согласно закону Бера – Ламберта, который гласит, что поглощение пропорционально концентрации: A λ = Clσ, где A λ - оптическая плотность при данной длине волны λ, C - концентрация в виде числовой плотности , а l - длина пути. Поглощение или поглощение излучения - это логарифм (декадный или, чаще, естественный ) обратной величины коэффициент пропускания T:

A λ = - log ⁡ T. {\ displaystyle A _ {\ lambda} = - \ log {\ mathcal {T}}.}

{\ displaystyle A _ {\ lambda} = - \ log {\ mathcal {T}}.}

Отношение к физическому размеру

Нет простой связи между сечением рассеяния и физическим размером частиц, так как сечение рассеяния зависит от длины волны используемого излучения. Это можно увидеть, глядя на ореол, окружающий Луну, в прилично туманный вечер: фотоны красного света испытывают большую площадь поперечного сечения капель воды, чем фотоны более высокой энергии. Таким образом, ореол вокруг Луны имеет периметр красного света из-за того, что фотоны с более низкой энергией рассеиваются дальше от центра Луны. Фотоны из остальной части видимого спектра остаются в центре ореола и воспринимаются как белый свет.

Метеорологический диапазон

Сечение рассеяния связано с метеорологическим диапазоном LV:

L V = 3,9 C σ scat. {\ displaystyle L _ {\ text {V}} = {\ frac {3.9} {C \ sigma _ {\ text {scat}}}}.}

{\ displaystyle L _ {\ text {V}} = {\ frac {3.9} {C \ sigma _ {\ text { scat}}}}.}

Иногда обозначается величина Cσ scat b scat, коэффициент рассеяния на единицу длины.

Примеры

Пример 1: упругое столкновение двух твердых сфер

упругое столкновение двух твердых сфер - поучительный пример, демонстрирующий смысл называть эту величину поперечным сечением. R и r - соответственно радиусы рассеивающего центра и рассеянной сферы. Полное сечение составляет

σ tot = π (r + R) 2. {\ displaystyle \ sigma _ {\ text {tot}} = \ pi \ left (r + R \ right) ^ {2}.}

{\ displaystyle \ sigma _ {\ text {tot}} = \ pi \ влево (г + р \ вправо) ^ {2}.}

Таким образом, в этом случае полное сечение рассеяния равно площади круг (с радиусом r + R), внутри которого должен прибыть центр масс падающей сферы, чтобы он отклонился, и за пределами которого он проходит мимо неподвижного центра рассеяния.

Пример 2: рассеяние света от двумерного круглого зеркала

Другой пример иллюстрирует детали вычисления простой модели рассеяния света, полученной путем уменьшения размера. Для простоты мы будем рассматривать рассеяние луча света на плоскости, рассматриваемой как однородная плотность параллельных лучей, и в рамках геометрической оптики от круга радиуса r с идеально отражающей границей. Поэтому его трехмерный эквивалент представляет собой более сложную проблему рассеяния света лазера или фонарика от зеркальной сферы, например, от шарика механического подшипника. Единица измерения поперечного сечения в одном измерении - это единица длины, например 1 м. Пусть α будет углом между световым лучом и радиусом, соединяющим точку отражения светового луча с центральной точкой кругового зеркала. Тогда увеличение длины элемента, перпендикулярного лучу света, выражается этим углом как

dx = r cos ⁡ α d α, {\ displaystyle \ mathrm {d} x = r \ cos \ alpha \, \ mathrm { d} \ alpha,}

{\ displaystyle \ mathrm { d} х = р \ соз \ альфа \, \ mathrm {d} \ alpha,}

тогда угол отражения этого луча относительно падающего луча равен 2α, а угол рассеяния равен

θ = π - 2 α. {\ displaystyle \ theta = \ pi -2 \ alpha.}

{\ displaystyle \ theta = \ pi -2 \ alpha.}

Энергия или количество фотонов, отраженных от светового луча с интенсивностью или плотностью фотонов I на длине dx, составляет

I d σ = I dx (x) = I r cos ⁡ α d α = I r 2 sin ⁡ (θ 2) d θ = I d σ d θ d θ. {\ Displaystyle I \, \ mathrm {d} \ sigma = I \, \ mathrm {d} x (x) = Ir \ cos \ alpha \, \ mathrm {d} \ alpha = I {\ frac {r} { 2}} \ sin \ left ({\ frac {\ theta} {2}} \ right) \, \ mathrm {d} \ theta = I {\ frac {\ mathrm {d} \ sigma} {\ mathrm {d } \ theta}} \, \ mathrm {d} \ theta.}

{\ displaystyle I \, \ mathrm {d} \ sigma = I \, \ mathrm {d} x (x) = Ir \ cos \ alpha \, \ mathrm {d} \ alpha = I {\ frac {r} {2}} \ sin \ left ({\ frac {\ theta} {2}} \ right) \, \ mathrm {d} \ theta = I {\ frac {\ mathrm {d} \ sigma} {\ mathrm {d} \ theta} } \, \ mathrm {d} \ theta.}

Следовательно, дифференциальное сечение равно (dΩ = dθ)

d σ d θ = r 2 sin ⁡ (θ 2). {\ displaystyle {\ frac {\ mathrm {d} \ sigma} {\ mathrm {d} \ theta}} = {\ frac {r} {2}} \ sin \ left ({\ frac {\ theta} {2 }} \ right).}

{\ displaystyle {\ гидроразрыв {\ mathrm {d} \ sigma} {\ mathrm {d} \ theta}} = {\ frac {r} {2}} \ sin \ left ({\ frac {\ theta} {2}} \ right).}

Как видно из поведения функции sine, эта величина имеет максимум для обратного рассеяния (θ = π; свет отражается перпендикулярно и возвращается), и нулевой минимум для рассеяния от края круга прямо вперед (θ = 0). Это подтверждает интуитивные ожидания о том, что зеркальный круг действует как расходящаяся линза, а тонкий луч тем более разбавлен, чем ближе он от края, определенного по отношению к входящему направлению. Полное сечение может быть получено путем суммирования (интегрирования) дифференциального сечения всего диапазона углов:

σ = ∫ 0 2 π d σ d θ d θ = ∫ 0 2 π r 2 sin ⁡ (θ 2) d θ = - r cos ⁡ (θ 2) | 0 2 π знак равно 2 р, {\ displaystyle \ sigma = \ int _ {0} ^ {2 \ pi} {\ frac {\ mathrm {d} \ sigma} {\ mathrm {d} \ theta}} \, \ mathrm {d} \ theta = \ int _ {0} ^ {2 \ pi} {\ frac {r} {2}} \ sin \ left ({\ frac {\ theta} {2}} \ right) \, \ mathrm {d} \ theta = \ left.-r \ cos \ left ({\ frac {\ theta} {2}} \ right) \ right | _ {0} ^ {2 \ pi} = 2r,}

{\ displaystyle \ sigma = \ int _ {0} ^ {2 \ pi} {\ frac {\ mathrm {d} \ sigma} {\ mathrm {d} \ theta}} \, \ mathrm {d} \ theta = \ int _ {0} ^ {2 \ pi} {\ frac {r} {2}} \ sin \ left ({\ frac {\ theta} {2}} \ right) \, \ mathrm {d} \ theta = \ left.-r \ cos \ left ({\ frac {\ theta} {2}} \ right) \ right | _ {0} ^ {2 \ pi} = 2r,}

, поэтому оно равно тому, насколько круглое зеркало полностью экранирует двумерное пространство для луча света. Следовательно, в трех измерениях для зеркального шара радиусом r он равен σ = πr.

Пример 3: рассеяние света от трехмерного сферического зеркала

Теперь мы можем использовать результат из Примера 2 для расчета дифференциального сечения рассеяния света от идеально отражающей сферы в трех измерениях.. Обозначим теперь радиус сферы как a. Параметризуем плоскость, перпендикулярную падающему световому лучу, цилиндрическими координатами r и φ. В любой плоскости входящего и отраженного луча мы можем записать из предыдущего примера:

r = a sin ⁡ α, dr = a cos ⁡ α d α, {\ displaystyle {\ begin {align} r = a \ sin \ alpha, \\\ mathrm {d} r = a \ cos \ alpha \, \ mathrm {d} \ alpha, \ end {align}}}

{\ displaystyle {\ begin {align} r = a \ sin \ alpha, \\\ mathrm {d} r = a \ соз \ альфа \, \ mathrm {d} \ alpha, \ end {align}}}

, а элемент области удара равен

d σ = dr (r) × rd φ = a 2 2 sin ⁡ (θ 2) cos ⁡ (θ 2) d θ d φ. {\ displaystyle \ mathrm {d} \ sigma = \ mathrm {d} r (r) \ times r \, \ mathrm {d} \ varphi = {\ frac {a ^ {2}} {2}} \ sin \ left ({\ frac {\ theta} {2}} \ right) \ cos \ left ({\ frac {\ theta} {2}} \ right) \, \ mathrm {d} \ theta \, \ mathrm {d } \ varphi.}

{\ displaystyle \ mathrm {d} \ sigma = \ mathrm {d} r (r) \ times r \, \ mathrm {d}\ varphi = {\ frac {a ^ {2}} {2}} \ sin \ left ({\ frac {\ theta} {2}} \ right) \ cos \ left ({\ frac {\ theta} {2 }} \ right) \, \ mathrm {d} \ theta \, \ mathrm {d} \ varphi.}

Используя соотношение для телесного угла в сферических координатах:

d Ω = sin ⁡ θ d θ d φ {\ displaystyle \ mathrm {d} \ Omega = \ sin \ theta \, \ mathrm {d} \ theta \, \ mathrm {d} \ varphi}

{\ displaystyle \ mathrm {d} \ Omega = \ sin \ theta \, \ mathrm {d} \ theta \, \ mathrm {d} \ varphi}

и тригонометрическое тождество

sin ⁡ θ = 2 sin ⁡ (θ 2) cos ⁡ (θ 2), {\ displaystyle \ sin \ theta = 2 \ sin \ left ({\ frac {\ theta} {2}} \ right) \ cos \ left ({\ frac {\ theta} {2}} \ right),}

{\ displaystyle \ sin \ theta = 2 \ sin \ left ({\ frac {\ theta} {2}} \ right) \ соз \ left ({\ frac {\ theta} {2}} \ right),}

получаем

d σ d Ω знак равно a 2 4, {\ displaystyle {\ frac {\ mathrm {d} \ sigma} {\ mathrm {d} \ Omega}} = {\ frac {a ^ {2}} {4} },}

{\ displaystyle {\ frac {\ mathrm {d} \ sigma} {\ mathrm {d} \ Omega} } = {\ frac {a ^ {2}} {4}},}

, а полное сечение, как мы и ожидали, составляет

σ = ∮ 4 π ⁡ d σ d Ω d Ω = π a 2. {\ displaystyle \ sigma = \ oint _ {4 \ pi} {\ frac {\ mathrm {d} \ sigma} {\ mathrm {d} \ Omega}} \, \ mathrm {d} \ Omega = \ pi a ^ {2}.}

{\ displaystyle \ sigma = \ oint _ {4 \ pi} {\ frac {\ mathrm {d} \ sigma} {\ mathrm {d} \ Omega}} \, \ mathrm {d} \ Omega = \ pi a ^ {2}.}

Как видно, это также согласуется с результатом из Примера 1, если предполагается, что фотон является жесткой сферой нулевого радиуса.