Свертка

Двоичная математическая операция над функциями Визуальное сравнение свертки, взаимной корреляции, и автокорреляции. Для операций с функцией f и при условии, что высота f равна 1,0, значение результата в различных точках указывается заштрихованной областью под каждой точкой. Кроме того, симметрия является причиной того, что $g\; \ast \; f\; \{\backslash \; displaystyle\; g\; *\; f\}$и $f\; \star \; g\; \{\backslash \; displaystyle\; f\; \backslash \; star\; g\}$являются идентичны в этом примере.

В математике (в частности, функциональным анализом ), свертка - это математическая операция над двумя функциями (f и g), которые составляют третью функцию ($f\; \ast \; g\; \{\backslash \; displaystyle\; f\; *\; g\}$), которая выражает, как форма одной изменяется другой. Термин свертка относится как к функции результата, так и к процессу ее вычислений. Он определяет как интеграл произведения двух функций после обращения и сдвига одной. И интеграл вычисляется для всех значений сдвига, создавая функцию свертки.

Некоторые функции свертки аналогичны взаимной корреляции : для функций с действительными значениями непрерывной или дискретной изменной корреляции она отличается от взаимной корреляции ($f\; \star \; g\; \{\backslash \; displaystyle\; f\; \backslash \; star\; g\}$) только в том, что либо f (x), либо g (x) отражается относительно оси y; таким образом, это взаимная корреляция f (x) и g (−x) или f (−x) и g (x). Для непрерывных функций оператор взаимной корреляции является сопряженным оператором свертки.

Свертка имеет приложения, которые включают вероятность, статистику, компьютерное зрение, обработку естественного языка, изображение и обработка сигналов, инженерные и дифференциальные уравнения.

Свертка может быть определена для функций в евклидовом пространстве и других группы. Например, периодические функции, такие как преобразование Фурье с дискретным временем, могут быть применимы в окружности и свернуты посредством периодической свертки. (См. Строку 18 в DTFT § Свойства.) Дискретная свертка может быть определена для функций на множестве целых чисел.

Обобщения свертки имеют применения в области численного анализа и числовая линейная алгебра, а также при разработке и реализации фильтров с конечной импульсной характеристикой при обработке сигналов.

Вычисление, обратное операции свертки, известно как деконволюция.

Содержание

• 1 Определение
  • 1.1 Обозначение
  • 1.2 Выводы
• 2 Визуальное объяснение
• 3 Исторические события
• 4 Круговая свертка
• 5 Дискретная свертка
  • 5.1 Круговая дискретная свертка
  • 5.2 Алгоритмы быстрой свертки
• 6 Область определения
  • 6.1 Функции с компактной поддержкой
  • 6.2 Интегрируемые функции
  • 6.3 Функции быстрого затухания
  • 6.4 Распределения
  • 6.5 Меры
• 7 Свойства
  • 7.1 Алгебраические свойства
  • 7.2 Интегрирование
  • 7.3 Дифференцирование
  • 7.4 Теорема о свертке
  • 7.5 Tr ансляционная эквивалентность
• 8 Свертки по группам
• 9 Свертка мер
• 10 Биалгебры
• 11 Приложения
• 12 См. также
• 13 Примечания
• 14 Ссылки
• 15 Дополнительная литература
• 16 Внешние ссылки

Определение

Свертка f и g записывается как f ∗ g, обозначающая оператор символом ∗. Он определен как интеграл двух произведений после обращения и сдвига одной. По сути, это особый вид интегрального преобразования :

$(f\; \ast \; g)\; (t)\; \triangleq \; \int \; -\; \infty \; \infty \; f\; (\tau )\; g\; (t\; -\; \tau )\; d\; \tau .\; \{\backslash \; Displaystyle\; (е\; *\; г)\; (т)\; \backslash \; треугольник\; \backslash \; \backslash \; int\; \_\; \{-\; \backslash \; infty\}\; ^\; \{\backslash \; infty\}\; е\; (\backslash \; тау)\; г\; (т-\; \backslash \; тау)\; \backslash ,\; д\; \backslash \; тау.\}$

эквивалентное определение (см. коммутативность):

$(f\; \ast \; g)\; (t)\; \triangleq \; \int \; -\; \infty \; \infty \; f\; (t\; -\; \tau )\; g\; (\tau )\; d\; \tau .\; \{\backslash \; Displaystyle\; (е\; *\; г)\; (т)\; \backslash \; треугольник\; \backslash \; \backslash \; int\; \_\; \{-\; \backslash \; infty\}\; ^\; \{\backslash \; infty\}\; f\; (т-\; \backslash \; тау)\; г\; (\backslash \; тау)\; \backslash ,\; д\; \backslash \; тау.\}$

Хотя символ t используется выше, он не обязательно должен использовать временную область. Но в этом контексте формулу свертки можно описать как средневзвешенное значение функции f (τ) в момент t, когда весовой коэффициент задается выражением g (–τ), просто сдвинутым на определение t. При изменении t весовая функция выделяет различные части входной функции.

Для функций f, g , поддерживаемых только на [0, ∞) (т. Е. Ноль для отрицательных аргументов), пределы интегрирования можно усечь, в результате получится:

$(\; fg)\; (t)\; знак\; равно\; \int \; 0\; tf\; (\tau )\; g\; (t\; -\; \tau )\; d\; \tau \; для\; f,\; g:\; [0,\; \infty )\; \to \; R.\; \{\backslash \; Displaystyle\; (е\; *\; г)\; (т)\; =\; \backslash \; int\; \_\; \{0\; \}\; ^\; \{т\}\; е\; (\backslash \; тау)\; г\; (т-\; \backslash \; тау)\; \backslash ,\; д\; \backslash \; тау\; \backslash \; квад\; \backslash \; \{\backslash \; текст\; \{для\}\}\; е,\; g:\; [0,\; \backslash \; infty)\; \backslash \; to\; \backslash \; mathbb\; \{R\}.\; \}$

Для многомерной формулировки свертки см. область определения (ниже).

Обозначение

Общее инженерное обозначение:

$f\; (t)\; \ast \; g\; (t)\; \triangleq \; \int \; -\; \infty \; \infty \; f\; (\tau )\; g\; (t\; -\; \tau )\; d\; \tau \; ⏟\; (е\; *\; г)\; (т),\; \{\backslash \; Displaystyle\; е\; (т)\; *\; г\; (т)\; \backslash ,\; \backslash \; треугольник\; \backslash \; \backslash \; underbrace\; \{\backslash \; int\; \_\; \{-\; \backslash \; infty\}\; ^\; \{\backslash \; infty\}\; е\; (\backslash \; тау)\; г\; (т\; -\; \backslash \; тау)\; \backslash ,\; d\; \backslash \; tau\}\; \_\; \{(f\; *\; g)\; (t)\},\}$

который следует интерпретировать осторожно, чтобы избежать путаницы. Например, f (t) ∗ g (t - t 0) эквивалентно (f ∗ g) (t - t 0), но f (t - t 0) ∗ g (t - t 0) практически эквивалентно (f ∗ g) (t - 2t 0).

Выводы

Свертка представленного вывода (в условиях ввода) важного класса операций, См. Теория систем LTI для получения свертки в результате ограничений LTI. В терминах Преобразование Фурье входа и выхода операции LTI, новые частотные компоненты не системы.. Существующие только изменяются (амплитуда и / или фаза). Другими словами, выходное преобразование точечным произведением входных преобразователей с третьим преобразованием (известное как передаточная функция ). См. теорема свертки для вывода И наоборот, свертка может быть получена как обратное преобразование Фурье поточечное произведение двух преобразований Фурье.

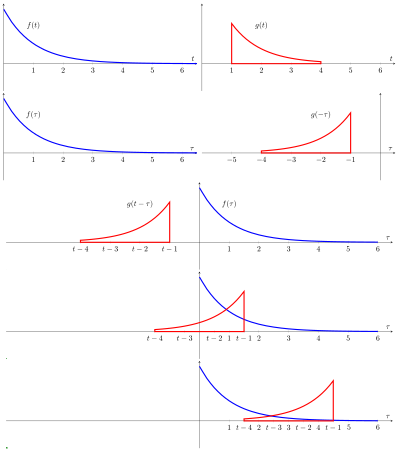
Визуальное объяснение

Визуальные объяснени я свертки
разите каждую функцию функции в терминах Выделившую функцию $\tau .\; \{\backslash \; displaystyle\; \backslash \; tau.\}$ Отражает одну из функций: $g\; (\tau )\; \{\backslash \; displaystyle\; g\; (\backslash \; tau)\}$→$g\; (-\; \tau ).\; \{\backslash \; displaystyle\; g\; (-\; \backslash \; tau).\}$ Добавить смещение по времени t, что позволяет $g\; (t\; -\; \tau )\; \{\backslash \; displaystyle\; g\; (t-\; \backslash \; tau)\}$для скольжения по оси $\tau \; \{\backslash \; displaystyle\; \backslash \; tau\}$. Начните t с −∞ и сдвиньте его до + ∞. Где бы ни пересекались две функции, найдите интеграл их произведения. Другими словами, вычислить скользящую, взвешенную сумму функции $f\; (\tau ),\; \{\backslash \; displaystyle\; f\; (\backslash \; tau),\}$, где весовая функция $g\; (-\; \tau ).\; \{\backslash \; displaystyle\; g\; (-\; \backslash \; tau).\}$ Результирующая форма волны (здесь не представляет) представляет собой свертку функций f и g. Если f (t) является единичный импульс, результатом этого процесса будет просто g (t). Формально: $\int \; -\; \infty \; \infty \; \delta \; (\tau )\; g\; (t\; -\; \tau )\; d\; \tau \; =\; g\; (t)\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{-\; \backslash \; infty\}\; ^\; \{\backslash \; infty\}\; \backslash \; delta\; (\backslash \; tau)\; g\; (\; t-\; \backslash \; tau)\; \backslash ,\; d\; \backslash \; tau\; =\; g\; (t)\}$
В этом примере красный «импульс», $g\; (\tau ),\; \{\backslash \; displaystyle\; \backslash \; g\; (\backslash \; tau),\}$- четная функция $(g\; (-\; \tau )\; =\; g\; (\tau )),\; \{\backslash \; displaystyle\; (\backslash \; g\; (-\; \backslash \; tau)\; =\; g\; (\backslash \; tau)\; \backslash ),\}$, поэтому свертка эквивалентна корреляции. Снимок этого "фильма" показывает функции $g\; (t\; -\; \tau )\; \{\backslash \; displaystyle\; g\; (t-\; \backslash \; tau)\}$и $f\; (\tau )\; \{\backslash \; displaystyle\; f\; (\backslash \; tau)\}$(синим цветом) для некоторого значения параметра $t,\; \{\backslash \; displaystyle\; t,\}$, которое произвольно определяется как расстояние от $\tau \; =\; 0\; \{\backslash \; displaystyle\; \backslash \; tau\; =\; 0\}$ось к центру красного импульса. Количество желтого - это площадь продукта $f\; (\tau )\; \cdot \; g\; (t\; -\; \tau ),\; \{\backslash \; displaystyle\; f\; (\backslash \; tau)\; \backslash \; cdot\; g\; (t-\; \backslash \; tau),\}$вычисляется с помощью интеграла свертки / корреляции. Фильм создается путем постоянного изменения $t\; \{\backslash \; displaystyle\; t\}$и пересчета интеграла. Результат (продемонстрирован черным) является функцией $t,\; \{\backslash \; displaystyle\; t,\}$, но отображается на той же оси, что и $\tau ,\; \{\backslash \; displaystyle\; \backslash \; tau,\}$для удобства и сравнения.
В этом изображении $f\; (\tau )\; \{\backslash \; displaystyle\; f\; (\backslash \; tau)\}$может вызвать реакцию RC-цепи на узкий импульс. которое происходит в $\tau \; =\; 0.\; \{\backslash \; displaystyle\; \backslash \; tau\; =\; 0.\}$Другими словами, если $g\; (\tau )\; =\; \delta \; (\tau ),\; \{\backslash \; displaystyle\; g\; (\backslash \; tau)\; =\; \backslash \; delta\; (\backslash \; tau),\}$результат свертки будет просто $f\; (t).\; \{\backslash \; displaystyle\; f\; (t).\}$Но когда $g\; (\tau )\; \{\backslash \; displaystyle\; g\; (\backslash \; tau)\}$- более широкий импульс (красный), ответ является " размазанной "версией $ф\; (т).\; \{\backslash \; displaystyle\; f\; (t).\}$Он начинается с $t\; =\; -\; 0,5,\; \{\backslash \; displaystyle\; t\; =\; -0,5,\}$, потому что мы определили $t\; \{\backslash \; displaystyle\; t\}$как расстояние от оси $\tau \; =\; 0\; \{\backslash \; displaystyle\; \backslash \; tau\; =\; 0\}$до center широкого спектраса ( вместо

Исторические события

Одно из самых ранних применений интеграла свертки появилось в выводе Даламбером теоремы Тейлора в Recherches sur différents points importants du système du monde, опубликовано в в 1754 г.

Также выражение типа:

$\int \; f\; (u)\; \cdot \; g\; (x\; -\; u)\; du\; \{\backslash \; displaystyle\; \backslash \; int\; f\; (u)\; \backslash \; cdot\; g\; (xu)\; \backslash ,\; du\}$

используется Сильвестром Франсуа Лакруа на странице 505 его книги под названием «Трактат о различных и сериях», которая является последним из трех томов энциклопедическая серия: Traité du Calcul différentiel et du Calcul intégral, Chez Courcier, Париж, 1797 –1800. Вскоре после этой операции свертки появляются на работе Пьера Симона Лапласа, Жан-Батиста Жозефа Фурье, Симеона Дени Пуассона и других. Сам термин не получил распространения до 1950-х или 60-х годов. До этого он иногда назывался Faltung (что означает сворачивание на немецком ), произведение композиции, интеграл суперпозиции и интеграл Карсона. Тем не менее, он появился еще в 1903 году, определение довольно незнакомо для более старых применений.

Операция:

- частный случай композиционных произведений, рассмотренный итальянским математиком Вито Вольтеррой в 1913 году.

Круговая свертка

Когда функция g T является периодическим, с периодом T, то для функций f, таких что f ∗ g T существует, свертка также периодическая и личность:

$(f\; \ast \; g\; T)\; (t)\; \equiv \; \int \; t\; 0\; T\; 0\; +\; T\; [\sum \; К\; =\; -\; \infty \; \infty \; е\; (\tau \; +\; К\; T)]\; г\; T\; (T\; -\; \tau )\; d\; \tau ,\; \{\backslash \; Displaystyle\; (F\; *\; G\_\; \{T\})\; (т)\; \backslash \; эквив\; \backslash \; int\; \_\; \{t\_\; \{0\}\}\; ^\; \{t\_\; \{0\}\; +\; T\}\; \backslash \; left\; [\backslash \; sum\; \_\; \{k\; =\; -\; \backslash \; infty\}\; ^\; \{\; \backslash \; infty\}\; f\; (\backslash \; tau\; +\; kT)\; \backslash \; right]\; g\_\; \{T\}\; (t-\; \backslash \; tau)\; \backslash ,\; d\; \backslash \; tau,\}$

где t 0 - произвольный выбор. Суммирование называется периодическим суммированием функции f.

Когда g Tявляется периодическим суммированием другой функции, g, тогда f ∗ g T называется круговой или циклической сверткой f и g.

И если периодическое суммирование выше заменено на f T, операция называется периодической сверткой f T и g T.

Дискретная свертка

Для комплексных функций f, g, определенные на множестве Z целых чисел, дискретная свертка f и g задается следующим образом:

$(f\; \ast \; g)\; [n]\; =\; \sum \; m\; Знак\; равно\; -\; \infty \; \infty \; е\; [м]\; г\; [n\; -\; м],\; \{\backslash \; displaystyle\; (f\; *\; g)\; [n]\; =\; \backslash \; sum\; \_\; \{m\; =\; -\; \backslash \; infty\}\; ^\; \{\backslash \; infty\}\; f\; [m]\; g\; [нм],\}$

или эквивалентным образом ( см. коммутативность) по:

$(f\; \ast \; g)\; [n]\; =\; \sum \; m\; =\; -\; \infty \; \infty \; f\; [n\; -\; m]\; g\; [m].\; \{\backslash \; displaystyle\; (f\; *\; g)\; [n]\; =\; \backslash \; sum\; \_\; \{m\; =\; -\; \backslash \; infty\}\; ^\; \{\backslash \; infty\}\; f\; [nm]\; g\; [m].\}$

Свертка двух конечных последовательностей определяется расширением последовательности к финитным функциям на множестве целых чисел. Когда устанавливают коэффициенты двух многочленов, тогда коэффициенты обычного произведения двух многочленов представляют собой свертку исходных двух последовательностей. Это известно как произведение Коши последовательнентов последовательностей.

Таким образом, когда g имеет конечный носитель в множестве $\{-\; M,\; -\; M\; +\; 1,\dots ,\; M\; -\; 1,\; M\}\; \{\backslash \; displaystyle\; \backslash \; \{-\; M,\; -M\; +\; 1,\; \backslash \; точки,\; M-1,\; M\; \backslash \}\}$(представляющий, например, конечную импульсную характеристику ), можно использовать конечное суммирование:

$(f\; \ast \; g)\; [n]\; =\; \sum \; m\; =\; -\; MM\; f\; [n\; -\; m]\; g\; [m].\; \{\backslash \; displaystyle\; (f\; *\; g)\; [n]\; =\; \backslash \; sum\; \_\; \{m\; =\; -M\}\; ^\; \{M\}\; f\; [nm]\; g\; [m].\}$

Круговая дискретная свертка

Когда функция g Nпериодичен с периодом N, то для функций f, таких что f ∗ g Nсуществует, свертка также периодична и идентична:

$(f\; \ast \; g\; N)\; [n]\; \equiv \; \sum \; m\; =\; 0\; N\; -\; 1\; (\; \sum \; k\; =\; -\; \infty \; \infty \; f\; [m\; +\; k\; N])\; g\; N\; [n\; -\; m].\; \{\backslash \; Displaystyle\; (е\; *\; г\_\; \{N\})\; [п]\; \backslash \; эквив\; \backslash \; сумма\; \_\; \{м\; =\; 0\}\; ^\; \{N-1\}\; \backslash \; влево\; (\backslash \; сумма\; \_\; \{к\; =\; -\; \backslash \; infty\}\; ^\; \{\backslash \; infty\}\; \{е\; \}\; [m\; +\; kN]\; \backslash \; right)\; g\_\; \{N\}\; [nm].\}$

Суммирование по k называется периодическим суммированием функции f.

Если g Nявляется периодическим суммированием другой функции, g, то f ∗ g Nизвестен как круговая свертка f и g.

Когда ненулевые длительности как f, так и g ограничены интервалом [0, N - 1], f ∗ g Nсводится к этим общим формам:

$(f\; \ast \; g\; N)\; [n]\; =\; \sum \; m\; =\; 0\; N\; -\; 1\; f\; [m]\; g\; N\; [n\; -\; m]\; =\; \sum \; m\; =\; 0\; nf\; [m]\; g\; [n\; -\; m]\; +\; \sum \; m\; =\; n\; +\; 1\; N\; -\; 1\; f\; [m]\; g\; [N\; +\; N\; -\; m]\; знак\; равно\; \sum \; m\; =\; 0\; N\; -\; 1\; f\; [m]\; g\; [(n\; -\; m)\; mod\; N]\; \triangleq \; (f\; *\; N\; g)\; [n]\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{выровнено\}\; (f\; *\; g\_\; \{N\})\; [n]\; =\; \backslash \; sum\; \_\; \{m\; =\; 0\}\; ^\; \{N-1\}\; f\; [m]\; g\_\; \{N\}\; [nm]\; \backslash \backslash \; =\; \backslash \; sum\; \_\; \{m\; =\; 0\}\; ^\; \{n\}\; f\; [m]\; g\; [nm]\; +\; \backslash \; sum\; \_\; \{m\; =\; n\; +\; 1\}\; ^\; \{N-1\}\; f\; [m]\; g\; [N\; +\; nm]\; \backslash \backslash \; =\; \backslash \; sum\; \_\; \{m\; =\; 0\}\; ^\; \{N\; -1\}\; f\; [m]\; g\; [(nm)\; \_\; \{\backslash \; bmod\; \{N\}\}]\; \backslash \; треугольникq\; (f\; *\; \_\; \{\_\; \{N\}\}\; g)\; [n]\; \backslash \; end\; \{align\}\}\}$

(уравнение 1)

Обозначение (f ∗ Ng) для циклической свертки обозначает свертку по циклической группе из целых чисел по модулю N.

Чаще всего возникает круговая свертка часто в контексте свертки с помощью алгоритма быстрого преобразования Фурье (FFT).

Алгоритмы быстрой свертки

Во многих дискретных свертках можно преобразовать в циклические свертки, так что быстрые преобразования со своим свертки выполнить реализацию для вычислений. Например, свертка последовательностей цифр - это операция ядра при умножении многозначных чисел, что, следовательно, может быть эффективно реализована с помощью методов преобразования (Knuth 1997, §4.3.3.C; von zur Gathen Gerhard 2003, §8.2).

Eq.1требует N арифметических операций для каждого выходного значения и N операций для N выходов. Это можно увеличить с помощью любого из нескольких быстрых алгоритмов. Цифровая обработка сигналов и другие приложения используют алгоритмы быстрой свертки, чтобы снизить стоимость свертки до сложности O (N log N).

Наиболее распространенные алгоритмы быстрой свертки используют алгоритмы быстрого преобразования Фурье (БПФ) с помощью теоремы о круговой свертке. В частности, циклическая свертка двух последовательностей конечной последовательности последовательного выполнения БПФ каждой последовательной, поточечного умножения и последующего выполнения обратного БПФ. Свертки типа, определенного выше, эффективно реализуются с использованием этого метода в сочетании с нулевым расширением и / или отбрасыванием частей вывода. Другие алгоритмы быстрой свертки, такие как алгоритм Шёнхаге - Штрассена или преобразование Мерсенна, используют быстрые преобразования Фурье в других кольцах .

. Нулевое расширение более короткой последовательности и быстрая циклическая свертка не является наиболее эффективными с вычислительной точки зрения доступными методами. Вместо этого разложения более длинной последовательности на блоки и свертка каждого блока позволяет использовать более быстрые алгоритмы, такие как метод сохранения и добавить метод перекрытия. Гибридный метод свертки, сочетающий блочные алгоритмы и алгоритмы FIR, обеспечивает нулевую задержку ввода-вывода, что полезно для вычислений свертки в реальном времени.

Область определения

свертка двух комплексных функций на R сама по себе является комплекснозначной функцией на R, определяемой следующим образом:

$(f\; \ast \; g)\; (Икс)\; знак\; равно\; \int \; R\; df\; (y)\; g\; (Икс\; -\; Y)\; dy\; знак\; равно\; \int \; R\; df\; (x\; -\; y)\; g\; (y)\; dy,\; \{\backslash \; displaystyle\; (f\; *\; g)\; (x)\; =\; \backslash \; int\; \_\; \{\backslash \; mathbf\; \{R\}\; ^\; \{d\}\}\; f\; (y)\; g\; (xy)\; \backslash ,\; dy\; =\; \backslash \; int\; \_\; \{\backslash \; mathbf\; \{R\}\; ^\; \{d\}\}\; f\; (xy)\; g\; (y)\; \backslash ,\; dy,\; \}$

и хорошо определен, только если f и g достаточно быстро затухают на бесконечности, чтобы интеграл существовал. Условия существования свертки могут быть хитрыми, так как раздутие g на бесконечности может быть легко компенсировано достаточно быстрым убыванием f. Таким образом, вопрос существования может исходить разные условия для f и g:

Функции с компактной поддержкой

Если f и g с компактной поддержкой непрерывные функции, то их свертка существует, а также имеет компактный носитель и непрерывна (Hörmander 1983, Глава 1). В более общем смысле, если одна функция (скажем, f) имеет компактный носитель, а другая локально интегрируема, то свертка f ∗ g корректно определена и непрерывна.

Свертка f и g также хорошо определена, когда обе функции являются локально квадратично интегрируемыми на R и поддерживаются на интервале формы [a, + ∞) (или обе поддерживаются на [−∞, a ]).

Интегрируемые функции

Свертка f и g существует, если обе f и g являются интегрируемыми по Лебегу функциями в L(R), и в этом случае f ∗ g также интегрируется (Stein Weiss 1971, теорема 1.3). Это следствие теоремы Тонелли. Это также верно для функций из L при дискретной свертке или, в более общем смысле, для свертки в любой группе.

. Аналогично, если f ∈ L (R ) и g ∈ L (R ), где 1 ≤ p ≤ ∞, тогда f ∗ g ∈ L (R ) и

$\Vert \; f\; \ast \; g\; \Vert \; p\; \le \; \Vert \; f\; \Vert \; 1\; \Vert \; g\; \Vert \; p.\; \{\backslash \; displaystyle\; \backslash \; |\; \{f\}\; *\; g\; \backslash \; |\; \_\; \{p\}\; \backslash \; leq\; \backslash \; |\; f\; \backslash \; |\; \_\; \{1\}\; \backslash \; |\; г\; \backslash \; |\; \_\; \{p\}.\}$

В частном случае p = 1 это показывает, что L является банаховой алгеброй относительно свертки (и равенство двух сторон выполнено, если f и g неотрицательны почти всюду).

В более общем смысле, неравенство Юнга подразумевает, что свертка - это непрерывное билинейное отображение между подходящими L пространствами. В частности, если 1 ≤ p, q, r ≤ ∞ удовлетворяют:

$1\; p\; +\; 1\; q\; =\; 1\; r\; +\; 1,\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{p\}\}\; +\; \{\backslash \; frac\; \{1\}\; \{\; q\}\}\; =\; \{\backslash \; frac\; \{1\}\; \{r\}\}\; +\; 1,\}$

, то

$\Vert \; f\; \ast \; g\; \Vert \; r\; \le \; \Vert \; f\; \Vert \; p\; \Vert \; g\; q,\; f\; \in \; L\; p,\; g\; \in \; L\; q,\; \{\backslash \; displaystyle\; \backslash \; left\; \backslash \; Vert\; f\; *\; g\; \backslash \; right\; \backslash \; Vert\; \_\; \{r\}\; \backslash \; leq\; \backslash \; left\; \backslash \; Vert\; f\; \backslash \; right\; \backslash \; Vert\; \_\; \{p\}\; \backslash \; left\; \backslash \; Vert\; g\; \backslash \; right\; \backslash \; Vert\; \_\; \{q\},\; \backslash \; quad\; f\; \backslash \; in\; \{\backslash \; mathcal\; \{L\}\}\; ^\; \{p\},\; \backslash \; g\; \backslash \; in\; \{\backslash \; mathcal\; \{L\}\}\; ^\; \{q\},\}$

, так что свертка является непрерывным билинейным отображением из L × L в L. Неравенство Юнга для свертки также верно в других контекстах (круговая группа, свертка на Z ). Предыдущее неравенство не является точным на вещественном прямой: когда 1 < p, q, r < ∞, there exists a constant Bp, q < 1 such that:

$\Vert \; f\; \ast \; g\; \Vert \; r\; \le \; B\; p,\; q\; \Vert \; f\; \Vert \; p\; \Vert \; g\; \Vert \; q,\; f\; \in \; L\; p,\; g\; \in \; L\; q.\; \{\backslash \; displaystyle\; \backslash \; left\; \backslash \; Vert\; f\; *\; g\; \backslash \; right\; \backslash \; Vert\; \_\; \{r\}\; \backslash \; leq\; B\_\; \{p,\; q\}\; \backslash \; left\; \backslash \; Vert\; f\; \backslash \; right\; \backslash \; Vert\; \_\; \{p\}\; \backslash \; left\; \backslash \; Vert\; g\; \backslash \; right\; \backslash \; Vert\; \_\; \{\; q\},\; \backslash \; quad\; f\; \backslash \; in\; \{\backslash \; mathcal\; \{L\}\}\; ^\; \{p\},\; \backslash \; g\; \backslash \; in\; \{\backslash \; mathcal\; \{L\}\}\; ^\; \{q\}.\}$

Оптимальное значение B p, q был открыт в 1975 году.

Более сильная оценка верна при условии 1 < p, q, r < ∞ :

$\Vert \; f\; \ast \; g\; \Vert \; r\; \le \; C\; p,\; q\; \Vert \; f\; \Vert \; p\; \Vert \; g\; \Vert \; q,\; w\; \{\backslash \; displaystyle\; \backslash \; |\; е\; *\; г\; \backslash \; |\; \_\; \{r\}\; \backslash \; leq\; C\_\; \{p,\; q\}\; \backslash \; |\; f\; \backslash \; |\; \_\; \{p\}\; \backslash \; |\; g\; \backslash \; |\; \_\; \{q,\; w\}\}$

где $\Vert \; g\; \Vert \; q,\; w\; \{\backslash \; displaystyle\; \backslash \; |\; g\; \backslash \; |\; \_\; \{q,\; w\}\}$- слабая норма L. Свертка также определяет билинейное непрерывное отображение $Lp,\; w\; \times \; L\; q,\; w\; \to \; L\; r,\; w\; \{\backslash \; displaystyle\; L\; ^\; \{p,\; w\}\; \backslash \; times\; L\; ^\; \{q,\; w\}\; \backslash \; to\; L\; ^\; \{r,\; w\}\}$для из-за слабого неравенства Юнга:

$\Vert \; f\; \ast \; g\; \Vert \; r,\; w\; \le \; C\; p,\; q\; \Vert \; f\; \Vert \; p,\; w\; \Vert \; g\; \Vert \; r,\; w.\; \{\backslash \; displaystyle\; \backslash \; |\; е\; *\; г\; \backslash \; |\; \_\; \{r,\; w\}\; \backslash \; leq\; C\_\; \{p,\; q\}\; \backslash \; |\; f\; \backslash \; |\; \_\; \{p,\; w\}\; \backslash \; |\; г\; \backslash \; |\; \_\; \{r,\; w\}.\}$

Функции быстрого убывания

В дополнение к функции с компактным носителем и интегрируемым функциям, функции, которые имеют достаточно большое затухание на бесконечности, также могут быть свернуты. Важная особенность свертки состоит в том, что если f и g быстро убывают, то f ∗ g также быстро убывает. В частности, если f и g - быстро убывающие функции, то свертка f ∗ g тоже. В сочетании с тем фактом, что свертка коммутирует с дифференцированием (см. #Properties), отсюда следует, что класс функций Шварца замкнут относительно свертки (Stein Weiss 1971, Теорема 3.3).

Распределения

При некоторых обстоятельствах можно определить свертку функции с распределением или двух распределений. Если f - функция с компактным носителем, а g - распределение, то f ∗ g - гладкая функция, определяемая формулой распределения, аналогичной

$\int \; R\; df\; (y)\; g\; (x\; -\; y)\; dy.\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{\backslash \; mathbf\; \{R\}\; ^\; \{d\}\}\; \{f\}\; (y)\; g\; (xy)\; \backslash ,\; dy.\}$

В более общем смысле, можно расширить определение свертки уникальным способом, так что ассоциативный закон

$f\; \ast \; (g\; \ast \; \phi )\; =\; (f\; \ast \; g)\; \ast \; \phi \; \{\backslash \; displaystyle\; f\; *\; (g\; *\; \backslash \; varphi)\; =\; (f\; *\; g)\; *\; \backslash \; varphi\}$

остается справедливо в случае, если f - распределение, а g - распределение с компактным носителем (Hörmander 1983, §4.2).

Меры

Свертка любых двух мер Бореля μ и ν ограниченные вариации - это мера $\mu \; \ast \; \nu \; \{\backslash \; displaystyle\; \backslash \; mu\; *\; \backslash \; nu\}$определено (Рудин 1962)

$\int \; R\; df\; (x)\; d\; (\mu \; \ast \; \nu )\; (x)\; =\; \int \; R\; d\; \int \; R\; df\; (x\; +\; y)\; d\; \mu \; (Икс)\; d\; \nu \; (Y),\; \{\backslash \; Displaystyle\; \backslash \; int\; \_\; \{\backslash \; mathbf\; \{R\}\; ^\; \{d\}\}\; f\; (x)\; \backslash ,\; d\; (\backslash \; mu\; *\; \backslash \; nu)\; (x)\; =\; \backslash \; int\; \_\; \{\backslash \; mathbf\; \{R\; \}\; ^\; \{d\}\}\; \backslash \; int\; \_\; \{\backslash \; mathbf\; \{R\}\; ^\; \{d\}\}\; f\; (x\; +\; y)\; \backslash ,\; d\; \backslash \; mu\; (x)\; \backslash ,\; d\; \backslash \; nu\; (y).\}$

В частности,

$(\mu \; \ast \; \nu )\; (A)\; знак\; равно\; \int \; р\; d\; \times \; р\; d\; 1\; A\; (x\; +\; y)\; d\; (\mu \; \times \; \nu )\; (x,\; y),\; \{\backslash \; displaystyle\; (\backslash \; mu\; *\; \backslash \; nu)\; (A)\; =\; \backslash \; int\; \_\; \{\backslash \; mathbf\; \{R\}\; ^\; \{d\}\; \backslash \; times\; \backslash \; mathbf\; \{R\}\; ^\; \{d\}\}\; 1\_\; \{A\}\; (x\; +\; y)\; \backslash ,\; d\; (\backslash \; mu\; \backslash \; times\; \backslash \; nu)\; (x,\; y),\}$

где $A\; \subset \; R\; d\; \{\backslash \; displaystyle\; A\; \backslash \; subset\; \backslash \; mathbf\; \{R\}\; ^\; \{d\}\}$- измеримое множество, а $1\; A\; \{\backslash \; displaystyle\; 1\_\; \{A\}\}$- это индикаторная функция для $A\; \{\backslash \; displaystyle\; A\}$.

Это согласуется со сверткой, обычно выше, когда рассматривает μ и ν. Как распределение, а также свертка L функци й, когда μ и ν равны abs исключительно непрерывно относительно меры Лебега.

Свертка мер также удовлетворяет следующую версию неравенства Юнга

$\Vert \; \mu \; \ast \; \nu \; \Vert \; \le \; \Vert \; \mu \; \Vert \; \Vert \; \nu \; \Vert \; \{\backslash \; displaystyle\; \backslash \; |\; \backslash \; му\; *\; \backslash \; ню\; \backslash \; |\; \backslash \; leq\; \backslash \; |\; \backslash \; му\; \backslash \; |\; \backslash \; |\; \backslash \; nu\; \backslash \; |\}$

, где норма - это общая вариация меры. Временное пространство ограничено вариациями банаховым пространством, свертка может обрабатываться стандартными методами функционального анализа, которые не для свертки распределений.

Свойства

Алгебраические свойства

Свертка выполняет произведение на линейном пространстве интегрируемых функций. Это произведение представляет собой следующее алгебраическое свойство, которое формально означает, что пространство интегрируемых функций с произведением, заданной сверткой, коммутативной ассоциативной алгеброй без тождества (Strichartz 1994, § 3.3). Другие линейные пространства функций, такие как пространство непрерывных функций с компактным носителем, замкнуты относительно свертки и, таким образом, также образуют коммутативные ассоциативные алгебры.

Коммутативность

$f\; \ast \; g\; =\; g\; \ast \; f\; \{\backslash \; displaystyle\; f\; *\; g\; =\; g\; *\; f\}$

Доказательство: по определению

$(f\; \ast \; g)\; (t)\; =\; \int \; -\; \infty \; \infty \; f\; (\; \tau )\; г\; (T\; -\; \tau )\; d\; \tau \; \{\backslash \; Displaystyle\; (е\; *\; г)\; (т)\; =\; \backslash \; int\; \_\; \{-\; \backslash \; infty\}\; ^\; \{\backslash \; infty\}\; е\; (\backslash \; тау)\; г\; (т-\; \backslash \; тау)\; \backslash ,\; d\; \backslash \; tau\}$

При изменении переменной интегрирования на $u\; =\; t\; -\; \tau \; \{\backslash \; displaystyle\; u\; =\; t-\; \backslash \; tau\}$результат будет следующим.

Ассоциативность

$f\; *\; (g\; *\; h)\; =\; (f\; *\; g)\; *\; h\; \{\backslash \; displaystyle\; f\; *\; (g\; *\; h)\; =\; (f\; *\; g)\; *\; h\}$

Доказательство: это следует из использования Теорема Фубини (т. Е. Двойные интегралы могут быть вычислены как повторные интегралы в любом порядке).

Распределимость

$f\; *\; (g\; +\; h)\; =\; (f\; *\; g)\; +\; (f\; *\; h)\; \{\backslash \; displaystyle\; f\; *\; (g\; +\; h)\; =\; (f\; *\; g)\; +\; (f\; *\; h)\}$

Доказательство: это следует из линейности интеграла.

Ассоциативность со скалярным умножением

$a\; (f\; \ast \; g)\; =\; (af)\; \ast \; g\; \{\backslash \; displaystyle\; a\; (f\; *\; g)\; =\; (af)\; *\; g\}$

для любого действительного (или комплексного) числа $a\; \{\backslash \; displaystyle\; a\}$.

Мультипликативное тождество

Никакая алгебра функций не обладает тождеством для свертки. Обычно не является серьезным неудобством, из-за набора функций, которые выполняются с помощью дельта-распределения или отсутствия крайней мере (как в случае L), допускают прибли к тождеству. Однако линейное пространство распределений с компактным носителем допускает тождество при свертке. В частности,

$f\; \ast \; \delta \; =\; f\; \{\backslash \; displaystyle\; f\; *\; \backslash \; delta\; =\; f\}$

, где δ - дельта-распределение.

Обратный элемент

Некоторые распределения имеют обратный элемент для свертки, S, который как определяется

$S\; (-\; 1)\; \ast \; S\; =\; \delta .\; \{\backslash \; displaystyle\; S\; ^\; \{(-\; 1)\}\; *\; S\; =\; \backslash \; delta.\}$

Набор обратимых распределений образует абелеву группу при свертке.

Комплексное спряжение

$f\; \ast \; g\; ¯\; =\; f\; ¯\; \ast \; g\; ¯\; \{\backslash \; displaystyle\; \{\backslash \; overline\; \{f\; *\; g\}\}\; =\; \{\backslash \; overline\; \{f\}\}\; *\; \{\backslash \; overline\; \{g\}\}\}$

Связь с дифференцированием

$(f\; \ast \; g)\; \prime \; =\; f\; \prime \; \ast \; g\; =\; f\; \ast \; g\; \prime \; \{\backslash \; displaystyle\; (f\; *\; g)\; \text{'}=\; f\text{'}\; *\; g\; =\; f\; *\; g\; \text{'}\}$

Доказательство:

$(f\; \ast \; g)\; \prime \; =\; ddt\; \int \; -\; \infty \; \infty \; f\; (\tau )\; g\; (t\; -\; \tau )\; d\; \tau \; =\; \int \; -\; \infty \; \infty \; f\; (\tau )\; \partial \; \partial \; tg\; (t\; -\; \tau )\; d\; \tau \; =\; \int \; -\; \infty \; \infty \; f\; (\; \tau )\; g\; \prime \; (t\; -\; \tau )\; d\; \tau \; =\; f\; \ast \; g\; \prime .\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; (f\; *\; g)\; \text{'}=\; \{\backslash \; frac\; \{d\}\; \{dt\}\}\; \backslash \; int\; \_\; \{-\; \backslash \; infty\}\; ^\; \{\backslash \; infty\}\; f\; (\backslash \; tau)\; g\; (t-\; \backslash \; tau)\; \backslash ,\; d\; \backslash \; tau\; \backslash \backslash \; [4pt]\; =\; \backslash \; int\; \_\; \{-\; \backslash \; infty\}\; ^\; \{\backslash \; infty\}\; f\; (\backslash \; tau)\; \{\backslash \; frac\; \{\backslash \; partial\}\; \{\backslash \; partial\; t\}\}\; g\; (t-\; \backslash \; tau)\; \backslash ,\; d\; \backslash \; tau\; \backslash \backslash \; [4pt]\; =\; \backslash \; int\; \_\; \{-\; \backslash \; infty\}\; ^\; \{\backslash \; infty\}\; f\; (\backslash \; tau)\; g\; \text{'}(t-\; \backslash \; tau)\; \backslash ,\; d\; \backslash \; tau\; =\; f\; *\; g\text{'}.\; \backslash \; end\; \{align\}\}\}$

Связь с интегрированием

Если $F\; (t)\; =\; \int \; -\; \infty \; tf\; (\tau )\; d\; \tau ,\; \{\backslash \; displaystyle\; F\; (t)\; =\; \backslash \; int\; \_\; \{\; -\; \backslash \; infty\}\; ^\; \{t\}\; е\; (\backslash \; тау)\; d\; \backslash \; тау,\}$и $G\; (t)\; =\; \int \; -\; \infty \; tg\; (\tau )\; d\; \tau ,\; \{\backslash \; displaystyle\; G\; (t)\; =\; \backslash \; int\; \_\; \{-\; \backslash \; infty\}\; ^\; \{t\}\; g\; (\backslash \; tau)\; \backslash ,\; d\; \backslash \; tau,\}$, тогда

$(F\; \ast \; g)\; (t)\; =\; (f\; \ast \; G)\; (t)\; =\; \int \; -\; \infty \; t\; (f\; \ast \; g)\; (\tau )\; d\; \tau .\; \{\backslash \; Displaystyle\; (F\; *\; g)\; (t)\; =\; (е\; *\; G)\; (t)\; =\; \backslash \; int\; \_\; \{-\; \backslash \; infty\}\; ^\; \{t\}\; (f\; *\; g)\; (\backslash \; tau)\; \backslash ,\; d\; \backslash \; tau.\}$

Интегрирование

Если f и g - интегрируемые функции, то интеграл от их свертки на всем визуализируется как произведение их интегралов:

$\int \; R\; d\; (f\; \ast \; g)\; (x)\; dx\; =\; (\int \; R\; df\; (x)\; dx)\; (\int \; R\; dg\; (x)\; dx).\; \{\backslash \; Displaystyle\; \backslash \; int\; \_\; \{\backslash \; mathbf\; \{R\}\; ^\; \{d\}\}\; (е\; *\; г)\; (х)\; \backslash ,\; dx\; =\; \backslash \; left\; (\backslash \; int\; \_\; \{\backslash \; mathbf\; \{R\}\; ^\; \{d\}\}\; е\; (х)\; \backslash ,\; dx\; \backslash \; right)\; \backslash \; left\; (\backslash \; int\; \_\; \{\backslash \; mathbf\; \{R\}\; ^\; \{d\}\}\; g\; (x)\; \backslash ,\; dx\; \backslash \; right).\}$

Это следует из теоремы Фубини. Тот же результат имеет место, если обязательным, что f и g являются только неотрицательными аппаратными средствами, функции, по теореме Тонелли.

Дифференцирование

В случае одной переменной

$ddx\; (f\; \ast \; g)\; =\; dfdx\; *\; g\; =\; f\; *\; dgdx\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\}\; \{dx\}\}\; (f\; *\; g)\; =\; \{\backslash \; frac\; \{df\}\; \{dx\}\}\; *\; g\; =\; f\; *\; \{\backslash \; frac\; \{dg\}\; \{dx\}\}\; \}$

где d / dx - производная. В более общем плане, в случае функций нескольких чисел, аналогичная формула верна с частной производной :

$\partial \; \partial \; x\; i\; (f\; \ast \; g)\; =\; \partial \; f\; \partial \; x\; i\; \ast \; g\; =\; f\; \ast \; \partial \; g\; \partial \; x\; i.\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\}\; \{\backslash \; partial\; x\_\; \{i\}\}\}\; (f\; *\; g)\; =\; \{\backslash \; frac\; \{\backslash \; partial\; f\}\; \{\backslash \; partial\; x\_\; \{i\}\}\}\; *\; g\; =\; f\; *\; \{\backslash \; frac\; \{\backslash \; partial\; g\}\; \{\backslash \; partial\; x\_\; \{i\}\}\}.\}$

Частным следствием этого является то, что свертку можно рассматривать как операцию "сглаживания": свертка f и g дифференцируема столько раз, сколько f и g - это сумма.

Эти тождества выполняются при точном условии, что f и g абсолютно интегрируемы и по крайней мере одно из них имеет абсолютно интегрируемую (L) слабую производную как следствие неравенства свертки Юнга. Например, когда непрерывно дифференцируема с компактным носителем, а g - произвольная локально интегрируемая функция,

$d\; d\; x\; (f\; \ast \; g)\; =\; d\; f\; d\; x\; \ast \; g.\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\}\; \{dx\}\}\; (f\; *\; g)\; =\; \{\backslash \; frac\; \{df\}\; \{dx\}\}\; *\; g.\}$

Эти тождества также имеют гораздо более широкое значение в смысле умеренных распределений, если одно из f или g является быстро убывающим умеренным распределением, умеренным распределением с компактной опорой или функцией Шварца, а другое - умеренным распределением. С другой стороны, две положительно интегрируемые и бесконечно дифференцируемые функции имеют нигде не непрерывную свертку.

В дискретном случае оператор разности D f (n) = f (n + 1) - f (n) удовлетворяетному применению:

$D\; (f\; \ast \; g)\; =\; (D\; f)\; \ast \; g\; =\; f\; \ast \; (D\; g).\; \{\backslash \; displaystyle\; D\; (f\; *\; g)\; =\; (Df)\; *\; g\; =\; f\; *\; (Dg).\}$

Теорема о свертке

Теорема о свертке утверждает, что

$F\; \{е\; *\; г\}\; знак\; равно\; К\; \cdot \; F\; \{е\}\; \cdot \; F\; \{g\}\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{F\}\}\; \backslash \; \{f\; *\; g\; \backslash \}\; =\; k\; \backslash \; cdot\; \{\backslash \; mathcal\; \{F\}\}\; \backslash \; \{f\; \backslash \}\; \backslash \; cdot\; \{\backslash \; mathcal\; \{F\}\}\; \backslash \; \{g\; \backslash \}\}$

где $F\; \{f\}\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{F\}\}\; \backslash \; \{f\; \backslash \}\}$обозначает преобразование Фурье из $f\; \{\backslash \; displaystyle\; f\}$и $k\; \{\backslash \; displaystyle\; k\}$- это константа, которая зависит от конкретного нормализация преобразования Фурье. Версии этой теоремы также верны для преобразования Лапласа, двустороннего преобразования Лапласа, Z-преобразования и преобразования Меллина.

См. Также менее тривиальная теорема Титчмарша о свертке.

С другой стороны, если $W\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{W\}\}\}$является матрицей преобразования Фурье, тогда.

$W\; (C\; (1)\; x\; \ast \; C\; (2)\; y)\; =\; (WC\; (1)\; \bullet \; WC\; (2))\; (x\; \otimes \; y)\; =\; WC\; (1)\; x\; \circ \; WC\; (2)\; y\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{W\}\}\; (C\; ^\; \{(1)\}\; x\; \backslash \; ast\; C\; ^\; \{(2)\}\; y)\; =\; (\{\backslash \; mathcal\; \{W\}\}\; C\; ^\; \{(1)\}\; \backslash \; bullet\; \{\backslash \; mathcal\; \{W))\}\}\; C\; ^\; \{(2)\})\; (x\; \backslash \; otimes\; y)\; =\; \{\backslash \; mathcal\; \{W\}\}\; C\; ^\; \{(1)\}\; x\; \backslash \; circ\; \{\backslash \; mathcal\; \{W\}\}\; C\; ^\; \{(2)\}\; y\; \}$,.

где $\bullet \; \{\backslash \; displaystyle\; \backslash \; bullet\}$- это разделительный продукт, $\otimes \; \{\backslash \; displaystyle\; \backslash \; otimes\}$означает произведение Кронекера, $\circ \; \{\backslash \; displaystyle\; \backslash \; circ\}$обозначает произведение Адамара (этот результат является развитием счетного эскиза свойств).

Трансляционная эквивалентность

Свертка коммутирует с переводами, что означает, что

$\tau \; x\; (f\; \ast \; g)\; =\; (\tau \; xf)\; \ast \; g\; =\; f\; \ast \; (\tau \; xg)\; \{\backslash \; displaystyle\; \backslash \; tau\; \_\; \{x\}\; (f\; *\; g)\; =\; (\backslash \; tau\; \_\; \{x\}\; f)\; *\; g\; =\; \{f\}\; *\; (\backslash \; tau\; \_\; \{x\}\; g)\}$

где τ x f представляет собой перенос функции f на x, как определенную

$(\tau \; xf)\; (y)\; =\; f\; (y\; -\; x).\; \{\backslash \; displaystyle\; (\backslash \; tau\; \_\; \{x\}\; f)\; (y)\; =\; f\; (yx).\}$

Если f - это функция Шварца, то τ x f - это свертка со сдвинутой дельта-функцией Дирака τ x f = f ∗ τ x δ. Таким образом, трансляционная инвариантность свертки функций Шварца является следствием ассоциативности свертки.

Кроме того, при определенных условиях свертка является наиболее общей инвариантной операцией преобразования. Неформально говоря, имеет место

• Предположим, что S - ограниченный линейный оператор, действующий на функции, коммутирующие со сдвигами: S (τ x f) = τ x (Sf) для всех x. Тогда S задается как свертка с функцией (или распределением) g S ; то есть Sf = g S ∗ f.

Таким образом, некоторые инвариантные операции трансляции могут быть представлены как свертка. Свертки играют важную роль в изучении систем, не зависящих от времени, и особенно теории систем LTI. Представляющая функция g S является импульсной характеристикой преобразования S.

Более точная версия приведенной выше теоремы требует указания класса функций, на которых свертка определена, а также требует дополнительного допущения, что S должен быть непрерывным линейным оператором по отношению к соответствующей топологии . Известно, например, что каждый непрерывный инвариантный относительно сдвига линейный непрерывный оператор на L является сверткой с конечной мерой Бореля. В более общем смысле, любой непрерывный инвариантный линейный оператор с непрерывным переносом на L для 1 ≤ p < ∞ is the convolution with a умеренного распределения, преобразование Фурье которого ограничено. То есть все они задаются ограниченными множителями Фурье.

Свёртки на группах

Если G - подходящая группа, наделенная мерой λ, и если f и g - действительные или комплексные интегрируемые функции на G, то мы можем определить их свертку как

$(f\; \ast \; g)\; (x)\; =\; \int \; G\; f\; (y)\; g\; (y\; -\; 1\; x)\; d\; \lambda \; (y).\; \{\backslash \; displaystyle\; (f\; *\; g)\; (x)\; =\; \backslash \; int\; \_\; \{G\}\; f\; (y)\; g\; (y\; ^\; \{-\; 1\}\; x)\; \backslash ,\; d\; \backslash \; lambda\; (y).\}$

Он не коммутативен в Генеральная. В типичных случаях, представляющих интерес, G является локально компактной топологической группой Хаусдорфа , а λ - (слева-) мерой Хаара. В этом случае, если G не унимодулярный, определенная таким образом свертка не совпадает с $\int \; f\; (xy\; -\; 1)\; g\; (y)\; d\; \lambda \; (y)\; \{\backslash \; displaystyle\; \backslash \; textstyle\; \{\backslash \; int\; f\; (xy\; ^\; \{-\; 1\})\; g\; (y)\; \backslash ,\; d\; \backslash \; lambda\; (y)\}\}$. Предпочтение одного перед другим сделано так, что свертка с фиксированной функцией g коммутирует с левым сдвигом в группе:

$L\; h\; (f\; \ast \; g)\; =\; (L\; h\; f)\; \ast \; g.\; \{\backslash \; displaystyle\; L\_\; \{h\}\; (f\; *\; g)\; =\; (L\_\; \{h\}\; f)\; *\; g.\}$

Кроме того, соглашение также требуется для согласования с определением свертки мер, приведенным ниже. Однако с правой вместо левой меры Хаара последний интеграл предпочтительнее первого.

На локально компактных абелевых группах верна версия теоремы о свертке : преобразование Фурье свертки является точечным произведением преобразований Фурье. Круговая группа Tс мерой Лебега является непосредственным примером. Для фиксированного g в L (T ) у нас есть следующий знакомый оператор, действующий в гильбертовом пространстве L(T):

$T\; f\; (x)\; =\; 1\; 2\; \pi \; \int \; T\; f\; (y)\; g\; (x\; -\; y)\; dy.\; \{\backslash \; displaystyle\; T\; \{f\}\; (x)\; =\; \{\backslash \; frac\; \{1\}\; \{2\; \backslash \; pi\}\}\; \backslash \; int\; \_\; \{\backslash \; mathbf\; \{T\}\}\; \{f\}\; (y)\; g\; (xy)\; \backslash ,\; dy.\}$

Оператор T компактный. Непосредственный расчет показывает, что сопряженный к нему T * является сверткой с

$g\; ¯\; (-\; y).\; \{\backslash \; displaystyle\; \{\backslash \; bar\; \{g\}\}\; (-\; y).\}$

В соответствии с указанным выше свойством коммутативности T нормальный : T * T = TT *. Кроме того, T коммутирует с оператора трансляции. Рассмотрим семейство операторов S, состоящее из всех таких сверток и операторов сдвига. Тогда S - коммутирующее семейство нормальных операторов. Согласно спектральной теории, существует ортонормированный базис {h k }, который одновременно диагонализирует S. Это характеризует свертки на окружности. В частности, у нас есть

$hk\; (x)\; =\; eikx,\; k\; \in \; Z,\; \{\backslash \; displaystyle\; h\_\; \{k\}\; (x)\; =\; e\; ^\; \{ikx\},\; \backslash \; quad\; k\; \backslash \; in\; \backslash \; mathbb\; \{Z\},\; \backslash ;\; \}$

, которые являются точностью символами из T . Каждая свертка представляет собой компактный оператор умножения в этом базисе. Это можно рассматривать как версию обсуждаемой выше теоремы о свертке.

Дискретным примером является конечная циклическая группа порядка n. Операторы свертки представлены здесь циркулянтными матрицами и могут быть диагонализованы с помощью дискретного преобразования Фурье.

.>образуют ортонормированный базис в L согласно теореме Питера - Вейля, и аналог Теорема свертки продолжает оставаться в силе, как и многие другие аспекты гармонического анализа, которые зависят от преобразования Фурье.

Свертка мер

Пусть G - (мультипликативно записанная) топологическая группа. Если μ и ν конечны борелевские меры на G, то их свертка μ ∗ ν означает как прямая мера действия группы и может быть записана как

$(\mu \; \ast \; \nu )\; (E)\; знак\; равно\; \iint \; 1\; E\; (ху)\; d\; \mu \; (x)\; d\; \nu \; (y)\; \{\backslash \; displaystyle\; (\backslash \; mu\; *\; \backslash \; nu)\; (E)\; =\; \backslash \; iint\; 1\_\; \{E\}\; (xy)\; \backslash ,\; d\; \backslash \; mu\; (x)\; \backslash ,\; d\; \backslash \; nu\; (y)\}$

для каждого измеримого подмножества E группы G. Свертка также является конечной мерой, полная вариация которая удовлетворяет

$\Vert \; {\rm M}\; \ast \; \nu \; \Vert \; \le \; \Vert \; {\rm M}\; \Vert \; \Vert \; \nu \; \Vert .\; \{\backslash \; displaystyle\; \backslash \; |\; \backslash \; му\; *\; \backslash \; ню\; \backslash \; |\; \backslash \; leq\; \backslash \; |\; \backslash \; му\; \backslash \; |\; \backslash \; |\; \backslash \; nu\; \backslash \; |.\}$

В случае, когда G локально компактный с (левый-) мера Хаара λ, а μ и ν являются абсолютно непрерывными относительно λ, , так что каждая функция имеет функцию плотности, тогда свертка μ ∗ ν равна также абсолютно непрерывный, и ее функция представляет собой просто свертку двух отдельных функций плотности.

Если μ и ν являются вероятностными мерами в топологической группе (R, +), то свертка μ ∗ ν представляет собой распределение вероятностей суммы X + Y двух независимых случайных величин X и Y, соответствующие распределения μ и ν.

Биалгебры

Пусть (X, Δ, ∇, ε, η) будет биалгеброй с коумножением Δ, умножением ∇, единицей η и счетчиком ε. Свертка - это произведение, определенное на алгебре эндоморфизмов Конец (X) следующим образом. Пусть φ, ψ ∈ End (X), то есть φ, ψ: X → X - функции, которые уважают всю алгебраическую преобразованную X, тогда свертка φ ∗ ψ определяется как композиция

$X\; \to \; ∆\; X\; \otimes \; X\; \to \; \varphi \; \otimes \; \psi \; X\; \otimes \; X\; \to \; \nabla \; X.\; \{\backslash \; displaystyle\; X\; \{\backslash \; xrightarrow\; \{\backslash \; Delta\}\}\; X\; \backslash \; otimes\; X\; \{\backslash \; xrightarrow\; \{\backslash \; phi\; \backslash \; otimes\; \backslash \; psi\}\}\; X\; \backslash \; otimes\; X\; \{\backslash \; xrightarrow\; \{\backslash \; nabla\}\}\; X.\}$

Заметно проявляется свертка в определении алгебр Хопфа (Кассель 1995, §III.3). Биалгебра является алгеброй Хопфа тогда и только тогда, когда у нее есть антипод: эндоморфизм S такой, что

$S\; \ast \; id\; X\; =\; id\; X\; \ast \; S\; =\; \eta \; \circ \; \epsilon .\; \{\backslash \; displaystyle\; S\; *\; \backslash \; operatorname\; \{id\}\; \_\; \{X\}\; =\; \backslash \; operatorname\; \{id\}\; \_\; \{X\}\; *\; S\; =\; \backslash \; eta\; \backslash \; circ\; \backslash \; varepsilon.\}$

Приложения

можно использовать размытие по Гауссу для получения гладкого цифрового изображения в градациях серого на полутоновом отпечатке.

Свертка и связанные с ней операции используются во многих приложениях в области науки, техники и математики.

• В обработка изображений

В обработка цифровых изображений сверточная фильтрация играет важную роль во многих важных алгоритмах в обнаружении краев и связанных процессах.

В оптике фотография вне фокуса - это свертка резкого изображения с функцией линзы. Фотографический термин для этого: боке.

в приложениях обработки изображений, таких как добавление размытия.

• в цифровой обработке данных

в аналитической химии, сглаживающие фильтры Савицки - Голея используются для анализа спектроскопических данных. Они могут улучшить отношение сигнал / шум с минимальным искажением спектров

В статистике взвешенное скользящее среднее представляет собой свертку.

• В акустике, реверберация - это свертка исходного звука с эхом от объектов, окружающих источник звука.

При цифровой обработке сигналов свертка используется для отображения импульсной характеристики Реальная комната на цифровой аудиосигнал.

В электронной музыке свертка - это наложение спектрального или ритмическая структура по звуку. Часто эта оболочка или структура берется из другого звука. Свертка двух сигналов - это фильтрация одного через другой.

• В электротехнике свертка одной функции (входной сигнал ) со второй функцией (импульсный отклик) дает результат линейной неизменной во времени <системы398>(LTI). В любой данный момент выходные данные представляют собой совокупный эффект всех обычно используемых значений входной функции, причем самые последние значения имеют наибольшее влияние (выраженные как мультипликативный коэффициент). Функция импульсной характеристики обеспечивает этот коэффициент как функцию времени, прошедшего с момента появления каждого входного значения.
• В физике, где есть линейная система с символом "принцип наложения ", появляется операция свертки. Например, в спектроскопии уширение линии из-за эффекта Доплера само по себе дает форму спектральной линии гауссова , а только столкновение уширение дает лоренцеву форма линии. Когда оба эффекта, форма линии представляет собой свертку гауссова и лоренциана, функция Фойгта.

В флуоресцентной спектроскопии с временным разрешением сигнал возбуждения можно рассматривать как цепочку дельта импульсов, измеренная флуоресценция представляет собой величину экспоненциальных затуханий от каждого дельта-импульса.

В вычислительной гидродинамике, моделирование вихрей (LES) Модель турбулентности использует операцию свертки для размера диапазона масштабов длины, необходимого для вычислений, тем самым мощая вычислительные затраты.

• В теории вероятностей, распределение вероятностей две ые случайные величины - это свертка их индивидуальных распределений.

В оценка плотности ядра распределение оценивается по точкам выборки путем свертки с ядром, например, изотропный гауссовский.

• В системах системы лучевой терапии большая часть современных кодов калорийности При вычислении использования.
• Сверточные нейронные сети применяют несколько ядер каскадной свертки с приложениями в машинном зрении и искусственном интеллекте. Хотя на самом деле это взаимные корреляции.
• В надежности индекса надежности может быть определен на основе теоремы свертки.

Определение показателя надежности для функций предельного состояния с ненормальным распределением может быть установлено в соответствии с совместная функция распределения. Фактически, совместная функция может быть получена с использованием теории свертки.

См. Также

• Обработка аналоговых сигналов
• Циркулянтная матрица
• Свертка для оптических характеристик широкого луча в рассеивающих средах
• Мощность свертки
• Свертка Дирихле
• Обобщенное усреднение сигнала
• Ян Микусински
• Список сверток вероятностных распределений
• Теория системы LTI # Импульсная характеристика и свертка
• Многомерная дискретная свертка
• Масштабированная корреляция
• Титчмарш теорема о свертке
• матрица Теплица (свертки можно рассматривать как матричную операцию Теплица, где каждая строка представляет собой сдвинутую копию ядра свертки)

Примечания

Ссылки

Дополнительная литература

• Брейсуэлл, Р. (1986), Преобразование Фурье и его приложения (2-е изд.), МакГроу - Хилл, ISBN 0-07-116043-4.
• Дамелин, С..; Миллер, В. (2011), Математика обработки сигналов, Cambridge University Press, ISBN 978-1107601048
• Diggle, PJ (1985), «Ядровый метод для сглаживания данных точечного процесса. ", Журнал Королевского статистического общества, серия C, 34 (2): 138–147, doi : 10.2307 / 2347366, JSTOR 2347366, S2CID 116746157
• Домингес-Торрес, Алехандро (2 ноября 2010 г.). «Происхождение и история свертки». 41 стр. http: //www.slideshare.net/Alexdfar/origin-adn-history-of-convolution. Крэнфилд, Бедфорд MK43 OAL, Великобритания. Проверено 13 марта 2013 г.
• Гасеми, С. Хуман; Новак, Анджей С.. (2017), «Индекс надежности для ненормальных распределений функций предельного состояния», Структурная инженерия и механика, 62 (3): 365–372, doi : 10.12989 / sem.2017.62.3.365
• Скриншпан, Аризона (2017), «Неравенство для множественных сверток вероятностной меры Дирихле», Успехи в прикладной математике, 82 (1): 102–119, doi : 10.1016 / j.aam.2016.08.001
• Хьюитт, Эдвин; Росс, Кеннет А. (1979), Абстрактный анализ. Том I, Grundle hren der Mathematischen Wissenschaften [Фундаментальные принципы математических наук], 115 (2-е изд.), Берлин, Нью-Йорк: Springer-Verlag, ISBN 978-3-540-09434-0, MR 0551496.
• Хьюитт, Эдвин; Росс, Кеннет А. (1970), Абстрактный гармонический анализ. Vol. II: Структура и анализ компактных групп. Анализ на локально компактных абелевых группах, Die Grundlehren der Mathematischen Wissenschaften, Band 152, Берлин, Нью-Йорк: Springer-Verlag, MR 0262773.
• Hörmander, L. (1983), Анализных частных дифференциальных операторы I, Grundl. Математика. Wissenschaft., 256, Springer, doi : 10.1007 / 978-3-642-96750-4, ISBN 3 -540-12104-8, MR 0717035.
• Kassel, Christian (1995), Quantum groups, Graduate Texts in Mathematics, 155, Berlin, New York: Springer-Verlag, doi : 10.1007 / 978-1-4612-0783-2, ISBN 978-0-387-94370 -1, MR 1321145.
• Knuth, Donald (1997), Seminumerical Algorithms (3-е изд.), Reading, Massachusetts: Addison-Wesley, ISBN 0-201 - 89684-2.
• ; (2011). Топологические информационные пространства. Чистая и прикладная математика (Второе изд.). Бока-Ратон, Флорида: CRC Press. ISBN 978-1584888666. OCLC 144216834.
• Рид, Майкл; Саймон, Барри (1975), Методы современной математической физики. II. Анализ Фурье, самосопряженность, Нью-Йорк-Лондон: Academic Press Harcourt Brace Jovanovich, Publishers, pp. Xv + 361, ISBN 0-12-585002-6, MR 0493420
• Рудин, Уолтер (1962), анализ Фурье по группам, Interscience Tracts in Pure and Applied Mathematics, 12, New York - London: Interscience Publishers, ISBN 0 - 471-52364-X, MR 0152834.
• Шефер, Гельмут Х. ; (1999). Топологические информационные пространства. GTM. 8(Второе изд.). Нью-Йорк, штат Нью-Йорк: Springer New York Выходные данные Springer. ISBN 978-1-4612-7155-0. OCLC 840278135.
• Стейн, Элиас ; Вайс, Гвидо (1971), Введение в анализ Фурье в евклидовых пространствах, Princeton University Press, ISBN 0-691-08078-X.
• Соболев В.И. (2001) [1994], Энциклопедия математики, EMS Press.
• Strichartz, R. (1994), A Guide to Distribution Theory and Fourier Transforms, CRC Press, ISBN 0-8493-8273-4.
• Титчмарш, E (1948), Введение в теорию интегралов Фурье (2-е изд.), Нью-Йорк, Нью-Йорк: Chelsea Pub. Co. (опубликовано в 1986 г.), ISBN 978-0-8284-0324-5.
• Трев, Франсуа (2006) [1967]. Топологические системы пространства, распределения и ядра. Минеола, Нью-Йорк: Dover Publications. ISBN 978-0-486-45352-1. OCLC 853623322.
• (1998), «О возможном плохом качестве гладкости при операции свертки», J. Math. Анальный. Appl., 227 (2): 335–358, doi : 10.1006 / jmaa.1998.6091
• von zur Gathen, J.; Герхард, Дж. (2003), Современная компьютерная алгебра, Cambridge University Press, ISBN 0-521-82646-2.

Внешние ссылки

Искать свертка в Викисловаре, бесплатном языке.

Викискладе есть носители, относящиеся к Свертка.

• Раннее использование: статья о Свертке содержит некоторую историческую информацию.
• Свертка, на Краткое руководство по анализу данных
• http://www.jhu.edu/~signals/convolve/index.html Java-апплет с визуальной сверткой
• http://www.jhu.edu/~signals/ diskteconv2 / index.html Java-апплет визуальной свертки для функций с дискретным временем
• https://lpsa.swarthmore.edu/Convolution/CI.html Демонстрация свертки и визуализация в javascript
• https: / /phiresky.github.io/convolution-demo/ Еще одна демонстрация свертки в javascript
• Лекции по обработке изображений: сборник из 18 лекций в формате pdf из Университета Вандербильта. Лекция 7 посвящена двумерной свертке., Алан Питерс
• * https://archive.org/details/Lectures_on_Image_Processing
• Свертка Операция с маским ядром Интерактивное руководство
• Свертка на MathWorld
• Процессор импульсных откликов Freeverb3 : процессор импульсных откликов с нулевой задержкой и открытым исходным кодом с плагинами VST
• Stanford University CS 178 интерактивная демонстрация Flash, как работает пространственная свертка.
• Видеолекция на тему свертки, прочитанная Салманом Кханом
• Пример свертки БПФ для распознавания образов (обработка изображений)