В обработке сигналов, гребенчатый фильтр представляет собой фильтр, реализованный путем добавления версии с задержкой сигнала самому себе, вызывая конструктивную и деструктивную помеху. АЧХ гребенчатого фильтра состоит из серии регулярно расположенных меток, что создает вид гребенки.
 Расширенный гребенчатый фильтр PAL-II (APCF-II, Motorola MC141627FT)
Расширенный гребенчатый фильтр PAL-II (APCF-II, Motorola MC141627FT) Гребенчатые фильтры используются во множестве приложений обработки сигналов. К ним относятся:
В акустике гребенчатая фильтрация может возникают нежелательными способами. Например, когда два громкоговорителя воспроизводят один и тот же сигнал на разных расстояниях от слушателя, на сигнал возникает эффект гребенчатой фильтрации. В любом замкнутом пространстве слушатели слышат смесь прямого и отраженного звука. Поскольку отраженный звук проходит более длинный путь, он представляет собой задержанную версию прямого звука, и создается гребенчатый фильтр, в котором они объединяются в слушателе.
гребенчатые фильтры существуют в двух разные формы, прямая связь и обратная связь ; имена относятся к направлению, в котором сигналы задерживаются перед добавлением на вход.
Гребенчатые фильтры могут быть реализованы в дискретном времени или непрерывном времени ; эта статья будет сосредоточена на реализациях с дискретным временем; Свойства гребенчатого фильтра непрерывного времени очень похожи.
 Структура гребенчатого фильтра с прямой связью
Структура гребенчатого фильтра с прямой связью Общая структура гребенчатого фильтра с прямой связью показана справа. Его можно описать следующим разностным уравнением :
![{\ displaystyle y [n] = x [n] + \ alpha x [nK]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/407d8d32def12f79789bde99eccb4d859fd98281)
где 

Мы определяем передаточную функцию как:

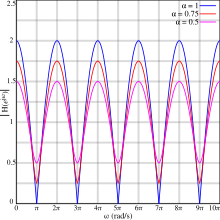 Амплитудно-частотная характеристика для различных положительных значений α и K = 1
Амплитудно-частотная характеристика для различных положительных значений α и K = 1  Прямая связь отклик амплитуды для различных отрицательных значений α и K = 1
Прямая связь отклик амплитуды для различных отрицательных значений α и K = 1 Чтобы получить частотную характеристику системы с дискретным временем, выраженную в z-области, мы делаем замену z = e. Следовательно, для нашего гребенчатого фильтра с прямой связью мы получаем:

Используя формулу Эйлера, мы находим, что частотная характеристика также определяется как
![{\ displaystyle H \ left (e ^ {j \ Omega} \ right) = {\ bigl [} 1+ \ alpha \ cos (\ Omega K) {\ bigr]} - j \ альфа \ sin (\ Omega K)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/076b5c3d97132991bd48c681c80650fe6c4c94a5)
Часто интерес представляет ответ величины, который игнорирует фазу. Это определяется как:

В случае гребенчатого фильтра с прямой связью это:

Обратите внимание, что член (1 + α) является постоянным, тогда как член 2α cos (ΩK) изменяется периодически. Следовательно, амплитудная характеристика гребенчатого фильтра является периодической.
Графики справа показывают реакцию величины для различных значений α, демонстрируя эту периодичность. Некоторые важные свойства:
 .
. , и наоборот.
, и наоборот.Гребенчатый фильтр с прямой связью является одним из простейших фильтров с конечной импульсной характеристикой. Его реакция - это просто начальный импульс со вторым импульсом после задержки.
Еще раз посмотрим на передаточную функцию в z-области гребенчатого фильтра с прямой связью:

мы видим, что числитель равен нулю всякий раз, когда z = −α. Это имеет K решений, равномерно распределенных по кругу в комплексной плоскости ; это нули передаточной функции. Знаменатель равен нулю при z = 0, что дает K полюсов при z = 0. Это приводит к графику полюс – ноль, подобному показанному ниже.
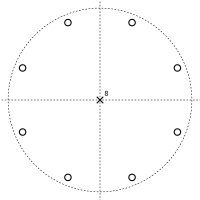 График «полюс – ноль» гребенчатого фильтра с прямой связью с K = 8 и α = 0,5 График «полюс – ноль» гребенчатого фильтра с прямой связью с K = 8 и α = 0,5 |  График «полюс – ноль» гребенчатого фильтра с прямой связью с K = 8 и α = −0,5 График «полюс – ноль» гребенчатого фильтра с прямой связью с K = 8 и α = −0,5 |
 гребенчатый фильтр обратной связи структура
гребенчатый фильтр обратной связи структура Аналогично, общая структура гребенчатого фильтра обратной связи показана справа. Его можно описать следующим разностным уравнением :
![{\ displaystyle y [n] = x [n] + \ alpha y [nK]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aab660dee16e819787a26d5de6162532f6da0da3)
Если мы изменим это уравнение так, чтобы все члены в 

Таким образом, передаточная функция имеет вид:

 Отклик величины обратной связи для различных положительных значений α и K = 2
Отклик величины обратной связи для различных положительных значений α и K = 2  Отклик величины обратной связи для различных отрицательных значений α и K = 2
Отклик величины обратной связи для различных отрицательных значений α и K = 2 Если мы сделаем замену z = e в выражение z-области для гребенчатого фильтра обратной связи, мы получаем:

ответ величины выглядит следующим образом:

Опять же, ответ периодический, как показывают графики справа. Гребенчатый фильтр обратной связи имеет некоторые общие свойства с формой прямого распространения:
 , и наоборот.
, и наоборот. .
.Однако есть и некоторые важные различия, потому что отклик величины имеет член в знаменателе :
Гребенчатый фильтр обратной связи представляет собой простой тип фильтра с бесконечной импульсной характеристикой. Если он стабилен, ответ просто состоит из повторяющейся серии импульсов, амплитуда которых уменьшается с течением времени.
Еще раз посмотрим на передаточную функцию в z-области гребенчатого фильтра обратной связи:

На этот раз числитель равен нулю при z = 0, что дает K нулей при z = 0. Знаменатель равен нулю, если z = α. Это имеет K решений, равномерно распределенных по кругу в комплексной плоскости ; это полюса передаточной функции. Это приводит к графику «полюс – ноль», как показано ниже.
 График «полюс – ноль» гребенчатого фильтра обратной связи с K = 8 и α = 0,5 График «полюс – ноль» гребенчатого фильтра обратной связи с K = 8 и α = 0,5 | 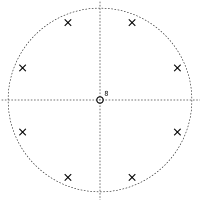 График «полюс – ноль» гребенчатого фильтра обратной связи с K = 8 и α = −0,5 График «полюс – ноль» гребенчатого фильтра обратной связи с K = 8 и α = −0,5 |
Гребенчатые фильтры также могут быть реализованы в непрерывном времени. Форма прямой связи может быть описана следующим уравнением:

где τ - задержка (измеряется в секундах). Он имеет следующую передаточную функцию:

Форма прямой связи состоит из бесконечного числа нулей, расположенных вдоль оси jω.
Форма обратной связи имеет уравнение:

и следующей передаточной функцией:

Форма обратной связи состоит из бесконечного числа полюсов, разнесенных по оси jω.
Реализации непрерывного времени разделяют все свойства соответствующих реализаций дискретного времени.