Теория приближений

редактировать

Теория приблизительного приближения к неточным математическим вычислениям

В математике, приближение Теория занимается тем, как функции могут быть наилучшим образом аппроксимированы более простыми функциями, а количественно характеризуют вызванные этим ошибки. Обратите внимание, что то, что подразумевается под лучшим и простым, будет зависеть от приложения.

Тесно связанной темой является приближение функций обобщенным рядом Фурье, то есть приближения, основанные на суммировании ряда членов, основанных на ортогональных многочленах.

Одна проблема Особый интерес представляет аппроксимация функции в математической библиотеке компьютер с использованием операций, которые могут выполняться на компьютере или калькуляторе (например, сложение и умножение), так что результат максимально приближен к фактической функции насколько возможно. Обычно это делается с помощью аппроксимаций полинома или рационального (отношение полиномов).

Цель состоит в том, чтобы сделать приближение как можно ближе к фактической функции, обычно с точностью, близкой к точности арифметики с плавающей запятой базового компьютера. Это достигается за счет использования полинома высокой степени и / или сужения области, в которой полином должен аппроксимировать функцию. Сужение области часто можно осуществить за счет использования различных формул сложения или масштабирования для аппроксимируемой функции. Современные математические библиотеки часто сокращают область до множества крошечных сегментов и используют полином низкой степени для каждого сегмента.

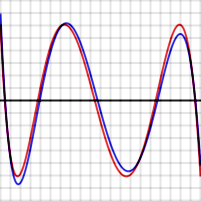Ошибка между оптимальным полиномом и log (x) (красный), и приближением Чебышева и log (x) (синий) на интервале [2, 4]. Вертикальные деления равны 10. Максимальная ошибка для оптимального полинома составляет 6,07 × 10.

Ошибка между оптимальным полиномом и exp (x) (красный), а также приближением Чебышева и exp (x) (синий) на интервале [−1, 1]. Вертикальное деление равно 10. Максимальная ошибка для оптимального полинома составляет 5,47 × 10.

Содержание

1 Оптимальные полиномы
2 Приближение Чебышева
3 Алгоритм Ремеза
4 Основные журналы
5 См. Также
6 Ссылки
7 Внешние ссылки

Оптимальные многочлены

После выбора области (обычно интервал) и степени многочлена выбирается сам многочлен таким образом, чтобы минимизировать наихудшая ошибка. То есть цель состоит в том, чтобы минимизировать максимальное значение $∣ P (x) - f (x) ∣ {\ displaystyle \ mid P (x) -f (x) \ mid}$ ${\ displaystyle \ mid P (x) -f (x) \ mid}$ , где P (x) - аппроксимирующий полином, f (x) - фактическая функция, а x изменяется в выбранном интервале. Для функций с хорошим поведением существует полином N-й степени, который приведет к кривой ошибки, которая колеблется взад и вперед между $+ ε {\ displaystyle + \ varepsilon}$ $+ \ varepsilon$ и $- ε {\ displaystyle - \ varepsilon}$ $- \ varepsilon$ всего N + 2 раз, что дает наихудшую ошибку $ε {\ displaystyle \ varepsilon}$ $\ varepsilon$ . Видно, что существует многочлен N-й степени, который может интерполировать N + 1 точку кривой. Такой многочлен всегда оптимален. Можно создать надуманные функции f (x), для которых такой многочлен не существует, но на практике это случается редко.

Например, графики, показанные справа, показывают ошибку аппроксимации log (x) и exp (x) для N = 4. Красные кривые для оптимального полинома имеют уровень, то есть они колеблются между $+ ε {\ displaystyle + \ varepsilon}$ $+ \ varepsilon$ и $- ε {\ displaystyle - \ varepsilon}$ $- \ varepsilon$ точно. Обратите внимание, что в каждом случае количество экстремумов равно N + 2, то есть 6. Два экстремума находятся в конечных точках интервала, на левом и правом краях графов.

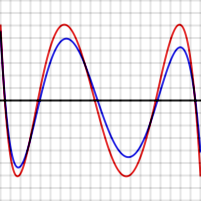Ошибка P (x) - f (x) для многочлена уровня (красный) и для предполагаемого лучшего многочлена (синий)

Чтобы доказать, что это в целом верно, предположим, что P - многочлен степени N, обладающий свойством описывается, то есть порождает функцию ошибок, которая имеет N + 2 экстремума, чередующихся знаков и равных величин. Красный график справа показывает, как эта функция ошибок может выглядеть для N = 4. Предположим, Q (x) (чья функция ошибок показана синим справа) - это еще один многочлен N-степени, который является лучшим приближением к f, чем P. В частности, Q ближе к f, чем P для каждого значения x i, где встречается крайнее значение P − f, поэтому

| Q (x i) - f (x i) | < | P ( x i) − f ( x i) |. {\displaystyle |Q(x_{i})-f(x_{i})|<|P(x_{i})-f(x_{i})|.}

| Q (x_ {i}) -f (x_ {i}) | <| P (x_ {i}) - f (x_ {i}) |.

Когда максимум P − f встречается в x i, тогда

Q (x i) - f (x i) ≤ | Q (x i) - f (x i) | < | P ( x i) − f ( x i) | = P ( x i) − f ( x i), {\displaystyle Q(x_{i})-f(x_{i})\leq |Q(x_{i})-f(x_{i})|<|P(x_{i})-f(x_{i})|=P(x_{i})-f(x_{i}),}

Q (x_ {i}) - f (x_ {i}) \ leq | Q (x_ {i}) - f (x_ {i}) | <| P (x_ {i }) - f (x_ {i}) | = P (x_ {i}) - f (x_ {i}),

И когда минимум P − f встречается в x i, тогда

f (x i) - Q (x i) ≤ | Q (x i) - f (x i) | < | P ( x i) − f ( x i) | = f ( x i) − P ( x i). {\displaystyle f(x_{i})-Q(x_{i})\leq |Q(x_{i})-f(x_{i})|<|P(x_{i})-f(x_{i})|=f(x_{i})-P(x_{i}).}

f (x_ {i}) - Q (x_ {i}) \ leq | Q (x_ {i}) - f (x_ {i}) | <| P (x_ {i}) - f (x_ {i }) | = f (x_ {i}) - P (x_ {i}).

Итак, как видно на графике, [P (x) - f (x)] - [Q (x) - f (x)] должны чередоваться по знаку для N + 2 значений x я. Но [P (x) - f (x)] - [Q (x) - f (x)] сводится к P (x) - Q (x), который является многочленом степени N. Эта функция меняет знак не менее N +1 раз, поэтому по теореме о промежуточном значении он имеет N + 1 нулей, что невозможно для многочлена степени N.

приближение Чебышева

Можно получить многочлены, очень близкие к оптимальному, расширяя данную функцию в терминах многочленов Чебышева и затем обрезая разложение в желаемой степени. Это похоже на анализ Фурье функции, использующий полиномы Чебышева вместо обычных тригонометрических функций.

Если вычислить коэффициенты в разложении Чебышева для функции:

f (x) ∼ ∑ i = 0 ∞ ci T i (x) {\ displaystyle f (x) \ sim \ sum _ {i = 0} ^ {\ infty} c_ {i} T_ {i} (x)}

f (x) \ sim \ sum _ {{i = 0}} ^ {\ infty} c_ {i} T_ {i} (x)

, а затем обрезает ряд после $TN {\ displaystyle T_ {N}}$ $T_ {N}$ , можно получить полином N-й степени, приближающий f (x).

Причина, по которой этот многочлен почти оптимален, заключается в том, что для функций с быстро сходящимися степенными рядами, если ряд обрезается после некоторого члена, общая ошибка, возникающая из-за обрезания, близка к первому члену после обрезания. То есть первый член после отсечения доминирует над всеми последующими членами. То же самое верно и в случае разложения в терминах полиномов противодействия. Если раскрытие Чебышева прерывается после $TN {\ displaystyle T_ {N}}$ $T_ {N}$ , ошибка примет форму, близкую к кратной $TN + 1 {\ displaystyle T_ {N +1}}$ $T_{{N+1}}$ . Многочлены Чебышева обладают тем свойством, что они являются уровнями - они колеблются между +1 и -1 в интервале [-1, 1]. $T N + 1 {\ displaystyle T_ {N + 1}}$ $T_{{N+1}}$ имеет N + 2 экстремумов уровня. Это означает, что ошибка между f (x) и его разложением Чебышева до $TN {\ displaystyle T_ {N}}$ $T_ {N}$ близка к функции уровня с N + 2 экстремумами, поэтому она близка к к оптимальному многочлену N-й степени.

На графиках выше обратите внимание, что синяя функция ошибки иногда лучше (внутри) красной функции, но иногда хуже, что означает, что это не совсем оптимальный полином. Расхождение менее серьезно для функции exp, которая имеет чрезвычайно быстро сходящийся степенной ряд, чем для функции log.

Чебышёвское приближение является основой для квадратур Кленшоу – Кертиса, метода численного интегрирования.

Алгоритм Ремеза

Алгоритм Ремеза (иногда пишется Ремес) используется для получения оптимального полинома P (x), приближающего заданную функцию f (x) по заданной интервал. Это итерационный алгоритм, который сходится к полиному, который имеет функцию ошибок с N + 2 экстремумами уровня. По теореме выше этот многочлен оптимален.

Алгоритм Ремеза использует тот факт, что можно построить многочлен N-й степени, который приводит к уровням и переменным значениям ошибок, учитывая N + 2 контрольных точки.

Дано N + 2 контрольных точки $x 1 {\ displaystyle x_ {1}}$ $x_ {1}$ , $x 2 {\ displaystyle x_ {2}}$ $x_ {2}$ ,... $x N + 2 {\ displaystyle x_ {N + 2}}$ $x _ {{N + 2}}$ (где $x 1 {\ displaystyle x_ {1}}$ $x_ {1}$ и $x N + 2 {\ displaystyle x_ {N + 2}}$ $x _ {{N + 2}}$ предположительно являются конечными точками интервала аппроксимации), эти уравнения необходимо решить:

P (x 1) - f (x 1) = + ε P (x 2) - f (x 2) = - ε P (x 3) - f (x 3) = + ε ⋮ P (x N + 2) - f (x N + 2) = ± ε. {\ Displaystyle {\ begin {align} P (x_ {1}) - f (x_ {1}) = + \ varepsilon \\ P (x_ {2}) - f (x_ {2}) = - \ варепсилон \\ P (x_ {3}) - f (x_ {3}) = + \ varepsilon \\ \ \ \ vdots \\ P (x_ {N + 2}) - f (x_ {N + 2}) = \ pm \ varepsilon. \ end {align}}}

{\ displaystyle {\ begin {выровнено} P (x_ {1}) - f (x_ {1}) = + \ varepsilon \\ P (x_ {2}) - f (x_ {2}) = - \ varepsilon \\ P (x_ {3}) - f (x_ {3}) = + \ varepsilon \\ \ \ \ vdots \\ P (x_ {N + 2}) - f (x_ {N + 2}) = \ pm \ varepsilon. \ end {align}}}

Правые части меняются знаками.

То есть

P 0 + P 1 x 1 + P 2 x 1 2 + P 3 x 1 3 + ⋯ + PN x 1 N - f (x 1) = + ε P 0 + П 1 Икс 2 + п 2 Икс 2 2 + п 3 Икс 2 3 + ⋯ + PN x 2 N - f (x 2) = - ε ⋮ {\ displaystyle {\ begin {align} P_ {0} + P_ {1 } x_ {1} + P_ {2} x_ {1} ^ {2} + P_ {3} x_ {1} ^ {3} + \ dots + P_ {N} x_ {1} ^ {N} -f ( x_ {1}) = + \ varepsilon \\ P_ {0} + P_ {1} x_ {2} + P_ {2} x_ {2} ^ {2} + P_ {3} x_ {2} ^ {3 } + \ dots + P_ {N} x_ {2} ^ {N} -f (x_ {2}) = - \ varepsilon \\ \ \ \ vdots \ end {align}}}

{\ displaystyle {\ begin {align} P_ {0} + P_ {1} x_ {1} + P_ {2} x_ {1} ^ {2} + P_ {3} x_ {1} ^ {3} + \ dots + P_ {N} x_ {1} ^ {N} -f (x_ {1}) = + \ varepsilon \\ P_ {0} + P_ {1} x_ {2} + P_ { 2} x_ {2} ^ {2} + P_ {3} x_ {2} ^ {3} + \ dots + P_ {N} x_ {2} ^ {N} -f (x_ {2}) = - \ varepsilon \\ \ \ \ vdots \ end {align}}}

Поскольку $x 1 {\ displaystyle x_ {1}}$ $x_ {1}$ ,..., $x N + 2 {\ displaystyle x_ {N + 2}}$ $x _ {{N + 2}}$ были заданы, все их мощности известны, и $f (x 1) {\ displaystyle f (x_ {1})}$ $f(x_{1})$ ,..., $f (x N + 2) {\ displaystyle f (x_ {N + 2})}$ $f (x _ {{N + 2}})$ также известны. Это означает, что приведенные выше уравнения представляют собой всего лишь N + 2 линейных уравнения от N + 2 переменных $P 0 {\ displaystyle P_ {0}}$ $P_ {0}$ , $P 1 {\ displaystyle P_ {1}}$ $P_{1}$ ,..., $PN {\ displaystyle P_ {N}}$ $P_ {N}$ и $ε {\ displaystyle \ varepsilon}$ $\ varepsilon$ . Учитывая контрольные точки $x 1 {\ displaystyle x_ {1}}$ $x_ {1}$ ,..., $x N + 2 {\ displaystyle x_ {N + 2}}$ $x _ {{N + 2}}$ , можно решить эту систему, чтобы получить многочлен P и число $ε {\ displaystyle \ varepsilon}$ $\ varepsilon$ .

На приведенном ниже графике показан пример этого, создавая полином четвертой степени, аппроксимирующий $ex {\ displaystyle e ^ {x}}$ $e^{x}$ больше [-1, 1]. Контрольные точки были установлены на -1, -0,7, -0,1, +0,4, +0,9 и 1. Эти значения показаны зеленым. Результирующее значение $ε {\ displaystyle \ varepsilon}$ $\ varepsilon$ составляет 4,43 × 10

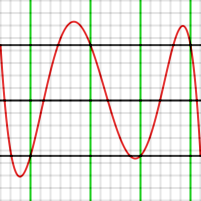Ошибка полинома, полученного на первом шаге алгоритма Ремеза, аппроксимирующего e в интервале [-1, 1 ]. Вертикальное деление равно 10.

Обратите внимание, что график ошибок действительно принимает значения $± ε {\ displaystyle \ pm \ varepsilon}$ $\ pm \ varepsilon$ в шести контрольных точках, включая конечные точки, но что эти точки не являются экстремальными. Если бы четыре внутренние контрольные точки были экстремумами (то есть, функция P (x) f (x) имела там максимум или минимум), полином был бы оптимальным.

Второй шаг алгоритма Ремеза состоит в перемещении контрольных точек в приблизительные места, где функция ошибок имела свои фактические локальные максимумы или минимумы. Например, глядя на график, можно сказать, что точка -0,1 должна была находиться примерно в -0,28. Способ сделать это в алгоритме - использовать один цикл метода Ньютона. Поскольку известна первая и вторая производные от P (x) - f (x), можно приблизительно вычислить, на сколько нужно переместить контрольную точку, чтобы производная была равна нулю.

Вычислить производные полинома несложно. Также необходимо уметь вычислять первую и вторую производные от f (x). Алгоритм Ремеза требует способности вычислять $f (x) {\ displaystyle f (x) \,}$ $f(x)\,$ , $f ′ (x) {\ displaystyle f '(x) \,}$ $f'(x)\,$ , и $f ″ (x) {\ displaystyle f '' (x) \,}$ $f''(x)\,$ с очень высокой точностью. Весь алгоритм должен выполняться с более высокой точностью, чем желаемая точность результата.

После перемещения контрольных точек часть линейного уравнения повторяется, получая новый многочлен, и снова используется метод Ньютона для повторного перемещения контрольных точек. Эта последовательность продолжается до тех пор, пока результат не достигнет желаемой точности. Алгоритм сходится очень быстро. Сходимость квадратичная для корректных функций - если контрольные точки находятся в пределах $10–15 {\ displaystyle 10 ^ {- 15}}$ $10^{-15}$ от правильного результата, они будут примерно в пределах $10–30 {\ displaystyle 10 ^ {- 30}}$ $10^{{-30}}$ правильного результата после следующего раунда.

Алгоритм Ремеза обычно запускается с выбора экстремумов полинома Чебышева $TN + 1 {\ displaystyle T_ {N + 1}}$ $T_{{N+1}}$ в качестве начальных точек, поскольку окончательная ошибка функция будет похожа на этот многочлен.

Основные журналы

См. Также

Литература

N. И. Ачиэзер (Ахиезер), Теория аппроксимации, Перевод Чарльза Дж. Хаймана Фредерика Унгара Паблишинг Ко., Нью-Йорк, 1956 x + 307 с. Тиман Ф. Теория приближения функций действительной переменной, 1963 ISBN 0-486-67830-X
C. Приближения Гастингса младшего для цифровых компьютеров. Princeton University Press, 1955.
Дж. Ф. Харт, Э. У. Чейни, К. Л. Лоусон, Х. Дж. Мэли, К. К. Мештеньи, Дж. Р. Райс, Х. К. Тэчер-младший, К. Витцгалл, Компьютерные приближения. Wiley, 1968, Lib. Конг. 67-23326.
Л. Фокс и И. Б. Паркер. «Многочлены Чебышева в численном анализе». Oxford University Press, Лондон, 1968.
Press, WH ; Теукольский С.А. ; Феттерлинг, штат Вашингтон; Фланнери, Б.П. (2007), «Раздел 5.8. Приближение Чебышева», Численные рецепты: Искусство научных вычислений (3-е изд.), Нью-Йорк: Cambridge University Press, ISBN 978-0-521-88068-8
W. Дж. Коди-младший, У. Уэйт, Руководство по программному обеспечению элементарных функций. Прентис-Холл, 1980, ISBN 0-13-822064-6.
E. Ремес [Ремез], "Sur le Calculated Effectif des Polynomes d'approximation de Tschebyscheff". 1934 C. R. Acad. Sci., Paris, 199, 337-340.
K.-G. Стеффенс, "История теории приближения: от Эйлера до Бернштейна", Биркхаузер, Бостон, 2006 ISBN 0-8176-4353-2.
T. Erdélyi, "Расширения теоремы Блоха-Полиа о числе различных действительных нулей многочленов", Journal de théorie des nombres de Bordeaux 20 (2008), 281–287.
Т. Эрдейи, "Неравенство Ремеза для линейных комбинаций сдвинутых гауссианов", Матем. Proc. Camb. Фил. Soc. 146 (2009), 523–530.
Л. Н. Трефетен, «Теория приближений и практика приближений», SIAM 2013. [1]

Внешние ссылки