Игра «Сороконожка»

редактировать

В теории игр, игра «Сороконожка», впервые представленная Робертом Розенталь в 1981 году - это расширенная игра, в которой два игрока по очереди выбирают либо взять немного большую долю увеличивающегося банка, либо передать банк другому игроку. Выплаты устроены так, что если кто-то передает банк своему противнику, а противник забирает банк в следующем раунде, он получает немного меньше, чем если бы он взял банк в этом раунде. Хотя традиционная игра с многоножкой имела ограничение в 100 раундов (отсюда и название), любая игра с такой структурой, но с другим количеством раундов, называется игрой в сороконожку.

Уникальное совершенное равновесие вспомогательной игры (и каждое равновесие Нэша ) этих игр указывает, что первый игрок забирает банк в первом раунде игры; однако в эмпирических тестах относительно мало игроков делают это, и в результате получают более высокий выигрыш, чем выигрыш, предсказанный анализом равновесия. Эти результаты используются, чтобы показать, что совершенное равновесие в подиграх и равновесие по Нэшу не могут предсказать игру человека в некоторых обстоятельствах. Игра «Сороконожка» обычно используется во вводных курсах и учебниках по теории игр, чтобы выделить концепцию обратной индукции и итеративного исключения доминирующих стратегий, которые показывают стандартный способ решения игра.

Содержание

1 Воспроизведение
- 1.1 Формальное определение
2 Анализ равновесия и обратная индукция
3 Эмпирические результаты
- 3.1 Пояснения
4 Значимость
5 См. Также
6 Ссылки
7 Внешние ссылки

Играть

В одну из возможных версий игры в сороконожку можно играть следующим образом:

Рассмотрим двух игроков: Алиса и Боб. Алиса ходит первой. В начале игры перед Алисой две стопки монет: одна стопка содержит 4 монеты, а другая - 1 монету. У каждого игрока есть два доступных хода: либо «взять» большую стопку монет и передать меньшую стопку другому игроку, либо «протолкнуть» обе стопки через стол другому игроку. Каждый раз, когда стопки монет проходят по столу, количество монет в каждой стопке удваивается. Например, предположим, что Алиса решает «раздвинуть» стопки на своем первом ходу, передав стопки из 1 и 4 монет Бобу, удваивая их до 2 и 8. Теперь Боб может использовать свой первый ход, чтобы «взять» стопку из 8 монет и отдайте 2 монеты Алисе, или он может «толкнуть» две стопки обратно через стол снова Алисе, снова увеличивая размер стопки до 4 и 16 монет. Игра продолжается в течение фиксированного количества раундов или до тех пор, пока игрок не решит закончить игру, положив в карман кучу монет.

Добавление монет считается внешним эффектом, поскольку не вносится любым игроком.

Формальное определение

Игра про многоножку может быть записана как $G (N, m 0, m 1) {\ displaystyle {\ mathcal {G}} (N, ~ m_ { 0}, ~ m_ {1})}$ ${\ displaystyle {\ mathcal {G}} (N, ~ m_ {0}, ~ m_ {1})}$ где $N, m 0, m 1 ∈ N {\ displaystyle N, m_ {0}, m_ {1} \ in \ mathbb {N} }$ ${\ displaystyle N, m_ {0}, m_ {1} \ in \ mathbb {N}}$ и $m 0>m 1 {\ displaystyle m_ {0}>m_ {1}}$ $m_{0}>m_ {1}$ . Игроки $I {\ displaystyle I}$ $I$ и $II {\ displaystyle II}$ ${\ displaystyle II}$ альтернативно, начиная с игрока $I {\ displaystyle I}$ $I$ , и может на каждом ходу делать ход от ${take, push} {\ displaystyle \ {\ mathrm {take}, \ mathrm {push} \}}$ ${\ displaystyle \ {\ mathrm {take}, \ mathrm {push} \}}$ с максимальным количеством $N {\ displaystyle N}$ $N$ раундов. Игра завершается, когда $take {\ displaystyle \ mathrm {take}}$ ${\ displaystyle \ mathrm {take} }$ разыгрывается впервые, в противном случае при $N {\ displaystyle N}$ $N$ перемещается, если $take {\ displaystyle \ mathrm {take}}$ ${\ displaystyle \ mathrm {take} }$ никогда не воспроизводится.

Предположим, игра заканчивается на раунде $t ∈ {0,…, N - 1} {\ displaystyle t \ in \ {0, \ ldots, N-1 \}}$ ${\ displaystyle t \ in \ {0, \ ldots, N-1 \}}$ с игроком $p ∈ {I, II} {\ displaystyle p \ in \ {I, II \}}$ ${\ displaystyle p \ in \ {I, II \}}$ , делающим последний ход. Тогда результат игры определяется следующим образом:

Если $p {\ displaystyle p}$ $p$ играл $take {\ displaystyle \ mathrm {take}}$ ${\ displaystyle \ mathrm {take} }$ , тогда $p {\ displaystyle p}$ $p$ получает $2 tm 0 {\ displaystyle 2 ^ {t} m_ {0}}$ ${\ displaystyle 2 ^ {t} m_ {0}}$ монет и $p ∗ {\ displaystyle p ^ {\ ast}}$ ${\ displaystyle p ^ {\ ast}}$ получает $2 tm 1 {\ displaystyle 2 ^ {t} m_ {1}}$ ${\ displaystyle 2 ^ {t} m_ {1}}$ .
Если $p {\ displaystyle p}$ $p$ сыграл $push {\ displaystyle \ mathrm {push}}$ ${\ displaystyle \ mathrm {push}}$ , затем $p {\ displaystyle p}$ $p$ получает $2 t + 1 m 1 {\ displaystyle 2 ^ {t + 1} m_ {1}}$ ${ \ displaystyle 2 ^ {t + 1} m_ {1}}$ монет и $p ∗ {\ displaystyle p ^ {\ ast}}$ ${\ displaystyle p ^ {\ ast}}$ прибыль $2 t + 1 м 0 {\ displaystyle 2 ^ {t + 1} m_ {0}}$ ${\ displaystyle 2 ^ {t + 1} m_ {0}}$ .

Здесь $p ∗ ∈ {I, II} {\ displaystyle p ^ {\ ast} \ in \ { I, II \}}$ ${\ displaystyle p ^ {\ ast} \ in \ {I, II \}}$ обозначает другого игрока.

Анализ равновесия и обратная индукция

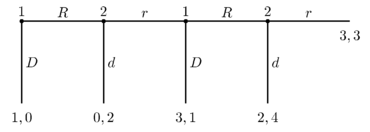Расширенная форма представление четырехэтапной игры с сороконожкой, которая заканчивается после четырех раундов разделением денег. Перемещение монет по столу представлено перемещением на R (переход через строку решетки, иногда также представленную как A для поперек), а размещение монет в карманах - это перемещение D (по решетке). Цифры 1 и 2 в верхней части диаграммы показывают чередование лиц, принимающих решения между двумя игроками, обозначенными здесь как 1 и 2, а числа внизу каждой ветви показывают выигрыш для игроков 1 и 2.

Стандартные теоретические инструменты игры предсказывают, что первый игрок откажется от игры в первом раунде, забрав кучу монет себе. В игре «сороконожка» чистая стратегия состоит из набора действий (по одному на каждую точку выбора в игре, даже если некоторые из этих точек выбора могут никогда не быть достигнуты) и смешанной стратегии - это распределение вероятностей по возможным чистым стратегиям. Существует несколько чистых стратегий равновесий по Нэшу игры о сороконожках и бесконечно много смешанных стратегий равновесий по Нэшу. Однако существует только одна подигра совершенное равновесие (популярное уточнение концепции равновесия по Нэшу).

В уникальной подигре идеальное равновесие, каждый игрок выбирает отступление при каждой возможности. Это, конечно, означает дезертирство на первом этапе. В равновесии Нэша, однако, действия, которые будут предприняты после первоначальных возможностей выбора (даже если они никогда не будут реализованы, так как первый игрок немедленно откажется), могут быть кооперативными.

Отклонение первого игрока - это уникальное идеальное равновесие в подигре, которое требуется для любого равновесия по Нэшу, оно может быть установлено с помощью обратной индукции. Предположим, два игрока дошли до финального раунда игры; второй игрок преуспеет, если дезертирует и заберет чуть большую долю банка. Поскольку мы предполагаем, что второй игрок откажется от участия, первый игрок добьется большего успеха, отказавшись от второго до последнего раунда, получив немного более высокий выигрыш, чем он получил бы, позволив второму игроку дезертировать в последнем раунде. Но зная это, второй игрок должен дезертировать в третьем-последнем раунде, получая немного более высокий выигрыш, чем он получил бы, позволив первому игроку дезертировать во втором-последнем раунде. Это рассуждение продолжается в обратном направлении по дереву игры до тех пор, пока не придет к выводу, что наилучшим действием является отказ первого игрока в первом раунде. То же самое можно применить к любому узлу в дереве игры.

Для игры, которая заканчивается после четырех раундов, это рассуждение происходит следующим образом. Если бы мы добрались до последнего раунда игры, игрок 2 преуспел бы, выбрав d вместо r, получив 4 монеты вместо 3. Однако, учитывая, что 2 выберет d, 1 должен выбрать D во предпоследнем раунде., получив 3 вместо 2. Учитывая, что 1 выберет D во втором и последнем раунде, 2 должен выбрать d в третьем и последнем раунде, получив 2 вместо 1. Но с учетом этого Игрок 1 должен выбрать D в первом раунде., получая 1 вместо 0.

Существует большое количество равновесий по Нэшу в игре с сороконожкой, но в каждой из них первый игрок не проходит в первом раунде, а второй игрок не выполняет в следующем раунде достаточно часто, чтобы первый игрок отказался от паса. Пребывание в равновесии по Нэшу не требует, чтобы стратегии были рациональными в каждой точке игры, как в идеальном равновесии во вспомогательной игре. Это означает, что стратегии, кооперативные в никогда не достигнутых более поздних раундах игры, все еще могут находиться в равновесии по Нэшу. В приведенном выше примере одно равновесие по Нэшу заключается в том, что оба игрока дезертируют в каждом раунде (даже в более поздних раундах, которые никогда не достигаются). Другое равновесие по Нэшу состоит в том, что игрок 1 дезертирует в первом раунде, но проходит в третьем раунде, а игрок 2 дезертирует при любой возможности.

Эмпирические результаты

Некоторые исследования продемонстрировали, что равновесие по Нэшу (а также совершенное равновесие в подиграх) наблюдается редко. Вместо этого субъекты регулярно демонстрируют частичное сотрудничество, играя «R» (или «r») в течение нескольких ходов, прежде чем в конечном итоге выбрать «D» (или «d»). Также редко субъекты сотрудничают на протяжении всей игры. Примеры см. В McKelvey and Palfrey (1992) и Nagel and Tang (1998). Как и во многих других теоретико-игровых экспериментах, ученые исследовали эффект увеличения ставок. Как и в случае с другими играми, например, ультиматумом, по мере увеличения ставок игра приближается (но не достигает) равновесной игры по Нэшу.

Пояснения

Поскольку эмпирические исследования дали результаты, несовместимые с традиционным анализом равновесия, было предложено несколько объяснений этого поведения. Розенталь (1981) предположил, что если у кого-то есть основания полагать, что его оппонент отклонится от поведения Нэша, то может быть выгодно не отступать в первом раунде.

Одна из причин предполагать, что люди могут отклоняться от равновесного поведения, заключается в том, что некоторые из них альтруистичны. Основная идея заключается в том, что если вы играете против альтруиста, этот человек всегда будет сотрудничать, и, следовательно, чтобы максимизировать выигрыш, вы должны дезертировать в последнем раунде, а не в первом. Если достаточное количество людей являются альтруистами, принесение в жертву побега в первом раунде стоит того, чтобы определить, является ли ваш противник альтруистом. Нагель и Танг (1998) предлагают это объяснение.

Другая возможность связана с ошибкой. Если существует значительная вероятность ошибки в действии, возможно, из-за того, что ваш оппонент не рассуждал полностью с помощью обратной индукции, может быть выгодно (и рационально) сотрудничать в начальных раундах.

Тем не менее, Parco, Rapoport и Stein (2002) показали, что уровень финансовых стимулов может иметь сильное влияние на результат в игре трех игроков: чем больше стимулы для отклонения, тем больше склонность к обучение поведению в повторяющейся экспериментальной схеме одиночной игры для продвижения к равновесию Нэша.

Паласиос-Уэрта и Волидж (2009) обнаружили, что опытные шахматисты играют иначе, чем студенты колледжа. При повышении Эло вероятность продолжения игры снижается; все гроссмейстеры в эксперименте остановились при первой же возможности. Они пришли к выводу, что шахматисты знакомы с аргументацией обратной индукции и поэтому им нужно меньше учиться, чтобы достичь равновесия. Однако, пытаясь воспроизвести эти результаты, Левитт, Лист и Садофф (2010) находят сильно противоречивые результаты: ноль из шестнадцати гроссмейстеров останавливает игру на первом узле.

Значение

Как и Дилемма заключенного, эта игра представляет собой конфликт между личными интересами и взаимной выгодой. Если бы это можно было применить, оба игрока предпочли бы, чтобы они оба сотрудничали на протяжении всей игры. Однако личный интерес игрока или недоверие игроков могут помешать и создать ситуацию, в которой у обоих будет хуже, чем если бы они сотрудничали вслепую. Хотя «Дилемма заключенного» привлекла значительное внимание из-за этого факта, «Игра многоножки» получила относительно меньше внимания.

Кроме того, Бинмор (2005) утверждал, что некоторые реальные ситуации могут быть описаны игрой «Сороконожка». Один из примеров, который он приводит, - это обмен товарами между сторонами, которые не доверяют друг другу. Другой пример, который Бинмор (2005) сравнивает с игрой «Сороконожка», - это брачное поведение морского окуня-гермафродита, который по очереди обменивает яйца для оплодотворения. В этих случаях мы находим сотрудничество в изобилии.

Поскольку вознаграждение за некоторое количество сотрудничества в игре Centipede намного больше, чем немедленное отступничество, «рациональные» решения, предлагаемые обратной индукцией, могут показаться парадоксальными. Это, в сочетании с тем фактом, что экспериментальные субъекты регулярно сотрудничают в игре «Сороконожка», вызвало дискуссию о полезности идеализаций, используемых в решениях обратной индукции, см. Aumann (1995, 1996) и Binmore (1996).

См. Также

Ссылки

Внешние ссылки

Статья EconPort об игре «Сороконожка»
Рациональность и теория игр - Колонка AMS об игре «Сороконожка»
Онлайн-эксперимент в VeconLab
Играйте в игру «Сороконожка» в браузере на gametheorygame.nl