Категория отношений

В математике, категория Rel имеет класс устанавливает как объекты и бинарные отношения как морфизмы.

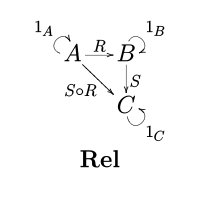
морфизм (или стрелка) R: A → B в этой категории - это отношение между множествами A и B, поэтому R ⊆ A × B.

композиция двух отношений R: A → B и S: B → C задается формулой

(a, c) ∈ S o R ⇔ для некоторых b ∈ B, (a, b) ∈ R и (b, c) ∈ S.

Rel также называлась «категорией соответствий множеств».

Свойства

Категория Rel имеет категорию устанавливает Установить как (широкую) подкатегорию, где стрелка f: X → Y в Set соответствует отношению F ⊆ X × Y, определенному как (x, y) ∈ F ⇔ f (x) = y.

Морфизм в Rel - это отношение, а соответствующий морфизм в противоположной категории к Rel имеет стрелки, перевернутые, поэтому это обратное отношение. Таким образом, Rel содержит свою противоположность и является самодвойственным.

. инволюция, представленная принятием обратного отношения, предоставляет кинжал для создания Отн a категория кинжала.

Категория имеет два функтора внутри себя, заданных гом-функтором : A бинарное отношение R ⊆ A × B и его транспонирование R ⊆ B × A может быть составлено либо как RR, либо как R R. Первая композиция приводит к однородному отношению на A, а вторая - к B. Поскольку изображения этих однородных функторы находятся в самом Rel, в этом случае hom - это внутренний функтор hom. Со своим внутренним функтором hom, Rel является закрытой категорией, и, кроме того, dagger compact category.

Категория Rel может быть получена из category Задайте как категорию Клейсли для монады, функтор которой соответствует набору степеней, интерпретируемой как ковариантный функтор.

Возможно, на первый взгляд немного удивителен тот факт, что product в Rel задается несвязным объединением (а не декартово произведение, как в наборе ), а также сопродукт.

отн является моноидально замкнутым, причем оба моноидального произведения A ⊗ B и внутренний hom A ⇒ B, заданный декартовым произведением множеств.

Категория Rel была прототипом алгебраической структуры, названной аллегорией Питером Дж. Фрейдом и Андре Щедровым в 1990 году. Начиная с регулярная категория и функтор F: A → B, они отмечают свойства индуцированного функтора Rel (A, B) → Rel (FA, FB). Например, он сохраняет композицию, преобразование и пересечение. Такие свойства затем используются для создания аксиом для аллегории.

Отношения как объекты

Дэвид Райдхард и Род Берстолл считают, что Rel имеет объекты, являющиеся однородными отношениями. Например, A - это множество, а R ⊆ A × A - бинарное отношение на A. Морфизмы этой категории - это функции между множествами, которые сохраняют отношение: скажем, S ⊆ B × B - второе отношение и f: A → B - функция такая, что $x\; R\; y\; ⟹\; f\; (x)\; S\; f\; (y),\; \{\backslash \; displaystyle\; xRy\; \backslash \; подразумевает\; f\; (x)\; Sf\; (y),\}$тогда f - морфизм.

Ту же идею выдвигают Адамек, Херрлих и Стрекер, где они обозначают объекты (A, R) и (B, S), набор и отношение.

Ссылки

• Фрэнсис Борсё (1994). Справочник по категориальной алгебре: Том 2, Категории и структуры. Издательство Кембриджского университета. п. 115. ISBN 978-0-521-44179-7.