Рассеяние носителей

редактировать

Типы дефектов включают атомные вакансии, адатомы, ступеньки и изгибы, которые чаще всего возникают на поверхностях из-за конечный размер материала, вызывающий нарушение сплошности кристалла. Общим для всех типов дефектов, будь то поверхностные или объемные дефекты, является то, что они создают оборванные связи, которые имеют определенные уровни энергии электронов, отличные от уровней основной энергии. Эта разница возникает из-за того, что эти состояния не могут быть описаны с помощью периодических блоховских волн из-за изменения потенциальной энергии электронов, вызванного отсутствием ионных остовов непосредственно за пределами поверхности. Следовательно, это локализованные состояния, которые требуют отдельных решений уравнения Шредингера, чтобы можно было правильно описать энергии электронов. Нарушение периодичности приводит к уменьшению проводимости из-за рассеяния на дефектах .

Содержание

1 Уровни энергии электронных полупроводниковых связей
2 Рассеяние на дефектах
3 Экспериментальные измерения
4 Пассивация
5 рассеяние фононов
6 акустических фононов
7 оптических фононов
8 примечаний

электронные уровни энергии полупроводниковых болтающихся связей

Рисунок 1: Энергетическая диаграмма Харрисона энергий электронов на разных этапах формирования Кристалл Si. Вертикальная ось - энергия. 3s- и 3p-орбитали гибридизуются на одном атоме Si, что энергетически невыгодно, потому что 2 3s-электроны получают больше энергии, чем теряют 2 3p-электроны. Благоприятное образование димера формирует связывающие (b) и антисвязывающие (b *) состояния, в конечном итоге приводя к чистой потере энергии, и последующее добавление атомов создает кристаллообразующие зоны проводимости (CB) и валентные зоны (VB). Состояния оборванных связей (db) эквивалентны отсутствию sp-связи.

Более простой и качественный способ определения уровней энергии оборванных связей - с помощью диаграмм Харрисона. Металлы имеют ненаправленное соединение и небольшую длину Дебая, что из-за их заряженной природы делает оборванные связи несущественными, если даже можно считать, что они существуют. Полупроводники - это диэлектрики, поэтому электроны могут ощущаться и захватываться в энергетических состояниях дефекта. Уровни энергии этих состояний определяются атомами, составляющими твердое тело. На рис. 1 показана диаграмма Хариссона для элементарного полупроводника Si. Слева направо, s-орбитальная и p-орбитальная гибридизация способствует sp-связыванию, которое, когда несколько sp-димеров Si-Si объединяются в твердое тело, определяет зону проводимости и валентную зону. Если бы вакансия существовала, например, на каждом атоме на границе твердое тело / вакуум, это привело бы, по крайней мере, к одной разорванной sp-связи, имеющей энергию, равную энергии одиночных самогибридизованных атомов Si, как показано на рисунке 1. Это энергия соответствует примерно середине запрещенной зоны Si, на ~ 0,55 эВ выше валентной зоны. Безусловно, это наиболее идеальный случай, тогда как ситуация была бы иной, если бы, например, имели место пассивация связи (см. Ниже) и реконструкция поверхности. Экспериментально энергии этих состояний можно определить с использованием абсорбционной спектроскопии или рентгеновской фотоэлектронной спектроскопии, например, если чувствительность прибора и / или плотность дефектов достаточно высоки.

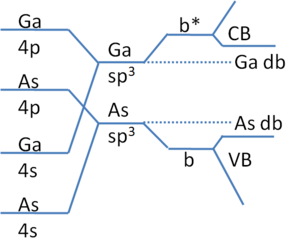
Рис. 2. Диаграмма энергии электронов Харрисона для полупроводникового соединения III-IV GaAs. Так же, как и для Si, кристалл построен с добавлением гибридизированных димеров GaAs. Поскольку вакансии вызывают оборванные связи Ga, образующие состояния вблизи CB. Вакансии Ga образуют оборванные связи As, энергия которых близка к VB. VB состоит в основном из «As-подобных» состояний, поскольку ионность помещает электроны на атомы As, и, как следствие, CB-состояния являются «Ga-подобными».

Составные полупроводники, такие как GaAs, имеют состояния оборванных связей, которые являются ближе к краям ленты (см. рисунок 2). Поскольку связывание становится все более ионным, эти состояния могут даже действовать как легирующие примеси. Это является причиной хорошо известной трудности легирования GaN p-типа, когда много N вакансий из-за высокого давления пара, что приводит к высокой плотности оборванных связей Ga. Эти состояния близки к краю зоны проводимости и поэтому действуют как доноры. Когда вводятся акцепторные примеси p-типа, они немедленно компенсируются N вакансиями. С этими мелкими состояниями их обработка часто рассматривается как аналог атома водорода следующим образом для случая анионных или катионных вакансий (эффективная масса дырки m * для катиона и электрон m * для анионных вакансий). Энергия связи, E c-Edb, равна. $E c - E db = U + KE = 1 2 U (1) {\ displaystyle E_ {c} -E_ {db} = U + KE = { \ frac {1} {2}} U \; \; (1)}$ ${\ displaystyle E_ {c} -E_ {db} = U + KE = {\ frac {1} {2}} U \; \; (1)}$ . где U = -q / (4πεε r r) - электростатический потенциал между электроном, занимающим оборванную связь, и его ионное ядро с ε, постоянной диэлектрической проницаемости в свободном пространстве, ε r, относительной диэлектрической проницаемостью и r разделением электрон-ионного ядра. Упрощение, заключающееся в том, что энергия поступательного движения электрона, KE = -U / 2, обусловлено теоремой вириала для центросимметричных потенциалов. Как описано в модели Бора, r подлежит квантованию. $n λ = 2 π r (2) {\ displaystyle n \ lambda = 2 \ pi r \; \; (2)}$ ${\ displaystyle n \ lambda = 2 \ pi r \; \; (2)}$ .. Импульс электрона равен p = mv = h / λ такой, что. $KE = p 2 2 m ∗ = h 2 n 2 8 m ∗ π 2 r 2 = - U 2 = q 2 8 π ε ε rr (3) {\ displaystyle KE = {\ frac {p ^ {2}} {2m ^ {*}}} = {\ frac {h ^ {2} n ^ {2}} {8m ^ {*} \ pi ^ {2} r ^ {2}}} = - {\ frac {U} {2}} = {\ frac {q ^ {2}} {8 \ pi \ varepsilon \ varepsilon _ {r } r}} \; \; (3)}$ ${\ displaystyle KE = {\ frac {p ^ {2}} {2m ^ {*} }} = {\ frac {h ^ {2} n ^ {2}} {8m ^ {*} \ pi ^ {2} r ^ {2}}} = - {\ frac {U} {2}} = {\ гидроразрыва {q ^ {2}} {8 \ pi \ varepsilon \ varepsilon _ {r} r}} \; \; (3)}$ ., что дает. $r = 4 π ℏ 2 n 2 ε ε rq 2 m ∗ (4) {\ displaystyle r = {\ frac {4 \ pi \ hbar ^ {2} n ^ {2} \ varepsilon \ varepsilon _ {r}} {q ^ {2} m ^ {*}}} \; \; (4)}$ ${\ displaystyle r = {\ frac {4 \ pi \ hbar ^ {2} n ^ {2} \ varepsilon \ varepsilon _ {r}} {q ^ {2} m ^ {*}}} \; \; (4)}$ . и. $E c - E db = U 2 = m ∗ q 4 8 h 2 (ε ε r) 2 (5) {\ displaystyle E_ {c} -E_ {db} = {\ frac {U} {2} } = {\ frac {m ^ {*} q ^ {4}} {8h ^ {2} (\ varepsilon \ varepsilon _ {r}) ^ {2}}} \; \; (5)}$ ${\ displaystyle E_ {c} -E_ {db} = {\ frac {U} {2}} = {\ frac {m ^ {*} q ^ {4}} {8h ^ {2} ( \ var эпсилон \ varepsilon _ {r}) ^ {2}} \; \; (5)}$ .. Эта обработка теряет точность, так как дефекты уходят от края ленты.

Рассеяние на дефектах

Уровни энергии оборванных связей являются собственными значениями волновых функций, которые описывают электроны в окрестности дефектов. В типичном рассмотрении рассеяния носителей это соответствует конечному состоянию в золотом правиле Ферми частоты рассеяния:. $S k 'k = 2 π ℏ | < f | H ′ | i>| 2 δ (E е - E я) (6) {\ displaystyle S_ {k'k} = {\ frac {2 \ pi} {\ hbar}} | | ^ {2} \ delta (E_ {f } -E_ {i}) \; \; (6)}$ $S_{k'k}={\frac {2\pi }{\hbar }}|<f|H'|i>| ^ {2} \ delta (E_ {f} -E_ {i}) \; \; (6)$ . где H 'является параметром взаимодействия, а Дельта-функция Дирака, δ (E f-Ei), указывающая на упругое рассеяние. Простое соотношение 1 / τ = Σ k ', k S k'k делает это уравнение полезным для определения свойств переноса материала при использовании вместе с σ = neτ / m * и правилом Маттиссена для включения других процессов рассеяния.

Значение S k'k в первую очередь определяется параметром взаимодействия H '. Этот член различается в зависимости от того, рассматриваются ли мелкие или глубокие состояния. Для мелких состояний H' - это член возмущения переопределенного гамильтониана H = H o + H ', где H o имеет энергию собственного значения E i. Матрица для этого случая имеет вид. $< f | H ′ | i>≡ M k ′ k = 1 V ∫ dr ¯ H ′ eir ¯ (k ¯ - k ¯ ′) = 1 V ∑ q ¯ ∫ dr ¯ H q ¯ eir ¯ (k ¯ - к ¯ ′ + q ¯) знак равно 1 В ∑ q ¯ H q ¯ δ k ¯ - k ¯ ′, q ¯ = 1 VH q ¯ (7) {\ displaystyle \ Equiv M_ {k'k} = { \ frac {1} {V}} \ int d {\ bar {r}} H'e ^ {i {\ bar {r}} ({\ bar {k}} - {\ bar {k}} ') } = {\ frac {1} {V}} \ sum _ {\ bar {q}} \ int d {\ bar {r}} H _ {\ bar {q}} e ^ {i {\ bar {r} } ({\ bar {k}} - {\ bar {k}} '+ {\ bar {q}})} = {\ frac {1} {V}} \ sum _ {\ bar {q}} H_ {\ bar {q}} \ delta _ {{\ bar {k}} - {\ bar {k}} '}, _ {\ bar {q}} = {\ frac {1} {V}} H_ { \ bar {q}} \; \; (7)}$ $<f|H'|i>\ Equiv M_ {k'k} = {\ frac {1} {V}} \ int d {\ bar {r}} H 'e ^ {i {\ bar {r}} ({\ bar {k}} - {\ bar {k}}')} = {\ frac {1} {V}} \ sum _ {\ bar {q }} \ int d {\ bar {r}} H _ {\ bar {q}} e ^ {i {\ bar {r}} ({\ bar {k}} - {\ bar {k}} '+ { \ bar {q}})} = {\ frac {1} {V}} \ sum _ {\ bar {q}} H _ {\ bar {q}} \ delta _ {{\ bar {k}} - { \ bar {k}} '}, _ {\ bar {q}} = {\ frac {1} {V}} H _ {\ bar {q}} \; \; (7)$ . где k '- волновой вектор конечного состояния, у которого есть только одно значение, поскольку плотность дефектов достаточно мала, чтобы не образовывать полосы (~ <10/cm). Using the Poisson equation for Fourier periodic point charges,. $∇ 2 V (r ¯) = - e δ ( r ¯) ε ε r = - ∑ q ¯ q ¯ 2 V q ¯ eiq ¯ r ¯ = - e V ε ε r ∑ q ¯ eiq ¯ r ¯ (8) {\ displaystyle \ nabla ^ {2} V ({ \ bar {r}}) = {\ frac {-e \ delta ({\ bar {r}})} {\ varepsilon \ varepsilon _ {r}}} = - \ sum _ {\ bar {q}} { \ bar {q}} ^ {2} V _ {\ bar {q}} e ^ {i {\ bar {q}} {\ bar {r}}} = {\ frac {-e} {V \ varepsilon \ varepsilon _ {r}}} \ \ sum _ {\ bar {q}} e ^ {i {\ bar {q}} {\ bar {r}}} \; \; (8)}$ ${\ displaystyle \ nabla ^ {2} V ({\ bar {r}}) = {\ frac {-e \ delta ({\ bar {r}})} {\ varepsilon \ varepsilon _ {r }}} = - \ sum _ {\ bar {q}} {\ bar {q}} ^ {2} V _ {\ bar {q}} e ^ {i {\ bar {q}} {\ bar {r }}} = {\ frac {-e} {V \ varepsilon \ varepsilon _ {r}}} \ \ sum _ {\ bar {q}} e ^ {i {\ bar {q}} {\ bar {r }}} \; \; (8)}$ ,. дает Коэффициент Фурье потенциала оборванной связи V q = e / (qε r V), где V - объем. В результате получаем. $H q ¯ = - e V q ¯ = - e 2 q ¯ 2 ε ε r V = - e 2 (q ¯ 2 + qs 2) ε ε r V (9) {\ displaystyle H _ {\ bar {q}} = - eV _ {\ bar {q}} = {\ frac {-e ^ {2}} {{\ bar {q}} ^ {2} \ varepsilon \ varepsilon _ {r } V}} = {\ frac {-e ^ {2}} {({\ bar {q}} ^ {2} + q_ {s} ^ {2}) \ varepsilon \ varepsilon _ {r} V}} \; \; (9)}$ ${\ displaystyle H _ {\ bar {q}} = - eV _ {\ bar {q}} = {\ frac {-e ^ {2}} {{\ bar {q}} ^ {2} \ varepsilon \ varepsilon _ {r} V}} = {\ frac {-e ^ {2}} {({\ bar {q}} ^ {2} + q_ {s} ^ {2}) \ varepsilon \ varepsilon _ {r} V}} \; \; (9)}$ . где q s - поправка волнового вектора длины Дебая из-за экранирования заряда. Тогда частота рассеяния равна. $1 τ = ∑ k ¯ ′, k ¯ S k ¯ ′ k ¯ = n ∑ k ¯ 2 π ℏ e 4 δ (E k ¯ - E k ¯ ′) ε ε r V [q ¯ 2 - qs 2] 2 = ne 4 4 π 2 ℏ ε ε r ∫ ∫ ∫ dkd θ d ϕ k 2 sin θ δ (E k ¯ - E k ¯ ′) [q ¯ 2 - qs 2] 2 (10) {\ displaystyle {\ frac {1} {\ tau}} = \ sum _ {{\ bar {k}} ', {\ bar {k}}} S _ {{\ bar {k} } '{\ bar {k}}} = n \ sum _ {\ bar {k}} {\ frac {2 \ pi} {\ hbar}} {\ frac {e ^ {4} \ delta (E _ {\ bar {k}} - E _ {{\ bar {k}} '})} {\ varepsilon \ varepsilon _ {r} V [{\ bar {q}} ^ {2} -q_ {s} ^ {2} ] ^ {2}}} = {\ frac {ne ^ {4}} {4 \ pi ^ {2} \ hbar \ varepsilon \ varepsilon _ {r}}} \ int \ int \ int dkd \ theta d \ phi {\ frac {k ^ {2} sin \ theta \; \ delta (E _ {\ bar {k}} - E _ {{\ bar {k}} '})} {[{\ bar {q}} ^ { 2} -q_ {s} ^ {2}] ^ {2}}} \; \; (10)}$ ${\frac {1}{\tau }}=\sum _{{\bar {k}}',{\bar {k}}}S_{{\bar {k}}'{\bar {k}}}=n\sum _{\bar {k}}{\frac {2\pi }{\hbar }}{\frac {e^{4}\delta (E_{\bar {k}}-E_{{\bar {k}}'})}{\varepsilon \varepsilon _{r}V[{\bar {q}}^{2}-q_{s}^{2}]^{2}}}={\frac {ne^{4}}{4\pi ^{2}\hbar \varepsilon \varepsilon _{r}}}\int \int \int dkd\theta d\phi {\frac {k^{2}sin\theta \;\delta (E_{\bar {k}}-E_{{\bar {k}}'})}{[{\bar {q}}^{2}-q_{s}^{2}]^{2}}}\;\;(10)$ . где n - объемная плотность дефектов. Выполнение интегрирования с использованием | k | = | k '| дает. $1 τ = ne 4 2 π 2 m ∗ (E c - E db) ℏ 2 ε ε r (1 qs 2 - 1 qs 2 + 8 м * (Е с - Е db) ℏ 2) (11) {\ displaystyle {\ frac {1} {\ tau}} = {\ frac {ne ^ {4}} {2 \ pi {\ sqrt {2m ^ {*} (E_ {c} -E_ {db})}} \ hbar ^ {2} \ varepsilon \ varepsilon _ {r}}} \ left ({\ frac {1} {q_ {s} ^ {2}}} - {\ frac {1} {q_ {s} ^ {2} + {\ frac {8m ^ {*} (E_ {c} -E_ {db})} {\ hbar ^ {2} }}}} \ right) \; \; (11)}$ ${\ displaystyle {\ frac {1} {\ tau}} = {\ frac {ne ^ {4}} {2 \ pi {\ sqrt {2m ^ {*} (E_ {c} -E_ {db})}} \ hbar ^ {2} \ varepsilon \ varepsilon _ {r} }} \ left ({\ frac {1} {q_ {s} ^ {2}}} - {\ frac {1} {q_ {s} ^ {2} + {\ frac {8m ^ {*} (E_ {c} -E_ {db})} {\ hbar ^ {2}}}}} \ right) \; \; (11)}$ .. Вышеупомянутая обработка не работает, если дефекты не являются периодическими, поскольку потенциалы оборванных связей представлены рядом Фурье. Упростить сумму в n раз в уравнении (10) было возможно только из-за низкой плотности дефектов. Если бы у каждого атома (или, возможно, у каждого другого) была бы одна оборванная связь, что вполне разумно для не реконструированной поверхности, интеграл по k 'также должен быть выполнен. Из-за использования теории возмущений при определении матрицы взаимодействия вышесказанное предполагает малые значения H 'или неглубокие дефектные состояния вблизи краев зоны. К счастью, само по себе золотое правило Ферми является довольно общим и может быть использовано для глубинных дефектов, если взаимодействие между электроном проводимости и дефектом изучено достаточно хорошо, чтобы смоделировать их взаимодействие в виде оператора, заменяющего H '.

Экспериментальные измерения

Рис. 3: (вверху) Простая развертка напряжения исток-сток с увеличением плотности дефектов может использоваться для определения скорости рассеяния носителей и энергии оборванных связей (красная кривая с большим количеством дефектов). (Внизу) Температурная зависимость удельного сопротивления. Вблизи абсолютного нуля выявляется влияние дефектов на рассеяние носителей.

Определение степени, в которой эти оборванные связи влияют на электрический транспорт, можно довольно легко экспериментально наблюдать. Путем изменения напряжения на проводнике (рис. 3), сопротивления и определенной геометрии можно определить проводимость образца. Как упоминалось ранее, σ = neτ / m *, где τ можно определить, зная n и m *, исходя из положения уровня Ферми и зонной структуры материала. К сожалению, это значение содержит эффекты от других механизмов рассеяния, например, за счет фононов. Это становится более полезным, когда измерение используется вместе с уравнением (11), где наклон графика зависимости 1 / τ от n делает E c-Edbвычисляемым, а точка пересечения определяет 1 / τ от всех процессов рассеяния, кроме дефектов. Это требует предположения, что рассеяние фононов (среди других, возможно, незначительных процессов) не зависит от концентрации дефектов.. В аналогичном эксперименте можно просто понизить температуру проводника (рис. 3), так что плотность фононов уменьшится до незначительной, допуская доминирующее сопротивление дефекта. В этом случае σ = neτ / m * можно использовать для прямого вычисления τ для рассеяния на дефектах.

Пассивация

Рис. 4. Пассивация водородом полевого транзистора Si-металл-оксид-полупроводник (MOSFET) для восстановления состояний интерфейса Si / SiO 2. Водородные связи с Si полностью удовлетворяют sp-гибридизацию, обеспечивая заселенность дефектных состояний, предотвращая рассеяние носителей в эти состояния.

Поверхностные дефекты всегда можно «пассивировать» атомами, чтобы целенаправленно занимать соответствующие энергетические уровни, чтобы электроны проводимости не могли рассеяться в эти состояния (эффективно уменьшение n в уравнении (10)). Например, пассивация Si на границе канал / оксид MOSFET водородом (рисунок 4) является типичной процедурой, помогающей снизить плотность дефектов ~ 10 см до 12 раз, тем самым улучшая подвижность и, следовательно, и скорости переключения. Удаление промежуточных состояний, которые в противном случае уменьшили бы туннельные барьеры, также снижает ток утечки затвора и увеличивает емкость затвора, а также переходную характеристику. Эффект заключается в том, что соединение Si sp становится полностью удовлетворенным. Очевидным требованием здесь является способность полупроводника окислять пассивирующий атом или, E c-Edb+ χ>E I, с полупроводником сродством к электрону χ и атому энергия ионизации EI.

Рассеяние фононов

Теперь рассмотрим рассеяние носителей с деформациями решетки, называемыми фононами. Рассмотрим объемное смещение, которое производит такая распространяющаяся волна, $Δ V 0 {\ displaystyle \ Delta V_ {0}}$ ${\ displaystyle \ Delta V_ {0}}$ , что, следовательно, приводит к деформации, зависящей от времени, $Δ V 0 / V 0 знак равно ▽ U (r, t) {\ displaystyle \ Delta V_ {0} / V_ {0} = \ bigtriangledown u (r, t)}$ ${\ displaystyle \ Delta V_ {0} / V_ {0} = \ bigtriangledown u (r, t)}$ где простая плоская волна используется для описания распространение фононов, $u (r, t) ∝ exp ± (iqr - i ω t) {\ displaystyle u (r, t) \ propto exp \ pm (iqr-i \ omega t)}$ ${\ displaystyle u (r, t) \ propto exp \ pm (iqr-i \ omega t)}$ . Смещение атомов от их положений равновесия обычно вызывает изменение электронной зонной структуры (рисунок 5), где для рассеяния мы имеем дело с электронами в зоне проводимости с энергией ~ E CB,. $Δ ECB знак равно d ECB d В 0 Δ V 0 знак равно V 0 d ECB d V 0 Δ V 0 V 0 знак равно ZDP ⋅ ▽ u (r, t) (12) {\ displaystyle \ Delta E_ {CB} = {\ frac {\ mathrm {d} E_ {CB}} {\ mathrm {d} V_ {0}}} \ Delta V_ {0} = V_ {0} {\ frac {\ mathrm {d} E_ {CB}} {\ mathrm { d} V_ {0}}} {\ frac {\ Delta V_ {0}} {V_ {0}}} = Z_ {DP} \ cdot \ bigtriangledown u (r, t) \; \; (12)}$ ${\ displaystyle \ Delta E_ {CB} = {\ frac {\ mathrm {d} E_ {CB}} {\ mathrm {d} V_ {0}}} \ Delta V_ {0} = V_ {0} {\ frac {\ mathrm {d} E_ {CB}} {\ mathrm {d } V_ {0}}} {\ frac {\ Delta V_ {0}} {V_ {0}}} = Z_ {DP} \ cdot \ bigtriangledown u (r, t) \; \; (12)}$ .. Эмпирический параметр Z DP называется деформационным потенциалом и описывает силу электрон-фононной связи. Умножение на фононную заселенность (распределение Бозе – Эйнштейна, N q) дает общий потенциал деформации,. $Δ ECBT ot = H ^ int = ZDP ⋅ ▽ u (г, t) N q + 1 2 ± 1 2 знак равно ± iq ZDP u (r, t) N q + 1 2 ± 1 2 (13) {\ displaystyle \ Delta E_ {CB} ^ {Tot} = {\ widehat {H}} _ {int} = Z_ {DP} \ cdot \ bigtriangledown u (r, t) {\ sqrt {N_ {q} + {\ frac {1} {2}} \ pm {\ frac {1 } {2}}}} = \ pm iqZ_ {DP} u (r, t) {\ sqrt {N_ {q} + {\ frac {1} {2}} \ pm {\ frac {1} {2} }}} \; \; (13)}$ ${\ displaystyle \ Delta E_ {CB} ^ {Tot} = {\ widehat {H}} _ {int} = Z_ {DP} \ cdot \ bigtriangledown u ( r, t) {\ sqrt {N_ {q} + {\ frac {1} {2}} \ pm {\ frac {1} {2}}}} = \ pm iqZ_ {DP} u (r, t) {\ sqrt {N_ {q} + {\ frac {1} {2}} \ pm {\ frac {1} {2}}}} \; \; (13)}$ .

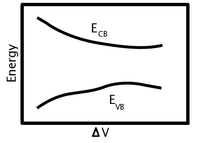
Рис. 5: Схема изменения краев энергетической зоны (зона проводимости, E CB и валентная зона E VB) как положения атомов кристалла смещены от равновесия, чтобы произвести объемную деформацию.

(причина возникновения корня будет очевидна ниже). Здесь + соответствует излучению фононов, а - поглощению фононов во время рассеяния. Примечание, поскольку для поперечных фононов $q ⊥ u (r, t) {\ displaystyle q \ perp u (r, t)}$ ${\ Displaystyle Q \ pe rp u (r, t)}$ , только взаимодействия с продольными фононами не равны нулю. Следовательно, полная матрица взаимодействия имеет вид. $< k ′ | H ^ i n t | k>= ± iq ZDP u (r, t) N q + 1 2 ± 1 2 δ k ′, k ± q (14) {\ displaystyle = \ pm iqZ_ {DP } u (r, t) {\ sqrt {N_ {q} + {\ frac {1} {2}} \ pm {\ frac {1} {2}}}} \ delta _ {k ', k \ pm q} \; \; (14)}$ $<k'|{\widehat {H}}_{int}|k>= \ pm iqZ_ {DP} u (r, t) {\ sqrt {N_ {q} + {\ frac {1} {2}} \ pm {\ frac {1} {2}}}} \ delta _ {k ', k \ pm q} \; \; (14)$ . где дельта Кронекера обеспечивает сохранение импульса и возникает в результате принятия электронных волновых функций (конечное состояние $< k ′ | {\displaystyle$ $<k'|$ и начальное состояние, $| k>{\ displaystyle | k>}$ $|k>$ ) также являются плоскими волнами.

Акустические фононы

Используя золотое правило Ферми, можно приблизительно определить скорость рассеяния акустических фононов низкой энергии. Матрица взаимодействия для этих фононов. $| < k ′ | H ^ i n t | k>| 2 знак равно ZDP 2 ℏ ω q 2 V ρ c 2 (N q + 1 2 ± 1 2) δ K ', k ± q (15) {\ displaystyle | | ^ {2} = Z_ {DP} ^ {2} {\ frac {\ hbar \ omega _ {q}} {2V \ rho c ^ {2}}} (N_ {q} + {\ frac {1} {2}} \ pm {\ frac {1 } {2}}) \ delta _ {k ', k \ pm q} \; \; (15)}$ $|<k'|{\widehat {H}}_{int}|k>| ^ {2} = Z_ {DP} ^ {2} {\ frac {\ hbar \ омега _ {q}} {2V \ rho c ^ {2}}} (N_ {q} + {\ frac {1} {2}} \ pm {\ frac {1} {2}}) \ delta _ { k ', k \ pm q} \; \; (15)$ . с радиальной частотой фононов ω q = cq, объемом V, плотностью твердого тела ρ и групповой скоростью фононов c. Подстановка этого в уравнение 6 дает. $S k ′ k A c = 2 π ℏ ZDP 2 ℏ ω q 2 V ρ c 2 (N q + 1 2 ± 1 2) δ k ′, k ± q δ [E (k ′) - E (k) ± ℏ ω q] (16) {\ displaystyle S_ {k'k} ^ {Ac} = {\ frac {2 \ pi} {\ hbar}} Z_ {DP} ^ {2} {\ frac {\ hbar \ omega _ {q}} {2V \ rho c ^ {2}}} (N_ {q} + {\ frac {1} {2}} \ pm {\ frac {1} {2}}) \ delta _ {k ', k \ pm q} \ delta [E (k') - E (k) \ pm \ hbar \ omega _ {q}] \; \; (16)}$ $S_{k'k}^{Ac}={\frac {2\pi }{\hbar }}Z_{DP}^{2}{\frac {\hbar \omega _{q}}{2V\rho c^{2}}}(N_{q}+{\frac {1}{2}}\pm {\frac {1}{2}})\delta _{k',k\pm q}\delta [E(k')-E(k)\pm \hbar \omega _{q}]\;\;(16)$ .. С предположениями, что N q>>1, ħω <сингулярность Ван Хова ) дает скорость рассеяния:. $1 τ = ∑ k ′ S k ′ k A c = ∑ k S к ± q, к A с {\ displaystyle {\ frac {1} {\ tau}} = \ sum _ {k '} S_ {k'k} ^ {Ac} = \ sum _ {k} S_ {k \ pm q, k} ^ {Ac}}$ ${\frac {1}{\tau }}=\sum _{k'}S_{k'k}^{Ac}=\sum _{k}S_{k\pm q,k}^{Ac}$ . $= 2 π ℏ ZDP 2 ℏ ω q 2 V ρ c 2 (k T ℏ ω q) ∑ k δ k ′, k ± q δ [E (k ′) - Е (к) ± ℏ ω q] {\ displaystyle = {\ frac {2 \ pi} {\ hbar}} Z_ {DP} ^ {2} {\ frac {\ hbar \ omega _ {q}} {2V \ rho c ^ {2}}} ({\ frac {kT} {\ hbar \ omega _ {q}}}) \ sum _ {k} \ delta _ {k ', k \ pm q} \ delta [E (к ') - Е (к) \ pm \ hbar \ omega _ {q}]}$ $={\frac {2\pi }{\hbar }}Z_{DP}^{2}{\frac {\hbar \omega _{q}}{2V\rho c^{2}}}({\frac {kT}{\hbar \omega _{q}}})\sum _{k}\delta _{k',k\pm q}\delta [E(k')-E(k)\pm \hbar \omega _{q}]$ . $= 2 π ℏ ZDP 2 k T 2 V ρ c 2 V × g (E) {\ displaystyle = {\ frac {2 \ pi} {\ hbar}} Z_ {DP} ^ {2} {\ frac {kT} {2V \ rho c ^ {2}}} V \ times g (E)}$ ${\ displaystyle = {\ frac {2 \ pi} {\ hbar}} Z_ {DP} ^ {2} {\ frac {kT} {2V \ rho c ^ {2}}} V \ times g (E)}$ . $= 2 π ZDP 2 м * 3 2 К T ρ ℏ 4 c 2 E - ECB (17) {\ displaystyle = {\ frac {\ sqrt {2}} {\ pi}} {\ frac {Z_ {DP} ^ {2} m ^ {* {\ frac {3} {2}}} kT} {\ rho \ hbar ^ {4} c ^ {2}}} {\ sqrt {E-E_ {CB}}} \; \; (17)}$ ${\ displaystyle = {\ frac {\ sqrt {2}} {\ pi}} {\ frac {Z_ {DP} ^ {2} m ^ {* { \ frac {3} {2}}} kT} {\ rho \ hbar ^ {4} c ^ {2}}} {\ sqrt {E-E_ {CB}}} \; \; (17)}$ . где g (E) - электронная плотность состояний, для которой для получения окончательного ответа использовалось 3-мерное решение с параболической дисперсией.

Оптические фононы

Как правило, фононы в оптических ветвях соотношений колебательной дисперсии имеют энергию порядка или больше kT, и поэтому приближения ħω <>1 не могут быть сделал. Тем не менее, разумным путем, который по-прежнему позволяет избежать сложных фононных дисперсий, является использование модели Эйнштейна, которая утверждает, что в твердых телах существует только одна фононная мода. Для оптических фононов этого приближения оказывается достаточно из-за очень небольшого изменения наклона ω (q), и, таким образом, мы можем утверждать, что ħω (q) ≅ ħω, постоянная. Следовательно, N q также является константой (зависит только от T). Последнее приближение, g (E ') = g (E ± ω) ~ g (E), не может быть выполнено, поскольку ħω ~ E и для него нет обходного пути, но добавленная сложность к сумме для τ минимальна.. $1 τ = ∑ k ′ S k ′ k O p = 2 π ℏ ZDP 2 ℏ ω 2 V ρ c 2 (N q + 1 2 ± 1 2) ∑ k ′ δ k ′, k ± q δ [E (k ') - E (k) ± ℏ ω] {\ displaystyle {\ frac {1} {\ tau}} = \ sum _ {k'} S_ {k'k} ^ {Op} = {\ frac {2 \ pi} {\ hbar}} Z_ {DP} ^ {2} {\ frac {\ hbar \ omega} {2V \ rho c ^ {2}}} (N_ {q} + {\ frac {1} {2}} \ pm {\ frac {1} {2}}) \ sum _ {k '} \ delta _ {k', k \ pm q} \ delta [E (k ') - E ( к) \ pm \ hbar \ omega]}$ ${\frac {1}{\tau }}=\sum _{k'}S_{k'k}^{Op}={\frac {2\pi }{\hbar }}Z_{DP}^{2}{\frac {\hbar \omega }{2V\rho c^{2}}}(N_{q}+{\frac {1}{2}}\pm {\frac {1}{2}})\sum _{k'}\delta _{k',k\pm q}\delta [E(k')-E(k)\pm \hbar \omega ]$ . $= ZDP 2 ℏ ω 8 π 2 ℏ ρ c 2 (N q + 1 2 ± 1 2) g (E ± ℏ ω) (18) {\ displaystyle = Z_ {DP} ^ {2} {\ frac {\ hbar \ omega} {8 \ pi ^ {2} \ hbar \ rho c ^ {2}}} (N_ {q} + {\ frac {1} {2}) } \ pm {\ frac {1} {2}}) g (E \ pm \ hbar \ omega) \; \; (18)}$ ${\ displaystyle = Z_ {DP} ^ {2} {\ frac {\ hbar \ omega} {8 \ pi ^ {2} \ hbar \ rho c ^ {2}}} (N_ {q} + {\ frac {1} {2}} \ pm {\ frac {1} {2}}) g (E \ pm \ hbar \ omega) \; \; (18)}$ .. Сумма превращается в плотность состояний в E 'и Распределение Бозе – Эйнштейна можно исключить из суммы, поскольку ħω (q) ≅ ħω.

Примечания

^Харрисон, Уолтер А., Электронная структура и свойства твердых тел: физика химической связи. Сан-Франциско: Freeman, 1980.
^Rockett, Angus, The Materials Science of Semiconductors. Нью-Йорк: Springer, 2007.
^Гесс, Карл, Продвинутая теория полупроводниковых приборов. Нью-Йорк: Wiley Interscience, 2000.
^Faughnan, B.; Ипри, А. С. IEEE Trans. Elec. Dev. 36, 101, 1999.
^Конвелл, Э. М., «Высокополевой перенос в полупроводниках», в физике твердого тела, под ред. Ф. Зейтц, Д. Тернбулл и Х. Эренрайх, Приложение 9. Нью-Йорк: Academic Press, 1967, с. 108.