Калориметрия

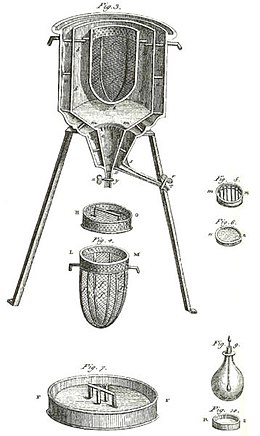
Измерение термодинамического состояния Первый в мире ледяной калориметр, использовавшийся зимой 1782–83 гг., Антуаном Лавуазье и Пьером-Симоном Лапласом, чтобы определить тепло, участвующее в различных химических изменениях ; расчеты, основанные на предыдущем открытии скрытой теплоты, сделанным Джозефом Блэком. Эти эксперименты положили начало термохимии. камеры прямой калориметрии Снеллена, Университет Оттавы. Тележка метаболизма непрямой калориметрии, измеряющая поглощение кислорода и производство CO2, спонтанно дышащим субъектом (метод разбавления с капюшоном).

Калориметрия - это наука или действие по измерению изменений достижение состояния цели с достижением теплопередачи, компоненты с изменениями его состояния, например, в химические реакции, физические изменения или фазовые переходы при определенных ограничениях. Калориметрия выполняется с помощью калориметра. Слово калориметрия происходит от латинского слова калор, означающего тепло, и греческого слова μέτρον (метрон), что означает мера. Шотландский врач и ученый Джозеф Блэк, который первым осознал различие между теплом и температурой, считается основателем калориметрии.

Косвенная калориметрия рассчитывает тепло, выделяемое путем либо производства диоксида углерода, либо азотных отходов (часто аммиака в водных организмах, или мочевина в земных), или от потребления ими кислорода. Лавуазье заметил в 1780 году, что производство тепла можно предсказать по потреблению кислорода таким образом, используя множественную регрессию. Теория динамического бюджета энергии объясняет, почему эта процедура верна. Тепло, выделяемое живыми организмами, также можно измерить с помощью прямых калориметрии, при этом весь организм помещается в калориметр для измерения.

Широко используемым современным прибором является дифференциальный сканирующий калориметр, устройство, которое позволяет получать тепловые данные на небольшого количества материала. Он включает нагревательный элемент с контролируемой скоростью и регистрацию теплового потока в образце или из него.

Содержание

• 1 Классический калориметрический расчет тепла
  • 1.1 Случаи дифференцируемого уравнения состояния однокомпонентного тела
    • 1.1.1 Базовый классический расчет по объему
    • 1.1.2 Классическая теория для калориметрии постоянного объема (изохорной)
    • 1.1.3 Классический расчет тепла по давлению
  • 1.2 Калориметрия через фазовый переход, уравнение состояний показывает скачкообразный переход
  • 1.3 Накопление перехода
  • 1.4 Математические аспекты из приведенных выше правил
  • 1.5 Физический объем вышеперечисленных правил калориметрии
• 2 Экспериментально удобно измеренные коэффициенты
  • 2.1 Повышение давления при постоянном объеме
  • 2.2 Расширение при постоянном давлении
  • 2.3 Сжимаемость при постоянной температуре
• 3 Связь между классическими калориметрическими величинами
• 4 Связь между калориметрией и термодинамикой
• 5 Особый интерес термодинамики в калориметрии: изотермические сегменты цикла Карно
• 6 Особый интерес калорим етрии в t Гермодинамика: соотношения между классическими калориметрическими величинами состояния
  • 6.1 Связь скрытой теплоты с объемом и уравнением
  • 6.2 Разница удельных теплоемкостей
• 7 Практическая калориметрия постоянного объема (калориметрия бомбы) для термодинамических исследований
• 8 См. Также
• 9 Ссылки
• 10 Книги
• 11ние ссылки

Классический калориметрический расчет тепла

Случаи с дифференцируемым уравнением состояния для однокомпонентного тела

Базовый классический расчет объема

Калориметрия требует, чтобы эталонный материал, изменяющая температура, обладал определенными термическими конститутивными свойствами. Классическое правило, признанное Клаузиусом и Кельвином, заключается в том, что давление, оказываемое калориметрическим материалом, полностью и быстро определяется исключительно его температурой и объемом; это правило применяется для изменений, не связанных с фазовым переходом, таких как таяние льда. Есть много материалов, которые не соответствуют этим правилам, и для них настоящая формула классической калориметрии не дает адекватного объяснения. Здесь принято, что классическое правило выполняется для используемого калориметрического материала, и утверждение математически записываются:

Тепловой отклик калориметрического материала полностью описывается его давлением $p\; \{\backslash \; displaystyle\; p\; \backslash \}$как значение его функции $p\; (V,\; T)\; \{\backslash \; displaystyle\; p\; (V,\; T)\; \backslash \}$только объем $V\; \{\backslash \; displaystyle\; V\; \backslash \}$и температура $Т\; \{\backslash \; Displaystyle\; T\; \backslash \}$. Все приращения здесь должны быть очень маленькими. Этот расчет относится к области объема и температуры тела, в которой не происходит фазового перехода и присутствует только одна фаза. Важным предположением здесь является непрерывность отношений собственности. Другой анализ необходим для изменения фазы

Когда калориметрическое тело получает небольшое приращение тепла с небольшими приращениями, $\delta \; V\; \{\backslash \; displaystyle\; \backslash \; delta\; V\; \backslash \}$его объем и $\delta \; T\; \{\backslash \; displaystyle\; \backslash \; delta\; T\; \backslash \}$его температуры, приращение тепла, $\delta \; Q\; \{\backslash \; displaystyle\; \backslash \; delta\; Q\; \backslash \}$, полученное телом калориметрического материала, определяется как

$\delta \; Q\; знак\; равно\; CT\; (V)\; (V,\; T)\; \delta \; V\; +\; CV\; (T)\; (V,\; T)\; \delta \; T\; \{\backslash \; displaystyle\; \backslash \; delta\; Q\; \backslash \; =\; C\_\; \{T\}\; ^\; \{(V)\}\; (V,\; T)\; \backslash ,\; \backslash \; дельта\; V\; \backslash ,\; +\; \backslash ,\; C\_\; \{V\}\; ^\; \{(T)\}\; (V,\; T)\; \backslash ,\; \backslash \; delta\; T\}$

где

$CT\; (V)\; (V,\; T)\; \{\backslash \; displaystyle\; C\_\; \{T\}\; ^\; \{(V)\}\; (V,\; T)\; \backslash \}$обозначает скрытую теплоту по отношению к объему калориметрический материал при контролируемой температуре $T\; \{\backslash \; displaystyle\; T\}$. Давление окружающей среды на материал инструментально регулируется, чтобы вызвать выбранное изменение объема с начальным объемом $V\; \{\backslash \; displaystyle\; V\; \backslash \}$. Для определения этой скрытой теплоты изменение фактически независимой инструментально изменяемой величиной. Это скрытое тепло не является одним из широко используемых, но представляет теоретический или концептуальный интерес.

$CV\; (T)\; (V,\; T)\; \{\backslash \; displaystyle\; C\_\; \{V\}\; ^\; \{(T)\}\; (V,\; T)\; \backslash \}$обозначает теплоемкость калориметрического материала при фиксированном постоянном объеме $V\; \{\backslash \; displaystyle\; V\; \backslash \}$, в то время как давление материала может свободно меняться, с начальной температурой $T\; \{\backslash \; displaystyle\; T\; \backslash \}$. Температура воздействием подходящей тепловой ванны. Обычно $CV\; (T)\; (V,\; T)\; \{\backslash \; displaystyle\; C\_\; \{V\}\; ^\; \{(T)\}\; (V,\; T)\; \backslash \}$просто как $CV\; (V,\; T)\; \{\backslash \; displaystyle\; C\_\; \{V\}\; (V,\; T)\; \backslash \}$, или, еще более кратко, $CV\; \{\backslash \; displaystyle\; C\_\; \{V\}\; \backslash \}$. Это скрытое тепло является одним из двух широко используемых.

Скрытое тепло по отношению к объему - это тепло, необходимое для увеличения объема на единицу при постоянной температуре. Можно сказать, что он «измеряется по изотерме», и давление, которое оказывает материал, может свободно меняться в соответствии с его основным законом $p\; =\; p\; (V,\; T)\; \{\backslash \; displaystyle\; p\; =\; p\; (V,\; Т)\; \backslash \; \}$. Для данного материала он может иметь положительный или отрицательный знак или, в исключительных случаях, может быть равен нулю, и это может зависеть от температуры, как это происходит для воды около 4 ° C. Концепция скрытой теплоты по отношению к объему, возможно, была впервые признана. Автор Джозеф Блэк в 1762 году. Также используется термин «скрытая теплота расширения». Скрытое тепло по отношению к объему также можно назвать «скрытой энергией по отношению к объему». Использование «скрытой теплоемкости» в более систематической терминологии используется «скрытая теплоемкость».

Теплоем при постоянном объеме - это количество тепла, необходимое для увеличения температуры на единицу при постоянном объеме. Можно сказать, что это «измеряется по изохоре», и опять же, давление, которое оказывает материал, может свободно изменяться. Это всегда имеет положительный знак. Это означает, что для повышения температуры тела без изменения его объема к нему необходимо подводить. Это согласуется с обычным опытом.

Такие величины, как $\delta \; Q\; \{\backslash \; displaystyle\; \backslash \; delta\; Q\; \backslash \}$, иногда называют «дифференциалом кривой», поскольку они измеряются вдоль кривых в $(V,\; T)\; \{\backslash \; displaystyle\; (V,\; T)\; \backslash \}$поверхность.

Классическая теория калориметрии постоянного объема (изохорная)

Калориметрия постоянного объема - это калориметрия, выполняемая при постоянном объеме. Это предполагает использование калориметра постоянного объема. Теплота по-прежнему устанавливается по вышеуказанному протоколу калориметрии.

Это означает, что в калориметре конструкции, называемой калориметром бомбы, приращение объема $\delta \; V\; \{\backslash \; displaystyle\; \backslash \; delta\; V\; \backslash \}$может быть обращено в ноль, $\delta \; В\; знак\; равно\; 0\; \{\backslash \; Displaystyle\; \backslash \; дельта\; V\; =\; 0\; \backslash \}$. Для калориметрии постоянного объема:

$\delta \; Q\; =\; CV\; \delta \; T\; \{\backslash \; displaystyle\; \backslash \; delta\; Q\; =\; C\_\; \{V\}\; \backslash \; delta\; T\; \backslash \}$

, где

$\delta \; T\; \{\backslash \; displaystyle\; \backslash \; delta\; T\; \backslash \}$обозначает приращение температуры, а

$CV\; \{\backslash \; displaystyle\; C\_\; \{V\}\; \backslash \}$обозначает теплоемкость при постоянном объеме.

Классический расчет тепла по давлению

Из приведенного выше правила расчета тепла по объему следует правилу по давлению.

В процессе небольших приращений $\delta \; p\; \{\backslash \; displaystyle\; \backslash \; delta\; p\; \backslash \}$его давление и $\delta \; T\; \{\backslash \; displaystyle\; \backslash \; delta\; T\; \backslash \}$его температура, приращение тепла $\delta \; Q\; \{\backslash \; displaystyle\; \backslash \; delta\; Q\; \backslash \}$, полученный телом калориметрического, определяется как

$\delta \; Q\; =\; CT\; (p)\; (p,\; T)\; \delta \; p\; +\; С\; п\; (T)\; (п,\; T)\; \delta \; T\; \{\backslash \; Displaystyle\; \backslash \; дельта\; Q\; \backslash \; =\; C\_\; \{T\}\; ^\; \{(p)\}\; (p,\; T)\; \backslash ,\; \backslash \; delta\; p\; \backslash ,\; +\; \backslash ,\; C\_\; \{p\}\; ^\; \{(T)\}\; (p,\; T)\; \backslash ,\; \backslash \; delta\; T\}$

где

$CT\; (p)\; (p,\; T)\; \{\backslash \; displaystyle\; C\_\; \{T\}\; ^\; \{(p)\}\; (p,\; T)\; \backslash \}$обозначает скрытую теплоту по отношению к давлению калориметрического материала при температуре, в то время как объем и давление могут свободно изменяться при давлении $p\; \{\backslash \; displaystyle\; p\; \backslash \}$и температура $T\; \{\backslash \; displaystyle\; T\; \backslash \}$;

$C\; p\; (T)\; (p,\; T)\; \{\backslash \; displaystyle\; C\_\; \{p\}\; ^\; \{(T)\}\; (p,\; T)\; \backslash \}$обозначает теплоемкость калориметрического материала при постоянном давлении, в то время как температура и объем тела свободно изменяться при давлении $p\; \{\backslash \; displaystyle\; p\; \backslash \}$и температуре $Т\; \{\backslash \; Displaystyle\; T\; \backslash \}$. Принято писать $C\; p\; (T)\; (p,\; T)\; \{\backslash \; displaystyle\; C\_\; \{p\}\; ^\; \{(T)\}\; (p,\; T)\; \backslash \}$просто как $C\; p\; (p,\; T)\; \{\backslash \; displaystyle\; C\_\; \{p\}\; (p,\; T)\; \backslash \}$, или даже более кратко, как $C\; p\; \{\backslash \; displaystyle\; C\_\; \{p\}\; \backslash \}$.

новые величины здесь связаны с предыдущими:

$CT\; (p)\; (p,\; T)\; =\; CT\; (V)\; (V,\; T)\; \partial \; p\; \partial \; V\; |\; (V,\; T)\; \{\backslash \; displaystyle\; C\_\; \{T\}\; ^\; \{(p)\}\; (p,\; T)\; =\; \{\backslash \; frac\; \{C\_\; \{T\}\; ^\; \{(V)\}\; (V,\; T)\}\; \{\backslash \; left.\; \{\backslash \; cfrac\; \{\backslash \; partial\; p\}\; \{\backslash \; partial\; V\}\}\; \backslash \; right\; |\; \_\; \{(V,\; T)\}\}\}\}$

$C\; p\; (T)\; (p,\; T)\; =\; CV\; (T)\; (V,\; T)\; -\; CT\; (V)\; (V,\; T)\; \partial \; p\; \partial \; T\; |\; (V,\; T)\; \partial \; p\; \partial \; V\; |\; (В,\; Т)\; \{\backslash \; Displaystyle\; C\_\; \{p\}\; ^\; \{(T)\}\; (p,\; T)\; =\; C\_\; \{V\}\; ^\; \{(T)\}\; (V,\; T)\; -C\_\; \{T\}\; ^\; \{(V)\}\; (V,\; T)\; \{\backslash \; frac\; \{\backslash \; left.\; \{\backslash \; Cfrac\; \{\backslash \; partial\; p\}\; \{\backslash \; partial\; T\}\}\; \backslash \; right\; |\; \_\; \{(V,\; T)\}\}\; \{\backslash \; left.\; \{\backslash \; Cfrac\; \{\backslash \; partial\; p\}\; \{\backslash \; partial\; V\}\}\; \backslash \; right\; |\; \_\; \{(V,\; T)\}\}\}\}$

где

$\partial \; p\; \partial \; V\; |\; (В,\; Т)\; \{\backslash \; Displaystyle\; \backslash \; влево.\; \{\backslash \; Frac\; \{\backslash \; partial\; p\}\; \{\backslash \; partial\; V\}\}\; \backslash \; right\; |\; \_\; \{(V,\; T)\}\}$обозначает частную производную из $p\; (V,\; T)\; \{\backslash \; displaystyle\; p\; (V,\; T)\; \backslash \}$по отношению к $V\; \{\backslash \; displaystyle\; V\; \backslash \}$оценено для $(V,\; T)\; \{\backslash \; displaystyle\; (V,\; T)\; \backslash \}$

и

$\partial \; p\; \partial \; Т\; |\; (В,\; Т)\; \{\backslash \; Displaystyle\; \backslash \; влево.\; \{\backslash \; Frac\; \{\backslash \; partial\; p\}\; \{\backslash \; partial\; T\}\}\; \backslash \; right\; |\; \_\; \{(V,\; T)\}\}$обозначает частную производную от $p\; (V,\; T)\; \{\backslash \; displaystyle\; p\; (V,\; T)\; \backslash \}$по отношению к $T\; \{\backslash \; displaystyle\; T\; \backslash \}$вычислено для $(V,\; T)\; \{\backslash \; displaystyle\; (V,\; T)\; \backslash \}$.

Скрытая теплота $CT\; (V)\; (V,\; T)\; \{\backslash \; Displaystyle\; C\_\; \{T\}\; ^\; \{(V)\}\; (V,\; T)\; \backslash \}$и $CT\; (p)\; (p,\; T)\; \{\backslash \; displaystyle\; C\_\; \{T\}\; ^\; \{(\; p)\}\; (p,\; T)\; \backslash \}$всегда противоположны знак.

Обычно отношение удельных теплоемкостей называют

$\gamma \; (V,\; T)\; =\; C\; p\; (T)\; (p,\; T)\; CV\; (T)\; (V,\; T)\; \{\backslash \; displaystyle\; \backslash \; gamma\; (V,\; T)\; =\; \{\backslash \; frac\; \{C\_\; \{p\}\; ^\; \{(T)\}\; (p,\; T)\}\; \{C\_\; \{V\}\; ^\; \{(T)\}\; (V,\; T)\}\}\}$часто просто записывается как $\gamma \; =\; C\; p\; CV\; \{\backslash \; displaystyle\; \backslash \; gamma\; =\; \{\backslash \; frac\; \{C\_\; \{p\}\}\; \{C\_\; \{V\}\}\}\}$.

Калориметрия через изменение фазы, уравнение состояния показывает прерывистость с одним скачком

Ранний калориметр использовался Лапласом и Лавуазье, как показано на рисунке выше. Он работал при постоянной температуре и атмосферном давлении. При этом задействованная скрытая теплота не была скрытой теплотой по отношению к объему или по отношению к давлению, как в приведенном выше описании калориметрии без фазового перехода. Скрытая теплота этого калориметра занимается с фазовым переходом, происходящим в природе при постоянной температуре. Этот вид калориметра работает путем измерения воды, образовавшейся при таянии льда, которая представляет собой фазовый переход.

накопление тепла

Для зависящего от времени процесса калориметрического материала., определяемый непрерывной совместной прогрессией $P\; (t\; 1,\; t\; 2)\; \{\backslash \; displaystyle\; P\; (t\_\; \{1\},\; t\_\; \{2\})\; \backslash \}$из $V\; (t)\; \{\backslash \; displaystyle\; V\; (t)\; \backslash \}$и $T\; (t)\; \{\backslash \; displaystyle\; T\; (t)\; \backslash \}$, начиная с момента $t\; 1\; \{\backslash \; displaystyle\; t\_\; \{1\; \}\; \backslash \}$и заканчивая в момент времени $t\; 2\; \{\backslash \; displaystyle\; t\_\; \{2\}\; \backslash \}$, можно вычислить накопленное количество доставленного тепла, $\Delta \; Q\; (п\; (\; t\; 1,\; t\; 2))\; \{\backslash \; displaystyle\; \backslash \; Delta\; Q\; (P\; (t\_\; \{1\},\; t\_\; \{2\}))\; \backslash ,\}$. Этот расчет выполняется путем математической интеграции по прогрессии по времени. Это потому, что приращения тепла являются «аддитивными»; но это не означает, что тепло - величина консервативная. Идея о том, что является тепло консервативной величиной, была изобретена Лавуазье и называется «теорией калорий »; к середине XIX века это было признано ошибочным. Записывается с помощью символа $\Delta \; \{\backslash \; displaystyle\; \backslash \; Delta\; \backslash \}$, величина $\Delta \; Q\; (P\; (t\; 1,\; t\; 2))\; \{\backslash \; displaystyle\; \backslash \; Delta\; Q\; (P\; (t\_\; \{1\; \},\; t\_\; \{2\}))\; \backslash ,\}$вовсе не ограничивается приращением с очень маленькими значениями; это контрастирует с $\delta \; Q\; \{\backslash \; displaystyle\; \backslash \; delta\; Q\; \backslash \}$.

Можно написать

$\Delta \; Q\; (P\; (t\; 1,\; t\; 2))\; \{\backslash \; displaystyle\; \backslash \; Delta\; Q\; (P\; (t\_\; \{1\},\; t\_\; \{2\}))\; \backslash \}$

$=\; \int \; P\; (t\; 1,\; t\; 2)\; Q\; \dot{}\; (t)\; dt\; \{\backslash \; displaystyle\; =\; \backslash \; int\; \_\; \{P\; (t\_\; \{1\},\; t\_\; \{2\})\}\; \{\backslash \; точка\; \{Q\}\}\; (t)\; dt\}$

$=\; \int \; P\; (t\; 1,\; t\; 2)\; CT\; (V)\; (V,\; T)\; V\; \dot{}\; (t)\; dt\; +\; \int \; P\; (t\; 1,\; t\; 2))\; CV\; (T)\; (V,\; T)\; T\; \dot{}\; (t)\; dt\; \{\backslash \; displaystyle\; =\; \backslash \; int\; \_\; \{P\; (t\_\; \{1\},\; t\_\; \{2\})\}\; C\_\; \{T\}\; ^\; \{(V)\}\; (V,\; T)\; \backslash ,\; \{\backslash \; dot\; \{V\}\}\; (t)\; \backslash ,\; dt\; \backslash ,\; +\; \backslash ,\; \backslash \; int\; \_\; \{P\; (t\_\; \{1\},\; t\_\; \{2\})\}\; C\_\; \{V\}\; ^\; \{(T)\}\; (V,\; T)\; \backslash ,\; \{\backslash \; dot\; \{T\}\}\; (t)\; \backslash ,\; dt\}$.

В этом выражении используются такие величины, как $Q\; \dot{}\; (t)\; \{\backslash \; displaystyle\; \{\backslash \; dot\; \{Q\}\}\; (t)\; \backslash \}$, которые указаны в разделе ниже, озаглавленном «Математические аспекты приведенных выше правил».

Математические аспекты приведенных выше правил

Использование «очень малых» величин, таких как $\delta \; Q\; \{\backslash \; displaystyle\; \backslash \; delta\; Q\; \backslash \}$, связано с физическим требованием, чтобы величина $p\; (V,\; T)\; \{\backslash \; displaystyle\; p\; (V,\; T)\; \backslash \}$«быстро определялась» с помощью $V\; \{\backslash \; displaystyle\; V\; \backslash \}$и $Т\; \{\backslash \; Displaystyle\; T\; \backslash \}$; такое «свойство определение» относится к физическому процессу. Эти «очень маленькие» величины используются в подходе Лейбница к исчислению бесконечно малых. В подходе Ньютона вместо этого используется «флюксии », например $V\; \dot{}\; (t)\; =\; d\; V\; d\; t\; |\; т\; \{\backslash \; Displaystyle\; \{\backslash \; точка\; \{V\}\}\; (т)\; =\; \backslash \; влево.\; \{\backslash \; frac\; \{dV\}\; \{dt\}\}\; \backslash \; right\; |\; \_\; \{t\}\}$, что делает более очевидным, что $p\; (V,\; T)\; \{\backslash \; displaystyle\; p\; (V,\; T)\; \backslash \}$должно быть «быстро определено».

В терминах потоков первое правило расчета, приведенное выше, может быть записано как

$Q\; \dot{}\; (t)\; =\; CT\; (V)\; (V,\; T)\; V\; \dot{}\; (t)\; +\; CV\; (T)\; (V,\; T)\; T\; \dot{}\; (T)\; \{\backslash \; Displaystyle\; \{\backslash \; dot\; \{Q\}\}\; (t)\; \backslash \; =\; C\_\; \{T\}\; ^\; \{(V)\}\; (V,\; T)\; \backslash ,\; \{\backslash \; dot\; \{V\}\}\; (t)\; \backslash ,\; +\; \backslash ,\; C\_\; \{V\}\; ^\; \{(T)\}\; (V,\; T)\; \backslash ,\; \{\backslash \; dot\; \{T\}\}\; (t)\}$

где

$t\; \{\backslash \; displaystyle\; t\; \backslash \}$обозначает время

$Q\; \dot{}\; (t)\; \{\backslash \; displaystyle\; \{\backslash \; dot\; \{Q\}\}\; (t)\; \backslash \}$обозначает временную скорость движения калориметрического материала в момент $t\; \{\backslash \; displaystyle\; t\; \backslash \}$

$V\; \dot{}\; (t)\; \{\backslash \; displaystyle\; \{\backslash \; dot\; \{V\}\}\; (t)\; \backslash \}$обозначает скорость изменения объема калориметрического материала во времени $t\; \{\backslash \; displaystyle\; t\; \backslash \}$

$T\; \dot{}\; (t)\; \{\backslash \; displaystyle\; \{\backslash \; dot\; \{T\}\}\; (t)\; \backslash \}$обозначает скорость изменения температуры калориметрического

Приращение $\delta \; Q\; \{\backslash \; displaystyle\; \backslash \; delta\; Q\; \backslash \}$и поток $Q\; \dot{}\; (t)\; \{\backslash \; displaystyle\; \{\backslash \; dot\; \{Q\}\}\; (t)\; \backslash \}$получены для определенного времени $t\; \{\backslash \; displaystyle\; t\; \backslash \; \}$, кот орое определяет значения величин в правых частях приведенных выше правил. Но это не повод ожидать, что должна существовать математическая функция $Q\; (V,\; T)\; \{\backslash \; displaystyle\; Q\; (V,\; T)\; \backslash \}$. По этой причине приращение $\delta \; Q\; \{\backslash \; displaystyle\; \backslash \; delta\; Q\; \backslash \}$называется «несовершенным дифференциалом» или «неточным дифференциалом ». В некоторых книгах это указывается записью $q\; \{\backslash \; displaystyle\; q\; \backslash \}$вместо $\delta \; Q\; \{\backslash \; displaystyle\; \backslash \; delta\; Q\; \backslash \}$. Кроме того, в некоторых книгах используется обозначение đQ. Невнимательность к этому может привести к ошибке.

Величина $\Delta \; Q\; (P\; (t\; 1,\; t\; 2))\; \{\backslash \; displaystyle\; \backslash \; Delta\; Q\; (P\; (t\_\; \{1\},\; t\_\; \{2\})))\; \backslash \}$называется функционалом непрерывной совместной прогрессии $P\; (t\; 1,\; t\; 2)\; \{\backslash \; displaystyle\; P\; (t\_\; \{1\},\; t\_\; \{2\})\; \backslash \}$из $V\; (t)\; \{\backslash \; displaystyle\; V\; (t)\; \backslash \}$и $T\; (t)\; \{\backslash \; displaystyle\; T\; (t)\; \backslash \}$, но в математическом определении функции $\Delta \; Q\; (P\; (t\; 1,\; t\; 2))\; \{\backslash \; displaystyle\; \backslash \; Delta\; Q\; (P\; (t\_\; \{1\},\; t\_\; \{2\}))\; \backslash \}$не является функция $(V,\; T)\; \{\backslash \; displaystyle\; (V,\; T)\; \backslash \}$. Хотя поток $Q\; \dot{}\; (t)\; \{\backslash \; displaystyle\; \{\backslash \; dot\; \{Q\}\}\; (t)\; \backslash \}$определяется здесь как функция времени $t\; \{\backslash \; displaystyle\; t\; \backslash \}$, символы $Q\; \{\backslash \; displaystyle\; Q\; \backslash \}$и $Q\; (V,\; T)\; \{\backslash \; displaystyle\; Q\; (V,\; T)\; \backslash \}$соответственно отдельно стоящие здесь не рекомендуется.

Физические приведенные выше правила калориметрии

Приведенные выше правила калориметрическим материалом. Термины «быстро» и «очень мало» требуют эмпирической физической проверки области применимости вышеуказанных правил.

Приведенные выше правила расчета тепла к чистой калориметрии. В них нет ссылки на термодинамику, и в основном они были поняты до появления термодинамики. Они составляют «термо» вклада в термодинамику. Вклад «теория» основан на идее работы, которая не используется в приведенных выше правилах расчета.

Экспериментально измеряемые коэффициенты

Эмпирически удобно измерять свойства калориметрических материалов в экспериментально контролируемых условиях.

Повышение давления при постоянном объеме

Для измерений при экспериментально контролируемом объеме можно использовать высказанное выше предположение, что давление тела калориметрического материала может быть выражено как функция его объем и температура.

Для измерения при постоянном экспериментально контролируемом объеме изохорный коэффициент повышения давления с температурой определяется как

$\alpha \; V\; (V,\; T)\; =\; \partial \; p\; \partial \; V\; |\; (V,\; T)п\; (В,\; Т)\; \{\backslash \; Displaystyle\; \backslash \; альфа\; \_\; \{V\}\; (V,\; T)\; \backslash \; =\; \{\backslash \; гидроразрыва\; \{\backslash \; слева.\; \{\backslash \; Cfrac\; \{\backslash \; partial\; p\}\; \{\backslash \; partial\; V\}\}\; \backslash \; right\; |\; \_\; \{(V,\; T)\}\}\; \{p\; (V,\; T)\}\}\}$.

Расширение при постоянном давлении

Для измерений при экспериментально контролируемом напряжении, давление $V\; \{\backslash \; displaystyle\; V\; \backslash \}$тела калориметрического материала может быть выражено как функция $V\; (T,\; p)\; \{\backslash \; displaystyle\; V\; (T,\; p)\; \backslash \}$его температура $T\; \{\backslash \; displaystyle\; T\; \backslash \}$и давление $p\; \{\backslash \; displaystyle\; p\; \backslash \}$. Предполагается, что это предположение связано с этим предположением, как известно, что это предположение связано с объемом калориметрического материала, как функция его объема и температуры; аномальное поведение материалов.

Величина, которую удобно измерять при постоянном экспериментально контролируемом давлении, коэффициент изобарного объемного расширения, как определяется

$\beta \; p\; (T,\; p)\; =\; \partial \; V\; \partial \; T\; |\; (Т,\; п)\; В\; (Т,\; п)\; \{\backslash \; Displaystyle\; \backslash \; бета\; \_\; \{р\}\; (Т,\; р)\; \backslash \; =\; \{\backslash \; гидроразрыва\; \{\backslash \; слева.\; \{\backslash \; Cfrac\; \{\backslash \; partial\; V\}\; \{\backslash \; partial\; T\}\}\; \backslash \; right\; |\; \_\; \{(T,\; p)\}\}\; \{V\; (T,\; p)\}\}\}$.

Сжимаемость при постоянной температуре

Для измерений при экспериментально контролируемой температуре снова, что объем $V\; \{\backslash \; displaystyle\; V\; \backslash \}$тела калориметрического материала может быть выражено как функция $V\; (T,\; p)\; \{\backslash \; displaystyle\; V\; (T,\; p)\; \backslash \}$его температуры $T\; \{\; \backslash \; displaystyle\; T\; \backslash \}$и давление $p\; \{\backslash \; displaystyle\; p\; \backslash \}$, с теми же условиями, что и упомянутые выше.

Величина, которая удобно измеряется при постоянной экспериментально контролируемой температуре, изотермическая сжимаемость, определяется как

$\kappa \; T\; (T,\; p)\; =\; -\; \partial \; V\; \partial \; p\; |\; (Т,\; п)\; В\; (Т,\; п)\; \{\backslash \; Displaystyle\; \backslash \; каппа\; \_\; \{Т\}\; (Т,\; р)\; \backslash \; =\; -\; \{\backslash \; гидроразрыва\; \{\backslash \; слева.\; \{\backslash \; Cfrac\; \{\backslash \; partial\; V\}\; \{\backslash \; partial\; p\}\}\; \backslash \; right\; |\; \_\; \{(T,\; p)\}\}\; \{V\; (T,\; p)\}\}\}$.

Связь между классическими калориметрическими величинами

Предполагаемая, что правило $p\; =\; p\; (V,\; T)\; \{\backslash \; displaystyle\; p\; =\; p\; (V,\; T)\; \backslash \}$известен, можно вывести функцию от $\partial \; p\; \partial \; T\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; p\}\; \{\backslash \; partial\; T\}\}\; \backslash \}$, который используется выше в классическом расчете тепла по отношению к давлению. Эту функцию можно найти экспериментально из коэффициентов $\beta \; p\; (T,\; p)\; \{\backslash \; displaystyle\; \backslash \; beta\; \_\; \{p\}\; (T,\; p)\; \backslash \}$и $\kappa \; T\; (T,\; p)\; \{\backslash \; displaystyle\; \backslash \; kappa\; \_\; \{T\}\; (T,\; p)\; \backslash \}$через математически выводимое соотношение

$\partial \; p\; \partial \; T\; =\; \beta \; p\; (T,\; p)\; \kappa \; T\; (T,\; p)\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; p\}\; \{\backslash \; partial\; T\}\}\; =\; \{\backslash \; frac\; \{\backslash \; beta\; \_\; \{p\}\; (T,\; p)\}\; \{\backslash \; kappa\; \_\; \{T\}\; (T,\; p)\}\}\}$.

Связь калориметрии и термодинамики

Термодинамика развивалась постепенно в течение первой половины девятнадцатого века, используя вышеупомянутой теории калориметрии, которая была добавлена ​​до нее и на других открытий. Согласно Гисласону и Крейгу (2005): «Большинство термодинамических данных поступает из калориметрии...» Согласно Кондепуди (2008): «Калориметрия широко используется в современных лабораториях».

С точки зрения термодинамики, внутренняя энергия $U\; \{\backslash \; displaystyle\; U\; \backslash \}$калориметрического материала может рассматриваться как значение функции $U\; (V,\; T)\; \{\backslash \; Displaystyle\; U\; (V,\; T)\; \backslash \}$из $(V,\; T)\; \{\backslash \; displaystyle\; (V,\; T)\; \backslash \}$, с частными производными $\partial \; U\; \partial \; V\; \{\backslash \; Displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; U\}\; \{\backslash \; partial\; V\}\}\; \backslash \}$и $\partial \; U\; \partial \; T\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; U\}\; \{\backslash \; частичный\; T\}\}\; \backslash \}$.

Тогда можно показать, что можно написать термодинамическую версию вышеуказанных калориметрических правил:

$\delta \; Q\; =\; [p\; (V,\; T)\; +\; \partial \; U\; \partial \; V\; |\; (V,\; T)]\; \delta \; V\; +\; \partial \; U\; \partial \; T\; |\; (В,\; Т)\; \delta \; Т\; \{\backslash \; Displaystyle\; \backslash \; дельта\; Q\; \backslash \; =\; \backslash \; влево\; [п\; (V,\; Т)\; \backslash ,\; +\; \backslash ,\; \backslash \; влево.\; \{\backslash \; Гидроразрыва\; \{\backslash \; partial\; U\}\; \{\backslash \; partial\; V\}\}\; \backslash \; вправо\; |\; \_\; \{(V,\; T)\}\; \backslash \; right]\; \backslash ,\; \backslash \; delta\; V\; \backslash ,\; +\; \backslash ,\; \backslash \; left.\; \{\backslash \; Frac\; \{\backslash \; partial\; U\}\; \{\backslash \; partial\; T\}\}\; \backslash \; right\; |\; \_\; \{(V,\; T)\}\; \backslash ,\; \backslash \; delta\; T\}$

с

$CT\; (V)\; (V,\; T)\; =\; p\; (V,\; T)\; +\; \partial \; U\; \partial \; V\; |\; (V,\; T)\; \{\backslash \; Displaystyle\; C\_\; \{T\}\; ^\; \{(V)\}\; (V,\; T)\; =\; p\; (V,\; T)\; \backslash ,\; +\; \backslash ,\; \backslash \; влево.\; \{\backslash \; Frac\; \{\backslash \; partial\; U\}\; \{\backslash \; partial\; V\}\}\; \backslash \; right\; |\; \_\; \{(V,\; T)\}\; \backslash \}$

и

$CV\; (T)\; (V,\; T)\; =\; \partial \; U\; \partial \; T\; |\; (В,\; Т)\; \{\backslash \; Displaystyle\; C\_\; \{V\}\; ^\; \{(T)\}\; (V,\; T)\; =\; \backslash \; слева.\; \{\backslash \; Frac\; \{\backslash \; partial\; U\}\; \{\backslash \; partial\; T\}\}\; \backslash \; right\; |\; \_\; \{(V,\; T)\}\; \backslash \}$.

Опять же, в терминах термодинамики, внутренняя энергия $U\; \{\backslash \; displaystyle\; U\; \backslash \}$калориметрического материала иногда может, в зависимости от калориметрический материал как анализ значения функции $U\; (p,\; T)\; \{\backslash \; displaystyle\; U\; (p,\; T)\; \backslash \}$of $(p,\; T)\; \{\backslash \; displaystyle\; (p,\; T))\; \backslash \}$, с частными производными $\partial \; U\; \partial \; p\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; U\}\; \{\backslash \; partial\; p\}\}\; \backslash \}$и $\partial \; U\; \partial \; T\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; U\}\; \{\backslash \; partial\; T\}\}\; \backslash \}$и с $V\; \{\backslash \; displaystyle\; V\; \backslash \}$выражается как значение функции $V\; (p,\; T)\; \{\backslash \; displaystyle\; V\; (p,\; T)\; \backslash \}$из $(p,\; T)\; \{\backslash \; displaystyle\; (p,\; T))\; \backslash \}$, с частными производными $\partial \; V\; \partial \; p\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; V\}\; \{\backslash \; partial\; p\}\}\; \backslash \}$и $\partial \; V\; \partial \; T\; \{\backslash \; displaystyle\; \{\; \backslash \; frac\; \{\backslash \; partial\; V\}\; \{\backslash \; partial\; T\}\}\; \backslash \}$.

Тогда, согласно Ссылаясь на Адкинса (1975), можно показать, что можно записать еще одну термодинамическу ю версию вышеуказанных калориметрических правил:

$\delta \; Q\; =\; [\partial \; U\; \partial \; p\; |\; (p,\; T)\; +\; p\; \partial \; V\; \partial \; p\; |\; (p,\; T)]\; \delta \; p\; +\; [\partial \; U\; \partial \; T\; |\; (p,\; T)\; +\; p\; \partial \; V\; \partial \; T\; |\; (п,\; T)]\; \delta \; T\; \{\backslash \; Displaystyle\; \backslash \; дельта\; Q\; \backslash \; =\; \backslash \; влево\; [\backslash \; влево.\; \{\backslash \; frac\; \{\backslash \; partial\; U\}\; \{\backslash \; partial\; p\}\}\; \backslash \; right\; |\; \_\; \{(p,\; T)\}\; \backslash ,\; +\; \backslash ,\; p\; \backslash \; left.\; \{\backslash \; frac\; \{\backslash \; partial\; V\}\; \{\backslash \; partial\; p\}\}\; \backslash \; right\; |\; \_\; \{(p,\; T)\}\; \backslash \; right]\; \backslash \; delta\; p\; \backslash ,\; +\; \backslash ,\; \backslash \; left\; [\backslash \; left.\; \{\backslash \; frac\; \{\backslash \; partial\; U\}\; \{\backslash \; partial\; T\}\}\; \backslash \; right\; |\; \_\; \{(p,\; T)\}\; \backslash ,\; +\; \backslash ,\; p\; \backslash \; left.\; \{\backslash \; frac\; \{\backslash \; partial\; V\}\; \{\backslash \; partial\; T\}\}\; \backslash \; right\; |\; \_\; \{(p,\; T)\}\; \backslash \; right]\; \backslash \; delta\; T\}$

с

$CT\; (p)\; (p,\; T)\; =\; \partial \; U\; \partial \; p\; |\; (p,\; T)\; +\; p\; \partial \; V\; \partial \; p\; |\; (п,\; Т)\; \{\backslash \; Displaystyle\; C\_\; \{T\}\; ^\; \{(р)\}\; (р,\; Т)\; =\; \backslash \; слева.\; \{\backslash \; frac\; \{\backslash \; partial\; U\}\; \{\backslash \; partial\; p\}\}\; \backslash \; right\; |\; \_\; \{(p,\; T)\}\; \backslash ,\; +\; \backslash ,\; p\; \backslash \; left.\; \{\backslash \; frac\; \{\backslash \; partial\; V\}\; \{\backslash \; partial\; p\}\}\; \backslash \; right\; |\; \_\; \{(p,\; T)\}\; \backslash \}$

и

$C\; p\; (T)\; (p,\; T)\; =\; \partial \; U\; \partial \; T\; |\; (p,\; T)\; +\; p\; \partial \; V\; \partial \; T\; |\; (п,\; Т)\; \{\backslash \; Displaystyle\; C\_\; \{р\}\; ^\; \{(Т)\}\; (р,\; Т)\; =\; \backslash \; слева.\; \{\backslash \; frac\; \{\backslash \; partial\; U\}\; \{\backslash \; partial\; T\}\}\; \backslash \; right\; |\; \_\; \{(p,\; T)\}\; \backslash ,\; +\; \backslash ,\; p\; \backslash \; left.\; \{\backslash \; frac\; \{\backslash \; partial\; V\}\; \{\backslash \; partial\; T\}\}\; \backslash \; right\; |\; \_\; \{(p,\; T)\}\; \backslash \}$.

Помимо отмеченного выше калориметрического факта, скрытая нагревает $CT\; (V)\; (V,\; T)\; \{\backslash \; displaystyle\; C\_\; \{T\}\; ^\; \{(V)\}\; (V,\; T)\; \backslash \}$и $CT\; (p)\; (p,\; T)\; \{\backslash \; displaystyle\; C\_\; \{T\}\; ^\; \{(p)\}\; (p,\; T)\; \backslash \}$всегда имеют противоположный знак, можно показать, используя термодинамическую концепцию работы, что также

$CT\; (V)\; (V,\; T)\; \partial \; p\; \partial \; T\; |\; (В,\; Т)\; \ge \; 0.\; \{\backslash \; Displaystyle\; C\_\; \{T\}\; ^\; \{(V)\}\; (V,\; T)\; \backslash ,\; \backslash \; влево.\; \{\backslash \; frac\; \{\backslash \; partial\; p\}\; \{\backslash \; partial\; T\}\}\; \backslash \; right\; |\; \_\; \{(V,\; T)\}\; \backslash \; geq\; 0\; \backslash ,.\}$

Особый интерес термодинамики в калориметрии: изотермические сегменты цикла Карно

Калориметрия имеет особое преимущество для термодинамики. Он сообщает о тепле, поглощенном или увеличивающемся в изотермическом сегменте цикла Карно.

Цикл Карно - это особый вид циклического процесса, воздействующего на тело, состоящее из материала, подходящего для использования в тепловой машине. Такой материал относится к типу, который охарактеризован выше, который имеет давление, которое очень быстро определяется только температурой и объемом. Говорят, что такое тело изменяется обратимо. Цикл Карно состоит из четырех последовательных стадий или сегментов:

(1) изменение объема $V\; a\; \{\backslash \; displaystyle\; V\_\; \{a\}\; \backslash \}$на объем $V\; b\; \{\backslash \; displaystyle\; V\_\; \{b\}\; \backslash \}$при постоянной температуре $T\; +\; \{\backslash \; displaystyle\; T\; ^\; \{+\}\; \backslash \}$, чтобы вызвать поток тепла в тело (известное как изотермическое изменение)

(2) изменение объема от $V\; b\; \{\backslash \; displaystyle\; V\_\; \{b\}\; \backslash \}$до объема $V\; c\; \{\backslash \; displaystyle\; V\_\; \{c\}\; \backslash \}$при модели, такой, чтобы не было потока тепла (известное как адиабатическое изменение)

(3) другой изотермический размер изменения от $V\; c\; \{\backslash \; displaystyle\; V\_\; \{c\}\; \backslash \; \}$до объема $V\; d\; \{\backslash \; displaystyle\; V\_\; \{d\}\; \backslash \}$при температуре $T\; -\; \{\backslash \; displaystyle\; T\; ^\; \{-\}\; \backslash \}$например, чтобы вызвать поток или тепло из тела и точно подготовиться к следующему изменению

(4) другое адиабатическое изменение объема от $V\; d\; \{\backslash \; displaystyle\; V\_\; \{d\}\; \backslash \}$назад к $V\; a\; \{\backslash \; displaystyle\; V\_\; \{a\}\; \backslash \}$как раз для того, чтобы вернуть тело к исходной температуре $T\; +\; \{\; \backslash \; displaystyle\; T\; ^\; \{+\}\; \backslash \}$.

В изотермическом сегменте (1) тепло, которое течет в теле, определяется как

$\Delta \; Q\; (V\; a,\; V\; b;\; T\; +)\; знак\; равно\; \int \; В\; a\; V\; b\; CT\; (V)\; (V,\; T\; +)\; d\; V\; \{\backslash \; displaystyle\; \backslash \; Delta\; Q\; (V\_\; \{a\},\; V\_\; \{b\};\; T\; ^\; \{+\})\; \backslash ,\; =\; \backslash ,\; \backslash ,\; \backslash ,\; \backslash ,\; \backslash ,\; \backslash ,\; \backslash ,\; \backslash ,\; \backslash \; int\; \_\; \{V\_\; \{a\}\}\; ^\; \{V\_\; \{b\}\}\; C\_\; \{T\}\; ^\; \{(V)\}\; (V,\; T\; ^\; \{+\})\; \backslash ,\; dV\; \backslash \}$

, в изотермическом сегменте (3) тепло, вытекающее из тела, определяется как

$-\; \Delta \; Q\; (V\; c,\; V\; d;\; T\; -)\; =\; -\; V\; c\; V\; d\; CT\; (V)\; (\; V,\; T\; -)\; d\; V\; \{\backslash \; displaystyle\; -\; \backslash \; Delta\; Q\; (V\_\; \{c\},\; V\_\; \{d\};\; T\; ^\; \{-\})\; \backslash ,\; =\; \backslash ,\; -\; \backslash \; int\; \_\; \{V\_\; \{c\}\}\; ^\; \{V\_\; \{\; d\}\}\; C\_\; \{T\}\; ^\; \{(V)\}\; (V,\; T\; ^\; \{-\})\; \backslash ,\; dV\; \backslash \}$.

Временные пункты (2) и (4) являются адиабатами, тепло не поступает внутрь или из тела во них, и, следовательно, чистое тепло, подводимое к телу во время цикла время, определяется как

$\Delta \; Q\; (V\; a,\; V\; b;\; T\; +;\; V\; c,\; V\; d;\; T\; -)\; =\; \Delta \; Q\; (V\; a,\; V\; b;\; T\; +)\; +\; \Delta \; Q\; (V\; c,\; V\; d;\; T\; -)\; =\; \int \; V\; a\; V\; b\; CT\; (V)\; (V,\; T\; +)\; d\; V\; +\; \int \; V\; c\; V\; d\; CT\; (V)\; (V,\; T\; -)\; d\; V\; \{\backslash \; displaystyle\; \backslash \; Delta\; Q\; (V\_\; \{a\},\; V\_\; \{b\};\; T\; ^\; \{+\};\; V\_\; \{c\},\; V\_\; \{d\};\; T\; ^\; \{-\})\; \backslash ,\; =\; \backslash ,\; \backslash \; Дельта\; Q\; (V\_\; \{a\},\; V\_\; \{b\};\; T\; ^\; \{+\})\; \backslash ,\; +\; \backslash ,\; \backslash \; Delta\; Q\; (V\_\; \{c\},\; V\_\; \{d\};\; T\; ^\; \{-\})\; \backslash ,\; =\; \backslash ,\; \backslash \; int\; \_\; \{V\_\; \{a\}\}\; ^\; \{V\_\; \{b\}\}\; C\_\; \{T\}\; ^\; \{(V)\}\; (V,\; T\; ^\; \{+\})\; \backslash ,\; dV\; \backslash ,\; +\; \backslash ,\; \backslash \; int\; \_\; \{V\_\; \{c\}\}\; ^\; \{V\_\; \{d\}\}\; C\_\; \{T\; \}\; ^\; \{(V)\}\; (V,\; T\; ^\; \{-\})\; \backslash ,\; dV\; \backslash \}$.

Ти Количество s используется термодинамикой и связано с чистой работой, выполняемой телом во время цикла Карно. Чистое изменение внутренней энергии тела во время цикла Карно, $\Delta \; U\; (V\; a,\; V\; b;\; T\; +;\; V\; c,\; V\; d;\; T\; -)\; \{\backslash \; displaystyle\; \backslash \; Delta\; U\; (V\_\; \{a\},\; V\_\; \{b\}\; ;\; T\; ^\; \{+\};\; V\_\; \{c\},\; V\_\; \{d\};\; T\; ^\; \{-\})\; \backslash \}$, равно нулю, потому что материал рабочего тела имеет особые свойства, текст выше.

Особый интерес калориметрии в термодинамике: соотношения между классическими калориметрическими величинами состояния

Отношение скрытой теплоты к объему и уравнение состояния

Величина $CT\; (V)\; (V,\; T)\; \{\backslash \; displaystyle\; C\_\; \{T\}\; ^\; \{(V)\}\; (V,\; T)\; \backslash \}$, скрытое тепло по отношению к объему, относится к классической калориметрии. Он объясняет возникновение передачи энергии в процессе, в котором также передается тепло; количество, однако, было рассмотрено до того, как связь между теплопередачей и работой была прояснена изобретением термодинамики. В свете термодинамики измерняется, что классическая калориметрическая связка связана с уравнением состояния калориметрического материала $p\; =\; p\; (V,\; T)\; \{\backslash \; displaystyle\; p\; =\; p\; (V,\; T)\; \backslash \}$. При условии, что температура $T\; \{\backslash \; displaystyle\; T\; \backslash ,\}$измеряется в термодинамической абсолютной шкале, соотношение выражается формулой

$CT\; (V)\; (V,\; T)\; =\; T\; \partial \; p\; \partial \; T\; |\; (В,\; Т)\; \{\backslash \; Displaystyle\; C\_\; \{T\}\; ^\; \{(V)\}\; (V,\; Т)\; =\; Т\; \backslash \; влево.\; \{\backslash \; Frac\; \{\backslash \; partial\; p\}\; \{\backslash \; partial\; T\}\}\; \backslash \; right\; |\; \_\; \{(V,\; T)\}\; \backslash \}$.

Разница удельных теплоемкостей

Расширенная термодинамика обеспечивает соотношение

$C\; p\; (p,\; T)\; -\; CV\; (V,\; T)\; =\; [p\; (V,\; T)\; +\; \partial \; U\; \partial \; V\; |\; (V,\; T)]\; \partial \; V\; \partial \; T\; |\; (п,\; T)\; \{\backslash \; Displaystyle\; C\_\; \{p\}\; (p,\; T)\; -C\_\; \{V\}\; (V,\; T)\; =\; \backslash \; left\; [p\; (V,\; T)\; \backslash ,\; +\; \backslash ,\; \backslash \; left.\; \{\backslash \; frac\; \{\backslash \; частичный\; U\}\; \{\backslash \; partial\; V\}\}\; \backslash \; right\; |\; \_\; \{(V,\; T)\}\; \backslash \; right]\; \backslash ,\; \backslash \; left.\; \{\backslash \; frac\; \{\backslash \; partial\; V\}\; \{\backslash \; partial\; T\}\}\; \backslash \; right\; |\; \_\; \{(p,\; T)\}\}$.

Из этого дальнейшие математические и термодинамические рассуждения приводят к другому соотношению между классическими калориметрическими величинами. Разница удельных теплоемкостей определяется как

$C\; p\; (p,\; T)\; -\; CV\; (V,\; T)\; =\; TV\; \beta \; p\; 2\; (T,\; p)\; \kappa \; T\; (T,\; p)\; \{\backslash \; displaystyle\; C\_\; \{p\}\; (\; p,\; T)\; -C\_\; \{V\}\; (V,\; T)\; =\; \{\backslash \; frac\; \{TV\; \backslash ,\; \backslash \; beta\; \_\; \{p\}\; ^\; \{2\}\; (T,\; p)\}\; \{\backslash \; kappa\; \_\; \{T\}\; (T,\; p)\; \}\}\}$.

Практическая калориметрия постоянного объема (калориметрия бомбы) для термодинамических исследований

Калориметрия постоянного объема - это калориметрия, выполняемая при постоянном объеме. Это предполагает использование калориметра постоянного объема.

В калориметрии постоянного объема никакой работы не выполняется, поэтому измеренное количество тепла равно изменению внутренней энергии системы. Предполагается, что теплоемкость при постоянном объеме не зависит от температуры.

Тепло измеряется по принципу калориметрии.

$q\; =\; CV\; \Delta \; T\; =\; \Delta \; U,\; \{\backslash \; displaystyle\; q\; =\; C\_\; \{V\}\; \backslash \; Delta\; T\; =\; \backslash \; Delta\; U\; \backslash ,,\}$

где

ΔU - изменение внутренней энергии,

ΔT - это изменение температуры, а

CV- теплоемкость при постоянном объеме.

В калориметрии постоянного объема давление не поддерживается постоянным. Если существует разница давлений между начальным и конечным состояниями, измеренное количество тепла требует корректировки, чтобы обеспечить изменение энтальпии. Тогда

$\Delta \; H\; =\; \Delta \; U\; +\; \Delta \; (PV)\; =\; \Delta \; U\; +\; V\; \Delta \; P,\; \{\backslash \; displaystyle\; \backslash \; Delta\; H\; =\; \backslash \; Delta\; U\; +\; \backslash \; Delta\; (PV)\; =\; \backslash \; Delta\; U\; +\; V\; \backslash \; Delta\; P\; \backslash ,,\}$

, где

ΔH - изменение энтальпии и

V - неизменный объем камеры для образца.

См. Также

• Изотермическая микрокалориметрия (IMC)
• Изотермическая калориметрия титрования
• Сорбционная калориметрия
• Реакционный калориметр

Ссылки

Книги

• Adkins, CJ (1975). Равновесная термодинамика, второе издание, McGraw-Hill, Лондон, ISBN 0-07-084057-1.
• Бейлин, М. (1994). Обзор термодинамики, Американский институт физики, Нью-Йорк, ISBN 0-88318-797-3.
• Брайан, Г.Х. (1907). Термодинамика. Вводный трактат, посвященный главным образом Первым принципам и их прямым приложениям, Б.Г. Tuebner, Leipzig.
• Callen, H.B. (1960/1985). Термодинамика и введение в термостатистику, второе издание, Wiley, New York, ISBN 981-253-185-8.
• Crawford, F.H. (1963). Тепло, термодинамика и статистическая физика, Rupert Hart-Davis, London, Harcourt, Brace, World.
• Guggenheim, E.A. (1949/1967). Термодинамика. Advanced Treatment for Chemists and Physicsists, North-Holland, Amsterdam.
• Ирибарн, Дж. В., Годсон, У. Л. (1973/1981), Атмосферная термодинамика, второе издание, D. Reidel, Kluwer Academic Publishers, Dordrecht, ISBN 90-277-1296-4.
• Кондепуди, Д. ( 2008 г.). Введение в современную термодинамику, Wiley, Chichester, ISBN 978-0-470-01598-8.
• Landsberg, P.T. (1978). Термодинамика и статистическая механика, Oxford University Press, Oxford, ISBN 0-19-851142-6.
• Льюис, Г.Н., Рэндалл, М. (1923/1961). Термодинамика, второе издание отредактировано К.С. Питцером, Л. Брюером, McGraw-Hil 1, Нью-Йорк.
• Максвелл, Дж. К. (1872 г.). Theory of Heat, третье издание, Longmans, Green, and Co., Лондон.
• Партингтон, Дж. Р. (1949). Расширенный трактат по физической химии, том 1, фундаментальные принципы. Свойства газов, Лонгманс, Грин и Ко, Лондон.
• Планк, М. (1923/1926). Трактат по термодинамике, третье английское издание, переведенное А. Оггом из седьмого немецкого издания, Longmans, Green Co., Лондон.
• Трусделл, К., Бхарата, С. (1977). Концепции и логика классической термодинамики как теории тепловых двигателей, строго построенные на основе, заложенной С. Карно и Ф. Ричем, Спрингер, Нью-Йорк, ISBN 0-387 -07971-8.

Внешние ссылки

Викиисточник содержит текст статьи Британской энциклопедии 1911 года Калориметрия.

• http: // www. Appropedia.org/Differential_scanning_calorimetry_protocol:_MOST